TL;DR#
Reasoning Language Models (RLMs) significantly improve AI’s problem-solving capabilities, but their high cost, proprietary nature, and complex architectures hinder accessibility and scalability. This creates a divide between institutions with access to advanced AI and those without. Current RLMs uniquely combine Reinforcement Learning (RL), search heuristics, and Large Language Models (LLMs), making them difficult to understand and reproduce.
To address these issues, this paper proposes a comprehensive blueprint that organizes RLM components into a modular framework. This framework includes various reasoning structures, strategies, RL concepts, and supervision schemes. The authors provide detailed mathematical formulations and algorithmic specifications to simplify RLM implementation, demonstrating the blueprint’s versatility by showing how existing RLMs fit as special cases. They also introduce x1, a modular implementation for rapid RLM prototyping and experimentation, and use it to provide key insights, like multi-phase training strategies. The goal is to democratize RLM construction and lower barriers to entry, fostering innovation and mitigating the gap between “rich AI” and “poor AI”.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the accessibility and scalability challenges of reasoning language models (RLMs). By providing a modular framework and open-source implementation, it democratizes RLM development, potentially fostering innovation and mitigating the gap between “rich AI” and “poor AI”. The blueprint and accompanying framework enable faster prototyping, experimentation, and comparison of different RLM designs, thus accelerating progress in AI research.
Visual Insights#

🔼 The figure illustrates the historical development of Reasoning Language Models (RLMs), highlighting the convergence of three key factors: advancements in Reinforcement Learning (as exemplified by AlphaZero), progress in Large Language Models (LLMs) and Transformer architectures (such as GPT-4), and the continuous increase in the computational power and data processing capabilities of high-performance computing systems. It shows how these three lines of research have intersected and built upon each other to create the field of RLMs.
read the caption
Figure 2: The history of RLMs. This class of models has been the result of the development of three lines of works: (1) Reinforcement Learning based models such as AlphaZero [79], (2) LLM and Transformer based models such as GPT-4o [65], and (3) the continuous growth of compute power and data processing capabilities of supercomputers and high performance systems.
| Reasoning | Reasoning Operator | Models | Pipeline | ||||||||||||||||
| Scheme | Structure | Traversal | Update | Evaluation | Remarks | ||||||||||||||
| Structure | Step | Strategy | Gen. | Ref. | Agg. | Pr. | Res. | Sel. | BT | Bp. | Inter. | Final. | PM | VM | Inf. | Tr. | DG | ||
| Explicit RLMs (Section 5.1) | |||||||||||||||||||
| rStar-Math [36] | E Tree | C Thought + Code Block | E MCTS | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | |
| PRIME [102, 26] | E Multiple Chains | F Token C Thought | E Best-of-N | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | |
| Marco-o1 [108] | E Tree | F Token Sequence C Thought | E MCTS | \faBatteryFull | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | |
| Journey Learning (Tr.) [69] | E Tree | E Thought | E Tree Search | \faBatteryFull | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryHalf* | \faBatteryFull | \faBatteryFull | *Separate Entry |
| OpenR [93] | E Tree | C Thought | E Best-of-N E Beam Search E MCTS | \faBatteryFull | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | |
| LLaMA-Berry [105] | E Tree of Chains | C Solution | E MCTS | \faBatteryFull | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | |
| ReST-MCTS* [106] | E Tree | C Thought | E MCTS | \faBatteryFull | \faBatteryHalf* | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | *Advice by critic |
| AlphaMath Almost Zero [18] | E Tree | F Thought | E MCTS | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryHalf* | \faBatteryHalf* | \faBatteryFull | \faBatteryFull | \faBatteryFull | *Single model |
| MCTS-DPO [99] | E Tree | F Token Sequence | E MCTS | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryHalf* | \faBatteryHalf* | \faBatteryFull | \faBatteryFull | \faBatteryFull | *Single model |
| AlphaLLM [89] | E Tree | C Option | E MCTS | \faBatteryFull | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | |
| TS-LLM [30] | E Tree | F Token F Sentence | E MCTS E Tree Search | \faBatteryFull | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faBatteryFull | |
| Implicit RLMs (Section 5.2) | |||||||||||||||||||
| QwQ [88] | I Chain* | F Token | \faTimes | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryHalf | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faTimes | *Linearized Tree |
| Journey Learning (Inf.) [69] | I Chain* | C Thought | I DFS | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryHalf | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faTimes | *Linearized Tree |
| Structured Prompting Schemes (Section 5.3) | |||||||||||||||||||
| Graph of Thoughts (GoT) [6] | E Graph* | C Thought | E Controller | \faBatteryFull | \faBatteryFull | \faBatteryFull | \faTimes | \faTimes | \faBatteryFull | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faTimes | \faBatteryHalf | \faBatteryFull | \faTimes | \faTimes | *DAG |
| Tree of Thoughts (ToT) [101] | E Tree | C Thought | E Tree Search | \faBatteryFull | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faTimes | \faBatteryFull | \faBatteryFull | \faTimes | \faBatteryHalf | \faBatteryFull | \faTimes | \faTimes | |
| Self-Consistency (SC) [97] | E Multiple Chains | C Thought | E Majority Voting | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faTimes | |
| Chain of Thought (CoT) [98] | I Chain | C Thought | \faTimes | \faBatteryFull | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faTimes | \faBatteryFull | \faTimes | \faTimes | |
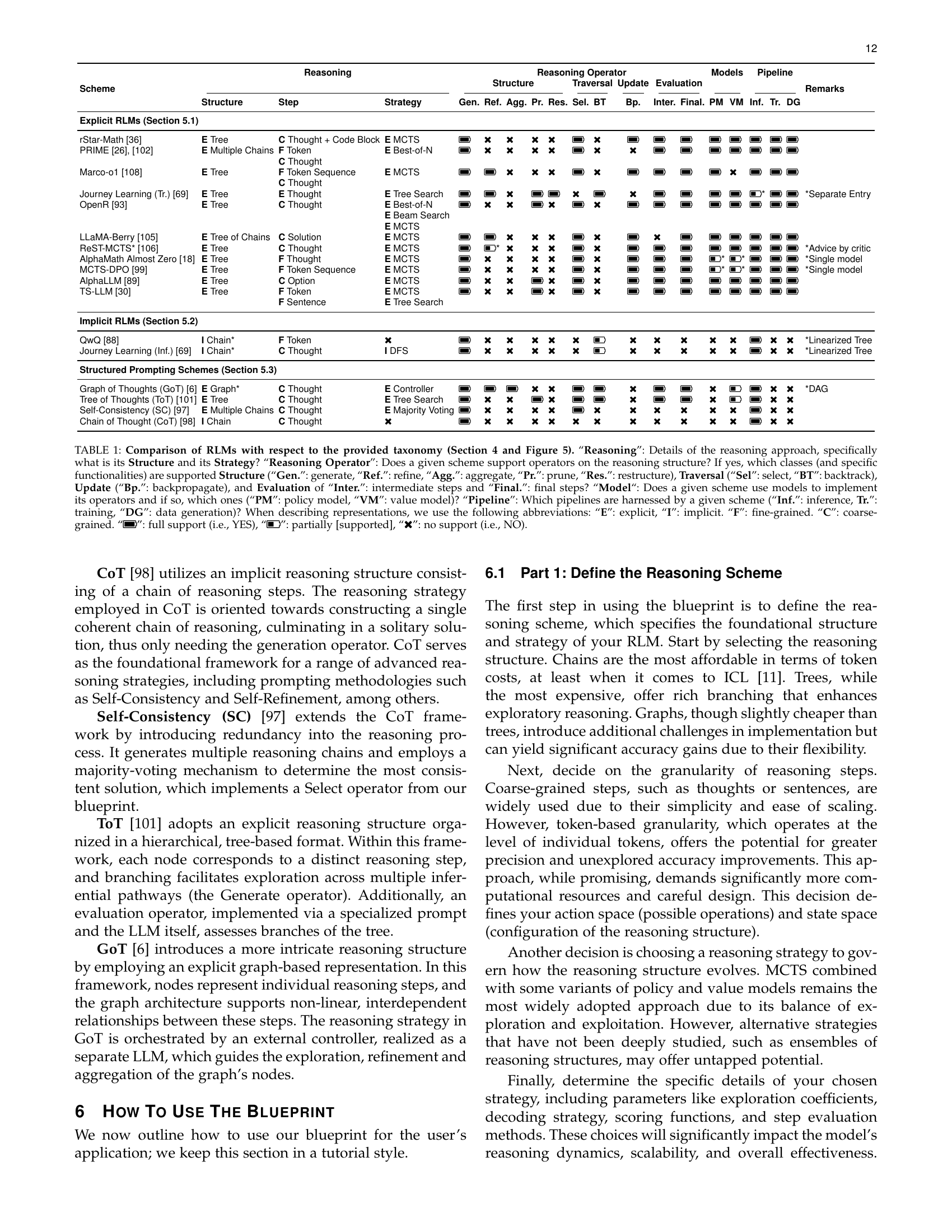
🔼 This table compares various Reasoning Language Models (RLMs) based on a taxonomy introduced in Section 4 of the paper. It details each RLM’s reasoning approach (structure and strategy), the types of operators used to manipulate the reasoning structure (generate, refine, aggregate, prune, restructure, select, backtrack, backpropagate, intermediate/final evaluation), the models employed (policy and/or value models), and the pipelines utilized (inference, training, data generation). Abbreviations are used for explicit/implicit reasoning, fine/coarse-grained steps, and the level of support for each operator/pipeline.
read the caption
TABLE I: Comparison of RLMs with respect to the provided taxonomy (Section 4 and Figure 5). “Reasoning”: Details of the reasoning approach, specifically what is its Structure and its Strategy? “Reasoning Operator”: Does a given scheme support operators on the reasoning structure? If yes, which classes (and specific functionalities) are supported Structure (“Gen.”: generate, “Ref.”: refine, “Agg.”: aggregate, “Pr.”: prune, “Res.”: restructure), Traversal (“Sel”: select, “BT”: backtrack), Update (“Bp.”: backpropagate), and Evaluation of “Inter.”: intermediate steps and “Final.”: final steps? “Model“: Does a given scheme use models to implement its operators and if so, which ones (“PM”: policy model, “VM”: value model)? “Pipeline”: Which pipelines are harnessed by a given scheme (“Inf.”: inference, Tr.”: training, “DG”: data generation)? When describing representations, we use the following abbreviations: “E”: explicit, “I”: implicit. “F”: fine-grained. “C”: coarse-grained. “\faBatteryFull”: full support (i.e., YES), “\faBatteryHalf”: partially [supported], “\faTimes”: no support (i.e., NO).
In-depth insights#
RLM Blueprint#
The “RLM Blueprint” section of this research paper proposes a modular framework for constructing reasoning language models (RLMs). It emphasizes modularity, allowing researchers to combine different reasoning structures (chains, trees, graphs), strategies (MCTS, beam search), and reinforcement learning concepts. The blueprint’s strength lies in its unifying power, demonstrating how various existing RLMs are special cases within this overarching framework. This modularity is crucial for democratizing RLM development, making sophisticated reasoning capabilities accessible to researchers with fewer resources. The detailed mathematical formulations and algorithmic specifications aim to remove the opaqueness often surrounding RLMs, facilitating reproducibility and innovation. The introduction of a new modular implementation, x1, further supports this goal by enabling rapid prototyping and experimentation, which will prove invaluable in fostering future research and development of more efficient and effective RLMs.
Modular RLMs#
The concept of Modular RLMs offers a compelling vision for overcoming current limitations in reasoning language models. By decomposing complex RLMs into smaller, independent modules, researchers can achieve greater flexibility and understandability. This modularity fosters easier experimentation and innovation, allowing for the selective replacement or addition of components to tailor RLMs to specific applications and datasets more effectively. Improved scalability is another key benefit, as modular designs can be adapted more readily for training on larger datasets or deployment on distributed computing infrastructure. However, the design and implementation of effective interfaces between modules present significant technical challenges. Careful attention must be given to ensuring seamless data flow and communication while maintaining modularity. Additionally, robust methods for training and evaluating individual modules are crucial for the success of modular RLMs. Thoroughly testing the performance of the combined system is essential to verify its reliability and accuracy compared to monolithic systems. The development of standardized interfaces and modular components would greatly accelerate RLM research and development, fostering broader accessibility to this powerful technology.
x1 Framework#
The x1 framework, as described in the research paper, is a modular and extensible system for prototyping and experimenting with reasoning language models (RLMs). Its minimalist design facilitates rapid development and experimentation, allowing researchers to test different RLM architectures and components without extensive overhead. The framework’s modularity allows users to easily swap out components like reasoning schemes, operators, and models, promoting flexibility and enabling the exploration of novel RLM designs. A key feature of x1 is its ability to support different training paradigms, such as supervised fine-tuning and reinforcement learning, facilitating comprehensive evaluation of RLM performance under various training schemes. Furthermore, x1 incorporates tools for data generation and management, streamlining the training process and allowing for effective experimentation. The framework’s focus on both theoretical understanding and practical implementation bridges the gap between complex RLM architectures and accessible experimentation, thereby democratizing the development and refinement of these advanced AI models. The combination of modularity, support for varied training approaches, and comprehensive data management tools positions x1 as a valuable resource for advancing the field of RLM research.**
Multi-Phase Training#
Multi-phase training for reasoning language models (RLMs) offers a structured approach to enhance model capabilities. It typically involves distinct phases, such as initial supervised fine-tuning to establish a foundational understanding of reasoning patterns, followed by reinforcement learning to refine strategies and improve performance. The initial phase often leverages labeled datasets, like chains of thought (CoT), providing a strong signal for the model to learn basic reasoning steps. Subsequently, reinforcement learning refines this foundation, often employing methods like proximal policy optimization (PPO) or direct preference optimization (DPO). This phase involves the iterative generation and evaluation of reasoning sequences within a search framework like Monte Carlo Tree Search (MCTS), generating more complex and nuanced data than the first phase. The use of MCTS allows the model to explore a wider range of solution paths and to develop more sophisticated strategies through continuous self-improvement. The value of this approach lies in its ability to combine the strengths of both supervised and reinforcement learning, yielding models that are both accurate and robust. Clear separation of training phases promotes model stability and enables better optimization of individual components. Careful consideration of data distributions used in each phase is crucial for efficient and effective training.
Future of RLMs#
The future of Reasoning Language Models (RLMs) appears incredibly promising, driven by several key factors. Improved scalability and efficiency are paramount; current RLMs’ high computational costs hinder widespread adoption. Future research will likely focus on more efficient architectures and training methods, potentially leveraging advancements in hardware and algorithm design. Enhanced reasoning capabilities are another critical area. While RLMs have demonstrated impressive reasoning abilities, their performance on complex, multi-step reasoning tasks remains limited. Future developments might incorporate more sophisticated reasoning strategies, such as hierarchical reasoning or the integration of external knowledge bases. Addressing the accessibility gap is crucial. The high cost and proprietary nature of many state-of-the-art RLMs limit their accessibility to researchers and developers with limited resources. Future progress hinges on creating more open-source and affordable models, fostering wider participation and innovation within the community. Finally, new benchmarks and evaluation metrics are needed. Existing benchmarks often lack the complexity and diversity to thoroughly evaluate the full range of RLM capabilities. The development of more comprehensive and nuanced evaluation metrics will be essential to guide future research and development.
More visual insights#
More on figures

🔼 This figure shows the relationship between different types of language models and the three key components that enable reasoning language models (RLMs): Large Language Models (LLMs), Reinforcement Learning (RL), and High-Performance Computing (HPC). The left side illustrates how LLMs, which are adept at generating human-like text but lack structured reasoning, and RL agents, which can find optimal solutions but lack world knowledge, are combined with the power of HPC to create RLMs. The right side presents a hierarchy showing how LLMs are a subset of language models, with RLMs being a more advanced type of LLM that incorporates reasoning capabilities.
read the caption
Figure 3: Hierarchy of language models (right) and the three pillars of RLMs (left).

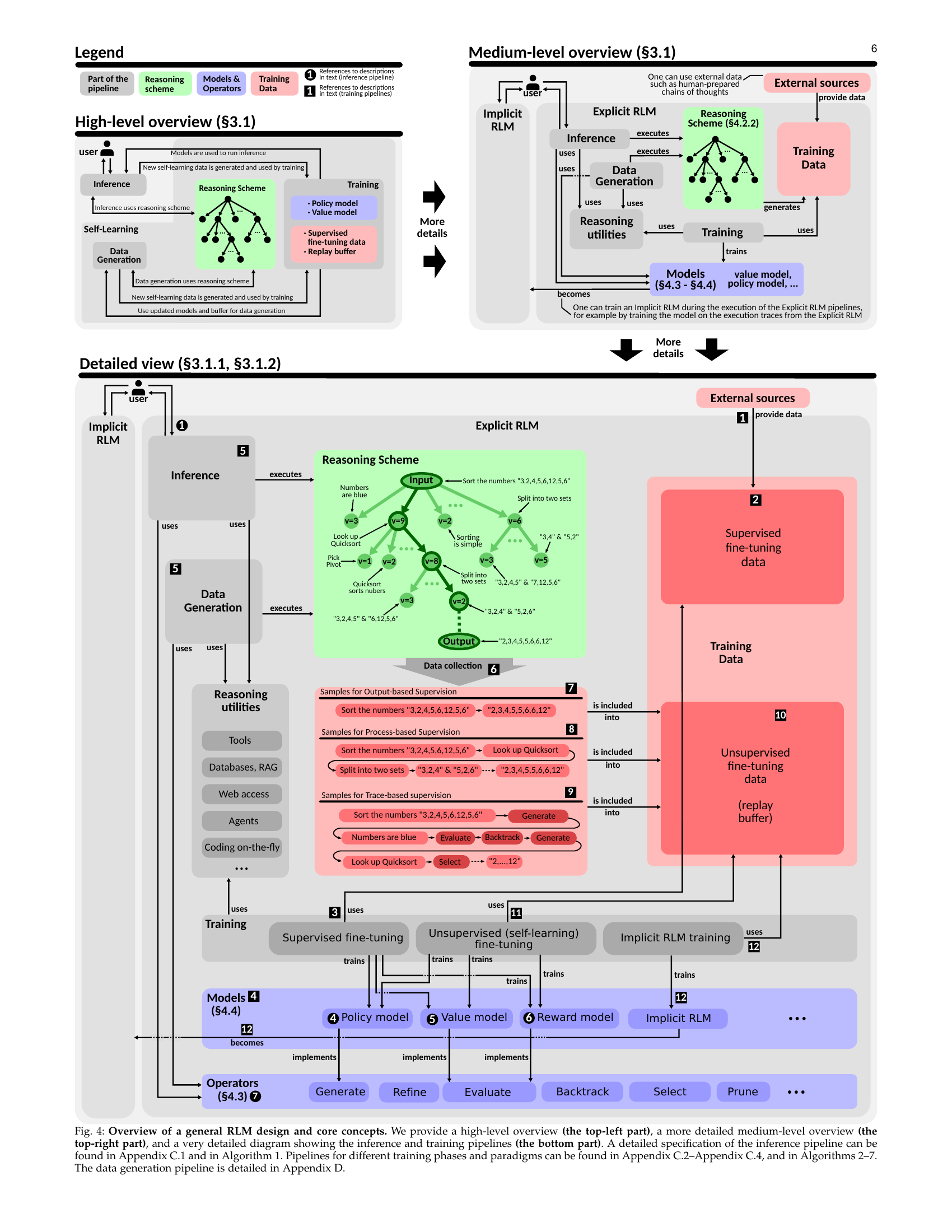
🔼 Figure 4 illustrates the architecture of a Reasoning Language Model (RLM). It starts with a high-level overview showing the three main pipelines: inference, training, and data generation. The medium-level overview zooms in on the inference and training processes, distinguishing between implicit and explicit RLMs. The bottom part provides a very detailed view of the processes, including the reasoning scheme (how the reasoning process evolves), operators, models, and various training data types (output-based, process-based, and trace-based supervision). The figure details the flow of data and how the different components interact to achieve reasoning. Appendices C and D provide further details on the algorithms and data generation.
read the caption
Figure 4: Overview of a general RLM design and core concepts. We provide a high-level overview (the top-left part), a more detailed medium-level overview (the top-right part), and a very detailed diagram showing the inference and training pipelines (the bottom part). A detailed specification of the inference pipeline can be found in Appendix C.1 and in Algorithm 1. Pipelines for different training phases and paradigms can be found in Appendix C.2–Appendix C.4, and in Algorithms 2–7. The data generation pipeline is detailed in Appendix D.

🔼 Figure 5 presents a comprehensive blueprint for building reasoning Language Models (RLMs). It’s structured around four key component categories: Reasoning Schemes (defining the overall reasoning strategy and structure), Operators (actions that modify the reasoning process), Models (neural networks used to implement operators), and Pipelines (workflows for inference, training, and data generation). The figure visually organizes these components, highlighting their interrelationships and providing references to detailed descriptions and algorithms found in the paper’s appendices.
read the caption
Figure 5: A blueprint for reasoning LMs. It consists of four main toolboxes: the reasoning scheme (the top part), operators (the bottom-left part), and models (the bottom-right part); pipelines are mentioned in the center and detailed in Appendix C.1 and in Algorithm 1 (the inference pipeline), Appendix C.2–Appendix C.4, and in Algorithms 2–7 (the training pipelines), and in Appendix D (the data generation pipeline).

🔼 The figure illustrates the x1 framework’s two-phase training process. Phase 1 initializes the models (policy and value models) using supervised fine-tuning. Phase 2 iteratively refines these models using reinforcement learning. This involves alternating between generating many Monte Carlo Tree Search (MCTS) trees and training the models using data derived from the MCTS process. This iterative refinement helps improve both model accuracy and efficiency.
read the caption
Figure 6: An overview of the x1 framework is presented, highlighting its two-phase training process. In phase 1, the models are initialized, while in phase 2, the models are iteratively refined by alternating between constructing a sufficient number of MCTS trees and training the models on data derived from these trees.

🔼 This figure displays an example of model output, highlighting the probabilities associated with individual tokens. The color-coding helps visualize the model’s confidence in its predictions: purple indicates low confidence (highest probability below 0.8), blue signifies high confidence with a potential for alternative predictions (second highest probability above 0.1), and red represents uncertainty (both conditions are met). This exemplifies how the model’s certainty is reflected in its token generation process.
read the caption
Figure 7: Example model output with highlighted tokens. The output has been colored in the following way: Purple if the highest probability is below 0.8 (not so certain but no contention), blue if the second highest probability is above 0.1 (very certain, but maybe another one) and red if both are true (uncertain).

🔼 This figure visualizes the token probability distributions generated by a language model during the reasoning process. For each token in the model’s output, it displays the probability of the two most likely tokens and the combined probability of all other less-likely tokens. This allows for a detailed analysis of the model’s certainty and uncertainty in each step, revealing potential areas of confidence and ambiguity in its reasoning.
read the caption
Figure 8: Token probabilities of example model outputs We show the two highest probabilities as well as the sum of the other probabilities.

🔼 This figure visualizes the uncertainty of token probabilities in a model’s output sequence, using four metrics: variance, entropy, VarEntropy, and the Gini coefficient. These metrics help analyze the model’s confidence in its predictions and can reveal where the model is most uncertain. The x-axis represents the position in the token sequence, and the y-axis shows the values of each metric. High values for variance, VarEntropy, and the Gini coefficient indicate high uncertainty, suggesting areas where the model may be making less informed predictions.
read the caption
Figure 9: Uncertainty metrics (variance, entropy, VarEntropy, and the Gini coefficient) plotted against the output token sequence.

🔼 This figure displays the relationship between the size of a question set and the length of the 95% confidence interval for the accuracy of large language models. The data was generated by sampling responses from a subset of 1000 questions, generating 8 answers for each question at a temperature of 1. The confidence interval was calculated across 32 randomly sampled sets with replacement for each question set size. The chart visually demonstrates how increasing the number of questions reduces the uncertainty in the model’s accuracy.
read the caption
Figure 10: Estimated 95%-confidence interval length for different question set sizes using sampled generated answers from a subset of 1000 questions with eight generated answers per question at temperature 1. The confidence interval is calculated over the eight different pass@1 subsets of each question with 32 sets randomly sampled with replacement for each set size.

🔼 This figure illustrates the different types of reward models used in reinforcement learning for reasoning tasks, specifically in the context of Monte Carlo Tree Search (MCTS). It compares Outcome-Based Reward Models (ORMs), which only consider the final outcome, with Process-Based Reward Models (PRMs), which evaluate intermediate steps. The figure also introduces Outcome-Driven Process-Based Reward Models (O-PRMs), a hybrid approach that combines elements of both ORMs and PRMs. Gray nodes in the diagrams represent terminal nodes (i.e., end of the reasoning process). The visual representation helps clarify the differences in how these reward models evaluate the quality of reasoning paths. This visualization helps to understand why PRMs are usually preferred, as they provide richer feedback signals during the training process.
read the caption
Figure 11: Comparison of Outcome vs. Process-Based label generation, and the introduction of Outcome-Driven Process Based Reward Models (O-PRMs). Gray nodes mark terminal nodes.

🔼 This figure illustrates the differences between reward models, V-value models, and Q-value models, specifically in scenarios with sparse rewards (only terminal states receive non-zero rewards). The reward model only provides information at the terminal state, indicating whether the solution is correct or incorrect. V-value models estimate a global value for each state, while Q-value models provide a more granular evaluation, estimating a value for each state-action pair. This more detailed information is especially useful for search algorithms like Monte Carlo Tree Search (MCTS) which make decisions based on the values of individual actions. Gray nodes in the figure represent terminal states.
read the caption
Figure 12: Comparison of reward, v-value and q-value models in a sparse reward setting (only terminal states receive non-zero rewards). Gray nodes mark terminal nodes. The reward model should predict the rewards for transitioning from one state to another which is 0 for non-terminal states and not providing information. V-VMs and Q-VMs however, predict a global value and are therefore informative for non-terminal states.

🔼 This figure illustrates an example of a tree structure generated by the Monte Carlo Tree Search (MCTS) algorithm used in the paper’s reasoning language model (RLM). Each node represents a reasoning step in the process of solving a problem, and the edges represent the transitions between steps. The tree expands by exploring multiple possible paths, guided by a policy model that predicts the likelihood of each next step and a value model that estimates the overall quality of each path.
read the caption
Figure 13: Example MCTS generated tree of reasoning sequences.

🔼 This figure illustrates the two-phase training pipeline for the Reasoning Language Model (RLM). Phase 1 focuses on supervised fine-tuning using Chain-of-Thought (CoT) and Monte Carlo Tree Search (MCTS) to initialize the policy and value models. Phase 2 uses reinforcement learning with Process-Based Reward Models to refine the models through iterative improvement based on data generated via the MCTS process. The process involves alternating between model training and MCTS simulations, each iteration enhancing model performance and data quality. Implicit and Explicit RLMs are shown to illustrate the generalizability of the pipeline.
read the caption
Figure 14: The two phases of the training pipeline.
Full paper#