TL;DR#
Large Language Models (LLMs) demand significant computational resources, hindering their wider use. Existing fine-tuning methods are often computationally expensive. Low-rank adaptation techniques, such as LoRA, offer a parameter-efficient alternative, but still face limitations.
This paper introduces novel methods combining low-rank adapters with neural architecture search (NAS) to tackle these challenges. It proposes elastic LoRA adapters and techniques such as LoNAS, Shears, and SQFT, which intelligently reduce model size while preserving accuracy. These innovations result in compressed LLMs with faster inference times and reduced memory needs, paving the way for broader deployment in resource-constrained environments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language model (LLM) optimization because it presents novel methods for efficient LLM compression and fine-tuning. It offers practical solutions to address resource constraints associated with LLMs, making them more accessible for broader applications. Furthermore, the study opens avenues for future research on efficient neural architecture search techniques and their integration with low-rank adaptations.
Visual Insights#

🔼 This figure illustrates the architecture of a vanilla LoRA adapter alongside two variations called elastic adapters. The vanilla LoRA adapter shows the standard low-rank decomposition of a weight matrix (W) into two smaller matrices (L1 and L2), which are trained while the original matrix remains frozen. In contrast, the elastic adapter offers two modes of operation. Mode A maintains the fixed dimensions of the input and output channels, but allows the rank (r) of the low-rank matrices (L1 and L2) to be dynamically adjusted during training, effectively providing a range of possible rank values. Mode B expands on this by additionally enabling the adjustment of the input and/or output channels’ dimensions, giving the model even more flexibility to adapt to different scenarios. This enhances efficiency by only training the smaller adapter matrices.
read the caption
Figure 1: Vanilla LoRA Adapter and two different modes of the elastic adapter. Mode A allows only the LoRA rank to be elastic, while Mode B also enables the input or output channels to be elastic.
| Method | Average Score | Relative Score | Total Params. | TFLOPs | Inference Speedup |
|---|---|---|---|---|---|
| LoRA | 65.8 | 100.0% | 6.7B | 1.7 | 1.00 |
| \cdashline1-12 LoNAS (Heuristic Subnet) | 65.2 | 99.1% | 5.6B | 1.4 | 1.23 |
| LoNAS (Search Subnet-1) | 67.1 | 102.0% | 5.6B | 1.4 | 1.28 |
| LoNAS (Search Subnet-2) | 65.6 | 99.7% | 5.1B | 1.3 | 1.41 |
🔼 This table presents the performance comparison of LoNAS (Low-Rank Neural Architecture Search) against the baseline LORA (Low-Rank Adaptation) method for fine-tuning a LLaMA-7B language model on a commonsense reasoning dataset. It demonstrates LoNAS’s efficiency in terms of accuracy, total parameters, floating point operations (FLOPs), and inference speedup. The results are averaged across eight different commonsense tasks, showcasing the consistent improvement of LoNAS over LORA in terms of compression and speed without significant accuracy loss. Different search strategies (heuristic and two search subnets) within LoNAS are compared, highlighting the impact of the search algorithm on the final model.
read the caption
Table 1: The performance of LoNAS using elastic adapters mode B, including accuracy score and model compression efficiency when fine-tuning LLaMA-7B on 15k unified commonsense reasoning dataset from LLM-Adapters (Hu et al. 2023). The average score represents the results across eight commonsense tasks. These results are reproduced from Muñoz et al. (2024)
In-depth insights#
Elastic LoRA#
Elastic LoRA adapters represent a significant advancement in efficient fine-tuning of large language models (LLMs). By introducing elasticity into the LoRA architecture, both the rank and the input/output channels of the adapter matrices can be dynamically adjusted. This flexibility allows for a more efficient search of optimal configurations during neural architecture search (NAS), leading to smaller, faster models with minimal accuracy loss. Mode A focuses on adjusting only the rank, while Mode B allows adjustment of both rank and channel dimensions, offering a broader search space and the potential for even greater compression. The integration with NAS techniques is key, allowing the search process to be guided by the low-rank structure of the adapters, making the overall NAS process more computationally feasible for LLMs. The resulting models are not only more efficient in terms of memory and inference time but also demonstrate an ability to adapt to various downstream tasks effectively, making LLMs more accessible for resource-constrained environments. This approach therefore represents a powerful combination of parameter-efficient fine-tuning and automated architecture optimization.
LoNAS Search#
LoNAS (Low-Rank Neural Architecture Search) presents a novel approach to efficiently compress and fine-tune Large Language Models (LLMs). It leverages the strengths of low-rank adapters, specifically focusing on the LoRA (Low-Rank Adaptation) technique, to significantly reduce the number of trainable parameters. This is achieved by only training the adapter weights while keeping the original model’s weights frozen. The integration of neural architecture search then allows for the exploration of various adapter configurations, identifying the most effective architecture. This search process is far more efficient than traditional NAS methods, as it operates on a much smaller search space defined by the adapter parameters, rather than the entire model. LoNAS aims to balance model compression with minimal accuracy loss. While traditional methods often suffer from significant computational costs, LoNAS offers a more practical and computationally feasible solution. Furthermore, heuristic strategies within the LoNAS search process enable quicker evaluations of promising architectures, accelerating the overall search process and making the methodology suitable for even very large LLMs. Overall, LoNAS signifies a substantial advancement in efficient LLM adaptation and demonstrates a viable pathway toward democratizing access to these powerful models by reducing the computational resources required for fine-tuning and deployment.
Sparsity & SQFT#
The concept of sparsity, applied within the context of SQFT (Sparse Quantized Fine-Tuning), is crucial for efficient large language model (LLM) adaptation. Sparsity reduces model size and computational costs by eliminating less important weights, thereby accelerating inference and reducing memory requirements. SQFT leverages this by integrating sparsity with low-rank adapters and low-numerical precision quantization. This combined approach addresses the challenge of merging low-rank adapters with sparse models, ensuring efficient fine-tuning without sacrificing accuracy. The key innovation is in techniques like SparsePEFT and QA-SparsePEFT, which maintain sparsity during the merging process by aligning the sparsity patterns of adapters and the base model or by considering quantization effects. The result is a significant improvement in efficiency without compromising model performance, making LLMs more accessible and scalable for various resource-constrained applications. Overall, SQFT’s approach to sparsity demonstrates a powerful strategy for achieving considerable efficiency gains in LLM compression and adaptation.
Low-Rank NAS#
Low-rank NAS represents a powerful paradigm shift in neural architecture search (NAS) by integrating low-rank matrix factorization techniques. This approach aims to significantly reduce the computational cost of NAS, which traditionally suffers from high resource demands, especially when applied to large language models (LLMs). By focusing on low-rank representations of model parameters, the search space is dramatically reduced, leading to faster and more efficient exploration of architectural designs. The key advantage is parameter efficiency, allowing for the exploration of a wider range of architectural possibilities without the need for extensive computational resources. Furthermore, low-rank NAS facilitates the discovery of models that are not only computationally efficient but also maintain high performance levels, making it a highly attractive method for deploying LLMs on resource-constrained devices. The integration of low-rank methods within the NAS framework promises a more practical and scalable approach to designing advanced neural architectures, potentially democratizing access to high-performing LLMs for a broader range of applications.
Future Works#
Future research could explore more sophisticated NAS techniques to guide the search for optimal elastic low-rank adapter configurations, potentially reducing computational costs. Investigating alternative sparsity patterns and quantization methods within the context of elastic adapters could improve both compression and efficiency. Combining elastic adapters with other PEFT methods like prefix-tuning or prompt-tuning is another promising avenue, potentially leading to even greater compression and performance gains. Additionally, a detailed investigation into the theoretical underpinnings of elastic adapters and their interactions with various base model architectures is needed. Exploring the performance of elastic adapters on different downstream tasks and with different model sizes would further solidify the approach’s viability. Finally, research should focus on developing more user-friendly tools and frameworks for easy implementation and deployment of the proposed techniques.
More visual insights#
More on figures

🔼 This figure illustrates how elastic adapters, specifically Mode B, facilitate model compression. Mode B allows the adapters to dynamically adjust the input and output channels, as well as the rank. By integrating with the frozen weights of the base model (shown as the ‘W’ matrix), the elastic adapters guide the selection of a smaller, more efficient subset of weights. This selective pruning results in a reduced model size with minimal performance degradation, as indicated by the smaller, high-performing model. The original frozen weights are shown with the elastic adapter’s output, emphasizing that the adapter is acting as a filter and only utilizing a portion of the original model’s parameters.
read the caption
Figure 2: Elastic adapters guide the removal of elements in the frozen model weights, resulting in smaller, high-performing models. This process exemplifies the application of Mode B as depicted in Figure 1.

🔼 Figure 3 illustrates how elastic low-rank adapters are used in the fine-tuning of sparse models. It shows that instead of adapting all weights in a dense layer, only a smaller subset of weights (the ones indicated by the non-zero values in the sparse weights matrix) are modified. The elastic adapters (L1 and L2) are applied only to these non-zero elements. This method, which is an example of Mode A from Figure 1, allows for efficient fine-tuning and reduces the number of parameters that need to be updated. The figure visually shows the integration of sparse weights with the elastic adapters, improving the efficiency of the fine-tuning process.
read the caption
Figure 3: Elastic low-Rank adapters for fine-tuning sparse efficient models. This style exemplifies the application of Mode A as depicted in Figure 1.

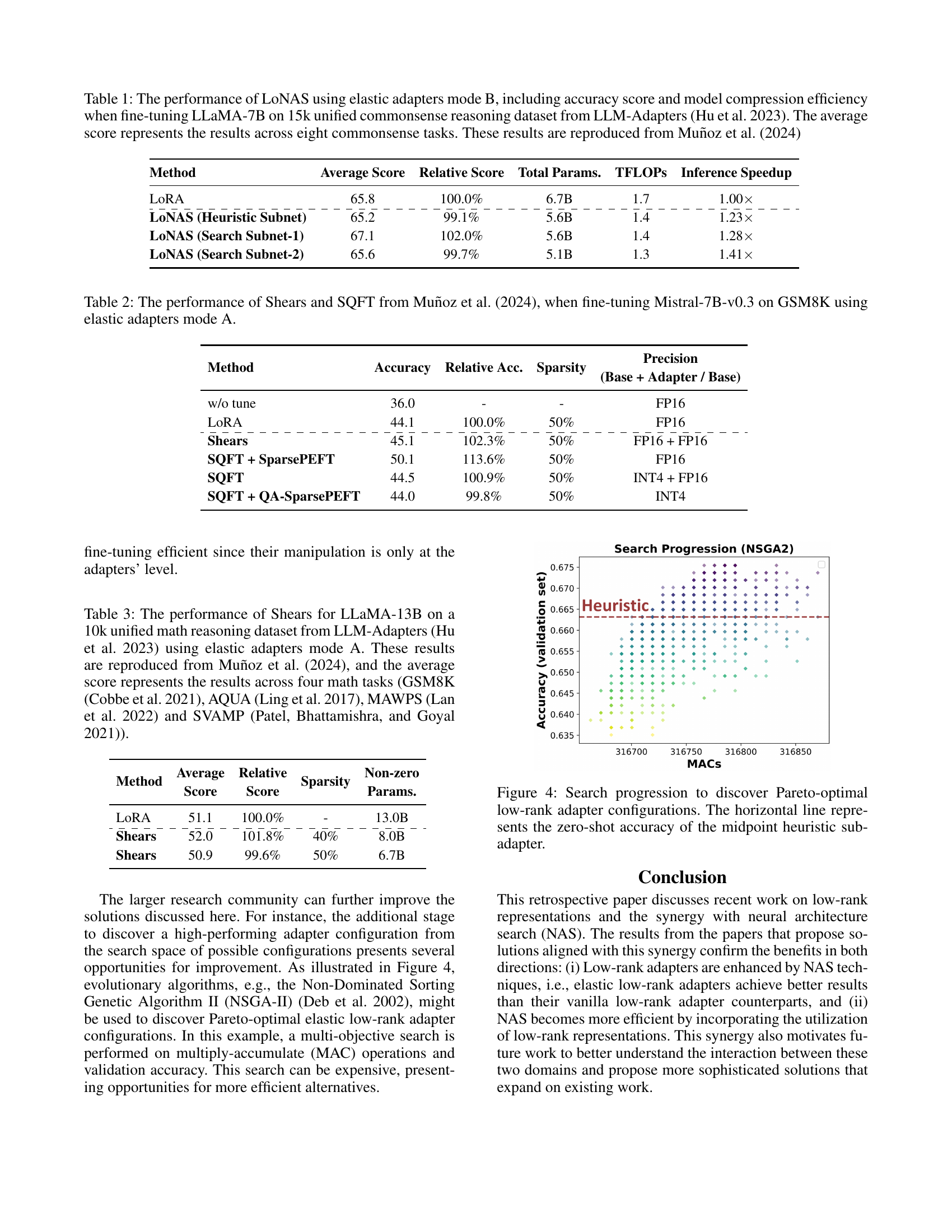
🔼 This figure visualizes the search process for finding the best low-rank adapter configurations using a multi-objective optimization algorithm (likely NSGA-II). The plot shows the trade-off between the number of multiply-accumulate (MAC) operations (a measure of computational cost) and the validation accuracy. Each point represents a different configuration tested during the search. The horizontal line indicates the accuracy achieved by a simpler heuristic method that evaluates a midpoint in the search space, providing a baseline for comparison against configurations found through the complete search process. The figure demonstrates how the search algorithm explores the design space and finds configurations that balance performance and efficiency.
read the caption
Figure 4: Search progression to discover Pareto-optimal low-rank adapter configurations. The horizontal line represents the zero-shot accuracy of the midpoint heuristic sub-adapter.
More on tables
| Method | Accuracy | Relative Acc. | Sparsity | Precision |
|---|---|---|---|---|
| (Base + Adapter / Base) | ||||
| w/o tune | 36.0 | - | - | FP16 |
| LoRA | 44.1 | 100.0% | 50% | FP16 |
| \cdashline1-5 Shears | 45.1 | 102.3% | 50% | FP16 + FP16 |
| SQFT + SparsePEFT | 50.1 | 113.6% | 50% | FP16 |
| SQFT | 44.5 | 100.9% | 50% | INT4 + FP16 |
| SQFT + QA-SparsePEFT | 44.0 | 99.8% | 50% | INT4 |
🔼 This table presents the performance comparison of different methods in fine-tuning the Mistral-7B-v0.3 language model on the GSM8K benchmark dataset. Specifically, it contrasts the accuracy, relative accuracy improvement compared to a baseline, sparsity level achieved, and precision used for the LoRA, Shears, and SQFT methods. Shears and SQFT utilize Elastic LoRA Adapters in Mode A, which means only the adapter ranks are allowed to be elastic. The table aims to illustrate how different model compression and fine-tuning techniques impact model performance and efficiency when working with large language models.
read the caption
Table 2: The performance of Shears and SQFT from Muñoz et al. (2024), when fine-tuning Mistral-7B-v0.3 on GSM8K using elastic adapters mode A.
| Method | Average | Relative | Sparsity | Non-zero |
|---|---|---|---|---|
| Score | Score | Params. | ||
| LoRA | 51.1 | 100.0% | - | 13.0B |
| \cdashline1-5 Shears | 52.0 | 101.8% | 40% | 8.0B |
| Shears | 50.9 | 99.6% | 50% | 6.7B |
🔼 This table presents the performance of the Shears method when fine-tuning a 13-billion parameter LLaMA model on a dataset of 10,000 unified math reasoning problems. The evaluation uses four different math reasoning tasks: GSM8K, AQUA, MAWPS, and SVAMP. The table shows the average score across these tasks, relative score compared to a baseline, the sparsity achieved, and the numerical precision used (floating-point 16-bit or integer 4-bit). The results are based on using Elastic Adapter Mode A, as detailed in the paper.
read the caption
Table 3: The performance of Shears for LLaMA-13B on a 10k unified math reasoning dataset from LLM-Adapters (Hu et al. 2023) using elastic adapters mode A. These results are reproduced from Muñoz et al. (2024), and the average score represents the results across four math tasks (GSM8K (Cobbe et al. 2021), AQUA (Ling et al. 2017), MAWPS (Lan et al. 2022) and SVAMP (Patel, Bhattamishra, and Goyal 2021)).
Full paper#