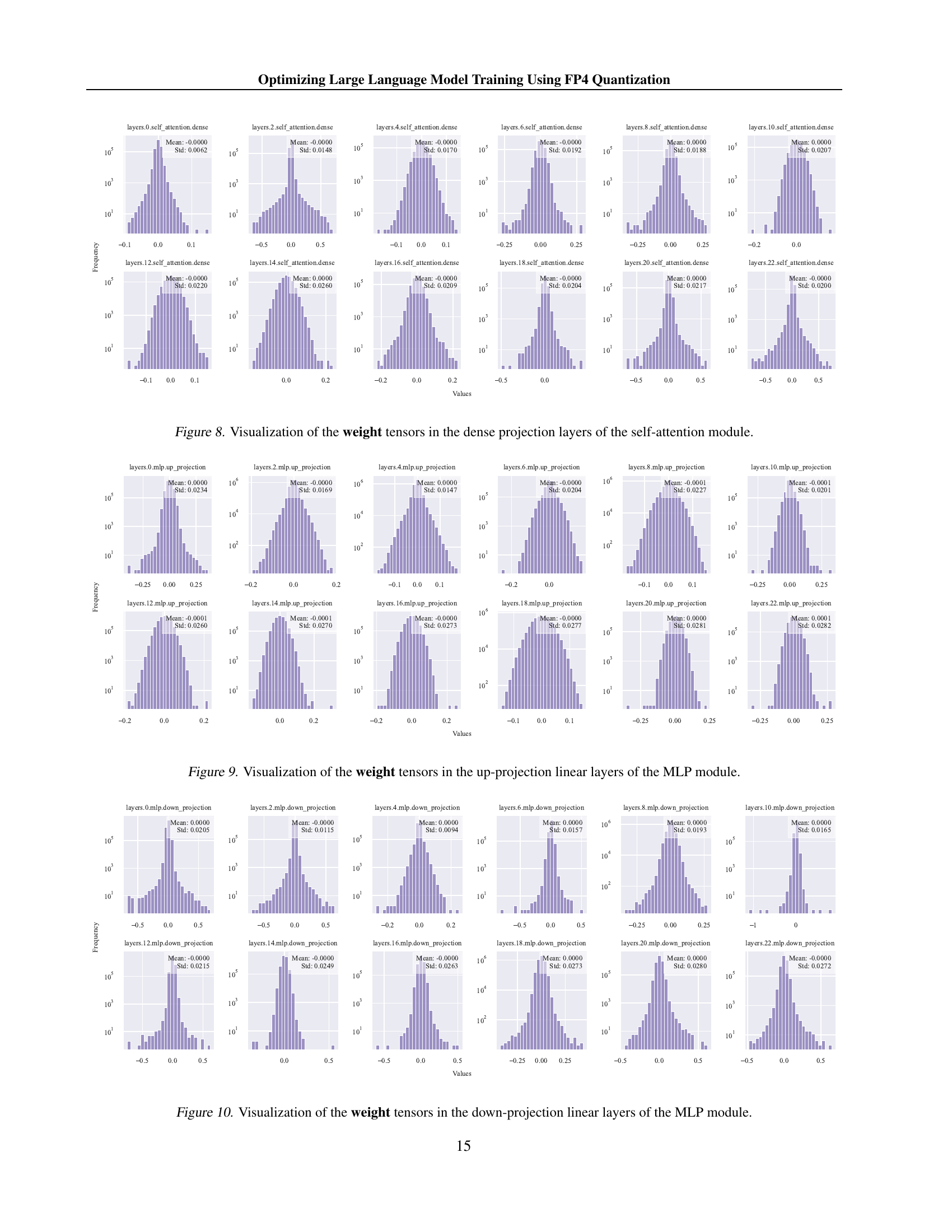
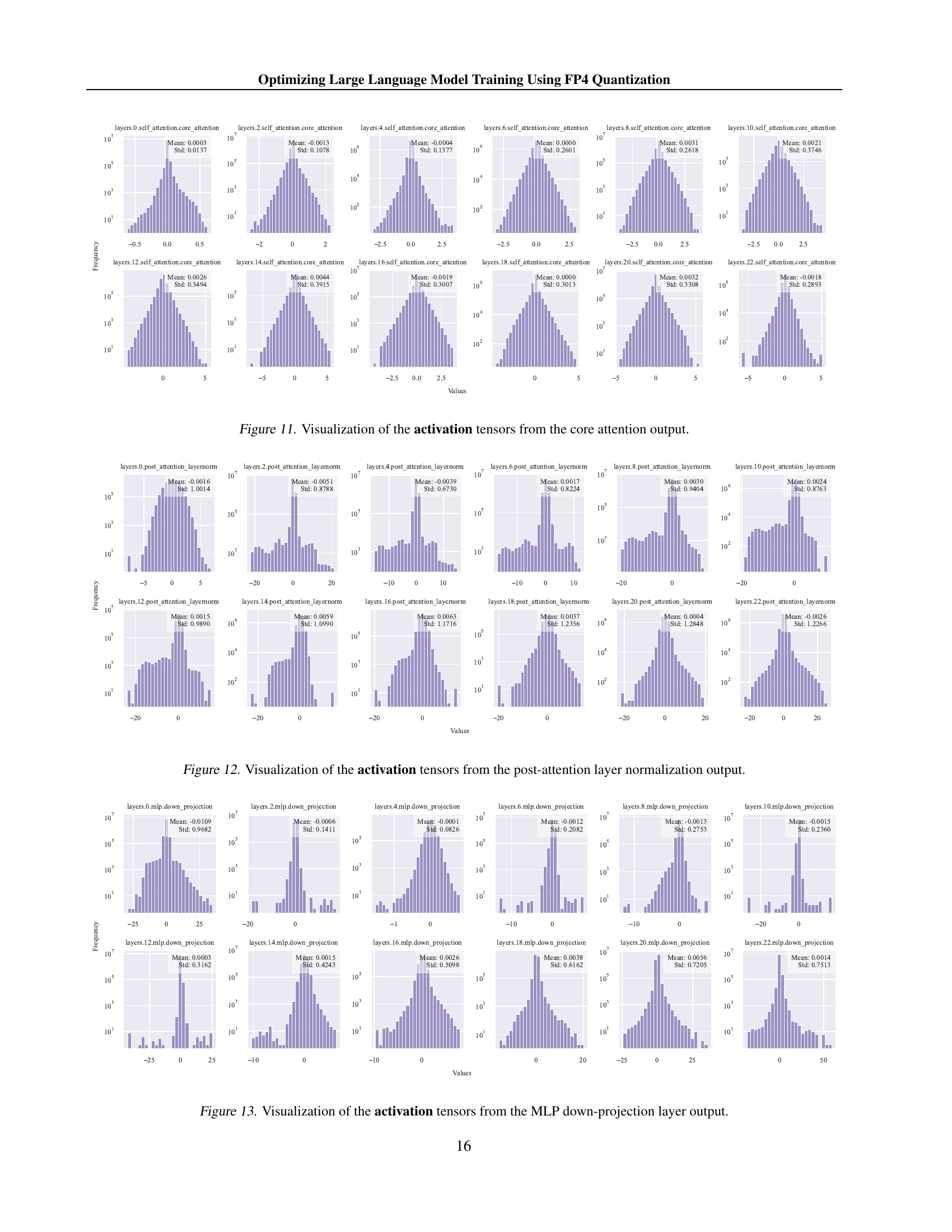
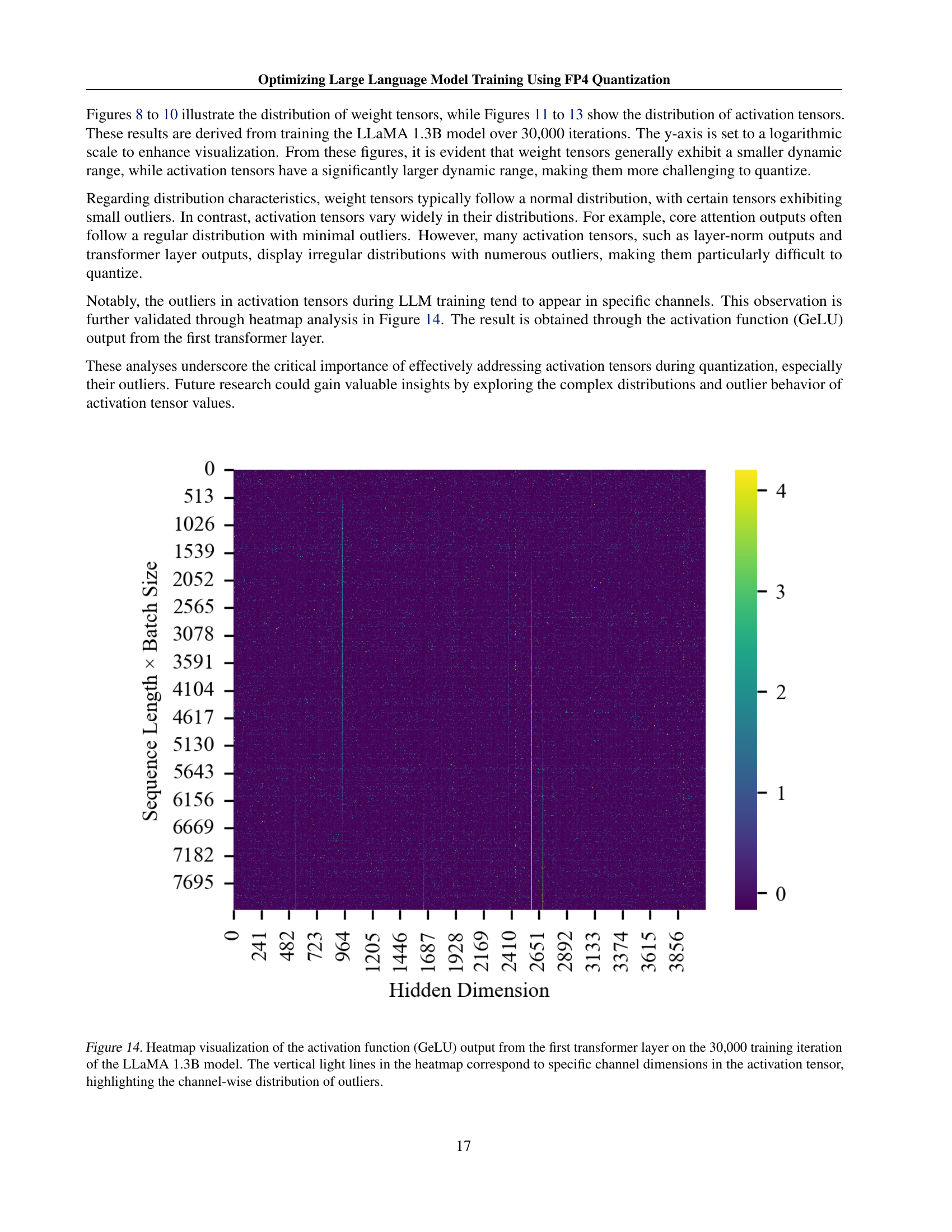
TL;DR#
Training large language models (LLMs) demands massive computational resources, driving the search for more efficient methods. Quantized training, using lower-precision numbers, is a promising approach, but achieving good accuracy with very low-precision (like 4-bit floating point, or FP4) has been challenging due to significant errors introduced by the quantization process. Prior work successfully demonstrated FP8 (8-bit) quantization, but extending this to FP4 has remained elusive.
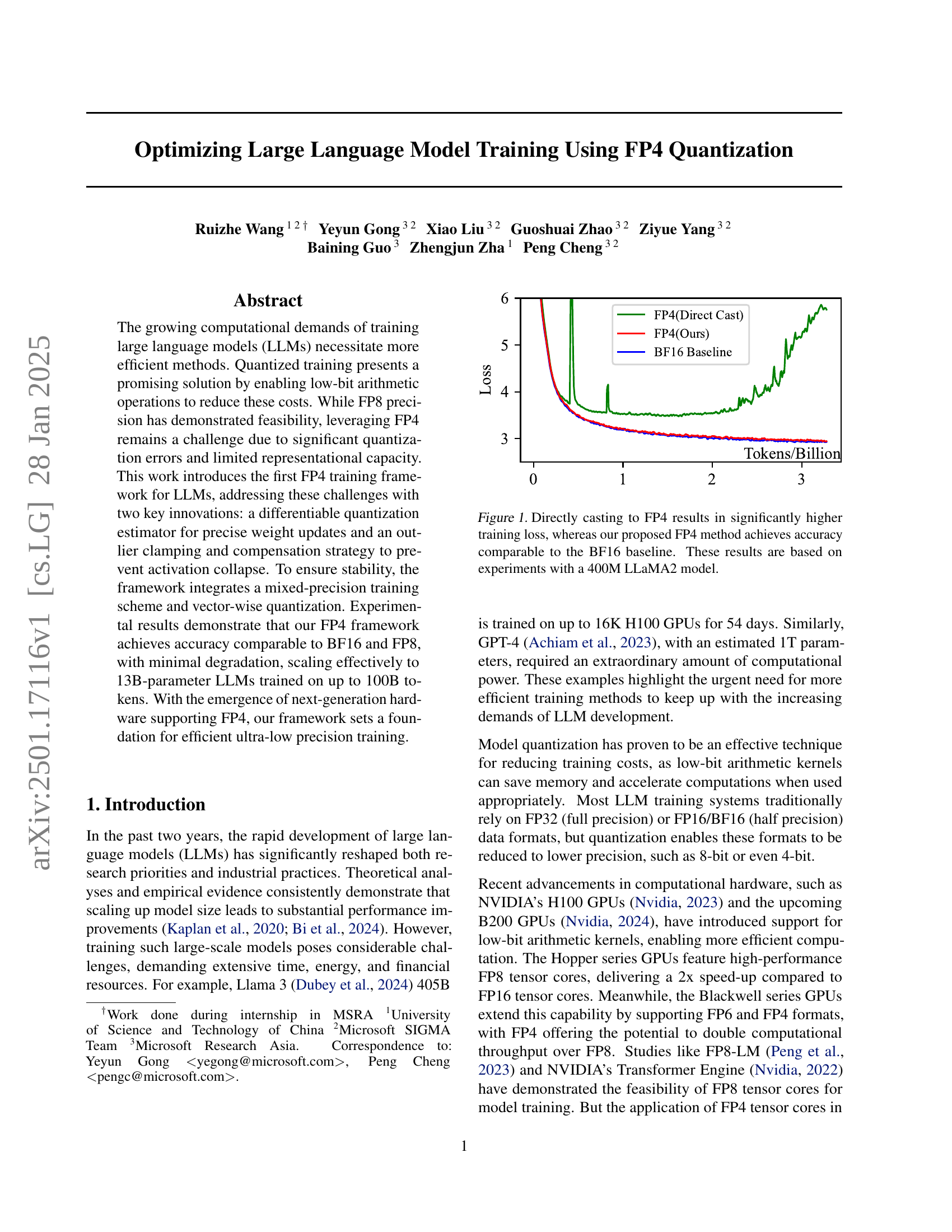
This work introduces the first-ever training framework for LLMs using FP4. The key innovation lies in two areas: a new differentiable quantization estimator that more accurately estimates weight updates during training, and a strategy to handle the problem of outlier values in activations (the outputs of neurons), preventing large errors. Experiments demonstrate that their approach achieves accuracy similar to BF16 and FP8, while scaling effectively to large models (13 billion parameters). The results suggest that FP4 may become a practical approach for efficient LLM training, especially with upcoming hardware supporting the format.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical need for efficient large language model (LLM) training, a major bottleneck in current AI research. By demonstrating the feasibility of FP4 quantization, it opens up new avenues for reducing training costs and energy consumption, paving the way for training even larger and more powerful models. The proposed methods and their validation are highly relevant to researchers working on LLM optimization and hardware acceleration, influencing the direction of future research.
Visual Insights#
| Clamp | Comp | Quantile | Sim | MSE | SNR |
|---|---|---|---|---|---|
| — | — | 92.19% | 0.1055 | 8.31 | |
| 99.9 | 98.83% | 0.0366 | 14.25 | ||
| 99.9 | 99.61% | 0.0245 | 15.31 | ||
| 99 | 100% | 0.0099 | 18.38 | ||
| 97 | 100% | 0.0068 | 20.88 |
🔼 This table presents a quantitative comparison of the mathematical accuracy between the original activation tensors (before quantization) and their quantized counterparts (after applying the outlier clamping and compensation method) from the LLaMA 1.3B model. The metrics used for comparison include cosine similarity (SIM), mean squared error (MSE), and signal-to-noise ratio (SNR). The results are averaged across all activation tensors and are based on data from 30,000 training iterations.
read the caption
Table 1: Quantitative analysis of mathematical accuracy between original and quantized activation tensors. Results represent the average values obtained across all activation tensors on the 30,000 training iterations of the LLaMA 1.3B model.
In-depth insights#
FP4 Training Framework#
An FP4 training framework for large language models (LLMs) is presented, addressing challenges of significant quantization errors and limited representational capacity inherent in ultra-low precision training. Two key innovations are introduced: a differentiable quantization estimator for accurate weight updates and an outlier clamping and compensation strategy to prevent activation collapse. The framework uses a mixed-precision training scheme and vector-wise quantization for stability. Results demonstrate comparable accuracy to BF16 and FP8, scaling effectively to 13B-parameter LLMs trained on up to 100B tokens, which sets a foundation for efficient ultra-low precision training on next-generation hardware supporting FP4. The differentiable quantization estimator improves gradient updates, while outlier clamping and compensation maintains accuracy by addressing outlier values in activation tensors. Overall, this framework presents a significant advancement in efficient LLM training, potentially leading to substantial cost and energy savings.
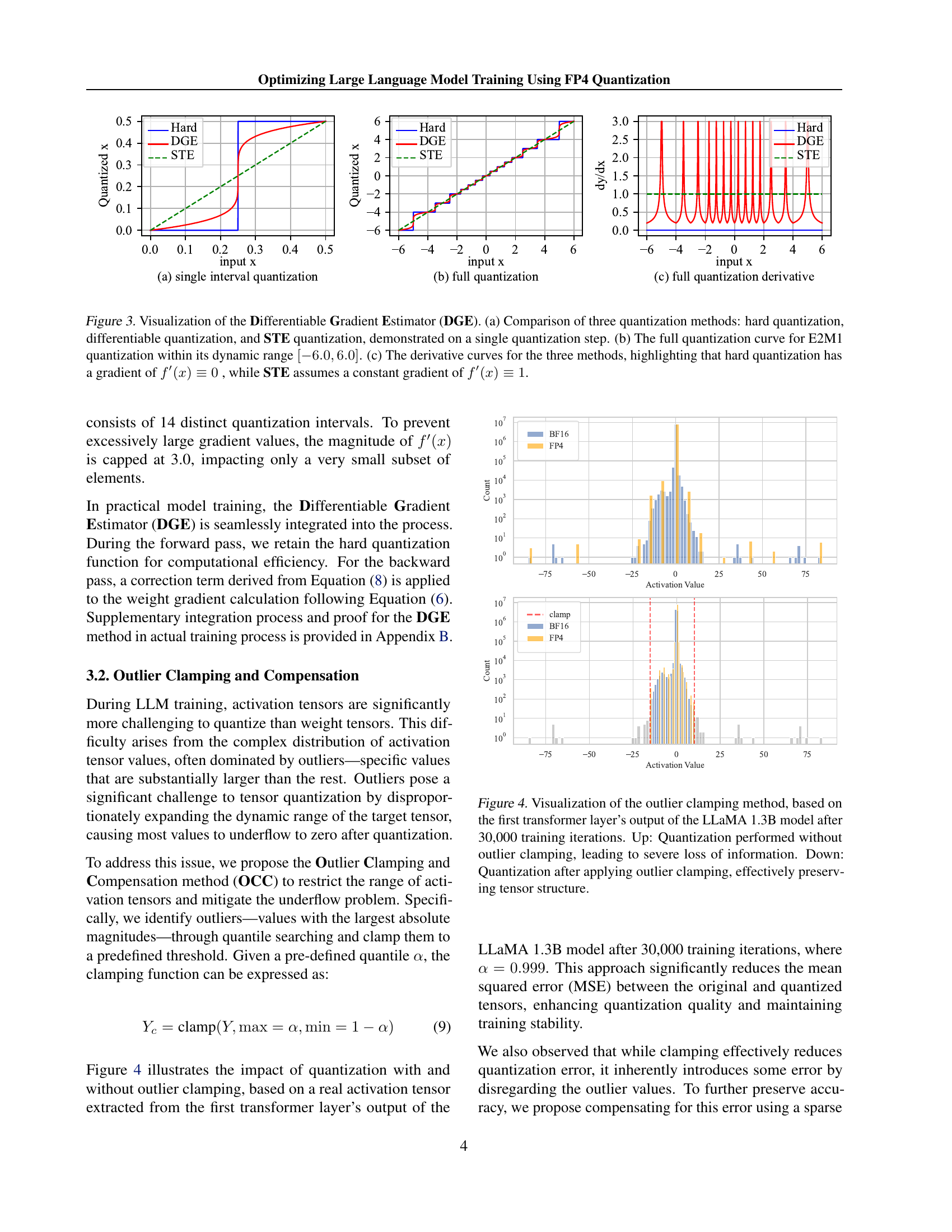
DGE & OCC Methods#
The research paper introduces two novel methods, Differentiable Gradient Estimator (DGE) and Outlier Clamping and Compensation (OCC), to address the challenges of training large language models (LLMs) using FP4 quantization. DGE tackles the non-differentiable nature of quantization functions by approximating them with a differentiable function, enabling more accurate gradient updates during backpropagation and mitigating vanishing gradients. This is crucial because direct quantization leads to significant errors. OCC addresses the issue of outlier activation values, which disproportionately increase the dynamic range of the tensors and cause underflow after quantization. It uses a combination of outlier clamping, limiting the extreme values, and compensation, using a sparse auxiliary matrix to preserve information lost through clamping. Together, DGE and OCC work synergistically, ensuring the stability of FP4 training by improving the precision of weight updates and preventing activation collapse. The effectiveness of these methods is demonstrated experimentally, showing that the accuracy of LLMs trained using FP4 is comparable to BF16 and FP8, paving the way for efficient, low-bit precision training using next-generation hardware.
LLM Quantization#
LLM quantization, the process of reducing the precision of large language model (LLM) parameters and activations, is a crucial technique for improving training efficiency and reducing computational costs. Lower precision (e.g., FP8, FP4) allows for faster computations and reduced memory footprint. However, this comes at the cost of potential accuracy degradation due to quantization errors. The paper explores the challenges of using extremely low-precision quantization, specifically FP4, and proposes innovative methods to mitigate accuracy loss. These include a differentiable quantization estimator for precise weight updates and an outlier clamping and compensation strategy to prevent activation collapse. The results show that the proposed framework can achieve accuracy comparable to higher-precision methods such as BF16, demonstrating the feasibility of ultra-low precision training for LLMs. This opens up possibilities for training even larger models with limited computational resources, and highlights the importance of hardware advancements to fully realize the potential of FP4.
Ablation Study Results#
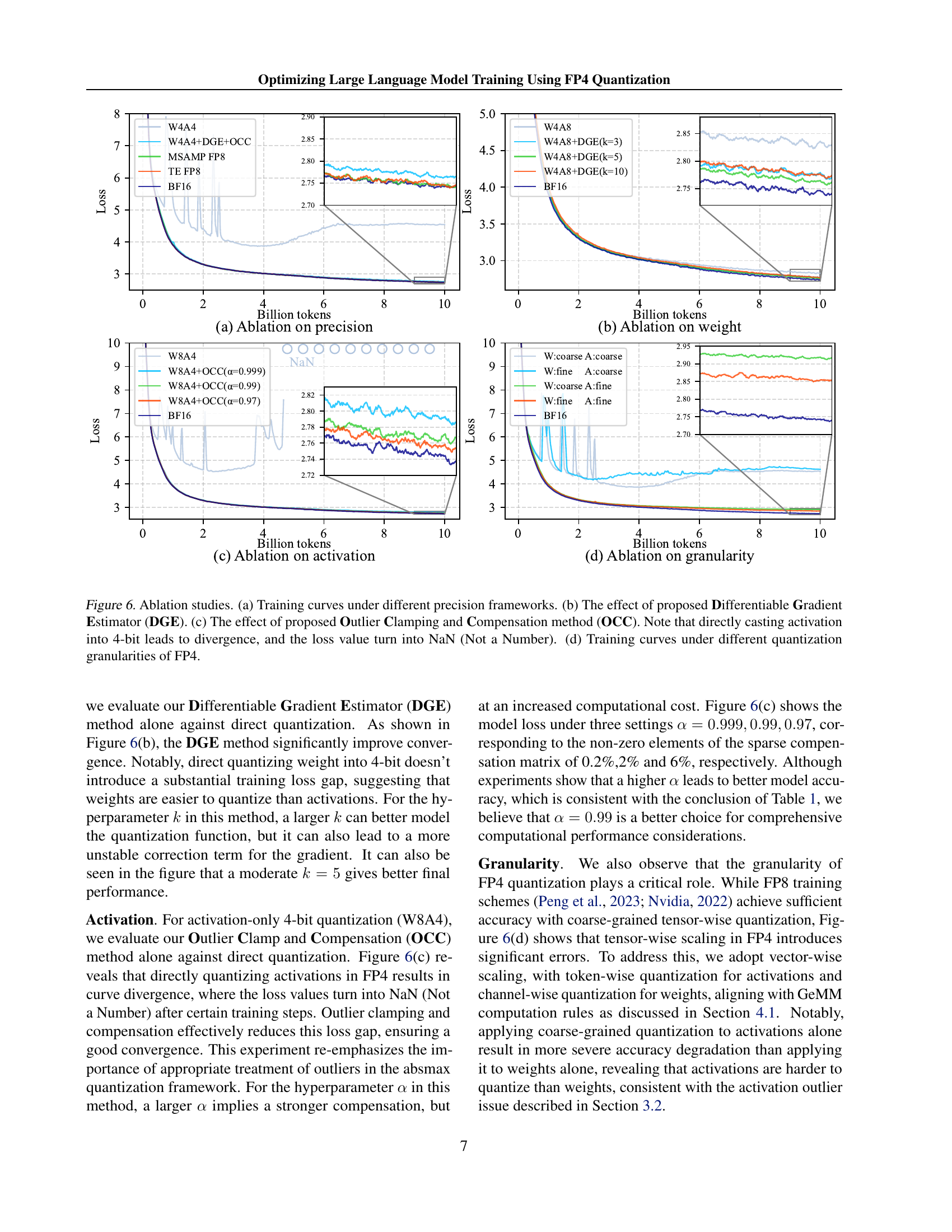
An ablation study systematically removes components of a proposed method to assess their individual contributions. In the context of this research paper, an ablation study on FP4 quantization for large language models (LLMs) would likely explore the impact of several key techniques. Removing the differentiable gradient estimator (DGE) would show how much it contributes to accurate gradient calculation, which is essential to prevent vanishing gradients inherent in low-precision training. Similarly, disabling the outlier clamping and compensation (OCC) strategy would reveal its role in handling the long-tailed distribution of activation values, which are often problematic during low-bit quantization. The results would quantify the accuracy degradation caused by each removed component, highlighting their importance to maintaining model performance with FP4. By comparing against the full method and various combinations, a comprehensive understanding of each technique’s relative contribution can be derived. The study may also analyze the tradeoffs involved, such as reduced computational cost versus accuracy loss, for each modification, providing a clear picture of the overall effectiveness and efficiency of the proposed FP4 framework.
Future Work#
Future research directions stemming from this FP4 quantization work on LLMs are plentiful. Extending the framework to support other LLM architectures beyond LLaMA 2 is crucial for broader applicability. The current implementation relies on FP8 emulation on H100 GPUs, limiting true performance gains; therefore, evaluating the framework on next-generation hardware with native FP4 support is essential to quantify speed and efficiency improvements. Investigating alternative quantization methods and exploring the trade-offs between accuracy and computational cost is important. Currently, the outlier clamping strategy addresses extreme values; a more nuanced technique could potentially improve results. Finally, deeper exploration of the interaction between FP4 quantization and other model optimization techniques, such as model pruning or knowledge distillation, could yield further performance boosts. The research also should include a thorough error analysis to pinpoint areas for optimization and guide future improvements.
More visual insights#
More on tables
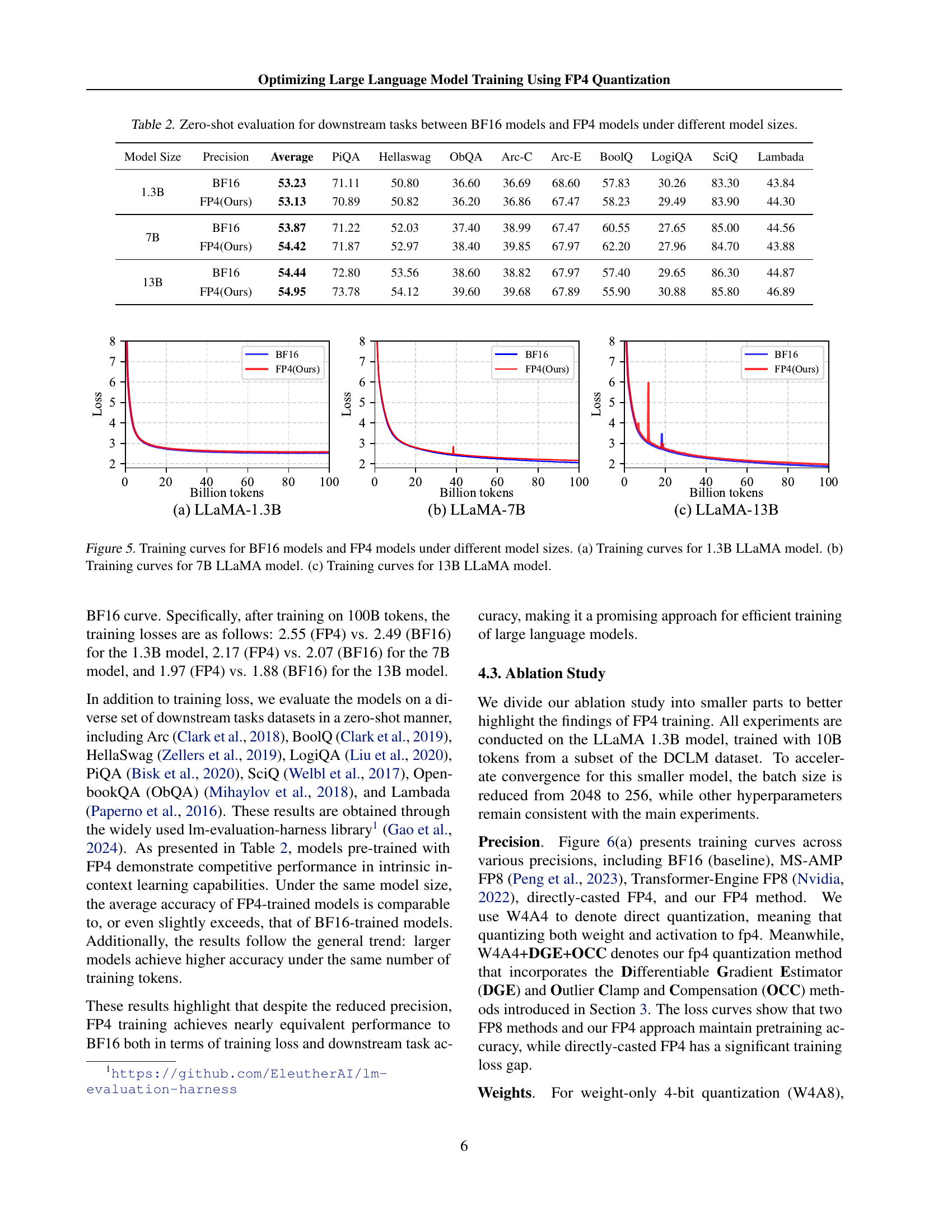
| Model Size | Precision | Average | PiQA | Hellaswag | ObQA | Arc-C | Arc-E | BoolQ | LogiQA | SciQ | Lambada |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.3B | BF16 | 53.23 | 71.11 | 50.80 | 36.60 | 36.69 | 68.60 | 57.83 | 30.26 | 83.30 | 43.84 |
| FP4(Ours) | 53.13 | 70.89 | 50.82 | 36.20 | 36.86 | 67.47 | 58.23 | 29.49 | 83.90 | 44.30 | |
| 7B | BF16 | 53.87 | 71.22 | 52.03 | 37.40 | 38.99 | 67.47 | 60.55 | 27.65 | 85.00 | 44.56 |
| FP4(Ours) | 54.42 | 71.87 | 52.97 | 38.40 | 39.85 | 67.97 | 62.20 | 27.96 | 84.70 | 43.88 | |
| 13B | BF16 | 54.44 | 72.80 | 53.56 | 38.60 | 38.82 | 67.97 | 57.40 | 29.65 | 86.30 | 44.87 |
| FP4(Ours) | 54.95 | 73.78 | 54.12 | 39.60 | 39.68 | 67.89 | 55.90 | 30.88 | 85.80 | 46.89 |
🔼 This table presents the results of zero-shot evaluations on several downstream tasks for language models trained using both BF16 (baseline) and FP4 precisions. Different model sizes (1.3B, 7B, and 13B parameters) are included to compare performance across scales. The tasks evaluated cover a range of reasoning and language understanding capabilities, and the table shows the average scores achieved by each model variant on each task, enabling a direct comparison of accuracy between the two training methods.
read the caption
Table 2: Zero-shot evaluation for downstream tasks between BF16 models and FP4 models under different model sizes.
| Binary Sequence | |||||||||||||||
| Format | 1111 | 1110 | 1101 | 1100 | 1011 | 1010 | 1101 | 1000/0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| e1m2 | -3.5 | -3 | -2.5 | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| e2m1 | -6 | -4 | -3 | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 6 |
| e3m0 | -16 | -8 | -4 | -2 | -1 | -0.5 | -0.25 | 0 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 |
🔼 This table shows the representation of numbers in different 4-bit floating-point formats (FP4). FP4 is an emerging format for low-precision computing, and different configurations exist, varying in the number of bits assigned to the exponent and mantissa. The table lists the binary representation and the corresponding numerical value for each possible combination in three different FP4 formats: E1M2, E2M1, and E3M0. The formats differ in their dynamic range and precision. Understanding these formats is crucial for implementing FP4 quantization in machine learning models.
read the caption
Table 3: FP4 Quantization Table under different FP4 formats.
Full paper#