TL;DR#
Current supervised fine-tuning (SFT) methods for language models face limitations, particularly diminishing returns with increased data size and quality, especially for already powerful models. This is a challenge because high-quality datasets are expensive and time-consuming to create. The paper also points out that applying SFT to already strong models can even decrease performance without stringent quality control.
This paper introduces Critique Fine-Tuning (CFT), a novel approach where models learn to critique noisy responses instead of simply imitating correct ones. The researchers created a 50K-sample dataset using GPT-40 to generate critiques, showing CFT consistently outperforms SFT on various mathematical reasoning benchmarks with improvements ranging from 4-10%. The CFT model trained on only 50K samples even matched or exceeded the performance of models trained on over 2 million samples, highlighting its efficiency. Ablation studies confirmed CFT’s robustness.
Key Takeaways#
Why does it matter?#
This paper is important because it challenges the dominant paradigm in language model training, proposing a more efficient and effective approach (Critique Fine-Tuning or CFT). CFT’s superior performance with significantly less data has major implications for researchers working with large language models, especially those facing resource constraints. It opens new avenues for research into critique-based learning, potentially transforming how we train and evaluate LLMs.
Visual Insights#

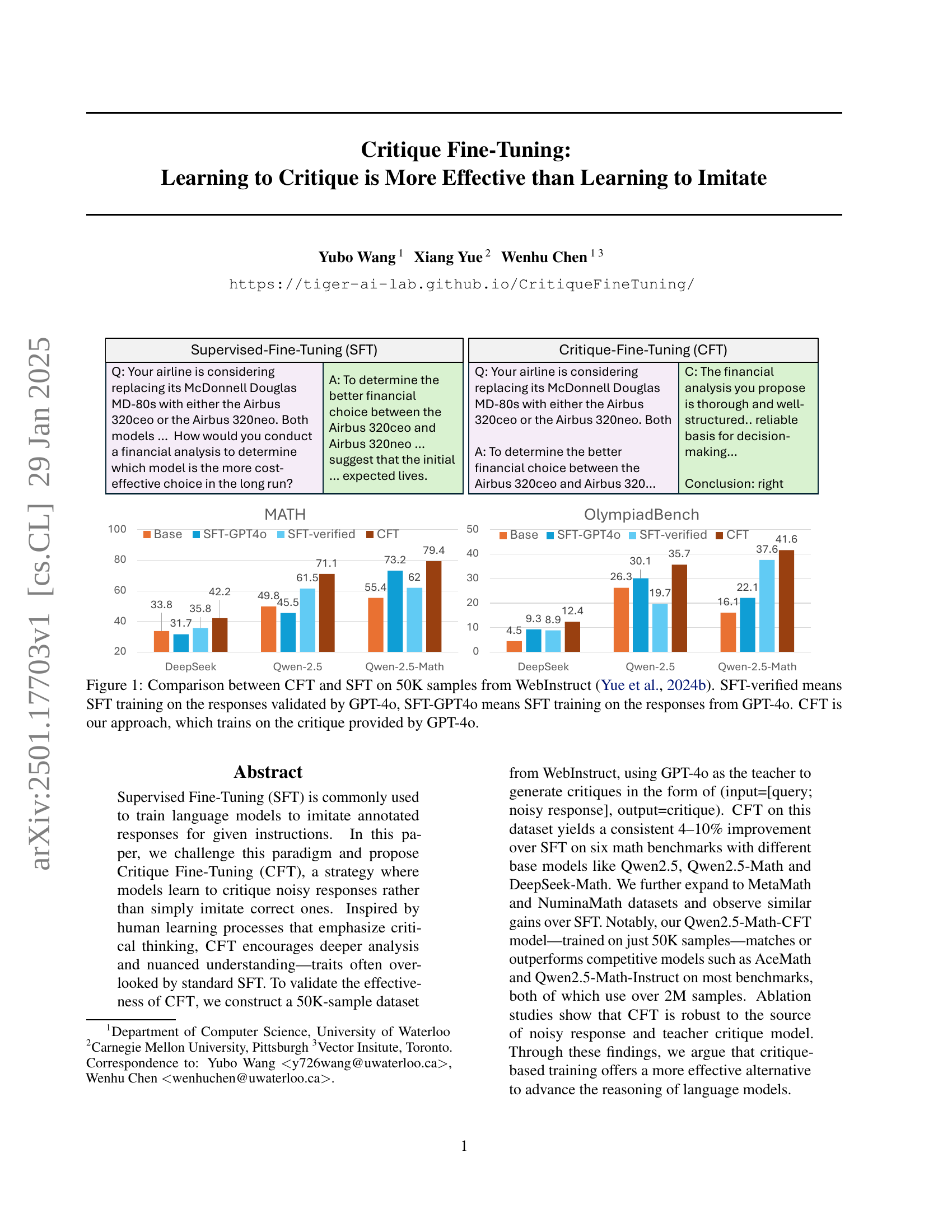
🔼 Figure 1 presents a comparison of the performance of Critique Fine-Tuning (CFT) and Supervised Fine-Tuning (SFT) methods on a dataset of 50,000 samples from WebInstruct. The figure showcases the effectiveness of CFT in improving model performance on different mathematical reasoning benchmarks. Three variants of SFT are shown: one trained on responses verified by GPT-40 (‘SFT-verified’), one trained directly on GPT-40’s generated responses (‘SFT-GPT40’), and a baseline SFT model. In contrast, CFT trains the model using critiques of noisy responses, also generated by GPT-40. The results demonstrate that CFT achieves consistently better performance than the SFT approaches across various benchmarks.
read the caption
Figure 1: Comparison between CFT and SFT on 50K samples from WebInstruct (Yue et al., 2024b). SFT-verified means SFT training on the responses validated by GPT-4o, SFT-GPT4o means SFT training on the responses from GPT-4o. CFT is our approach, which trains on the critique provided by GPT-4o.
| Dataset | Size | Source or Seed | Discipline |
|---|---|---|---|
| Supervised Fine-Tuning Data | |||
| WizardMath | 96K | GSM8K, MATH | Math |
| MathInstruct | 260K | GSM8K, MATH, etc | Math |
| MetaMathQA | 395K | GSM8K, MATH | Math |
| XwinMath | 1.4M | GSM8K, MATH | Math |
| OrcaMath | 200K | GSM8K | Math |
| NuminaMath | 860K | GSM8K, MATH, AIME | Math |
| AceMath | 1.6M | GSM8K, MATH, AIME | Math |
| OpenMath-2 | 14M | GSM8K, MATH | Math |
| Critique Fine-Tuning Data (Ours) | |||
| CFT | 50K | WebInstruct | STEM |
| CFT-tiny | 4K | WebInstruct | STEM |
🔼 This table compares the MAmmoTH3 dataset with other Supervised Fine-Tuning (SFT) and Reinforcement Learning (RL) datasets used for training language models on mathematical reasoning tasks. It lists the dataset name, size (number of examples), source or seed dataset(s) used to create it, and the main discipline or subject area it covers (Math or STEM). The table highlights the differences in scale and source data between MAmmoTH3 and other approaches to mathematical reasoning.
read the caption
Table 1: The comparison of MAmmoTH3 vs other SFT and RL models including WizardMath (Luo et al., 2023), MathInstruct (Yue et al., 2024a), MetaMathQA (Yu et al., 2024), XWinMath (Li et al., 2024a), OrcaMath (Mitra et al., 2024), NuminaMath (Li et al., 2024b), AceMath (Liu et al., 2024), OpenMathInsstruct-2 (Toshniwal et al., 2024) and Qwen2.5-Math (Yang et al., 2024c).
In-depth insights#
Critique Fine-tuning#
Critique fine-tuning (CFT) presents a novel approach to training language models, shifting the focus from imitation to critique. Instead of directly mimicking annotated responses, CFT trains models to analyze and evaluate noisy responses, identifying flaws and suggesting improvements. This approach is inspired by human learning processes, emphasizing critical thinking and nuanced understanding. The core idea is that learning to critique fosters a deeper understanding than simply memorizing correct answers. Experimental results demonstrate that CFT consistently outperforms traditional supervised fine-tuning (SFT) across various benchmarks, achieving comparable or even better performance with significantly less training data. This data efficiency is a crucial advantage. While CFT exhibits limitations regarding noisy critique data and self-critique, it still offers a compelling alternative for enhancing the reasoning abilities of language models and improving their overall performance.
CFT vs. SFT#
The study compares Critique Fine-Tuning (CFT) and Supervised Fine-Tuning (SFT), two methods for training language models. CFT trains models to critique noisy responses, while SFT trains models to imitate correct ones. The results show that CFT consistently outperforms SFT across various benchmarks, achieving a consistent 4-10% improvement. This is particularly notable because CFT uses significantly less training data (50K samples) compared to SFT, highlighting its efficiency. The superior performance of CFT suggests that learning to critique fosters a deeper understanding and more nuanced analysis than simple imitation, leading to more effective language models. Furthermore, CFT demonstrates robustness to the source of noisy responses and the choice of teacher critique model, adding to its practicality. The findings strongly advocate for CFT as a more effective alternative to traditional SFT for training advanced language models.
CFT Datasets#
The effectiveness of Critique Fine-Tuning (CFT) hinges heavily on the quality of its datasets. A well-constructed CFT dataset needs to balance the inclusion of noisy responses with insightful critiques. Simply providing correct answers for imitation is insufficient; the dataset must offer opportunities for the model to learn by identifying flaws, proposing improvements, and refining responses. A key consideration is the source of the noisy responses and critiques. Using high-quality models for critique generation can minimize the introduction of erroneous feedback, but even advanced models occasionally produce imperfect critiques. This necessitates mechanisms for validation, potentially through human review or cross-verification with multiple expert models to ensure data reliability. Furthermore, dataset size is important, but not the only defining factor. CFT’s efficiency is highlighted by achieving competitive results with comparatively smaller datasets compared to traditional SFT approaches. Thus, the focus shifts from sheer volume to the strategic selection of informative examples, capable of driving significant improvements in model reasoning abilities.
Ablation Studies#
Ablation studies in this research paper systematically investigate the impact of various factors on the performance of the proposed Critique Fine-Tuning (CFT) approach. The studies are crucial for understanding the relative contributions of different components and establishing the robustness of the method. Key aspects explored include the source of the noisy response data, the choice of the teacher critique model, and the impact of dataset source variations. The results from these ablation studies demonstrate that CFT is surprisingly robust to these factors, achieving consistent improvements even with weaker components. This robustness highlights a key strength of CFT; its effectiveness isn’t overly dependent on perfect data or extremely powerful models, suggesting practical applicability. The insights gained from these studies offer valuable guidance for future development and deployment of critique-based learning methods. The detailed analysis helps to isolate the core mechanisms driving CFT’s success, enhancing the overall credibility and understanding of the approach. The emphasis on robustness strengthens the paper’s claims regarding CFT’s potential for broader adoption in various machine learning scenarios.
Future Work#
The authors acknowledge limitations in their current Critique Fine-Tuning (CFT) approach and outline several promising avenues for future research. Improving the quality of critique data is paramount; the current dataset, while showing strong results, contains inaccuracies in the GPT-40-generated critiques. Future efforts could focus on developing automated verification methods or employing human verification to create a more reliable and accurate dataset. Furthermore, exploring the potential of self-critique mechanisms is identified as a key area for future development. Although initial attempts showed underperformance compared to direct inference, refining self-critique techniques could lead to models capable of iterative self-improvement and enhanced performance. Finally, the authors suggest expanding CFT to broader domains and tasks, investigating the theoretical underpinnings of CFT, and combining CFT with other training methods such as reinforcement learning to potentially improve its efficiency and effectiveness.
More visual insights#
More on tables
| Model | Method | MATH | Minerva-Math | GSM8K | OlympiadBench | AIME24 | AMC23 | AVG |
|---|---|---|---|---|---|---|---|---|
| DeepSeek-Math-7B | Base | 33.8 | 9.2 | 64.3 | 4.5 | 0.0 | 10.0 | 20.3 |
| WebInstruct-SFT | 26.3 | 12.1 | 34.7 | 6.2 | 0.0 | 17.5 | 16.1 | |
| WebInstruct-verified-SFT | 35.8 | 10.7 | 67.5 | 9.3 | 0.0 | 7.5 | 21.8 | |
| WebInstruct-GPT4o-SFT | 31.7 | 11.8 | 70.9 | 8.9 | 3.3 | 17.5 | 24.0 | |
| WebInstruct-CFT | 42.2 | 12.5 | 74.5 | 12.4 | 3.3 | 20.0 | 27.5 | |
| = CFT- SFTbest | 6.4 | 0.4 | 3.6 | 3.1 | 0.0 | 2.5 | 3.5 | |
| Qwen2.5-7B | Base | 49.8 | 15.1 | 85.4 | 26.3 | 10.0 | 37.5 | 37.4 |
| WebInstruct-SFT | 30.8 | 6.6 | 59.5 | 5.8 | 3.3 | 15.0 | 20.2 | |
| WebInstruct-verified-SFT | 61.5 | 16.2 | 70.8 | 30.1 | 13.3 | 37.5 | 38.2 | |
| WebInstruct-GPT4o-SFT | 45.5 | 18.4 | 77.4 | 19.7 | 10.0 | 50.0 | 36.8 | |
| WebInstruct-CFT | 71.1 | 27.9 | 88.8 | 35.7 | 13.3 | 55.0 | 48.6 | |
| = CFT- SFTbest | 9.6 | 9.5 | 11.4 | 5.6 | 0.0 | 5.0 | 10.4 | |
| Qwen2.5-Math-7B | Base | 55.4 | 13.6 | 91.6 | 16.1 | 10.0 | 40.0 | 37.8 |
| WebInstruct-SFT | 59.0 | 13.2 | 77.4 | 19.9 | 3.3 | 37.5 | 35.1 | |
| WebInstruct-verified-SFT | 62.0 | 12.5 | 78.8 | 22.1 | 16.7 | 50.0 | 40.4 | |
| WebInstruct-GPT4o-SFT | 73.2 | 25.7 | 90.0 | 37.6 | 13.3 | 62.5 | 50.4 | |
| WebInstruct-CFT | 79.4 | 36.8 | 90.9 | 41.6 | 20.0 | 67.5 | 56.0 | |
| = CFT- SFTbest | 6.2 | 11.1 | 0.9 | 4.0 | 3.3 | 5.0 | 5.7 |
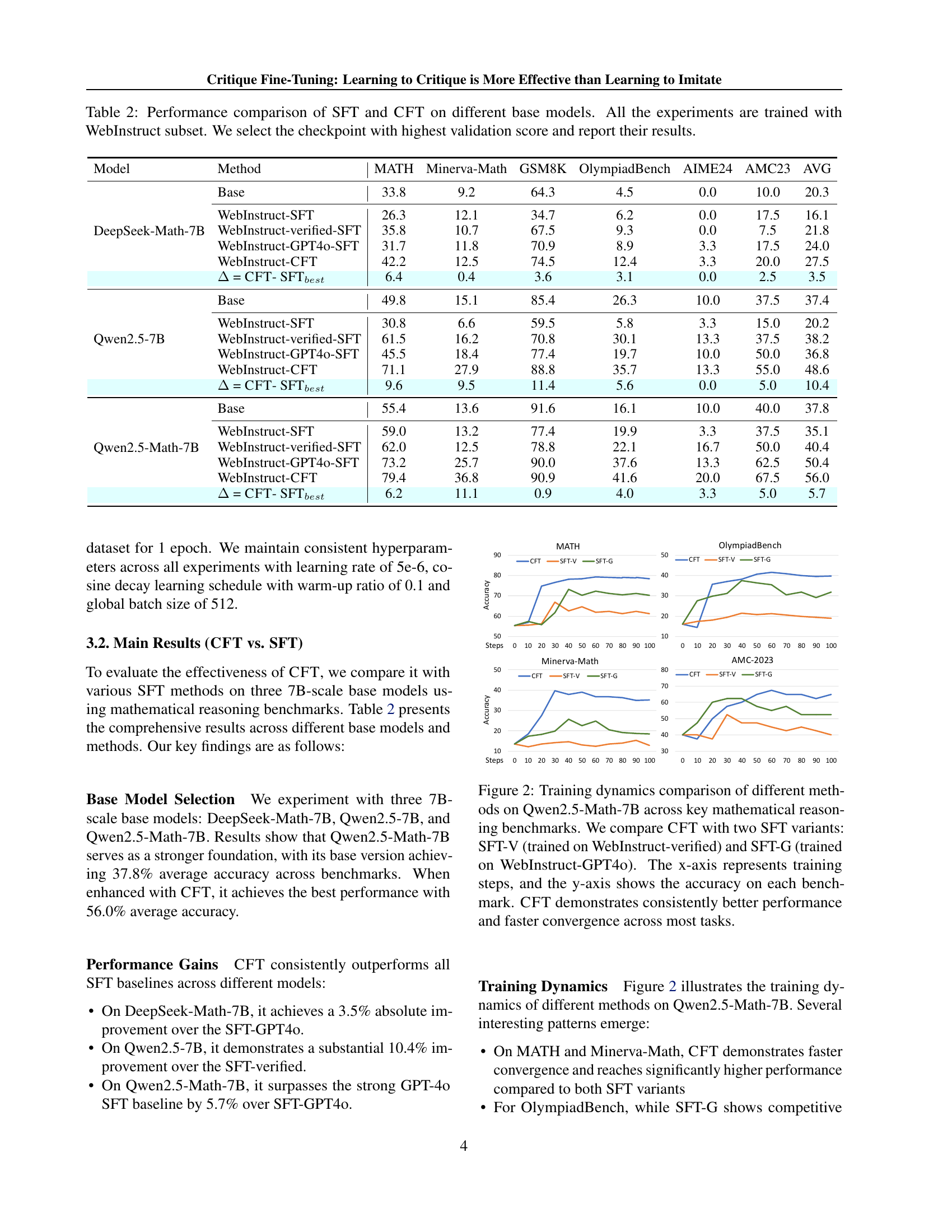
🔼 This table compares the performance of Supervised Fine-Tuning (SFT) and Critique Fine-Tuning (CFT) on three different 7B-scale base language models: DeepSeek-Math-7B, Qwen2.5-7B, and Qwen2.5-Math-7B. For each model, it shows the performance using four different training methods: standard SFT, SFT with GPT-40-validated responses, SFT using GPT-40 generated responses, and CFT. The performance is measured across six mathematical reasoning benchmarks: MATH, Minerva-Math, GSM8K, OlympiadBench, AIME24, and AMC23. The table highlights the improvement achieved by CFT over the various SFT methods. All models were trained using the WebInstruct subset, and the checkpoint with the highest validation score was selected for reporting.
read the caption
Table 2: Performance comparison of SFT and CFT on different base models. All the experiments are trained with WebInstruct subset. We select the checkpoint with highest validation score and report their results.
| Model | #Data | MATH | GPQA | TheoremQA | MMLU-Pro | OlympiadBench | AIME24 | AMC23 | AVG |
|---|---|---|---|---|---|---|---|---|---|
| Frontier Models | |||||||||
| GPT-4o (2024-08-06) | - | 81.1 | 51.6 | 54.7 | 74.7 | 43.3 | 9.3 | 47.5 | 51.7 |
| GPT-o1-mini | - | 90.0 | 60.0 | 57.2 | 80.3 | 65.3 | 56.7 | 95.0 | 72.1 |
| Other Open-sourced Reasoning LLMs | |||||||||
| Deepseek-Math-7B-Instruct | - | 44.3 | 31.8 | 23.7 | 35.3 | 13.6 | 3.3 | 15.0 | 23.9 |
| Mathstral-7B-v0.1 | - | 56.6 | 32.2 | 28.4 | 42.5 | 21.5 | 6.7 | 42.4 | 32.9 |
| NuminaMath-7B-CoT | - | 55.2 | 30.6 | 28.6 | 38.6 | 19.9 | 6.7 | 30.0 | 29.9 |
| Llama-3.1-8B-Instruct | - | 51.9 | 30.4 | 30.3 | 48.3 | 14.4 | 6.7 | 30.0 | 30.3 |
| Llama-3.1-70B-Instruct | - | 65.7 | 42.2 | 51.3 | 62.8 | 14.4 | 16.7 | 30.0 | 40.4 |
| NuminaMath-72B-CoT | - | 68.0 | 35.3 | 24.9 | 55.0 | 35.0 | 3.3 | 52.5 | 39.1 |
| Qwen2.5-Math-72B-Instruct | - | 85.9 | 49.0 | 50.3 | 60.3 | 49.0 | 30.0 | 70.0 | 56.4 |
| Initialized from Qwen2.5-Math-7B-Base | |||||||||
| Qwen2.5-Math-Base | 0 | 55.4 | 31.0 | 37.4 | 39.3 | 16.1 | 10.0 | 40.0 | 32.7 |
| Eurus-2-SFT | 230 K | 62.4 | 32.1 | 38.0 | 44.2 | 29.8 | 3.3 | 30.1 | 34.3 |
| rStar-Math@Greedy | 747 K | 78.4 | - | - | - | 47.1 | 26.7 | 47.5 | - |
| AceMath-Qwen2.5-Math | 2.3 M | 83.1 | 26.1 | 24.6 | 48.1 | 42.2 | 16.7 | 60.0 | 43.0 |
| Qwen2.5-Math-7B-Instruct | 2.5 M | 83.6 | 31.1 | 37.0 | 39.5 | 41.6 | 16.7 | 62.5 | 44.6 |
| Qwen2.5-Math-7B-CFT | 50 K | 79.4 | 39.4 | 40.4 | 47.5 | 41.6 | 20.0 | 67.5 | 48.0 |
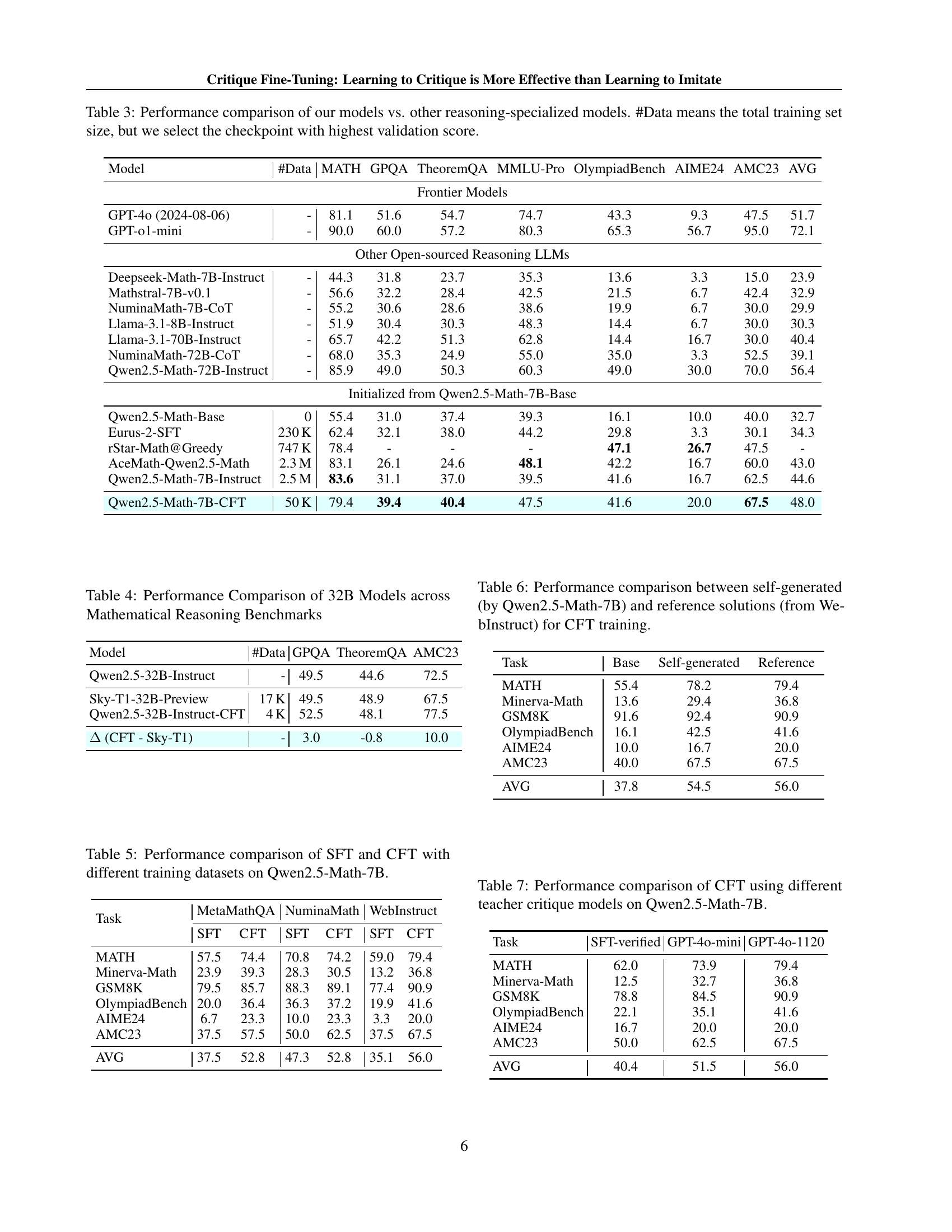
🔼 This table compares the performance of the models developed by the authors against other state-of-the-art reasoning-specialized models. The comparison is across multiple benchmarks (MATH, GPQA, TheoremQA, MMLU-Pro, OlympiadBench, AIME24, AMC23), providing a comprehensive evaluation of performance. The table includes the total size of the training dataset used for each model (#Data), highlighting the data efficiency of the authors’ approach. Note that the checkpoint with the best validation score was selected for reporting results, rather than simply using the final checkpoint after training.
read the caption
Table 3: Performance comparison of our models vs. other reasoning-specialized models. #Data means the total training set size, but we select the checkpoint with highest validation score.
| Model | #Data | GPQA | TheoremQA | AMC23 |
|---|---|---|---|---|
| Qwen2.5-32B-Instruct | - | 49.5 | 44.6 | 72.5 |
| Sky-T1-32B-Preview | 17 K | 49.5 | 48.9 | 67.5 |
| Qwen2.5-32B-Instruct-CFT | 4 K | 52.5 | 48.1 | 77.5 |
| (CFT - Sky-T1) | - | 3.0 | -0.8 | 10.0 |
🔼 This table compares the performance of two 32B language models on various mathematical reasoning benchmarks. It shows the performance of Qwen2.5-32B-Instruct-CFT (Critique Fine-Tuning) and Sky-T1-32B-Preview on GPQA, TheoremQA, and AMC23. The table highlights the data efficiency of the CFT model, which achieves competitive or superior performance using significantly less training data (4K samples) compared to Sky-T1-32B-Preview (17K samples).
read the caption
Table 4: Performance Comparison of 32B Models across Mathematical Reasoning Benchmarks
| Task | MetaMathQA | NuminaMath | WebInstruct | |||
|---|---|---|---|---|---|---|
| SFT | CFT | SFT | CFT | SFT | CFT | |
| MATH | 57.5 | 74.4 | 70.8 | 74.2 | 59.0 | 79.4 |
| Minerva-Math | 23.9 | 39.3 | 28.3 | 30.5 | 13.2 | 36.8 |
| GSM8K | 79.5 | 85.7 | 88.3 | 89.1 | 77.4 | 90.9 |
| OlympiadBench | 20.0 | 36.4 | 36.3 | 37.2 | 19.9 | 41.6 |
| AIME24 | 6.7 | 23.3 | 10.0 | 23.3 | 3.3 | 20.0 |
| AMC23 | 37.5 | 57.5 | 50.0 | 62.5 | 37.5 | 67.5 |
| AVG | 37.5 | 52.8 | 47.3 | 52.8 | 35.1 | 56.0 |
🔼 This table presents a comparison of the performance of Supervised Fine-Tuning (SFT) and Critique Fine-Tuning (CFT) methods on the Qwen2.5-Math-7B language model. The comparison is made across three different training datasets: MetaMathQA, NuminaMath, and WebInstruct. For each dataset and method, the table shows the performance on several mathematical reasoning benchmarks, including MATH, GSM8K, Minerva-Math, OlympiadBench, AIME24, and AMC23. This allows for an assessment of how the choice of training data and training method affects the model’s performance on various mathematical tasks.
read the caption
Table 5: Performance comparison of SFT and CFT with different training datasets on Qwen2.5-Math-7B.
| Task | Base | Self-generated | Reference |
|---|---|---|---|
| MATH | 55.4 | 78.2 | 79.4 |
| Minerva-Math | 13.6 | 29.4 | 36.8 |
| GSM8K | 91.6 | 92.4 | 90.9 |
| OlympiadBench | 16.1 | 42.5 | 41.6 |
| AIME24 | 10.0 | 16.7 | 20.0 |
| AMC23 | 40.0 | 67.5 | 67.5 |
| AVG | 37.8 | 54.5 | 56.0 |
🔼 This table compares the performance of Critique Fine-Tuning (CFT) using two different sources of solutions for training: solutions generated by the Qwen2.5-Math-7B model itself and reference solutions taken from the WebInstruct dataset. The comparison is made across multiple mathematical reasoning benchmarks, showing the average performance and the performance on each individual benchmark. This helps assess the impact of the quality of training data on the effectiveness of the CFT approach.
read the caption
Table 6: Performance comparison between self-generated (by Qwen2.5-Math-7B) and reference solutions (from WebInstruct) for CFT training.
| Task | SFT-verified | GPT-4o-mini | GPT-4o-1120 |
|---|---|---|---|
| MATH | 62.0 | 73.9 | 79.4 |
| Minerva-Math | 12.5 | 32.7 | 36.8 |
| GSM8K | 78.8 | 84.5 | 90.9 |
| OlympiadBench | 22.1 | 35.1 | 41.6 |
| AIME24 | 16.7 | 20.0 | 20.0 |
| AMC23 | 50.0 | 62.5 | 67.5 |
| AVG | 40.4 | 51.5 | 56.0 |
🔼 This table compares the performance of Critique Fine-Tuning (CFT) using different teacher critique models on the Qwen2.5-Math-7B language model. It shows how the choice of critique model (GPT-40-mini vs. GPT-40-1120) affects the final model’s performance across several mathematical reasoning benchmarks (MATH, Minerva-Math, GSM8K, OlympiadBench, AIME24, AMC23). This allows for an assessment of CFT’s robustness to different critique model strengths.
read the caption
Table 7: Performance comparison of CFT using different teacher critique models on Qwen2.5-Math-7B.
| Method | Temperature | MATH | Minerva-Math |
| Direct inference | 0.0 | 79.4 | 36.8 |
| 0.1 | 78.8 | 35.9 | |
| 0.3 | 77.5 | 34.7 | |
| 0.6 | 75.2 | 33.1 | |
| Single-pass self-critique | 0.1 | 77.2 | 33.7 |
| 0.3 | 76.1 | 32.2 | |
| 0.6 | 73.5 | 31.3 | |
| Two-stage self-critique | 0.1 | 77.9 | 35.2 |
| 0.3 | 75.8 | 32.4 | |
| 0.6 | 74.6 | 31.5 |
🔼 This table compares the performance of three different inference methods: direct inference, single-pass self-critique, and two-stage self-critique. Each method is tested at various temperature settings (0.0, 0.1, 0.3, 0.6), which affect the randomness of the model’s output. The performance is measured on two mathematical reasoning benchmarks: MATH and Minerva-Math. The results show how the choice of inference method and temperature setting impact the accuracy of the model’s solutions.
read the caption
Table 8: Performance comparison of different inference methods across various temperature settings.
Full paper#