TL;DR#
Current discrete diffusion models for language modeling have limitations in exploiting iterative refinement due to signal loss during transitions between discrete states, while existing continuous approaches lack performance. Also, the unclear link between discrete and continuous diffusion models hinders development.
This research introduces Riemannian Diffusion Language Model (RDLM), a continuous diffusion framework that leverages the geometry of the underlying categorical distribution, effectively linking discrete and continuous modeling. RDLM’s novel simulation-free training and generalization to various data modalities (images, DNA sequences) showcase superior performance compared to previous methods, reaching near autoregressive model performance. This advance has significant implications for generative modeling and various related fields.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in natural language processing and machine learning because it bridges the gap between discrete and continuous diffusion models for discrete data. It introduces a novel framework that outperforms existing methods, offering a more efficient and effective approach to generative modeling. The simulation-free training method and generalization to various data modalities open exciting avenues for future work, potentially impacting various applications.
Visual Insights#
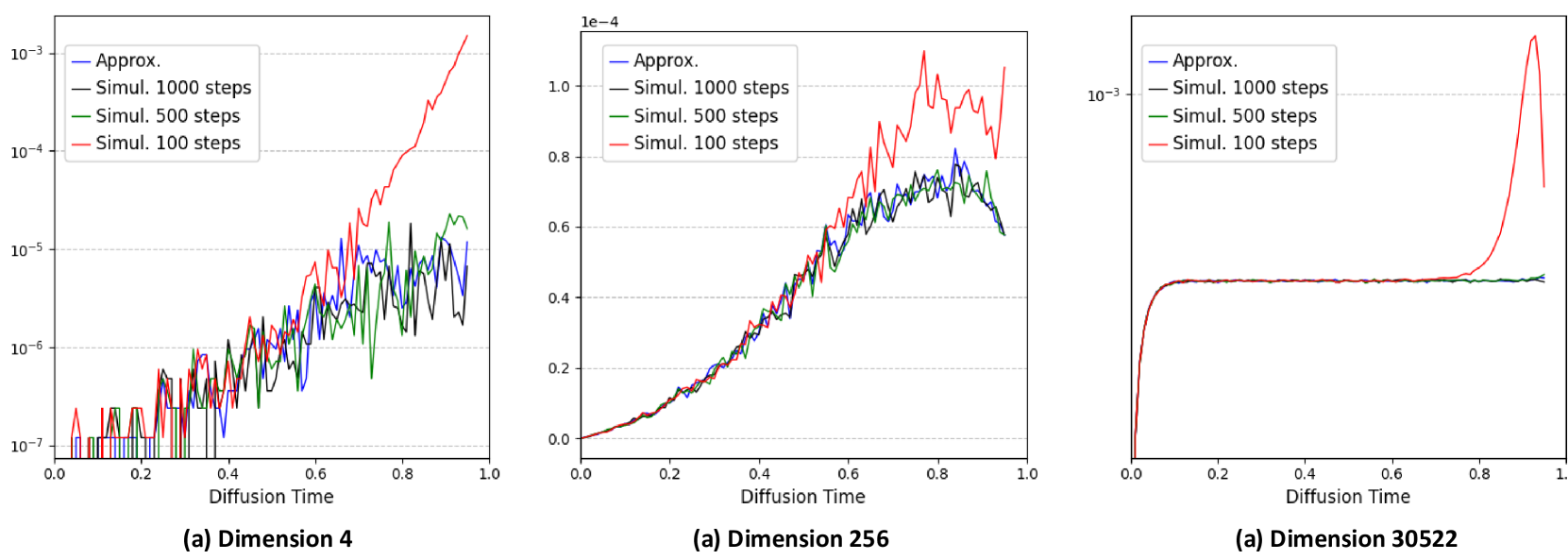
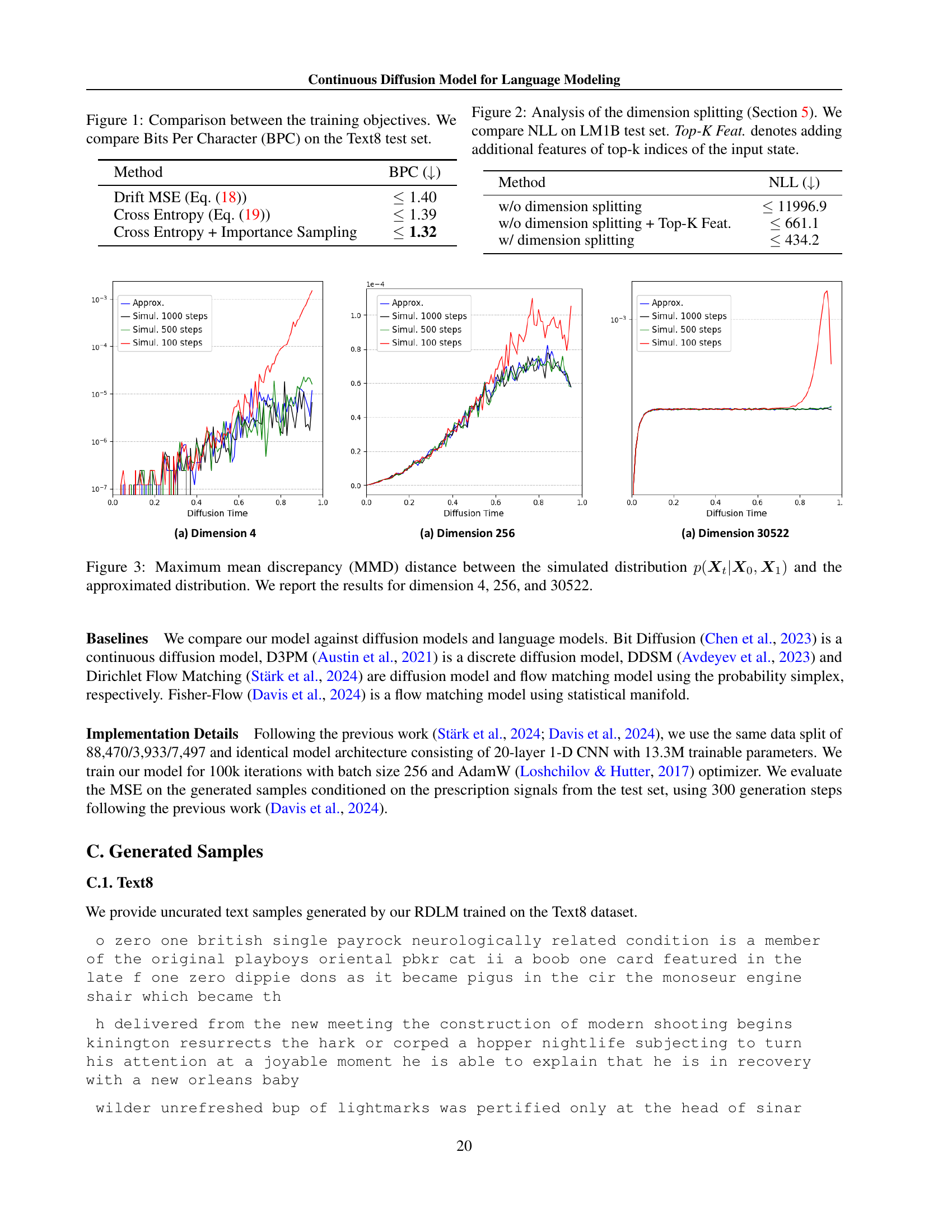
🔼 This figure compares the performance of three different training objective functions for a continuous diffusion model on the Text8 dataset. The three objectives are minimizing the mean squared error of the drift approximation, minimizing the cross-entropy between the predicted probability vector and the target one-hot vector, and the cross-entropy with importance sampling. The results are presented as Bits Per Character (BPC) on the Text8 test set. The figure shows that the cross-entropy method with importance sampling achieves the best performance, followed by cross-entropy, with the mean squared error performing the worst.
read the caption
Figure 1: Comparison between the training objectives. We compare Bits Per Character (BPC) on the Text8 test set.
| Method | BPC () |
| Autoregressive | |
| IAF/SCF | 1.88 |
| AR Argmax Flow | 1.39 |
| Transformer AR | 1.23 |
| Discrete Flow | 1.23 |
| Any-order Autoregressive | |
| ARDM | 1.43 |
| MAC | 1.40 |
| Discrete Diffusion | |
| Multinomial Diffusion | 1.72 |
| D3PM Uniform | 1.61 |
| D3PM Absorb | 1.45 |
| SEDD Absorb | 1.39 |
| MDLM | 1.40 |
| MD4 | 1.37 |
| Continuous Diffusion | |
| Plaid | 1.48 |
| BFN | 1.41 |
| RDLM (Ours) | 1.32 |
🔼 This table presents a comparison of different language models’ performance on the Text8 benchmark dataset, measured by Bits Per Character (BPC). It includes both autoregressive and diffusion models, allowing for a direct comparison of these two major approaches to language modeling. The lowest BPC value indicates the best performance. The results for each model are sourced directly from their respective papers. Bold values highlight the best-performing model within either the autoregressive or diffusion model categories.
read the caption
Table 1: Bits Per Character (BPC) results on Text8 test set. Results are taken from the corresponding papers. Bold denotes the best result in autoregressive or diffusion models.
In-depth insights#
Discrete Diffusion Models#
Discrete diffusion models offer a compelling approach to generative modeling of discrete data, leveraging the power of iterative refinement inherent in diffusion processes. Unlike autoregressive models that generate data sequentially, discrete diffusion models process the entire sequence in parallel, enabling bidirectional generation and faster sampling. However, these models face challenges in fully exploiting iterative refinement because signals can be lost during transitions between discrete states. This limitation arises from the inherent stochasticity of the Markov chains used to model the process, leading to jumps between states that may obscure valuable information. Several methods exist for mitigating this, such as carefully designed transition matrices (e.g., masked diffusion), but improvements are continually sought to bridge the performance gap with autoregressive models and enhance controllability over the generative process.
Riemannian Diffusion#
The concept of “Riemannian Diffusion” in the context of language modeling presents a novel approach to address the limitations of existing diffusion models when applied to discrete data. Traditional diffusion models excel in continuous domains but struggle with discrete data due to the loss of information during the transition between states. A key innovation is leveraging the geometry of the underlying categorical distribution, specifically using the statistical manifold and its Riemannian geometry. This allows the model to not just treat discrete tokens as points but to consider the relationships between them based on their inherent probabilities, effectively moving the process from a discrete jump between states to a continuous flow on a hypersphere. This continuous flow allows for smoother refinement during the generative process, improving performance and controllability. Radial symmetry is employed to simplify the parameterization and training process, which avoids the computational challenges of simulations on complex manifolds. The framework thus elegantly bridges discrete and continuous perspectives, resulting in a model that better utilizes iterative refinement and potentially surpasses the performance of existing discrete diffusion models.
Simulation-Free Training#
The concept of ‘Simulation-Free Training’ in the context of diffusion models addresses a critical computational bottleneck. Traditional training methods often require computationally expensive simulations of stochastic processes, particularly when dealing with complex, high-dimensional spaces. Simulation-free training aims to bypass these computationally expensive simulations, instead relying on efficient mathematical approximations or alternative training strategies. This approach is crucial for scalability, making it possible to train these models on large datasets and complex problems that would otherwise be intractable. Key to the success of simulation-free training is finding accurate, yet efficient approximations of the underlying stochastic processes. This typically involves leveraging the mathematical properties of the system, such as symmetries or specific probability distributions, to simplify the calculations. One common strategy is to replace the simulation with a closed-form solution or a tractable approximation that captures the essential characteristics of the stochastic process. This might involve using variational inference or devising clever parameterizations that allow for direct computation of gradients without explicit simulation. Another important aspect is the careful design of the training objective and algorithm. The training algorithm needs to be designed such that it accurately reflects the behavior of the approximated system and that the training objective is effectively optimized within the simulation-free framework. This often requires careful consideration of the trade-off between accuracy and computational efficiency. Successfully developing a simulation-free training method for diffusion models is a significant advancement, opening the door to broader applications and accelerating the pace of research in this area.
Generative Process#
The generative process in this research paper is a crucial component, detailing how the model produces new data instances. It is a continuous diffusion model, meaning it operates in a continuous space rather than a discrete one. This contrasts with discrete diffusion models, which often face limitations in fully exploiting iterative refinement. The model leverages the geometry of the underlying statistical manifold, specifically the hypersphere, which offers several advantages. The use of radial symmetry simplifies parameterization and training, leading to a simulation-free approach. The framework generalizes existing discrete models and incorporates the concept of a continuous flow on the manifold, enabling the model to smoothly transition between states and correct wrong predictions during the process. A key innovation is the simulation-free training scheme, making it efficient and scalable. The design addresses high-dimensionality issues, enhancing the effectiveness of the method, particularly for large vocabulary tasks. The continuous nature of the process and the incorporation of geometric information allow for a more nuanced generation process, potentially surpassing discrete methods in terms of performance and controllability. The model’s ability to learn complex relationships is a key strength, but exploring the limitations of its continuous representation relative to real-world data remains an area for future investigation.
Future Work#
The paper’s ‘Future Work’ section hints at several promising research avenues. Extending the model to handle autoregressive-like generation is crucial, potentially improving the model’s efficiency and controllability by strategically adjusting the noise schedule to guide token generation sequentially, mimicking autoregressive models’ strengths. Exploring different noise schedules for varying positions within a sequence could further refine this approach. Beyond language, the authors suggest applying RDLM to diverse modalities. The success of continuous diffusion models in image generation and molecular design strongly suggests that RDLM’s adaptation to these areas holds substantial potential, requiring further investigation into effective data representations and training strategies within these new contexts. Finally, the integration of guidance methods from continuous diffusion models for enhanced control over the generation process warrants exploration, promising more directed and refined outputs in various applications.
More visual insights#
More on tables
| Method | # Param. | PPL () |
| Autoregressive | ||
| Transformer-X Base | 0.46B | 23.5 |
| 100M | 21.5 | |
| Transformer | 110M | 22.32 |
| Discrete Diffusion | ||
| BERT-Mouth | 110M | 142.89 |
| D3PM Absorb | 70M | 76.90 |
| DiffusionBert | 110M | 63.78 |
| SEDD | 110M | 32.79 |
| MDLM | 110M | 27.04 |
| Continuous Diffusion | ||
| Diffusion-LM | 80M | 118.62 |
| RDLM (Ours) | 110M | 29.72 |
🔼 This table presents the test perplexity (PPL) scores achieved by various language models on the LM1B benchmark dataset. It compares both autoregressive and diffusion models, highlighting the performance of different approaches, including both discrete and continuous diffusion models. Baseline results are included from Sahoo et al. (2024) for reference.
read the caption
Table 2: Test perplexity (PPL) results on LM1B dataset. Baseline results are taken from Sahoo et al. (2024).
| Method | # Param. | BPD () |
| Autoregressive | ||
| PixelRNN | 3.00 | |
| Gated PixelCNN | 3.03 | |
| PixelCNN++ | 53M | 2.92 |
| PixelSNAIL | 46M | 2.85 |
| Image Transformer | 2.90 | |
| Sparse Transformer | 59M | 2.80 |
| Discrete Diffusion | ||
| D3PM Absorb | 37M | 4.40 |
| D3PM Gauss | 36M | 3.44 |
| LDR | 36M | 3.59 |
| MD4 | 28M | 2.78 |
| Continuous Diffusion | ||
| RDLM (Ours) | 35M | 2.74 |
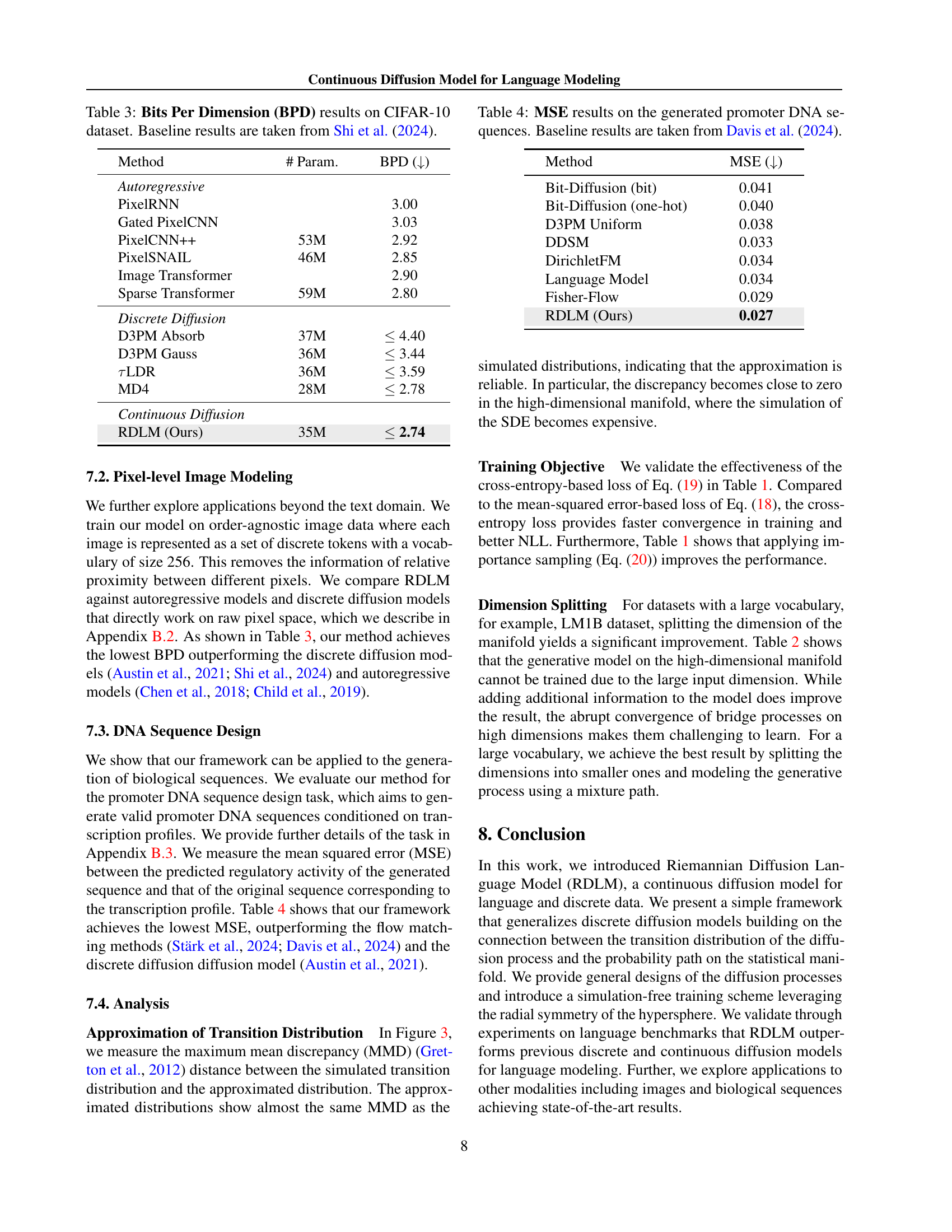
🔼 This table presents a comparison of Bits Per Dimension (BPD) achieved by various generative models on the CIFAR-10 image dataset. It specifically highlights the performance of different approaches, including autoregressive models and discrete diffusion models, as well as the model proposed in the paper. The baseline results are taken from a prior publication by Shi et al. (2024), allowing for a direct comparison of the presented method against state-of-the-art techniques. Lower BPD values indicate better performance in image generation.
read the caption
Table 3: Bits Per Dimension (BPD) results on CIFAR-10 dataset. Baseline results are taken from Shi et al. (2024).
| Method | MSE () |
| Bit-Diffusion (bit) | 0.041 |
| Bit-Diffusion (one-hot) | 0.040 |
| D3PM Uniform | 0.038 |
| DDSM | 0.033 |
| DirichletFM | 0.034 |
| Language Model | 0.034 |
| Fisher-Flow | 0.029 |
| RDLM (Ours) | 0.027 |
🔼 This table presents the mean squared error (MSE) achieved by different models in generating promoter DNA sequences. The MSE is a measure of the difference between the predicted regulatory activity of the generated sequences and the actual activity of the original sequences. Lower MSE values indicate better performance. The results are compared to the baselines established in Davis et al. (2024), providing a benchmark for evaluating the performance of the proposed method against existing state-of-the-art techniques.
read the caption
Table 4: MSE results on the generated promoter DNA sequences. Baseline results are taken from Davis et al. (2024).
Full paper#