Eager Updates For Overlapped Communication and Computation in DiLoCo

2502.12996

Satyen Kale et el.

🤗 2025-02-19

TL;DR
#

Training extremely large language models requires distributed computing, but communication between machines can be a major bottleneck. Existing methods like DiLoCo reduce communication but still suffer from delays due to synchronization steps. This creates idle time on the computing machines, wasting resources and slowing down the overall training process.

This paper introduces a new technique called “eager updates” that overlaps communication with computation in the DiLoCo algorithm. Eager updates use locally computed gradients to start the next step before waiting for all gradients to be collected, thus greatly reducing idle time. Experiments show that eager updates are highly efficient, offering performance similar to standard DiLoCo while significantly improving compute utilization, particularly in low-bandwidth situations.

Key Takeaways
#

Why does it matter?
#

This paper is crucial for researchers in distributed machine learning, especially those working with large language models. It directly addresses the communication bottleneck that hinders efficient training of large models across multiple machines. The proposed method, eager updates, offers a practical solution to improve training speed and resource utilization, which is highly relevant to current research trends in scaling deep learning. It also opens up new avenues for optimizing distributed training algorithms, inviting further exploration in this important field.

Visual Insights
#

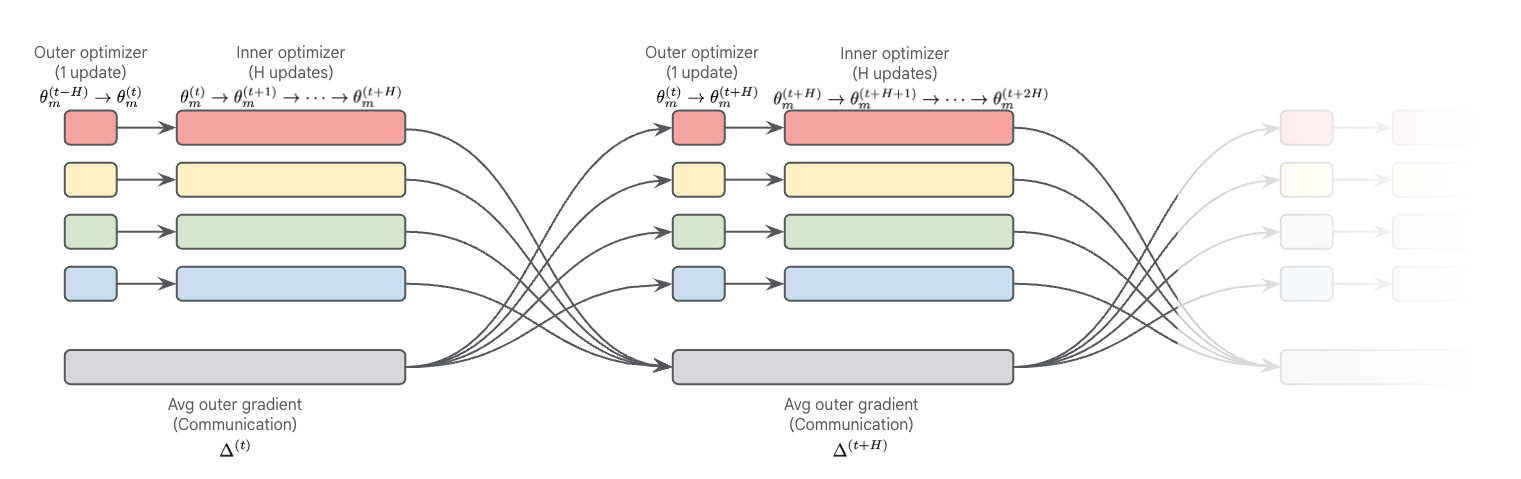
🔼 Figure 1 illustrates the data flow and operations within the standard DiLoCo algorithm. DiLoCo divides the training process into inner and outer optimization phases. In the inner phase, four workers (shown in the diagram) concurrently perform multiple optimization steps using their local data. This phase involves only local computation. Then, in the outer phase, these workers communicate their updates (outer gradients) and collectively average them. This averaged outer gradient is then applied to update the global model parameters, thus completing one iteration. The process repeats, alternating between parallel inner optimization and synchronized outer gradient averaging.
read the caption
Figure 1: Data flow and operations in standard DiLoCo. Here, 4 workers execute in parallel and alternate sequentially computation (the outer and inner optimization steps) and communication (averaging outer gradients across workers).

Method	Token Budget	Hours spent w/ $+\infty$ Gbits/s	Hours spent w/ 1 Gbits/s	Terabytes exchanged	Eval Loss $\downarrow$	HellaSwag $\uparrow$	Piqa $\uparrow$	Arc Easy $\uparrow$
Data-Parallel	25B	0.67	109	441	2.67	42.09	67.35	40.42
	100B	2.7	438	1,767	2.52	49.78	69.15	44.03
	250B	6.75	1097	4,418	2.45	53.86	70.45	44.21
Streaming DiLoCo with 1-inner-step overlap	25B	0.67	0.88	1.10	2.66	42.08	67.46	38.42
	100B	2.7	3.5	4.42	2.51	49.98	69.96	44.03
	250B	6.75	8.75	11.05	2.45	54.24	71.38	41.92
Streaming DiLoCo with 1-outer-step overlap	25B	0.67	0.67	1.10	2.69	40.51	66.87	39.12
	100B	2.7	2.7	4.42	2.53	49.48	68.82	41.05
	250B	6.75	6.75	11.05	2.46	53.30	69.00	41.93

🔼 This table compares the performance of Data-Parallel and the proposed method (1-outer-step eager overlap) on the Dolma dataset when training a 1-billion parameter model. The key finding is that the proposed method achieves comparable or slightly better performance while requiring significantly less communication. Specifically, it reduces the total bits exchanged by a factor of 400 and the peak bandwidth by a factor of 8. Importantly, this improved efficiency is achieved while allowing communication latency to extend to the length of a complete inner optimization phase.
read the caption
Table 1: Overtraining Data-Parallel and our method on Dolma with a 1 billion parameters model. The latter performs slightly better despite exchanging in total 400×400\times400 × fewer bits, reducing the peak bandwidth by 8×8\times8 ×, and with a significantly relaxed training communication latency constraint: allowing communication to be as long as a full inner optimization phase.

In-depth insights
#

Eager Updates’ Impact
#

The impact of eager updates in the context of distributed model training, specifically within the DiLoCo framework, is multifaceted. Eager updates significantly improve compute utilization by overlapping communication and computation. This is particularly beneficial in settings with low bandwidth between workers, a common challenge in large-scale distributed training. The eager approach, while showing competitive performance to standard DiLoCo in terms of training loss, demonstrates a considerable reduction in the required bandwidth to achieve comparable compute utilization. This is crucial because it reduces the overall training time by minimizing idle periods where workers wait for inter-worker communication to complete. However, a naive implementation of overlapped updates can lead to worse convergence, emphasizing the importance of the proposed ’eager’ modification which skillfully leverages local gradients as a proxy for the final aggregated outer gradients. The experimental results highlight the tradeoff between bandwidth efficiency and speed of convergence, showing that this tradeoff is model and dataset size dependent. While eager updates do not always achieve lower loss than other approaches, the substantial gains in compute utilization and reduced bandwidth requirements make it a powerful technique for large-scale distributed model training.

Overlapping Comm
#

The concept of “Overlapping Comm,” likely referring to overlapping communication with computation, is a crucial optimization strategy in distributed training, especially for large language models. The core idea is to reduce the idle time during communication phases by performing computation concurrently. This is particularly beneficial in settings with high computational power but limited bandwidth between workers, which is a common constraint in large-scale distributed training. The paper likely explores different techniques to achieve this overlap, such as initiating the next inner optimization phase before the current outer communication phase is fully completed, potentially using locally computed gradients as proxies for fully aggregated results until the latter becomes available. The effectiveness of such techniques is evaluated based on various factors, including training speed, convergence, and compute utilization. The results likely demonstrate that carefully designed overlapping communication strategies can significantly enhance the efficiency of distributed training while maintaining performance comparable to standard methods that lack the overlap. Eager updates, a particular variant of overlapping communication, may be introduced and investigated, showcasing its competitive performance and compute efficiency compared to other approaches.

DiLoCo Algorithm
#

The DiLoCo algorithm is a distributed optimization method particularly effective for training large language models. It cleverly divides the training process into inner and outer optimization phases. The inner phase involves independent optimization steps on local data by multiple workers, minimizing communication overhead. The outer phase synchronizes these local updates through an all-reduce operation, updating global parameters. This two-stage approach significantly reduces communication compared to traditional data-parallel methods. However, the synchronization step can become a bottleneck in low-bandwidth settings. This paper introduces eager updates, a modification that aims to alleviate this issue by overlapping communication with computation, allowing the outer optimization to commence before the previous all-reduce operation is complete. This overlap is achieved by using locally computed outer gradients as a proxy for the full all-reduced gradients, thereby reducing idle time. Eager updates demonstrate competitive performance with standard DiLoCo in low-bandwidth scenarios, improving compute efficiency, but further research into convergence guarantees and optimal hyperparameter settings is recommended.

Large-Scale Training
#

Large-scale training of large language models (LLMs) presents significant challenges. Computational resources required are enormous, demanding powerful hardware and infrastructure. Data requirements are equally massive, necessitating vast datasets for effective training. Communication overhead becomes a major bottleneck in distributed settings, as massive amounts of data need to be transferred between numerous machines. Techniques to overcome these challenges include model parallelism, data parallelism, pipeline parallelism, and various optimization strategies. Efficient communication protocols are crucial for reducing the communication bottleneck. Quantized communication methods reduce the bandwidth needed, but at the potential cost of accuracy. Overlapping communication with computation is a key strategy to improve efficiency, and the research paper explores this through the use of eager updates. Algorithm design plays a critical role, with methods like DiLoCo attempting to reduce communication needs. Scalability is paramount, with algorithms needing to perform effectively across different hardware configurations and model sizes. Overtraining issues might arise due to large datasets and computational power, so careful monitoring and techniques are needed. Hardware advancements, like specialized AI accelerators, are critical to enabling large-scale training. Ultimately, successful large-scale training requires careful integration of efficient algorithms, optimized hardware, and effective communication strategies.

Future Directions
#

Future research could explore several promising avenues. Extending the eager update mechanism to other distributed optimization algorithms beyond DiLoCo would broaden its applicability and impact. Investigating the theoretical convergence properties of eager updates under various network conditions and model architectures is crucial for establishing its robustness. Developing more sophisticated techniques for handling stragglers in the distributed setting would further enhance the efficiency and stability of the proposed method. Additionally, exploring the interplay between eager updates and different quantization methods could lead to significant improvements in communication efficiency. Finally, a deeper investigation into the optimal choice of hyperparameters, such as the synchronization frequency and the number of inner optimization steps, could unlock further performance gains.

More visual insights
#

More on figures

🔼 Figure 2 illustrates the process of DiLoCo with delayed outer gradients. Multiple workers perform inner optimization steps concurrently. The communication for averaging the outer gradients happens in parallel with the next inner optimization phase. The application of the averaged outer gradient in the outer optimizer is delayed until after the next inner phase completes. This overlapping of communication and computation reduces idle time.
read the caption
Figure 2: Data flow and operations in DiLoCo with delayed outer gradients. Here, 4 workers execute optimization steps in parallel with each other, as well as with the communication required for averaging outer gradients. This is accomplished by delaying the application of the averaged outer gradient in the outer optimizer.

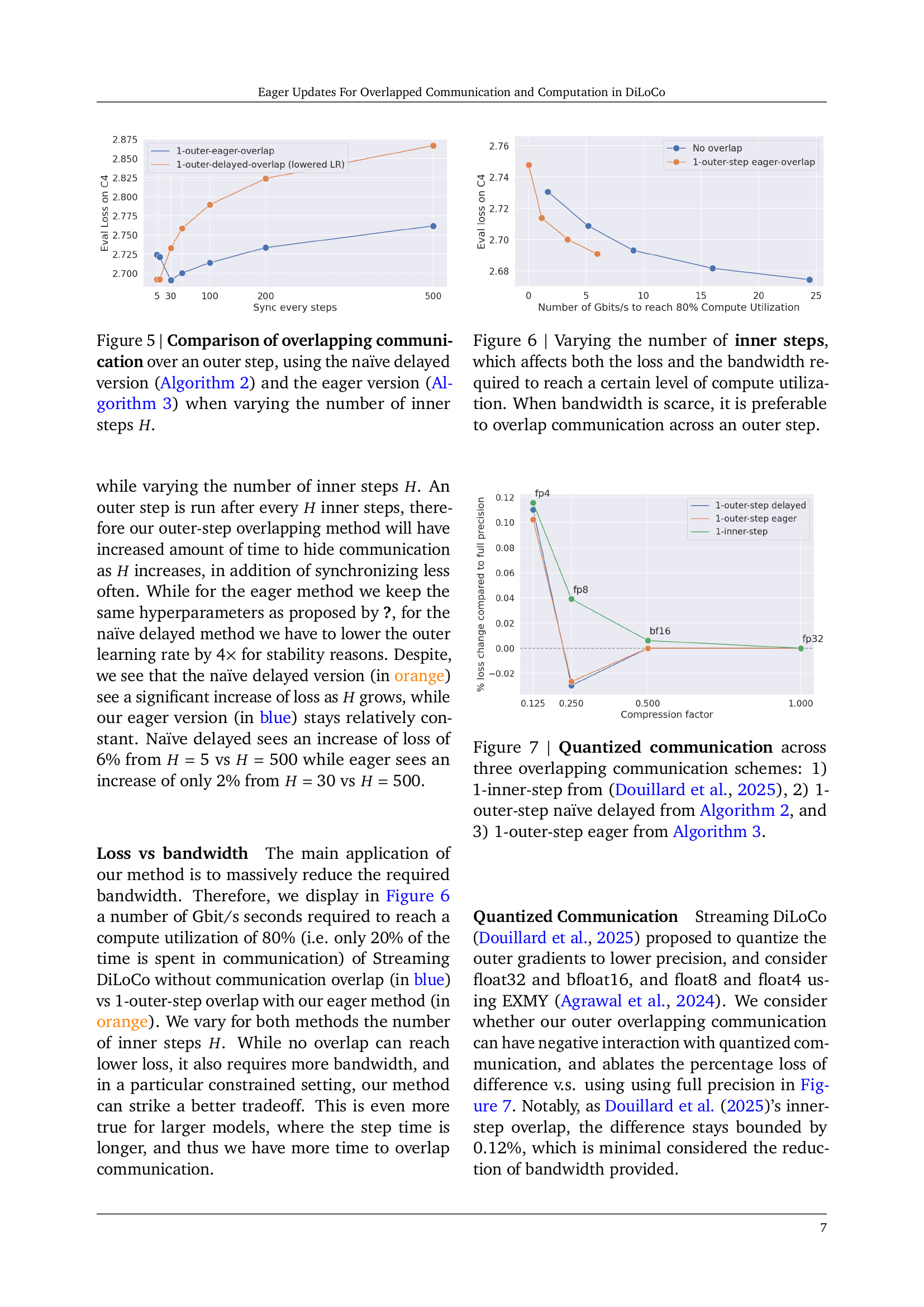
🔼 The figure shows the compute utilization simulated across a range of bandwidth for a model with 1 billion parameters. Compute utilization is defined as the percentage of time spent on computation versus communication. The plot illustrates how different methods (Data-Parallel, Streaming DiLoCo with various overlapping strategies) perform across different bandwidths, revealing the impact of bandwidth limitations on compute efficiency. It highlights the improvements achieved using the proposed eager updates method in reducing the communication overhead and maximizing compute utilization, particularly in low-bandwidth scenarios.
read the caption
(a) 1B parameters model.

🔼 This figure displays the compute utilization simulated across various bandwidths for a 10 billion parameter model. Compute utilization is defined as the percentage of time spent on computation, with the remaining time dedicated to communication. The graph compares different distributed training methods, illustrating how the compute utilization changes as bandwidth varies. This helps visualize the efficiency of each method in balancing computational work with communication overhead.
read the caption
(b) 10B parameters model

🔼 This figure shows the compute utilization simulated across a range of bandwidth for a model with 100 billion parameters. Compute utilization is defined as the percentage of time spent on computation versus communication. The figure compares different distributed training methods: Data-Parallel, Streaming DiLoCo (with various overlap configurations for inner and outer optimization steps), and Streaming DiLoCo with 1-inner-step and 1-outer-step overlapped forward and backward passes. It demonstrates the effect of bandwidth on compute utilization for each method, showing that the proposed methods significantly improve compute utilization, especially at lower bandwidths.
read the caption
(c) 100B parameters model

🔼 This figure illustrates the compute utilization achieved by various distributed training methods across a range of network bandwidths. Compute utilization represents the percentage of time spent on actual computation versus communication. The results show that the proposed ’eager updates’ method significantly improves compute utilization, achieving nearly 95% utilization for models with 1B, 10B, and 100B parameters, even with relatively low bandwidth (1-5 Gbit/s). In contrast, the standard data-parallel method requires much higher bandwidth (100-300 Gbit/s) to achieve comparable utilization.
read the caption
Figure 3: Compute Utilization simulated across a range of bandwidth. A compute utilization of 0.8 means 80% of the time is spent in computation, and 20% in communication. Our best method reaches a compute utilization of 95% for models 1B, 10B, and 100B with a bandwidth roughly constant between 1 and 5 Gbit/s. Data-Parallel on the other hand requires 100, 200, and 300Gbit/s.

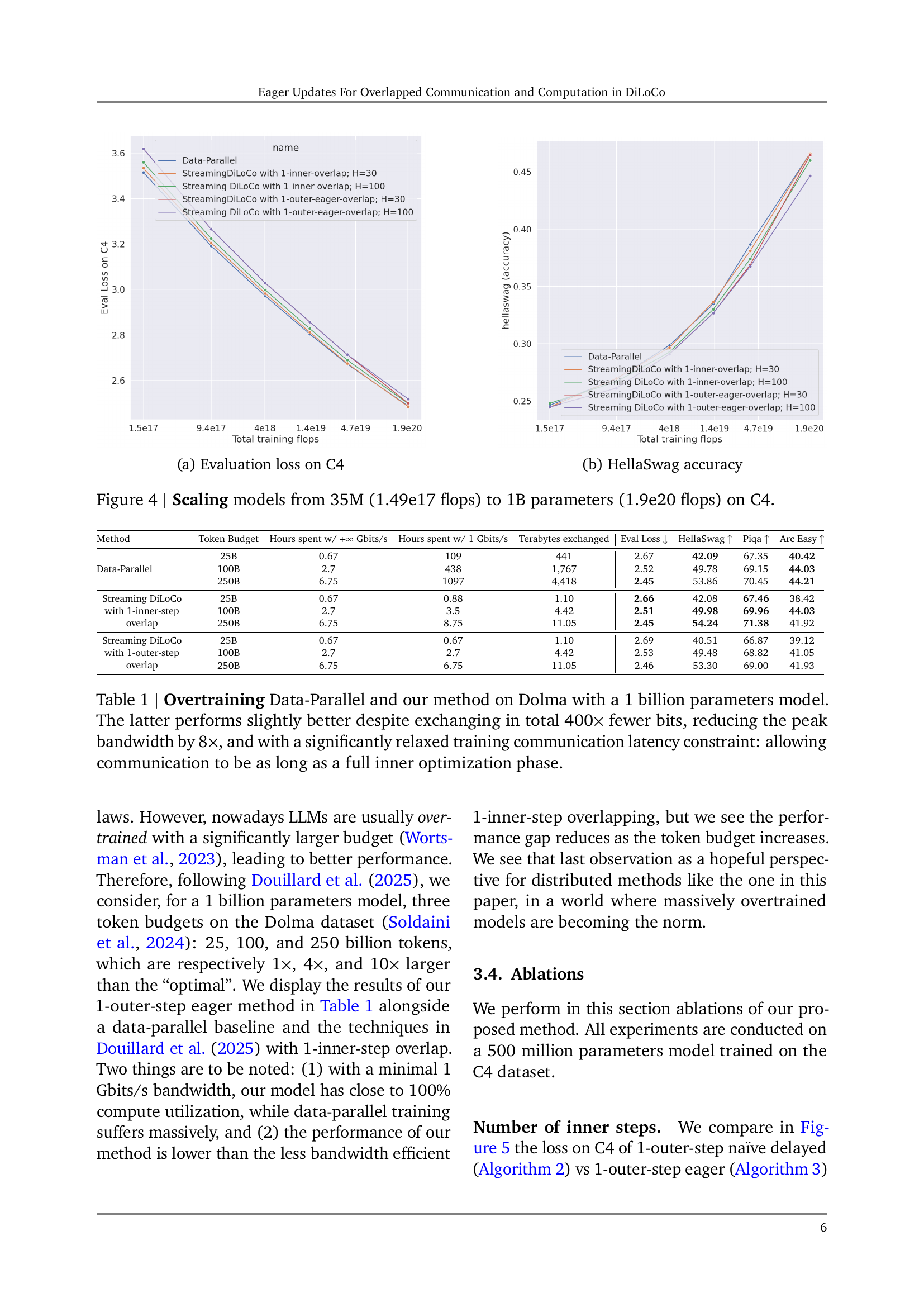
🔼 The figure shows the evaluation loss on the C4 dataset for various models, comparing the performance of different distributed training methods. The x-axis represents the total training FLOPs, and the y-axis represents the evaluation loss. This provides insights into how different training methods scale with model size and computational resources.
read the caption
(a) Evaluation loss on C4

🔼 The plot shows how the HellaSwag accuracy changes as the total training FLOPS increases for different distributed training methods. The x-axis represents the total number of floating point operations (FLOPs) performed during training, while the y-axis shows the HellaSwag accuracy achieved. Each line corresponds to a different training method: Data-Parallel, Streaming DiLoCo with 1-inner-step overlap (H=30 and H=100), and Streaming DiLoCo with 1-outer-eager-overlap (H=30 and H=100). The figure illustrates how the accuracy improves as the total training FLOPS increases, but at different rates for each training method, providing insights into their comparative performance and efficiency at various scales.
read the caption
(b) HellaSwag accuracy

🔼 This figure displays scaling results for language models trained on the C4 dataset, demonstrating model performance across different scales. The x-axis represents the total number of training FLOPs (floating-point operations), ranging from 1.49e17 for the 35M parameter model to 1.9e20 for the 1B parameter model. The y-axis shows two key performance metrics: evaluation loss on the C4 dataset (Figure 4a) and HellaSwag accuracy (Figure 4b). Each line represents a different training method. The purpose is to visualize how model performance (loss and accuracy) changes with model size, comparing various distributed training methods.
read the caption
Figure 4: Scaling models from 35M (1.49e17 flops) to 1B parameters (1.9e20 flops) on C4.

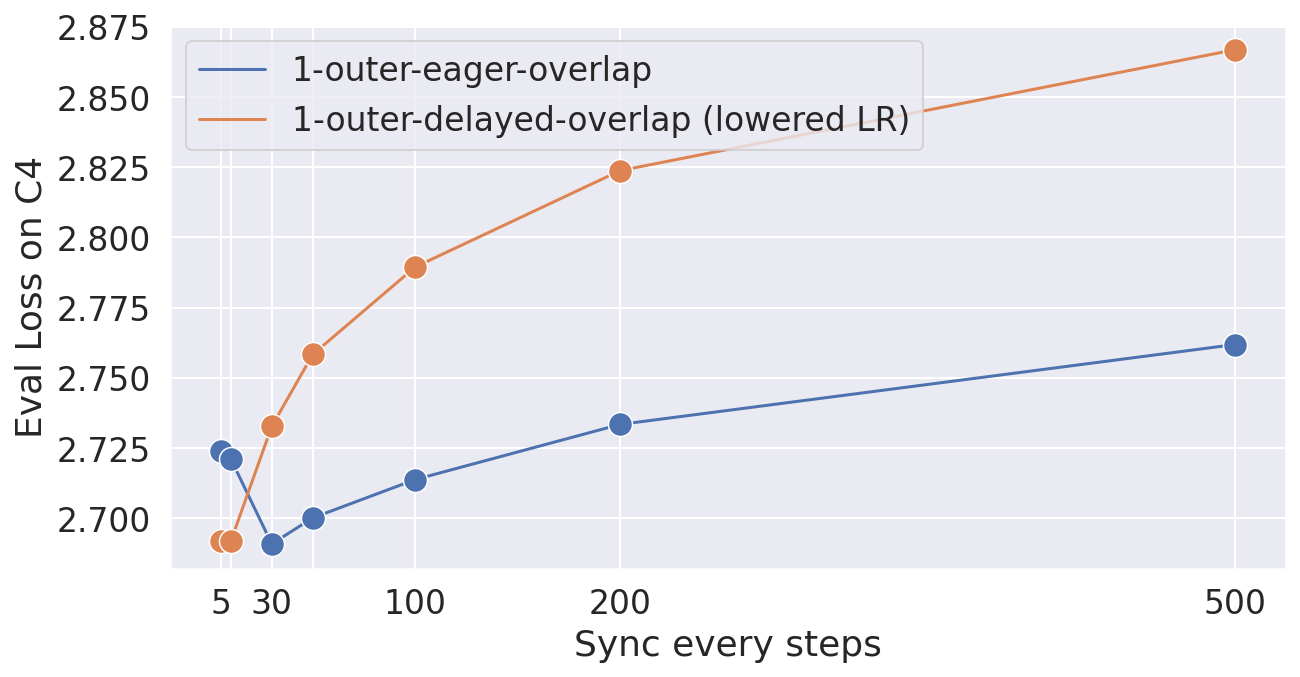
🔼 This figure compares two approaches for overlapping communication with computation in DiLoCo, a distributed optimization method. The x-axis represents the number of inner optimization steps (H) performed before a synchronization step. The y-axis shows the evaluation loss on a benchmark dataset. The blue line shows the performance of the ’eager updates’ method, which starts the next inner optimization step immediately after sending the outer gradient, using a local outer gradient estimate as a proxy. The orange line shows the performance of the ’naïve delayed outer gradients’ method, which only starts the next inner step after the synchronization step is complete. The results show that the eager update strategy maintains performance even with a large H, while the naive delayed version suffers significantly increased loss as H grows.
read the caption
Figure 5: Comparison of overlapping communication over an outer step, using the naïve delayed version (Algorithm 2) and the eager version (Algorithm 3) when varying the number of inner steps H𝐻Hitalic_H.

More on tables

Communication overlap	Tolerated latency in sec. $\uparrow$	Eval Loss $\downarrow$	HellaSwag $\uparrow$	Piqa $\uparrow$	Arc-Easy $\uparrow$
No overlap	0	2.67	38.26	66.59	34.91
1-inner-step	0.08	2.67	37.96	66.10	36.14
1-outer-step delayed	2.4	3.01	29.40	60.93	34.73
1-outer-step delayed, lowered LR	2.4	2.73	35.83	64.96	34.21
1-outer-step eager	2.4	2.69	37.52	66.86	34.91
2-outer-steps eager	4.8	2.73	36.47	64.85	35.43

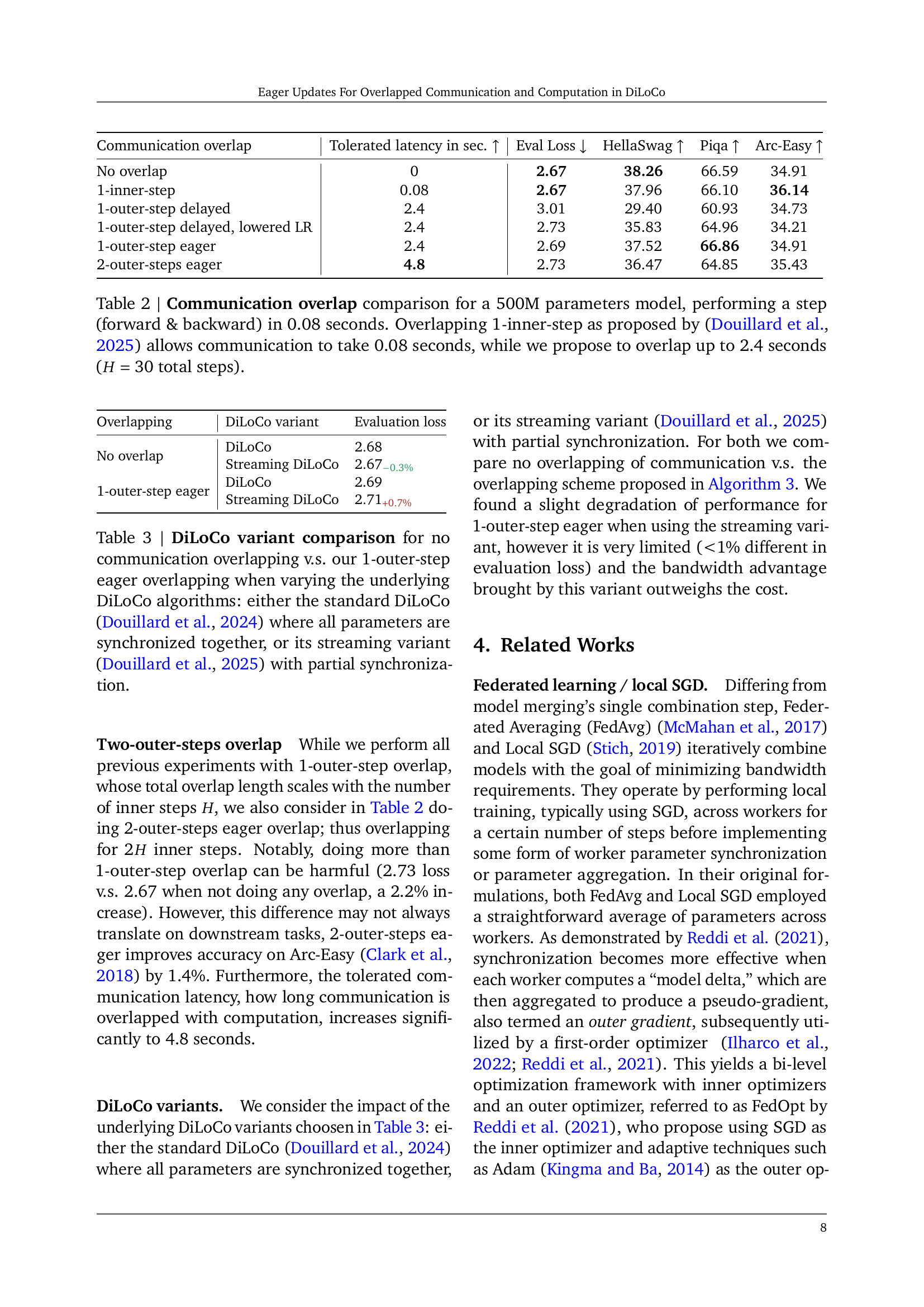
🔼 Table 2 showcases the effects of different communication overlap strategies on model training performance for a 500 million parameter model. It compares the standard approach with no overlap, overlapping one inner optimization step (as suggested in prior work by Douillard et al.), and the proposed approach which overlaps a single outer optimization step with up to 2.4 seconds of communication. The impact on training loss, HellaSwag accuracy, Piqa accuracy, and Arc-Easy accuracy is evaluated. The table highlights the trade-offs between communication efficiency and overall training speed/convergence.
read the caption
Table 2: Communication overlap comparison for a 500M parameters model, performing a step (forward & backward) in 0.08 seconds. Overlapping 1-inner-step as proposed by (Douillard et al., 2025) allows communication to take 0.08 seconds, while we propose to overlap up to 2.4 seconds (H=30𝐻30H=30italic_H = 30 total steps).

Overlapping	DiLoCo variant	Evaluation loss
No overlap	DiLoCo	$2.68$
No overlap	Streaming DiLoCo	$2.67_{{\color[rgb]{0,0.88,0}\definecolor[named]{pgfstrokecolor}{rgb}{0,0.88,0}% \pgfsys@color@cmyk@stroke{0.91}{0}{0.88}{0.12}\pgfsys@color@cmyk@fill{0.91}{0}% {0.88}{0.12}-0.3\%}}$
1-outer-step eager	DiLoCo	2.69
1-outer-step eager	Streaming DiLoCo	$2.71_{{\color[rgb]{0.72,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{0.72,0,0}% \pgfsys@color@cmyk@stroke{0}{0.89}{0.94}{0.28}\pgfsys@color@cmyk@fill{0}{0.89}% {0.94}{0.28}+0.7\%}}$

🔼 This table compares the performance of different DiLoCo variants with and without the proposed 1-outer-step eager communication overlap. It shows the evaluation loss for both standard DiLoCo (all parameters synchronized) and its streaming version (partial synchronization), with and without the overlap technique. This allows for an assessment of the method’s impact across various DiLoCo configurations.
read the caption
Table 3: DiLoCo variant comparison for no communication overlapping v.s. our 1-outer-step eager overlapping when varying the underlying DiLoCo algorithms: either the standard DiLoCo (Douillard et al., 2024) where all parameters are synchronized together, or its streaming variant (Douillard et al., 2025) with partial synchronization.

Model scale	Hidden dim	Num layers	Num heads	Token budget
35M	$2{,}048$	6	8	700M
100M	$3{,}072$	9	12	1.5B
200M	$4{,}096$	12	16	3.5B
300M	$5{,}120$	15	20	6B
500M	$6{,}144$	18	24	11B
1B	$8{,}192$	24	32	25B

🔼 This table presents the architectural hyperparameters used for training language models of varying sizes, ranging from 35 million to 1 billion parameters. These hyperparameters include the hidden dimension, number of layers, number of attention heads, and the Chinchilla-optimal token budget. The vocabulary size remains constant at 32,000 for all model sizes. This information is crucial for understanding and replicating the experimental setup of the paper.
read the caption
Table 4: Architecture hyperparameters: we consider model from 35M to 1B with the following hyperameters and chinchilla-optimal token budget. For all model scale, the vocabulary size is 32,0003200032{,}00032 , 000.

Model size	# layers	Step time	Method	Gbit/s to reach a compute utilization $\texttt{CU}=$ ?
Model size	# layers	Step time	Method	$50\%$	$80\%$	$90\%$	$95\%$	$99\%$
1B	24	0.1s	Data-Parallel	86.8	152.6	184.2	222.3	569.0
			Streaming DiLoCo	1.4	5.2	9.1	16.0	28.1
			Streaming DiLoCo with 1-inner-step overlapped FP4 com. H=30	2.4	3.6	4.3	4.3	4.3
			Streaming DiLoCo with 1-inner-step overlapped FP4 com. H=100	0.4	0.9	1.7	2.0	3.0
			Streaming DiLoCo with 1-outer-step overlapped FP4 com. H=30	1.1	2.0	2.0	2.0	2.4
			Streaming DiLoCo with 1-outer-step overlapped FP4 com. H=100	0.1	0.2	0.2	0.2	0.2
10B	48	0.8s	Data-Parallel	104.8	222.3	222.3	268.3	471.5
			Streaming DiLoCo	1.7	5.2	9.1	13.3	19.3
			Streaming DiLoCo with 1-inner-step overlapped FP4 com. H=30	1.4	2.4	2.4	3.0	3.0
			Streaming DiLoCo with 1-inner-step overlapped FP4 com. H=100	0.4	0.9	1.4	1.4	1.7
			Streaming DiLoCo with 1-outer-step overlapped FP4 com. H=30	0.7	1.1	1.4	1.4	1.4
			Streaming DiLoCo with 1-outer-step overlapped FP4 com. H=100	0.1	0.2	0.2	0.3	0.3
100B	108	4.9s	Data-Parallel	184.2	323.8	390.7	390.7	471.5
			Streaming DiLoCo	2.4	6.2	9.1	11.0	19.3
			Streaming DiLoCo with 1-inner-step overlapped FP4 com. H=30	0.9	1.7	2.0	2.0	2.0
			Streaming DiLoCo with 1-inner-step overlapped FP4 com. H=100	0.5	0.9	1.1	1.1	1.4
			Streaming DiLoCo with 1-outer-step overlapped FP4 com. H=30	0.5	0.8	0.9	0.9	0.9
			Streaming DiLoCo with 1-outer-step overlapped FP4 com. H=100	0.2	0.3	0.3	0.3	0.4

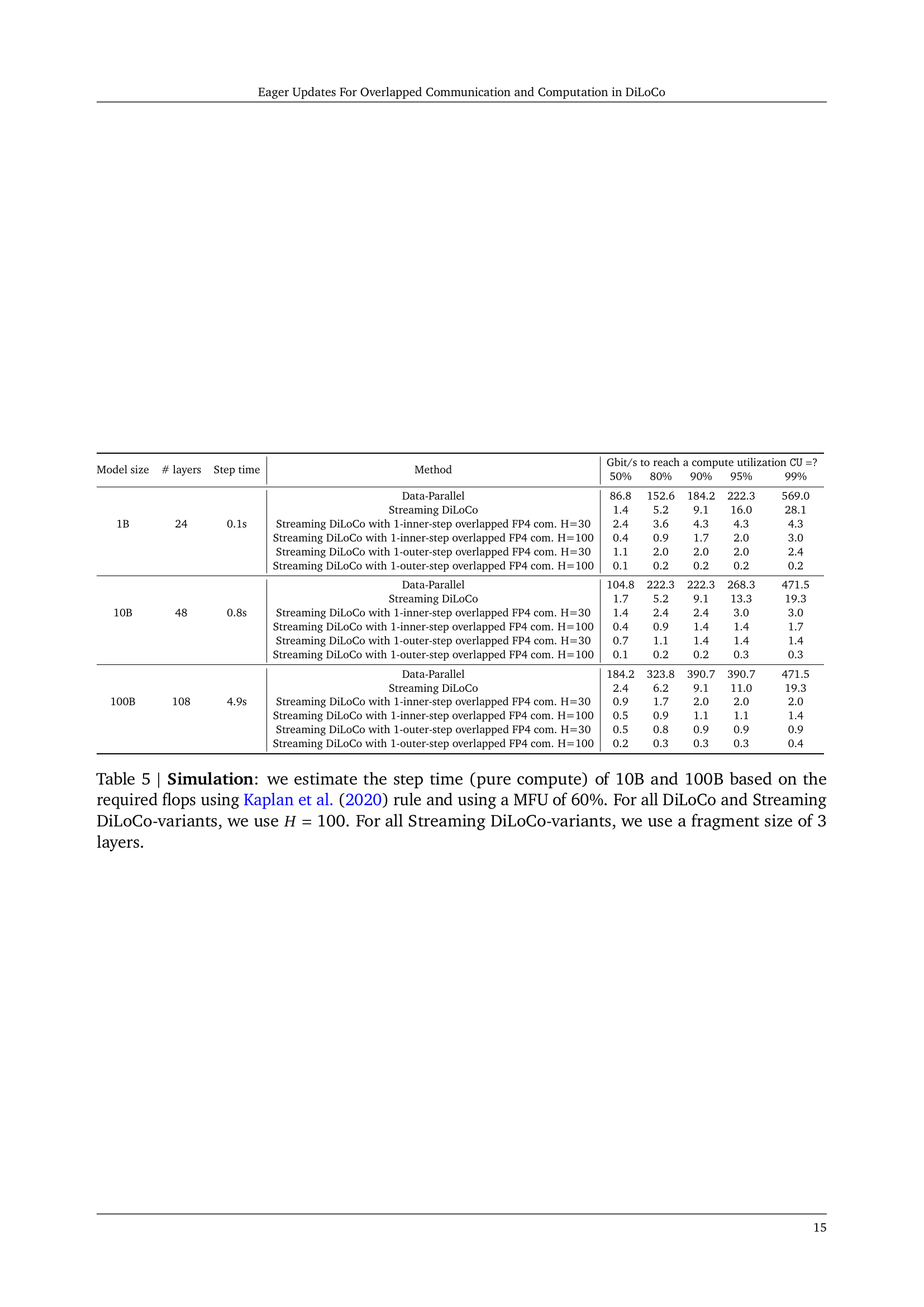
🔼 This table presents a simulation comparing different distributed training methods’ compute utilization across various WAN bandwidths. The simulation estimates step times for 1B, 10B, and 100B parameter models based on FLOPS requirements from Kaplan et al. (2020), assuming a 60% model-level compute utilization. It shows the Gbit/s required to achieve specific compute utilization targets (50%, 80%, 90%, 95%, 99%) for each method. The methods include Data-Parallel, Streaming DiLoCo (with and without inner- and outer-step communication overlaps). The hyperparameters H (synchronization frequency) is set to 100 for DiLoCo and its variants, and a fragment size of 3 layers is used for Streaming DiLoCo variants.
read the caption
Table 5: Simulation: we estimate the step time (pure compute) of 10B and 100B based on the required flops using Kaplan et al. (2020) rule and using a MFU of 60%. For all DiLoCo and Streaming DiLoCo-variants, we use H=100𝐻100H=100italic_H = 100. For all Streaming DiLoCo-variants, we use a fragment size of 3 layers.

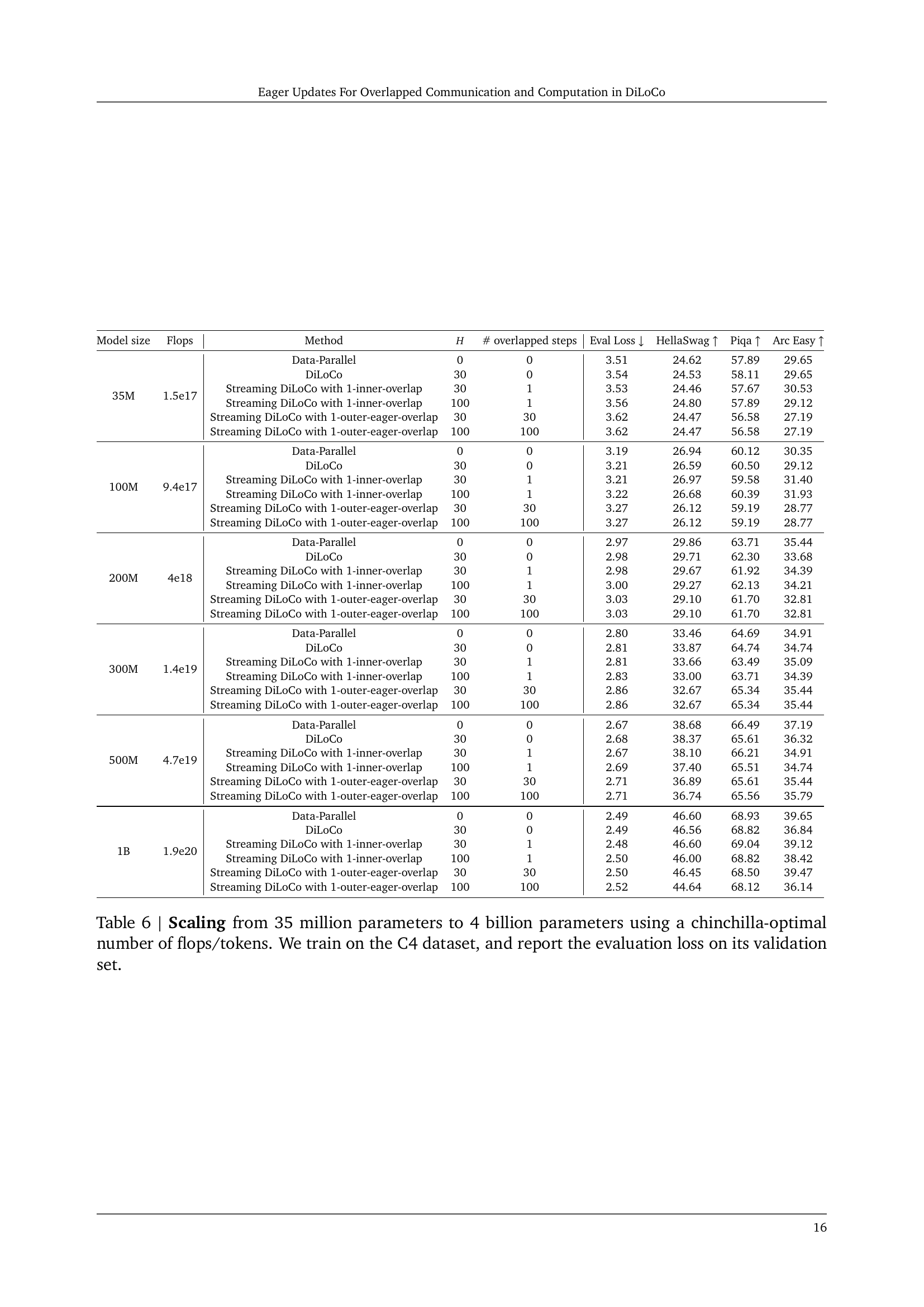
Model size	Flops	Method	$H$	# overlapped steps	Eval Loss $\downarrow$	HellaSwag $\uparrow$	Piqa $\uparrow$	Arc Easy $\uparrow$
35M	1.5e17	Data-Parallel	0	0	3.51	24.62	57.89	29.65
		DiLoCo	30	0	3.54	24.53	58.11	29.65
		Streaming DiLoCo with 1-inner-overlap	30	1	3.53	24.46	57.67	30.53
		Streaming DiLoCo with 1-inner-overlap	100	1	3.56	24.80	57.89	29.12
		Streaming DiLoCo with 1-outer-eager-overlap	30	30	3.62	24.47	56.58	27.19
		Streaming DiLoCo with 1-outer-eager-overlap	100	100	3.62	24.47	56.58	27.19
100M	9.4e17	Data-Parallel	0	0	3.19	26.94	60.12	30.35
		DiLoCo	30	0	3.21	26.59	60.50	29.12
		Streaming DiLoCo with 1-inner-overlap	30	1	3.21	26.97	59.58	31.40
		Streaming DiLoCo with 1-inner-overlap	100	1	3.22	26.68	60.39	31.93
		Streaming DiLoCo with 1-outer-eager-overlap	30	30	3.27	26.12	59.19	28.77
		Streaming DiLoCo with 1-outer-eager-overlap	100	100	3.27	26.12	59.19	28.77
200M	4e18	Data-Parallel	0	0	2.97	29.86	63.71	35.44
		DiLoCo	30	0	2.98	29.71	62.30	33.68
		Streaming DiLoCo with 1-inner-overlap	30	1	2.98	29.67	61.92	34.39
		Streaming DiLoCo with 1-inner-overlap	100	1	3.00	29.27	62.13	34.21
		Streaming DiLoCo with 1-outer-eager-overlap	30	30	3.03	29.10	61.70	32.81
		Streaming DiLoCo with 1-outer-eager-overlap	100	100	3.03	29.10	61.70	32.81
300M	1.4e19	Data-Parallel	0	0	2.80	33.46	64.69	34.91
		DiLoCo	30	0	2.81	33.87	64.74	34.74
		Streaming DiLoCo with 1-inner-overlap	30	1	2.81	33.66	63.49	35.09
		Streaming DiLoCo with 1-inner-overlap	100	1	2.83	33.00	63.71	34.39
		Streaming DiLoCo with 1-outer-eager-overlap	30	30	2.86	32.67	65.34	35.44
		Streaming DiLoCo with 1-outer-eager-overlap	100	100	2.86	32.67	65.34	35.44
500M	4.7e19	Data-Parallel	0	0	2.67	38.68	66.49	37.19
		DiLoCo	30	0	2.68	38.37	65.61	36.32
		Streaming DiLoCo with 1-inner-overlap	30	1	2.67	38.10	66.21	34.91
		Streaming DiLoCo with 1-inner-overlap	100	1	2.69	37.40	65.51	34.74
		Streaming DiLoCo with 1-outer-eager-overlap	30	30	2.71	36.89	65.61	35.44
		Streaming DiLoCo with 1-outer-eager-overlap	100	100	2.71	36.74	65.56	35.79
1B	1.9e20	Data-Parallel	0	0	2.49	46.60	68.93	39.65
		DiLoCo	30	0	2.49	46.56	68.82	36.84
		Streaming DiLoCo with 1-inner-overlap	30	1	2.48	46.60	69.04	39.12
		Streaming DiLoCo with 1-inner-overlap	100	1	2.50	46.00	68.82	38.42
		Streaming DiLoCo with 1-outer-eager-overlap	30	30	2.50	46.45	68.50	39.47
		Streaming DiLoCo with 1-outer-eager-overlap	100	100	2.52	44.64	68.12	36.14

🔼 This table presents the results of scaling experiments conducted on language models with varying sizes, ranging from 35 million to 4 billion parameters. The experiments utilized the C4 dataset for training and measured the evaluation loss on a validation set. The table compares several model variations and training strategies, such as Data-Parallel training, Streaming DiLoCo (with and without overlapping communication), and DiLoCo with different numbers of inner steps and overlapping configurations. The purpose is to demonstrate the scaling performance and the effectiveness of different approaches, especially focusing on the impact of overlapping communication and computation within the DiLoCo framework.
read the caption
Table 6: Scaling from 35 million parameters to 4 billion parameters using a chinchilla-optimal number of flops/tokens. We train on the C4 dataset, and report the evaluation loss on its validation set.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Eager Updates’ Impact#

Overlapping Comm#

DiLoCo Algorithm#

Large-Scale Training#

Future Directions#

More visual insights#

Full paper#