TL;DR#
Current methods for compressing long text sequences into shorter vectors for use in LLMs have limitations, with compression ratios rarely exceeding x10. This is surprising given the theoretically high information capacity of large vectors. The authors explore this discrepancy and aim to discover the true limits of compression using optimized techniques.
The researchers used a per-sample optimization procedure to replace traditional encoders and demonstrate significantly higher compression ratios. They show that compression limits depend on the uncertainty to be reduced (cross-entropy loss), not input length. The results reveal a considerable gap between the theoretical capacity of input embeddings and their practical use, suggesting opportunities to significantly enhance LLM design and efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the prevailing assumptions about the capacity of input embeddings in large language models (LLMs). By demonstrating significantly higher compression ratios than previously thought possible, it opens new avenues for optimizing LLM design, improving efficiency, and potentially enabling entirely new functionalities. This has significant implications for researchers working on LLM efficiency, memory augmentation, and long-context processing.
Visual Insights#
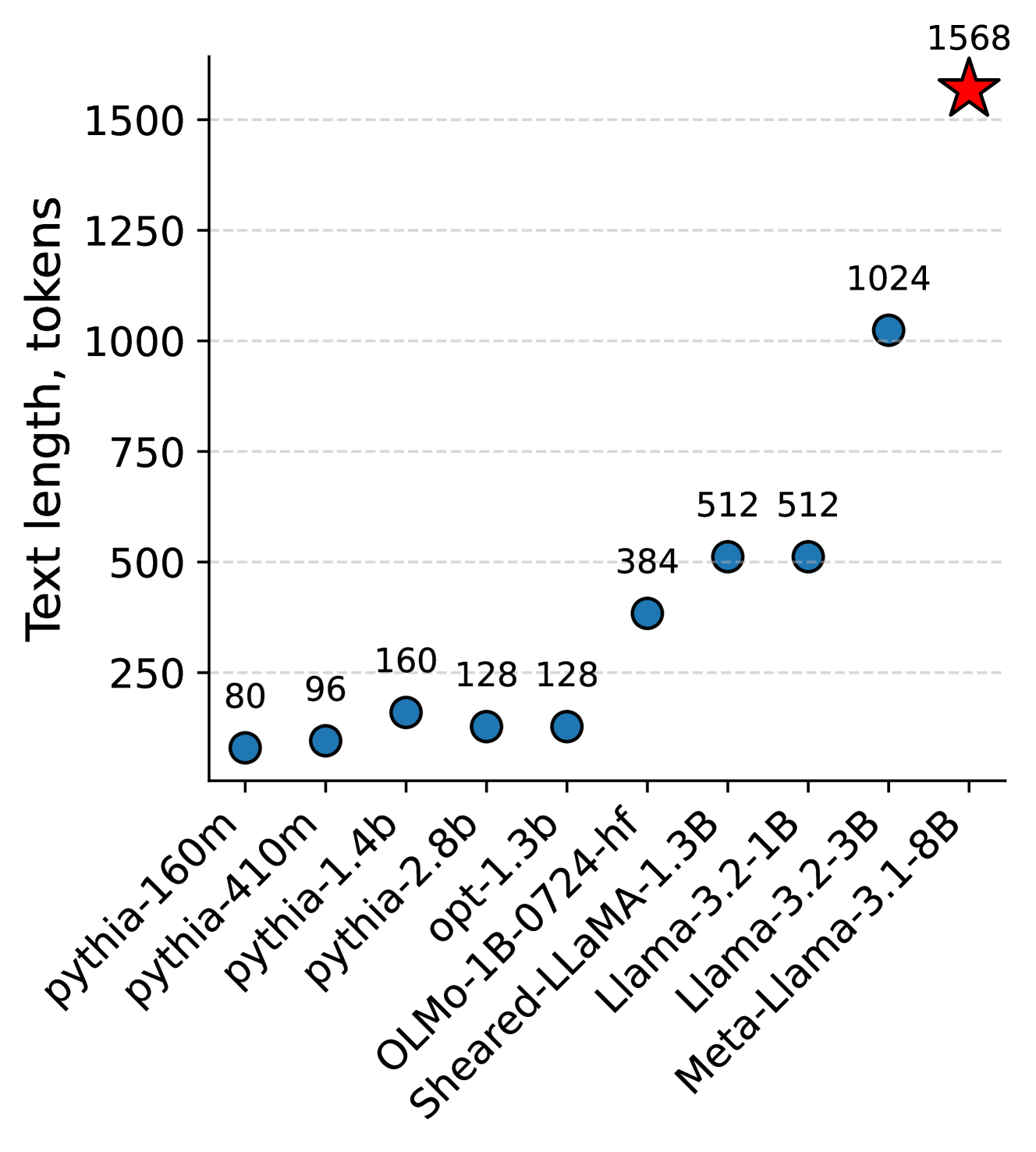
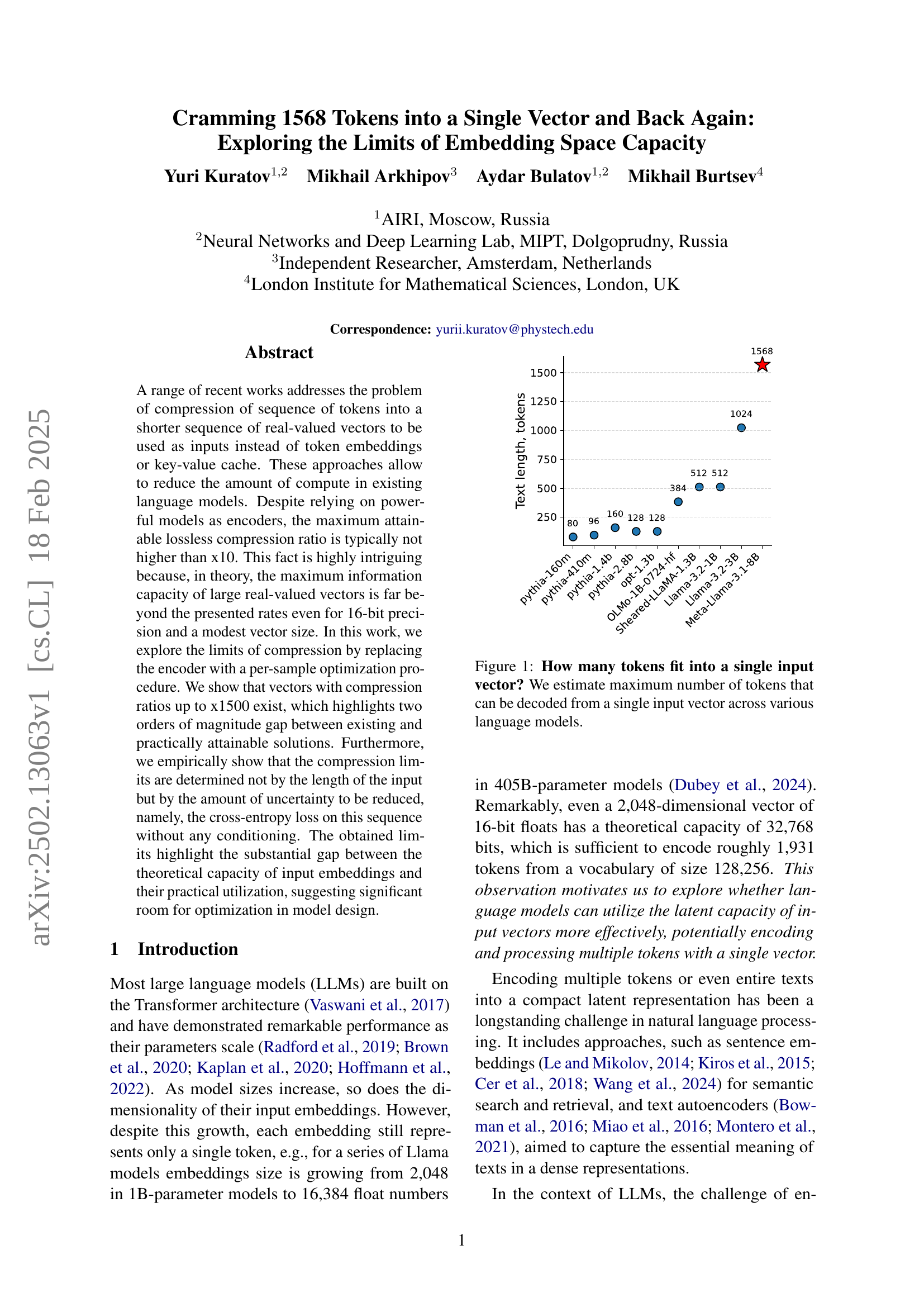
🔼 This figure shows the maximum number of tokens that different language models can process within a single input vector. The x-axis represents the number of tokens in the input text, and the y-axis represents the model’s capacity to handle those tokens. Each bar represents a different language model, showing how many tokens each model can effectively process before encountering performance limitations. This illustrates the varying capacities of different language models in compressing text information into a single vector, highlighting the limitations and potential for improvement.
read the caption
Figure 1: How many tokens fit into a single input vector? We estimate maximum number of tokens that can be decoded from a single input vector across various language models.
| Pythia-160M | Pythia-410M | Pythia-1.4B | Llama-3.2-1B | Llama-3.2-3B | Llama-3.1-8B | ||
| PG-19 | Max, tokens | 80 | 96 | 160 | 512 | 1024 | 1568 |
| Gain, tokens | 70.911.0 | 81.312.0 | 158.029.1 | 426.279.2 | 720.380.2 | 1094.1127.6 | |
| Information Gain | 396.446.0 | 431.451.6 | 792.8143.4 | 2119.9364.8 | 3292.2320.0 | 4865.7546.6 | |
| Fanfics | Max, tokens | 80 | 96 | 192 | 512 | 1024 | 1568 |
| Gain, tokens | 70.910.5 | 81.211.6 | 152.928.0 | 449.683.7 | 734.185.0 | 1071.8168.6 | |
| Information Gain | 378.145.9 | 429.846.2 | 776.9132.5 | 2213.8365.8 | 3354.5344.9 | 4768.9622.6 | |
| Random | Max, tokens | 65 | 72 | 139 | 316 | 460 | 792 |
| Gain, tokens | 61.36.6 | 76.98.7 | 144.417.5 | 294.964.8 | 456.972.1 | 623.297.3 | |
| Information Gain | 500.838.9 | 630.465.2 | 1108.2136.2 | 2265.2498.7 | 3382.6585.2 | 4541.2758.6 |
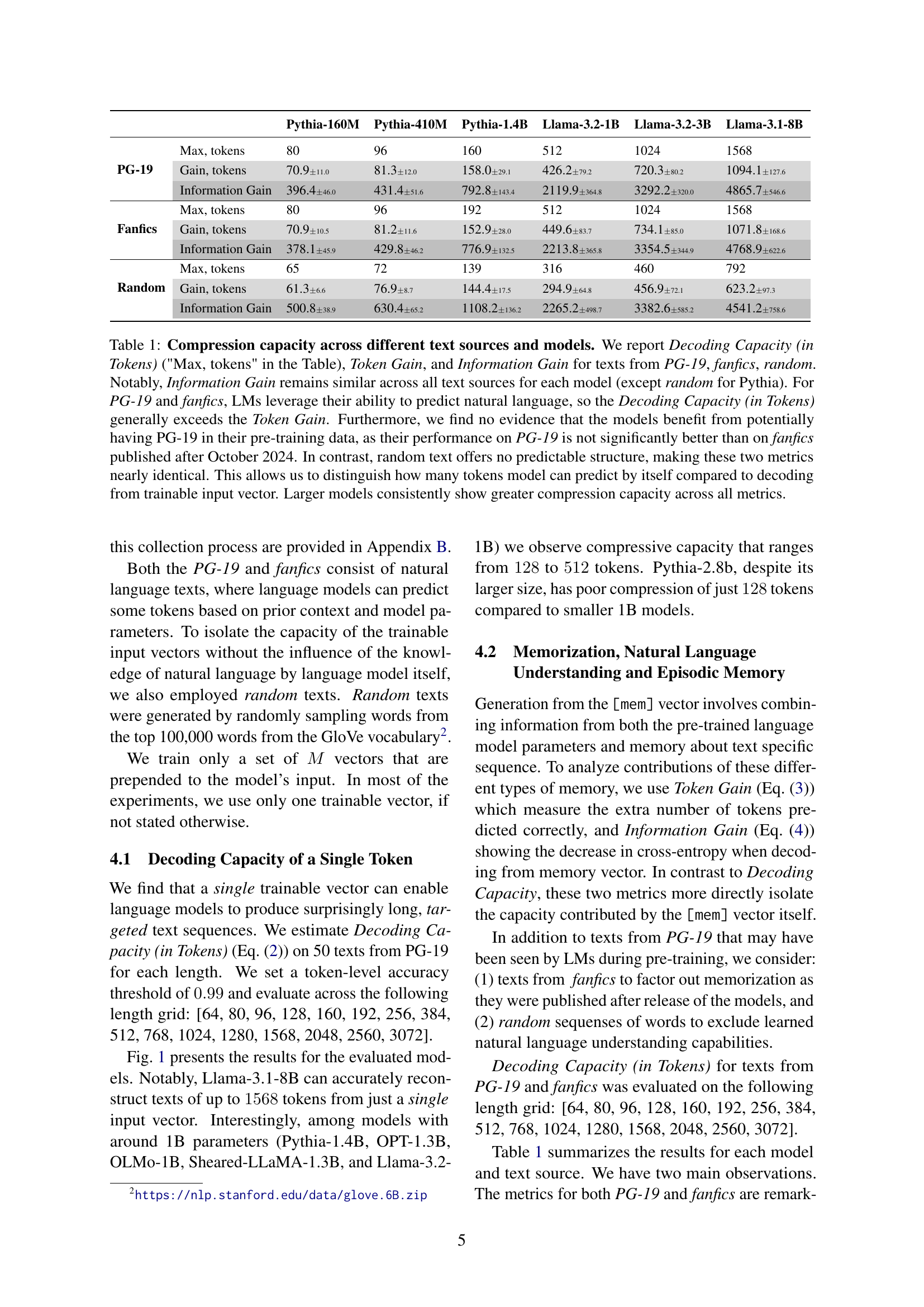
🔼 This table shows how different language models compress text from three sources: PG-19 (a book dataset), fanfics (fan fiction stories written after the models’ training), and random text. Three metrics are reported: Decoding Capacity (the maximum number of tokens a model can accurately reconstruct from a compressed vector), Token Gain (additional tokens correctly predicted due to the compressed vector), and Information Gain (reduction in uncertainty measured by cross-entropy). The results show that Information Gain is consistent across text sources for each model (except for random text with the Pythia model), indicating that the compression ability is not heavily reliant on memorization of the training data. Decoding Capacity is higher for natural language texts (PG-19 and fanfics) than for random text. Larger models consistently demonstrate better compression across all metrics.
read the caption
Table 1: Compression capacity across different text sources and models. We report Decoding Capacity (in Tokens) ('Max, tokens' in the Table), Token Gain, and Information Gain for texts from PG-19, fanfics, random. Notably, Information Gain remains similar across all text sources for each model (except random for Pythia). For PG-19 and fanfics, LMs leverage their ability to predict natural language, so the Decoding Capacity (in Tokens) generally exceeds the Token Gain. Furthermore, we find no evidence that the models benefit from potentially having PG-19 in their pre-training data, as their performance on PG-19 is not significantly better than on fanfics published after October 2024. In contrast, random text offers no predictable structure, making these two metrics nearly identical. This allows us to distinguish how many tokens model can predict by itself compared to decoding from trainable input vector. Larger models consistently show greater compression capacity across all metrics.
In-depth insights#
Embedding Limits#
The concept of “Embedding Limits” in the context of large language models (LLMs) explores the boundaries of information that can be effectively encoded and decoded within a fixed-size embedding vector. The research highlights a significant gap between the theoretical capacity of these vectors and their practical utilization. Existing methods, while leveraging powerful models, achieve compression ratios far below what’s theoretically possible. This suggests considerable room for improvement in model design and optimization techniques. The study challenges the conventional approach of representing one token per embedding, demonstrating lossless compression ratios up to x1500 by optimizing a vector to encode an entire text sequence. This breakthrough reveals that the limiting factor isn’t sequence length, but rather the amount of uncertainty inherent in the text. Focusing on reducing cross-entropy during the encoding process, rather than simply the length of the input, unlocks far greater embedding capacity. The results underscore the need to re-evaluate our understanding of embedding efficiency within LLMs and further investigate how to exploit the latent potential of these representations for more efficient context encoding and processing.
Compression via Optimization#
The concept of ‘Compression via Optimization’ in the context of large language models (LLMs) presents a novel approach to handling long text sequences. Instead of relying on pre-trained encoders or traditional compression methods, this technique uses a per-sample optimization procedure to directly compress token sequences into significantly shorter, real-valued vectors. This method offers the potential to overcome the limitations of existing techniques, which typically achieve compression ratios no higher than 10x. By replacing the encoder with an optimization process, it pushes the boundaries of compression, demonstrating ratios up to 1500x. This substantial increase highlights the vast difference between theoretical capacity of large vectors and their practical utilization in current LLMs. Moreover, the research indicates that compression limits are not determined by text length, but rather by the uncertainty to be reduced, specifically measured by cross-entropy loss. This finding suggests that future model designs could benefit significantly from focusing on optimizing the utilization of embedding space for efficient information storage and retrieval rather than solely increasing model size.
Capacity Scaling Laws#
Capacity scaling laws in large language models (LLMs) explore how the model’s ability to process and generate text scales with its size, specifically focusing on the relationship between model parameters and the maximum context length or the number of tokens that can be encoded and decoded effectively. Understanding these laws is crucial for optimizing model design and resource allocation. The research paper likely investigates if this scaling is linear, sublinear, or superlinear; whether there are diminishing returns with increasing size; and what architectural choices (e.g., attention mechanisms) influence the scaling behavior. A key aspect would be examining the capacity utilization – how efficiently the model utilizes its parameter space to achieve the observed capacity. The investigation would probably also consider the trade-offs between capacity and other metrics like performance (accuracy, fluency) and computational cost. Ultimately, a deep understanding of capacity scaling laws can help developers build more efficient and powerful LLMs capable of handling longer sequences and complex tasks.
Beyond Memorization#
The concept of moving beyond memorization in large language models (LLMs) is crucial for achieving true artificial intelligence. Current LLMs often excel at pattern recognition and mimicking training data, essentially memorizing relationships. To surpass this limitation, research must focus on developing models that exhibit genuine understanding and reasoning capabilities. This involves shifting from simply predicting the next word to inferring meaning, generating novel content, and making logical deductions. Achieving this requires advancements in model architecture, training methodologies, and evaluation metrics. Instead of relying solely on massive datasets, emphasis should be placed on creating models capable of learning from limited examples and generalizing effectively. Developing methods to assess true comprehension, rather than just mimicking learned patterns, is a major hurdle in this field. Ultimately, the goal is to create LLMs that exhibit contextual awareness, critical thinking, and the ability to solve complex problems – capabilities far exceeding mere memorization. This would signify a true leap forward in AI, paving the way for more sophisticated and adaptable AI systems.
Future Directions#
Future research should prioritize a deeper investigation into the semantic properties of the compressed vectors and their utility in downstream tasks. Exploring alternative model architectures, especially recurrent and memory-augmented models, and scaling the methodology to larger models with greater parameter counts is essential. Understanding the relationship between model capacity, compression effectiveness, and the specific training data used requires further study. Furthermore, the impact of different text complexities and sources on compression performance necessitates detailed analysis. Investigating the potential for exploiting these compact representations in various applications, including efficient information storage and retrieval and enhanced reasoning capabilities, offers exciting possibilities. Finally, rigorous examination of the ethical implications surrounding the potential misuse of compressed information and related data security issues is crucial for responsible development and deployment.
More visual insights#
More on figures

🔼 This figure illustrates the process of compressing a sequence of tokens into a smaller set of memory vectors using a pre-trained language model. The pre-trained language model’s weights are frozen; only the memory vectors are trainable parameters. These memory vectors are prepended to the input token sequence and serve as a compact representation to be processed by the frozen language model. The model is trained to predict the original token sequence from these memory vectors. Importantly, the memory vectors are trained independently for each text sequence, emphasizing the per-sample optimization approach used in this study.
read the caption
Figure 2: Compressing text into a [mem] vector. The pre-trained LLM is frozen, and we only finetune one or multiple [mem] vectors to decode the sequence of tokens [t1,t2,…,tN]subscript𝑡1subscript𝑡2…subscript𝑡𝑁[t_{1},t_{2},\ldots,t_{N}][ italic_t start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT , italic_t start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT , … , italic_t start_POSTSUBSCRIPT italic_N end_POSTSUBSCRIPT ]. [mem] vectors are trained for each text separately.

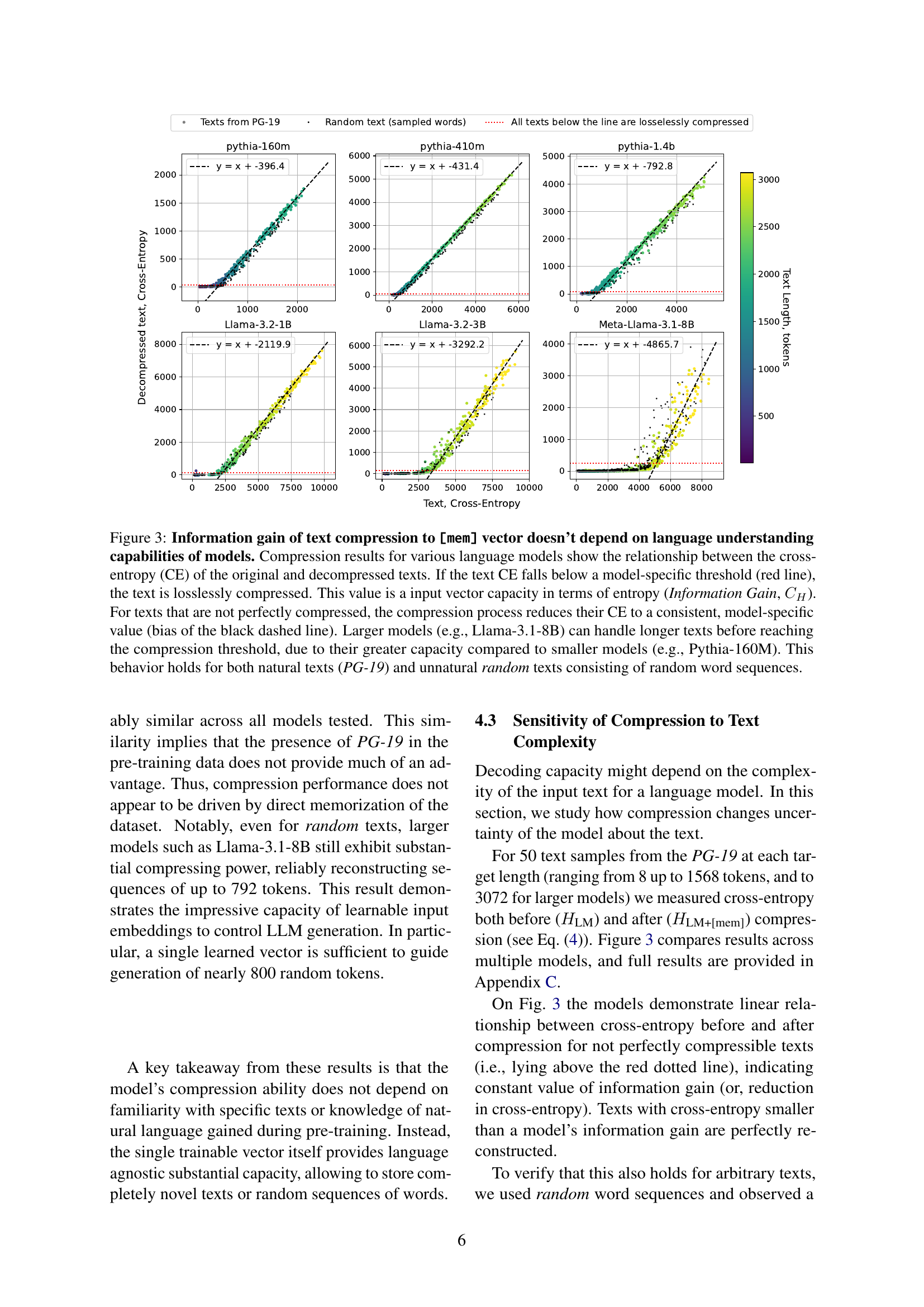
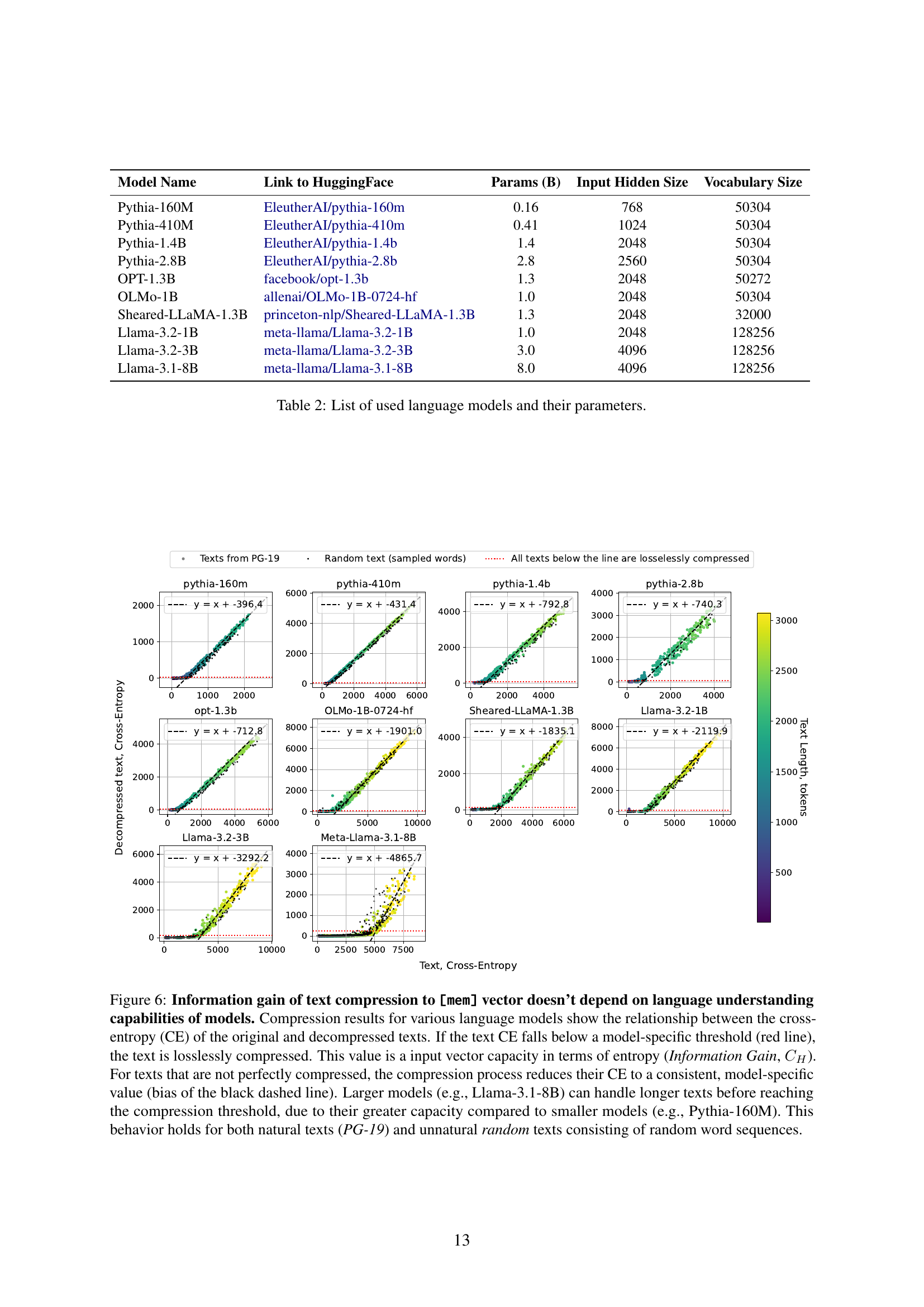
🔼 Figure 3 examines the relationship between the cross-entropy of original and compressed texts across various language models, demonstrating that compression capacity is independent of the model’s language understanding capabilities. The x-axis shows the original text’s cross-entropy, and the y-axis represents the cross-entropy after compression. Lossless compression occurs when the compressed text’s cross-entropy falls below a model-specific threshold (red line), representing the model’s information gain. Texts above this line show a consistent cross-entropy reduction to a model-specific value (black dashed line). Larger models demonstrate a higher compression capacity than smaller models. The same pattern holds true for both natural language texts and synthetic random text sequences.
read the caption
Figure 3: Information gain of text compression to [mem] vector doesn’t depend on language understanding capabilities of models. Compression results for various language models show the relationship between the cross-entropy (CE) of the original and decompressed texts. If the text CE falls below a model-specific threshold (red line), the text is losslessly compressed. This value is a input vector capacity in terms of entropy (Information Gain, CHsubscript𝐶𝐻C_{H}italic_C start_POSTSUBSCRIPT italic_H end_POSTSUBSCRIPT). For texts that are not perfectly compressed, the compression process reduces their CE to a consistent, model-specific value (bias of the black dashed line). Larger models (e.g., Llama-3.1-8B) can handle longer texts before reaching the compression threshold, due to their greater capacity compared to smaller models (e.g., Pythia-160M). This behavior holds for both natural texts (PG-19) and unnatural random texts consisting of random word sequences.

🔼 This figure displays the linear relationship between the number of trainable memory vectors ([mem] vectors) used and the model’s ability to compress and decompress text. The dashed lines show the ideal linear scaling. Shaded areas represent the standard deviation (±1 std). For the Pythia-160M model, the maximum input context is 2048 tokens; it successfully encoded up to 2016 tokens with 32 [mem] vectors. The Llama-3.2-1B model perfectly decoded texts of 7168 tokens using just 16 [mem] vectors, demonstrating that the compression capacity scales effectively with the number of trainable memory vectors.
read the caption
Figure 4: Compression scales linearly with the number of trainable [mem] vectors. Dashed lines represent ideal linear scaling, and shaded regions indicate ±1plus-or-minus1\pm 1± 1 std. Pythia-160m reaches its maximum input context length of 2048 tokens and can successfully encode texts of up to 2016 tokens into 32 [mem] input vectors. Llama-3.2-1B can perfectly decode texts of 7168 tokens from just 16 input vectors.

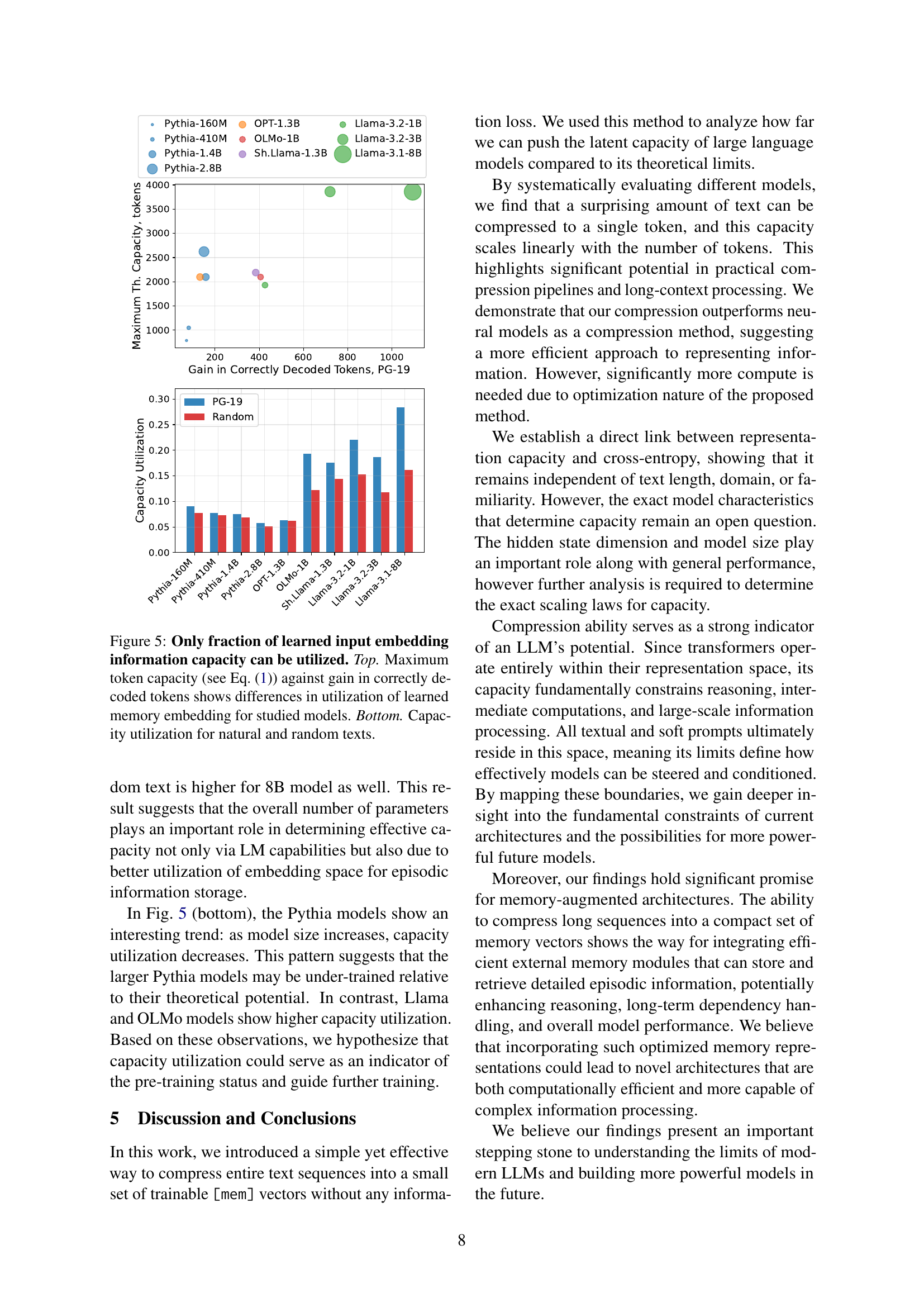
🔼 Figure 5 analyzes the efficiency of different language models in using their input embedding capacity for text compression. The top panel plots the theoretical maximum number of tokens that can be encoded in the input embedding (calculated using Equation 1) against the actual gain in correctly decoded tokens achieved through compression. This comparison reveals variations in how effectively different models utilize their embedding space. The bottom panel further examines capacity utilization by contrasting performance on natural language text with that of randomly generated text, providing insights into how model architecture and training data affect the capacity to represent text information in the input embeddings.
read the caption
Figure 5: Only fraction of learned input embedding information capacity can be utilized. Top. Maximum token capacity (see Eq. 1) against gain in correctly decoded tokens shows differences in utilization of learned memory embedding for studied models. Bottom. Capacity utilization for natural and random texts.

🔼 Figure 6 illustrates the relationship between the cross-entropy of original and compressed texts for various language models. The x-axis represents the cross-entropy of the original text, and the y-axis represents the cross-entropy after compression using a trainable memory vector. The red line indicates a model-specific threshold: if the compressed text’s cross-entropy falls below this line, the compression is lossless. The black dashed lines show the consistent, model-specific cross-entropy reduction for texts not perfectly compressed. Larger models demonstrate a greater capacity to handle longer texts before reaching this lossless compression threshold. This consistent behavior is observed for both naturally occurring and randomly generated texts.
read the caption
Figure 6: Information gain of text compression to [mem] vector doesn’t depend on language understanding capabilities of models. Compression results for various language models show the relationship between the cross-entropy (CE) of the original and decompressed texts. If the text CE falls below a model-specific threshold (red line), the text is losslessly compressed. This value is a input vector capacity in terms of entropy (Information Gain, CHsubscript𝐶𝐻C_{H}italic_C start_POSTSUBSCRIPT italic_H end_POSTSUBSCRIPT). For texts that are not perfectly compressed, the compression process reduces their CE to a consistent, model-specific value (bias of the black dashed line). Larger models (e.g., Llama-3.1-8B) can handle longer texts before reaching the compression threshold, due to their greater capacity compared to smaller models (e.g., Pythia-160M). This behavior holds for both natural texts (PG-19) and unnatural random texts consisting of random word sequences.

🔼 This figure displays the distribution of cosine similarity scores between different embeddings of the same text sequence (intra-sample) and between embeddings of different text sequences (inter-sample). The cosine similarity measures how similar two vector representations are, with a score of 1 indicating identical vectors and 0 indicating orthogonal vectors. The distributions show that intra-sample similarities are not strongly clustered around a high similarity value (e.g. 1), indicating the model can generate diverse vector representations for the same input. Furthermore, the overlap between the intra-sample and inter-sample distributions suggests that the uniqueness of the embedding for a given input is not guaranteed and that there is a significant amount of variation in the representation of different input sequences.
read the caption
Figure 7: Intra/inter-sample embeddings cosine similarity. Empirical probability densities of cosine similarity between intra-sample and inter-sample embeddings. Intra-sample similarities are measured between of the same sequence of tokens, while inter-sample between different ones. Measured on GovReport Huang et al. (2021) and Sheared-Llama-1.3B Xia et al. (2024).

🔼 Figure 8 visualizes the accuracy of reconstructing text sequences from linear interpolations between different embeddings of the same input sequence. For each input sequence, 32 different embeddings were generated using the method described in the paper. Then, linear interpolations were performed between all pairs of these embeddings. The plot shows the accuracy of reconstructing the original text at various points along these interpolation lines. The higher density of lines in certain areas indicates a higher concentration of interpolation points with similar reconstruction accuracy. The grey lines represent the minimum and maximum accuracies observed across all interpolations for a given interpolation parameter (θ). This helps illustrate the variability in reconstruction accuracy across different interpolations between embeddings of the same sequence.
read the caption
Figure 8: Intra-sample Interpolation Accuracies. Interpolation lines are provided for all pairs between 32 embeddings of the same input sequence. All interpolation lines are printed with high transparency to show denser regions. Grey lines depict minimums and maximums of the accuracy for a given interpolation parameter θ𝜃\thetaitalic_θ.
Full paper#