TL;DR#
Current multimodal large language models (MLLMs) suffer from high computational costs due to their quadratic complexity and the need for separate vision encoders. This limits their deployment and scalability. The high cost is due to the quadratic complexity of the Transformer architecture used in most current models.
This paper introduces mmMamba, a framework that directly converts trained decoder-only MLLMs into linear-complexity models through a three-stage distillation process. This method leverages the similarity between the Transformer attention mechanism and the Mamba-2 state space model, significantly reducing the computational demands. mmMamba achieves competitive performance against existing models, offering both a purely linear and a hybrid architecture that balances efficiency and performance. The results demonstrate significant speedup and memory savings, paving the way for more efficient and scalable multimodal AI systems.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the crucial limitations of current multimodal large language models (MLLMs): quadratic complexity and reliance on separate vision encoders. By introducing mmMamba, a novel framework for developing linear-complexity multimodal state space models, it significantly improves computational efficiency without sacrificing performance. This opens new avenues for deploying MLLMs on resource-constrained devices and for developing more scalable and efficient multimodal AI systems. The proposed distillation-based approach is also highly significant, as it circumvents the need for pre-trained linear-complexity LLMs, making the development of such models more accessible.
Visual Insights#

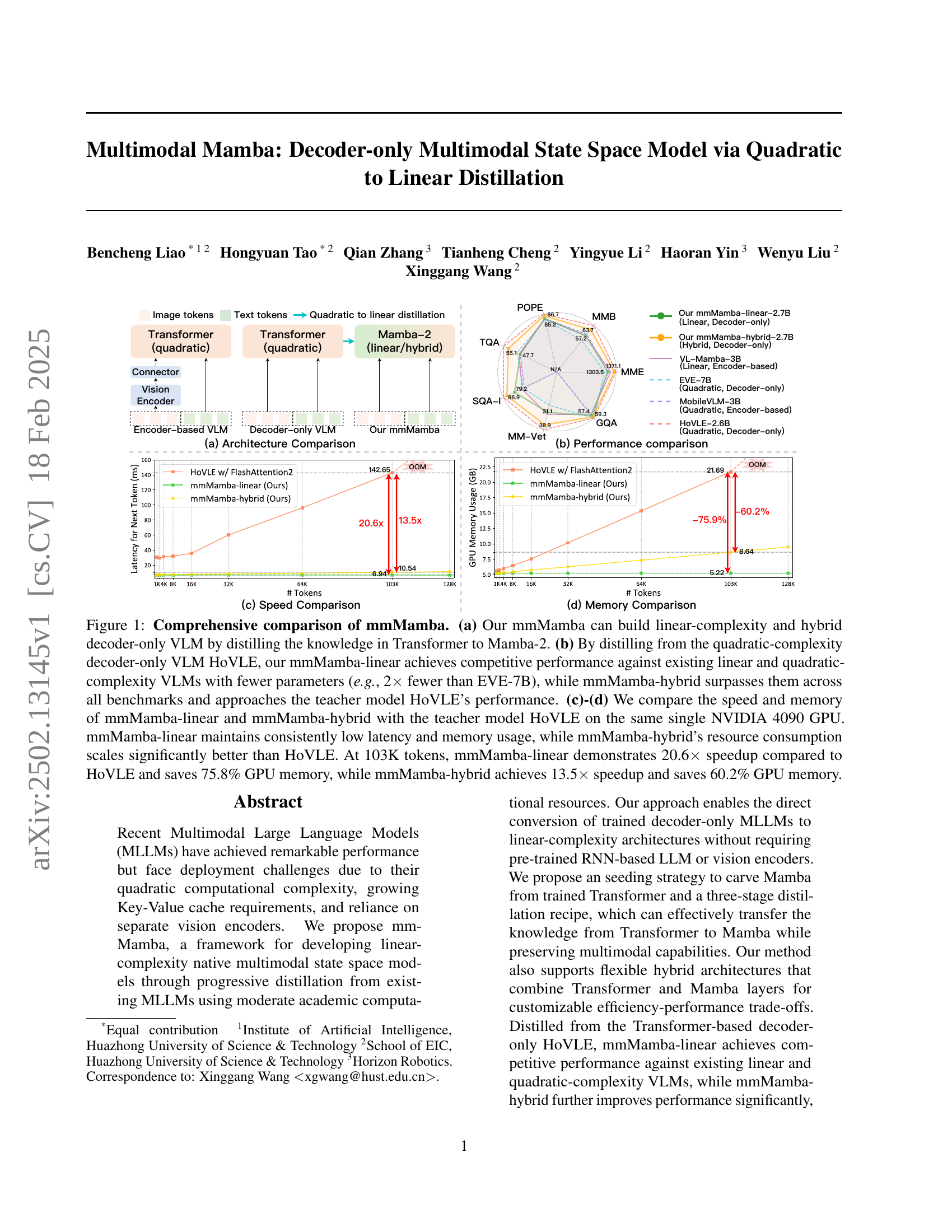
🔼 Figure 1 provides a comprehensive comparison of the proposed multimodal Mamba model. Subfigure (a) illustrates the architecture of mmMamba, highlighting its linear-complexity and hybrid decoder-only VLM design achieved through knowledge distillation from Transformer to Mamba-2. Subfigure (b) presents a performance comparison showing that mmMamba-linear achieves competitive results against existing models, while mmMamba-hybrid outperforms them across various benchmarks. Subfigures (c) and (d) compare the speed and memory usage of mmMamba with the teacher model HoVLE on an NVIDIA 4090 GPU. mmMamba-linear exhibits significantly lower latency and memory consumption than HoVLE, while mmMamba-hybrid scales more efficiently with increasing sequence length. Specifically, at 103K tokens, mmMamba-linear achieves a 20.6x speedup and 75.8% memory saving, whereas mmMamba-hybrid shows a 13.5x speedup and 60.2% memory saving compared to HoVLE.
read the caption
Figure 1: Comprehensive comparison of mmMamba. (a) Our mmMamba can build linear-complexity and hybrid decoder-only VLM by distilling the knowledge in Transformer to Mamba-2. (b) By distilling from the quadratic-complexity decoder-only VLM HoVLE, our mmMamba-linear achieves competitive performance against existing linear and quadratic-complexity VLMs with fewer parameters (e.g., 2×\times× fewer than EVE-7B), while mmMamba-hybrid surpasses them across all benchmarks and approaches the teacher model HoVLE’s performance. (c)-(d) We compare the speed and memory of mmMamba-linear and mmMamba-hybrid with the teacher model HoVLE on the same single NVIDIA 4090 GPU. mmMamba-linear maintains consistently low latency and memory usage, while mmMamba-hybrid’s resource consumption scales significantly better than HoVLE. At 103K tokens, mmMamba-linear demonstrates 20.6×\times× speedup compared to HoVLE and saves 75.8% GPU memory, while mmMamba-hybrid achieves 13.5×\times× speedup and saves 60.2% GPU memory.
| Method | Recipe | Complexity | # P. | # T.P. | MME | MMB | POPE | SEED | MMMU | MM-Vet | TQA | SQA-I | GQA |
| Encoder-based VLMs | |||||||||||||
| OpenFlamingo (Awadalla et al., 2023) | PT, SFT | Quadratic | 9B | 96.6% | - | 4.6 | - | - | - | - | 33.6 | - | - |
| MiniGPT-4 (Zhu et al., 2023) | PT, SFT | Quadratic | 13B | 94.8% | 581.7 | 23.0 | - | - | - | 22.1 | - | - | 32.2 |
| Qwen-VL (Bai et al., 2023b) | PT, SFT | Quadratic | 7B | 100.0% | - | 38.2 | - | 56.3 | - | - | 63.8 | 67.1 | 59.3 |
| LLaVA-Phi (Zhu et al., 2024) | PT, SFT | Quadratic | 3B | 90.0% | 1335.1 | 59.8 | 85.0 | - | - | 28.9 | 48.6 | 68.4 | - |
| MobileVLM-3B (Chu et al., 2023) | PT, SFT | Quadratic | 3B | 90.0% | 1288.9 | 59.6 | 84.9 | - | - | - | 47.5 | 61.0 | 59.0 |
| VisualRWKV (Hou et al., 2024) | PT, SFT | Linear | 3B | 90.0% | 1369.2 | 59.5 | 83.1 | - | - | - | 48.7 | 65.3 | 59.6 |
| VL-Mamba (Qiao et al., 2024) | PT, SFT | Linear | 3B | 90.0% | 1369.6 | 57.0 | 84.4 | - | - | 32.6 | 48.9 | 65.4 | 56.2 |
| Cobra (Zhao et al., 2024) | PT, SFT | Linear | 3.5B | 82.6% | - | - | 88.4 | - | - | - | 58.2 | - | 62.3 |
| Decoder-only VLMs | |||||||||||||
| Fuyu-8B (HD) (Bavishi et al., 2023) | PT, SFT | Quadratic | 8B | 100.0% | 728.6 | 10.7 | 74.1 | - | - | 21.4 | - | - | - |
| SOLO (Chen et al., 2024a) | PT, SFT | Quadratic | 7B | 100.0% | 1001.3 | - | - | 64.4 | - | - | - | 73.3 | - |
| Chameleon-7B (Team, 2024) | PT, SFT | Quadratic | 7B | 100.0% | 170 | 31.1 | - | 30.6 | 25.4 | 8.3 | 4.8 | 47.2 | - |
| EVE-7B (Diao et al., 2024) | PT, SFT | Quadratic | 7B | 100.0% | 1217.3 | 49.5 | 83.6 | 61.3 | 32.3 | 25.6 | 51.9 | 63.0 | 60.8 |
| Emu3 (Wang et al., 2024b) | PT, SFT | Quadratic | 8B | 100.0% | - | 58.5 | 85.2 | 68.2 | 31.6 | 37.2 | 64.7 | 89.2 | 60.3 |
| HoVLE (Tao et al., 2024) | DT, PT, SFT | Quadratic | 2.6B | 100.0% | 1433.5 | 71.9 | 87.6 | 70.7 | 33.7 | 44.3 | 66.0 | 94.8 | 60.9 |
| mmMamba | DT | Linear | 2.7B | 14.7% | 1303.5 | 57.2 | 85.2 | 62.9 | 30.7 | 31.1 | 47.7 | 79.2 | 57.4 |
| mmMamba | DT | Hybrid | 2.7B | 11.2% | 1371.1 | 63.7 | 86.7 | 66.3 | 32.3 | 36.9 | 55.1 | 86.9 | 59.3 |
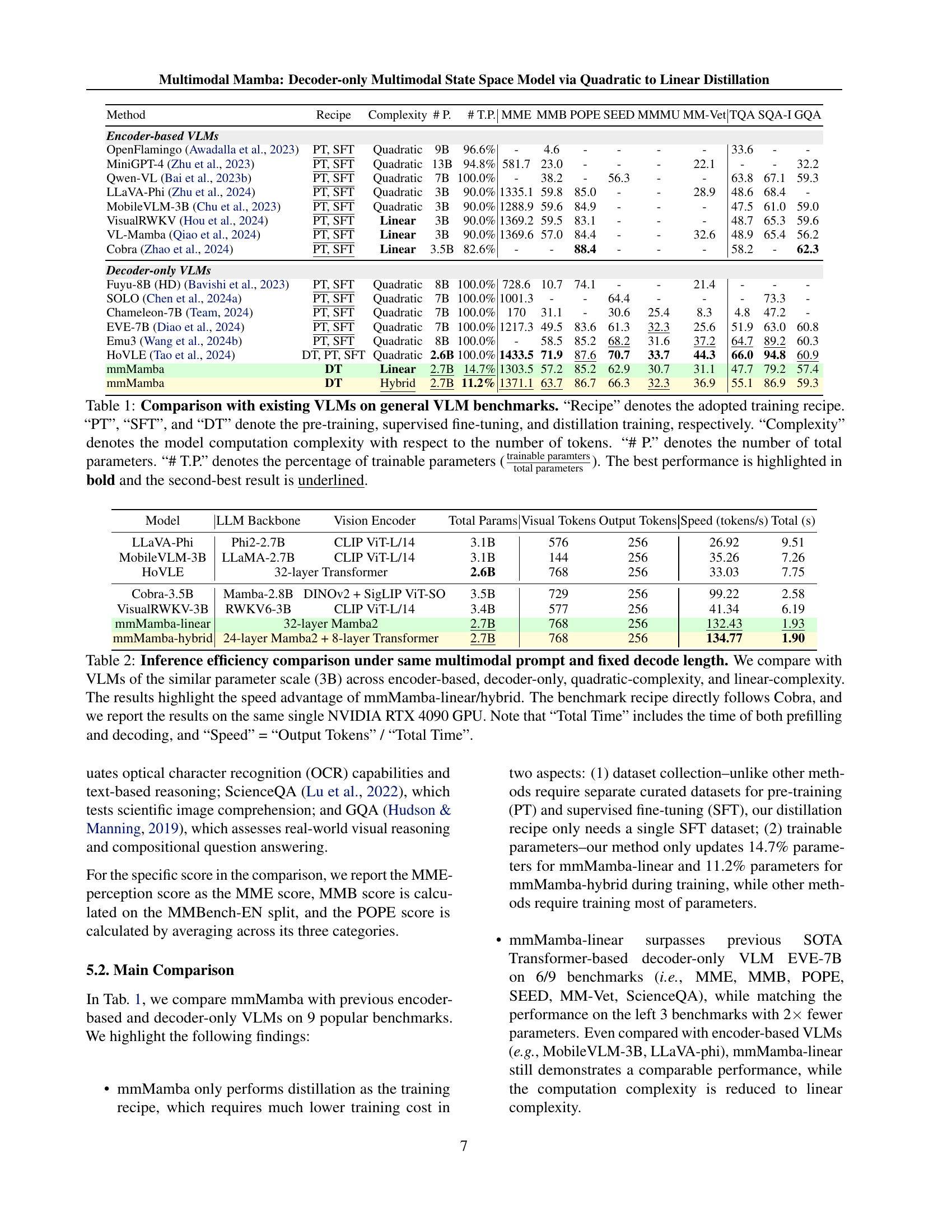
🔼 This table compares various Vision-Language Models (VLMs) on their performance across several benchmark datasets. It contrasts different model architectures (encoder-based vs. decoder-only) and training methods (pre-training, supervised fine-tuning, and distillation). Key metrics include the overall performance on each benchmark, model size (# of parameters), the proportion of trainable parameters, and the computational complexity (quadratic or linear) in relation to the input sequence length. The best performing model for each benchmark is highlighted in bold, while the second-best is underlined. This allows for a direct comparison of the trade-offs between performance, model size, and computational efficiency among different VLMs.
read the caption
Table 1: Comparison with existing VLMs on general VLM benchmarks. “Recipe” denotes the adopted training recipe. “PT”, “SFT”, and “DT” denote the pre-training, supervised fine-tuning, and distillation training, respectively. “Complexity” denotes the model computation complexity with respect to the number of tokens. “# P.” denotes the number of total parameters. “# T.P.” denotes the percentage of trainable parameters (trainable paramterstotal parameterstrainable paramterstotal parameters\frac{\text{trainable paramters}}{\text{total parameters}}divide start_ARG trainable paramters end_ARG start_ARG total parameters end_ARG). The best performance is highlighted in bold and the second-best result is underlined.
In-depth insights#
Quadratic to Linear#
The core concept of “Quadratic to Linear” in the context of the research paper likely revolves around optimizing the computational complexity of large multimodal language models (MLLMs). Traditional transformer-based models exhibit quadratic complexity, making them computationally expensive, especially for long sequences. This section likely details the techniques used to distill knowledge from these quadratic models into more efficient linear models. This involves transferring the core capabilities and understanding from a computationally expensive architecture to a more resource-friendly one, significantly reducing the computational burden without sacrificing performance too drastically. The process probably involves architectural modifications, potentially introducing linear-complexity mechanisms like the Mamba-2 state space model, and sophisticated distillation strategies to effectively transfer knowledge between the two architectures. The result is a MLLM that maintains performance while boasting a significant advantage in terms of speed and memory efficiency, making it more practical for real-world applications.
Decoder-only VLMs#
Decoder-only Vision Language Models (VLMs) represent a significant shift in multimodal architecture design. Unlike encoder-decoder models, which process visual and textual information separately before combining them, decoder-only VLMs process both modalities within a unified decoder network. This approach simplifies the architecture, potentially reducing computational complexity and improving efficiency. However, decoder-only VLMs often present challenges in effectively integrating heterogeneous data types. Successfully training and deploying effective decoder-only VLMs requires careful consideration of pre-training strategies, the ability to handle long sequences of visual and textual information, and the inherent trade-offs between model size and performance. While some approaches address these challenges through innovative training techniques or architectural modifications, there remains a need for improved methods to enhance their performance, efficiency, and generalizability to various vision-language tasks. The advantages of a unified approach, especially concerning inference speed and reduced resource requirements, make decoder-only VLMs an active area of research with promising potential for real-world applications.
Progressive Distillation#
Progressive distillation, as described in the context of the research paper, is a multi-stage training strategy designed to effectively transfer knowledge from a complex, quadratic-complexity model (like a Transformer-based VLM) to a simpler, linear-complexity model (like a Mamba-2 based VLM). This approach is crucial because it tackles the challenge of directly converting a pre-trained, high-performing model into a more efficient architecture without significant performance degradation. The methodology appears to involve three main stages: initializing the simpler model with parameters from the complex model, followed by layer-wise training and alignment, and finally, end-to-end fine-tuning to optimize overall performance. This stepwise refinement process mitigates the difficulties associated with a direct transfer, allowing for a gradual adaptation and stabilization of the linear model. The use of different loss functions at each stage, such as MSE and KL-divergence, also suggests a tailored approach to address varying aspects of model behavior. This progressive method is key to obtaining a linear-complexity model that maintains the multimodal capabilities of its teacher model. By incrementally transferring knowledge, the method overcomes the challenges of simply initializing the target model with the source’s parameters. The three-stage approach, therefore, ensures the success of the distillation while addressing the complexities of adapting between different model architectures.
Efficiency Analysis#
The efficiency analysis section of the paper focuses on evaluating the computational performance gains achieved by the proposed mmMamba model. The key aspect is the comparison of inference speed and memory usage between mmMamba and existing models, particularly HoVLE, a quadratic-complexity model. Experiments demonstrate that mmMamba significantly outperforms HoVLE in terms of speed and memory efficiency, especially when processing longer sequences, highlighting its suitability for real-world applications demanding high throughput and low latency. The analysis also explores architectural variations of mmMamba, comparing a purely linear version (mmMamba-linear) with a hybrid version (mmMamba-hybrid). The results show a trade-off between performance and resource consumption, where the hybrid model offers a balance between speed and accuracy. The substantial speedup and memory savings achieved by mmMamba underscore its potential for deploying large-scale multimodal language models efficiently on resource-constrained devices. This is a significant contribution, as it tackles the major bottleneck of high computational costs typically associated with large, transformer-based models.
Hybrid Architecture#
The research explores a hybrid architecture combining the strengths of Transformer and Mamba-2 layers. This approach offers a flexible trade-off between computational efficiency and model capability. By strategically interleaving Transformer layers (which excel in complex feature representation) with Mamba-2 layers (known for linear computational complexity), the model adapts to diverse deployment needs. The number of interleaved Transformer layers can be adjusted to fine-tune this balance, making it highly adaptable to resource constraints. Experiments demonstrate that a hybrid model incorporating both architecture types significantly improves performance over a purely linear model while maintaining computational benefits compared to full Transformer models, showing the hybrid model’s effectiveness in balancing performance and efficiency.
More visual insights#
More on tables
| Model | LLM Backbone | Vision Encoder | Total Params | Visual Tokens | Output Tokens | Speed (tokens/s) | Total (s) |
| LLaVA-Phi | Phi2-2.7B | CLIP ViT-L/14 | 3.1B | 576 | 256 | 26.92 | 9.51 |
| MobileVLM-3B | LLaMA-2.7B | CLIP ViT-L/14 | 3.1B | 144 | 256 | 35.26 | 7.26 |
| HoVLE | 32-layer Transformer | 2.6B | 768 | 256 | 33.03 | 7.75 | |
| Cobra-3.5B | Mamba-2.8B | DINOv2 + SigLIP ViT-SO | 3.5B | 729 | 256 | 99.22 | 2.58 |
| VisualRWKV-3B | RWKV6-3B | CLIP ViT-L/14 | 3.4B | 577 | 256 | 41.34 | 6.19 |
| mmMamba-linear | 32-layer Mamba2 | 2.7B | 768 | 256 | 132.43 | 1.93 | |
| mmMamba-hybrid | 24-layer Mamba2 + 8-layer Transformer | 2.7B | 768 | 256 | 134.77 | 1.90 | |
🔼 Table 2 presents a comparison of the inference efficiency of various Vision-Language Models (VLMs), focusing on speed and resource utilization. Models with similar parameter scales (around 3 billion parameters) are compared across different architectural categories: encoder-based, decoder-only, quadratic complexity, and linear complexity. The experiment uses the same multimodal prompt and fixed decode length for a fair comparison. The results demonstrate the significant speed advantage of the mmMamba-linear and mmMamba-hybrid models, especially when considering the total time (prefilling + decoding). The metrics reported are speed in tokens per second and total inference time, highlighting the efficiency gains achieved by the proposed mmMamba models on a single NVIDIA RTX 4090 GPU.
read the caption
Table 2: Inference efficiency comparison under same multimodal prompt and fixed decode length. We compare with VLMs of the similar parameter scale (3B) across encoder-based, decoder-only, quadratic-complexity, and linear-complexity. The results highlight the speed advantage of mmMamba-linear/hybrid. The benchmark recipe directly follows Cobra, and we report the results on the same single NVIDIA RTX 4090 GPU. Note that “Total Time” includes the time of both prefilling and decoding, and “Speed” = “Output Tokens” / “Total Time”.
| ID | Stage1 | Stage2 | Stage3 | MME | POPE | TextVQA | SQA-I |
| 1 | NAN | NAN | NAN | NAN | |||
| 2 | ✓ | 969.8 | 70.6 | 13.47 | 40.8 | ||
| 3 | ✓ | 1007.1 | 72.9 | 25.5 | 52.1 | ||
| 4 | ✓ | 1188.4 | 83.0 | 40.0 | 63.4 | ||
| 5 | ✓ | ✓ | 1108.9 | 75.3 | 28.0 | 59.3 | |
| 6 | ✓ | ✓ | 1263.1 | 84.0 | 42.5 | 77.1 | |
| 7 | ✓ | ✓ | 1255.5 | 83.5 | 41.1 | 72.1 | |
| 8 | ✓ | ✓ | ✓ | 1303.5 | 85.2 | 47.7 | 79.2 |
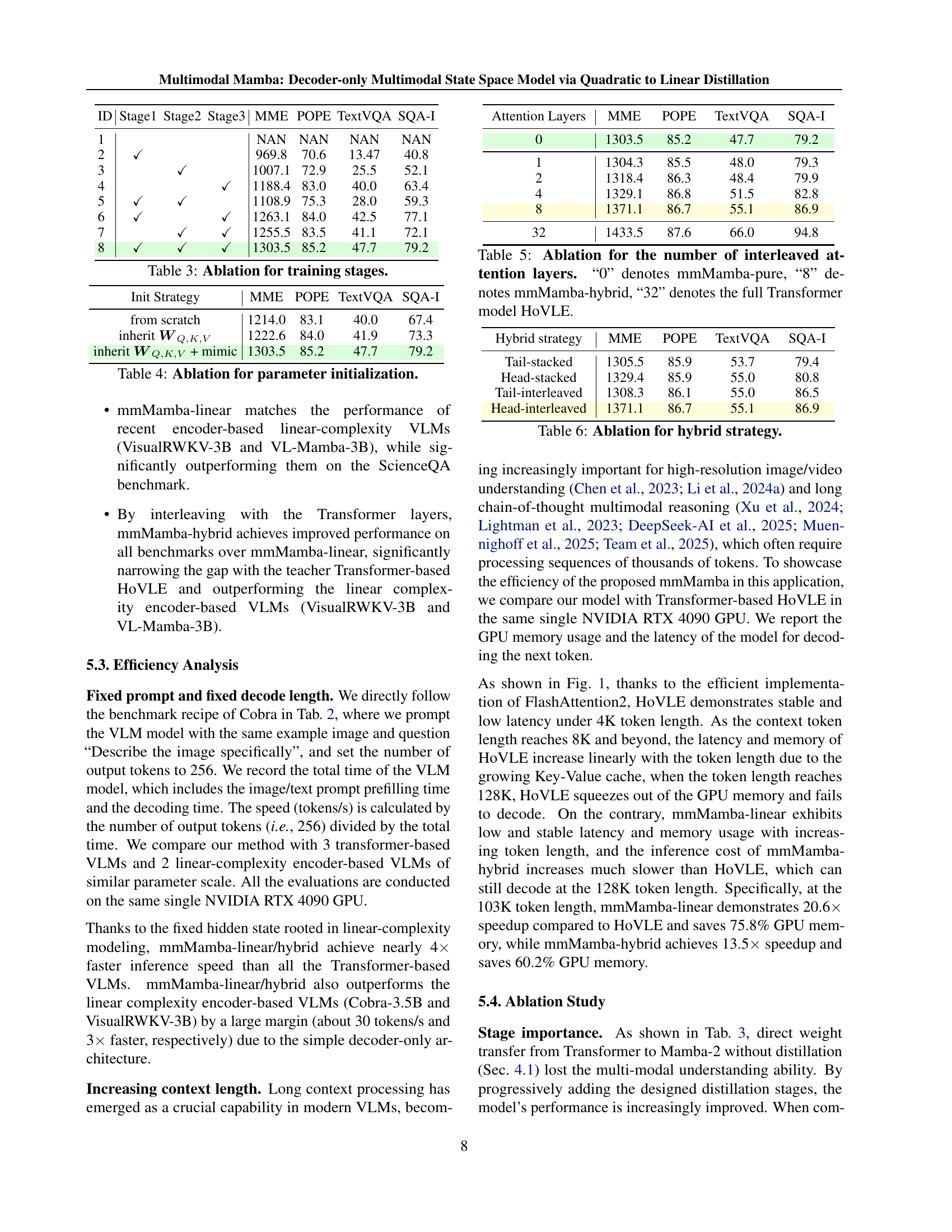
🔼 This table presents the ablation study on the effect of different training stages in the mmMamba model. It shows the performance on four metrics (MME, POPE, TextVQA, SQA-I) when only the first stage, the first two stages, and all three stages of the distillation process are used. The results demonstrate the progressive improvement in performance as more stages are included.
read the caption
Table 3: Ablation for training stages.
| Init Strategy | MME | POPE | TextVQA | SQA-I |
| from scratch | 1214.0 | 83.1 | 40.0 | 67.4 |
| inherit | 1222.6 | 84.0 | 41.9 | 73.3 |
| inherit + mimic | 1303.5 | 85.2 | 47.7 | 79.2 |
🔼 This table presents an ablation study on different parameter initialization strategies for the mmMamba model. It compares the performance of three approaches: initializing parameters randomly from scratch, inheriting only the weight matrices WQ, WK, and WV from the Transformer, and a combined approach inheriting those weights while also mimicking the original Transformer’s behavior. The results show the impact of each initialization method on the model’s performance across multiple vision-language benchmarks (MME, POPE, TextVQA, and SQA-I).
read the caption
Table 4: Ablation for parameter initialization.
| Attention Layers | MME | POPE | TextVQA | SQA-I |
| 0 | 1303.5 | 85.2 | 47.7 | 79.2 |
| 1 | 1304.3 | 85.5 | 48.0 | 79.3 |
| 2 | 1318.4 | 86.3 | 48.4 | 79.9 |
| 4 | 1329.1 | 86.8 | 51.5 | 82.8 |
| 8 | 1371.1 | 86.7 | 55.1 | 86.9 |
| 32 | 1433.5 | 87.6 | 66.0 | 94.8 |
🔼 This table presents an ablation study on the number of interleaved Transformer layers in the mmMamba model. It shows how performance varies across different vision-language tasks (MME, POPE, TextVQA, SQA-I) when using only Mamba-2 layers (mmMamba-pure, denoted by ‘0’), a hybrid architecture with 8 interleaved Transformer layers (mmMamba-hybrid, denoted by ‘8’), and the full Transformer-based HoVLE model (denoted by ‘32’) as a baseline for comparison. The results illustrate the trade-off between efficiency and performance achieved by varying the proportion of Mamba-2 and Transformer layers.
read the caption
Table 5: Ablation for the number of interleaved attention layers. “0” denotes mmMamba-pure, “8” denotes mmMamba-hybrid, “32” denotes the full Transformer model HoVLE.
| Hybrid strategy | MME | POPE | TextVQA | SQA-I |
| Tail-stacked | 1305.5 | 85.9 | 53.7 | 79.4 |
| Head-stacked | 1329.4 | 85.9 | 55.0 | 80.8 |
| Tail-interleaved | 1308.3 | 86.1 | 55.0 | 86.5 |
| Head-interleaved | 1371.1 | 86.7 | 55.1 | 86.9 |
🔼 This table presents an ablation study on the hybrid strategy used in the mmMamba model. It investigates the impact of different ways of interleaving Transformer and Mamba-2 layers on the model’s performance across various metrics (MME, POPE, TextVQA, SQA-I). The hybrid strategy aims to balance computational efficiency and performance by selectively replacing Transformer layers with Mamba-2 layers, thus exploring the optimal configuration for a given task.
read the caption
Table 6: Ablation for hybrid strategy.
Full paper#