TL;DR#
Inspired by DeepSeek-R1, this paper explores rule-based reinforcement learning (RL) to improve reasoning in LLMs using synthetic logic puzzles due to their controllable nature and answer verification. To address challenges with naive training, the authors make key technical contributions. This includes a system prompt to emphasize thinking, a format reward function to penalize shortcuts and a training recipe to achieve convergence. By doing so, the model can develop the ability to reflect, verify and summarize.
This paper introduces Logic-RL, a framework using the REINFORCE++ algorithm and designs from DeepSeek-R1. After training a 7B model on 5K logic problems, it demonstrated generalization to math benchmarks like AIME and AMC. During training, the model allocated more steps to reason, expanding from hundreds to thousands of tokens. Key findings include: language mixing hinders reasoning, increased ’thinking’ tokens help, and RL generalizes better than SFT.
Key Takeaways#
Why does it matter?#
This paper introduces Logic-RL, which develops advanced reasoning skills such as reflection and verification that generalizes to math benchmarks. This work suggests rule-based RL can unlock emergent abilities in LLMs, offering new directions for reasoning research and task adaptation.
Visual Insights#

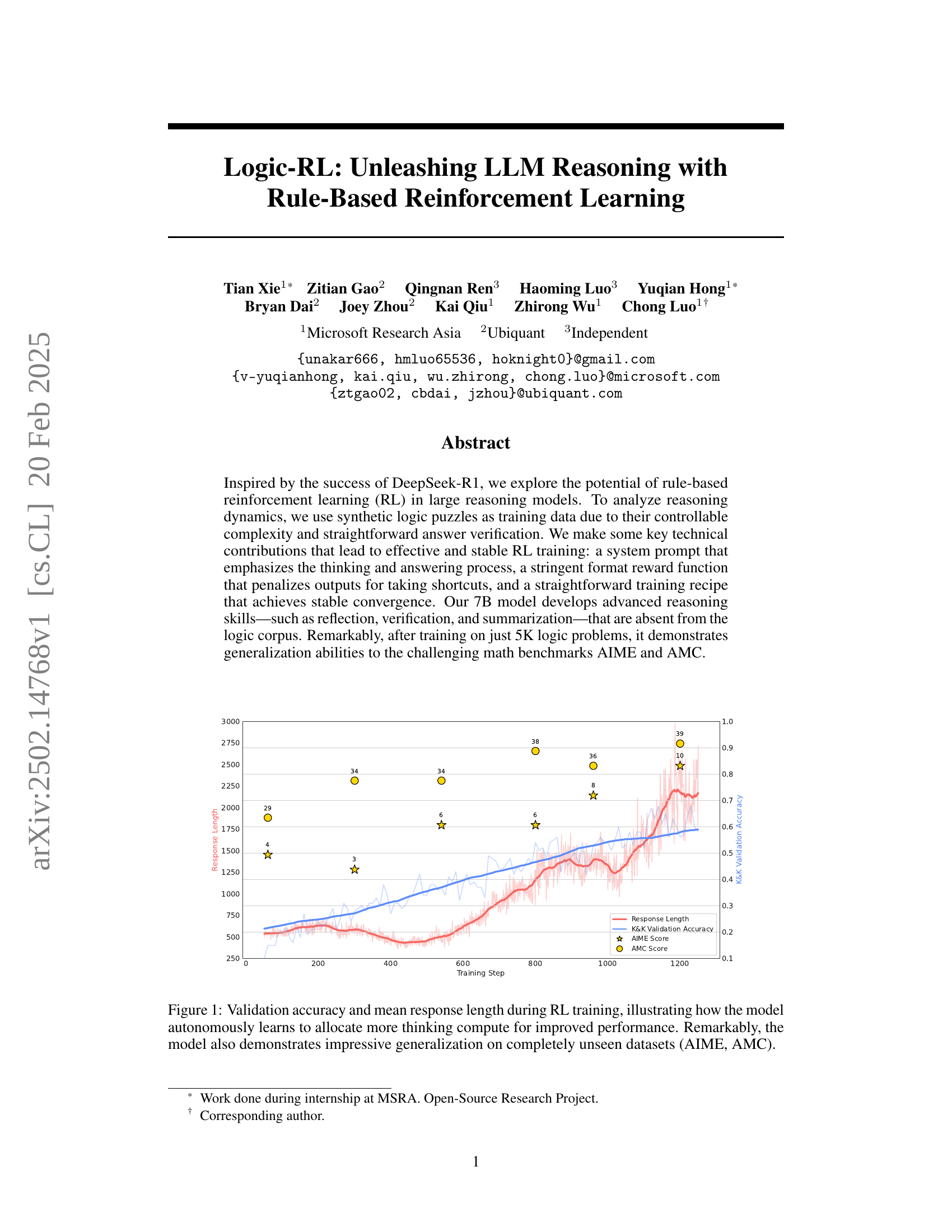
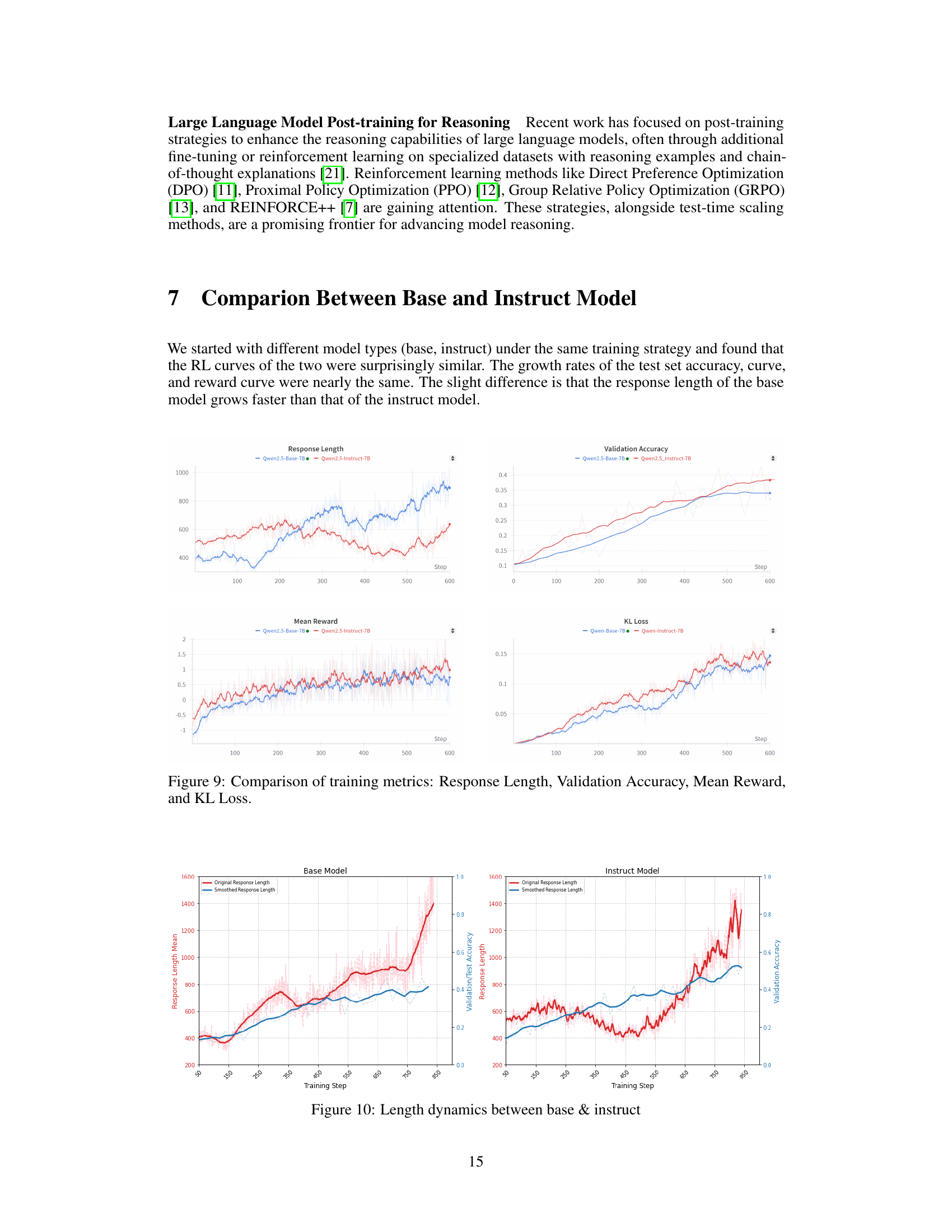
🔼 This figure displays the validation accuracy and average response length of a language model during reinforcement learning (RL) training. The x-axis represents the training step, showing progress over time. The y-axis on the left shows validation accuracy, indicating how well the model performs on unseen data. The y-axis on the right shows the mean response length, demonstrating the model’s increasing use of ’thinking’ steps. The plot shows a clear correlation: as the model’s performance improves, it allocates more resources to deliberation. The plot also includes the performance on two external, unseen benchmarks (AIME and AMC) that demonstrate the model’s generalization ability after training.
read the caption
Figure 1: Validation accuracy and mean response length during RL training, illustrating how the model autonomously learns to allocate more thinking compute for improved performance. Remarkably, the model also demonstrates impressive generalization on completely unseen datasets (AIME, AMC).
| Algorithm | Train Batch Size | Rollout N | KL Coef | Max Response Len |
| REINFORCE++ | 8 | 8 | 0.001 | 4096 |
🔼 This table lists the hyperparameters used during the training process of the Logic-RL model. It shows the algorithm used (REINFORCE++), the batch size for training, the number of rollouts per update, the coefficient for the KL divergence penalty, and the maximum response length allowed during training. These parameters are crucial for controlling the training process and achieving optimal performance. Understanding these values helps in interpreting the results of the Logic-RL model and potentially reproducing or adapting the training process for similar tasks.
read the caption
Table 1: Important Training Parameters
In-depth insights#
Logic-RL Intro#
The paper introduces Logic-RL, a novel framework leveraging rule-based reinforcement learning for enhancing reasoning capabilities in LLMs. Inspired by DeepSeek-R1’s success, it explores RL’s potential using synthetic logic puzzles as training data due to their controllable complexity and straightforward answer verification. A key contribution lies in a system prompt emphasizing the thinking process, alongside a strict reward function that penalizes shortcuts, leading to stable convergence. The paper highlights the development of advanced reasoning skills like reflection, verification, and summarization in a 7B model, trained on a small logic corpus, demonstrating generalization to challenging math benchmarks like AIME and AMC, suggesting the emergence of abstract problem-solving schemata rather than mere domain-specific pattern matching. This cross-domain transfer is remarkable given the limited training data.
K&K Data Design#
The paper leverages the Knights and Knaves (K&K) puzzles due to their structured nature, enabling controlled experiments on reasoning dynamics. The procedural generation ensures consistency and infinite variability, serving as unseen data for generalization testing. Difficulty is precisely adjustable, allowing for curriculum learning design by varying characters and logical operations. The puzzles have unambiguous ground truth, facilitating accurate evaluation and minimizing reward hacking. These features make K&K ideal for studying reasoning dynamics in isolation, distinguishing genuine reasoning from superficial memorization. Its well-defined nature allows for precise study. This is essential when you need an accurate result.
Aha: Gradual Rise#
The concept of an “Aha!” moment, often associated with sudden insights, takes on a different character in the context of LLM reasoning. Instead of a singular, dramatic breakthrough, the rise to complex reasoning capabilities seems to be gradual. There is no instantaneous leap in performance; rather, skills such as self-reflection, exploration, and verification emerge incrementally. The model refines its approach over time, exhibiting a steady increase in sophistication. This gradualism suggests that the underlying mechanisms involve progressive adjustments to the model’s parameters. The “Aha!” is not a flash of brilliance, but the result of sustained learning. This makes RL, a more appropriate framework for inducing such capabilities. RL relies on incremental feedback and iterative adjustments, leading to gradual refinement. It aligns with the observed phenomenon of skills development, where reasoning abilities accumulate through trial and error. The journey is marked by incremental improvements, not sudden transformations.
RL>SFT Ability#
Reinforcement Learning (RL) often fosters greater generalization compared to Supervised Fine-Tuning (SFT). While SFT excels at mimicking training data patterns, RL encourages exploration and independent problem-solving. This leads to models that don’t just memorize but develop enhanced reasoning capabilities. RL models adapts to unseen data more effectively as RL optimizes for rewards, not exact replication. SFT can overfit to the training format, RL cultivates robust skills that transfer across diverse scenarios. SFT is more likely to struggle with modified input because RL encourages active learning, it can adapt in real-time. RL-trained models have greater problem-solving flexibility by building true reasoning capabilities.
Scale Logic-RL#
Scaling Logic-RL is a promising avenue for enhancing LLM reasoning. Moving beyond small logic datasets is crucial. Future research should prioritize real-world mathematical and coding scenarios. This involves exploring diverse, complex datasets. Addressing limitations like long response lengths and high computational cost is essential. Chain-of-thought shortening methods and more stable RL training techniques can help. Also, the use of code-switching as a tool.
More visual insights#
More on figures
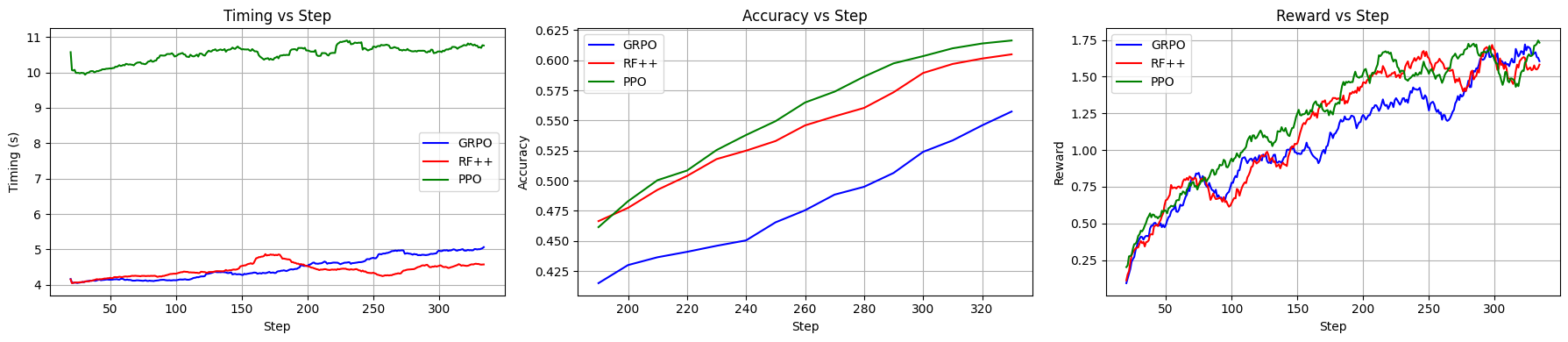
🔼 This figure compares the performance of three reinforcement learning algorithms: GRPO, REINFORCE++, and PPO. The comparison is made across three key metrics: training speed (time taken to reach a certain number of training steps), accuracy (how well the model performs on a validation set), and reward gain (the amount of reward accumulated during training). The results are averaged using a sliding window of 50 steps to smooth out any noise and highlight the overall trends. The graph visually represents how each algorithm performs over a set of training steps.
read the caption
Figure 2: Comparison of GRPO (Blue), REINFORCE++ (Red), and PPO (Green) performance (averaged by sliding window = 50) in terms of training speed, accuracy, and reward gain.

🔼 This figure examines the effects of complex reasoning behaviors and language mixing on the model’s performance. The analysis focuses on the impact of specific tokens, such as ‘verify’ and ’re-evaluate,’ which are associated with higher scores when present in the model’s responses. Conversely, the inclusion of tokens from languages other than English leads to lower scores, highlighting the model’s sensitivity to language consistency and its preference for explicit verification during the reasoning process. The bar chart visually represents the average answer scores with and without these key tokens and language mixing, providing a clear comparison of their influence on the model’s reasoning abilities.
read the caption
Figure 3: Impact of complex reasoning behaviours and language mixing on reasoning performance. We analyzed the model’s answer rewards for responses containing the tokens shown in the figure. Responses with 'verify' and 're-evaluate' scored significantly higher than those without these words. Conversely, responses containing certain tokens from other languages generally received lower scores.

🔼 The figure shows the frequency of the word ‘verify’ appearing in the model’s responses during the first 1800 training steps. The frequency increases gradually over time, indicating that the model increasingly uses the word ‘verify’ as it learns to perform more complex reasoning, which involves self-verification. This is consistent with the model’s development of emergent reasoning behaviors like reflection and verification discussed in the paper.
read the caption
(a) Verify

🔼 The figure shows the impact of specific tokens on reasoning performance. The word ’re-evaluate’ is highlighted because its presence in the model’s reasoning process leads to significantly higher average answer scores compared to when it is absent. This suggests that the act of reconsidering and refining one’s reasoning process is a key factor in improved performance. The graph visually demonstrates this effect by comparing average answer scores with and without the token ’re-evaluate’.
read the caption
(b) Re-evaluate

🔼 The figure shows the frequency of the word ‘check’ appearing in the model’s responses during training. The frequency increases gradually over time, suggesting that the model’s self-verification behavior develops steadily, not suddenly.
read the caption
(c) Check

🔼 This figure displays the frequency of the word ‘yet’ appearing in the model’s responses during the first 1800 training steps of the reinforcement learning process. The steady, gradual increase in frequency suggests there was no sudden ‘aha moment’ or breakthrough in the model’s reasoning abilities. Instead, the development of more complex reasoning behaviors, including reflection and self-verification, appears to have been incremental and continuous.
read the caption
(d) Yet

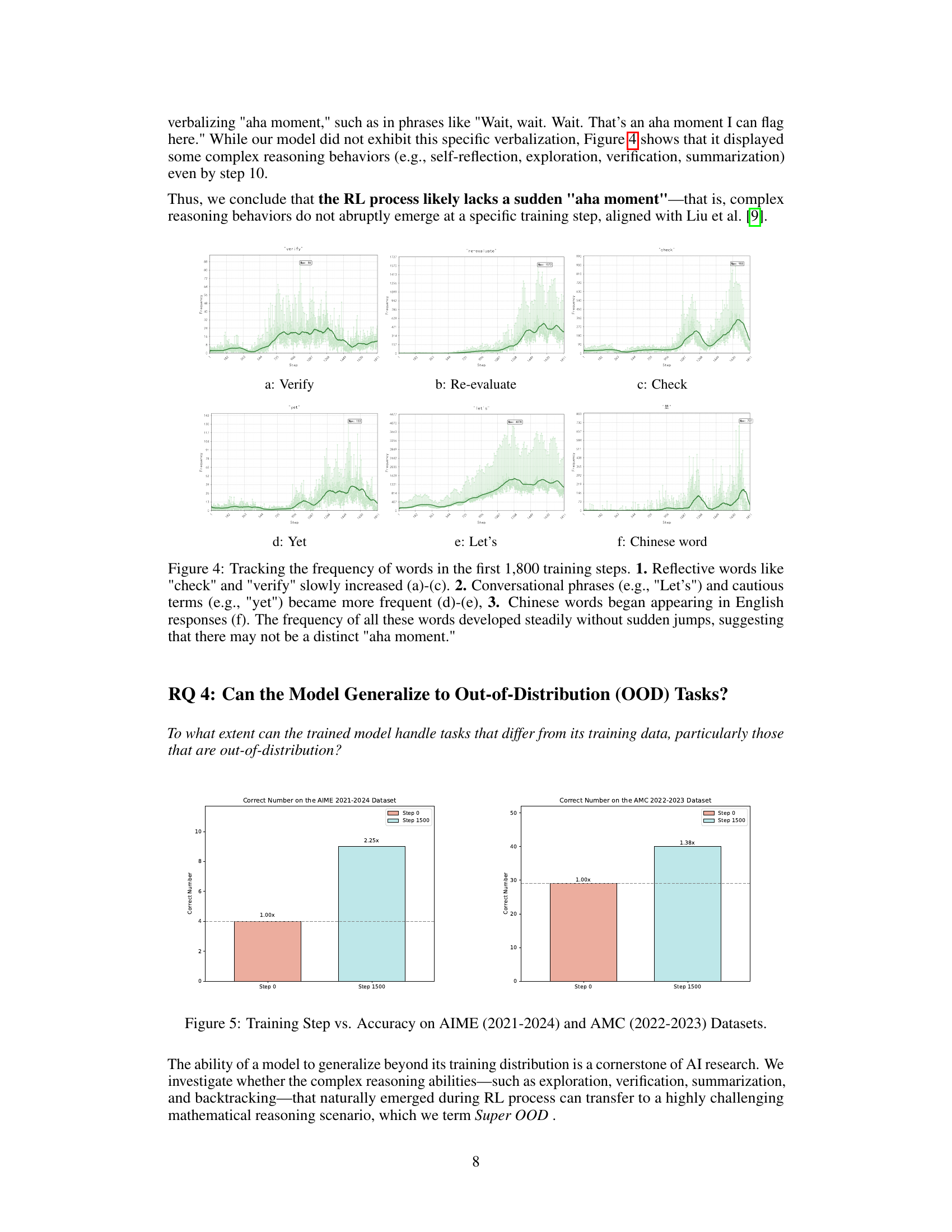
🔼 The figure displays the frequency of specific words during the first 1800 steps of the RL training process. It visualizes how the frequency of words related to reflection (‘verify’, ’re-evaluate’, ‘check’), cautiousness (‘yet’), conversational phrases (’let’s’), and even a Chinese word, changed over time. The relatively gradual and consistent increase in frequency of these words, rather than a sudden spike, suggests a lack of a distinct ‘aha moment’ in the model’s learning process.
read the caption
(e) Let’s

🔼 The figure shows the frequency of Chinese words appearing in the English responses generated by the model during the RL training process. This unexpected appearance of Chinese words within responses primarily written in English suggests the model might be utilizing or accessing internal representations or mechanisms that involve Chinese vocabulary, even when the task and training data primarily use English.
read the caption
(f) Chinese word

🔼 This figure displays the frequency of specific words over the initial 1800 training steps. It visually demonstrates the gradual increase in the use of reflective words (‘check’, ‘verify’), conversational phrases (‘Let’s’), and cautious terms (‘yet’). Interestingly, the appearance of Chinese words in English responses is also tracked. The steady, non-abrupt increase in word frequency suggests a continuous learning process rather than a sudden ‘aha moment’ of understanding.
read the caption
Figure 4: Tracking the frequency of words in the first 1,800 training steps. 1. Reflective words like 'check' and 'verify' slowly increased (a)-(c). 2. Conversational phrases (e.g., 'Let’s') and cautious terms (e.g., 'yet') became more frequent (d)-(e), 3. Chinese words began appearing in English responses (f). The frequency of all these words developed steadily without sudden jumps, suggesting that there may not be a distinct 'aha moment.'

🔼 This figure displays the model’s accuracy on the American Invitational Mathematics Examination (AIME) from 2021-2024 and the American Mathematics Competitions (AMC) from 2022-2023, demonstrating its generalization capabilities to out-of-distribution datasets. The x-axis represents the training step, showing the model’s performance improvement over time. The y-axis shows the accuracy on each dataset. The figure showcases the model’s ability to generalize its learned reasoning skills beyond the specific training data.
read the caption
Figure 5: Training Step vs. Accuracy on AIME (2021-2024) and AMC (2022-2023) Datasets.

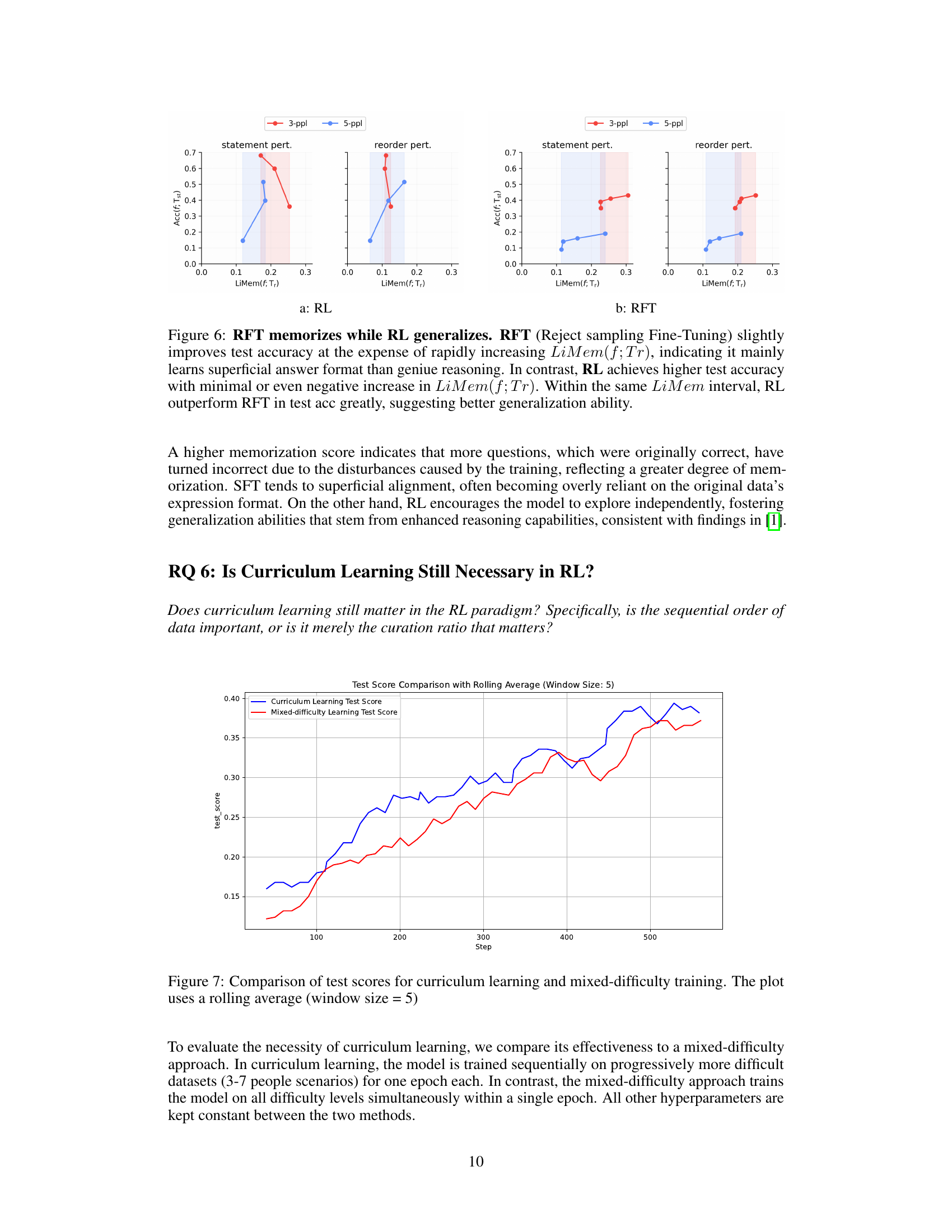
🔼 Figure 6 presents a comparison of the generalization capabilities of Reinforcement Learning (RL) and Reject Sampling Fine-Tuning (RFT). The x-axis represents the Local Inconsistency-based Memorization Score (LiMem), which measures how sensitive the model is to changes in problem structure. A high LiMem indicates memorization of training data, whereas a low LiMem signifies robust generalization. The y-axis depicts test accuracy on unseen data. The results demonstrate that RL achieves significantly higher accuracy on perturbed test instances (i.e., those with changes to wording or order) compared to RFT, indicating that RL learns true reasoning skills rather than memorizing superficial patterns. In contrast, RFT prioritizes superficial pattern matching, resulting in higher memorization, and diminished accuracy on unseen data.
read the caption
(a) RL

🔼 Figure 6b presents the results of a Reject Sampling Fine-Tuning (RFT) experiment. It displays the relationship between the model’s memorization level (LiMem) and its accuracy on unseen test data. The x-axis represents LiMem, measuring the extent to which the model has memorized the training data. The y-axis shows the accuracy on test data, indicating the model’s ability to generalize to unseen examples. The figure showcases that as the model memorizes more training data (increasing LiMem), its ability to generalize to new data decreases (lower accuracy). This contrasts sharply with the results shown in Figure 6a, which illustrate the generalization capability of reinforcement learning, where the model’s ability to generalize to new data increases along with its memorization of training data.
read the caption
(b) RFT

🔼 This figure compares the generalization capabilities of Reinforcement Learning (RL) and Reject sampling Fine-Tuning (RFT). The x-axis represents the memorization score (LiMem(f;Tr)), measuring how much a model relies on memorizing the training data rather than learning underlying reasoning principles. The y-axis shows the test accuracy. RFT initially shows higher test accuracy but quickly increases its memorization score, demonstrating superficial learning focused on memorizing answer formats. In contrast, RL achieves higher test accuracy with minimal or even negative increases in the memorization score, indicating a genuine understanding of reasoning principles and superior generalization ability.
read the caption
Figure 6: RFT memorizes while RL generalizes. RFT (Reject sampling Fine-Tuning) slightly improves test accuracy at the expense of rapidly increasing LiMem(f;Tr)𝐿𝑖𝑀𝑒𝑚𝑓𝑇𝑟LiMem(f;Tr)italic_L italic_i italic_M italic_e italic_m ( italic_f ; italic_T italic_r ), indicating it mainly learns superficial answer format than geniue reasoning. In contrast, RL achieves higher test accuracy with minimal or even negative increase in LiMem(f;Tr)𝐿𝑖𝑀𝑒𝑚𝑓𝑇𝑟LiMem(f;Tr)italic_L italic_i italic_M italic_e italic_m ( italic_f ; italic_T italic_r ). Within the same LiMem𝐿𝑖𝑀𝑒𝑚LiMemitalic_L italic_i italic_M italic_e italic_m interval, RL outperform RFT in test acc greatly, suggesting better generalization ability.
More on tables
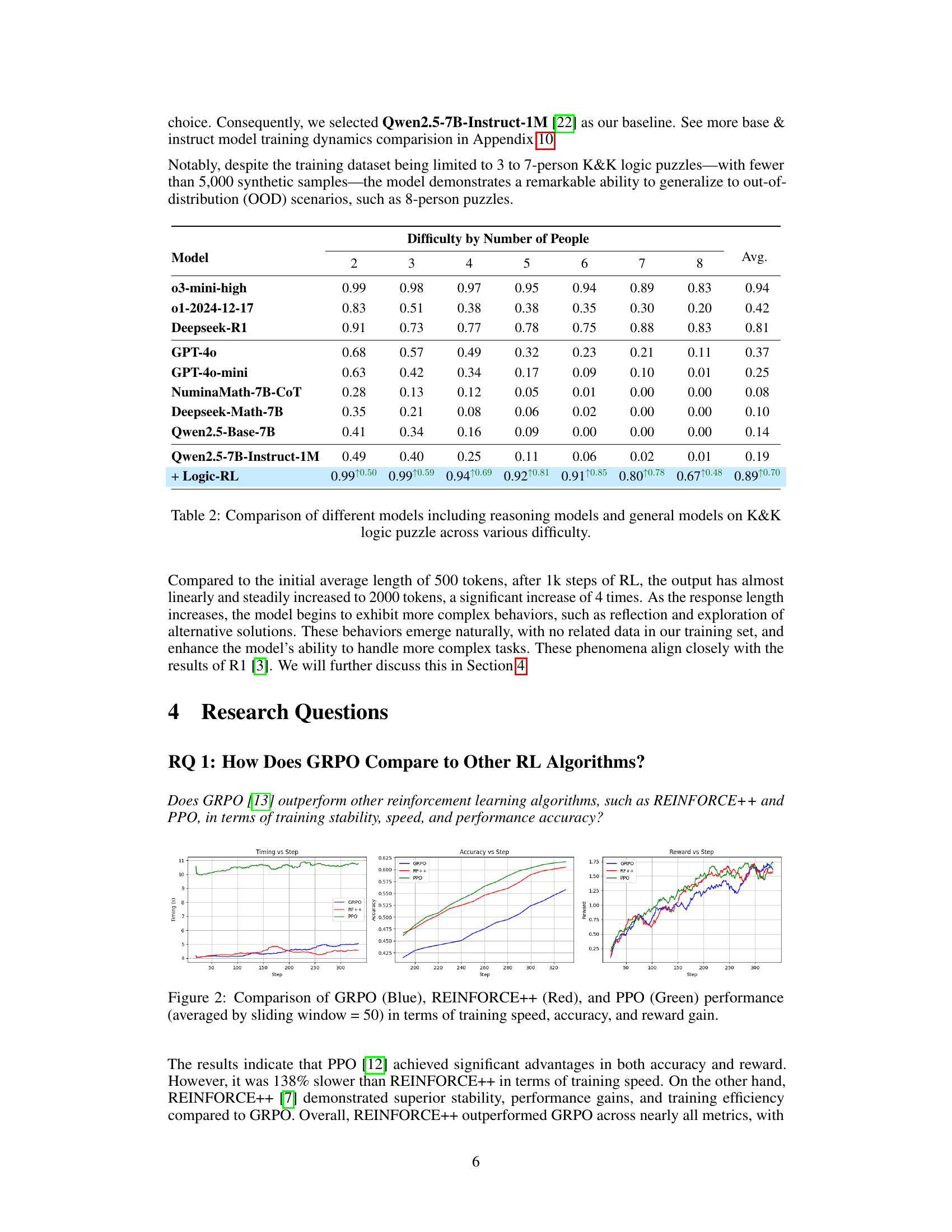
| Model | Difficulty by Number of People | |||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | Avg. | |
| o3-mini-high | 0.99 | 0.98 | 0.97 | 0.95 | 0.94 | 0.89 | 0.83 | 0.94 |
| o1-2024-12-17 | 0.83 | 0.51 | 0.38 | 0.38 | 0.35 | 0.30 | 0.20 | 0.42 |
| Deepseek-R1 | 0.91 | 0.73 | 0.77 | 0.78 | 0.75 | 0.88 | 0.83 | 0.81 |
| GPT-4o | 0.68 | 0.57 | 0.49 | 0.32 | 0.23 | 0.21 | 0.11 | 0.37 |
| GPT-4o-mini | 0.63 | 0.42 | 0.34 | 0.17 | 0.09 | 0.10 | 0.01 | 0.25 |
| NuminaMath-7B-CoT | 0.28 | 0.13 | 0.12 | 0.05 | 0.01 | 0.00 | 0.00 | 0.08 |
| Deepseek-Math-7B | 0.35 | 0.21 | 0.08 | 0.06 | 0.02 | 0.00 | 0.00 | 0.10 |
| Qwen2.5-Base-7B | 0.41 | 0.34 | 0.16 | 0.09 | 0.00 | 0.00 | 0.00 | 0.14 |
| Qwen2.5-7B-Instruct-1M | 0.49 | 0.40 | 0.25 | 0.11 | 0.06 | 0.02 | 0.01 | 0.19 |
| + Logic-RL | 0.99↑0.50 | 0.99↑0.59 | 0.94↑0.69 | 0.92↑0.81 | 0.91↑0.85 | 0.80↑0.78 | 0.67↑0.48 | 0.89↑0.70 |
🔼 This table compares the performance of various large language models (LLMs) on a dataset of Knights and Knaves (K&K) logic puzzles. The models are tested across different difficulty levels of the puzzles, which are determined by the number of characters involved. The table shows the average accuracy of each model across all difficulties, allowing for a direct comparison of their reasoning abilities. The models compared include both those specifically designed for reasoning tasks and general-purpose LLMs.
read the caption
Table 2: Comparison of different models including reasoning models and general models on K&K logic puzzle across various difficulty.
| Question: |
| A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie. Five residents (William, Chloe, Lily, Jack, and Logan) made the following statements: (1) William said: "William is a knight and Chloe is a knight." (2) Chloe said: "Lily is a knight." (3) Lily said: "William is a knave and Jack is a knight." (4) Jack said: "William is a knave." (5) Logan said: "Lily is a knave if and only if William is a knave." So who is a knight and who is a knave? |
| Response: <think> |
| To solve this, let’s start analyzing the statements one by one, beginning with William’s statement since it’s a good starting point due to its self-referential nature. |
| William’s statement: "William is a knight and Chloe is a knight." |
| - If William is telling the truth (i.e., he is a knight), then both parts of his statement must be true. However, if William is a knight, the statement "William is a knight" is true, but the statement "Chloe is a knight" cannot determine the truth about Chloe at this point since we haven’t analyzed Chloe’s statement yet. (Hesitate) Therefore, William cannot be a knight because it would lead to a contradiction. |
| … |
| Let’s test both possibilities. (Explore) |
| Testing Chloe as a knight: If Chloe is a knight, then her statement "Lily is a knight" is true, so Lily is a knight. |
| Analyzing Lily’s statement: "William is a knave and Jack is a knight." |
| … |
| Now, we have determined: (Summerize) |
| - William is a knave. |
| - Chloe is a knight. |
| … |
| Let’s verify all statements: (Verify) |
| - "William is a knight and Chloe is a knight" (False, since William is a knave). |
| - "Lily is a knight" (True). |
| … |
🔼 This table showcases an example of a large language model’s reasoning process after undergoing reinforcement learning. The model demonstrates several key emergent reasoning behaviors not present in its original training data. These include: hesitation and self-verification (expressed through phrases such as ‘I am not entirely sure; let’s re-check this step’), multi-path exploration and backtracking (where the model tries multiple solution approaches and revisits earlier steps), summarization of its reasoning process (condensing the reasoning into key points), and explicit verification of steps. The example problem is a logic puzzle involving knights and knaves, requiring the model to use deductive reasoning to determine the identity of each character based on their statements. The model’s response shows a thought process that resembles human problem-solving strategies, involving trial and error, exploration of different possibilities, and self-correction. This highlights the model’s ability to develop sophisticated reasoning skills during reinforcement learning without explicit instruction.
read the caption
Table 3: An example of a large language model trained through reinforcement learning naturally exhibiting reasoning behaviors such as hesitation, exploration, summarization, and verification, even though these behaviors were not present in the training data.
| Question: |
| A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie. Three residents (Jack, Samuel, Lily) made the following statements: (1) Jack said, "If Samuel is a knight, then Lily is a knave." (2) Samuel said, "If Jack is a knight, then Lily is a knave." (3) Lily said, "Jack is a knight." So who is a knight and who is a knave? |
| Response: <think> |
| Let’s analyze the statements step by step. |
| 1. Jack’s statement is: "If Samuel is a knight then Lily is a knave." |
| … |
| Now that we know Samuel is a knave, let’s analyze Samuel’s statement again: |
| - Samuel’s statement: "If Jack is a knight then Lily is a knave." |
| - An implication "If P then Q" is false only when P is true and Q is false. (Formula Application) Here, "If Jack is a knight then Lily is a knave" is false when Jack is a knight and Lily is not a knave. This is consistent with our previous conclusion that Jack is a knight and Lily is a knight. |
| … |
🔼 This table presents an example of how the model uses logical formulas to solve a Knights and Knaves puzzle. It demonstrates the model’s ability to apply formal logical reasoning, such as the implication formula (‘If P, then Q’), in solving the puzzle. This is particularly notable because these formal logical reasoning skills are not explicitly taught or demonstrated in the training data. The example shows the model’s step-by-step reasoning process, where it analyzes the statements given by the characters in the puzzle and reaches a conclusion based on its understanding of the logic involved. This illustrates the emergence of advanced reasoning capabilities in the model that are not present in its initial training.
read the caption
Table 4: An example of using logical formulas to solve a Knights and Knaves puzzle.
| Question:A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie. Six residents (Benjamin, Michael, Evelyn, Sophia, James, and Jacob) made the following statements: (1) Benjamin said, "If Sophia is a knight, then Evelyn is also a knight." (2) Michael said, "Benjamin is a knave, or James is a knight." (3) Evelyn said, "Sophia is a knight, or James is a knave." (4) Sophia said, "If Michael is a knave, then James is a knight." (5) James said, "Sophia is a knight, or Evelyn is a knight." (6) Jacob said, "Benjamin is a knave, and Sophia is a knight." So who is a knight and who is a knave? |
| Response: <think> |
| Let’s analyze each statement step-by-step based on whether the speaker is a knight or a knave. |
| 1. Benjamin: "If Sophia is a knight then Evelyn is a knight" |
| - If Benjamin is a knight, then the statement must be true. Thus, if Sophia is a knight, Evelyn has to be a knight. |
| 2. Michael: "Benjamin is a knave or James is a knight" |
| … |
| From Jacob’s statement, if Jacob is a knight then Sophia must be a knight and Benjamin must be a knave. |
| {CJK*}UTF8gbsn 以卡文的方式推理: - 假设 Jacob 是骑士,那么 Jacob 的声明 "Benjamin 是背叛者且 Sophia 是骑士" 就是真的。这意味着 Benjamin 是背叛者而 Sophia 是骑士。 - 既然 Sophia 是骑士,根据 Benjamin 的声明 "如果 Sophia 是骑士那么 Evelyn 也是骑士",Evelyn 也是骑士。 … 综上所述,Sophia, Evelyn, 和 Jacob 是骑士,而 Benjamin, Michael, 和 James 是背叛者。 (Language Switching) … |
🔼 This table showcases an example of the model’s reasoning process where it uses a mix of English and Chinese to solve a Knights and Knaves puzzle, highlighting the model’s ability to incorporate different linguistic structures during its problem-solving steps.
read the caption
Table 5: An example of our model used language switching to solve a Knights and Knaves puzzle.
Full paper#