TL;DR#
Current 3D human pose estimation methods often lack anatomical accuracy, limiting their use in biomechanics. These methods frequently violate joint angle limits, leading to unnatural and unrealistic poses. This gap highlights the need for approaches aligned with biomechanically accurate skeleton models. The paper aims to bridge this by creating predictions that respect anatomical constraints.
The study introduces a method named HSMR, which reconstructs humans using a biomechanically accurate skeleton from a single image. It uses the SKEL model and trains a transformer to estimate model parameters. Addressing the lack of training data, they create a pipeline to generate pseudo ground truth and iteratively refine it. HSMR matches state-of-the-art performance on benchmarks and improves results in extreme poses, ensuring realistic joint rotations.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the biomechanical accuracy in 3D human pose estimation, a critical factor for applications like biomechanics. By using a biomechanically accurate skeleton model, this research opens avenues for more realistic and reliable human pose estimation, advancing both computer vision and biomechanical simulations.
Visual Insights#

🔼 This figure illustrates the Human Skeleton and Mesh Recovery (HSMR) method. The method takes a single image of a person as input and outputs a 3D biomechanically accurate skeleton and a surface mesh. The skeleton is based on the SKEL model, and a transformer network is trained to estimate the model’s parameters from the input image. The figure shows example input images and corresponding side and top views of the recovered skeleton and mesh. To see more detailed results, the reader is directed to the project page.
read the caption
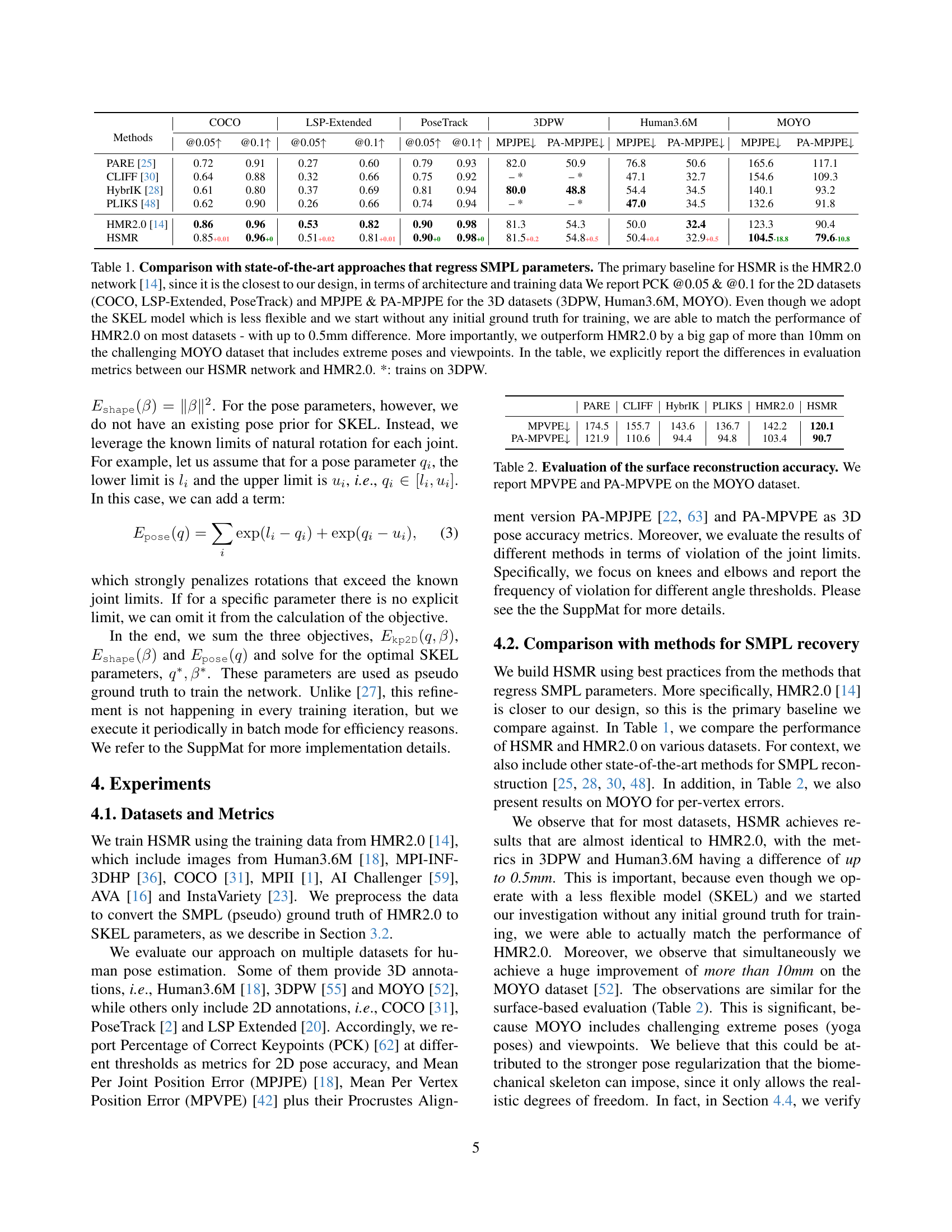
Figure 1: Human Skeleton and Mesh Recovery (HSMR). We propose an approach that recovers the biomechanical skeleton and the surface mesh of a human from a single image. We adopt a recent biomechanical model, SKEL [24] and train a transformer to estimate the parameters of the model. We encourage the reader to see the skeleton and surface reconstructions in our project page.
| Methods | COCO | LSP-Extended | PoseTrack | 3DPW | Human3.6M | MOYO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| @0.05 | @0.1 | @0.05 | @0.1 | @0.05 | @0.1 | MPJPE | PA-MPJPE | MPJPE | PA-MPJPE | MPJPE | PA-MPJPE | ||
| PARE [25] | 0.72 | 0.91 | 0.27 | 0.60 | 0.79 | 0.93 | 82.0 | 50.9 | 76.8 | 50.6 | 165.6 | 117.1 | |
| CLIFF [30] | 0.64 | 0.88 | 0.32 | 0.66 | 0.75 | 0.92 | – * | – * | 47.1 | 32.7 | 154.6 | 109.3 | |
| HybrIK [28] | 0.61 | 0.80 | 0.37 | 0.69 | 0.81 | 0.94 | 80.0 | 48.8 | 54.4 | 34.5 | 140.1 | 93.2 | |
| PLIKS [48] | 0.62 | 0.90 | 0.26 | 0.66 | 0.74 | 0.94 | – * | – * | 47.0 | 34.5 | 132.6 | 91.8 | |
| HMR2.0 [14] | 0.86 | 0.96 | 0.53 | 0.82 | 0.90 | 0.98 | 81.3 | 54.3 | 50.0 | 32.4 | 123.3 | 90.4 | |
| HSMR | 0.85 +0.01 | 0.96 +0 | 0.51 +0.02 | 0.81 +0.01 | 0.90 +0 | 0.98 +0 | 81.5 +0.2 | 54.8 +0.5 | 50.4 +0.4 | 32.9 +0.5 | 104.5 -18.8 | 79.6 -10.8 | |
🔼 Table 1 compares the performance of the proposed HSMR method with state-of-the-art human pose estimation methods that predict SMPL parameters. HMR2.0 serves as the primary baseline due to its similar architecture and training data to HSMR. The table reports PCK (Percentage of Correct Keypoints) for 2D datasets (COCO, LSP Extended, PoseTrack) and MPJPE (Mean Per Joint Position Error) and PA-MPJPE (Procrustes Aligned MPJPE) for 3D datasets (3DPW, Human3.6M, MOYO). Despite using the less flexible SKEL model and lacking initial ground truth for training, HSMR achieves comparable performance to HMR2.0 (within 0.5mm difference) on most datasets. Significantly, HSMR substantially outperforms HMR2.0 on the MOYO dataset (more than 10mm improvement), which contains challenging extreme poses and viewpoints. The table highlights these differences in evaluation metrics between HSMR and HMR2.0. Note that one method (*) uses 3DPW for training.
read the caption
Table 1: Comparison with state-of-the-art approaches that regress SMPL parameters. The primary baseline for HSMR is the HMR2.0 network [14], since it is the closest to our design, in terms of architecture and training data We report PCK @0.05 & @0.1 for the 2D datasets (COCO, LSP-Extended, PoseTrack) and MPJPE & PA-MPJPE for the 3D datasets (3DPW, Human3.6M, MOYO). Even though we adopt the SKEL model which is less flexible and we start without any initial ground truth for training, we are able to match the performance of HMR2.0 on most datasets - with up to 0.5mm difference. More importantly, we outperform HMR2.0 by a big gap of more than 10mm on the challenging MOYO dataset that includes extreme poses and viewpoints. In the table, we explicitly report the differences in evaluation metrics between our HSMR network and HMR2.0. *: trains on 3DPW.
In-depth insights#
BioMech. Skeleton#
The biomechanical skeleton is a crucial component for realistic human modeling, as it ensures anatomical accuracy and plausible movements. Unlike simplified skeletons, a biomechanical skeleton incorporates joint limits and constraints, preventing unnatural poses often seen in models using basic skeletal structures. This accuracy is vital for applications like biomechanics and simulations where realistic human motion is essential. Models like SKEL aim to integrate biomechanical fidelity with surface mesh representations, improving the accuracy of 3D human reconstruction. The challenge lies in accurately estimating the parameters of these complex skeletons from input data like images, requiring sophisticated methods and datasets.
Pseudo GT Refine#
The iterative pseudo-label refinement is a crucial aspect. It addresses the lack of real data, where we iteratively improve the quality of the labels used for training. It enables training of more accurate and reliable models. The process is inspired by previous works. Specifically, a network estimate is refined iteratively to align with the 2D keypoints. The optimized estimates serve as more accurate pseudo-ground truth. This entire process helps the model to supervise the network more accurately.
Extreme Pose++#
While the title “Extreme Pose++” isn’t present in the paper, one can speculate on its meaning based on the content. It likely refers to an enhanced method for handling extreme poses in 3D human reconstruction. The “++” suggests an improvement over existing techniques, possibly addressing limitations in accurately capturing and representing challenging poses. This might involve novel data augmentation strategies, specialized network architectures, or biomechanical constraints, to better regularize the estimated pose. Robustness in extreme poses is vital for real-world applications where human movement isn’t always constrained, so the proposed method tackles this, while achieving competitive performance on standard benchmarks.
SKEL vs. SMPL#
The comparison between SKEL and SMPL focuses on anatomical accuracy and biomechanical plausibility. SMPL, while widely used, employs a simplified skeleton with ball-and-socket joints, which can lead to unrealistic joint rotations. SKEL, in contrast, incorporates a biomechanically accurate skeleton, limiting degrees of freedom to match actual human joint movement. This results in more realistic and physically plausible poses, crucial for applications in biomechanics and simulation. The trade-off is that SKEL might be less flexible in representing certain extreme or unnatural poses compared to SMPL, but the gained accuracy is vital for specific use cases. SKEL models the degrees of freedom by carefully considering kinematic constraints. This makes the model anatomically plausible. The key difference lies in how each model represents joints, which directly impacts the realism of generated poses. The use of SKEL allows a better analysis of joint constraints as opposed to SMPL.
Joint Limit Viol.#
Analysis of joint limit violations is crucial in evaluating the realism of human pose estimation methods. Biomechanical constraints dictate the natural range of motion for joints, and models that fail to respect these limits often produce unrealistic or physically implausible poses. This analysis helps to identify methods that prioritize statistical accuracy over anatomical correctness. Quantifying the frequency and magnitude of joint limit violations provides a valuable metric for assessing the suitability of a model for biomechanical applications. Lower violation rates indicate more realistic and anatomically accurate pose estimations, leading to more reliable simulations and analyses of human movement. Methods incorporating biomechanical priors or constraints tend to exhibit fewer joint limit violations, demonstrating the effectiveness of explicitly enforcing anatomical plausibility during pose estimation.
More visual insights#
More on figures

🔼 Figure 2 illustrates the HSMR (Human Skeleton and Mesh Recovery) approach. HSMR uses the SKEL model, a biomechanically accurate skeleton, which is a key design choice. A transformer network processes a single image of a person as input. The network outputs estimates of the SKEL model’s pose (q), shape (β), and camera parameters (π). To improve model accuracy during training, the approach iteratively refines pseudo ground truth data by aligning the HSMR’s estimations with ground-truth 2D keypoints through an optimization step called ‘SKELify.’ The refined parameters then serve as updated supervision targets for subsequent training iterations.
read the caption
Figure 2: Overview of our HSMR approach. A key design choice of HSMR is the adoption of the SKEL parametric body model [24] which uses a biomechanically accurate skeleton. We employ a transformer-based architecture that takes as input a single image of a person and estimates the pose q𝑞qitalic_q and shape parameters β𝛽\betaitalic_β of SKEL, as well as the camera π𝜋\piitalic_π. During training, we iteratively update the pseudo ground truth we use to supervise our model, aiming to improve its quality. For this, we optimize the HSMR estimate to align with the ground-truth 2D keypoints (SKELify). The output parameters of the optimization are used in future training iterations as supervision target.

🔼 This figure showcases instances where converting a SMPL mesh to a SKEL mesh results in issues. The conversion process, while feasible, doesn’t always produce accurate or realistic SKEL meshes. The visualization compares the original SMPL mesh (in light green) against the resulting SKEL mesh (in light blue) after applying the optimization method described in reference [24]. The discrepancies highlight the challenges and potential inaccuracies of this direct conversion approach.
read the caption
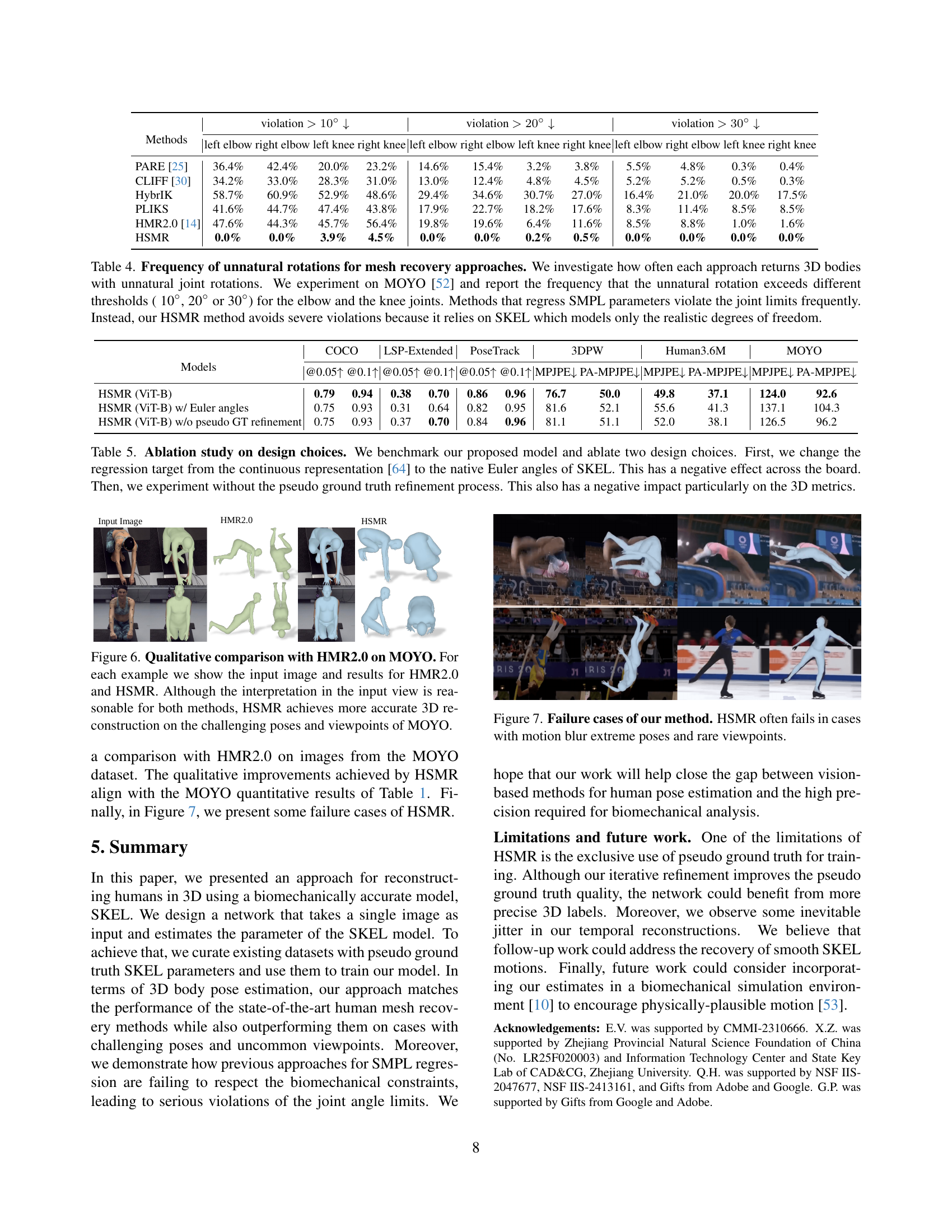
Figure 3: Failure cases of SMPL-to-SKEL conversion. While we can technically fit SKEL to an instance of the SMPL model, this conversion can often lead to problematic SKEL results. Here, we visualize SMPL meshes (light green), and the SKEL meshes we get when we try to fit the SKEL model to the SMPL mesh (light blue). For the fitting, we use the optimization code of [24].

🔼 Figure 4 illustrates the limitations of using simplified human body models like SMPL for pose estimation. The SMPL model represents joints, such as the knee, with a ball-and-socket joint, which allows for unnatural rotations not found in real human anatomy. The figure compares pose estimations from the HMR2.0 method (light green) showing exaggerated or impossible knee bends. In contrast, the HSMR method (light blue) utilizes the biomechanically accurate SKEL model, resulting in more natural and anatomically correct knee positions that respect joint limitations.
read the caption
Figure 4: Examples of unnatural joint rotation for SMPL. SMPL represents the knee with a ball (socket) joint. This allows mesh recovery methods like HMR2.0 [14] to generate invalid rotations. We visualize examples from HMR2.0 (light green) where the knee is bend in unnatural ways. In comparison, the HSMR output (light blue) respects the biomechanical constraints.

🔼 Figure 5 presents a qualitative assessment of the HSMR (Human Skeleton and Mesh Recovery) model. For each example, the input image is displayed alongside four additional views: (b) an overlay of the SKEL biomechanical skeleton on the input image providing a direct comparison between the model’s reconstruction and the original image; (c) a side view of the 3D reconstruction, showing the mesh and the skeleton; and (d) a top view of the 3D reconstruction, again showcasing both the mesh and the skeleton. These multiple viewpoints enable a comprehensive evaluation of the model’s ability to accurately reconstruct the human’s pose and mesh.
read the caption
Figure 5: Qualitative evaluation of HSMR. For each input example we show: a) the input image, b) the overlay of SKEL in the input view, c) a side view, d) the top view. We visualize both the skeleton and the transparent mesh of the estimated SKEL.
More on tables
| PARE | CLIFF | HybrIK | PLIKS | HMR2.0 | HSMR | |
|---|---|---|---|---|---|---|
| MPVPE | 174.5 | 155.7 | 143.6 | 136.7 | 142.2 | 120.1 |
| PA-MPVPE | 121.9 | 110.6 | 94.4 | 94.8 | 103.4 | 90.7 |
🔼 Table 2 presents a quantitative evaluation of the surface mesh reconstruction accuracy achieved by the proposed HSMR model and other state-of-the-art methods. The evaluation is performed using the MOYO dataset, which is known for its challenging poses and viewpoints. The metrics used for the evaluation are Mean Per Vertex Position Error (MPVPE) and its Procrustes Aligned version (PA-MPVPE). Lower values for both metrics indicate more accurate surface reconstruction. This table provides a comparison showing how well the different approaches reconstruct the 3D surface mesh in terms of both vertex positions and overall shape alignment.
read the caption
Table 2: Evaluation of the surface reconstruction accuracy. We report MPVPE and PA-MPVPE on the MOYO dataset.
| Methods | COCO | LSP-Extended | PoseTrack | 3DPW | Human3.6M | MOYO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| @0.05 | @0.1 | @0.05 | @0.1 | @0.05 | @0.1 | MPJPE | PA-MPJPE | MPJPE | PA-MPJPE | MPJPE | PA-MPJPE | ||
| HMR2.0 [14] | 0.86 | 0.96 | 0.53 | 0.82 | 0.90 | 0.98 | 81.3 | 54.3 | 50.0 | 32.4 | 123.3 | 90.4 | |
| HMR2.0 + SKEL fit | 0.78 | 0.95 | 0.49 | 0.79 | 0.90 | 0.98 | 81.0 | 54.4 | 53.6 | 34.1 | 130.5 | 93.7 | |
| HSMR | 0.85 | 0.96 | 0.51 | 0.81 | 0.90 | 0.98 | 81.5 | 54.8 | 50.4 | 32.9 | 104.5 | 79.6 | |
🔼 This table compares the performance of the proposed HSMR method with a two-stage baseline approach for recovering a biomechanically accurate skeleton (SKEL). The baseline first uses the HMR2.0 method to predict SMPL parameters, then iteratively fits the SKEL model to the SMPL prediction. The comparison demonstrates that the end-to-end HSMR approach significantly outperforms the two-stage baseline in terms of accuracy, while also being substantially faster (3 minutes per frame vs. HSMR’s speed).
read the caption
Table 3: Comparison with baseline for SKEL recovery. We start from the SMPL prediction of HMR2.0 [14] and we fit the SKEL model to it with terative optimization [24]. This baseline corresponds to the “HMR2.0 + SKEL fit” row. We observe that this two-stage baseline for SKEL recovery performs worse than HSMR, while it is also significantly slower (3 minutes for a single frame).
| Methods | violation | violation | violation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| left elbow | right elbow | left knee | right knee | left elbow | right elbow | left knee | right knee | left elbow | right elbow | left knee | right knee | ||
| PARE [25] | 36.4% | 42.4% | 20.0% | 23.2% | 14.6% | 15.4% | 3.2% | 3.8% | 5.5% | 4.8% | 0.3% | 0.4% | |
| CLIFF [30] | 34.2% | 33.0% | 28.3% | 31.0% | 13.0% | 12.4% | 4.8% | 4.5% | 5.2% | 5.2% | 0.5% | 0.3% | |
| HybrIK | 58.7% | 60.9% | 52.9% | 48.6% | 29.4% | 34.6% | 30.7% | 27.0% | 16.4% | 21.0% | 20.0% | 17.5% | |
| PLIKS | 41.6% | 44.7% | 47.4% | 43.8% | 17.9% | 22.7% | 18.2% | 17.6% | 8.3% | 11.4% | 8.5% | 8.5% | |
| HMR2.0 [14] | 47.6% | 44.3% | 45.7% | 56.4% | 19.8% | 19.6% | 6.4% | 11.6% | 8.5% | 8.8% | 1.0% | 1.6% | |
| HSMR | 0.0% | 0.0% | 3.9% | 4.5% | 0.0% | 0.0% | 0.2% | 0.5% | 0.0% | 0.0% | 0.0% | 0.0% | |
🔼 This table compares different human pose estimation methods’ frequency of producing unnatural joint rotations (elbows and knees) exceeding specified thresholds (10°, 20°, and 30°). The dataset used is MOYO [52], known for its challenging poses. Methods using SMPL, a simplified model, show high rates of unnatural joint angles, unlike the HSMR method, which leverages the biomechanically accurate SKEL model, exhibiting far fewer unnatural rotations.
read the caption
Table 4: Frequency of unnatural rotations for mesh recovery approaches. We investigate how often each approach returns 3D bodies with unnatural joint rotations. We experiment on MOYO [52] and report the frequency that the unnatural rotation exceeds different thresholds ( 10∘, 20∘ or 30∘) for the elbow and the knee joints. Methods that regress SMPL parameters violate the joint limits frequently. Instead, our HSMR method avoids severe violations because it relies on SKEL which models only the realistic degrees of freedom.
| Models | COCO | LSP-Extended | PoseTrack | 3DPW | Human3.6M | MOYO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| @0.05 | @0.1 | @0.05 | @0.1 | @0.05 | @0.1 | MPJPE | PA-MPJPE | MPJPE | PA-MPJPE | MPJPE | PA-MPJPE | ||
| HSMR (ViT-B) | 0.79 | 0.94 | 0.38 | 0.70 | 0.86 | 0.96 | 76.7 | 50.0 | 49.8 | 37.1 | 124.0 | 92.6 | |
| HSMR (ViT-B) w/ Euler angles | 0.75 | 0.93 | 0.31 | 0.64 | 0.82 | 0.95 | 81.6 | 52.1 | 55.6 | 41.3 | 137.1 | 104.3 | |
| HSMR (ViT-B) w/o pseudo GT refinement | 0.75 | 0.93 | 0.37 | 0.70 | 0.84 | 0.96 | 81.1 | 51.1 | 52.0 | 38.1 | 126.5 | 96.2 | |
🔼 This table presents an ablation study evaluating the impact of two key design choices in the HSMR model: the regression target for pose parameters and the pseudo ground truth refinement process. The first experiment replaces the continuous rotation representation of pose parameters with SKEL’s native Euler angles, showing a negative effect across all metrics. The second experiment removes the iterative refinement of pseudo ground truth labels, resulting in a more significant performance drop, especially for 3D metrics.
read the caption
Table 5: Ablation study on design choices. We benchmark our proposed model and ablate two design choices. First, we change the regression target from the continuous representation [64] to the native Euler angles of SKEL. This has a negative effect across the board. Then, we experiment without the pseudo ground truth refinement process. This also has a negative impact particularly on the 3D metrics.
Full paper#