TL;DR#
Four-dimensional computed tomography (4D CT) captures anatomical changes, crucial for medical imaging. However, current methods discretize time into phases using respiratory gating devices, causing misalignment and limiting practicality. These rely on external hardware, are uncomfortable for patients, and often produce artifacts that obscure fine tissue details. Recent advances like Neural Radiance Fields(NeRF) and Gaussian Splatting(GS) improve 3D reconstruction but still struggle with continuous motion and hardware dependency.
This paper introduces X2-Gaussian, a novel framework for continuous-time 4D CT reconstruction. It integrates dynamic radiative Gaussian splatting with self-supervised respiratory motion learning. The method models dynamics via a spatiotemporal encoder-decoder predicting time-varying Gaussian deformations, eliminating phase discretization. A physiology-driven consistency loss learns breathing cycles directly from projections. X2-Gaussian achieves state-of-the-art performance and advances high-fidelity 4D CT for clinical imaging.
Key Takeaways#
Why does it matter?#
This research addresses the critical need for accurate 4D CT reconstruction, improving clinical workflows and patient comfort by removing hardware dependencies and enabling continuous motion modeling. It opens new avenues for dynamic medical imaging and radiomic feature extraction.
Visual Insights#
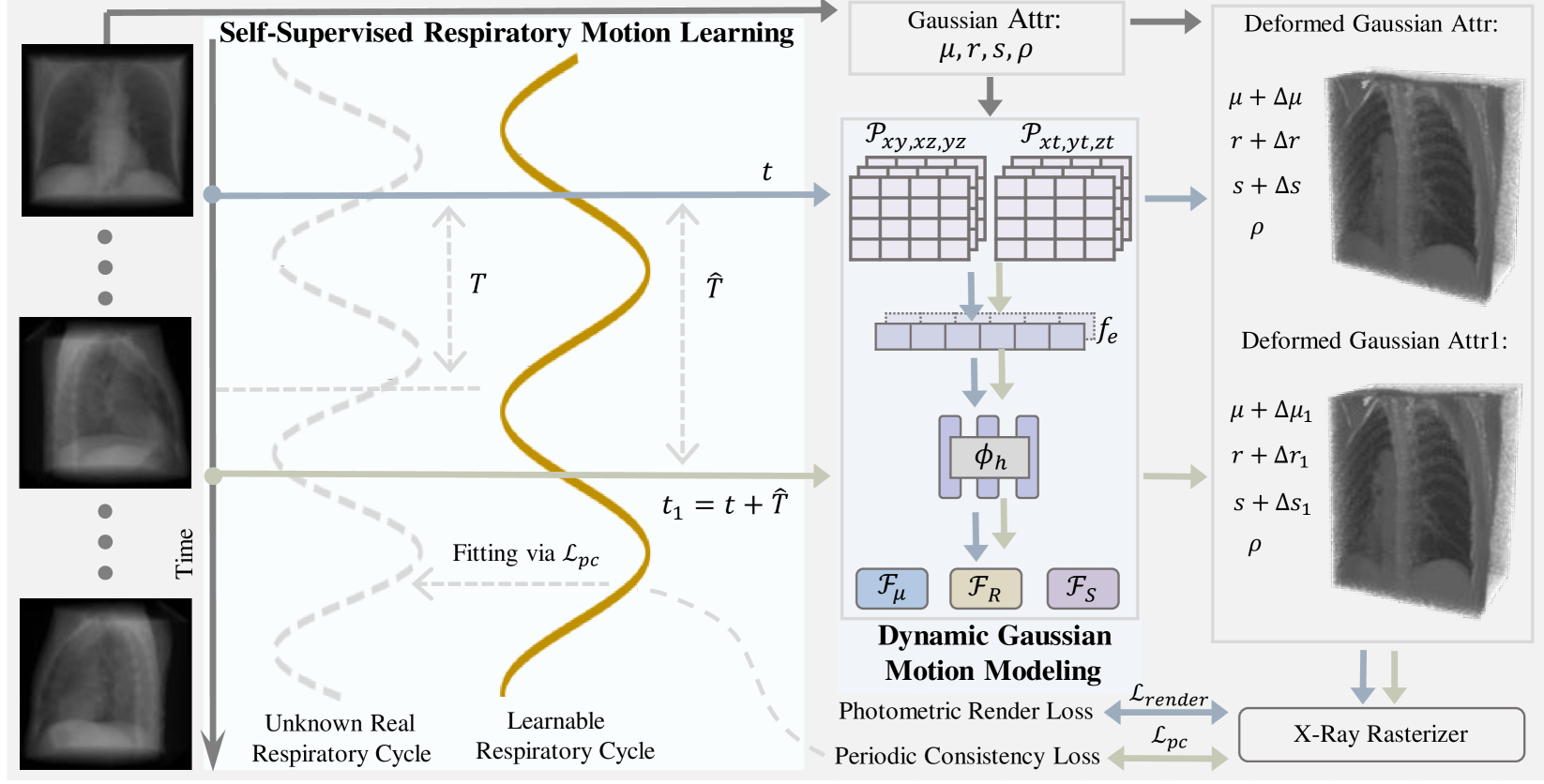
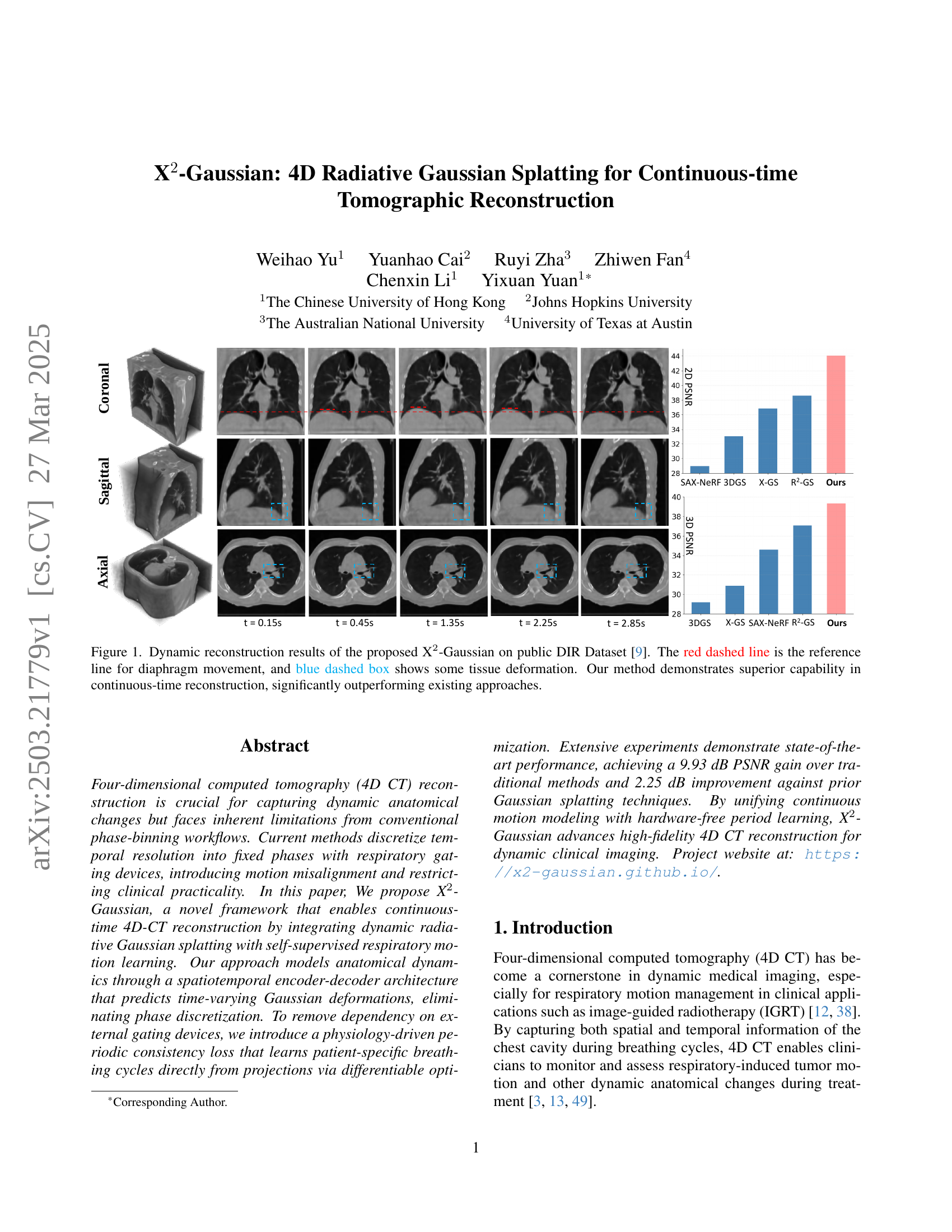
🔼 This figure illustrates the X2-Gaussian framework, which is a novel method for 4D CT reconstruction. It highlights two key components: 1) Dynamic Gaussian motion modeling, which captures continuous anatomical changes over time using a time-dependent deformation field applied to Gaussian splatting. This allows for continuous-time reconstruction rather than discrete phase binning. 2) Self-supervised respiratory motion learning, which automatically learns the patient’s breathing cycle directly from the projection data, eliminating the need for external gating devices. The framework is presented as a flowchart showing the data flow and interactions between these components.
read the caption
Figure 1: Framework of our X2-Gaussian, which consists of two innovative components: (1) Dynamic Gaussian motion modeling for continuous-time reconstruction; (2) Self-Supervised respiratory motion learning for estimating breathing cycle autonomously.
| Method | Patient1 | Patient2 | Patient3 | Patient4 | Patient5 | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| FDK [42] | ||||||||||||
| IntraTomo [58] | ||||||||||||
| NeRF [37] | ||||||||||||
| TensoRF [10] | ||||||||||||
| NAF [59] | ||||||||||||
| SAX-NeRF [7] | ||||||||||||
| 3D-GS [29] | ||||||||||||
| X-GS [6] | ||||||||||||
| R2-GS [60] | ||||||||||||
| Ours | ||||||||||||
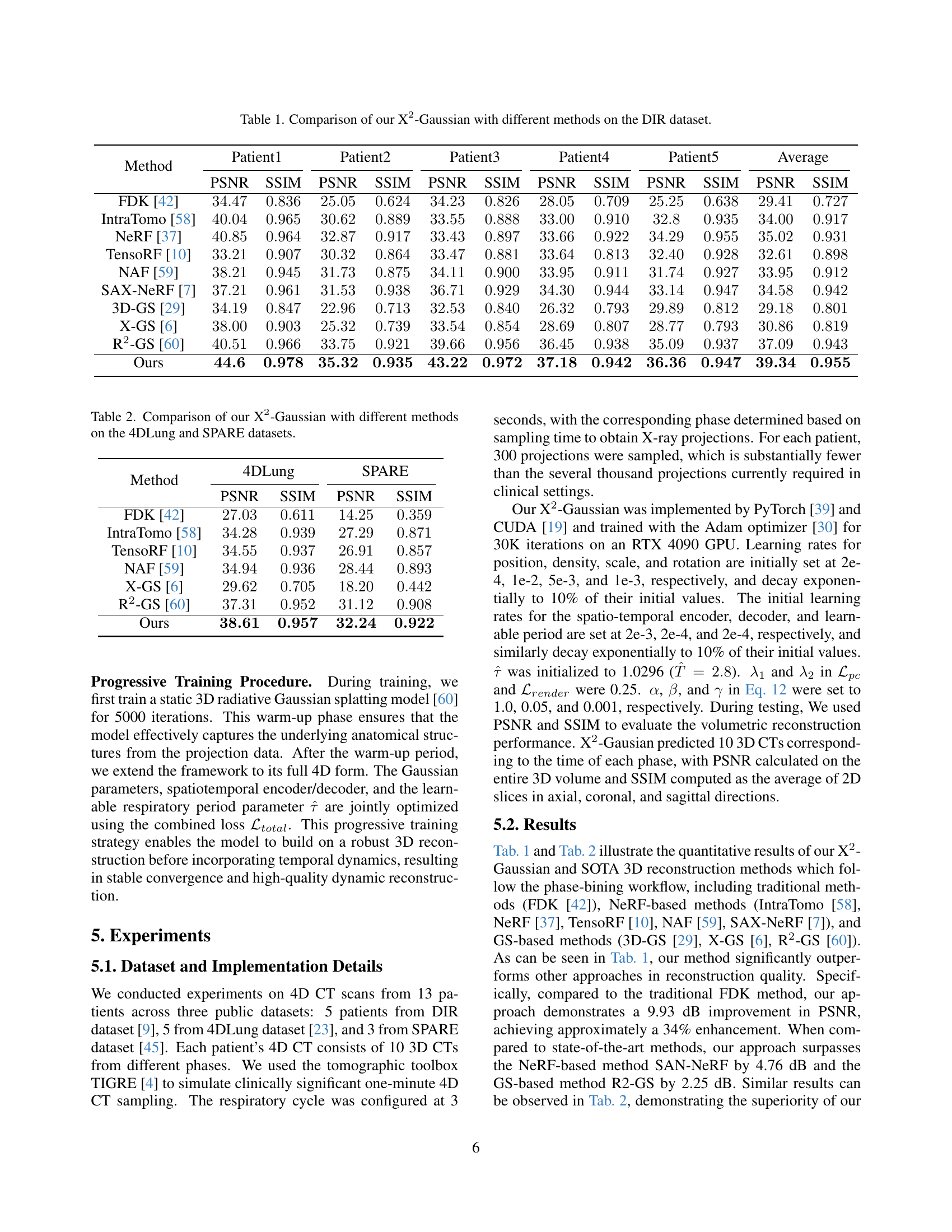
🔼 Table 1 presents a quantitative comparison of the proposed X2-Gaussian method against several state-of-the-art techniques for 4D CT reconstruction. The comparison is performed on the DIR public dataset, a collection of 4D CT scans from patients with malignant thoracic tumors. The table shows the performance of each method in terms of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) for each of five patients, as well as an average across all patients. Higher PSNR and SSIM values indicate better reconstruction quality.
read the caption
Table 1: Comparison of our X2-Gaussian with different methods on the DIR dataset.
In-depth insights#
Continuous 4D-CT#
Continuous 4D-CT aims to overcome limitations of traditional phase-binning methods in dynamic medical imaging. Current 4D-CT methods discretize temporal resolution, introducing motion misalignment and limiting clinical practicality. By directly modeling continuous anatomical motion without discrete phase binning, it enables motion analysis at arbitrary temporal resolutions. The core idea involves extending static radiative Gaussian splatting into the temporal domain, capturing continuous deformation of anatomical structures over time using a spatiotemporal encoder-decoder architecture. It eliminates external gating devices and estimates breathing period directly from projection data through physiology-driven periodic consistency, automatically discovering and adapting to patient-specific breathing patterns.
Motion Learning#
Motion learning, particularly in the context of 4D CT reconstruction, is a critical aspect for accurately capturing dynamic anatomical changes. Traditional methods rely on external gating devices and phase-binning, which discretize temporal resolution and introduce motion artifacts. Newer methods attempt to predict patient-specific motion patterns and improve reconstruction quality, they often still treat time as discrete. The ideal motion learning approach would be self-supervised, learning directly from projection data without external devices, and capable of modeling continuous anatomical motion throughout the respiratory cycle. It should capture periodic nature of respiratory motion while adapting to patient-specific breathing patterns. The goal is to achieve high-fidelity 4D CT reconstruction for dynamic clinical imaging, enabling better monitoring of respiratory-induced changes and more accurate radiotherapy planning. Effectively this involves learning to predict time-varying deformations in the data.
Gaussian Splatting#
Gaussian Splatting emerges as a pivotal technique, particularly 3DGS, initially conceived for novel view synthesis. Leveraging millions of 3D Gaussian point clouds, it achieves impressive scene and object representation. Its rapid evolution spans diverse applications, including scene modeling, SLAM, 3D generation, and medical imaging, underscoring its versatility. However, challenges persist in dynamic CT volume reconstruction, where existing algorithms struggle. The text highlights the development of techniques like X-GS and R2GS that are built on gaussian splatting, however there are inherent limitations of these techniques. This study introduces a novel approach that leverages Gaussian Splatting with the aim to resolve these limitations and advance the state-of-the-art performance. With the method the study strives to reconstruct the CT volumes, the study aims to cope with the mentioned problems.
Periodic Loss#
A periodic loss function in the context of 4D CT reconstruction likely aims to enforce temporal consistency by leveraging the periodic nature of respiratory motion. This means that images reconstructed at time t should be similar to those at time t + nT, where T is the respiratory period and n is an integer. By penalizing deviations from this periodic behavior, the loss function can help to regularize the reconstruction process, reduce noise, and improve the overall quality, especially in dynamic regions. The effectiveness of periodic loss hinges on the accurate estimation or learning of the respiratory period T, either through external gating or self-supervised techniques, potentially making model more robust in dynamic scenarios.
Clinical Params#
The paper touches on the potential extraction of clinically relevant parameters, which is a significant step towards practical application in medicine. The ability to quantify Tidal Volume (TV), Minute Ventilation (MV), and I:E Ratio directly from the reconstructed 4D CT volumes opens up avenues for enhanced patient monitoring and treatment personalization. This suggests the method can serve as a powerful tool for radiomic feature analysis, offering insights into disease progression and treatment response. While the paper showcases preliminary results, the integration of such quantitative measures holds promise for improved clinical decision-making and personalized radiotherapy planning, paving the way for a more tailored approach to patient care. This is a crucial area for future research and development.
More visual insights#
More on figures

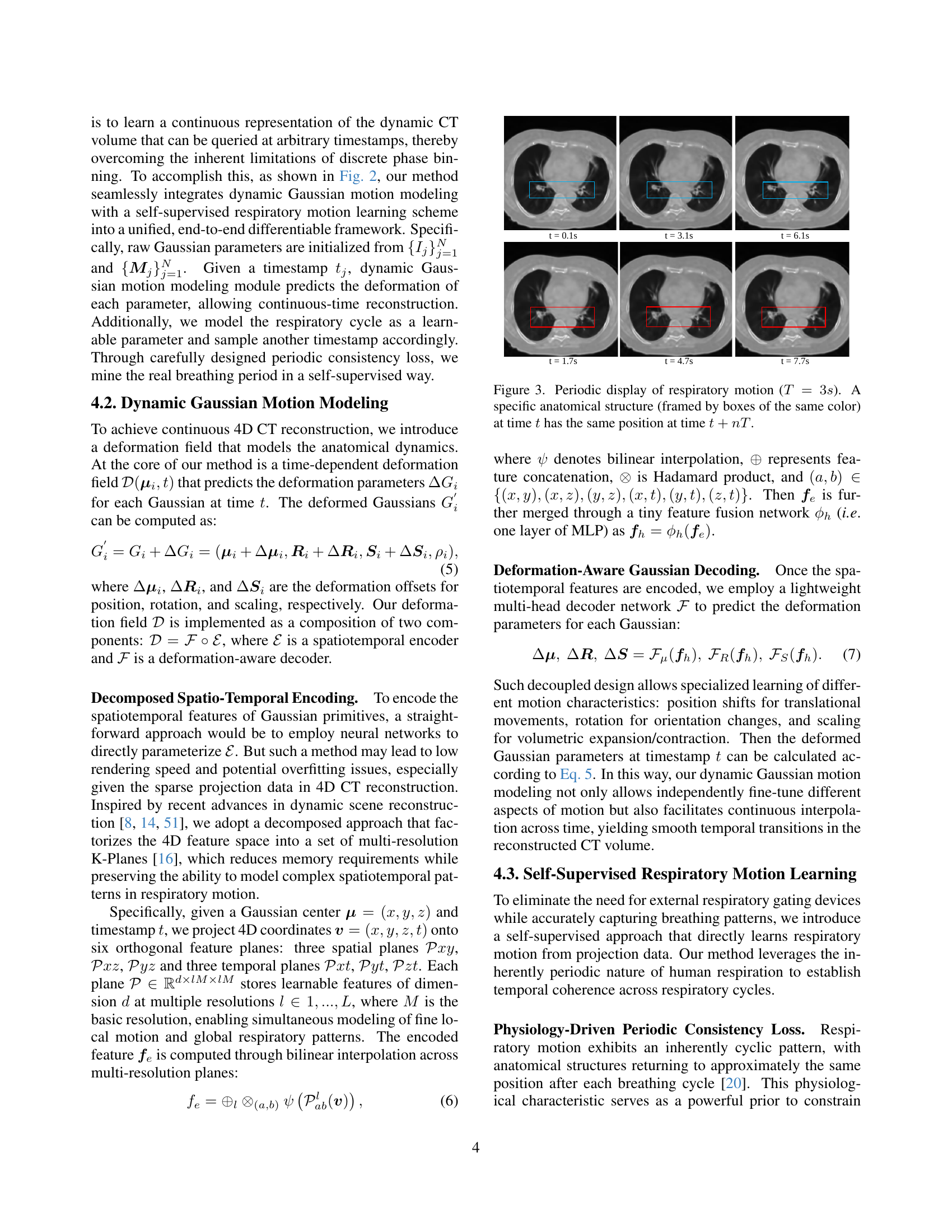
🔼 Figure 3 visualizes the periodic nature of respiratory motion. It shows snapshots of a 3-second respiratory cycle (T=3s), highlighting the cyclical movement of specific anatomical structures. The colored boxes track the same anatomical region across different time points (t) within the cycle and at corresponding points in subsequent cycles (t+nT), demonstrating the repetitive pattern of breathing.
read the caption
Figure 2: Periodic display of respiratory motion (T=3s𝑇3𝑠T=3sitalic_T = 3 italic_s). A specific anatomical structure (framed by boxes of the same color) at time t𝑡titalic_t has the same position at time t+nT𝑡𝑛𝑇t+nTitalic_t + italic_n italic_T.

🔼 This figure shows the impact of two key techniques, Bounded Cycle Shifts and Log-Space Parameterization, on the learning process of the respiratory cycle period (T). The x-axis represents the number of iterations during training, and the y-axis represents the estimated period (T). The blue line (‘Ours’) demonstrates the stable and accurate convergence to the true respiratory period when both techniques are used. The orange line (‘w/o Bounded Cycle Shifts’) shows the instability where the estimated period oscillates and approaches half the true value. The green line (‘w/o Log-Space Parameterization’) shows significant oscillations in the estimated period. This visualization clearly illustrates the importance of these two methods in ensuring stable and accurate learning of the breathing cycle.
read the caption
Figure 3: Convergence behavior of the learnable period T^^𝑇\hat{T}over^ start_ARG italic_T end_ARG. Without Bounded Cycle Shifts, T^^𝑇\hat{T}over^ start_ARG italic_T end_ARG undergoes wide-ranging oscillations approaching half the true period. Without Log-Space Parameterization, the optimization curve exhibits large oscillations. With both techniques implemented, T^^𝑇\hat{T}over^ start_ARG italic_T end_ARG converges stably and accurately to the correct breathing cycle.

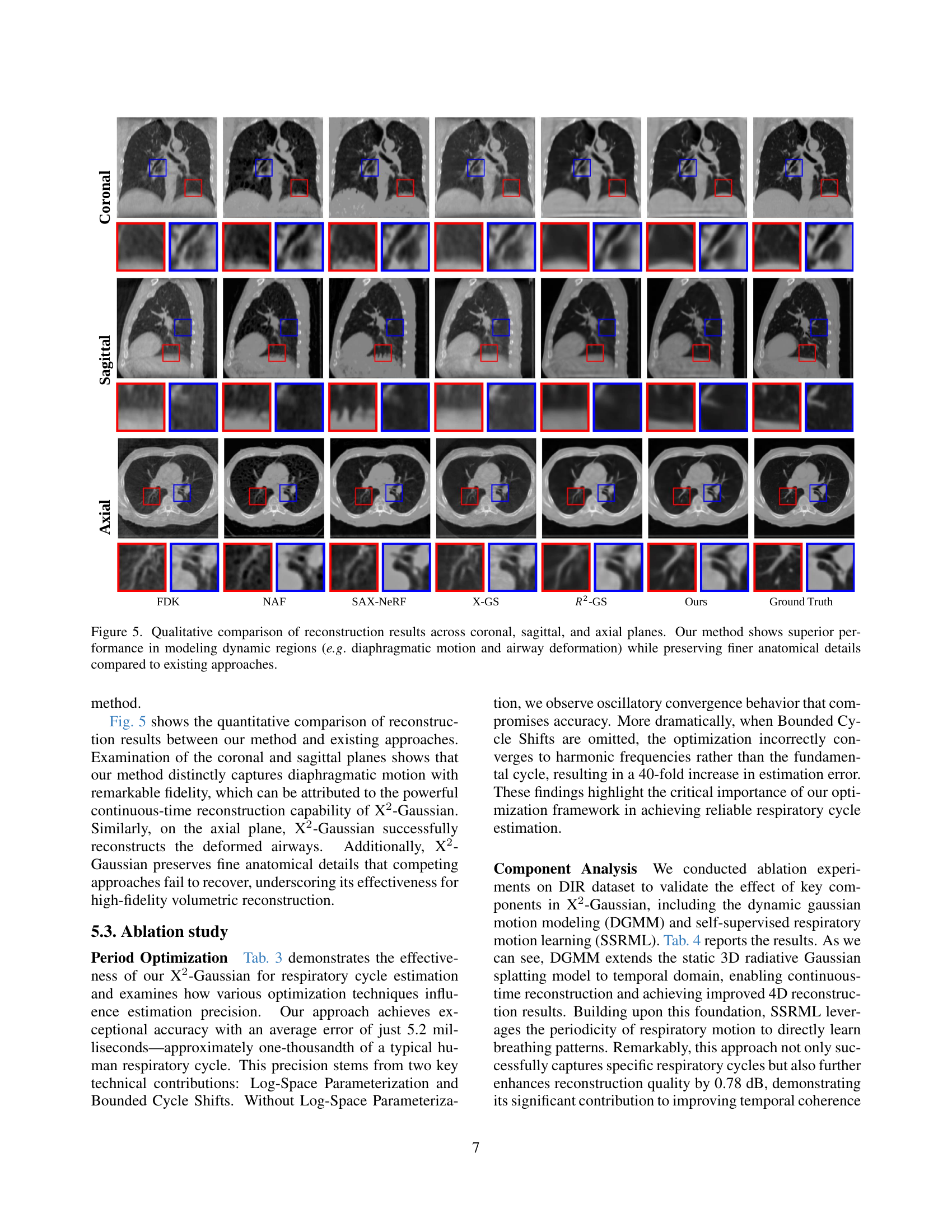
🔼 Figure 5 presents a qualitative comparison of 4D CT reconstruction results obtained using different methods across coronal, sagittal, and axial views. The images showcase the ability of each method to model dynamic anatomical structures, such as the diaphragm and airways, during respiration. X2-Gaussian, the proposed method, demonstrates superior performance in capturing the continuous movement of these structures, resulting in clearer and more detailed representations than existing methods. This superiority is particularly evident in the accurate depiction of finer anatomical details, which are often blurred or lost in other reconstruction approaches. The comparison highlights X2-Gaussian’s enhanced ability to resolve the complexities of dynamic imaging.
read the caption
Figure 4: Qualitative comparison of reconstruction results across coronal, sagittal, and axial planes. Our method shows superior performance in modeling dynamic regions (e.g. diaphragmatic motion and airway deformation) while preserving finer anatomical details compared to existing approaches.

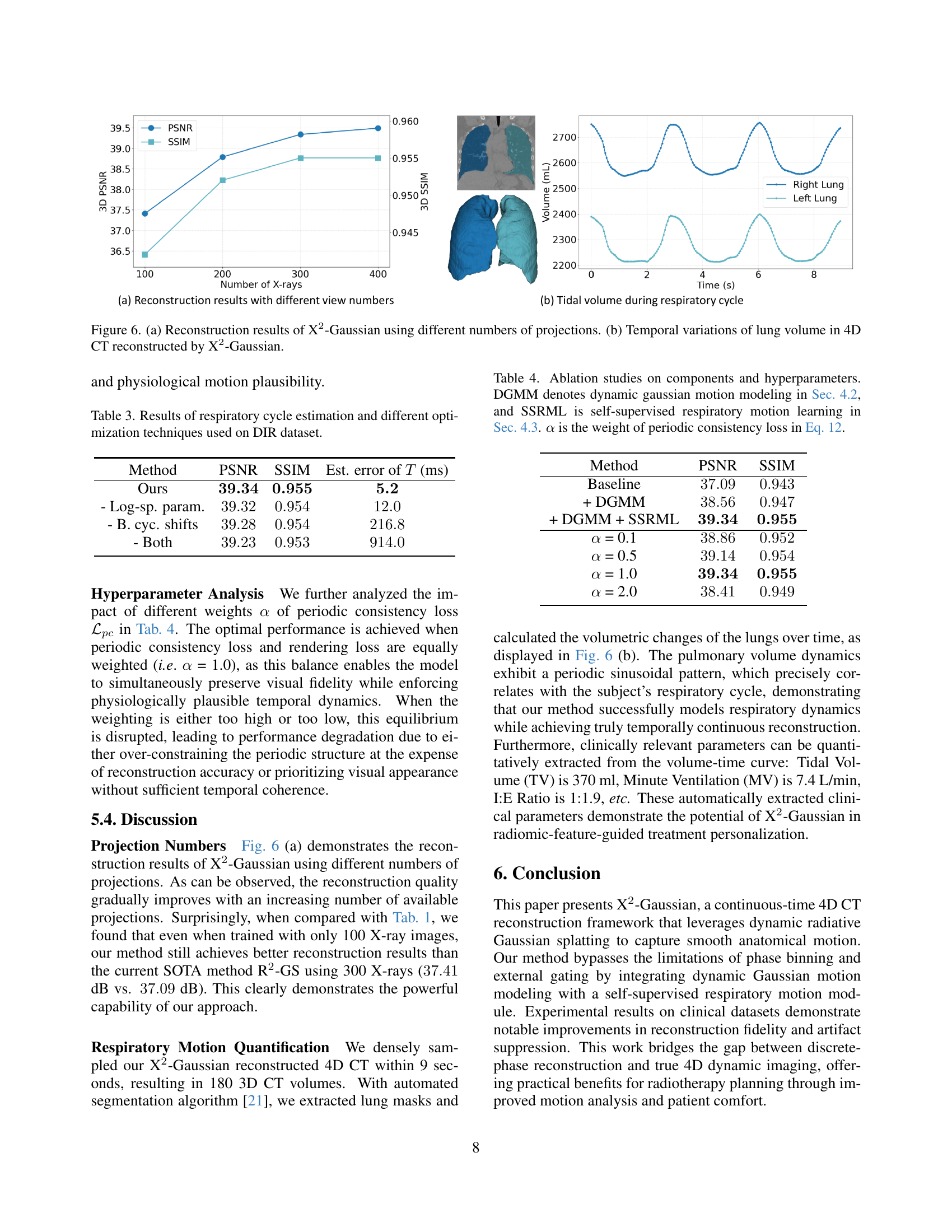
🔼 Figure 6 presents a two-part visualization of the X2-Gaussian model’s performance. Subfigure (a) shows a graph illustrating the relationship between the number of X-ray projections used for reconstruction and the resulting 3D PSNR (Peak Signal-to-Noise Ratio) and 3D SSIM (Structural Similarity Index). The graph demonstrates the improvement in reconstruction quality as the number of projections increases. Subfigure (b) displays the temporal changes in lung volume over a respiratory cycle, as obtained from the 4D CT scan reconstructed by X2-Gaussian. The plot shows the volume variations of both the right and left lungs over time, highlighting the model’s ability to capture the dynamic nature of respiratory motion.
read the caption
Figure 5: (a) Reconstruction results of X2-Gaussian using different numbers of projections. (b) Temporal variations of lung volume in 4D CT reconstructed by X2-Gaussian.
More on tables
🔼 Table 2 presents a quantitative comparison of the proposed X2-Gaussian method against several state-of-the-art 4D CT reconstruction techniques on two publicly available datasets: 4DLung and SPARE. The table shows the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) metrics, which are common image quality assessment measures. Higher PSNR and SSIM values indicate better reconstruction quality. By comparing the performance of X2-Gaussian to other methods across these datasets, the table demonstrates the superior reconstruction capabilities of the proposed approach in terms of both quantitative metrics.
read the caption
Table 2: Comparison of our X2-Gaussian with different methods on the 4DLung and SPARE datasets.
| Method | PSNR | SSIM | Est. error of (ms) |
|---|---|---|---|
| Ours | |||
| - Log-sp. param. | |||
| - B. cyc. shifts | |||
| - Both |
🔼 This table presents a ablation study on the impact of different optimization techniques on the accuracy of respiratory cycle estimation using the DIR dataset. It compares the performance of the proposed method with and without key optimization components such as log-space parameterization and bounded cycle shifts, highlighting their importance in achieving accurate and stable period estimation.
read the caption
Table 3: Results of respiratory cycle estimation and different optimization techniques used on DIR dataset.
| Method | PSNR | SSIM |
|---|---|---|
| Baseline | ||
| + DGMM | ||
| + DGMM + SSRML | ||
| = 0.1 | ||
| = 0.5 | ||
| = 1.0 | ||
| = 2.0 |
🔼 This table presents the results of ablation studies conducted to analyze the impact of different components and hyperparameters on the performance of the X2-Gaussian model. It specifically examines the contributions of dynamic Gaussian motion modeling (DGMM), self-supervised respiratory motion learning (SSRML), and the weight (α) assigned to the periodic consistency loss (Equation 12). By comparing the performance metrics (PSNR and SSIM) across various configurations, the table helps to quantify the individual contributions of each component and the optimal setting for the hyperparameter α.
read the caption
Table 4: Ablation studies on components and hyperparameters. DGMM denotes dynamic gaussian motion modeling in Sec. 4.2, and SSRML is self-supervised respiratory motion learning in Sec. 4.3. α𝛼\alphaitalic_α is the weight of periodic consistency loss in Eq. 12.
| Method | Patient1 | Patient2 | Patient3 | Patient4 | Patient5 | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| FDK [42] | ||||||||||||
| IntraTomo [58] | ||||||||||||
| TensoRF [10] | ||||||||||||
| NAF [59] | ||||||||||||
| X-GS [6] | ||||||||||||
| R2-GS [60] | ||||||||||||
| Ours | ||||||||||||
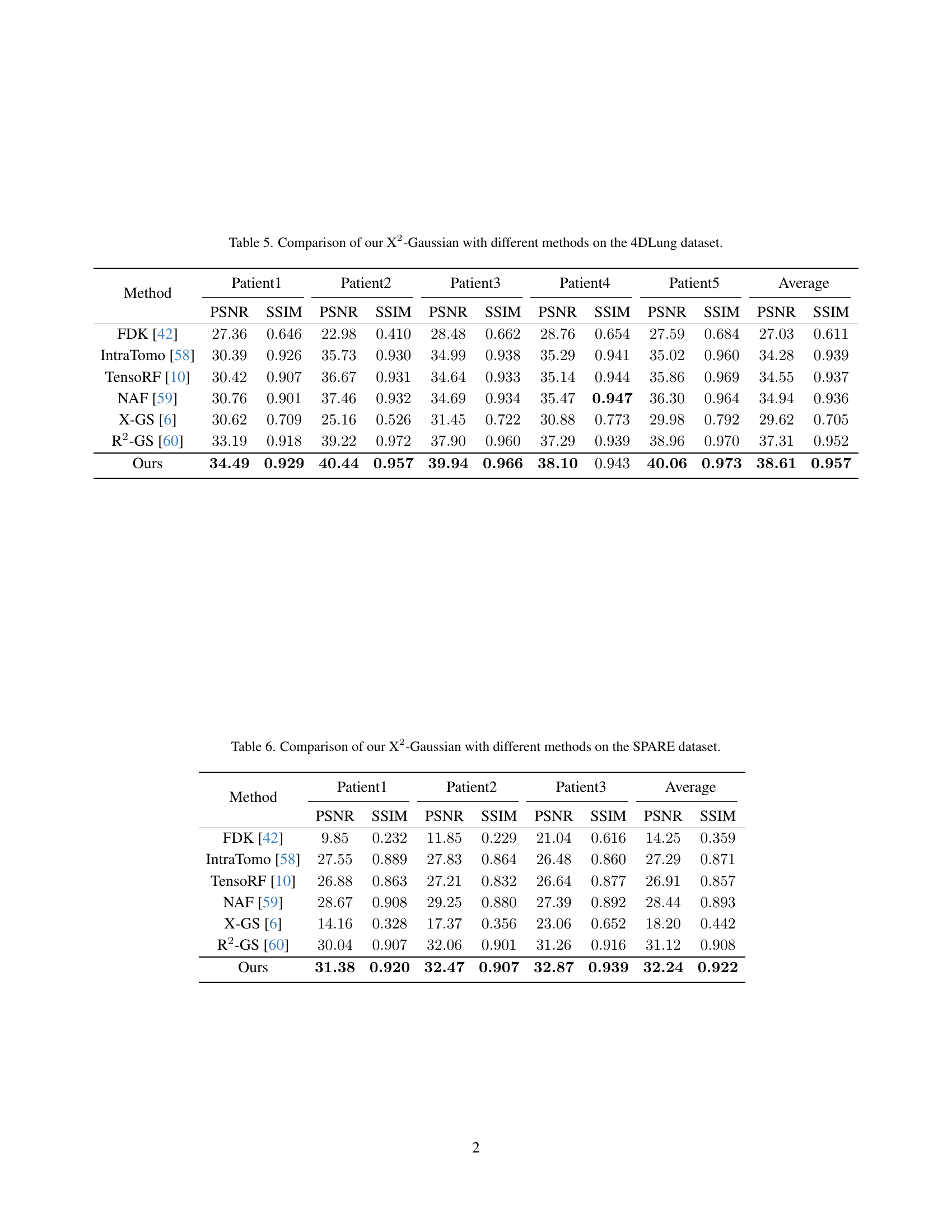
🔼 This table presents a quantitative comparison of the proposed X2-Gaussian method against several state-of-the-art techniques for 4D CT reconstruction. The evaluation is performed on the 4DLung dataset, a publicly available dataset containing 4D CT scans of patients with lung cancer. The comparison metrics used are PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index), both common measures of image quality. Results are provided for each of five patients in the dataset, as well as an overall average, allowing for a comprehensive assessment of the performance differences between the methods. The methods compared encompass traditional analytical approaches, novel neural radiance field (NeRF)-based methods, and other Gaussian splatting techniques.
read the caption
Table 5: Comparison of our X2-Gaussian with different methods on the 4DLung dataset.
| Method | Patient1 | Patient2 | Patient3 | Average | ||||
|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| FDK [42] | ||||||||
| IntraTomo [58] | ||||||||
| TensoRF [10] | ||||||||
| NAF [59] | ||||||||
| X-GS [6] | ||||||||
| R2-GS [60] | ||||||||
| Ours | ||||||||
🔼 This table presents a quantitative comparison of the proposed X2-Gaussian method against several state-of-the-art techniques for 4D CT reconstruction. The comparison is performed on the SPARE dataset, a publicly available benchmark dataset for 4D lung CT scans. The metrics used for comparison are PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index), which measure the image quality and structural similarity respectively. The results for each patient in the dataset are shown, alongside average values across all patients. This allows for a comprehensive evaluation of the relative performance of different methods in reconstructing 4D CT data from sparse projections.
read the caption
Table 6: Comparison of our X2-Gaussian with different methods on the SPARE dataset.
Full paper#