TL;DR#
AI models have shown promise in math, yet physics remains a hurdle. Existing physics datasets often consist of multiple-choice questions or focus on primary-high school level problems that frontier models perform well on. To fill the gap, the study introduces PHYSICS, a benchmark consisting of 1,297 expert-annotated problems spanning six core areas that need advanced physics knowledge and mathematical reasoning.
PHYSICS assesses AI using open-ended questions. The benchmark reveals limitations: the best model only achieves 59.9% accuracy. Key issues include incorrect assumptions, data understanding, calculation accuracy, and question interpretation. The study explores diverse prompting strategies and Retrieval-Augmented Generation (RAG) to improve performance, identifying areas for future advancement.
Key Takeaways#
Why does it matter?#
This PHYSICS benchmark provides a critical tool for evaluating and improving AI models in advanced physics problem-solving. It is important for researchers because it highlights current limitations and guides future development toward more robust, scientifically grounded AI.
Visual Insights#

🔼 Figure 1 showcases a sample problem from the PHYSICS benchmark dataset, specifically focusing on classical mechanics. The problem presents a diagram of a siphon and asks for calculations related to water flow speed and maximum height, requiring application of Bernoulli’s equation. The caption highlights PHYSICS as a comprehensive benchmark comprising 1,297 expert-annotated university-level physics problems.
read the caption
Figure 1: An example of classical mechanics problem in \ours. \oursis a comprehensive benchmark for university-level physics problem solving which contains 1,297 expert-annotated problems.
| Benchmark | Multi-modal | Size | Level | Question Type | Evaluation | Reasoning Steps |
| JEEBench Arora et al. (2023) | ✗ | 515 | CEE | OE, MC | Rule-Based | - |
| MATH Hendrycks et al. (2021) | ✗ | 12,500 | K12-Comp | OE | Rule-Based | - |
| HARDMath Fan et al. (2024) | ✗ | 1,466 | Graduate | OE | Rule + Model | - |
| GSM8K(Cobbe et al., 2021) | ✗ | 8,500 | K8 | OE | Rule-Based | 5.0 |
| GPQA(Rein et al., 2024) | ✗ | 227 | Graduate | OE | Rule-Based | 3.6 |
| SciQ Welbl et al. (2017) | ✗ | 13,679 | K4-K8 | MC, OE | Rule-Based | - |
| SciEval Sun et al. (2023) | ✗ | 1657 | - | OE, MC | Rule-Based | - |
| SciBench Wang et al. (2024) | ✓ | 295 | University | OE | Rule-Based | 2.8 |
| MMMU Yue et al. (2024a) | ✓ | 443 | University | OE, MC | Rule-Based | - |
| MMMU-Pro Yue et al. (2024b) | ✓ | 3,460 | University | MC | Rule-Based | - |
| MMVU Zhao et al. (2025) | ✓ | 3,000 | University | OE, MC | Rule + Model | - |
| ScienceQA Lu et al. (2022) | ✓ | 617 | K1-K12 | MC | Rule-Based | 2.4 |
| OlympiadBench(He et al., 2024) | ✓ | 2334 | Comp | OE | Rule-Based | 3.7 |
| PutnamBench Tsoukalas et al. (2024) | ✗ | 1692 | University | OE | Rule-Based | - |
| \ours | ✓ | 1297 | University | OE | Rule + Model | 5.7 |
🔼 This table compares the PHYSICS benchmark with other existing benchmarks across several key features. These features include the modality (whether the benchmark uses text only or text and images), the size of the benchmark (number of questions), the educational level of the questions (ranging from elementary school to graduate level), the type of questions (multiple choice or open-ended), the evaluation method used, and the average number of reasoning steps required to solve the problems. The table provides a context for understanding the relative difficulty and scope of the PHYSICS benchmark in comparison to others.
read the caption
Table 1: Comparison of \ourswith other benchmarks. For Level, comp: Competition, CEE: University Entrance Examination, K1-K12: Elementary and High School Level. For Question Type, OE: Open-ended Questions, MC: Multiple-choice Questions. Reasoning Steps are based on the statistics provided in the corresponding reference.
In-depth insights#
Physics FM Limits#
Foundation Models (FM) face considerable limits when applied to physics due to the domain’s reliance on precise mathematical formulations and complex reasoning. Unlike tasks where FMs can leverage pattern recognition, physics demands a deep understanding of underlying principles and accurate equation manipulation. Current FMs often struggle with multi-step problem-solving requiring the integration of diverse concepts. Furthermore, FMs may lack the inherent physical intuition necessary to correctly apply formulas and interpret results within real-world contexts. Addressing these limits requires improving FMs’ ability to handle symbolic mathematics, integrate domain-specific knowledge, and perform robust reasoning.
PHYSICS Dataset#
The PHYSICS dataset appears to be a specifically curated collection intended for evaluating foundation models in their capacity to tackle university-level physics problems. The key strength likely resides in its composition of problems demanding advanced knowledge and mathematical reasoning, potentially sourced from PhD qualifying exams to ensure high difficulty. It is designed to assesses the models’ abilities in core physics areas such as classical mechanics, quantum mechanics, thermodynamics, electromagnetism, atomic physics, and optics. By incorporating expert-annotated problems with a high level of complexity, the dataset avoids the limitations of multiple-choice formats. This helps in enabling a more thorough and accurate evaluation of the models’ physics problem-solving skills in open-ended scenarios and complex reasoning tasks.
Automated Eval#
The automated evaluation component is a critical aspect of modern benchmarking. It allows for objective and consistent assessment of model performance. Key considerations include ensuring the system can accurately extract solutions, especially in formats such as LaTeX, and handle varying symbolic representations. A robust automated evaluation framework is characterized by its ability to standardize mathematical expressions, verify correctness through rule-based equivalence checking (e.g., using SymPy), and accurately assess models in cases where results do not directly match. This evaluation should also address the inherent challenges of AI such as logical reasoning, conceptual physics problems, and mathematical precision. GPT-4 assisted evaluation can augment rule-based assessments. This is important to evaluate nuanced solutions. This ensures the system does not dismiss correct, but unconventionally derived answers, enhancing reliability and fairness. High-quality automated evaluation is an essential part to reduce costs and make the research more reproducible.
RAG for Physics#
Retrieval-Augmented Generation (RAG) for Physics is a promising avenue for enhancing the capabilities of foundation models in this domain. Since physics problems often demand integrating diverse knowledge pieces, RAG enables models to retrieve relevant information from external sources like textbooks or scientific literature. This augmentation mitigates the limitations of models’ internal knowledge, particularly when dealing with specialized concepts or complex derivations. By grounding the reasoning process in retrieved evidence, RAG can improve the accuracy and reliability of solutions. However, challenges include formulating effective search queries, selecting relevant information from retrieved content, and seamlessly integrating retrieved knowledge into the reasoning process. This requires models to discern essential concepts and relationships within complex physics problems and formulate queries that retrieve precise and contextually relevant information. Effectively managing the retrieved information and combining it with existing knowledge to produce accurate physics problem solutions is the key to success for RAG in physics.
Multi-Modal Data#
Multi-modal data is crucial for a comprehensive understanding of complex phenomena. Integrating diverse data types, such as text, images, and audio, provides a richer context and enables more nuanced analysis. For example, in medical diagnosis, combining patient history (text), X-ray images, and heart sounds (audio) can improve accuracy. Challenges include data synchronization, feature extraction across modalities, and dealing with heterogeneous data formats. Deep learning models, particularly those with attention mechanisms, are effective in learning cross-modal representations. Future research should focus on developing robust and interpretable methods for multi-modal fusion. This will drive advances in various fields, from AI to scientific discovery.
More visual insights#
More on figures

🔼 The figure illustrates the workflow of the PHYSICS benchmark dataset creation and model evaluation. First, annotators contribute problems (§3.2). These problems then undergo validation to create a refined dataset. Next, this dataset is used to prompt various language models (§4.1). The models’ responses are processed using regular expressions and the SymPy library for symbolic mathematics (§4.2). Finally, an automated system performs the final evaluation.
read the caption
Figure 2: For the overall process, we begin by collecting annotated problems from annotators (§3.2), followed by validation to create a processed dataset. This dataset is then used to prompt models (§4.1). The responses from models undergo regular expression pre-processing and SymPy-based processing before final evaluation using an automated system (§4.2).

🔼 This histogram displays the frequency distribution of reasoning steps needed to solve the physics problems in the PHYSICS benchmark dataset. The x-axis represents the number of reasoning steps, and the y-axis shows the percentage of problems requiring that many steps. The distribution helps illustrate the complexity of the problems, indicating that a substantial portion require multiple steps to solve, highlighting the challenge for AI models.
read the caption
Figure 3: Reasoning steps distribution.
More on tables
| Category | Value |
| Dataset Overview | |
| Total Questions | 1,297 |
| Questions with Figures | 298 |
| Validation : Test Split | 297 : 1,000 |
| Hard : Regular Questions | 523 : 774 |
| Subject Distribution | |
| Number of Subjects | 6 |
| Atomic Physics | 200 |
| Electromagnetism | 242 |
| Classical Mechanics | 221 |
| Optics | 158 |
| Quantum Mechanics | 236 |
| Statistical Physics | 240 |
| Question Complexity | |
| Avg. Question Length (words) | 83.7 |
| Solution Statistics | |
| Avg. Solution Length (words) | 234.75 |
| Avg. Reasoning Steps | 5.38 |
🔼 Table 2 presents a detailed statistical overview of the PHYSICS dataset, a benchmark for evaluating AI models’ ability to solve university-level physics problems. It shows the total number of questions, the number of questions with figures, the split of the dataset into validation and test sets, the breakdown of questions by physics subject area, the average length of questions and solutions (in words), and the average number of reasoning steps required to solve the problems. It also provides a breakdown of questions categorized as ‘hard’ based on annotator assessment. This comprehensive statistical summary allows researchers to understand the characteristics of the PHYSICS dataset and to assess its suitability for their research needs.
read the caption
Table 2: Dataset statistics of \ours.
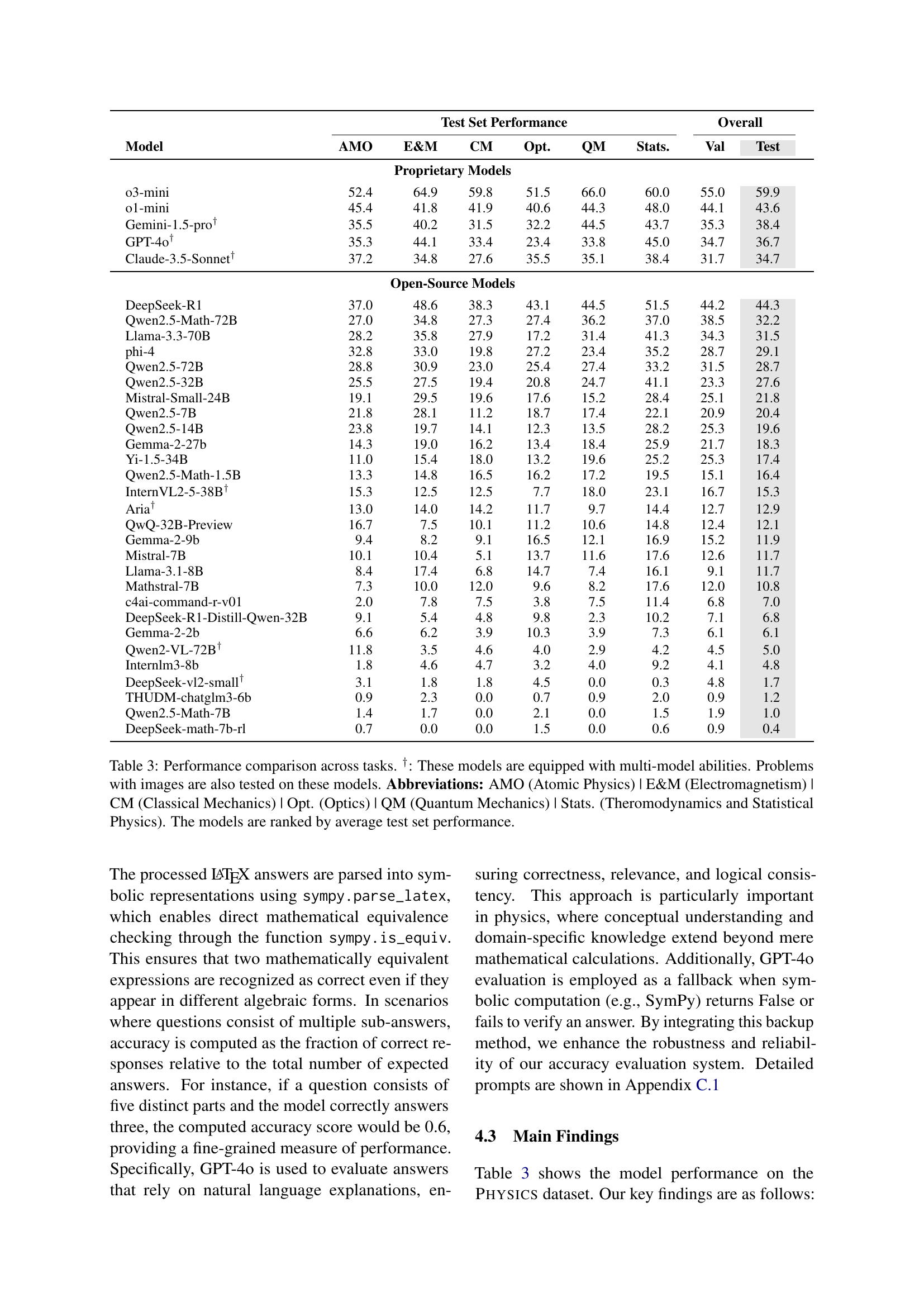
| Test Set Performance | Overall | |||||||
| Model | AMO | E&M | CM | Opt. | QM | Stats. | Val | Test |
| Proprietary Models | ||||||||
| o3-mini | 52.4 | 64.9 | 59.8 | 51.5 | 66.0 | 60.0 | 55.0 | 59.9 |
| o1-mini | 45.4 | 41.8 | 41.9 | 40.6 | 44.3 | 48.0 | 44.1 | 43.6 |
| Gemini-1.5-pro† | 35.5 | 40.2 | 31.5 | 32.2 | 44.5 | 43.7 | 35.3 | 38.4 |
| GPT-4o† | 35.3 | 44.1 | 33.4 | 23.4 | 33.8 | 45.0 | 34.7 | 36.7 |
| Claude-3.5-Sonnet† | 37.2 | 34.8 | 27.6 | 35.5 | 35.1 | 38.4 | 31.7 | 34.7 |
| Open-Source Models | ||||||||
| DeepSeek-R1 | 37.0 | 48.6 | 38.3 | 43.1 | 44.5 | 51.5 | 44.2 | 44.3 |
| Qwen2.5-Math-72B | 27.0 | 34.8 | 27.3 | 27.4 | 36.2 | 37.0 | 38.5 | 32.2 |
| Llama-3.3-70B | 28.2 | 35.8 | 27.9 | 17.2 | 31.4 | 41.3 | 34.3 | 31.5 |
| phi-4 | 32.8 | 33.0 | 19.8 | 27.2 | 23.4 | 35.2 | 28.7 | 29.1 |
| Qwen2.5-72B | 28.8 | 30.9 | 23.0 | 25.4 | 27.4 | 33.2 | 31.5 | 28.7 |
| Qwen2.5-32B | 25.5 | 27.5 | 19.4 | 20.8 | 24.7 | 41.1 | 23.3 | 27.6 |
| Mistral-Small-24B | 19.1 | 29.5 | 19.6 | 17.6 | 15.2 | 28.4 | 25.1 | 21.8 |
| Qwen2.5-7B | 21.8 | 28.1 | 11.2 | 18.7 | 17.4 | 22.1 | 20.9 | 20.4 |
| Qwen2.5-14B | 23.8 | 19.7 | 14.1 | 12.3 | 13.5 | 28.2 | 25.3 | 19.6 |
| Gemma-2-27b | 14.3 | 19.0 | 16.2 | 13.4 | 18.4 | 25.9 | 21.7 | 18.3 |
| Yi-1.5-34B | 11.0 | 15.4 | 18.0 | 13.2 | 19.6 | 25.2 | 25.3 | 17.4 |
| Qwen2.5-Math-1.5B | 13.3 | 14.8 | 16.5 | 16.2 | 17.2 | 19.5 | 15.1 | 16.4 |
| InternVL2-5-38B† | 15.3 | 12.5 | 12.5 | 7.7 | 18.0 | 23.1 | 16.7 | 15.3 |
| Aria† | 13.0 | 14.0 | 14.2 | 11.7 | 9.7 | 14.4 | 12.7 | 12.9 |
| QwQ-32B-Preview | 16.7 | 7.5 | 10.1 | 11.2 | 10.6 | 14.8 | 12.4 | 12.1 |
| Gemma-2-9b | 9.4 | 8.2 | 9.1 | 16.5 | 12.1 | 16.9 | 15.2 | 11.9 |
| Mistral-7B | 10.1 | 10.4 | 5.1 | 13.7 | 11.6 | 17.6 | 12.6 | 11.7 |
| Llama-3.1-8B | 8.4 | 17.4 | 6.8 | 14.7 | 7.4 | 16.1 | 9.1 | 11.7 |
| Mathstral-7B | 7.3 | 10.0 | 12.0 | 9.6 | 8.2 | 17.6 | 12.0 | 10.8 |
| c4ai-command-r-v01 | 2.0 | 7.8 | 7.5 | 3.8 | 7.5 | 11.4 | 6.8 | 7.0 |
| DeepSeek-R1-Distill-Qwen-32B | 9.1 | 5.4 | 4.8 | 9.8 | 2.3 | 10.2 | 7.1 | 6.8 |
| Gemma-2-2b | 6.6 | 6.2 | 3.9 | 10.3 | 3.9 | 7.3 | 6.1 | 6.1 |
| Qwen2-VL-72B† | 11.8 | 3.5 | 4.6 | 4.0 | 2.9 | 4.2 | 4.5 | 5.0 |
| Internlm3-8b | 1.8 | 4.6 | 4.7 | 3.2 | 4.0 | 9.2 | 4.1 | 4.8 |
| DeepSeek-vl2-small† | 3.1 | 1.8 | 1.8 | 4.5 | 0.0 | 0.3 | 4.8 | 1.7 |
| THUDM-chatglm3-6b | 0.9 | 2.3 | 0.0 | 0.7 | 0.9 | 2.0 | 0.9 | 1.2 |
| Qwen2.5-Math-7B | 1.4 | 1.7 | 0.0 | 2.1 | 0.0 | 1.5 | 1.9 | 1.0 |
| DeepSeek-math-7b-rl | 0.7 | 0.0 | 0.0 | 1.5 | 0.0 | 0.6 | 0.9 | 0.4 |
🔼 Table 3 presents a detailed performance comparison of various large language models (LLMs) across six core physics subfields. It shows the accuracy of each model on problems from Atomic Physics (AMO), Electromagnetism (E&M), Classical Mechanics (CM), Optics (Opt), Quantum Mechanics (QM), and Thermodynamics & Statistical Physics (Stats). The table distinguishes between proprietary and open-source models and indicates which models can handle multimodal problems (those including images). Models are ranked by their average performance on a held-out test set. This provides a comprehensive evaluation of the strengths and weaknesses of different LLMs in solving physics problems, highlighting the challenges that remain for even state-of-the-art models.
read the caption
Table 3: Performance comparison across tasks. †: These models are equipped with multi-model abilities. Problems with images are also tested on these models. Abbreviations: AMO (Atomic Physics) | E&M (Electromagnetism) | CM (Classical Mechanics) | Opt. (Optics) | QM (Quantum Mechanics) | Stats. (Theromodynamics and Statistical Physics). The models are ranked by average test set performance.
| ID | Year | Major | Assigned Subject(s) |
| 1 | 2nd Year Undergraduate | Physics | Classical Mechanics, Electromagnetism |
| 2 | 3rd Year Undergraduate | Physics | Quantum Mechanics, Optics |
| 3 | 2nd Year Undergraduate | Theoretical Physics | Quantum Mechanics, Thermodynamics and Statistical Mechanics |
| 4 | 3rd Year Undergraduate | Applied Physics | Thermodynamics and Statistical Mechanics, Atomic Physics |
| 5 | 2nd Year Undergraduate | Engineering Physics | Electromagnetism, Classical Mechanics |
| 6 | 3rd Year Undergraduate | Physics | Thermodynamics and Statistical Mechanics, Atomic Physics |
| 7 | 2nd Year Undergraduate | Astrophysics | Classical Mechanics, Optics |
🔼 Table 4 provides detailed biographical information for the seven expert annotators who contributed to the creation of the PHYSICS benchmark dataset. For each annotator, the table lists their ID number, academic year (as an undergraduate student), their major, and the specific physics subfields they were responsible for annotating. This information is crucial for understanding the qualifications and expertise of the individuals who created the dataset, thereby ensuring the reliability and accuracy of the benchmark’s annotation.
read the caption
Table 4: Biographies of 7 annotators involved in the Physics benchmark construction
Full paper#