Decoupling Angles and Strength in Low-rank Adaptation

2503.18225

Massimo Bini et el.

🤗 2025-04-01

TL;DR
#

Parameter-Efficient Fine-Tuning (PEFT) methods are popular for adapting large models, but LoRA is sensitive to hyperparameters and can degrade with extended training. ETHER is more robust, but limited to low-rank adaptations, reducing expressiveness. This work identifies the need for a method that balances robustness and expressiveness, addressing the limitations of existing PEFT techniques. The key problem is achieving stable and efficient adaptation without compromising performance.

This paper introduces DeLoRA, a novel PEFT method that normalizes and scales learnable low-rank matrices. By bounding the transformation distance, DeLoRA decouples angular learning from adaptation strength, enhancing robustness without sacrificing performance. Evaluations across image generation, NLU, and instruction tuning demonstrate that DeLoRA matches or exceeds existing PEFT methods while exhibiting stronger robustness, making it an effective approach for adapting large-scale models.

Key Takeaways
#

Why does it matter?
#

This paper introduces DeLoRA, a novel parameter-efficient finetuning method that enhances robustness and performance in adapting large-scale pretrained models. By decoupling angular learning from adaptation strength, DeLoRA offers a more stable and effective approach, opening new avenues for research in image generation, natural language understanding, and instruction tuning.

Visual Insights
#

🔼 Figure 1 provides a visual comparison of the original LoRA method and the proposed DeLoRA method. The left panel illustrates the LoRA architecture, showing the low-rank matrices B and A being multiplied and added to the original weight matrix W. The right panel shows the DeLoRA architecture, which incorporates a normalization factor (Ξ) and a scaling factor (λ) in addition to the low-rank matrices. These added components are designed to decouple the learning of the transformation’s direction (angle) from its magnitude (strength), resulting in improved robustness and adaptability. The figure highlights the key differences between the two methods by emphasizing the additional components incorporated into DeLoRA.
read the caption
Figure 1: Visualizations (Left) of the original LoRA (Hu et al., 2022) and (Right) of our proposed method DeLoRA. In addition to the low-rank matrices B,A𝐵𝐴B,Aitalic_B , italic_A, we introduce a normalization ΞΞ\Xiroman_Ξ and a scaling factor λ𝜆\lambdaitalic_λ, which effectively decouple the angular learning from the adaptation strength.

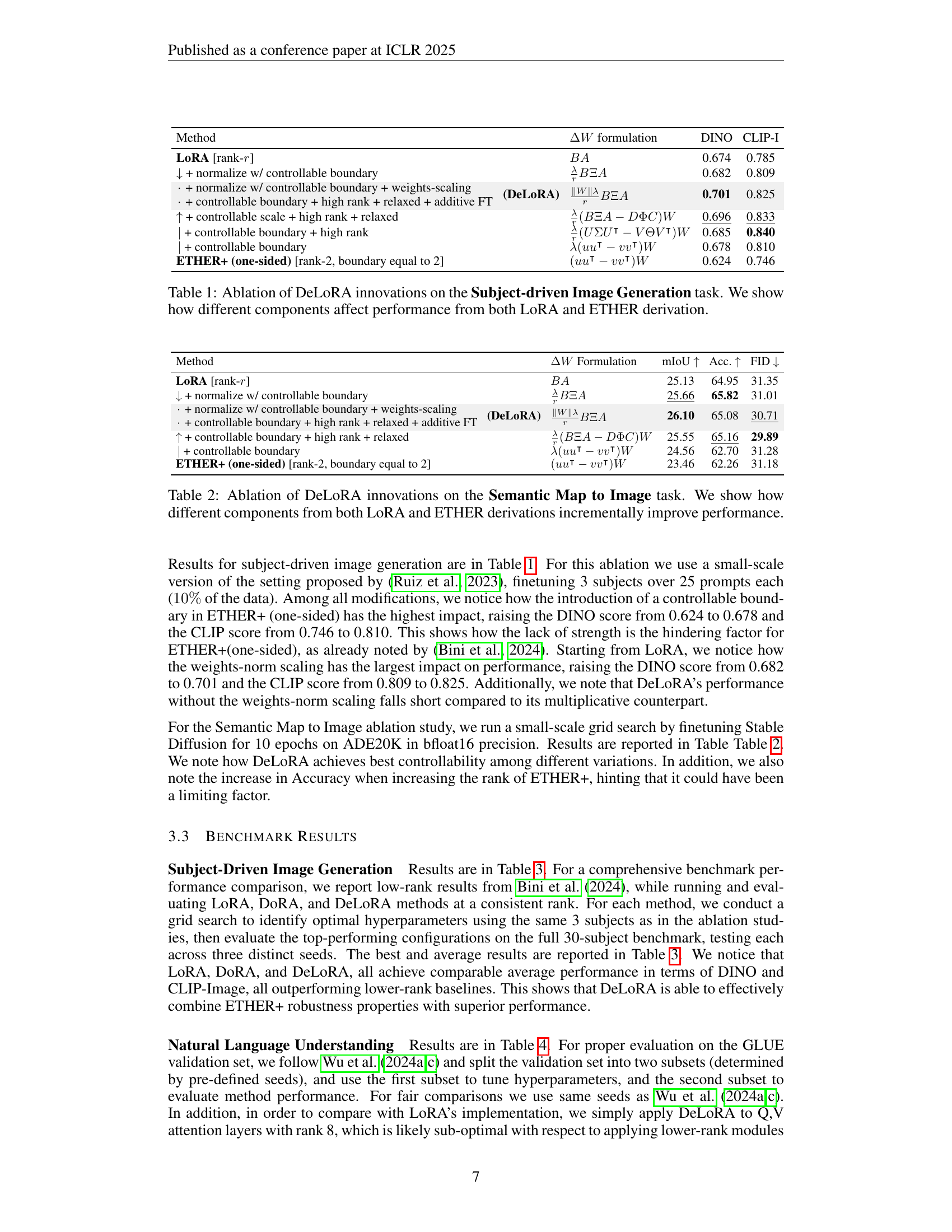
Method		$\Delta W$ formulation	DINO	CLIP-I
LoRA [rank- $r$ ]		$BA$	0.674	0.785
$\downarrow$ + normalize w/ controllable boundary		$\frac{\lambda}{r}B\Xi A$	0.682	0.809
$\cdot$ + normalize w/ controllable boundary + weights-scaling
$\cdot$ + controllable boundary + high rank + relaxed + additive FT	(DeLoRA)	$\frac{\\|W\\|\lambda}{r}B\Xi A$	0.701	0.825
$\uparrow$ + controllable scale + high rank + relaxed		$\frac{\lambda}{r}(B\Xi A-D\Phi C)W$	0.696	0.833
$\|$ + controllable boundary + high rank		$\frac{\lambda}{r}(U\Sigma U^{\intercal}-V\Theta V^{\intercal})W$	0.685	0.840
$\|$ + controllable boundary		$\lambda(uu^{\intercal}-vv^{\intercal})W$	0.678	0.810
ETHER+ (one-sided) [rank-2, boundary equal to 2]		$(uu^{\intercal}-vv^{\intercal})W$	0.624	0.746

🔼 This table presents an ablation study evaluating the impact of individual components of the DeLoRA model on the Subject-driven Image Generation task. It shows the performance improvements achieved by incrementally adding features from both LoRA (Low-Rank Adaptation) and ETHER (Efficient finetuning with Hyperplane Reflections) methods. Each row represents a variation of the model, starting from the basic LoRA, and progressively incorporating features such as normalization with a controllable boundary, weights scaling, high-rank updates, and relaxed constraints. The performance is measured using DINO and CLIP-I scores, indicating the subject-fidelity of the generated images.
read the caption
Table 1: Ablation of DeLoRA innovations on the Subject-driven Image Generation task. We show how different components affect performance from both LoRA and ETHER derivation.

In-depth insights
#

DeLoRA: Angles+
#

The “DeLoRA: Angles+” concept, though not explicitly defined in the provided paper, likely pertains to the innovative approach of decoupling angular learning from adaptation strength in low-rank adaptation (LoRA). It is used to achieve robustness and expressivity. The “Angles” aspect probably refers to the normalized low-rank matrices (BΞA) which control the direction of weight updates, independent of their magnitude. The “+” implies additional mechanisms enhancing this angular control. These could include the scaling factor (λ) which is used to tune the adaptation strength or weights norm scaling which makes the update proportional to the pretrained weight’s norm. By decoupling the angular update with this normalized learning, DeLoRA offers superior control during finetuning avoiding catastrophic overwriting. This contributes to DeLoRA’s learning rate robustness.

Robustness Focus
#

The paper demonstrates a robustness focus achieved through the DeLoRA method. This method normalizes and scales low-rank matrices, effectively decoupling angular learning from adaptation strength. This is crucial because it reduces sensitivity to hyperparameter choices and extended training regimes, problems common in LoRA. The method mitigates catastrophic overwriting of pre-trained weights, enhancing stability and reducing performance degradation. The findings revealed that DeLoRA maintains performance, whereas the LoRA performance degrades with higher learning rates. Robustness is seen through better performance retentions during extended fine-tuning, making DeLoRA more reliable for diverse applications. Ultimately, robustness is a key aspect of DeLoRA, making it a valuable contribution to parameter-efficient fine-tuning.

LoRA & ETHER
#

LoRA excels in parameter-efficient finetuning, offering simplicity and effectiveness, but struggles with hyperparameter sensitivity and performance degradation during extended training. ETHER provides robustness but is limited by low-rank adaptations and fixed-strength transformations. This impacts expressive power, hindering the extent to which the model can adapt to specific tasks and datasets. These limitations highlight a trade-off between efficiency, robustness and expressivity. Balancing these aspects is key for optimal performance across diverse applications.

Weights vs. Norms
#

The research paper explores the nuances of weight normalization within the context of parameter-efficient fine-tuning (PEFT) methods, particularly in image generation. The analysis reveals that different modules in the U-Net architecture exhibit systematic variations in weight norms, underscoring the importance of layer-adaptive strategies. This heterogeneity suggests that a universal scaling approach might not be optimal, and PEFT techniques should account for the unique characteristics of each layer. The study introduces a weights-norm scaling technique that demonstrates improved performance, suggesting that aligning weight updates with the inherent structure of the pretrained model can be beneficial. Further exploration of more sophisticated methods to incorporate layer-wise differences is indicated as a promising avenue for future research, potentially leading to more effective and robust fine-tuning strategies.

Vision & Language
#

While the provided research paper doesn’t explicitly have a “Vision & Language” section, its core theme strongly aligns with this interdisciplinary field. The paper’s exploration of adapting large-scale pretrained models for tasks like subject-driven image generation and semantic map-to-image translation directly tackles challenges at the intersection of vision and language. The key idea of parameter-efficient finetuning (PEFT), specifically through the proposed DeLoRA method, aims to bridge the gap between textual prompts/semantic layouts and the generation/manipulation of visual content. By decoupling angular learning from adaptation strength, DeLoRA enhances the robustness of these models, allowing for more reliable and controllable generation based on linguistic inputs. The experiments in subject-driven image generation demonstrate how well the models can understand and recontextualize a subject based on text, while the semantic map to image task evaluates the model’s ability to translate spatial information derived from language into realistic images. Furthermore, its evaluation on Natural Language Understanding tasks shows that it not only excels in vision-language tasks but also captures intricate linguistic information. This ability to work with both vision and language is a hallmark of a good vision and language model.

More visual insights
#

More on figures

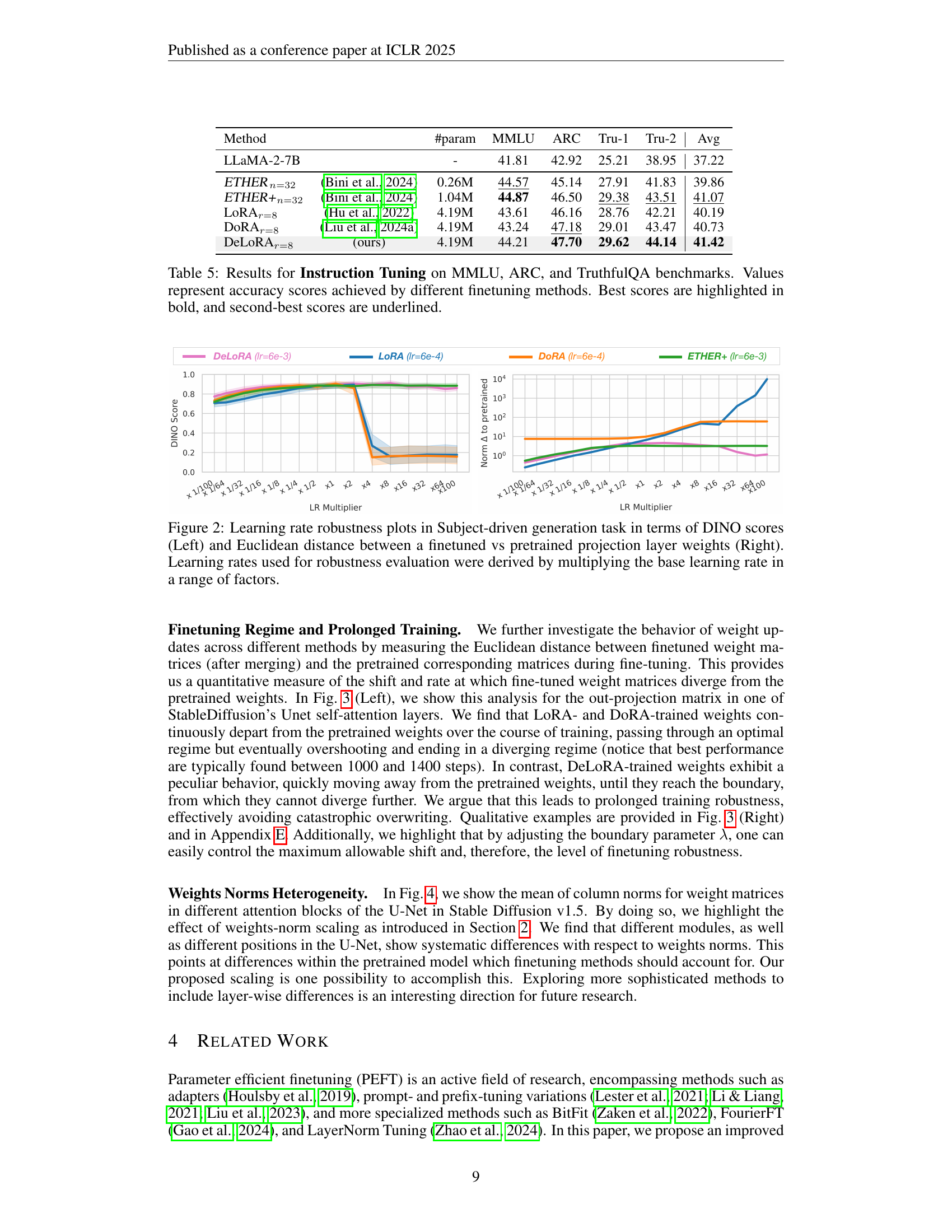
🔼 This figure displays the results of an experiment evaluating the robustness of different parameter-efficient fine-tuning (PEFT) methods to variations in the learning rate. The left panel shows DINO scores, a measure of subject fidelity in image generation, for various learning rates. The scores are obtained by multiplying the base learning rate by a range of factors, demonstrating how model performance changes with different learning rates. The right panel shows the Euclidean distance between the weights of a finetuned model and those of its pretrained counterpart for the same range of learning rates. This distance provides insight into how much the model’s parameters change during fine-tuning, which is relevant to stability and the risk of catastrophic forgetting. The figure helps to assess how each method’s performance and parameter shift is affected by the choice of learning rate.
read the caption
Figure 2: Learning rate robustness plots in Subject-driven generation task in terms of DINO scores (Left) and Euclidean distance between a finetuned vs pretrained projection layer weights (Right). Learning rates used for robustness evaluation were derived by multiplying the base learning rate in a range of factors.

🔼 Figure 3 presents a comparative analysis of the training dynamics of LoRA and DeLoRA. The left panel shows a line graph plotting the Euclidean distance between the weights of the finetuned model and the pretrained model’s weights over the course of training. This distance represents the magnitude of changes made to the model during finetuning. The right panel provides qualitative results showcasing image generation using LoRA and DeLoRA. This visual comparison demonstrates how LoRA produces images with noticeable artifacts earlier in the training process, while DeLoRA generates higher-quality images that maintain a better visual fidelity. This illustrates DeLoRA’s improved robustness and stability during training.
read the caption
Figure 3: (Left) Euclidean Distance of finetuned weights to pretrained weights as a function of the number of training steps. (Right) Qualitative examples show that LoRA exhibits significant artifacts earlier in the process compared to DeLoRA, which maintains better image quality.

🔼 This figure visualizes the average column norms of the parameters within the attention modules of Stable Diffusion’s U-Net. It displays these norms for various layers and blocks within the U-Net, including the down blocks, up blocks, and mid block. The x-axis represents the different layers and blocks, and the y-axis shows the average column norms. This visualization helps to illustrate the heterogeneity of parameter norms across the different components of the model. Understanding these norm distributions can be important for designing and interpreting parameter-efficient fine-tuning techniques for generative models like Stable Diffusion.
read the caption
Figure 4: Average column norms of parameters in the attention modules of Stable Diffusion’s Unet

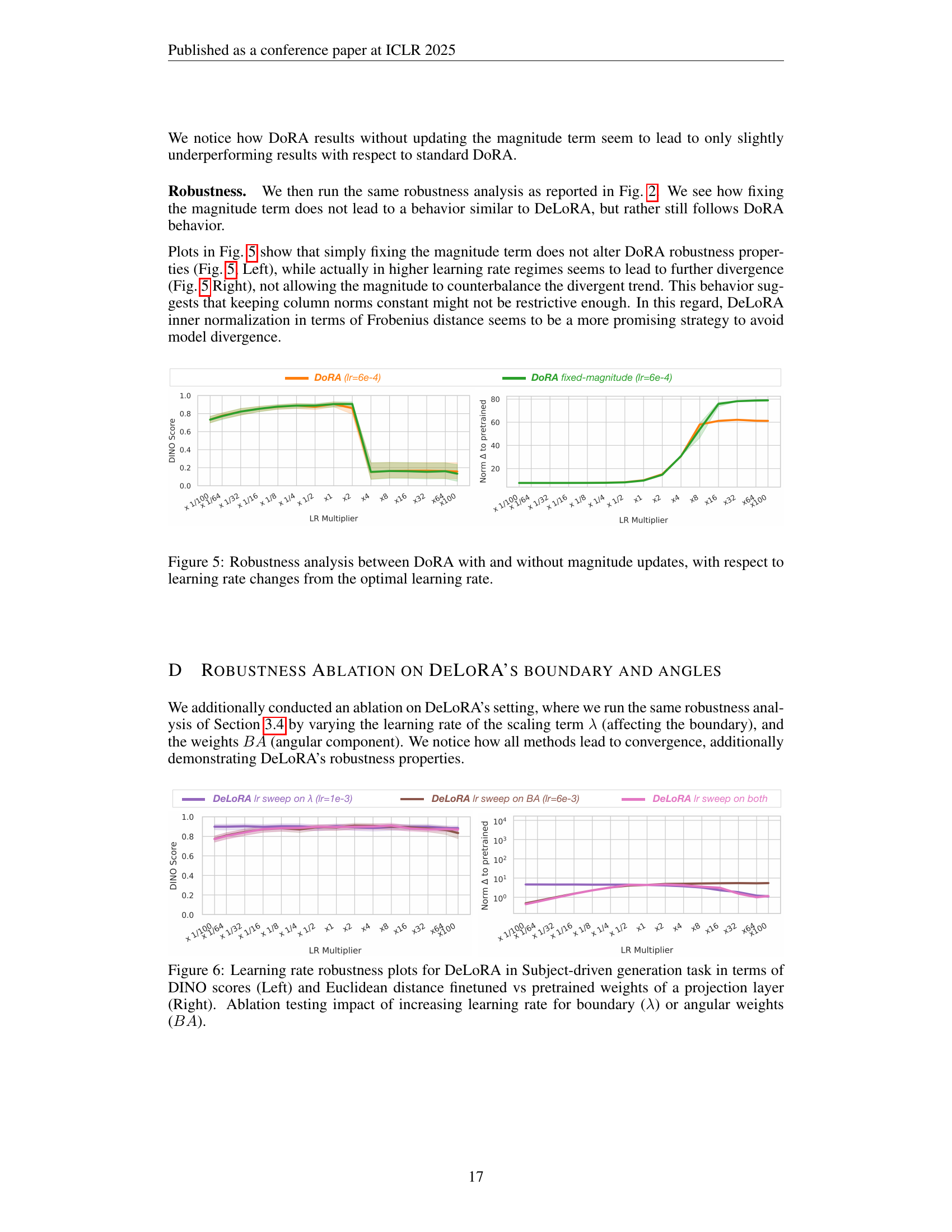
🔼 Figure 5 presents a comparative analysis of DoRA’s robustness with and without magnitude updates. It illustrates how the performance of DoRA changes when the learning rate deviates from its optimal value. The left subplot showcases the DINO scores while the right one displays the Euclidean distance between the finetuned and pretrained projection layer weights. This visualization helps in understanding the impact of magnitude updates on DoRA’s robustness against learning rate variations.
read the caption
Figure 5: Robustness analysis between DoRA with and without magnitude updates, with respect to learning rate changes from the optimal learning rate.

🔼 Figure 6 presents an ablation study on DeLoRA’s robustness to learning rate variations in the context of subject-driven image generation. The left panel displays DINO scores, a measure of subject fidelity in generated images, plotted against different learning rates for the scaling parameter (λ) and the angular weights (BA). The right panel shows the Euclidean distance between the finetuned and pretrained weights of a projection layer, also as a function of the learning rate for λ and BA. This dual visualization allows for a comprehensive assessment of how changes in learning rate affect both the performance (DINO score) and the stability (distance from pretrained weights) of DeLoRA. The results show the impact of varying learning rates on DeLoRA’s performance and stability.
read the caption
Figure 6: Learning rate robustness plots for DeLoRA in Subject-driven generation task in terms of DINO scores (Left) and Euclidean distance finetuned vs pretrained weights of a projection layer (Right). Ablation testing impact of increasing learning rate for boundary (λ𝜆\lambdaitalic_λ) or angular weights (B⁢A𝐵𝐴BAitalic_B italic_A).

🔼 This figure shows examples of image generation results obtained using DeLoRA, a parameter-efficient fine-tuning method. The left side displays images generated for a personalized generation task, where Stable Diffusion is fine-tuned to generate images of a specific subject in various contexts based on given text prompts. The right side shows results from a semantic map to image task, where DeLoRA fine-tunes Stable Diffusion to generate realistic images that closely adhere to the structure of a provided segmentation map (ADE20K dataset). This visually demonstrates DeLoRA’s ability to adapt a large-scale pre-trained model to various downstream image generation tasks with high fidelity.
read the caption
Figure 7: Examples generated by DeLoRA-finetuned Stable Diffusion for personalized generation on a small set of subject-specific images (left), and for semantic map to image on ADE20K (right).

🔼 Figure 8 presents a qualitative comparison of image generation results from DeLoRA, LoRA, and DoRA models after prolonged training, up to 2600 time steps. The images visually showcase the differences in output quality and stability across the three methods, providing insights into each model’s ability to maintain image coherence and avoid artifacts during extended training.
read the caption
Figure 8: Prolonged finetuning generated examples generated by DeLoRA, LoRA, and DoRA methods, up to time step 2600.

More on tables

Method		$\Delta W$ Formulation	mIoU $\uparrow$	Acc. $\uparrow$	FID $\downarrow$
LoRA [rank- $r$ ]		$BA$	25.13	64.95	31.35
$\downarrow$ + normalize w/ controllable boundary		$\frac{\lambda}{r}B\Xi A$	25.66	65.82	31.01
$\cdot$ + normalize w/ controllable boundary + weights-scaling
$\cdot$ + controllable boundary + high rank + relaxed + additive FT	(DeLoRA)	$\frac{\\|W\\|\lambda}{r}B\Xi A$	26.10	65.08	30.71
$\uparrow$ + controllable boundary + high rank + relaxed		$\frac{\lambda}{r}(B\Xi A-D\Phi C)W$	25.55	65.16	29.89
$\|$ + controllable boundary		$\lambda(uu^{\intercal}-vv^{\intercal})W$	24.56	62.70	31.28
ETHER+ (one-sided) [rank-2, boundary equal to 2]		$(uu^{\intercal}-vv^{\intercal})W$	23.46	62.26	31.18

🔼 This table presents an ablation study evaluating the impact of different design choices in the DeLoRA model on its performance for the Semantic Map to Image task. It systematically adds components from both the LoRA and ETHER methods to demonstrate the incremental improvements achieved by each addition. The table shows how each component contributes to the overall performance improvement, highlighting the relative importance of various design aspects of the DeLoRA model.
read the caption
Table 2: Ablation of DeLoRA innovations on the Semantic Map to Image task. We show how different components from both LoRA and ETHER derivations incrementally improve performance.

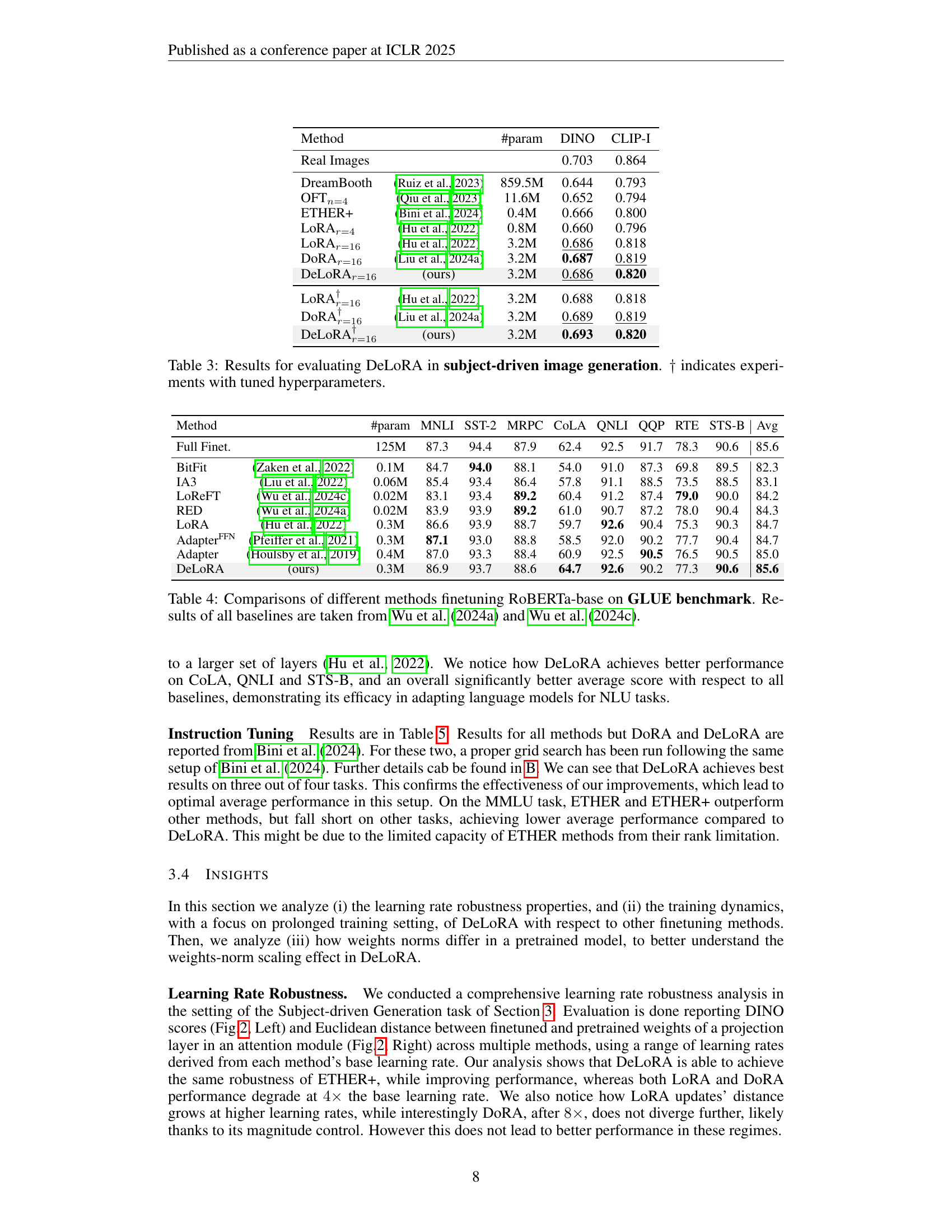
Method		#param	DINO	CLIP-I
Real Images			0.703	0.864
DreamBooth	(Ruiz et al., 2023)	859.5M	0.644	0.793
OFT_n=4	(Qiu et al., 2023)	11.6M	0.652	0.794
ETHER+	(Bini et al., 2024)	0.4M	0.666	0.800
LoRA_r=4	(Hu et al., 2022)	0.8M	0.660	0.796
LoRA_r=16	(Hu et al., 2022)	3.2M	0.686	0.818
DoRA_r=16	(Liu et al., 2024a)	3.2M	0.687	0.819
DeLoRA_r=16	(ours)	3.2M	0.686	0.820
LoRA ${}^{\dagger}_{r=16}$	(Hu et al., 2022)	3.2M	0.688	0.818
DoRA ${}^{\dagger}_{r=16}$	(Liu et al., 2024a)	3.2M	0.689	0.819
DeLoRA ${}^{\dagger}_{r=16}$	(ours)	3.2M	0.693	0.820

🔼 This table presents a comparison of different parameter-efficient fine-tuning (PEFT) methods on a subject-driven image generation task. The task involves adapting a pre-trained Stable Diffusion model to generate images of a specific subject according to a given prompt. The table shows the performance of various methods, including LoRA, DORA, and the proposed DeLoRA, in terms of two metrics: DINO and CLIP-I. These metrics evaluate the similarity between generated images and real images of the subject, measuring the faithfulness of the generation. The number of parameters used by each method is also reported. Some results may include tuned hyperparameters, indicated by a dagger symbol.
read the caption
Table 3: Results for evaluating DeLoRA in subject-driven image generation. ††\dagger† indicates experiments with tuned hyperparameters.

Method		#param	MNLI	SST-2	MRPC	CoLA	QNLI	QQP	RTE	STS-B	Avg
Full Finet.		125M	87.3	94.4	87.9	62.4	92.5	91.7	78.3	90.6	85.6
BitFit	(Zaken et al., 2022)	0.1M	84.7	94.0	88.1	54.0	91.0	87.3	69.8	89.5	82.3
IA3	(Liu et al., 2022)	0.06M	85.4	93.4	86.4	57.8	91.1	88.5	73.5	88.5	83.1
LoReFT	(Wu et al., 2024c)	0.02M	83.1	93.4	89.2	60.4	91.2	87.4	79.0	90.0	84.2
RED	(Wu et al., 2024a)	0.02M	83.9	93.9	89.2	61.0	90.7	87.2	78.0	90.4	84.3
LoRA	(Hu et al., 2022)	0.3M	86.6	93.9	88.7	59.7	92.6	90.4	75.3	90.3	84.7
Adapter ${}^{\text{FFN}}$	(Pfeiffer et al., 2021)	0.3M	87.1	93.0	88.8	58.5	92.0	90.2	77.7	90.4	84.7
Adapter	(Houlsby et al., 2019)	0.4M	87.0	93.3	88.4	60.9	92.5	90.5	76.5	90.5	85.0
DeLoRA	(ours)	0.3M	86.9	93.7	88.6	64.7	92.6	90.2	77.3	90.6	85.6

🔼 This table presents a comparison of various parameter-efficient fine-tuning (PEFT) methods on the GLUE benchmark, using the RoBERTa-base model. It shows the performance of each method in terms of accuracy across different GLUE tasks, including MNLI, SST-2, MRPC, CoLA, QNLI, QQP, RTE, and STS-B. The table also includes the number of parameters used by each method, providing a context for comparing performance efficiency. Results for all baseline methods (other than DeLoRA) are taken from previously published work by Wu et al. (2024a) and Wu et al. (2024c), ensuring a consistent basis for comparison.
read the caption
Table 4: Comparisons of different methods finetuning RoBERTa-base on GLUE benchmark. Results of all baselines are taken from Wu et al. (2024a) and Wu et al. (2024c).

Method		#param	MMLU	ARC	Tru-1	Tru-2	Avg
LLaMA-2-7B		-	41.81	42.92	25.21	38.95	37.22
ETHER_n=32	(Bini et al., 2024)	0.26M	44.57	45.14	27.91	41.83	39.86
ETHER+_n=32	(Bini et al., 2024)	1.04M	44.87	46.50	29.38	43.51	41.07
LoRA_r=8	(Hu et al., 2022)	4.19M	43.61	46.16	28.76	42.21	40.19
DoRA_r=8	(Liu et al., 2024a)	4.19M	43.24	47.18	29.01	43.47	40.73
DeLoRA_r=8	(ours)	4.19M	44.21	47.70	29.62	44.14	41.42

🔼 This table presents the results of instruction tuning experiments conducted on three widely used benchmarks: MMLU, ARC, and TruthfulQA. Different parameter-efficient fine-tuning (PEFT) methods were evaluated, and their accuracy scores are reported for each benchmark. The best performing method for each benchmark is highlighted in bold, while the second-best is underlined. This allows for a direct comparison of the effectiveness of various PEFT approaches in adapting large language models for instruction following tasks.
read the caption
Table 5: Results for Instruction Tuning on MMLU, ARC, and TruthfulQA benchmarks. Values represent accuracy scores achieved by different finetuning methods. Best scores are highlighted in bold, and second-best scores are underlined.

Method		DINO	CLIP-I
LoRA_r=16	(Hu et al., 2022)	0.686_±.0012	0.818_±.0017
DoRA_r=16	(Liu et al., 2024a)	0.687_±.0015	0.819_±.0015
DeLoRA_r=16	(ours)	0.686_±.0056	0.820_±.0027

🔼 This table presents a quantitative comparison of different methods for subject-driven image generation, focusing on their performance as measured by two metrics: DINO and CLIP-I. The results are shown for three different low-rank methods: LoRA, DORA, and DeLoRA. Each method’s performance is evaluated across multiple trials, with standard deviations provided to illustrate the variability in performance. The best-performing method for each metric is highlighted in bold, while the second-best is underlined.
read the caption
Table 6: Results with standard deviation for subject-driven image generation trained methods. Best scores are highlighted in bold, and second-best scores are underlined.

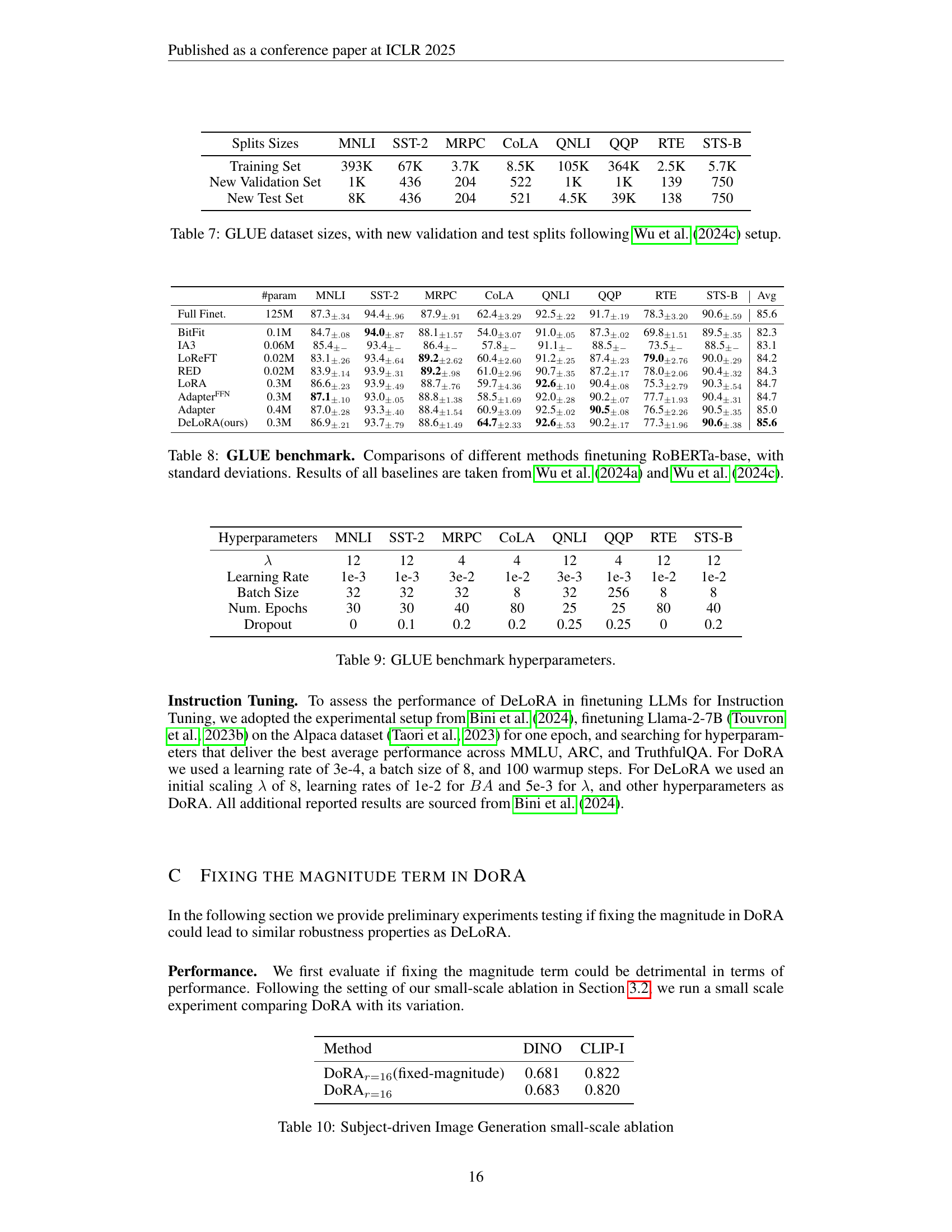
Splits Sizes	MNLI	SST-2	MRPC	CoLA	QNLI	QQP	RTE	STS-B
Training Set	393K	67K	3.7K	8.5K	105K	364K	2.5K	5.7K
New Validation Set	1K	436	204	522	1K	1K	139	750
New Test Set	8K	436	204	521	4.5K	39K	138	750

🔼 This table presents the sizes of the datasets used in the GLUE benchmark for natural language understanding. It shows the number of samples in the training, validation, and test sets for each of the tasks included in the GLUE benchmark (MNLI, SST-2, MRPC, CoLA, QNLI, QQP, RTE, and STS-B). Importantly, it highlights that the validation and test set sizes have been adjusted following the methodology described in Wu et al. (2024c) to ensure consistency and fairness in the experimental results.
read the caption
Table 7: GLUE dataset sizes, with new validation and test splits following Wu et al. (2024c) setup.

	#param	MNLI	SST-2	MRPC	CoLA	QNLI	QQP	RTE	STS-B	Avg
Full Finet.	125M	87.3_±.34	94.4_±.96	87.9_±.91	62.4_±3.29	92.5_±.22	91.7_±.19	78.3_±3.20	90.6_±.59	85.6
BitFit	0.1M	84.7_±.08	94.0_±.87	88.1_±1.57	54.0_±3.07	91.0_±.05	87.3_±.02	69.8_±1.51	89.5_±.35	82.3
IA3	0.06M	85.4_±-	93.4_±-	86.4_±-	57.8_±-	91.1_±-	88.5_±-	73.5_±-	88.5_±-	83.1
LoReFT	0.02M	83.1_±.26	93.4_±.64	89.2_±2.62	60.4_±2.60	91.2_±.25	87.4_±.23	79.0_±2.76	90.0_±.29	84.2
RED	0.02M	83.9_±.14	93.9_±.31	89.2_±.98	61.0_±2.96	90.7_±.35	87.2_±.17	78.0_±2.06	90.4_±.32	84.3
LoRA	0.3M	86.6_±.23	93.9_±.49	88.7_±.76	59.7_±4.36	92.6_±.10	90.4_±.08	75.3_±2.79	90.3_±.54	84.7
Adapter ${}^{\text{FFN}}$	0.3M	87.1_±.10	93.0_±.05	88.8_±1.38	58.5_±1.69	92.0_±.28	90.2_±.07	77.7_±1.93	90.4_±.31	84.7
Adapter	0.4M	87.0_±.28	93.3_±.40	88.4_±1.54	60.9_±3.09	92.5_±.02	90.5_±.08	76.5_±2.26	90.5_±.35	85.0
DeLoRA(ours)	0.3M	86.9_±.21	93.7_±.79	88.6_±1.49	64.7_±2.33	92.6_±.53	90.2_±.17	77.3_±1.96	90.6_±.38	85.6

🔼 This table presents a comparison of different parameter-efficient fine-tuning (PEFT) methods on the GLUE benchmark, specifically focusing on their performance when applied to the RoBERTa-base model. It shows the performance metrics (accuracy, correlation, etc.) achieved by each method for various subtasks within the GLUE benchmark. Standard deviations are included to indicate the variability in the results. The results for baseline methods (other than DeLoRA) are sourced from Wu et al. (2024a) and Wu et al. (2024c), ensuring a consistent comparison framework.
read the caption
Table 8: GLUE benchmark. Comparisons of different methods finetuning RoBERTa-base, with standard deviations. Results of all baselines are taken from Wu et al. (2024a) and Wu et al. (2024c).

Hyperparameters	MNLI	SST-2	MRPC	CoLA	QNLI	QQP	RTE	STS-B
$\lambda$	12	12	4	4	12	4	12	12
Learning Rate	1e-3	1e-3	3e-2	1e-2	3e-3	1e-3	1e-2	1e-2
Batch Size	32	32	32	8	32	256	8	8
Num. Epochs	30	30	40	80	25	25	80	40
Dropout	0	0.1	0.2	0.2	0.25	0.25	0	0.2

🔼 Table 9 presents the hyperparameters used in the GLUE benchmark experiments for various methods, including the learning rate, batch size, number of epochs, and dropout rate. It shows the specific settings employed for each method and dataset, which is crucial for reproducibility and understanding the experimental conditions.
read the caption
Table 9: GLUE benchmark hyperparameters.

Method	DINO	CLIP-I
DoRA_r=16(fixed-magnitude)	0.681	0.822
DoRA_r=16	0.683	0.820

🔼 This table presents results from a small-scale ablation study on the Subject-driven Image Generation task. It compares the performance of DoRA with and without fixing the magnitude term, evaluating both methods using the DINO and CLIP-I metrics to assess subject fidelity. The purpose is to investigate if constraining magnitude in DoRA leads to similar robustness properties as observed in DeLoRA.
read the caption
Table 10: Subject-driven Image Generation small-scale ablation

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

DeLoRA: Angles+#

Robustness Focus#

LoRA & ETHER#

Weights vs. Norms#

Vision & Language#

More visual insights#

Full paper#