TL;DR#
Large Language Models(LLMs) leverage self-generated reasoning paths to refine their mathematical problem-solving. Self-training uses this data, but treats all examples equally, missing the varying value of each data point and limiting learning effectiveness. This paper asks if reweighting training data could improve reasoning and which data should be prioritized.
To address this, the paper introduces Entropy-Based Adaptive Weighting for Self-Training (EAST), which adaptively weights data based on the model’s uncertainty. It uses a mapping function with a tunable parameter to prioritize uncertain data, guiding the model to focus on challenging examples. Evaluated on benchmarks like GSM8K and MATH, EAST shows performance gains over vanilla methods, highlighting its effectiveness.
Key Takeaways#
Why does it matter?#
This paper introduces EAST, a novel weighting method for self-training that enhances reasoning capabilities by emphasizing uncertain data. This is important for researchers because it offers a new strategy to improve LLMs without manual effort. It addresses a critical challenge in self-training and opens avenues for exploring adaptive weighting.
Visual Insights#

🔼 This figure illustrates the difference between standard self-training and the proposed EAST method. In standard self-training, a large language model (LLM) generates multiple responses to a given question. Responses are grouped by their final answer. If all responses for a question are incorrect, that question is discarded. The remaining correct responses are used for fine-tuning the model, with each response given equal weight. EAST modifies this process by assigning weights to the questions based on the diversity of the responses. Questions with a wide variety of answers (indicating uncertainty in the model) receive higher weights, while those with consistent answers (showing model confidence) receive lower weights. This adaptive weighting strategy allows EAST to focus the model’s training on more challenging and informative examples.
read the caption
Figure 1: Comparison between the traditional self-training pipeline and EAST. The LLM generates n𝑛nitalic_n responses per question, clustered by final answers. Questions with all incorrect answers are discarded. Self-training fine-tunes uniformly on the rest, while EAST assigns higher weights to questions with diverse (uncertain) answers and lower weights to consistent (confident) ones.
In-depth insights#
Self-Training++#
Self-Training++ could represent an advanced iteration of traditional self-training techniques in machine learning. This likely involves augmenting the core self-training loop with innovative strategies to overcome inherent limitations, such as confirmation bias and noisy pseudo-labels. Potential enhancements might include sophisticated methods for pseudo-label filtering or refinement, adaptive weighting schemes to prioritize high-confidence or informative examples, or the integration of auxiliary tasks to improve model robustness. Furthermore, Self-Training++ may explore novel ways to leverage unlabeled data, such as incorporating contrastive learning objectives or employing generative models to create synthetic training examples. The goal would be to yield more effective and reliable performance gains compared to conventional self-training.
Uncertainty Rules#
The concept of ‘Uncertainty Rules’ in the context of AI, especially Large Language Models (LLMs), is multifaceted. In essence, it means that models’ predictions aren’t always definitive; they exist on a spectrum of possibilities. This uncertainty stems from various factors, including the inherent ambiguity in language, the limitations of training data, and the model’s architecture. Embracing uncertainty is critical for robust AI. Quantifying uncertainty is the first step, using techniques like entropy to measure the diversity of predictions. Adaptive weighting strategies like EAST leverage this uncertainty, prioritizing training on examples where the model is less confident. This focuses learning on more informative data, improving reasoning and preventing overfitting. However, not all uncertainty is equal; the source matters. Token-level uncertainty (perplexity) differs from distributional uncertainty (entropy), with the latter proving more effective. Finally, ‘Uncertainty Rules’ highlight the need for AI systems to communicate their confidence levels, fostering trust and enabling users to make informed decisions based on the model’s output. Ignoring uncertainty leads to overconfident, brittle models prone to failure in novel situations.
Weighting Edge#
Weighting edges in self-training offers a promising avenue for refining large language model reasoning. Instead of treating all self-generated data equally, a strategic weighting scheme can emphasize more informative examples. Prioritizing uncertain data, where the model struggles, encourages exploration and prevents overfitting. The weighting should consider factors such as entropy, accuracy, and rejection. By weighting, we can guide the model towards optimal knowledge. This helps improve the learning effectiveness.
LLM Reasoning#
LLM Reasoning is a critical area of research, focusing on enhancing logical consistency and problem-solving. Self-generated reasoning paths refine models by capturing step-by-step processes, using only correct answers for supervision. Adaptive weighting strategies, like EAST, prioritize uncertain data during training. This emphasizes informative examples, boosting reasoning ability. Prioritizing uncertain data enhances training effectiveness by focusing on challenging questions where the model struggles. Entropy-based weighting leverages model uncertainty to guide focus. Studies explore constructing preference pairs from negative samples and aligning methods for fine-tuning. Techniques assigning equal importance to all examples overlook the varying value of data points, impacting the model’s ability to prioritize effectively. Reweighting training data can improve reasoning. It’s vital to emphasize prioritizing uncertain data, and determining how much data should be prioritized.
Beyond SFT#
Moving beyond Supervised Fine-Tuning (SFT) is critical for advancing LLMs. SFT, while effective as a starting point, often leads to models that simply mimic the training data, lacking true reasoning capabilities. To surpass these limitations, research explores various avenues. One approach involves Reinforcement Learning from Human Feedback (RLHF), which aligns models with human preferences, leading to more helpful and safer outputs. However, RLHF is data-intensive and requires careful reward design. Another promising direction is self-training, where the model iteratively learns from its own generated data, refining its reasoning abilities over time. This approach reduces reliance on external data and can uncover hidden patterns. Contrastive learning is also emerging as a powerful technique, training models to distinguish between correct and incorrect reasoning paths, improving their accuracy and robustness. Furthermore, innovative architectures and training objectives, like adversarial training, can enhance a model’s ability to generalize and handle challenging inputs. Ultimately, a holistic approach combining these techniques is likely needed to unlock the full potential of LLMs and move beyond the limitations of SFT.
More visual insights#
More on figures

🔼 Figure 2 illustrates the EAST framework, a novel weighting method for self-training. For each training question, a large language model (LLM) generates multiple responses. These responses are grouped (clustered) based on their final answers. The diversity of answers within each question is quantified using entropy. This entropy value represents the model’s uncertainty about the question; higher entropy indicates more uncertainty. The entropy is then transformed by a mapping function, which introduces a tunable parameter to control the sharpness of the weighting. Finally, this transformed entropy value (the weight) is incorporated into the loss function to guide the self-training process. Questions with high entropy (more uncertainty) receive higher weights during training, effectively steering the model towards focusing on more challenging and informative examples.
read the caption
Figure 2: The framework of EAST. For each training question, the LLM generates n𝑛nitalic_n responses, clustered by final answers. Entropy value is computed from the cluster distribution, transformed via mapping function, and integrated as weight into the loss objective.

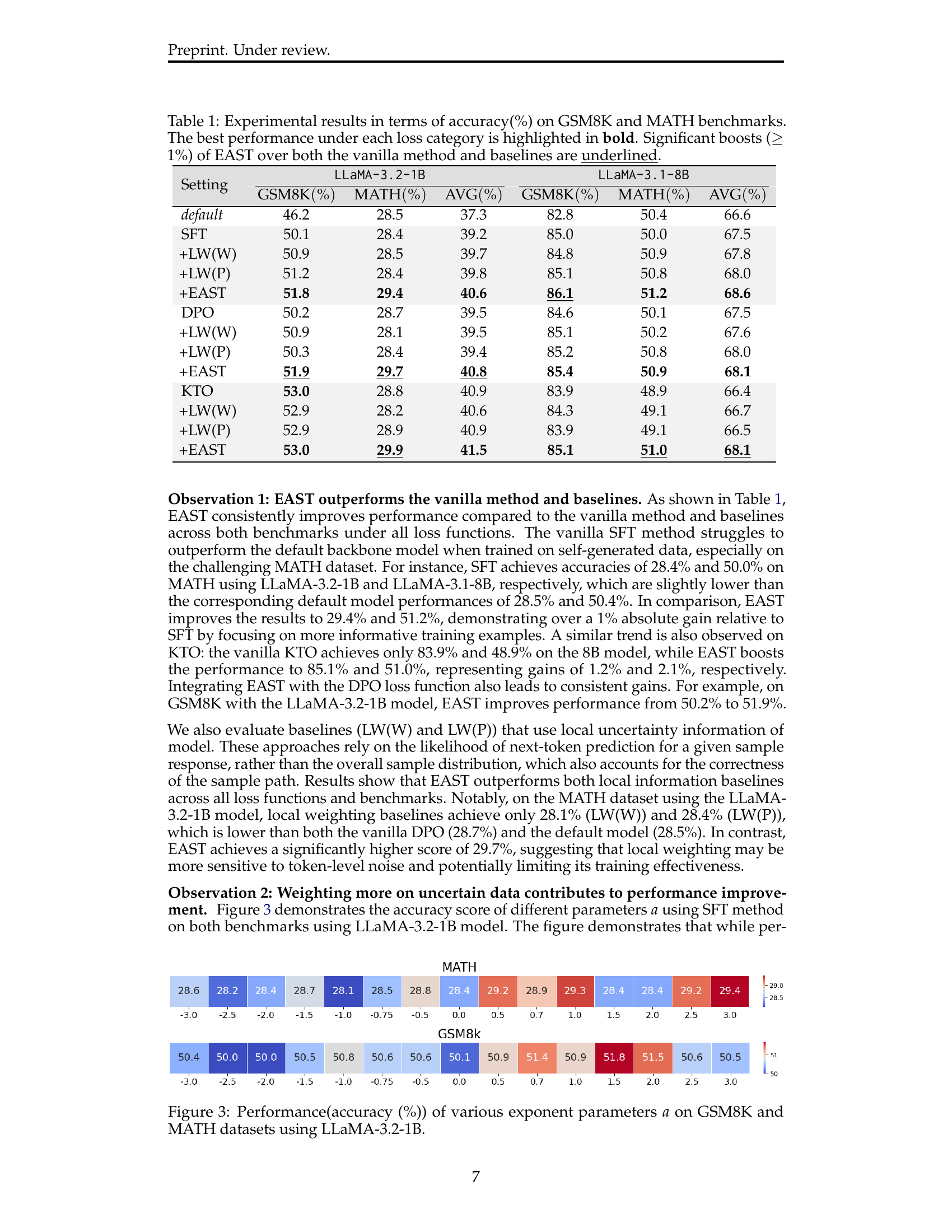
🔼 This figure displays the accuracy achieved by the EAST model on the GSM8K and MATH datasets using different values for the exponent parameter ‘a’. The x-axis represents the values of ‘a’, ranging from -3 to +3. The y-axis shows the accuracy percentage achieved. Two separate lines are shown, one for each dataset (GSM8K and MATH). This graph illustrates how different values of the exponent parameter affect the model’s performance across various mathematical reasoning tasks. The results show the impact of the mapping function’s sharpness on the model’s performance, highlighting how the emphasis on uncertain data influences accuracy.
read the caption
Figure 3: Performance(accuracy (%)) of various exponent parameters a𝑎aitalic_a on GSM8K and MATH datasets using LLaMA-3.2-1B.

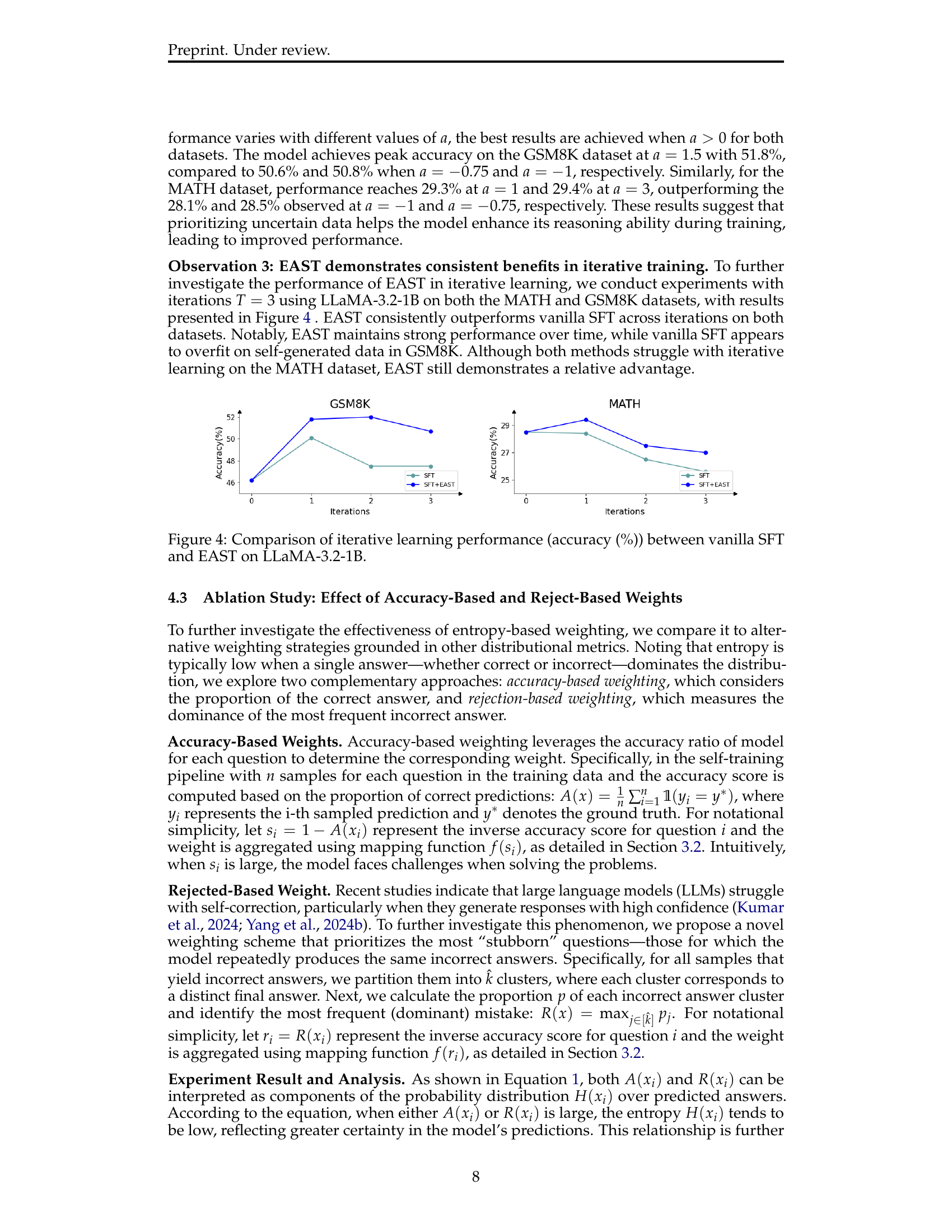
🔼 Figure 4 presents a comparison of the performance of vanilla supervised fine-tuning (SFT) and the proposed Entropy-Based Adaptive Weighting for Self-Training (EAST) method over multiple iterative training rounds. The results are shown separately for the GSM8K and MATH datasets, using the LLaMA-3.2-1B language model. The plots display the accuracy achieved at each iteration, highlighting the difference in performance between vanilla SFT and EAST. This visualization allows for the assessment of the impact of iterative training and the efficacy of EAST in preventing overfitting and maintaining performance over multiple iterations.
read the caption
Figure 4: Comparison of iterative learning performance (accuracy (%)) between vanilla SFT and EAST on LLaMA-3.2-1B.

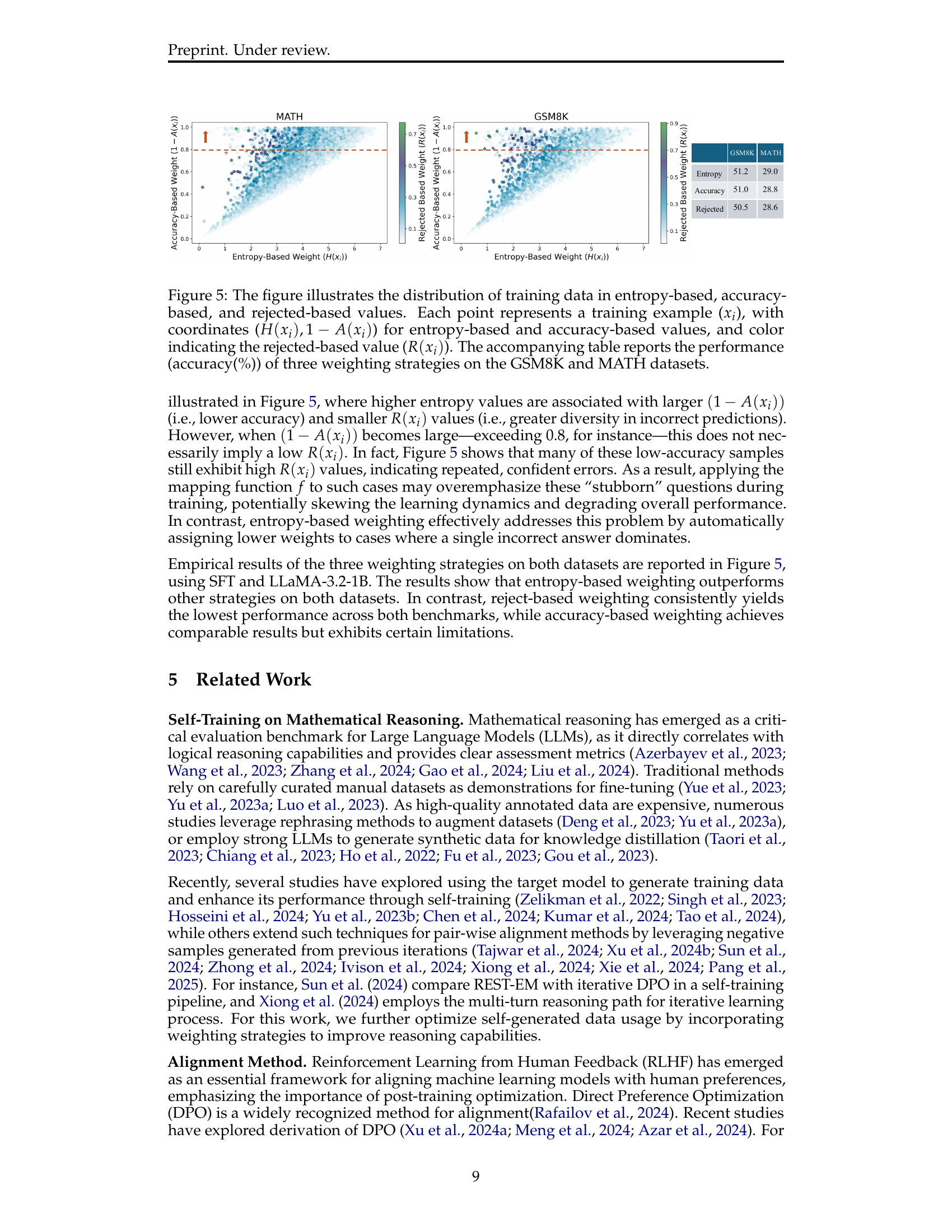
🔼 Figure 5 visualizes the relationship between three different weighting strategies (entropy-based, accuracy-based, and rejection-based) and their impact on model performance. Each point on the scatter plot represents a single training example, plotted according to its entropy and accuracy. The color of the point indicates the rejected-based value for that example. The accompanying table summarizes the accuracy achieved by each weighting method on the GSM8K and MATH datasets, allowing for a direct comparison of their effectiveness in improving model performance.
read the caption
Figure 5: The figure illustrates the distribution of training data in entropy-based, accuracy-based, and rejected-based values. Each point represents a training example (xisubscript𝑥𝑖x_{i}italic_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT), with coordinates (H(xi),1−A(xi)𝐻subscript𝑥𝑖1𝐴subscript𝑥𝑖H(x_{i}),1-A(x_{i})italic_H ( italic_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT ) , 1 - italic_A ( italic_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT )) for entropy-based and accuracy-based values, and color indicating the rejected-based value (R(xi)𝑅subscript𝑥𝑖R(x_{i})italic_R ( italic_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT )). The accompanying table reports the performance (accuracy(%)) of three weighting strategies on the GSM8K and MATH datasets.
Full paper#