↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Training and deploying large neural networks is hampered by limited on-device memory. While techniques like quantization exist, they often compromise model performance. This paper introduces a novel solution to this problem.
The proposed method, NeuZip, uses a lossless compression algorithm for training, focusing on the low-entropy nature of the exponent bits in floating-point numbers. For inference, a lossy variant offers further memory reduction by controlling the relative change of each parameter. Experiments on various models showed that NeuZip significantly reduces memory usage (e.g., Llama-3 8B model training memory reduced from 31GB to under 16GB) while maintaining, or even improving, performance, surpassing existing techniques like quantization.
Key Takeaways#
Why does it matter?#
This paper is important because it presents NeuZip, a novel and effective method for memory-efficient training and inference of large neural networks. This addresses a critical limitation in deep learning, enabling researchers to train and deploy larger, more powerful models with limited resources. The proposed technique offers a significant improvement over existing methods, opening up new avenues for research in memory optimization and large model deployment.
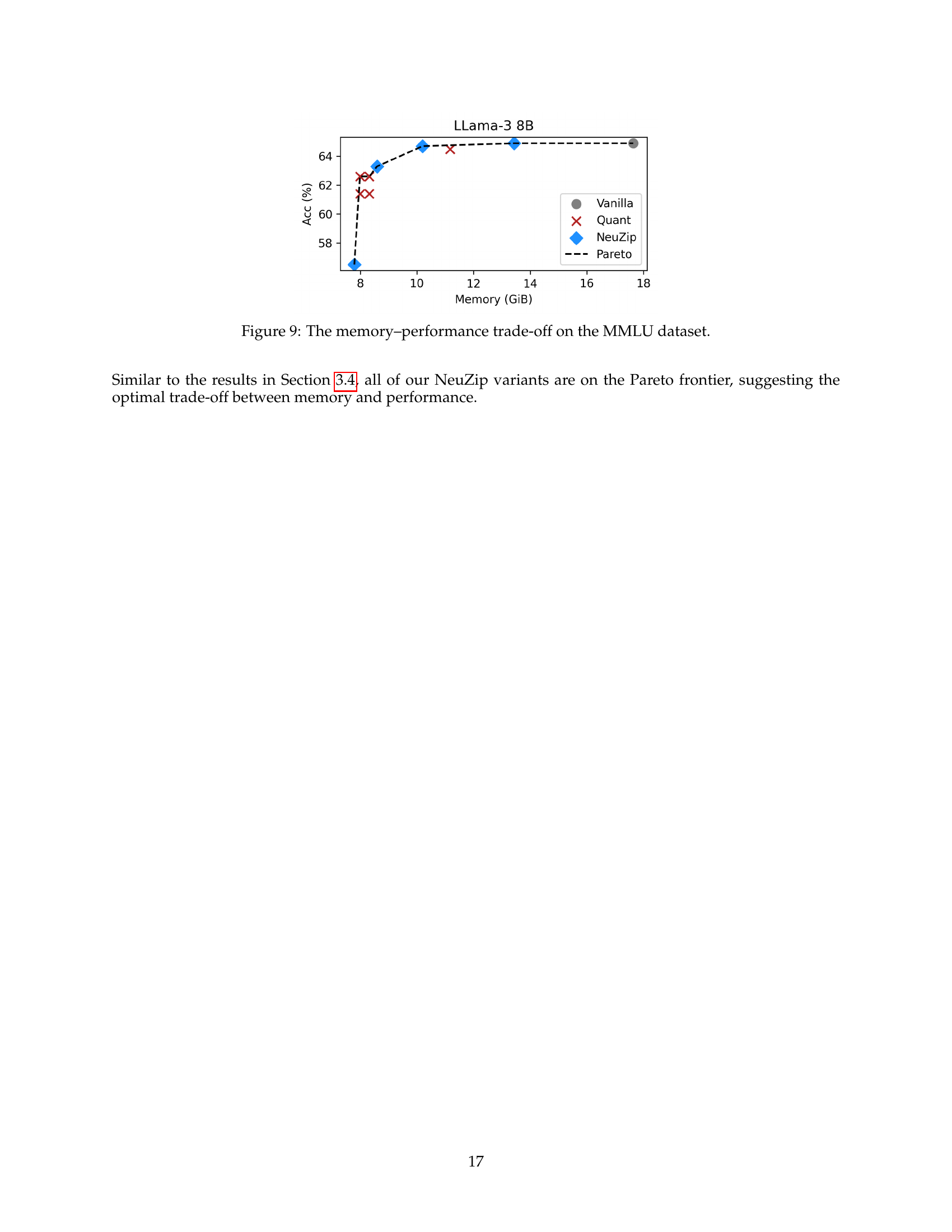
Visual Insights#

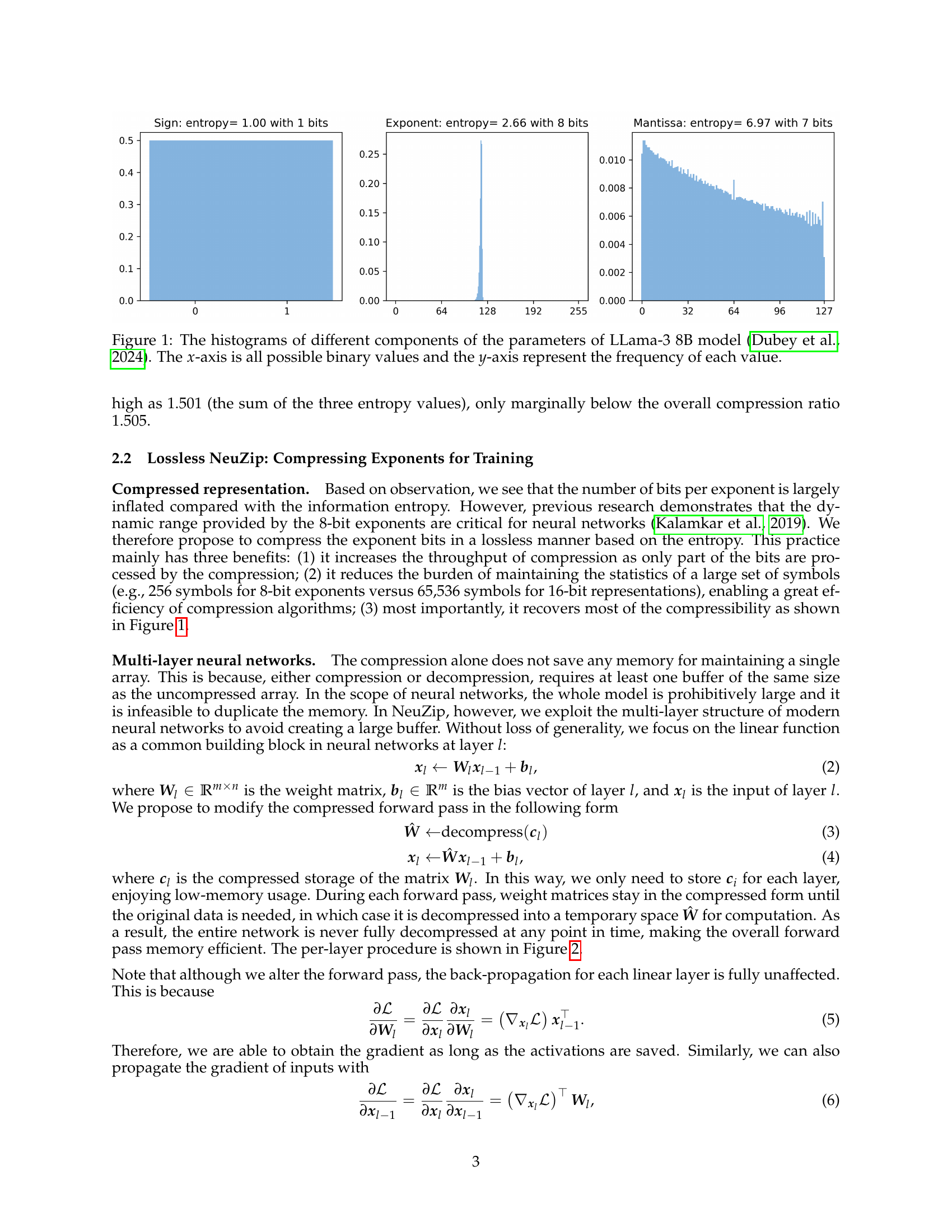
🔼 Figure 1 presents histograms visualizing the distribution of sign bits, exponent bits, and mantissa bits within the parameters of the LLama-3 8B model. Each histogram shows the frequency of occurrence for each possible binary value (represented on the x-axis), providing insights into the entropy of each component. This analysis is crucial to understanding NeuZip’s compression strategy, which focuses on the low-entropy nature of specific bits to achieve memory efficiency.
read the caption
Figure 1: The histograms of different components of the parameters of LLama-3 8B model (Dubey et al., 2024). The x𝑥xitalic_x-axis is all possible binary values and the y𝑦yitalic_y-axis represent the frequency of each value.
| Name | GPT-Neo-XL 2.7B Loss | GPT-Neo-XL 2.7B Mem | GPT-Neo-XL 2.7B Speed | Llama-3 8B Loss | Llama-3 8B Mem | Llama-3 8B Speed | LLama-2 13B Loss | LLama-2 13B Mem | LLama-2 13B Speed |
|---|---|---|---|---|---|---|---|---|---|
| Vanilla | 8.81 | 11.22 | 0.96 | 8.61 | 30.97 | 0.77 | - | OOM | - |
| LOMO | 8.81 | 6.97 | 0.94 | 8.61 | 19.47 | 0.78 | 9.10 | 26.26 | 0.49 |
| +NeuZip Lossless | 8.81 | 5.54 | 0.70 | 8.61 | 15.25 | 0.45 | 9.10 | 18.58 | 0.28 |
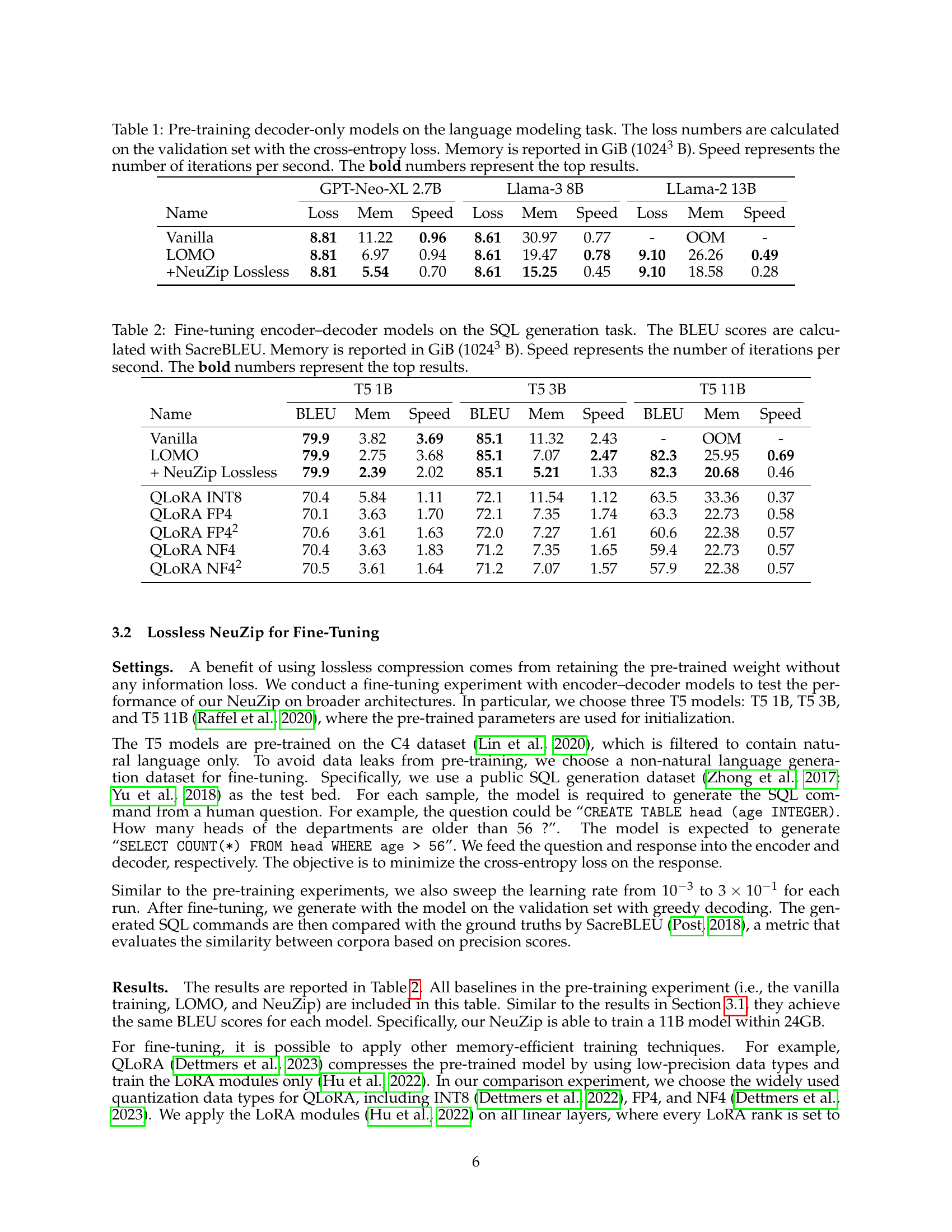
🔼 This table presents the results of pre-training three different decoder-only language models (GPT-Neo-XL 2.7B, Llama-3 8B, and Llama-2 13B) on a language modeling task. The models were trained using four different methods: a standard training approach (Vanilla), an approach using the Layer-wise Optimization with Memory Optimization (LOMO) technique, LOMO combined with lossless NeuZip compression, and LOMO combined with lossless NeuZip. The table shows for each model and training method the cross-entropy loss calculated on a validation set, the peak memory usage during training (measured in gibibytes, GiB), and the training speed (number of iterations per second). The best performing method for each model is highlighted in bold.
read the caption
Table 1: Pre-training decoder-only models on the language modeling task. The loss numbers are calculated on the validation set with the cross-entropy loss. Memory is reported in GiB (10243superscript102431024^{3}1024 start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT B). Speed represents the number of iterations per second. The bold numbers represent the top results.
In-depth insights#
Low-Entropy Weights#
The research paper section on “Low-Entropy Nature of Neural Network Parameters” posits that neural network weights exhibit low entropy. This is primarily attributed to weight initialization strategies, which often center weights around zero (e.g., Gaussian initialization), and the effects of regularization techniques (e.g., weight decay) that consistently reduce weight magnitudes during training. This central tendency, alongside the implicit regularization effect of stochastic gradient descent, contributes to the low-entropy characteristic. The paper highlights that this property, specifically the low entropy of exponent bits in the floating-point representation of weights, makes these weights highly compressible, offering a pathway for efficient memory management in training and inference without significantly sacrificing model performance. The low entropy is key to the success of NeuZip’s compression algorithm, as it forms the fundamental basis for achieving significant memory savings.
ANS Compression#
The research paper introduces Asymmetric Numeral Systems (ANS) as a lossless compression algorithm for the exponent bits of floating-point numbers in neural network weights. This is motivated by the observation that the exponent bits exhibit low entropy due to the concentration of weights around zero, a common characteristic resulting from initialization and training dynamics. ANS is chosen due to its high throughput on parallel computing devices like GPUs, essential for efficient training. Lossless compression ensures that no precision is lost during training, maintaining the full capability of the network while simultaneously reducing memory usage. The algorithm efficiently handles the dynamic range of exponents by treating each bit as a base-n number with a variable base determined by symbol frequency. The authors leverage the multi-layer structure of neural networks to compress and decompress on a per-layer basis, minimizing the overall memory footprint, and fully preserving backpropagation capabilities. The choice of ANS allows NeuZip to successfully reduce memory consumption without sacrificing model performance during training.
Lossy Inference#
The research paper introduces NeuZip, a memory-efficient technique for neural network training and inference. Its lossy inference component focuses on reducing memory usage during inference by selectively compressing the mantissa bits of floating-point numbers. This is motivated by the observation that inference is less sensitive to precision loss than training. By controlling the relative change in each parameter through controlled rounding and truncation of mantissa bits, NeuZip achieves significant memory reduction. The effectiveness is empirically demonstrated on various models and tasks, showing a favorable trade-off between memory usage and performance. Lossy NeuZip is presented as a practical approach to enable deployment of large models on resource-constrained devices, maintaining high accuracy despite the lossy compression scheme.
Memory Benchmarks#
The provided text does not contain a heading explicitly titled ‘Memory Benchmarks’. Therefore, a summary cannot be generated. To create the summary, please provide the relevant text from the PDF’s section on memory benchmarks. The summary would then analyze the memory usage results reported for various models and techniques (e.g., vanilla training, LOMO, NeuZip variants, and quantization methods) to determine their memory efficiency. It would likely highlight the significant memory savings achieved by the proposed NeuZip method, especially compared to the baseline and quantization approaches, while maintaining or even improving model performance. The summary might also touch upon the impact of hyperparameter choices such as block size on memory usage and performance trade-offs, focusing on NeuZip’s position on the Pareto frontier, which indicates a superior memory-performance balance. In addition, the summary might discuss the memory efficiency achieved during both training and inference phases and emphasize the achievability of training large language models (LLMs) on consumer-grade GPUs due to NeuZip’s efficiency.
Future Directions#
The research paper does not include a section specifically titled ‘Future Directions’. Therefore, it is not possible to provide a summary about a heading that does not exist in the provided document. To generate the requested summary, please provide a PDF containing a ‘Future Directions’ section.
More visual insights#
More on figures

🔼 This figure illustrates the reverse-mode automatic differentiation (backpropagation) process for a linear layer in a neural network, comparing different memory-saving techniques. (a) Vanilla shows the standard approach, where both weights and activations/gradients are stored in memory throughout the entire process. This contrasts with methods like (b) activation checkpointing (AC), (c) AC combined with Low-Memory Optimization (LOMO), and (d) NeuZip. These optimized techniques utilize various strategies to reduce memory usage during backpropagation, either by recomputing certain values or leveraging compressed representations, as seen in NeuZip’s compressed weight storage.
read the caption
(a) Vanilla

🔼 This figure shows the memory usage pattern of the activation checkpointing (AC) method for a linear layer in a neural network during reverse-mode automatic differentiation (backpropagation). Blue blocks represent data temporarily loaded into memory for calculations, while red blocks denote data constantly residing in memory. Activation checkpointing saves memory by recomputing activations during backpropagation, but still needs to store weights and other intermediate variables. The image visually compares vanilla, AC, AC with Layer-wise Optimization using Memory Optimization (LOMO), and NeuZip, which is the proposed method in the paper.
read the caption
(b) AC

🔼 This figure shows the reverse-mode automatic differentiation (backpropagation) process for a linear layer in a neural network using the AC+LOMO memory-saving technique. Blue blocks represent data temporarily loaded into memory during computation for the current layer, while red blocks show data that remains in memory throughout the entire training process. AC+LOMO combines activation checkpointing (AC) and Layer-wise Ordering of Memory Optimization (LOMO) to reduce memory usage. Activation checkpointing recomputes activations instead of storing them, while LOMO optimizes memory usage by efficiently managing memory allocation and deallocation across layers. This visualization contrasts AC+LOMO with other memory-saving approaches, highlighting its efficiency in reducing peak memory usage during training.
read the caption
(c) AC+LOMO

🔼 This figure shows a diagram illustrating the reverse-mode automatic differentiation (backpropagation) process in a linear layer of a neural network using NeuZip. It compares NeuZip’s memory-saving approach with other methods like vanilla, activation checkpointing (AC), and AC combined with LOMO. Blue blocks represent data temporarily loaded into memory, while red blocks represent data persistently stored in memory. NeuZip significantly reduces memory usage by compressing weight matrices and utilizing the multi-layer structure of neural networks to avoid storing large buffers.
read the caption
(d) NeuZip

🔼 This figure illustrates the memory usage of different training methods for a single linear layer during backpropagation. It compares vanilla training, activation checkpointing (AC), AC with Layer-wise Optimization using Memory Optimization (AC+LOMO), and the proposed NeuZip method. Blue blocks represent data loaded into memory temporarily for a single layer’s computation, while red blocks denote data persistently stored throughout training. NeuZip is shown to reduce memory usage by strategically compressing parameters.
read the caption
Figure 2: Reverse-mode automatic differentiation (e.g., back-propagation) with different memory-saving techniques for a linear layer. Blocks colored blue are loaded in memory temporarily for the calculation of this layer, whereas the blocks colored red are always in memory throughout training.

🔼 This figure illustrates the Pareto frontier for different model compression techniques, showing the trade-off between memory usage and model performance. The x-axis represents memory consumption (in GiB), and the y-axis represents model performance (e.g., perplexity). Three different model sizes (Llama-3 8B, Llama-2 13B, Yi-1.5 34B) are shown, each with results for a vanilla (uncompressed) model, a quantization method, and several NeuZip variants. Points closer to the bottom-left corner indicate better memory efficiency and higher performance. The results demonstrate that NeuZip variants generally lie closer to or on the Pareto frontier compared to quantization methods, indicating a better balance between memory efficiency and performance.
read the caption
Figure 3: The trade-off between memory and performance for different methods.

🔼 This figure compares the throughput (in GiB/s) of various methods for compressing and decompressing matrices of varying sizes in neural network training. Panel (a) shows the compression throughput of CPU offloading, quantization, lossy NeuZip, and lossless NeuZip. Panel (b) displays the decompression throughput of GPU reloading, de-quantization, lossy NeuZip decompression, and lossless NeuZip decompression. The results illustrate the relative efficiency of each method in terms of data transfer rate and memory usage.
read the caption
Figure 4: The throughput experiment. (a) Comparison of CPU-offloading, quantization, lossy NeuZip compression, and lossless NeuZip compression. (b) Comparison of GPU-reloading, de-quantization, lossy NeuZip decompression, and lossless NeuZip decompression.

🔼 This figure displays histograms illustrating the distribution of sign bits, exponent bits, and mantissa bits within the floating-point numbers representing the parameters of a randomly initialized Llama-3 8B model. The x-axis of each histogram represents the possible values for each component (bits), while the y-axis represents the frequency of occurrence for each value in the model’s parameters. The histograms visually demonstrate the low entropy nature of the exponent bits, a key observation supporting the NeuZip compression method described in the paper.
read the caption
Figure 5: The histograms of different floating-point components of the parameters of a randomly initialized Llama-3 8B model.
More on tables
| Name | T5 1B BLEU | T5 1B Mem | T5 1B Speed | T5 3B BLEU | T5 3B Mem | T5 3B Speed | T5 11B BLEU | T5 11B Mem | T5 11B Speed |
|---|---|---|---|---|---|---|---|---|---|
| Vanilla | 79.9 | 3.82 | 3.69 | 85.1 | 11.32 | 2.43 | - | OOM | - |
| LOMO | 79.9 | 2.75 | 3.68 | 85.1 | 7.07 | 2.47 | 82.3 | 25.95 | 0.69 |
| + NeuZip Lossless | 79.9 | 2.39 | 2.02 | 85.1 | 5.21 | 1.33 | 82.3 | 20.68 | 0.46 |
| QLoRA INT8 | 70.4 | 5.84 | 1.11 | 72.1 | 11.54 | 1.12 | 63.5 | 33.36 | 0.37 |
| QLoRA FP4 | 70.1 | 3.63 | 1.70 | 72.1 | 7.35 | 1.74 | 63.3 | 22.73 | 0.58 |
| QLoRA FP42 | 70.6 | 3.61 | 1.63 | 72.0 | 7.27 | 1.61 | 60.6 | 22.38 | 0.57 |
| QLoRA NF4 | 70.4 | 3.63 | 1.83 | 71.2 | 7.35 | 1.65 | 59.4 | 22.73 | 0.57 |
| QLoRA NF42 | 70.5 | 3.61 | 1.64 | 71.2 | 7.07 | 1.57 | 57.9 | 22.38 | 0.57 |
🔼 This table presents the results of fine-tuning various encoder-decoder models on an SQL generation task. It compares different model compression techniques (including the proposed NeuZip method) in terms of their impact on model performance (measured by BLEU score using SacreBLEU), memory usage (reported in GiB), and training speed (iterations per second). The top-performing model for each metric in each model size is highlighted in bold.
read the caption
Table 2: Fine-tuning encoder–decoder models on the SQL generation task. The BLEU scores are calculated with SacreBLEU. Memory is reported in GiB (10243superscript102431024^{3}1024 start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT B). Speed represents the number of iterations per second. The bold numbers represent the top results.
| Name | Llama-3 8B PPL | Llama-3 8B Mem | Llama-3 8B Speed | Llama-2 13B PPL | Llama-2 13B Mem | Llama-2 13B Speed | Yi-1.5 34B PPL | Yi-1.5 34B Mem | Yi-1.5 34B Speed |
|---|---|---|---|---|---|---|---|---|---|
| Vanilla | 9.89 | 15.08 | 5.07 | 10.87 | 24.36 | 3.59 | - | OOM | - |
| Quant INT8 | 10.07 | 8.63 | 3.54 | 10.97 | 12.74 | 2.27 | 10.87 | 33.41 | 1.13 |
| Quant FP4 | 11.51 | 5.77 | 3.45 | 11.38 | 7.37 | 1.87 | 11.57 | 19.54 | 1.75 |
| Quant NF4 | 10.75 | 5.77 | 3.38 | 11.15 | 7.37 | 1.83 | 11.06 | 19.54 | 1.67 |
| Quant FP42 | 11.50 | 5.44 | 3.41 | 11.38 | 6.87 | 1.86 | 11.57 | 18.11 | 1.61 |
| Quant NF42 | 10.75 | 5.44 | 3.34 | 11.15 | 6.87 | 1.81 | 11.06 | 18.11 | 1.54 |
| NeuZip 0-bit | 13.64 | 5.24 | 3.44 | 12.46 | 6.30 | 1.87 | 12.06 | 16.20 | 0.94 |
| NeuZip 1-bit | 10.77 | 6.05 | 3.38 | 11.17 | 7.77 | 1.86 | 11.04 | 20.14 | 0.93 |
| NeuZip 3-bit | 9.93 | 7.70 | 3.38 | 10.90 | 10.73 | 1.84 | 10.76 | 27.92 | 0.93 |
| NeuZip 7-bit (lossless) | 9.89 | 10.95 | 3.39 | 10.87 | 16.66 | 1.84 | 10.72 | 43.40 | 0.94 |
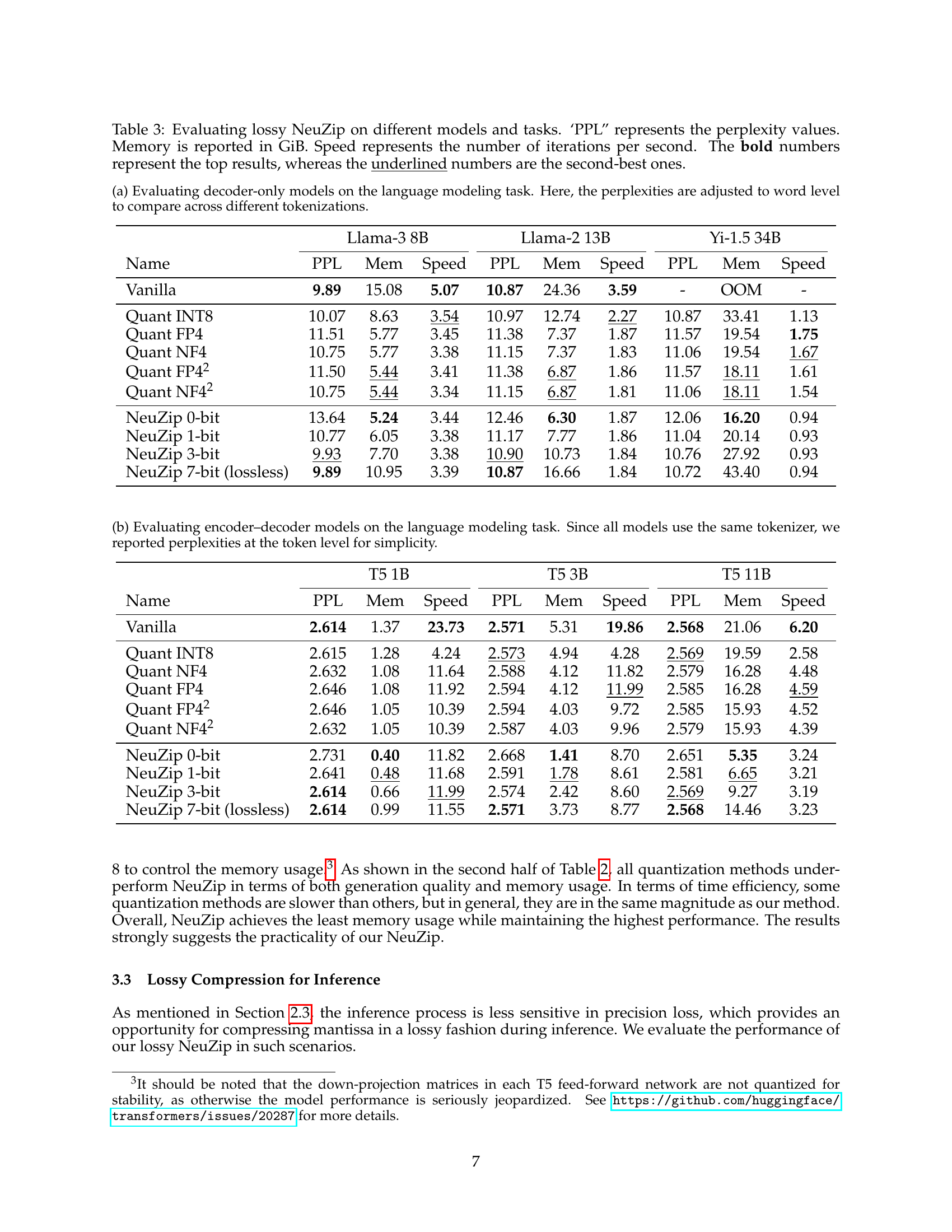
🔼 Table 3 presents a comprehensive evaluation of the lossy NeuZip compression technique on various neural network models and tasks. It compares the performance (perplexity), memory usage (in GiB), and training speed (iterations per second) of lossy NeuZip against several baseline methods, including standard models and various quantization techniques (INT8, FP4, NF4). The table shows the perplexity scores, memory requirements, and iteration speeds achieved by each method, enabling a detailed comparison of the trade-off between memory efficiency and model accuracy. The bold values indicate the best results for each model and task, while the underlined numbers highlight the second-best performing methods.
read the caption
Table 3: Evaluating lossy NeuZip on different models and tasks. ‘PPL” represents the perplexity values. Memory is reported in GiB. Speed represents the number of iterations per second. The bold numbers represent the top results, whereas the underlined numbers are the second-best ones.
| Name | T5 1B PPL | T5 1B Mem | T5 1B Speed | T5 3B PPL | T5 3B Mem | T5 3B Speed | T5 11B PPL | T5 11B Mem | T5 11B Speed |
|---|---|---|---|---|---|---|---|---|---|
| Vanilla | 2.614 | 1.37 | 23.73 | 2.571 | 5.31 | 19.86 | 2.568 | 21.06 | 6.20 |
| Quant INT8 | 2.615 | 1.28 | 4.24 | 2.573 | 4.94 | 4.28 | 2.569 | 19.59 | 2.58 |
| Quant NF4 | 2.632 | 1.08 | 11.64 | 2.588 | 4.12 | 11.82 | 2.579 | 16.28 | 4.48 |
| Quant FP4 | 2.646 | 1.08 | 11.92 | 2.594 | 4.12 | 11.99 | 2.585 | 16.28 | 4.59 |
| Quant FP42 | 2.646 | 1.05 | 10.39 | 2.594 | 4.03 | 9.72 | 2.585 | 15.93 | 4.52 |
| Quant NF42 | 2.632 | 1.05 | 10.39 | 2.587 | 4.03 | 9.96 | 2.579 | 15.93 | 4.39 |
| NeuZip 0-bit | 2.731 | 0.40 | 11.82 | 2.668 | 1.41 | 8.70 | 2.651 | 5.35 | 3.24 |
| NeuZip 1-bit | 2.641 | 0.48 | 11.68 | 2.591 | 1.78 | 8.61 | 2.581 | 6.65 | 3.21 |
| NeuZip 3-bit | 2.614 | 0.66 | 11.99 | 2.574 | 2.42 | 8.60 | 2.569 | 9.27 | 3.19 |
| NeuZip 7-bit (lossless) | 2.614 | 0.99 | 11.55 | 2.571 | 3.73 | 8.77 | 2.568 | 14.46 | 3.23 |
🔼 This table presents the results of evaluating decoder-only language models on a language modeling task. The models are compared across three metrics: perplexity (PPL), memory usage (in GiB), and training speed (iterations per second). Perplexity scores are adjusted to the word level to allow for fair comparison across models with different tokenization schemes. The table includes results for a vanilla (uncompressed) model, several quantization methods (INT8, FP4, NF4, FP42, NF42), and different variations of the NeuZip algorithm (0-bit, 1-bit, 3-bit, and 7-bit (lossless)). This allows for a comprehensive comparison of model performance, efficiency, and memory footprint.
read the caption
(a) Evaluating decoder-only models on the language modeling task. Here, the perplexities are adjusted to word level to compare across different tokenizations.
| Name | Block 32 | Block 32 | Block 64 | Block 64 | Block 128 | Block 128 | Block 256 | Block 256 | Block 512 | Block 512 |
|---|---|---|---|---|---|---|---|---|---|---|
| PPL | Mem | PPL | Mem | PPL | Mem | PPL | Mem | PPL | Mem | |
| NeuZip 0-bit | 6.341 | 35.7 | 6.694 | 34.6 | 6.853 | 34.2 | 7.639 | 33.8 | 7.104 | 33.5 |
| NeuZip 1-bit | - | OOM | 4.611 | 42.7 | 4.662 | 42.2 | 4.640 | 41.8 | 4.649 | 41.4 |
🔼 This table presents the results of evaluating encoder-decoder models (T5 models of various sizes) on a language modeling task. Because all models used the same tokenizer, perplexity is reported at the token level for simpler comparison and easier interpretation of the results. The table likely shows metrics like perplexity (PPL), memory usage (Mem), and training speed (Speed) for different model sizes and/or compression techniques. The focus is on comparing the impact of different methods on efficiency and accuracy.
read the caption
(b) Evaluating encoder–decoder models on the language modeling task. Since all models use the same tokenizer, we reported perplexities at the token level for simplicity.
Full paper#