↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large Language Models (LLMs) are powerful but demand significant memory, hindering their use on devices with limited resources. Traditional compression methods often necessitate pre-defined ratios and separate processes for each setting, thus posing challenges for deployment in dynamic memory environments. This limits adaptability and efficiency.
BitStack tackles this problem with a novel, training-free weight compression approach. It leverages weight decomposition, allowing dynamic model size adjustments based on available memory. BitStack iteratively decomposes weights, prioritizing significant parameters, achieving approximately 1-bit per parameter in residual blocks. These blocks are then efficiently sorted and stacked for dynamic loading. Experiments demonstrate that BitStack consistently matches or outperforms existing methods, especially at extreme compression levels.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical challenge in deploying large language models (LLMs) on resource-constrained devices. BitStack offers a novel solution for dynamic model size adjustment, enabling efficient LLM deployment in variable memory environments. This is highly relevant to current research trends focusing on efficient LLM deployment and opens new avenues for research on memory-efficient model compression techniques. The results demonstrate significant performance gains, especially in extreme compression scenarios, making it a valuable contribution to the field.
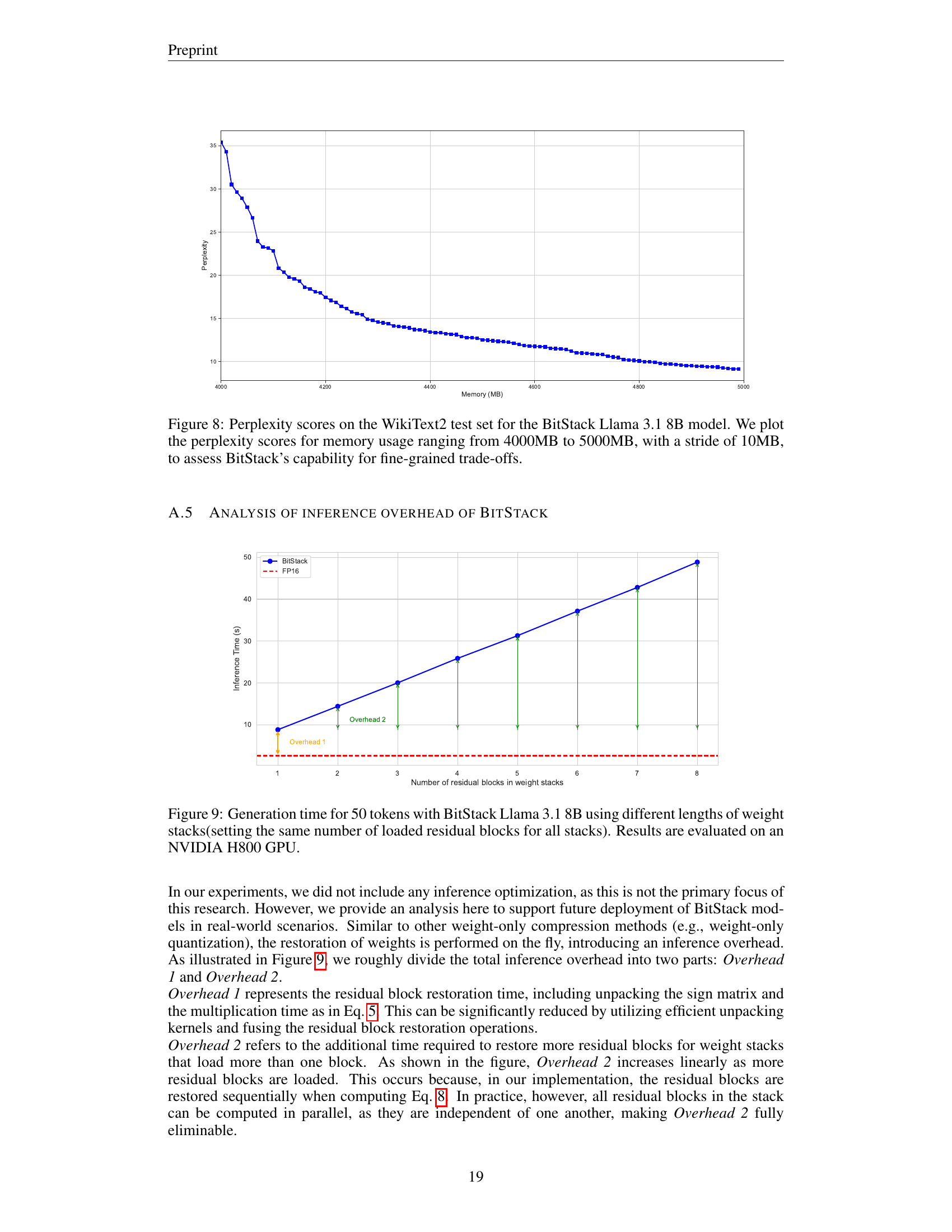
Visual Insights#

🔼 This figure demonstrates BitStack’s ability to dynamically adjust the model size in response to varying memory availability. The left panel (a) shows a schematic illustration of how BitStack operates at different memory levels, adjusting its size at a megabyte-level granularity. This allows it to handle different memory constraints on various devices without sacrificing model performance. The actual caption only states ‘(a)’, without further explanation.
read the caption
(a)
| Model | Memory (MB) | Method | Wiki2 ( ) ) | ARC-e ( ) ) | ARC-c ( ) ) | PIQA ( ) ) | HellaS. ( ) ) | WinoG. ( ) ) | LAMBADA ( ) ) | Avg. ( ) ) |
|---|---|---|---|---|---|---|---|---|---|---|
| 8B | 15316 | FP 16 | 6.24 | 81.1±0.8 | 53.6±1.5 | 81.2±0.9 | 78.9±0.4 | 73.9±1.2 | 75.8±0.6 | 74.1±0.9 |
| 3674(76%) | GPTQw2 | 1.2e6 | 26.0±0.9 | 27.1±1.3 | 51.7±1.2 | 26.0±0.4 | 48.5±1.4 | 0.0±0.0 | 29.9±0.9 | |
| AWQw2 | 1.1e6 | 24.9±0.9 | 23.6±1.2 | 49.6±1.2 | 26.2±0.4 | 52.2±1.4 | 0.0±0.0 | 29.4±0.9 | ||
| BitStack | 3.3e3 | 29.3±0.9 | 23.4±1.2 | 53.4±1.2 | 27.9±0.4 | 50.7±1.4 | 0.2±0.1 | 30.8±0.9 | ||
| 3877(75%) | GPTQw2g128 | 1.7e5 | 25.9±0.9 | 26.0±1.3 | 53.9±1.2 | 26.5±0.4 | 49.6±1.4 | 0.0±0.0 | 30.3±0.9 | |
| AWQw2g128 | 1.5e6 | 24.6±0.9 | 24.7±1.3 | 50.0±1.2 | 26.4±0.4 | 46.7±1.4 | 0.0±0.0 | 28.7±0.9 | ||
| BitStack | 79.28 | 48.4±1.0 | 26.0±1.3 | 66.5±1.1 | 41.0±0.5 | 57.1±1.4 | 15.5±0.5 | 42.4±1.0 | ||
| 4506(71%) | GPTQw3 | 260.86 | 34.7±1.0 | 24.5±1.3 | 57.6±1.2 | 30.4±0.5 | 53.0±1.4 | 3.0±0.2 | 33.9±0.9 | |
| AWQw3 | 17.01 | 67.0±1.0 | 42.9±1.4 | 72.6±1.0 | 67.3±0.5 | 62.6±1.4 | 53.3±0.7 | 61.0±1.0 | ||
| BitStack | 12.55 | 68.5±1.0 | 39.4±1.4 | 75.5±1.0 | 63.4±0.5 | 65.8±1.3 | 66.2±0.7 | 63.1±1.0 | ||
| 4709(69%) | GPTQw3g128 | 38.28 | 55.3±1.0 | 33.9±1.4 | 66.9±1.1 | 53.1±0.5 | 61.9±1.4 | 46.9±0.7 | 53.0±1.0 | |
| AWQw3g128 | 8.06 | 74.5±0.9 | 48.4±1.5 | 77.7±1.0 | 73.9±0.4 | 70.6±1.3 | 67.8±0.7 | 68.8±0.9 | ||
| BitStack | 10.91 | 72.7±0.9 | 41.6±1.4 | 76.7±1.0 | 65.9±0.5 | 67.8±1.3 | 69.6±0.6 | 65.7±1.0 | ||
| 5338(65%) | GPTQw4 | 20.88 | 74.7±0.9 | 45.6±1.5 | 77.2±1.0 | 54.6±0.5 | 64.5±1.3 | 40.9±0.7 | 59.6±1.0 | |
| AWQw4 | 7.12 | 78.4±0.8 | 51.1±1.5 | 79.9±0.9 | 77.5±0.4 | 73.3±1.2 | 70.6±0.6 | 71.8±0.9 | ||
| BitStack | 8.39 | 76.6±0.9 | 47.9±1.5 | 79.0±1.0 | 71.6±0.4 | 69.6±1.3 | 76.1±0.6 | 70.1±0.9 | ||
| 5541(64%) | GPTQw4g128 | 6.83 | 78.6±0.8 | 51.5±1.5 | 79.1±0.9 | 77.0±0.4 | 71.2±1.3 | 72.9±0.6 | 71.7±0.9 | |
| AWQw4g128 | 6.63 | 79.3±0.8 | 51.2±1.5 | 81.0±0.9 | 78.2±0.4 | 72.1±1.3 | 74.2±0.6 | 72.7±0.9 | ||
| BitStack | 8.14 | 77.6±0.9 | 49.7±1.5 | 79.5±0.9 | 72.4±0.4 | 70.6±1.3 | 76.0±0.6 | 71.0±0.9 | ||
| 70B | 134570 | FP 16 | 2.81 | 86.7±0.7 | 64.8±1.4 | 84.3±0.8 | 85.1±0.4 | 79.8±1.1 | 79.2±0.6 | 80.0±0.8 |
| 20356(85%) | GPTQw2 | NaN | 24.8±0.9 | 26.2±1.3 | 50.8±1.2 | 26.4±0.4 | 51.4±1.4 | 0.0±0.0 | 29.9±0.9 | |
| AWQw2 | 9.6e5 | 25.0±0.9 | 25.5±1.3 | 51.7±1.2 | 26.6±0.4 | 50.4±1.4 | 0.0±0.0 | 29.9±0.9 | ||
| BitStack | 1.0e3 | 27.9±0.9 | 23.9±1.2 | 52.3±1.2 | 30.4±0.5 | 49.6±1.4 | 2.6±0.2 | 31.1±0.9 | ||
| 22531(83%) | GPTQw2g128 | 4.4e5 | 23.9±0.9 | 25.6±1.3 | 51.1±1.2 | 26.4±0.4 | 50.4±1.4 | 0.0±0.0 | 29.6±0.9 | |
| AWQw2g128 | 1.8e6 | 24.9±0.9 | 26.2±1.3 | 51.3±1.2 | 26.8±0.4 | 49.4±1.4 | 0.0±0.0 | 29.8±0.9 | ||
| BitStack | 8.50 | 76.8±0.9 | 50.6±1.5 | 77.9±1.0 | 74.2±0.4 | 73.7±1.2 | 73.2±0.6 | 71.1±0.9 | ||
| 28516(79%) | GPTQw3 | 3.7e6 | 24.7±0.9 | 26.8±1.3 | 51.1±1.2 | 26.3±0.4 | 50.5±1.4 | 0.0±0.0 | 29.9±0.9 | |
| AWQw3 | 10.76 | 57.4±1.0 | 37.0±1.4 | 71.1±1.1 | 63.8±0.5 | 59.0±1.4 | 49.5±0.7 | 56.3±1.0 | ||
| BitStack | 6.38 | 81.7±0.8 | 56.7±1.4 | 81.8±0.9 | 79.3±0.4 | 76.6±1.2 | 76.8±0.6 | 75.5±0.9 | ||
| 30691(77%) | GPTQw3g128 | 4.4e5 | 24.2±0.9 | 24.2±1.3 | 51.7±1.2 | 26.0±0.4 | 49.3±1.4 | 0.0±0.0 | 29.2±0.9 | |
| AWQw3g128 | 4.68 | 84.0±0.8 | 60.6±1.4 | 83.1±0.9 | 82.5±0.4 | 79.2±1.1 | 75.8±0.6 | 77.5±0.9 | ||
| BitStack | 5.94 | 82.6±0.8 | 58.3±1.4 | 82.9±0.9 | 80.9±0.4 | 78.8±1.1 | 78.4±0.6 | 77.0±0.9 | ||
| 36676(73%) | GPTQw4 | NaN | 24.9±0.9 | 25.3±1.3 | 51.4±1.2 | 26.8±0.4 | 51.1±1.4 | 0.0±0.0 | 29.9±0.9 | |
| AWQw4 | 4.24 | 83.4±0.8 | 61.3±1.4 | 83.5±0.9 | 83.4±0.4 | 63.5±1.4 | 69.1±0.6 | 74.0±0.9 | ||
| BitStack | 4.97 | 84.8±0.7 | 61.4±1.4 | 83.2±0.9 | 82.1±0.4 | 79.3±1.1 | 79.4±0.6 | 78.4±0.9 | ||
| 38851(71%) | GPTQw4g128 | 6.5e4 | 23.4±0.9 | 27.3±1.3 | 51.9±1.2 | 26.6±0.4 | 49.9±1.4 | 0.0±0.0 | 29.8±0.9 | |
| AWQw4g128 | 3.27 | 86.6±0.7 | 63.3±1.4 | 83.9±0.9 | 84.4±0.4 | 78.8±1.1 | 77.3±0.6 | 79.1±0.8 | ||
| BitStack | 4.96 | 85.1±0.7 | 61.3±1.4 | 83.5±0.9 | 82.6±0.4 | 78.8±1.1 | 78.7±0.6 | 78.3±0.9 |
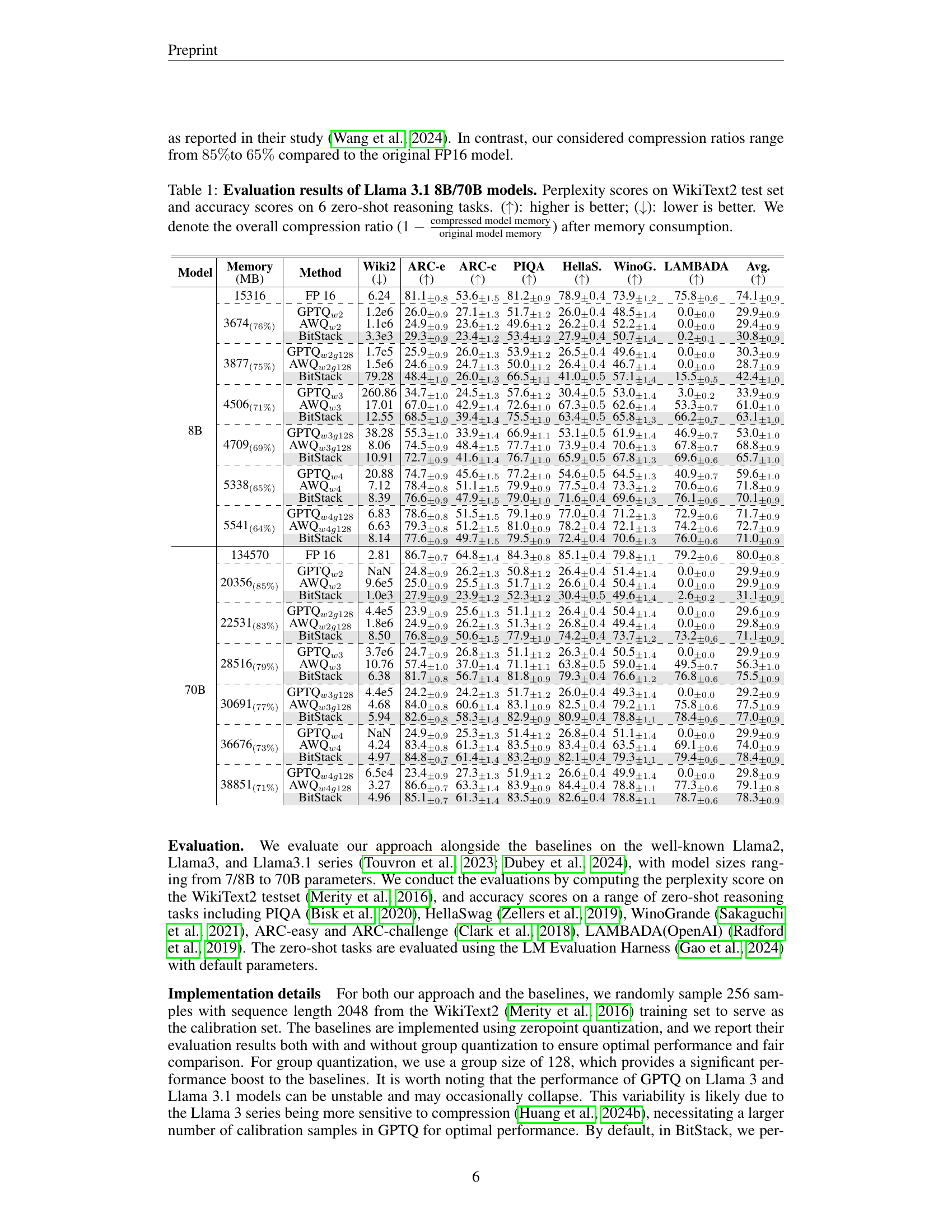
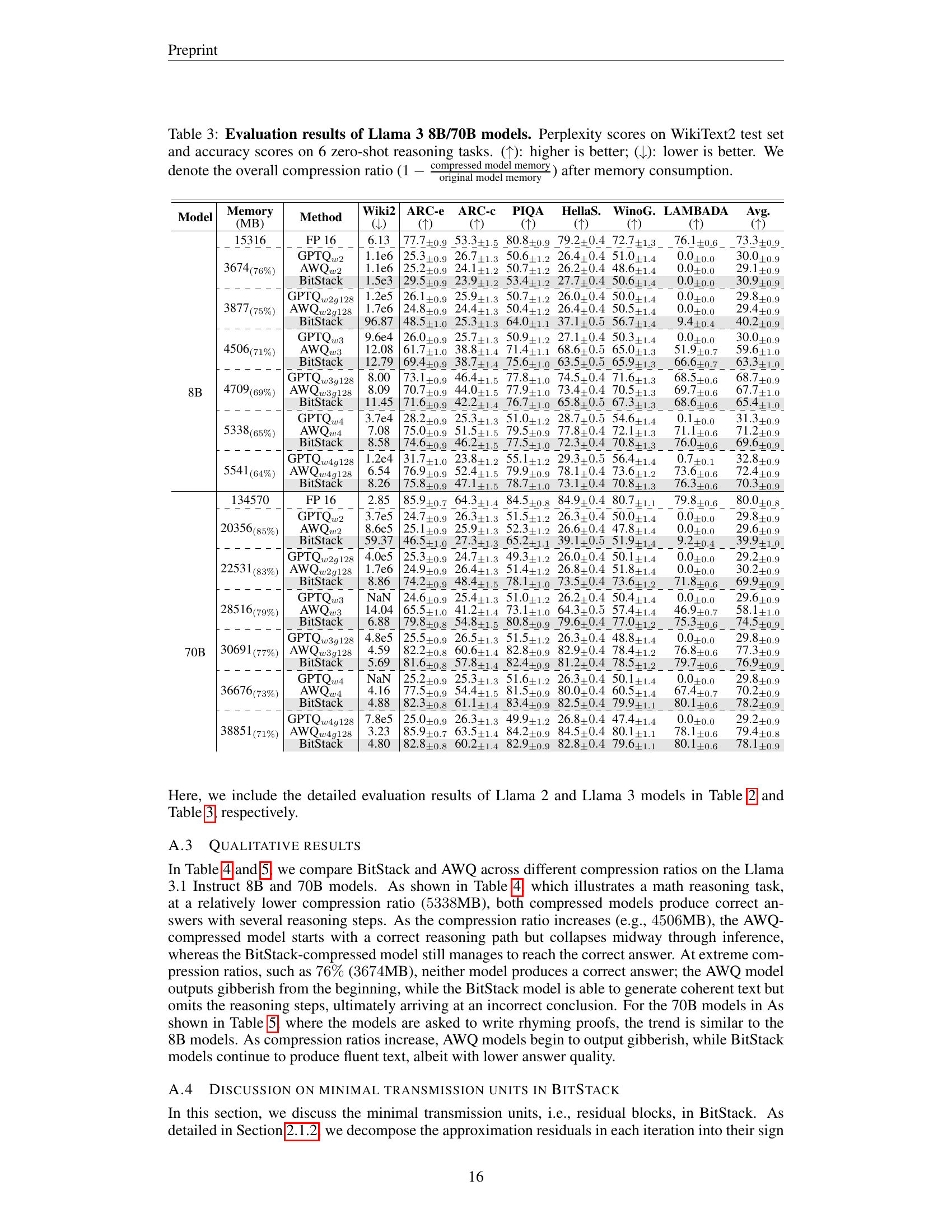
🔼 This table presents a comprehensive evaluation of the BitStack model’s performance on Llama 3.1 8B and 70B models across various compression ratios. It compares BitStack against several baselines (GPTQ and AWQ) using two key metrics: perplexity (lower is better) on the WikiText2 benchmark, a common language modeling task, and accuracy (higher is better) across six zero-shot reasoning tasks. The table shows perplexity and accuracy scores for each method at different compression levels, indicated by the model size in MB and the corresponding compression ratio (calculated as 1 minus the ratio of compressed model size to the original model size). This detailed comparison allows for a thorough assessment of BitStack’s effectiveness under various memory constraints.
read the caption
Table 1: Evaluation results of Llama 3.1 8B/70B models. Perplexity scores on WikiText2 test set and accuracy scores on 6 zero-shot reasoning tasks. (↑↑\uparrow↑): higher is better; (↓↓\downarrow↓): lower is better. We denote the overall compression ratio (1−compressed model memoryoriginal model memory1compressed model memoryoriginal model memory1-\frac{\text{compressed model memory}}{\text{original model memory}}1 - divide start_ARG compressed model memory end_ARG start_ARG original model memory end_ARG) after memory consumption.
In-depth insights#
Fine-grained LLM Control#
The research paper section on “Fine-grained LLM Control” focuses on addressing the challenge of deploying large language models (LLMs) in resource-constrained environments. Existing compression techniques often lack the flexibility to dynamically adjust model size based on available memory. BitStack, the proposed method, offers a novel solution by employing a training-free weight decomposition approach. This allows for megabyte-level granularity in adjusting model size, enabling seamless adaptation to varying memory conditions. The key innovation is the iterative decomposition of weight matrices, creating residual blocks that can be selectively loaded/unloaded from storage. This dynamic memory management is highly effective in bridging the performance gap between traditional quantization and less practical decomposition methods, achieving competitive results while offering superior size control. BitStack’s efficiency and fine-grained control make it suitable for deploying LLMs on resource-limited devices.
BitStack Architecture#
BitStack’s architecture centers on a training-free weight compression method that dynamically adjusts model size based on available memory. It employs iterative absolute value decomposition of weight matrices, prioritizing significant parameters. The resulting residual blocks are then sorted by importance and stored, enabling flexible loading/unloading. This approach allows megabyte-level granularity in size control, bridging the gap between the performance of quantization-based methods and the flexibility of decomposition. Unlike fixed-ratio methods, BitStack enables dynamic memory-performance trade-offs, making it suitable for variable memory environments.
Decomposition Method#
The research paper introduces BitStack, a novel decomposition-based weight compression method for LLMs. BitStack dynamically adjusts model size based on available memory, achieving megabyte-level trade-offs between memory usage and performance. Unlike traditional methods requiring pre-defined compression ratios, BitStack leverages iterative weight decomposition. This iterative process involves scaling weights based on activation magnitudes, applying SVD decomposition, and sorting/stacking resulting residual blocks. The sorted blocks are dynamically loaded/unloaded based on memory availability, enabling fine-grained size control. Importantly, BitStack’s decomposition-based approach bridges the gap to the performance of quantization techniques, even surpassing them at extreme compression ratios. Its training-free nature and effectiveness make it suitable for deployment in variable memory environments.
Experimental Results#
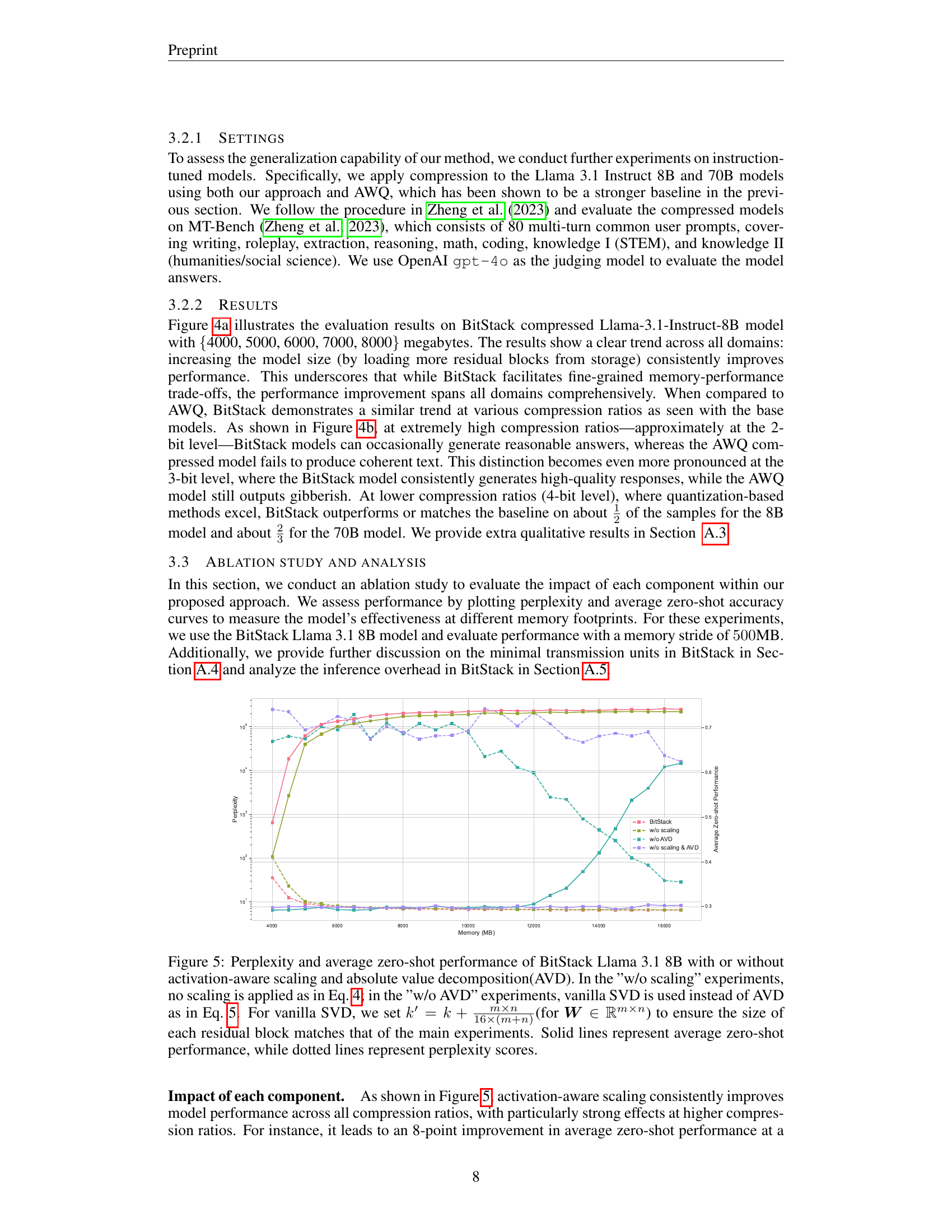
The experimental results section demonstrates BitStack’s effectiveness across various LLMs (Llama 2, 3, and 3.1) and tasks. BitStack consistently matches or surpasses the performance of strong quantization baselines (GPTQ and AWQ), especially at extreme compression ratios. This is a significant finding, as prior decomposition methods struggled in this regime. The experiments also highlight BitStack’s ability to achieve megabyte-level granularity in size control, dynamically adjusting model size based on available memory. Fine-grained control is demonstrated through consistent performance across a wide range of memory footprints. Furthermore, the results show BitStack’s robustness across different tasks, including zero-shot reasoning and perplexity tests. The ablation studies confirm the importance of key components within BitStack, notably activation-aware scaling and absolute value decomposition for achieving high compression rates while maintaining accuracy.
Future Work#
The paper’s ‘Future Work’ section highlights several promising avenues for improvement. Reducing inference overhead is a primary goal, achievable through optimizations in residual block restoration and parallel computation. The authors plan to explore more advanced sorting algorithms for residual blocks, potentially leveraging machine learning techniques to optimize memory-performance trade-offs. Further investigation into the impact of various decomposition methods and their suitability for different model architectures is also anticipated. Finally, extending BitStack’s applicability to other LLM tasks and modalities beyond those evaluated in the current work is a key objective for future research.
More visual insights#
More on figures

🔼 This figure shows the zero-shot performance of different LLMs at various memory footprints. BitStack consistently matches or surpasses the performance of GPTQ and AWQ, especially at extreme compression ratios. The x-axis represents memory usage in MB, and the y-axis represents the average zero-shot performance across six different tasks. The various lines represent different LLMs and compression techniques.
read the caption
(b)

🔼 Figure 1 demonstrates BitStack’s ability to dynamically adjust the size of large language models (LLMs) in environments with varying memory constraints. The left panel (a) shows how BitStack enables fine-grained size control at the megabyte level. The right panel (b) illustrates BitStack’s performance, showing that it achieves comparable or superior results to existing state-of-the-art compression methods such as GPTQ and AWQ, even when operating within the same limited memory footprint.
read the caption
Figure 1: BitStack enables LLMs to dynamically adjust their size in variable memory environments (1(a)) at a megabyte-level, while still matching or surpassing the performance of practical compression methods such as GPTQ (Frantar et al., 2022) and AWQ (Lin et al., 2024) with the same memory footprint(1(b)).

🔼 This figure demonstrates BitStack’s ability to dynamically adjust the size of LLMs in environments with varying memory availability. Panel (a) illustrates how BitStack can adapt to low and high memory scenarios by loading a different number of residual blocks (representing different levels of model compression) at a megabyte-level granularity. This allows the model to seamlessly trade off memory usage and performance as needed.
read the caption
(a)

🔼 The figure shows the zero-shot performance of various LLMs compressed using different methods, including BitStack, GPTQ, and AWQ, across a range of memory footprints. The x-axis represents the memory in MB, and the y-axis represents the average zero-shot performance across six tasks. Different colored lines correspond to different compression methods. The plot highlights the performance of BitStack at various memory levels, demonstrating its ability to match or surpass the performance of other compression techniques at the same memory footprint. The results indicate BitStack’s effectiveness in dynamically adjusting model size and maintaining comparable performance in variable memory environments.
read the caption
(b)

🔼 Figure 2 illustrates BitStack’s dynamic memory management. BitStack uses weight decomposition to create smaller, residual blocks of model weights that can be stored separately on a storage device. When more RAM is available, BitStack loads additional residual blocks from storage to increase model size and performance. Conversely, if available memory decreases, BitStack offloads blocks back to storage. All residual blocks from all layers are stored in a single stack on the storage device, allowing for efficient management. For clarity, the figure omits positional embeddings, normalization, and residual connections.
read the caption
Figure 2: Overview of BitStack. BitStack dynamically loads and offloads weight residual blocks (Figure 3) between RAM and storage devices based on current memory availability. We can load more weight residuals from storage when available memory increases (2(a)), or offload them otherwise (2(b)). The residual blocks for all weights across all layers are universally stored in the same stack on the storage device (grey blocks denote residual blocks for weights in other layers). Note that we omit positional embeddings, normalization layers, and residual connections in the figure for clarity.

🔼 Figure 3 illustrates a residual block, the fundamental unit of data in BitStack’s compression method. Each block is generated through the absolute value decomposition (AVD) of a weight matrix. This process yields two components: a sign matrix containing only +1 or -1 values, and the singular vectors from the singular value decomposition (SVD). The sign matrix is particularly efficient, as its binary nature allows for compact storage using GPU-optimized data types, which reduces memory usage. The figure visually represents these components, showing the original sign matrix and its compressed packed version for storage. The packed sign matrix (denoted by a different symbol) takes up much less memory space than the original sign matrix.
read the caption
Figure 3: Illustration of a residual block in BitStack. A residual block consists of a sign matrix and singular vectors obtained through absolute value decomposition. The sign matrix can be packed into GPU-supported data types to minimize memory usage. denotes the sign matrix while denotes the packed sign matrix.

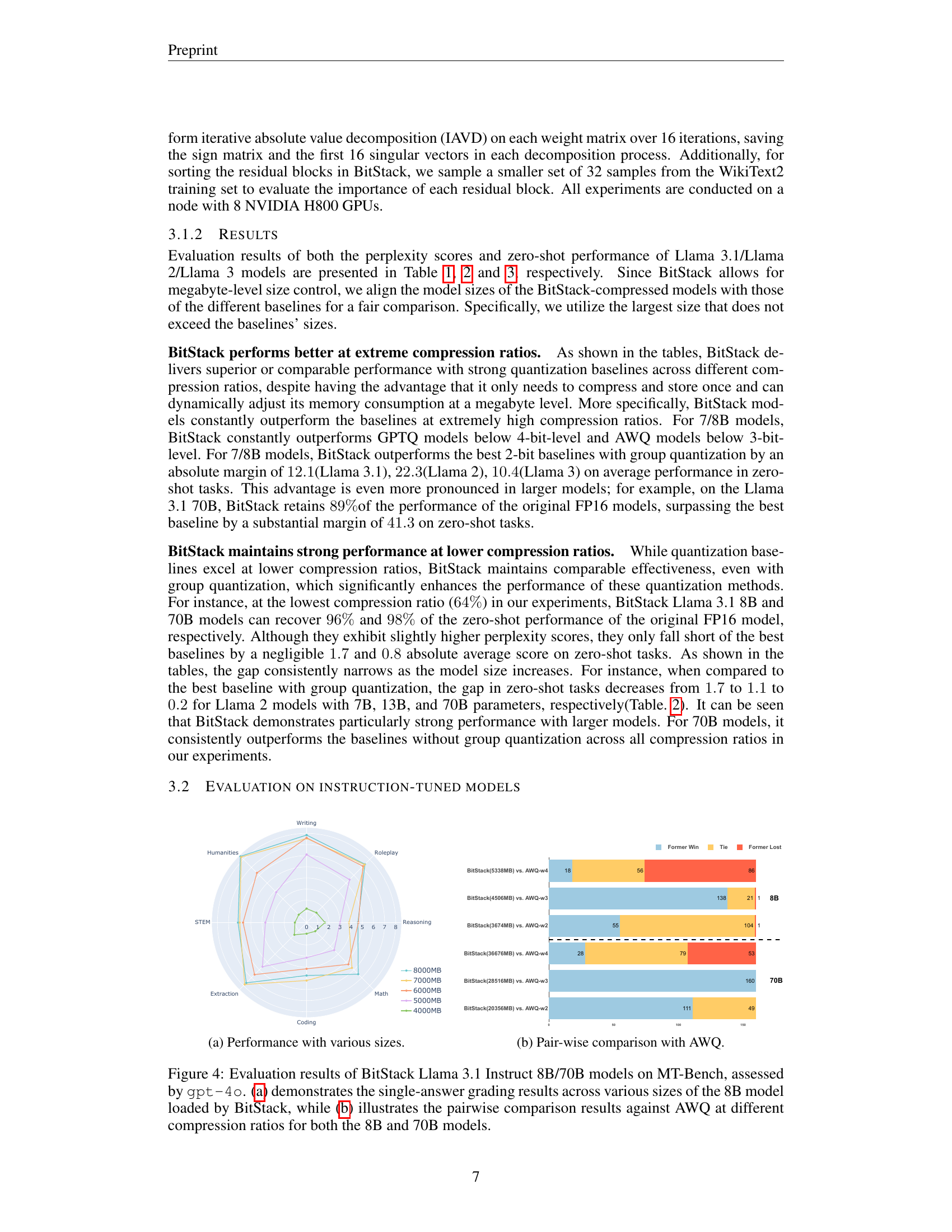
🔼 This figure demonstrates the performance of BitStack on instruction-tuned Llama 3.1 models of different sizes (8B and 70B) across various tasks in the MT-Bench benchmark. The x-axis represents different memory footprints achieved by loading varying numbers of residual blocks, while the y-axis represents the performance scores. The figure illustrates BitStack’s capability to dynamically adjust the model’s size based on available memory, showcasing its effectiveness across various scales and tasks.
read the caption
(a) Performance with various sizes.

🔼 This figure presents a pairwise comparison of BitStack’s performance against AWQ (Activation-Aware Weight Quantization) across various model sizes (8B and 70B parameters) and different compression ratios. The chart likely displays performance metrics, possibly perplexity scores or accuracy on benchmark tasks, to illustrate how BitStack’s performance compares to AWQ under different memory constraints.
read the caption
(b) Pair-wise comparison with AWQ.

🔼 Figure 4 presents a comprehensive evaluation of BitStack’s performance on instruction-tuned LLMs. Specifically, it uses the MT-Bench benchmark, which assesses performance across various tasks like writing, role-playing, reasoning, and coding. Part (a) shows how the performance of the 8B BitStack model improves as more memory is allocated to it; this demonstrates the fine-grained control BitStack offers. Part (b) provides a direct pairwise comparison of BitStack against AWQ (another compression method) across various compression ratios, for both the 8B and 70B models, highlighting the competitive performance of BitStack.
read the caption
Figure 4: Evaluation results of BitStack Llama 3.1 Instruct 8B/70B models on MT-Bench, assessed by gpt-4o. (4(a)) demonstrates the single-answer grading results across various sizes of the 8B model loaded by BitStack, while (4(b)) illustrates the pairwise comparison results against AWQ at different compression ratios for both the 8B and 70B models.

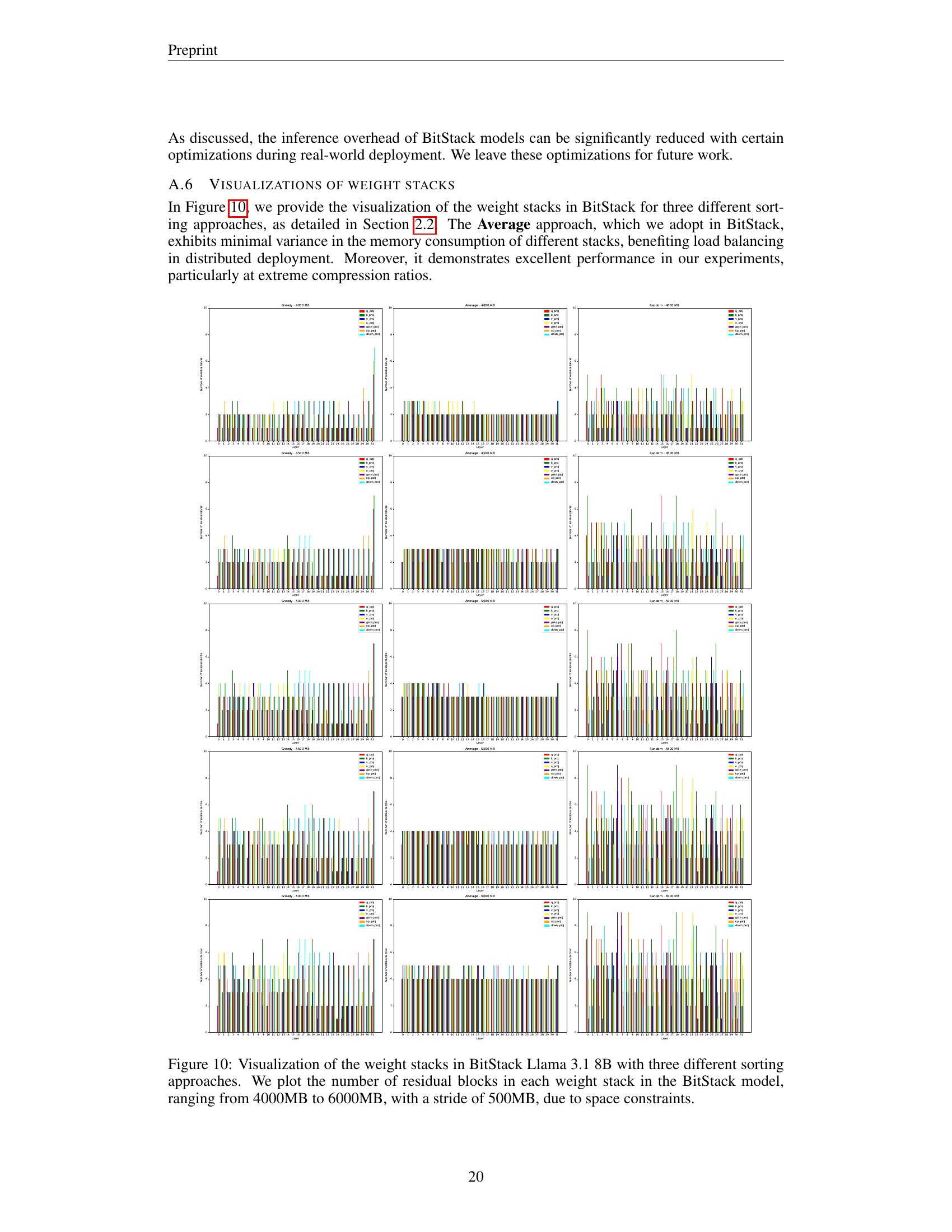
🔼 Figure 5 presents a comprehensive ablation study on the BitStack model (Llama 3.1 8B). It analyzes the impact of two key components: activation-aware scaling and absolute value decomposition (AVD). The experiments systematically remove one or both of these components, comparing their performance to the full BitStack model. When scaling is omitted, the performance significantly degrades. Similarly, replacing AVD with standard SVD (while adjusting the number of singular values to maintain a comparable residual block size) also causes significant performance drops. This highlights the crucial role of both scaling and AVD in BitStack’s efficiency and accuracy, especially at high compression ratios. The results are shown via perplexity and average zero-shot performance across a range of memory footprints.
read the caption
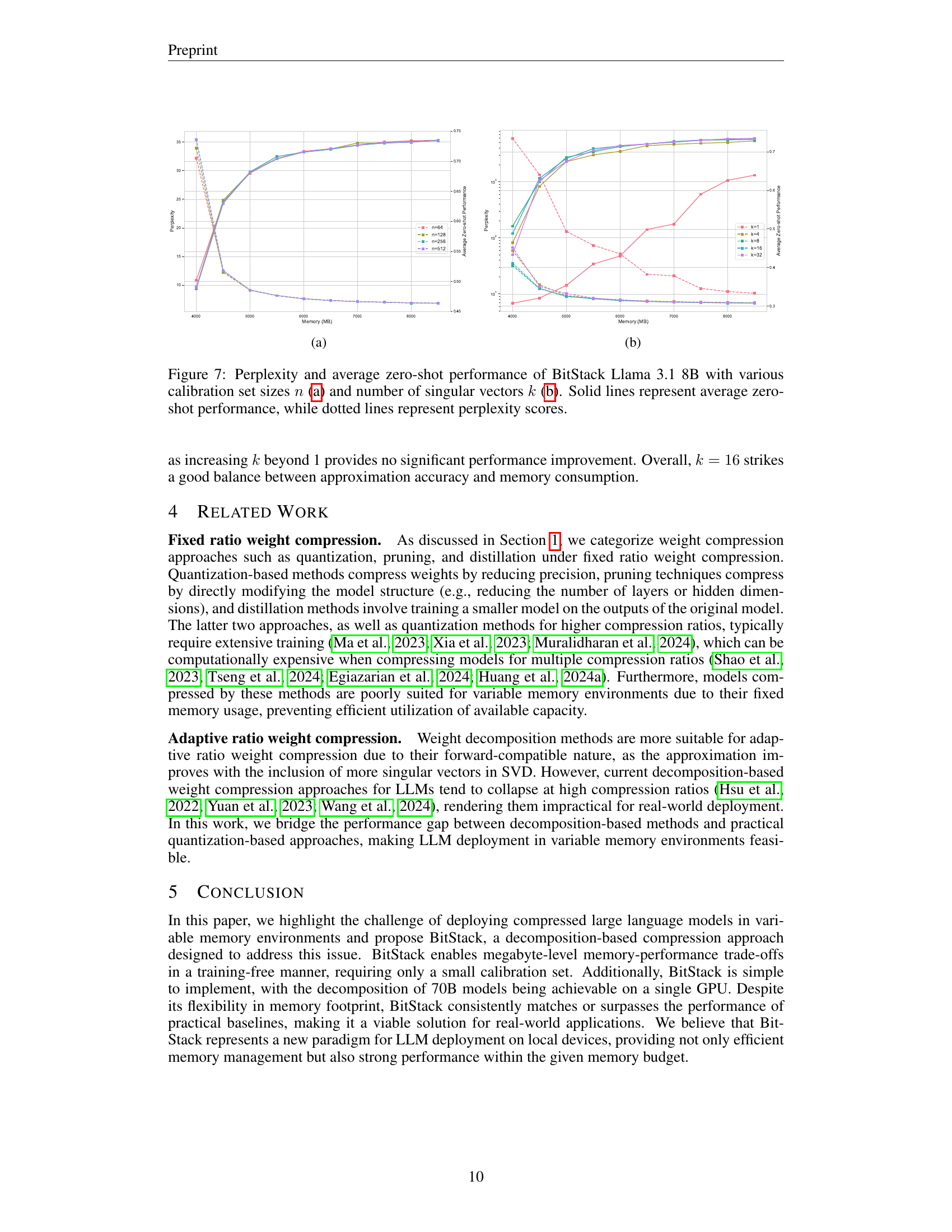
Figure 5: Perplexity and average zero-shot performance of BitStack Llama 3.1 8B with or without activation-aware scaling and absolute value decomposition(AVD). In the ”w/o scaling” experiments, no scaling is applied as in Eq. 4; in the ”w/o AVD” experiments, vanilla SVD is used instead of AVD as in Eq. 5. For vanilla SVD, we set k′=k+m×n16×(m+n)superscript𝑘′𝑘𝑚𝑛16𝑚𝑛k^{\prime}=k+\frac{m\times n}{16\times(m+n)}italic_k start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT = italic_k + divide start_ARG italic_m × italic_n end_ARG start_ARG 16 × ( italic_m + italic_n ) end_ARG(for 𝑾∈ℝm×n𝑾superscriptℝ𝑚𝑛{\bm{W}}\in\mathbb{R}^{m\times n}bold_italic_W ∈ blackboard_R start_POSTSUPERSCRIPT italic_m × italic_n end_POSTSUPERSCRIPT) to ensure the size of each residual block matches that of the main experiments. Solid lines represent average zero-shot performance, while dotted lines represent perplexity scores.

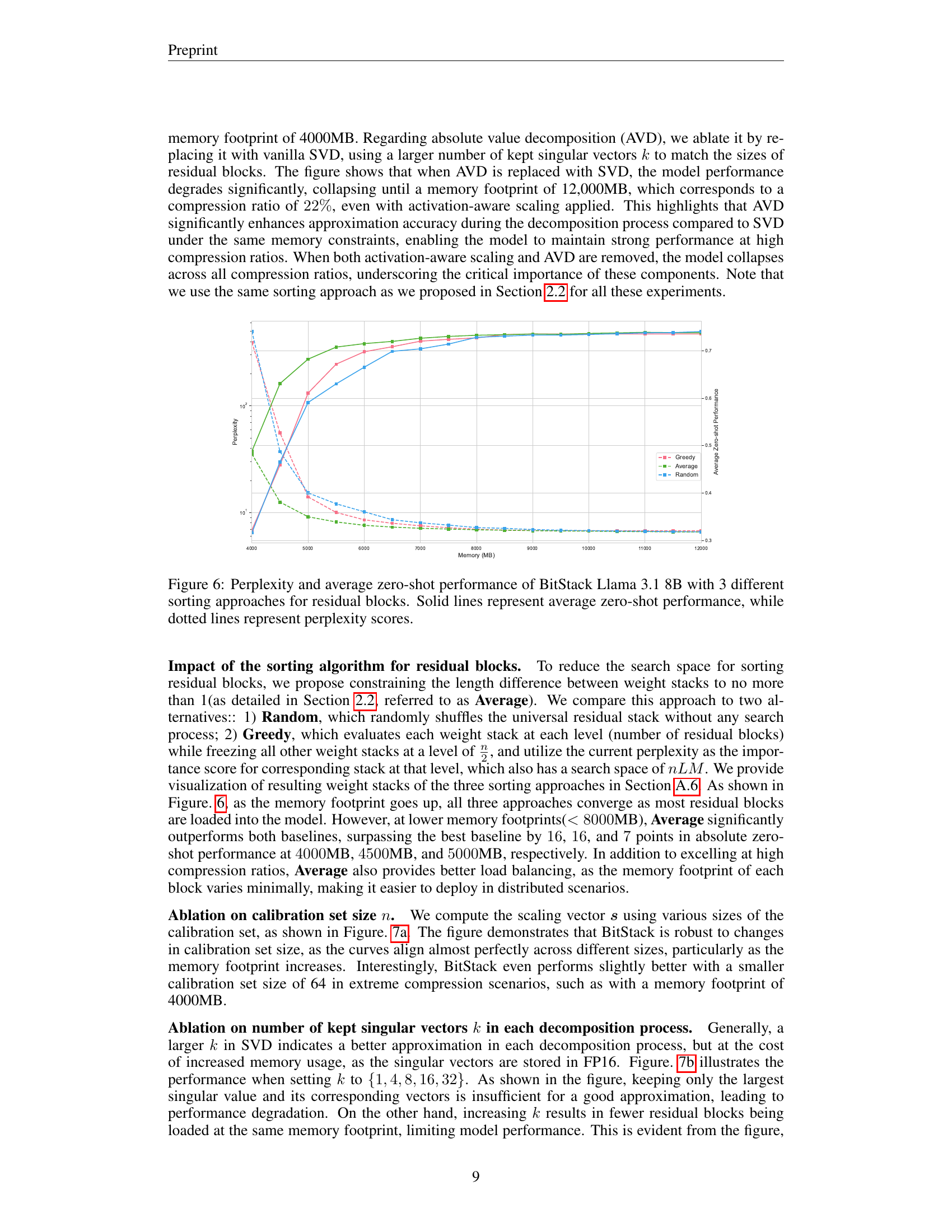
🔼 Figure 6 compares the performance of three different sorting algorithms for residual blocks in the BitStack model, specifically using Llama 3.1 8B. The algorithms are Average, Greedy, and Random. The graph displays both perplexity (dotted lines) and average zero-shot performance (solid lines) across a range of memory footprints. This shows how the choice of sorting algorithm affects the tradeoff between model size and performance.
read the caption
Figure 6: Perplexity and average zero-shot performance of BitStack Llama 3.1 8B with 3 different sorting approaches for residual blocks. Solid lines represent average zero-shot performance, while dotted lines represent perplexity scores.

🔼 This figure demonstrates BitStack’s ability to dynamically adjust its size in environments with varying memory availability. The left panel (a) shows how BitStack adapts its size at a megabyte-level granularity, illustrating the flexibility offered by the approach. Different llama models are shown to have different memory footprints (MB) given their size. The right panel (b) complements this, showing that BitStack maintains or exceeds the performance of other methods (GPTQ, AWQ) at the same memory footprint.
read the caption
(a)

🔼 The figure shows the zero-shot performance of various compressed language models across different memory footprints. BitStack consistently matches or surpasses the performance of GPTQ and AWQ, particularly at extreme compression ratios (low memory). This demonstrates BitStack’s effectiveness in dynamically adjusting model size for optimal performance within variable memory environments. Different colors represent different compression methods.
read the caption
(b)
More on tables
| Model | Memory (MB) | Method | Wiki2 (↓) | ARC-e (↑) | ARC-c (↑) | PIQA (↑) | HellaS. (↑) | WinoG. (↑) | LAMBADA (↑) | Avg. (↑) |
|---|---|---|---|---|---|---|---|---|---|---|
| 7B | 12852 | FP 16 | 5.47 | 74.5 ±0.9 | 46.2 ±1.5 | 79.1 ±0.9 | 76.0 ±0.4 | 69.1 ±1.3 | 73.9 ±0.6 | 69.8 ±0.9 |
| 2050(84%) | GPTQw2 | 2.8e4 | 26.5 ±0.9 | 27.6 ±1.3 | 48.4 ±1.2 | 25.9 ±0.4 | 50.3 ±1.4 | 0.0 ±0.0 | 29.8 ±0.9 | |
| AWQw2 | 1.8e5 | 26.3 ±0.9 | 26.7 ±1.3 | 50.9 ±1.2 | 26.5 ±0.4 | 49.3 ±1.4 | 0.0 ±0.0 | 30.0 ±0.9 | ||
| BitStack | 29.93 | 32.3 ±1.0 | 25.6 ±1.3 | 62.4 ±1.1 | 42.8 ±0.5 | 53.6 ±1.4 | 24.7 ±0.6 | 40.2 ±1.0 | ||
| 2238(83%) | GPTQw2g128 | 156.37 | 28.2 ±0.9 | 27.1 ±1.3 | 51.7 ±1.2 | 28.0 ±0.4 | 51.1 ±1.4 | 0.3 ±0.1 | 31.1 ±0.9 | |
| AWQw2g128 | 2.3e5 | 25.8 ±0.9 | 26.7 ±1.3 | 50.2 ±1.2 | 26.1 ±0.4 | 49.8 ±1.4 | 0.0 ±0.0 | 29.8 ±0.9 | ||
| BitStack | 12.49 | 51.8 ±1.0 | 30.1 ±1.3 | 71.1 ±1.1 | 53.0 ±0.5 | 61.1 ±1.4 | 53.3 ±0.7 | 53.4 ±1.0 | ||
| 2822(78%) | GPTQw3 | 9.38 | 58.1 ±1.0 | 34.0 ±1.4 | 71.9 ±1.0 | 61.7 ±0.5 | 60.6 ±1.4 | 53.3 ±0.7 | 56.6 ±1.0 | |
| AWQw3 | 14.33 | 52.7 ±1.0 | 33.0 ±1.4 | 68.3 ±1.1 | 56.3 ±0.5 | 59.3 ±1.4 | 36.3 ±0.7 | 51.0 ±1.0 | ||
| BitStack | 7.45 | 62.5 ±1.0 | 37.5 ±1.4 | 74.8 ±1.0 | 67.0 ±0.5 | 66.5 ±1.3 | 68.5 ±0.6 | 62.8 ±1.0 | ||
| 3010(77%) | GPTQw3g128 | 922.54 | 26.3 ±0.9 | 25.3 ±1.3 | 52.4 ±1.2 | 27.4 ±0.4 | 49.0 ±1.4 | 0.1 ±0.0 | 30.1 ±0.9 | |
| AWQw3g128 | 6.14 | 70.2 ±0.9 | 43.7 ±1.4 | 78.0 ±1.0 | 73.9 ±0.4 | 67.6 ±1.3 | 71.4 ±0.6 | 67.5 ±1.0 | ||
| BitStack | 7.10 | 63.8 ±1.0 | 38.2 ±1.4 | 76.0 ±1.0 | 68.4 ±0.5 | 65.9 ±1.3 | 70.7 ±0.6 | 63.8 ±1.0 | ||
| 3594(72%) | GPTQw4 | 5.91 | 71.8 ±0.9 | 43.7 ±1.4 | 77.7 ±1.0 | 74.5 ±0.4 | 68.7 ±1.3 | 71.1 ±0.6 | 67.9 ±1.0 | |
| AWQw4 | 5.81 | 70.9 ±0.9 | 44.5 ±1.5 | 78.5 ±1.0 | 74.8 ±0.4 | 69.2 ±1.3 | 71.5 ±0.6 | 68.2 ±1.0 | ||
| BitStack | 6.36 | 67.0 ±1.0 | 41.4 ±1.4 | 77.1 ±1.0 | 71.4 ±0.5 | 69.5 ±1.3 | 73.1 ±0.6 | 66.6 ±1.0 | ||
| 3782(71%) | GPTQw4g128 | 5.73 | 73.6 ±0.9 | 45.3 ±1.5 | 78.7 ±1.0 | 75.4 ±0.4 | 67.6 ±1.3 | 72.7 ±0.6 | 68.9 ±0.9 | |
| AWQw4g128 | 5.61 | 73.3 ±0.9 | 45.2 ±1.5 | 78.6 ±1.0 | 75.2 ±0.4 | 68.7 ±1.3 | 72.7 ±0.6 | 68.9 ±0.9 | ||
| BitStack | 6.27 | 67.8 ±1.0 | 43.3 ±1.4 | 77.2 ±1.0 | 72.2 ±0.4 | 68.6 ±1.3 | 73.9 ±0.6 | 67.2 ±1.0 | ||
| 13B | 24825 | FP 16 | 4.88 | 77.4 ±0.9 | 49.1 ±1.5 | 80.5 ±0.9 | 79.4 ±0.4 | 72.2 ±1.3 | 76.8 ±0.6 | 72.6 ±0.9 |
| 3659(85%) | GPTQw2 | 1.2e4 | 26.4 ±0.9 | 28.2 ±1.3 | 50.2 ±1.2 | 26.3 ±0.4 | 48.4 ±1.4 | 0.0 ±0.0 | 29.9 ±0.9 | |
| AWQw2 | 9.6e4 | 27.3 ±0.9 | 28.0 ±1.3 | 49.9 ±1.2 | 26.0 ±0.4 | 50.4 ±1.4 | 0.0 ±0.0 | 30.3 ±0.9 | ||
| BitStack | 68.64 | 38.1 ±1.0 | 23.5 ±1.2 | 57.3 ±1.2 | 32.2 ±0.5 | 51.6 ±1.4 | 14.0 ±0.5 | 36.1 ±1.0 | ||
| 4029(84%) | GPTQw2g128 | 3.9e3 | 26.2 ±0.9 | 28.8 ±1.3 | 50.7 ±1.2 | 26.9 ±0.4 | 48.6 ±1.4 | 0.1 ±0.0 | 30.2 ±0.9 | |
| AWQw2g128 | 1.2e5 | 26.9 ±0.9 | 27.5 ±1.3 | 50.0 ±1.2 | 26.1 ±0.4 | 50.8 ±1.4 | 0.0 ±0.0 | 30.2 ±0.9 | ||
| BitStack | 9.26 | 64.5 ±1.0 | 34.2 ±1.4 | 73.0 ±1.0 | 60.9 ±0.5 | 64.9 ±1.3 | 65.3 ±0.7 | 60.5 ±1.0 | ||
| 5171(79%) | GPTQw3 | 6.20 | 68.2 ±1.0 | 42.8 ±1.4 | 77.1 ±1.0 | 71.4 ±0.5 | 67.6 ±1.3 | 63.1 ±0.7 | 65.0 ±1.0 | |
| AWQw3 | 6.46 | 71.1 ±0.9 | 44.4 ±1.5 | 77.6 ±1.0 | 71.2 ±0.5 | 66.8 ±1.3 | 61.9 ±0.7 | 65.5 ±1.0 | ||
| BitStack | 6.32 | 74.4 ±0.9 | 45.1 ±1.5 | 77.1 ±1.0 | 71.9 ±0.4 | 69.2 ±1.3 | 74.8 ±0.6 | 68.8 ±0.9 | ||
| 5541(78%) | GPTQw3g128 | 5.85 | 73.4 ±0.9 | 45.2 ±1.5 | 78.2 ±1.0 | 74.4 ±0.4 | 68.0 ±1.3 | 67.6 ±0.7 | 67.8 ±1.0 | |
| AWQw3g128 | 5.29 | 75.3 ±0.9 | 48.5 ±1.5 | 79.4 ±0.9 | 77.1 ±0.4 | 70.8 ±1.3 | 75.1 ±0.6 | 71.0 ±0.9 | ||
| BitStack | 6.04 | 74.4 ±0.9 | 46.2 ±1.5 | 77.9 ±1.0 | 72.6 ±0.4 | 70.6 ±1.3 | 76.6 ±0.6 | 69.7 ±0.9 | ||
| 6684(73%) | GPTQw4 | 5.09 | 75.8 ±0.9 | 48.0 ±1.5 | 79.6 ±0.9 | 77.8 ±0.4 | 72.4 ±1.3 | 74.5 ±0.6 | 71.4 ±0.9 | |
| AWQw4 | 5.07 | 78.2 ±0.8 | 49.7 ±1.5 | 80.4 ±0.9 | 78.6 ±0.4 | 71.6 ±1.3 | 76.1 ±0.6 | 72.4 ±0.9 | ||
| BitStack | 5.53 | 76.7 ±0.9 | 48.4 ±1.5 | 79.0 ±1.0 | 75.2 ±0.4 | 71.7 ±1.3 | 77.4 ±0.6 | 71.4 ±0.9 | ||
| 7054(72%) | GPTQw4g128 | 4.97 | 76.4 ±0.9 | 49.2 ±1.5 | 79.9 ±0.9 | 78.8 ±0.4 | 71.7 ±1.3 | 76.0 ±0.6 | 72.0 ±0.9 | |
| AWQw4g128 | 4.97 | 77.1 ±0.9 | 48.5 ±1.5 | 80.4 ±0.9 | 78.8 ±0.4 | 73.1 ±1.2 | 76.8 ±0.6 | 72.5 ±0.9 | ||
| BitStack | 5.47 | 76.5 ±0.9 | 48.0 ±1.5 | 79.0 ±1.0 | 75.7 ±0.4 | 71.7 ±1.3 | 77.8 ±0.6 | 71.4 ±0.9 | ||
| 70B | 131562 | FP 16 | 3.32 | 81.1 ±0.8 | 57.3 ±1.4 | 82.7 ±0.9 | 83.8 ±0.4 | 78.0 ±1.2 | 79.6 ±0.6 | 77.1 ±0.9 |
| 17348(87%) | GPTQw2 | 152.31 | 26.8 ±0.9 | 26.0 ±1.3 | 49.0 ±1.2 | 26.1 ±0.4 | 49.8 ±1.4 | 0.0 ±0.0 | 29.6 ±0.9 | |
| AWQw2 | 8.0e4 | 25.8 ±0.9 | 28.8 ±1.3 | 50.1 ±1.2 | 25.7 ±0.4 | 48.3 ±1.4 | 0.0 ±0.0 | 29.8 ±0.9 | ||
| BitStack | 9.41 | 67.8 ±1.0 | 42.1 ±1.4 | 75.9 ±1.0 | 65.1 ±0.5 | 67.7 ±1.3 | 65.7 ±0.7 | 64.1 ±1.0 | ||
| 19363(85%) | GPTQw2g128 | 7.79 | 53.0 ±1.0 | 32.0 ±1.4 | 66.9 ±1.1 | 51.1 ±0.5 | 60.2 ±1.4 | 34.8 ±0.7 | 49.7 ±1.0 | |
| AWQw2g128 | 7.2e4 | 26.0 ±0.9 | 28.9 ±1.3 | 49.8 ±1.2 | 25.7 ±0.4 | 51.0 ±1.4 | 0.0 ±0.0 | 30.2 ±0.9 | ||
| BitStack | 5.30 | 74.5 ±0.9 | 50.0 ±1.5 | 79.7 ±0.9 | 75.1 ±0.4 | 74.4 ±1.2 | 79.3 ±0.6 | 72.2 ±0.9 | ||
| 25508(81%) | GPTQw3 | 4.49 | 75.9 ±0.9 | 52.1 ±1.5 | 80.7 ±0.9 | 79.2 ±0.4 | 75.3 ±1.2 | 74.3 ±0.6 | 72.9 ±0.9 | |
| AWQw3 | 4.30 | 79.8 ±0.8 | 55.4 ±1.5 | 81.4 ±0.9 | 81.2 ±0.4 | 73.6 ±1.2 | 73.1 ±0.6 | 74.1 ±0.9 | ||
| BitStack | 4.33 | 78.9 ±0.8 | 54.9 ±1.5 | 81.7 ±0.9 | 79.9 ±0.4 | 76.6 ±1.2 | 80.1 ±0.6 | 75.3 ±0.9 | ||
| 27523(79%) | GPTQw3g128 | 55.43 | 27.8 ±0.9 | 27.4 ±1.3 | 50.9 ±1.2 | 29.8 ±0.5 | 48.9 ±1.4 | 9.5 ±0.4 | 32.4 ±0.9 | |
| AWQw3g128 | 3.74 | 79.0 ±0.8 | 56.7 ±1.4 | 82.8 ±0.9 | 82.3 ±0.4 | 76.6 ±1.2 | 79.3 ±0.6 | 76.1 ±0.9 | ||
| BitStack | 4.07 | 79.8 ±0.8 | 55.4 ±1.5 | 82.4 ±0.9 | 80.7 ±0.4 | 77.3 ±1.2 | 81.6 ±0.5 | 76.2 ±0.9 | ||
| 33668(74%) | GPTQw4 | 3.59 | 79.3 ±0.8 | 54.9 ±1.5 | 82.2 ±0.9 | 82.8 ±0.4 | 77.2 ±1.2 | 79.1 ±0.6 | 75.9 ±0.9 | |
| AWQw4 | 3.48 | 80.6 ±0.8 | 57.9 ±1.4 | 82.8 ±0.9 | 83.2 ±0.4 | 76.5 ±1.2 | 78.8 ±0.6 | 76.6 ±0.9 | ||
| BitStack | 3.76 | 79.3 ±0.8 | 57.4 ±1.4 | 82.4 ±0.9 | 81.8 ±0.4 | 77.9 ±1.2 | 81.0 ±0.5 | 76.6 ±0.9 | ||
| 35683(73%) | GPTQw4g128 | 3.42 | 81.3 ±0.8 | 57.8 ±1.4 | 83.0 ±0.9 | 83.6 ±0.4 | 76.8 ±1.2 | 79.4 ±0.6 | 77.0 ±0.9 | |
| AWQw4g128 | 3.41 | 80.3 ±0.8 | 56.7 ±1.4 | 83.1 ±0.9 | 83.4 ±0.4 | 78.1 ±1.2 | 79.6 ±0.6 | 76.9 ±0.9 | ||
| BitStack | 3.71 | 79.7 ±0.8 | 57.1 ±1.4 | 82.2 ±0.9 | 82.1 ±0.4 | 77.9 ±1.2 | 81.7 ±0.5 | 76.8 ±0.9 |
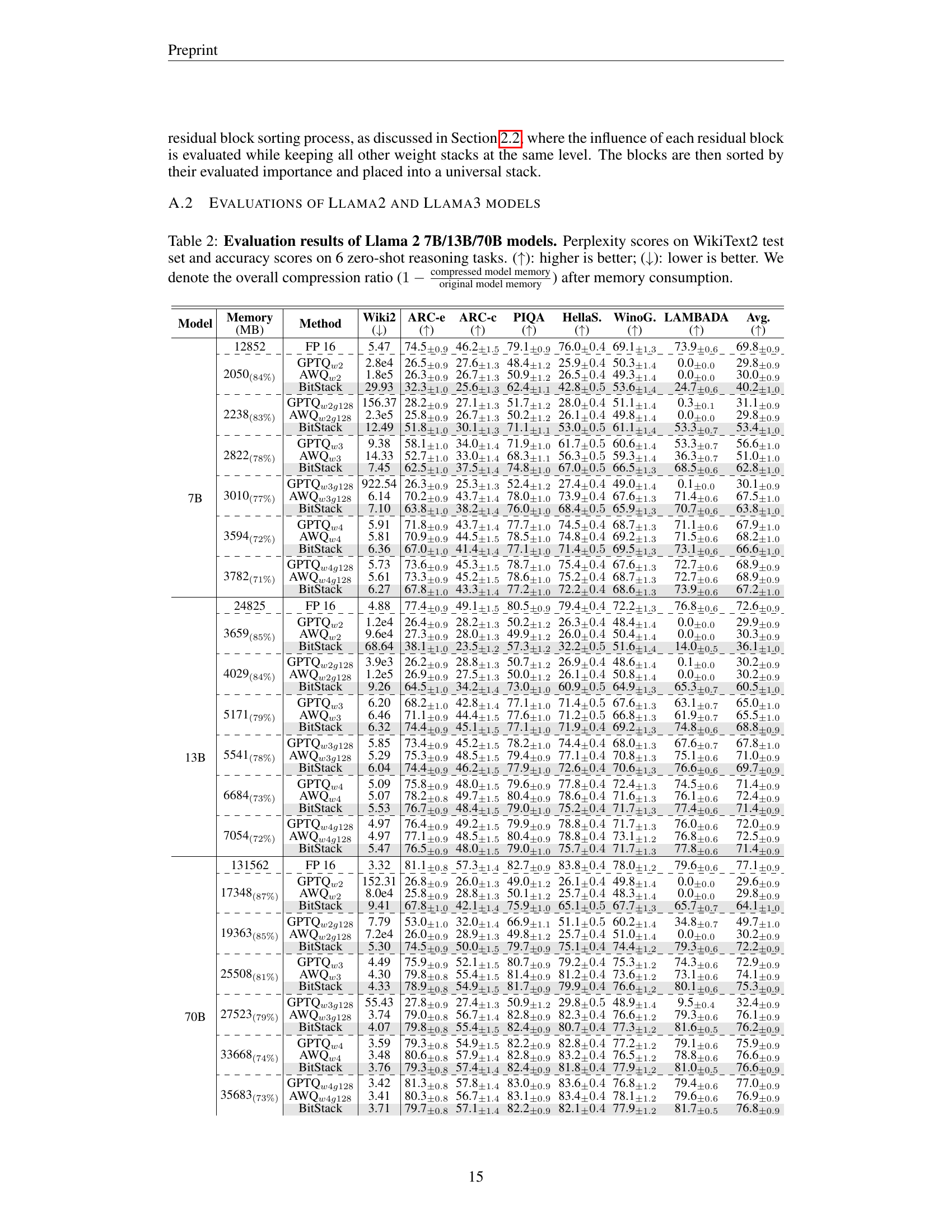
🔼 Table 2 presents a comprehensive evaluation of the BitStack model’s performance on three different sizes of Llama 2 language models (7B, 13B, and 70B parameters). The evaluation includes two key metrics: perplexity scores (lower is better) on the WikiText2 dataset, a common benchmark for language model performance, and accuracy scores (higher is better) across six zero-shot reasoning tasks. These zero-shot tasks assess the model’s ability to perform reasoning tasks without any explicit training on those specific tasks. The table also shows the memory consumption of the compressed models using BitStack, as well as the corresponding compression ratio (percentage reduction in memory usage compared to the original FP16 model). The results are compared to those obtained using other widely used compression methods like GPTQ and AWQ, allowing for a direct performance comparison. This comprehensive evaluation helps to demonstrate the effectiveness of BitStack in achieving a balance between model size and performance in variable memory environments.
read the caption
Table 2: Evaluation results of Llama 2 7B/13B/70B models. Perplexity scores on WikiText2 test set and accuracy scores on 6 zero-shot reasoning tasks. (↑↑\uparrow↑): higher is better; (↓↓\downarrow↓): lower is better. We denote the overall compression ratio (1−compressed model memoryoriginal model memory1compressed model memoryoriginal model memory1-\frac{\text{compressed model memory}}{\text{original model memory}}1 - divide start_ARG compressed model memory end_ARG start_ARG original model memory end_ARG) after memory consumption.
| Model | Memory (MB) | Method | Wiki2 ( ) ) | ARC-e ( ) ) | ARC-c ( ) ) | PIQA ( ) ) | HellaS. ( ) ) | WinoG. ( ) ) | LAMBADA ( ) ) | Avg. ( ) ) |
|---|---|---|---|---|---|---|---|---|---|---|
| 8B | 15316 | FP 16 | 6.13 | 77.7±0.9 | 53.3±1.5 | 80.8±0.9 | 79.2±0.4 | 72.7±1.3 | 76.1±0.6 | 73.3±0.9 |
| 3674(76%) | GPTQw2 | 1.1e6 | 25.3±0.9 | 26.7±1.3 | 50.6±1.2 | 26.4±0.4 | 51.0±1.4 | 0.0±0.0 | 30.0±0.9 | |
| AWQw2 | 1.1e6 | 25.2±0.9 | 24.1±1.2 | 50.7±1.2 | 26.2±0.4 | 48.6±1.4 | 0.0±0.0 | 29.1±0.9 | ||
| BitStack | 1.5e3 | 29.5±0.9 | 23.9±1.2 | 53.4±1.2 | 27.7±0.4 | 50.6±1.4 | 0.0±0.0 | 30.9±0.9 | ||
| 3877(75%) | GPTQw2g128 | 1.2e5 | 26.1±0.9 | 25.9±1.3 | 50.7±1.2 | 26.0±0.4 | 50.0±1.4 | 0.0±0.0 | 29.8±0.9 | |
| AWQw2g128 | 1.7e6 | 24.8±0.9 | 24.4±1.3 | 50.4±1.2 | 26.4±0.4 | 50.5±1.4 | 0.0±0.0 | 29.4±0.9 | ||
| BitStack | 96.87 | 48.5±1.0 | 25.3±1.3 | 64.0±1.1 | 37.1±0.5 | 56.7±1.4 | 9.4±0.4 | 40.2±0.9 | ||
| 4506(71%) | GPTQw3 | 9.6e4 | 26.0±0.9 | 25.7±1.3 | 50.9±1.2 | 27.1±0.4 | 50.3±1.4 | 0.0±0.0 | 30.0±0.9 | |
| AWQw3 | 12.08 | 61.7±1.0 | 38.8±1.4 | 71.4±1.1 | 68.6±0.5 | 65.0±1.3 | 51.9±0.7 | 59.6±1.0 | ||
| BitStack | 12.79 | 69.4±0.9 | 38.7±1.4 | 75.6±1.0 | 63.5±0.5 | 65.9±1.3 | 66.6±0.7 | 63.3±1.0 | ||
| 4709(69%) | GPTQw3g128 | 8.00 | 73.1±0.9 | 46.4±1.5 | 77.8±1.0 | 74.5±0.4 | 71.6±1.3 | 68.5±0.6 | 68.7±0.9 | |
| AWQw3g128 | 8.09 | 70.7±0.9 | 44.0±1.5 | 77.9±1.0 | 73.4±0.4 | 70.5±1.3 | 69.7±0.6 | 67.7±1.0 | ||
| BitStack | 11.45 | 71.6±0.9 | 42.2±1.4 | 76.7±1.0 | 65.8±0.5 | 67.3±1.3 | 68.6±0.6 | 65.4±1.0 | ||
| 5338(65%) | GPTQw4 | 3.7e4 | 28.2±0.9 | 25.3±1.3 | 51.0±1.2 | 28.7±0.5 | 54.6±1.4 | 0.1±0.0 | 31.3±0.9 | |
| AWQw4 | 7.08 | 75.0±0.9 | 51.5±1.5 | 79.5±0.9 | 77.8±0.4 | 72.1±1.3 | 71.1±0.6 | 71.2±0.9 | ||
| BitStack | 8.58 | 74.6±0.9 | 46.2±1.5 | 77.5±1.0 | 72.3±0.4 | 70.8±1.3 | 76.0±0.6 | 69.6±0.9 | ||
| 5541(64%) | GPTQw4g128 | 1.2e4 | 31.7±1.0 | 23.8±1.2 | 55.1±1.2 | 29.3±0.5 | 56.4±1.4 | 0.7±0.1 | 32.8±0.9 | |
| AWQw4g128 | 6.54 | 76.9±0.9 | 52.4±1.5 | 79.9±0.9 | 78.1±0.4 | 73.6±1.2 | 73.6±0.6 | 72.4±0.9 | ||
| BitStack | 8.26 | 75.8±0.9 | 47.1±1.5 | 78.7±1.0 | 73.1±0.4 | 70.8±1.3 | 76.3±0.6 | 70.3±0.9 | ||
| 70B | 134570 | FP 16 | 2.85 | 85.9±0.7 | 64.3±1.4 | 84.5±0.8 | 84.9±0.4 | 80.7±1.1 | 79.8±0.6 | 80.0±0.8 |
| 20356(85%) | GPTQw2 | 3.7e5 | 24.7±0.9 | 26.3±1.3 | 51.5±1.2 | 26.3±0.4 | 50.0±1.4 | 0.0±0.0 | 29.8±0.9 | |
| AWQw2 | 8.6e5 | 25.1±0.9 | 25.9±1.3 | 52.3±1.2 | 26.6±0.4 | 47.8±1.4 | 0.0±0.0 | 29.6±0.9 | ||
| BitStack | 59.37 | 46.5±1.0 | 27.3±1.3 | 65.2±1.1 | 39.1±0.5 | 51.9±1.4 | 9.2±0.4 | 39.9±1.0 | ||
| 22531(83%) | GPTQw2g128 | 4.0e5 | 25.3±0.9 | 24.7±1.3 | 49.3±1.2 | 26.0±0.4 | 50.1±1.4 | 0.0±0.0 | 29.2±0.9 | |
| AWQw2g128 | 1.7e6 | 24.9±0.9 | 26.4±1.3 | 51.4±1.2 | 26.8±0.4 | 51.8±1.4 | 0.0±0.0 | 30.2±0.9 | ||
| BitStack | 8.86 | 74.2±0.9 | 48.4±1.5 | 78.1±1.0 | 73.5±0.4 | 73.6±1.2 | 71.8±0.6 | 69.9±0.9 | ||
| 28516(79%) | GPTQw3 | NaN | 24.6±0.9 | 25.4±1.3 | 51.0±1.2 | 26.2±0.4 | 50.4±1.4 | 0.0±0.0 | 29.6±0.9 | |
| AWQw3 | 14.04 | 65.5±1.0 | 41.2±1.4 | 73.1±1.0 | 64.3±0.5 | 57.4±1.4 | 46.9±0.7 | 58.1±1.0 | ||
| BitStack | 6.88 | 79.8±0.8 | 54.8±1.5 | 80.8±0.9 | 79.6±0.4 | 77.0±1.2 | 75.3±0.6 | 74.5±0.9 | ||
| 30691(77%) | GPTQw3g128 | 4.8e5 | 25.5±0.9 | 26.5±1.3 | 51.5±1.2 | 26.3±0.4 | 48.8±1.4 | 0.0±0.0 | 29.8±0.9 | |
| AWQw3g128 | 4.59 | 82.2±0.8 | 60.6±1.4 | 82.8±0.9 | 82.9±0.4 | 78.4±1.2 | 76.8±0.6 | 77.3±0.9 | ||
| BitStack | 5.69 | 81.6±0.8 | 57.8±1.4 | 82.4±0.9 | 81.2±0.4 | 78.5±1.2 | 79.7±0.6 | 76.9±0.9 | ||
| 36676(73%) | GPTQw4 | NaN | 25.2±0.9 | 25.3±1.3 | 51.6±1.2 | 26.3±0.4 | 50.1±1.4 | 0.0±0.0 | 29.8±0.9 | |
| AWQw4 | 4.16 | 77.5±0.9 | 54.4±1.5 | 81.5±0.9 | 80.0±0.4 | 60.5±1.4 | 67.4±0.7 | 70.2±0.9 | ||
| BitStack | 4.88 | 82.3±0.8 | 61.1±1.4 | 83.4±0.9 | 82.5±0.4 | 79.9±1.1 | 80.1±0.6 | 78.2±0.9 | ||
| 38851(71%) | GPTQw4g128 | 7.8e5 | 25.0±0.9 | 26.3±1.3 | 49.9±1.2 | 26.8±0.4 | 47.4±1.4 | 0.0±0.0 | 29.2±0.9 | |
| AWQw4g128 | 3.23 | 85.9±0.7 | 63.5±1.4 | 84.2±0.9 | 84.5±0.4 | 80.1±1.1 | 78.1±0.6 | 79.4±0.8 | ||
| BitStack | 4.80 | 82.8±0.8 | 60.2±1.4 | 82.9±0.9 | 82.8±0.4 | 79.6±1.1 | 80.1±0.6 | 78.1±0.9 |
🔼 This table presents a comprehensive evaluation of the BitStack model’s performance on Llama 3 8B and 70B models. It assesses both the perplexity scores (lower is better) on the WikiText2 test set and accuracy scores (higher is better) across six distinct zero-shot reasoning tasks. Crucially, the table highlights the impact of different compression ratios achieved by BitStack, showing how performance varies as the model size is reduced. This allows for a direct comparison of BitStack against other compression techniques on a range of performance metrics, showcasing the efficiency of BitStack at different model sizes.
read the caption
Table 3: Evaluation results of Llama 3 8B/70B models. Perplexity scores on WikiText2 test set and accuracy scores on 6 zero-shot reasoning tasks. (↑↑\uparrow↑): higher is better; (↓↓\downarrow↓): lower is better. We denote the overall compression ratio (1−compressed model memoryoriginal model memory1compressed model memoryoriginal model memory1-\frac{\text{compressed model memory}}{\text{original model memory}}1 - divide start_ARG compressed model memory end_ARG start_ARG original model memory end_ARG) after memory consumption.
| Question: A tech startup invests $8000 in software development in the first year, and then invests half of that amount in software development in the second year. What’s the total amount the startup invested in software development over the two years? |
|---|
| AWQ-w4: ## Step 1: Identify the amount invested in the first year. The startup invests $8000 in software development in the first year. ## Step 2: Calculate the amount invested in the second year. The amount invested in the second year is half of the first year’s investment, which is $8000 / 2 = $4000. ## Step 3: Calculate the total amount invested over the two years. Add the investments of the first and second year to get the total amount invested: $8000 + $4000 = $12000. The final answer is: $12000. |
| BitStack(5338MB): ## Step 1: Calculate the amount invested in the first year. The startup invests $8000 in software development in the first year. ## Step 2: Calculate the amount invested in the second year. The startup invests half of the first year’s investment in the second year, which is $8000 / 2 = $4000. ## Step 3: Calculate the total amount invested over the two years. The total amount invested is the sum of the first year’s investment and the second year’s investment, which is $8000 + $4000 = $12000. The final answer is: . |
| \cdashline 1-1 AWQ-w3: ## Step 1: Calculate the total investment in the first year The total amount invested in the first year is 8000. ## Step 2: Calculate the total investment in the second year The total amount invested in the second year is half of the first year’s amount, which is 4000. ## Step 3: Calculate the total investment over both periods. To find the total amount invested in software development over the two years, we need to add the investment in the first year and the second year. The total amount = 8000 + (half of pound eight thousand five hundred six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six six ( concatenated.) |
| BitStack(4506MB): To find the total amount invested in software development over the two years, we need to add the amount invested in the first year to the amount invested in the second year. The amount invested in the first year is $8000, and the amount invested in the second year is half of that amount, which is $4000. So, the total amount invested in software development over the two years is $8000 + $4000, which is $12000. |
| \cdashline 1-1 AWQ-w2: blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank blank0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti0̆16 1ti0̆161ti0̆161ti0̆161ti0̆161ti0̆161ti( concatenated.) |
| BitStack(3674MB): The total amount of the startup is $8000. |
🔼 This table presents a qualitative comparison of the BitStack and AWQ model’s performance on a math reasoning task across various compression ratios. It shows the generated responses for each model at different memory footprints (representing various compression levels), highlighting the differences in reasoning capability and correctness as the model size decreases. The goal is to demonstrate BitStack’s ability to maintain reasonable performance even under extreme compression.
read the caption
Table 4: Qualitative results of BitStack Llama-3.1-8B-Instruct at different compression ratios comparing to AWQ.
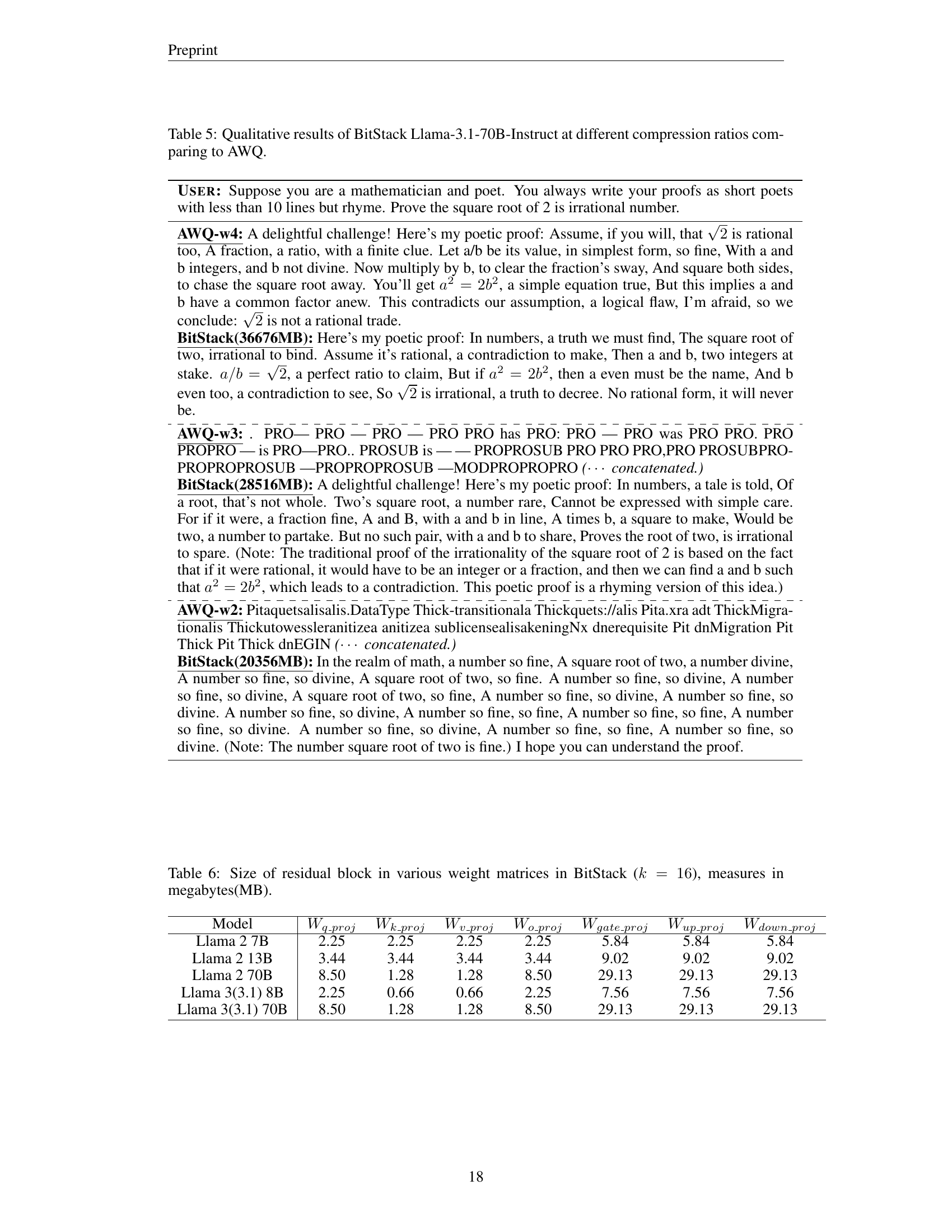
🔼 This table presents a qualitative comparison of the BitStack and AWQ model compression techniques on the Llama-3.1-70B-Instruct model. The comparison focuses on the quality of generated text responses at various compression ratios, illustrating the performance differences between the two methods under different memory constraints. The table uses examples to showcase how response quality degrades as compression increases, revealing the relative strengths and weaknesses of each approach.
read the caption
Table 5: Qualitative results of BitStack Llama-3.1-70B-Instruct at different compression ratios comparing to AWQ.
| Model | $W_{q_proj}$ | $W_{k_proj}$ | $W_{v_proj}$ | $W_{o_proj}$ | $W_{gate_proj}$ | $W_{up_proj}$ | $W_{down_proj}$ |
|---|---|---|---|---|---|---|---|
| Llama 2 7B | 2.25 | 2.25 | 2.25 | 2.25 | 5.84 | 5.84 | 5.84 |
| Llama 2 13B | 3.44 | 3.44 | 3.44 | 3.44 | 9.02 | 9.02 | 9.02 |
| Llama 2 70B | 8.50 | 1.28 | 1.28 | 8.50 | 29.13 | 29.13 | 29.13 |
| Llama 3(3.1) 8B | 2.25 | 0.66 | 0.66 | 2.25 | 7.56 | 7.56 | 7.56 |
| Llama 3(3.1) 70B | 8.50 | 1.28 | 1.28 | 8.50 | 29.13 | 29.13 | 29.13 |
🔼 This table shows the size of each residual block in megabytes (MB) for various weight matrices within the BitStack model. The residual blocks are created during the iterative decomposition process, where the original weight matrices are broken down into smaller, manageable units for dynamic loading. The number of singular values retained during singular value decomposition is set to 16 (k=16). The table provides insights into the memory footprint of different weight matrices in BitStack across various model sizes and helps illustrate the fine-grained size control that the model offers.
read the caption
Table 6: Size of residual block in various weight matrices in BitStack (k=16𝑘16k=16italic_k = 16), measures in megabytes(MB).
Full paper#