↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Dense 3D motion tracking from monocular videos remains a challenge due to limitations in computational efficiency and the difficulty of maintaining pixel-level precision over long sequences. Existing methods often struggle with either accuracy or speed. Some approaches prioritize speed, but this often results in lower accuracy. Others sacrifice speed for enhanced accuracy.
This research introduces DELTA, a novel method that addresses these issues by combining a reduced-resolution tracking phase with a transformer-based upsampler to achieve high-resolution, accurate predictions. DELTA leverages a joint global-local attention mechanism for efficiency and achieves state-of-the-art accuracy, outperforming prior methods by a significant margin (more than 8x faster) while maintaining high precision. The researchers also demonstrate the superiority of log-depth representation compared to standard Euclidean and inverse depth representations. These findings offer a highly robust and scalable solution for applications requiring dense and continuous 3D motion tracking.
Key Takeaways#
Why does it matter?#
This paper is important because it presents DELTA, a novel and efficient method for dense 3D tracking from monocular videos. It addresses the long-standing challenge of achieving pixel-level accuracy over long sequences, offering significant improvements over existing approaches. This opens new avenues for applications requiring precise and continuous 3D motion tracking and provides a robust baseline for future research in this area. The efficient architecture also makes it highly relevant to researchers focusing on computational efficiency in computer vision.
Visual Insights#

🔼 Figure 1 showcases the capabilities of DELTA, a novel dense 3D tracking method. Panel (a) demonstrates DELTA’s ability to track every pixel within a monocular video sequence. Panel (b) highlights that these pixel tracks are consistent and accurately represented in 3D space. Finally, panel (c) presents a performance comparison graph, illustrating that DELTA achieves state-of-the-art (SoTA) accuracy on 3D tracking benchmarks while exhibiting significantly faster processing speeds than existing dense 3D tracking approaches.
read the caption
Figure 1: DELTA is a dense 3D tracking approach that (a) tracks every pixel from a monocular video, (b) provides consistent trajectories in 3D space, and (c) achieves state-of-the-art accuracy on 3D tracking benchmarks while being significantly faster than previous approaches in the dense setting.
| Method | Dense | 3D | Long-term | Feed-forward |
|---|---|---|---|---|
| RAFT [Teed & Deng, 2020] | ✓ | ✓ | ||
| TAPIR [Doersch et al., 2023] | △ | ✓ | ✓ | |
| CoTracker [Karaev et al., 2023] | △ | ✓ | ✓ | |
| SpatialTracker [Xiao et al., 2024] | △ | ✓ | ✓ | ✓ |
| SceneTracker [Wang et al., 2024a] | △ | ✓ | ✓ | ✓ |
| DOT [Le Moing et al., 2024] | ✓ | ✓ | ✓ | |
| OmniMotion [Wang et al., 2023a] | △ | ✓ | ||
| DELTA (Ours) | ✓ | ✓ | ✓ | ✓ |
🔼 This table compares various motion estimation methods, highlighting their capabilities in terms of handling dense 3D data, long-term tracking, and whether they employ a feed-forward architecture. The symbol ‘△’ indicates methods theoretically capable of dense tracking, but computationally infeasible in practice due to their high time complexity.
read the caption
Table 1: Comparison of different types of motion estimation methods. △△\triangle△ denotes that the method is technically applicable to dense tracking but will be extremely time-consuming.
In-depth insights#
Dense 3D Tracking#
The research paper section on ‘Dense 3D Tracking’ introduces DELTA, a novel method for achieving accurate and efficient 3D motion tracking of every pixel in monocular videos. DELTA overcomes limitations of previous approaches by leveraging a joint global-local attention mechanism at a reduced resolution, followed by a transformer-based upsampler for high-resolution predictions. This coarse-to-fine strategy dramatically improves computational efficiency, making dense 3D tracking feasible at scale. The method’s effectiveness is demonstrated through extensive experiments, surpassing state-of-the-art accuracy on multiple benchmarks while being significantly faster than existing methods. Key contributions include the introduction of a novel spatial attention architecture and a sophisticated attention-based upsampler, both designed to achieve optimal performance and efficiency. Furthermore, the impact of depth representation on accuracy is studied, revealing log-depth as the most suitable choice for 3D motion tracking.
Coarse-to-Fine#
The paper introduces a novel coarse-to-fine strategy for efficient dense 3D tracking. It begins with reduced-resolution tracking using a spatio-temporal attention mechanism to capture the global spatial structure and temporal correlations. This approach significantly reduces computational complexity compared to directly processing high-resolution data. The low-resolution tracks are then upsampled to high resolution using an attention-based upsampler, carefully designed to preserve sharp motion boundaries and achieve pixel-level accuracy. This two-stage process allows DELTA to efficiently track every pixel in 3D space across long video sequences, achieving state-of-the-art results while maintaining high speed. The coarse stage’s efficiency is crucial for handling the computational burden of dense tracking, while the fine stage ensures high-resolution accuracy, making the strategy both efficient and accurate. This design choice balances computational cost and performance, resulting in an effective and scalable solution for long-range 3D dense tracking.
Attention Mechanisms#
The paper’s “Attention Mechanisms” section delves into the core of DELTA’s efficiency and accuracy in dense 3D tracking. It highlights the use of a novel spatio-temporal attention mechanism operating at a reduced resolution. This approach significantly reduces computational cost compared to traditional methods, especially for high-resolution videos. The reduced-resolution tracking is then enhanced by a transformer-based upsampler, cleverly designed to achieve high-resolution predictions efficiently. The authors also discuss key architectural choices, comparing different spatial attention designs. They demonstrate that incorporating both global and local spatial attention is crucial for achieving optimal performance, as the design effectively captures both global scene structure and local spatial details crucial for high accuracy. Finally, the design of the spatial attention is carefully tuned to avoid the computational burden of typical methods, ultimately achieving linear complexity in relation to the number of tracks.
Depth Representation#
The research explores the impact of depth representation on 3D tracking performance, comparing Euclidean depth, inverse depth (1/d), and log depth (log(d)). Log depth emerges as the superior representation, significantly improving accuracy. This is attributed to its enhanced precision for nearby objects, where depth estimation tends to be more accurate, while being more tolerant of uncertainty at greater distances. The choice of log depth is further justified by its alignment with the concept of optical expansion, where the apparent size of objects changes proportionally to their inverse distance from the camera. Representing depth changes as ratios (log(dt/d1)) further enhances robustness against imperfections in depth map input, making the model less sensitive to the absolute scale of depth values.
Future of 3D Tracking#
The provided text does not contain a section or heading explicitly titled ‘Future of 3D Tracking’. Therefore, it’s impossible to generate a summary based on that specific heading. To create the requested summary, please provide the relevant text from the PDF’s ‘Future of 3D Tracking’ section.
More visual insights#
More on figures

🔼 DELTA, a novel method for efficient dense 3D tracking, is illustrated. It uses a coarse-to-fine approach: starting with reduced-resolution tracking using a spatio-temporal attention mechanism (Sections 3.1 and 3.2), and then upsampling to high-resolution predictions via an attention-based upsampler (Section 3.3). The input is RGB-D video, and the output is efficient dense 3D tracking.
read the caption
Figure 2: Overview of DELTA. DELTA takes RGB-D videos as input and achieves efficient dense 3D tracking using a coarse-to-fine strategy, beginning with coarse tracking through a spatio-temporal attention mechanism at reduced resolution (Sec. 3.1, 3.2), followed by an attention-based upsampler for high-resolution predictions (Sec. 3.3).

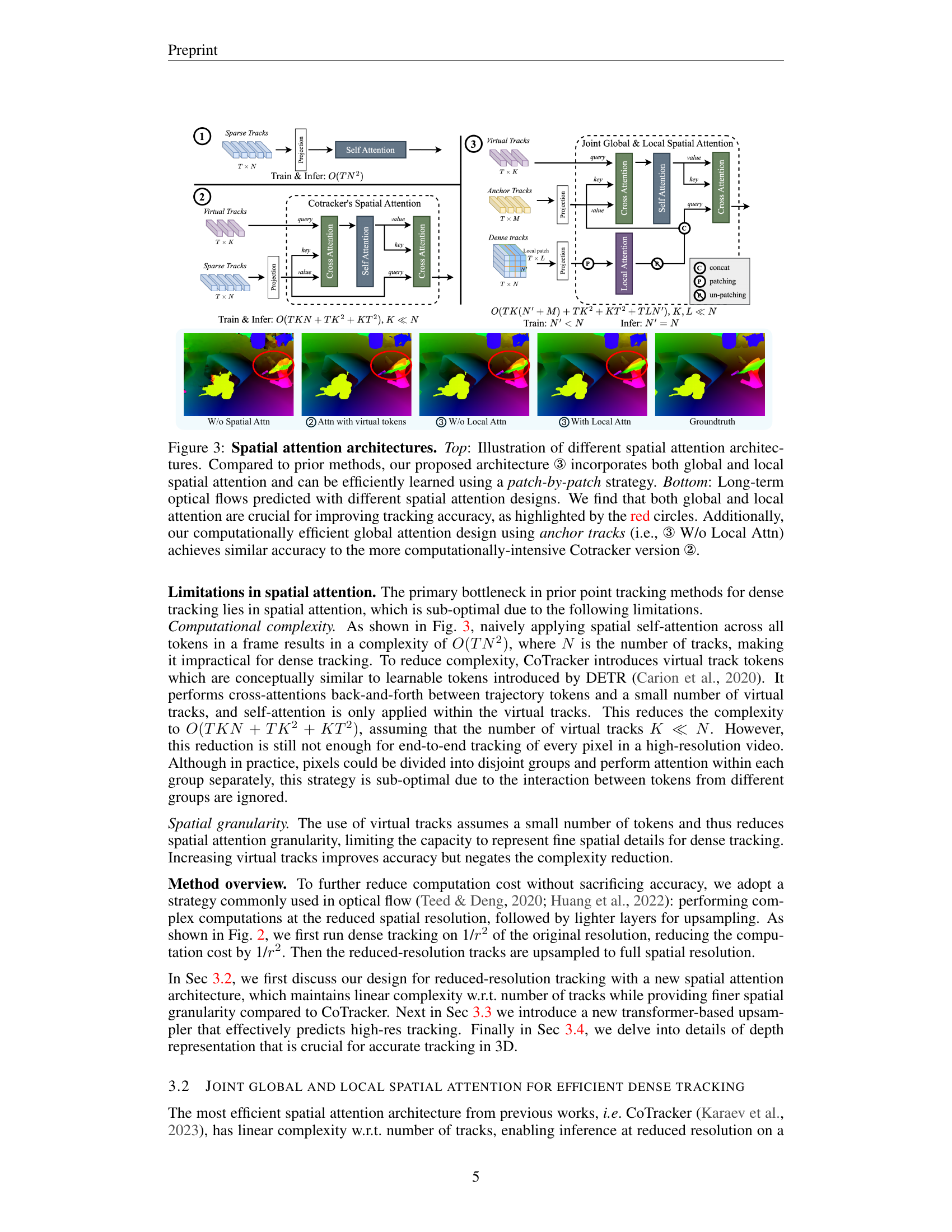
🔼 Figure 3 illustrates different spatial attention mechanisms used in dense tracking. The top part compares various architectures, highlighting how the proposed method (③) uniquely combines global and local spatial attention for efficient learning via a patch-by-patch approach. This contrasts with previous methods, which are shown to be less efficient. The bottom of the figure shows the long-term optical flow predictions obtained using each architecture, demonstrating the improved accuracy resulting from the inclusion of both global and local attention, especially noticeable in the red-circled regions. It also shows that the computationally efficient global attention using anchor tracks performs similarly to the computationally more expensive Cotracker architecture.
read the caption
Figure 3: Spatial attention architectures. Top: Illustration of different spatial attention architectures. Compared to prior methods, our proposed architecture ③ incorporates both global and local spatial attention and can be efficiently learned using a patch-by-patch strategy. Bottom: Long-term optical flows predicted with different spatial attention designs. We find that both global and local attention are crucial for improving tracking accuracy, as highlighted by the red circles. Additionally, our computationally efficient global attention design using anchor tracks (i.e., ③ W/o Local Attn) achieves similar accuracy to the more computationally-intensive Cotracker version ②.

🔼 This figure illustrates the attention-based upsampling module used in the DELTA architecture. The left panel shows the module’s architecture, highlighting how multiple blocks of local cross-attention are used to learn the upsampling weights for each pixel in the high-resolution output. These weights refine the predictions from a lower-resolution stage, making it computationally efficient. The right panel provides a qualitative comparison, using long-term optical flow maps. Red circles show areas where the attention-based upsampler outperforms RAFT’s standard convolution-based approach, indicating improved accuracy in challenging regions.
read the caption
Figure 4: Attention-based upsample module. Left: We apply multiple blocks of local cross-attention to learn the upsampling weights for each pixel in the fine resolution. Right: The red circles highlight regions in the long-term flow maps where our attention-based upsampler produces more accurate predictions compared to RAFT’s convolution-based upsampler.

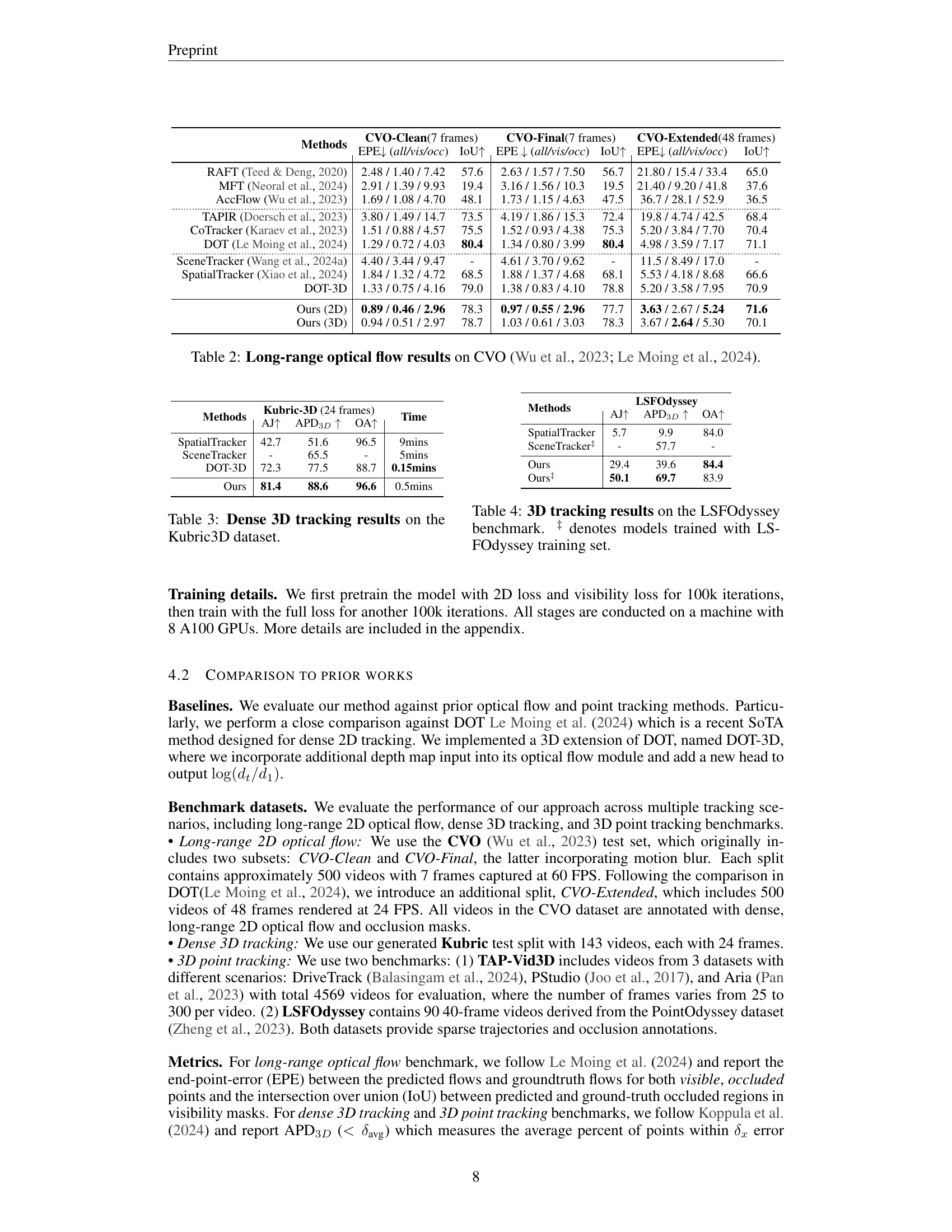
🔼 This table presents a quantitative comparison of different methods for dense 3D tracking on the Kubric3D benchmark dataset. It shows the performance of various methods across three key metrics: Average Jaccard index (AJ), Average Point-to-Point Distance in 3D space (APD3D), and Overall Accuracy (OA). The table also includes the time taken by each method, illustrating the computational efficiency of each approach.
read the caption
Table 3: Dense 3D tracking results on the Kubric3D dataset.

🔼 This table presents a comparison of different methods’ performance on the LSFOdyssey benchmark for 3D tracking. The metrics used likely include Average Jaccard (AJ), Average 3D Positional Accuracy (APD3D), and Occlusion Accuracy (OA). The ‘‡’ symbol indicates models that were specifically trained using the LSFOdyssey dataset, allowing for a fairer comparison against those trained on other datasets. The table helps to highlight the relative effectiveness of different 3D tracking approaches in a real-world video scenario.
read the caption
Table 4: 3D tracking results on the LSFOdyssey benchmark. ‡ denotes models trained with LSFOdyssey training set.

🔼 Figure 5 presents a qualitative comparison of dense 3D tracking performance on real-world videos. Four different methods are compared: CoTracker++ with UniDepth, SceneTracker, SpatialTracker, and the proposed DELTA method. Each method’s tracking results are visualized, showing 3D trajectories of every pixel over time. Moving objects are color-coded with rainbow colors to highlight their movement. The figure demonstrates the superior accuracy and stability of DELTA in tracking moving objects in complex scenes while maintaining consistent background estimates.
read the caption
Figure 5: Qualitative results of dense 3D tracking on in-the-wild videos between CoTracker +++ UniDepth, SceneTracker, SpatialTracker and our method. We densely track every pixel from the first frame of the video in 3D space, the moving objects are highlighted as rainbow color. Our method accurately tracks the motion of foreground objects while maintaining stable backgrounds.

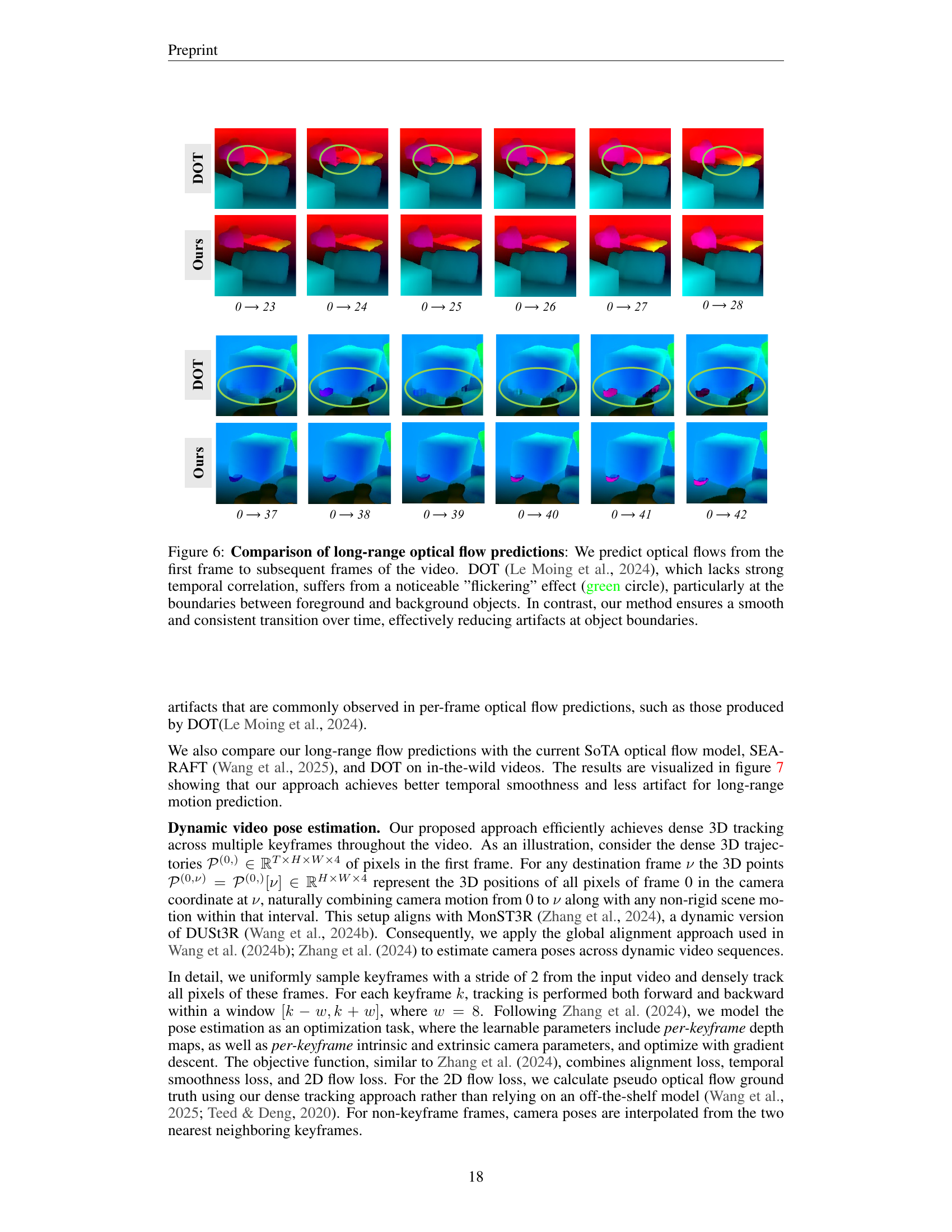
🔼 Figure 6 presents a comparison of long-range optical flow predictions generated by the proposed method and DOT (Le Moing et al., 2024). The figure displays optical flow predictions from the first frame to subsequent frames for both methods. The comparison highlights the significant improvement in temporal consistency achieved by the proposed method. DOT, lacking strong temporal correlation, exhibits a noticeable ‘flickering’ effect, especially where foreground and background objects meet. In contrast, the proposed method’s predictions show a much smoother and more consistent transition over time, effectively minimizing artifacts around object boundaries.
read the caption
Figure 6: Comparison of long-range optical flow predictions: We predict optical flows from the first frame to subsequent frames of the video. DOT (Le Moing et al., 2024), which lacks strong temporal correlation, suffers from a noticeable ”flickering” effect (green circle), particularly at the boundaries between foreground and background objects. In contrast, our method ensures a smooth and consistent transition over time, effectively reducing artifacts at object boundaries.
More on tables
| Methods | CVO-Clean(7 frames) | CVO-Final(7 frames) | CVO-Extended(48 frames) | |||
|---|---|---|---|---|---|---|
| EPE↓ (all/vis/occ) | IoU↑ | EPE↓ (all/vis/occ) | IoU↑ | EPE↓ (all/vis/occ) | IoU↑ | |
| RAFT (Teed & Deng, 2020) | 2.48 / 1.40 / 7.42 | 57.6 | 2.63 / 1.57 / 7.50 | 56.7 | 21.80 / 15.4 / 33.4 | 65.0 |
| MFT (Neoral et al., 2024) | 2.91 / 1.39 / 9.93 | 19.4 | 3.16 / 1.56 / 10.3 | 19.5 | 21.40 / 9.20 / 41.8 | 37.6 |
| AccFlow (Wu et al., 2023) | 1.69 / 1.08 / 4.70 | 48.1 | 1.73 / 1.15 / 4.63 | 47.5 | 36.7 / 28.1 / 52.9 | 36.5 |
| TAPIR (Doersch et al., 2023) | 3.80 / 1.49 / 14.7 | 73.5 | 4.19 / 1.86 / 15.3 | 72.4 | 19.8 / 4.74 / 42.5 | 68.4 |
| CoTracker (Karaev et al., 2023) | 1.51 / 0.88 / 4.57 | 75.5 | 1.52 / 0.93 / 4.38 | 75.3 | 5.20 / 3.84 / 7.70 | 70.4 |
| DOT (Le Moing et al., 2024) | 1.29 / 0.72 / 4.03 | 80.4 | 1.34 / 0.80 / 3.99 | 80.4 | 4.98 / 3.59 / 7.17 | 71.1 |
| SceneTracker (Wang et al., 2024a) | 4.40 / 3.44 / 9.47 | - | 4.61 / 3.70 / 9.62 | - | 11.5 / 8.49 / 17.0 | - |
| SpatialTracker (Xiao et al., 2024) | 1.84 / 1.32 / 4.72 | 68.5 | 1.88 / 1.37 / 4.68 | 68.1 | 5.53 / 4.18 / 8.68 | 66.6 |
| DOT-3D | 1.33 / 0.75 / 4.16 | 79.0 | 1.38 / 0.83 / 4.10 | 78.8 | 5.20 / 3.58 / 7.95 | 70.9 |
| Ours (2D) | 0.89 / 0.46 / 2.96 | 78.3 | 0.97 / 0.55 / 2.96 | 77.7 | 3.63 / 2.67 / 5.24 | 71.6 |
| Ours (3D) | 0.94 / 0.51 / 2.97 | 78.7 | 1.03 / 0.61 / 3.03 | 78.3 | 3.67 / 2.64 / 5.30 | 70.1 |
🔼 Table 2 presents a comprehensive comparison of different methods for long-range optical flow estimation on the challenging CVO dataset. The table shows the performance of various methods across three variations of the dataset: CVO-Clean (7 frames), CVO-Final (7 frames), and CVO-Extended (48 frames). For each method and dataset variation, the table reports the End-Point Error (EPE) for all pixels, visible pixels, and occluded pixels, as well as the Intersection over Union (IoU) metric. This allows for a detailed assessment of each method’s ability to accurately estimate optical flow over both short and long sequences, and to handle challenging scenarios involving occlusions.
read the caption
Table 2: Long-range optical flow results on CVO (Wu et al., 2023; Le Moing et al., 2024).
| Methods | Kubric-3D (24 frames) AJ↑ | Kubric-3D (24 frames) APD3D↑ | Kubric-3D (24 frames) OA↑ | Time |
|---|---|---|---|---|
| SpatialTracker | 42.7 | 51.6 | 96.5 | 9mins |
| SceneTracker | - | 65.5 | - | 5mins |
| DOT-3D | 72.3 | 77.5 | 88.7 | 0.15mins |
| Ours | 81.4 | 88.6 | 96.6 | 0.5mins |
🔼 Table 5 presents a comprehensive comparison of different 3D tracking methods on the TAP-Vid3D benchmark dataset. The benchmark consists of three diverse subsets: Aria, DriveTrack, and PStudio. The table reports three key metrics for each method: Average Jaccard Index (AJ), Average 3D Position Accuracy (APD3D), and Occlusion Accuracy (OA). Results are shown for methods that use either UniDepth or ZoeDepth for depth estimation. The table also includes results for methods that lift 2D tracking results to 3D (indicated by †). For the sake of consistent evaluation, the authors re-implemented SpatialTracker and SceneTracker using publicly available code and checkpoints and performed evaluation using the same inference procedure as their proposed method. Slight discrepancies in results compared to the original TAP-Vid3D paper are noted.
read the caption
Table 5: 3D tracking results on the TAP-Vid3D Benchmark. We report the 3D average jaccard (AJ), average 3D position accuracy (APD3D), and occlusion accuracy (OA) across datasets Aria, DriveTrack, and PStudio using UniDepth and ZoeDepth for depth estimation.† denotes using depth to lift 2D tracks to 3D tracks. We re-evaluated SpatialTracker and SceneTracker using their publicly available code and checkpoints, following the same inference procedure as our method. We note that the results differ slightly from the numbers reported in the TAP-Vid3D paper.
| Methods | LSFOdyssey AJ↑ | LSFOdyssey APD3D↑ | LSFOdyssey OA↑ |
|---|---|---|---|
| SpatialTracker | 5.7 | 9.9 | 84.0 |
| SceneTracker‡ | - | 57.7 | - |
| Ours | 29.4 | 39.6 | 84.4 |
| Ours‡ | 50.1 | 69.7 | 83.9 |
🔼 This table shows the ablation study on different depth representations used in the 3D tracking task. It compares the performance (measured by Average Jaccard Index (AJ) and Average Positional Deviation in 3D (APD3D)) of three different depth representations: Euclidean depth (d), inverse depth (1/d), and log depth (log(d)). The results demonstrate the superiority of log depth, which is consistent with the trends in monocular depth estimation.
read the caption
(a) Depth representation
| Methods | Aria AJ↑ | Aria APD₃D↑ | Aria OA↑ | DriveTrack AJ↑ | DriveTrack APD₃D↑ | DriveTrack OA↑ | PStudio AJ↑ | PStudio APD₃D↑ | PStudio OA↑ | Average AJ↑ | Average APD₃D↑ | Average OA↑ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TAPIR† + COLMAP | 7.1 | 11.9 | 72.6 | 8.9 | 14.7 | 80.4 | 6.1 | 10.7 | 75.2 | 7.4 | 12.4 | 76.1 |
| CoTracker† + COLMAP | 8.0 | 12.3 | 78.6 | 11.7 | 19.1 | 81.7 | 8.1 | 13.5 | 77.2 | 9.3 | 15.0 | 79.1 |
| BoostTAPIR† + COLMAP | 9.1 | 14.5 | 78.6 | 11.8 | 18.6 | 83.8 | 6.9 | 11.6 | 81.8 | 9.3 | 14.9 | 81.4 |
| CoTracker† + UniDepth | 13.0 | 20.9 | 84.9 | 12.5 | 19.9 | 80.1 | 6.2 | 13.5 | 67.8 | 10.6 | 18.1 | 77.6 |
| SpatialTracker + UniDepth | 13.6 | 20.9 | 90.5 | 8.3 | 14.5 | 82.8 | 8.0 | 15.0 | 75.8 | 10.0 | 16.8 | 83.0 |
| SceneTracker + UniDepth | - | 23.1 | - | - | 6.8 | - | - | 12.7 | - | - | 14.2 | - |
| DOT-3D + UniDepth | 13.8 | 22.1 | 85.5 | 11.8 | 17.9 | 82.3 | 3.2 | 5.3 | 52.5 | 9.6 | 15.1 | 73.4 |
| Ours + UniDepth | 16.6 | 24.4 | 86.8 | 14.6 | 22.5 | 85.8 | 8.2 | 15.0 | 76.4 | 13.1 | 20.6 | 83.0 |
| TAPIR† + ZoeDepth | 9.0 | 14.3 | 79.7 | 5.2 | 8.8 | 81.6 | 10.7 | 18.2 | 78.7 | 8.3 | 13.8 | 80.0 |
| CoTracker† + ZoeDepth | 10.0 | 15.9 | 87.8 | 5.0 | 9.1 | 82.6 | 11.2 | 19.4 | 80.0 | 8.7 | 14.8 | 83.4 |
| BoostTAPIR† + ZoeDepth | 9.9 | 16.3 | 86.5 | 5.4 | 9.2 | 85.3 | 11.3 | 19.0 | 82.7 | 8.8 | 14.8 | 84.8 |
| SpatialTracker + ZoeDepth | 9.2 | 15.1 | 89.9 | 5.8 | 10.2 | 82.0 | 9.8 | 17.7 | 78.0 | 8.3 | 14.3 | 83.3 |
| SceneTracker + ZoeDepth | - | 15.1 | - | - | 5.6 | - | - | 16.3 | - | - | 12.3 | - |
| Ours + ZoeDepth | 10.1 | 16.2 | 84.7 | 7.8 | 12.8 | 87.2 | 10.2 | 17.8 | 74.5 | 9.4 | 15.6 | 82.1 |
🔼 Table 6b presents ablation study results focusing on the impact of different spatial attention mechanisms on the overall performance of the DELTA model. It compares various designs, including the use of virtual tracks, global and local spatial attention, and different combinations thereof, to analyze their effect on accuracy and computational efficiency. The goal is to find an optimal balance between these two factors.
read the caption
(b) Spatial attention design
🔼 This table presents ablation study results on the effect of different upsampling methods used in the DELTA model for high-resolution track prediction. It compares the performance of various upsampling techniques, such as bilinear interpolation, a convolution-based upsampler (similar to that used in RAFT), and the proposed attention-based upsampler. The comparison is based on metrics such as end-point error (EPE), which measures the accuracy of optical flow predictions, and occlusion accuracy (OA), which measures the accuracy of visibility prediction on the CVO Extended dataset.
read the caption
(c) Upsampler design
| Depth | Network | TAP-Vid3D (Avg.) | |
|---|---|---|---|
| Repr. | Output | AJ | APD |
| 9.0 | 15.0 | ||
| 9.4 | 15.6 | ||
| 13.1 | 20.6 | ||
🔼 This table presents ablation studies evaluating different design choices in the DELTA model. It is broken down into three parts: (a) compares the impact of using different depth representations (Euclidean depth, inverse depth, and log depth) on the TAP-Vid3D benchmark; (b) examines the effect of various spatial attention architectures (with and without global/local attention) on the extended CVO dataset; and (c) analyzes the performance of different upsampling techniques (bilinear, a convnet-based upsampler, and an attention-based upsampler) also on the extended CVO dataset. The goal is to demonstrate the effectiveness of the chosen design choices for improved performance.
read the caption
Table 6: Ablation studies (a) different depth representations on TAP-Vid3D (b) different spatial attention designs on the CVO (Extended) (c) different upsampler designs on CVO (Extended).
| Global | Local | CVO (Extended) | |
|---|---|---|---|
| Attn. | Attn. | EPE↓ | OA↑ |
| ✗ | ✗ | 10.0 / 4.84 / 18.1 | 65.7 |
| ✗ | ✓ | 8.01 / 3.89 / 13.91 | 69.0 |
| ② CoTracker | ✗ | 3.72 / 2.78 / 5.44 | 70.1 |
| ③ Ours | ✗ | 3.73 / 2.78 / 5.47 | 70.0 |
| ③ Ours | ✓ | 3.67 / 2.64 / 5.30 | 70.1 |
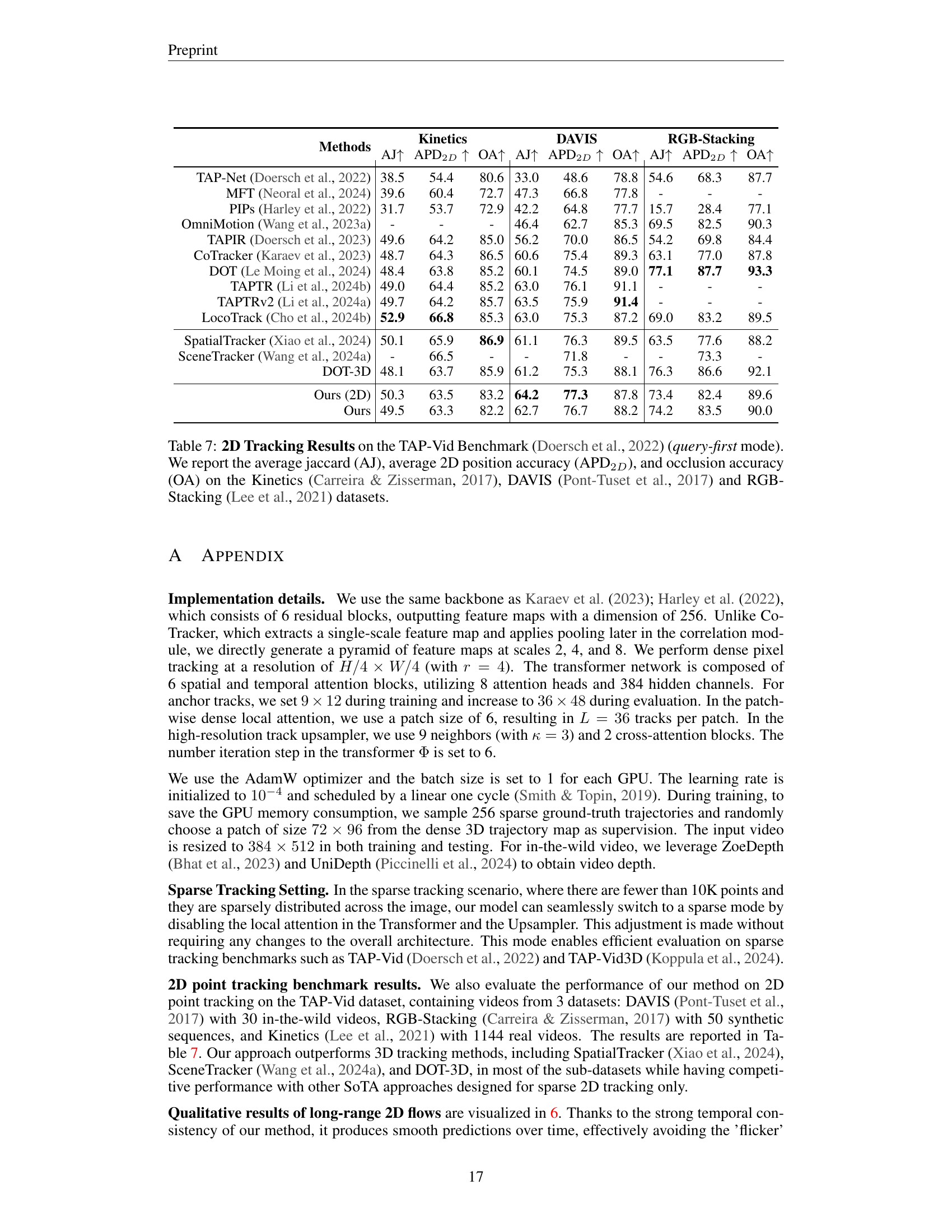
🔼 Table 7 presents a comprehensive comparison of various 2D tracking methods’ performance on the TAP-Vid benchmark dataset, using the query-first mode. The benchmark is composed of three subsets: Kinetics, DAVIS, and RGB-Stacking, each representing different video characteristics and challenges. The table shows the average Jaccard index (AJ), average 2D positional accuracy (APD2D), and occlusion accuracy (OA) for each method across all three subsets. Higher values for AJ, APD2D, and OA indicate better tracking performance. This allows for a detailed assessment of the strengths and weaknesses of each method across a variety of video scenarios.
read the caption
Table 7: 2D Tracking Results on the TAP-Vid Benchmark (Doersch et al., 2022) (query-first mode). We report the average jaccard (AJ), average 2D position accuracy (APD2D), and occlusion accuracy (OA) on the Kinetics (Carreira & Zisserman, 2017), DAVIS (Pont-Tuset et al., 2017) and RGB-Stacking (Lee et al., 2021) datasets.
| Upsample | CVO (Extended) | |
|---|---|---|
| Method | EPE ↓ | OA ↑ |
| Bilinear | 5.31 / 4.14 / 7.94 | 68.9 |
| NN | 5.34 / 4.17 / 7.98 | 66.9 |
| 3D KNN | 4.59 / 3.41 / 7.07 | 68.9 |
| ConvUp | 4.27 / 3.09 / 6.73 | 70.2 |
| AttentionUp | 3.73 / 2.73 / 5.35 | 70.3 |
| AttentionUp + Alibi | 3.67 / 2.64 / 5.30 | 70.1 |
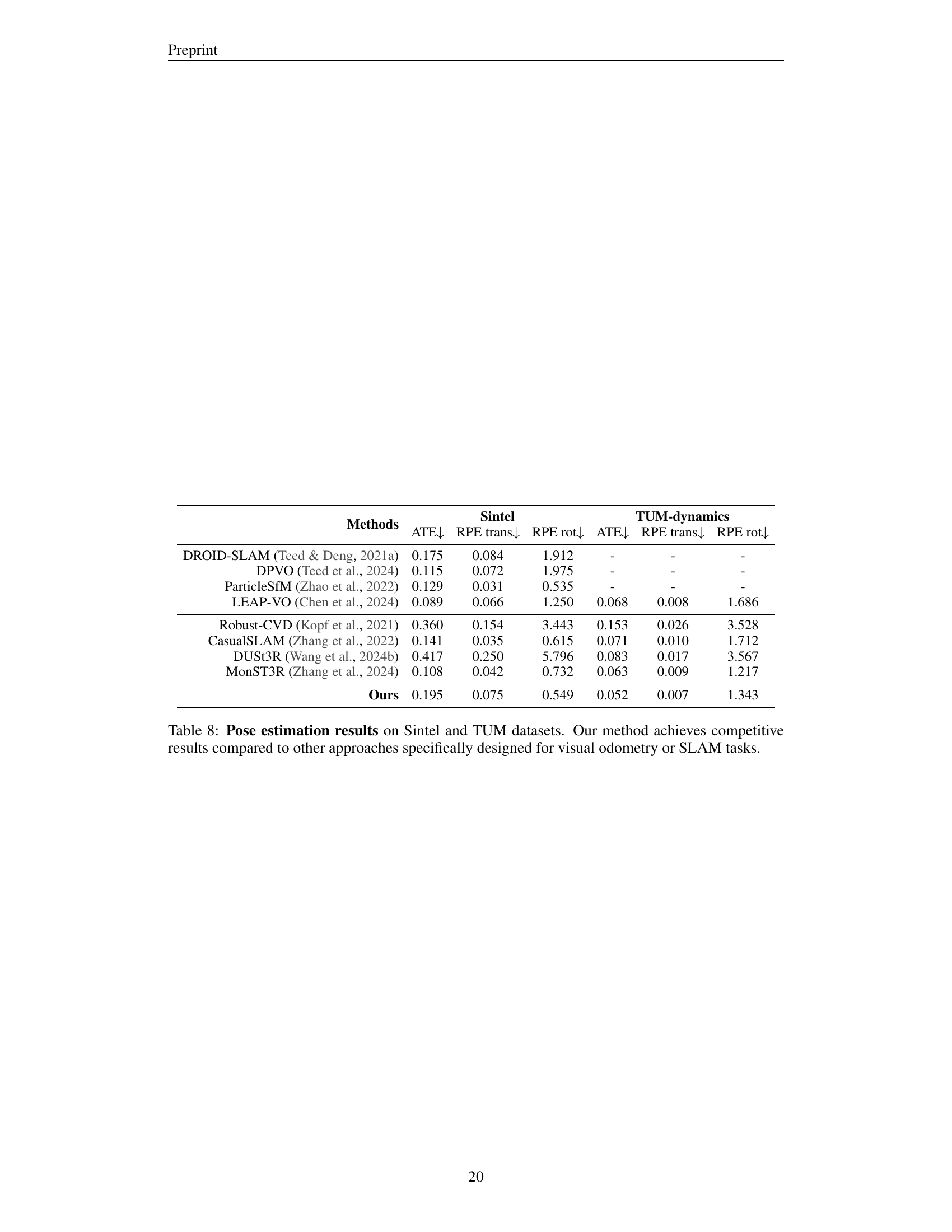
🔼 Table 8 presents a comparison of pose estimation performance metrics on the Sintel and TUM datasets. The metrics evaluated are Absolute Translation Error (ATE), Relative Translation Error (RPE) for translation and rotation. The table shows that the proposed method achieves competitive results compared to other state-of-the-art visual odometry (VO) and simultaneous localization and mapping (SLAM) methods. This demonstrates the effectiveness of the method even when not explicitly designed for these specific tasks.
read the caption
Table 8: Pose estimation results on Sintel and TUM datasets. Our method achieves competitive results compared to other approaches specifically designed for visual odometry or SLAM tasks.
Full paper#