TL;DR#
Current Vision-Language Models (VLMs) excel at solving mathematical problems, but their performance significantly drops when problem variations—changes in numerical values or functions—are introduced, revealing a lack of robustness. This paper introduces DynaMath, a new dynamic visual math benchmark to address this issue. DynaMath comprises 501 seed questions, each represented as a Python program, which generates numerous variants, allowing for a thorough assessment of the models’ ability to generalize and handle variations. The study shows that the worst-case accuracy of these VLMs is significantly lower than their average-case accuracy, highlighting a critical weakness that requires further investigation.
The DynaMath benchmark is designed to encourage the development of more robust VLMs by focusing on their ability to generalize and handle various input conditions, as opposed to simply memorizing answers. The results emphasize the need for more research on the robustness of VLM reasoning capabilities and provide valuable insights for developing more reliable mathematical reasoning models. This benchmark is a significant step forward in evaluating and advancing the field of vision-language models by providing a more rigorous and comprehensive evaluation of the generalization ability of these models.
Key Takeaways#
Why does it matter?#
This paper is crucial because it highlights the limitations of current Vision-Language Models (VLMs) in mathematical reasoning. By introducing DynaMath, it provides a benchmark that directly addresses the need for more robust and reliable VLMs, paving the way for future research and development in this vital field. The findings have broader implications for AI safety and trustworthiness, as they reveal vulnerabilities in advanced AI systems that need to be addressed.
Visual Insights#

🔼 Figure 1 shows an example where GPT-4 consistently fails to correctly identify the location of a sharp corner in a shifted absolute value function graph. Variant 9 of seed question 78 consistently produces an incorrect answer from GPT-4 with a repetition consistency of 90%. In contrast, variant 7, with the same function but a different shift, generates correct answers consistently. Across 7 other similar variants with varying shifts, GPT-4 makes the same error, claiming that the sharp corner is always at x=0, even though the function is shifted.
read the caption
Figure 1: An example of consistent failures in GPT-4o. Seed question 78 in our DynaMath benchmark generates a graph of a shifted absolute value function. GPT-4o consistently provides incorrect answers for variant 9 (left) with 90% repetition consistency, while it can successfully answer variant 7 (right) with 100% repetition consistency. We tested 7 other variants involving non-zero shifts of the absolute value function, and in each case, GPT-4o insists incorrectly that the “sharp corner” is at x=0𝑥0x=0italic_x = 0, leading to incorrect answers for all 7 variants. More failure examples are in Appendix F.
| Statistic | Number |
|---|---|
| Total seed questions (programs) | 501 |
| - Created from existing dataset | 227 (45.3%) |
| - Newly designed questions | 274 (54.7%) |
| Topics | |
| - Solid geometry (SG) | 15 (3.0%) |
| - Puzzle test (PT) | 17 (3.4%) |
| - Arithmetic (AR) | 26 (5.2%) |
| - Scientific figure (SF) | 45 (9.0%) |
| - Graph theory (GT) | 48 (9.6%) |
| - Algebra (AL) | 51 (10.2%) |
| - Plane geometry (PG) | 77 (15.4%) |
| - Analytic geometry (AG) | 97 (19.4%) |
| - Statistics (ST) | 125 (25.0%) |
| Levels | |
| - Elementary school (EL) | 63 (12.6%) |
| - High school (HI) | 277 (55.3%) |
| - Undergraduate (UN) | 161 (32.1%) |
| Question Types | |
| - Multiple-choice questions | 177 (35.3%) |
| - Free-form questions | 324 (64.7%) |
🔼 Table 1 provides a comprehensive overview of the DYNAMATH dataset, detailing its composition and characteristics. It shows the total number of seed questions (programs), categorized by whether they originate from existing datasets or are newly designed. Furthermore, it breaks down the seed questions by topic (covering areas like geometry, algebra, statistics, etc.), difficulty level (elementary, high school, undergraduate), and question type (multiple-choice versus free-form). This granular breakdown helps to understand the scope and diversity of the dataset, highlighting the balance between established problems and novel questions across different mathematical domains and difficulty levels.
read the caption
Table 1: Statistics of DynaMath.
In-depth insights#
VLM Robustness#
The research paper investigates the robustness of Vision-Language Models (VLMs) in mathematical reasoning. It reveals that state-of-the-art VLMs struggle to reliably solve even simple math problems when presented with slight variations, such as changes in visual numerical values or function graphs. This inconsistency highlights a significant limitation in current VLMs’ mathematical reasoning capabilities. The authors emphasize the need to study VLM robustness rigorously and introduce a new benchmark, DYNAMATH, specifically designed to evaluate this aspect. The findings underscore that the worst-case accuracy of VLMs is substantially lower than their average-case accuracy, demonstrating that the failure to solve a variant of a problem is not random but consistent. This points to a need for more reliable models that can generalize their reasoning abilities to varied input conditions, and DYNAMATH provides a valuable tool to guide the development of more robust VLMs.
Dynamic Bench#
The ‘Dynamic Bench’ section details a novel benchmark for evaluating the robustness of Vision-Language Models (VLMs) in mathematical reasoning. Unlike static benchmarks, it uses programmatically generated questions, allowing for diverse variations in visual and textual elements while assessing the model’s ability to generalize. This dynamic approach reveals that current state-of-the-art VLMs show significant inconsistencies in performance under different variants of the same problem. The benchmark includes diverse question types and difficulty levels, making it a more comprehensive evaluation tool for VLM reasoning capabilities. The worst-case accuracy metric is crucial, highlighting models’ tendency to fail consistently on certain variants, revealing limitations beyond average performance.
Python Program Gen#
The research paper section ‘Python Program Gen’ details the methodology for dynamically generating math problems. Each problem is encoded as a Python program, enabling the automatic creation of numerous variations by adjusting parameters within the program. This approach moves beyond static datasets, allowing for a more comprehensive evaluation of model robustness. The programs are designed to randomly vary aspects such as numerical values, geometric transformations, function types, graph structures, and real-world contexts. This dynamic generation allows for a much more rigorous assessment of generalization capability than traditional static benchmarks, which can be memorized by models. The process ensures that the core mathematical reasoning remains consistent, while the superficial details change, revealing the true robustness of Vision-Language Models (VLMs) in handling varying inputs.
Consistent Failure#
The research section, ‘Consistent Failure Cases’, highlights a critical weakness in current Vision-Language Models (VLMs). It reveals that VLMs often exhibit consistent errors on seemingly minor variations of a problem, even when these variations would be easily handled by humans. This consistent failure is not attributed to random errors, as demonstrated by high repetition consistency, but rather to a fundamental limitation in the models’ ability to generalize and apply their reasoning skills robustly across problem variations. The study emphasizes that this is not a matter of occasional mistakes but rather systematic shortcomings that hinder the reliable application of VLMs to real-world scenarios where slight changes in problem parameters are common. The presence of these consistent failures underscores the importance of researching robustness and generalizability in VLM development to build more dependable and practical systems.
Future Work#
The ‘Future Work’ section of this research paper outlines several promising avenues for future research. Expanding the dataset is a primary goal, aiming to include more complex problems and a wider range of mathematical topics. The researchers also plan to explore different model architectures and training techniques to enhance the robustness of vision-language models (VLMs) in mathematical reasoning. This includes investigating the use of adversarial training to improve VLM resilience to variations in input data, and utilizing reinforcement learning methods incorporating human feedback to guide model development toward more reliable and consistent performance. Furthermore, developing more sophisticated evaluation metrics that better capture the nuances of mathematical reasoning is seen as crucial. The aim is to move beyond simple accuracy measurements to assess the reasoning process itself, and identify areas for improvement. Finally, application to real-world problems is highlighted as a long-term goal, emphasizing the potential of robust VLMs to improve mathematical problem-solving across various disciplines.
More visual insights#
More on figures

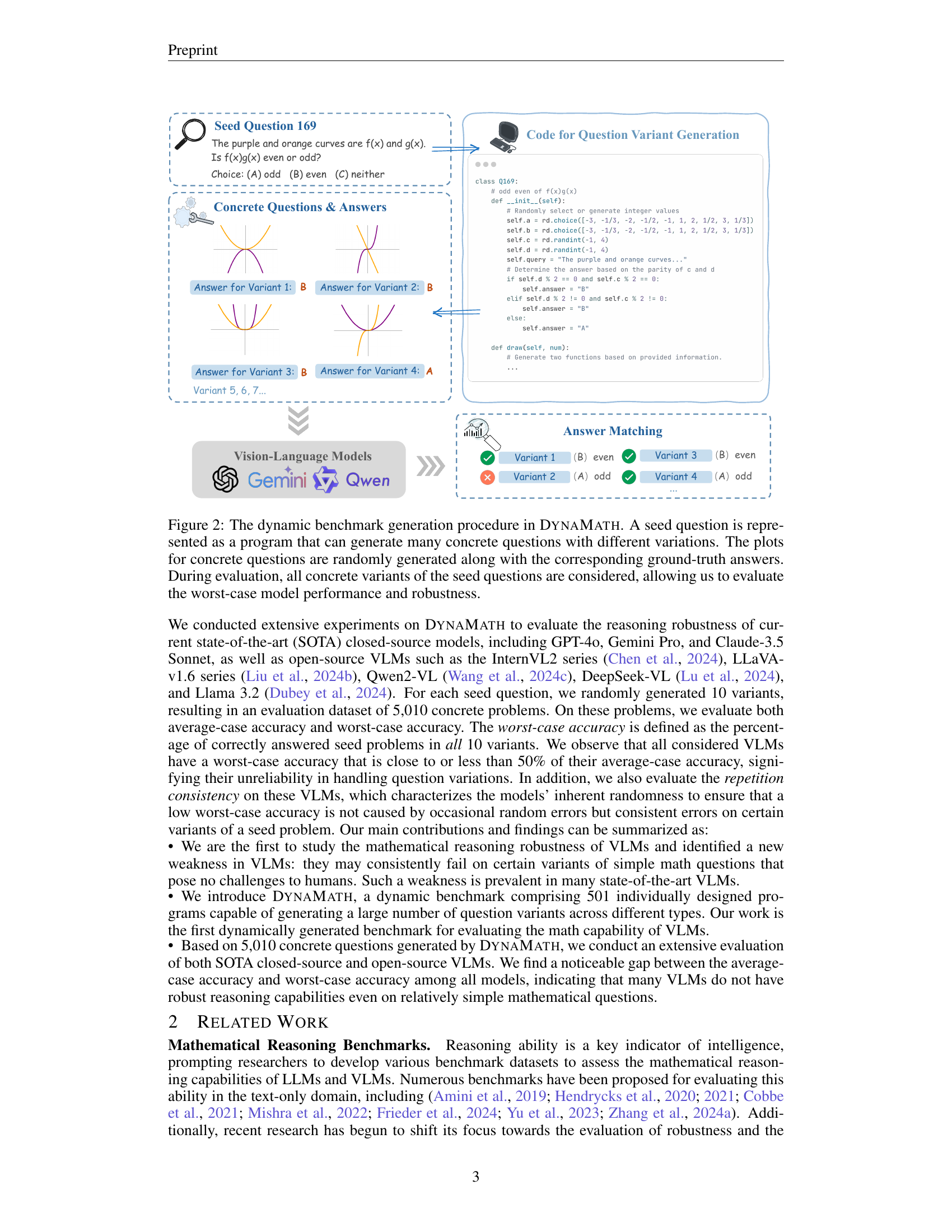
🔼 The figure illustrates the process of generating a dynamic benchmark dataset for evaluating the robustness of vision-language models (VLMs) in mathematical reasoning. It starts with a seed question, represented as a Python program. This program generates numerous concrete question variants by randomly altering parameters (numerical values, function types, etc.), producing different visual representations (plots, graphs, etc.). Each variant has a corresponding ground-truth answer. During the evaluation phase, all generated variants of each seed question are used to assess the model’s performance, enabling the calculation of both average-case and worst-case accuracy, providing a comprehensive measure of robustness against variations.
read the caption
Figure 2: The dynamic benchmark generation procedure in DynaMath. A seed question is represented as a program that can generate many concrete questions with different variations. The plots for concrete questions are randomly generated along with the corresponding ground-truth answers. During evaluation, all concrete variants of the seed questions are considered, allowing us to evaluate the worst-case model performance and robustness.

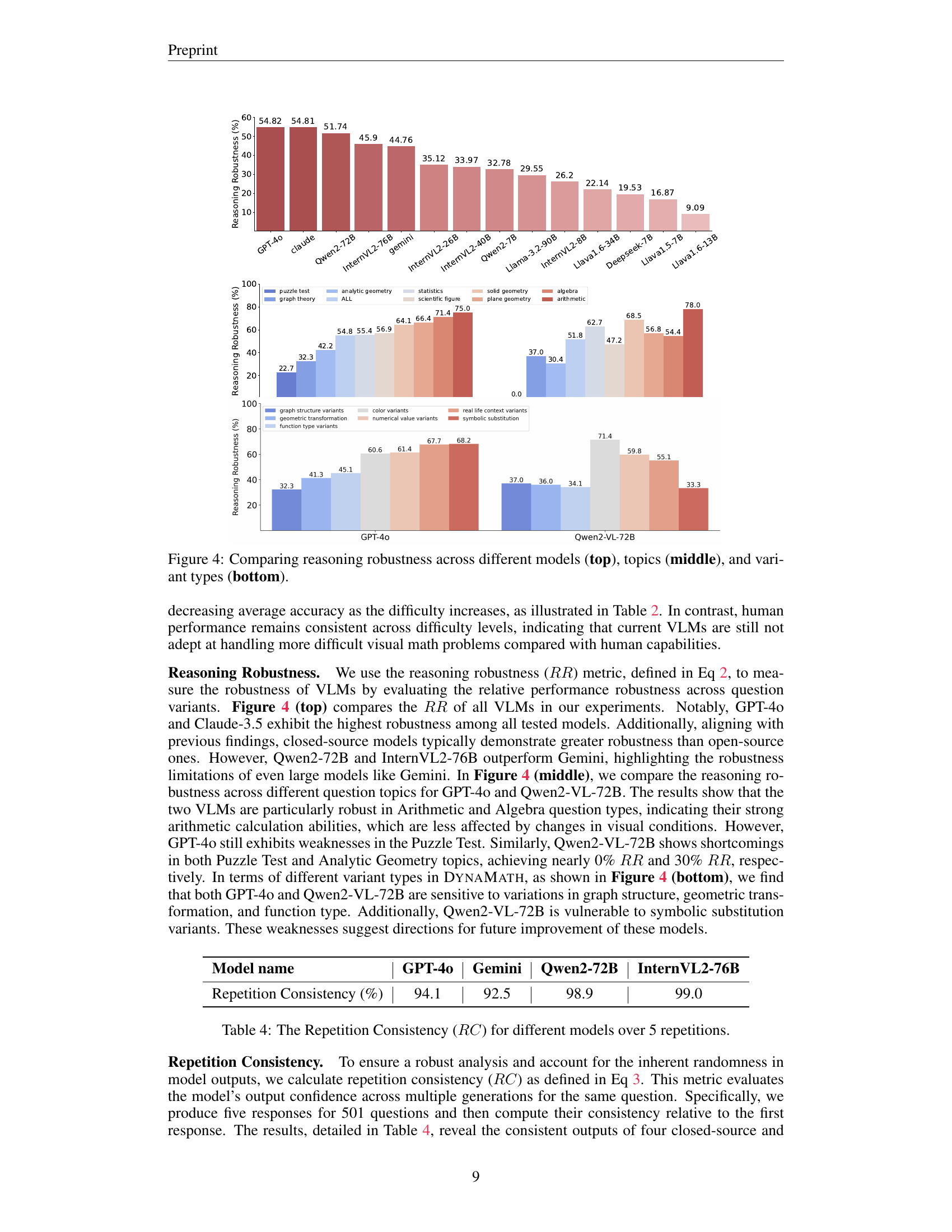
🔼 This figure compares the reasoning robustness of various vision-language models (VLMs) across different aspects. The top panel shows the overall reasoning robustness of each model, indicating how consistently each model performs across various question variants. The middle panel breaks down the robustness performance across different math problem topics, showing variations in the models’ abilities across diverse mathematical domains. The bottom panel analyzes the robustness concerning various types of question variations, assessing how sensitive the models are to changes in numerical values, geometric transformations, functional representations, and so on.
read the caption
Figure 5: Comparing reasoning robustness across different models (top), topics (middle), and variant types (bottom).

🔼 Figure 6 demonstrates the memorization phenomenon observed in Claude 3.5 Sonnet. Five variants of seed question 12, each with a different visual representation of a periodic function, were generated. Despite the varying inputs, the model consistently predicted the period of the function as 2π. This indicates that instead of performing actual calculations based on the diagram’s details, the model may be relying on memorized patterns or heuristics. The high probability of the model giving the same answer, regardless of visual changes in the input, highlights a significant limitation in its reasoning capability and emphasizes the need for more robust evaluation of vision-language models.
read the caption
Figure 6: Example of the Memorization Phenomenon: the generated variants of seed Question 12 and the corresponding responses from Claude 3.5 Sonnet. The model’s response remains 2π2𝜋2\pi2 italic_π with high probability, regardless of changes in the conditions depicted in the diagram.

🔼 The figure shows a pie chart that breaks down the types of errors made by the Claude-3.5 Sonnet model on the DYNAMATH benchmark. It visually represents the proportion of errors attributed to five categories: figure reading errors, calculation errors, reasoning errors, knowledge errors, and hallucination errors. This allows for a quick understanding of the model’s failure modes and their relative frequencies.
read the caption
Figure 7: Error Analysis of Claude-3.5 Sonnet.

🔼 Figure 7 visualizes six distinct variation types incorporated within the DynaMath benchmark. These variations manipulate different aspects of mathematical problems to assess the robustness of Vision-Language Models (VLMs). The variations include altering numerical values, performing geometric transformations, modifying function types, applying symbolic substitutions, incorporating real-life contexts, and changing graph structures. Each variation type challenges VLMs’ ability to generalize their reasoning processes across diverse problem instances.
read the caption
Figure 8: Variation types considered in our DynaMath benchmark

🔼 Figure 9 shows six variations of Question 169 from the DynaMath benchmark. Question 169 asks whether the product of two functions, f(x) and g(x), represented graphically, is even or odd. Each variant displays a slightly altered version of the graphs of f(x) and g(x), testing the model’s robustness to changes in visual representation. The figure also includes the corresponding answers generated by GPT-40 for each variant. The differences in the answers highlight GPT-40’s inconsistency in solving similar problems with minor visual changes.
read the caption
Figure 9: Example of the generated variants of Question 169 and the corresponding responses from GPT-4o.

🔼 Figure 10 presents six variations of Question 75 from the DYNAMATH benchmark, each showing different visual representations of two lines. The question asks whether the lines are parallel. Gemini’s responses to each variant are included, demonstrating inconsistencies in its ability to correctly assess parallelism based on these different visual presentations.
read the caption
Figure 10: Example of the generated variants of Question 75 and the corresponding responses from Gemini.
More on tables
| Model | ALL | PG | SG | AG | AL | PT | GT | ST | SF | AR | EL | HI | UN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Closed-sourced Large Multimodal Models (LMMs) | |||||||||||||
| Zero-shot GPT-4o | 63.7 | 56.8 | 52.0 | 61.0 | 76.9 | 51.8 | 58.1 | 69.3 | 62.4 | 61.5 | 68.6 | 61.8 | 36.8 |
| Zero-shot Claude-3.5 | 64.8 | 49.9 | 49.3 | 55.3 | 81.0 | 44.1 | 69.4 | 78.2 | 62.2 | 61.2 | 66.7 | 62.6 | 33.3 |
| Zero-shot Gemini Pro 1.5 | 60.5 | 52.7 | 42.7 | 61.6 | 70.8 | 20.6 | 65.2 | 69.8 | 50.2 | 54.2 | 62.9 | 59.2 | 37.1 |
| 3-shot CoT GPT-4o | 64.9 | 58.1 | 59.3 | 57.7 | 84.1 | 51.2 | 61.9 | 71.0 | 60.9 | 57.7 | 66.2 | 62.5 | 34.8 |
| 3-shot CoT Claude-3.5 | 62.5 | 49.1 | 48.0 | 50.6 | 80.2 | 37.1 | 58.1 | 78.2 | 64.9 | 55.0 | 63.0 | 61.5 | 30.5 |
| 3-shot CoT Gemini Pro 1.5 | 58.7 | 52.6 | 45.3 | 56.7 | 72.9 | 21.8 | 57.9 | 66.0 | 54.9 | 48.1 | 59.0 | 58.3 | 34.2 |
| Open-sourced Vision Language Models (VLMs) | |||||||||||||
| Qwen2-VL-72B | 55.1 | 48.1 | 48.7 | 50.9 | 57.6 | 28.2 | 45.0 | 68.9 | 56.4 | 54.2 | 61.3 | 57.4 | 30.7 |
| Qwen2-VL-7B | 42.1 | 40.3 | 38.7 | 39.9 | 37.1 | 8.2 | 44.8 | 52.1 | 41.1 | 39.2 | 47.6 | 42.2 | 24.4 |
| InternVL2-76B | 54.0 | 44.5 | 34.7 | 43.8 | 67.6 | 35.3 | 51.0 | 66.7 | 55.1 | 51.5 | 60.3 | 52.9 | 26.4 |
| InternVL2-40B | 41.8 | 31.3 | 21.3 | 38.8 | 42.9 | 15.3 | 38.3 | 58.1 | 43.1 | 38.1 | 51.0 | 41.5 | 23.4 |
| InternVL2-26B | 41.0 | 35.8 | 26.0 | 37.3 | 38.8 | 13.5 | 46.9 | 51.9 | 39.6 | 40.4 | 52.1 | 38.5 | 22.5 |
| InternVL2-8B | 39.7 | 33.9 | 37.3 | 32.5 | 46.9 | 15.9 | 42.1 | 47.8 | 39.1 | 37.3 | 51.1 | 37.4 | 19.6 |
| Llama-3.2-90B | 44.0 | 47.5 | 37.3 | 36.8 | 46.5 | 12.4 | 44.8 | 56.8 | 39.8 | 30.0 | 45.4 | 43.8 | 22.2 |
| Deepseek-VL-7B-chat | 21.5 | 16.0 | 13.3 | 26.5 | 12.9 | 4.7 | 32.7 | 24.3 | 24.2 | 15.0 | 28.3 | 19.0 | 16.0 |
| Llava-v1.6-34B | 27.1 | 21.4 | 25.3 | 27.6 | 14.9 | 7.6 | 32.7 | 36.8 | 27.8 | 23.1 | 35.9 | 23.8 | 16.6 |
| Llava-v1.6-vicuna-13B | 19.8 | 14.7 | 10.0 | 23.4 | 8.2 | 10.0 | 21.5 | 28.2 | 19.6 | 10.0 | 27.1 | 16.5 | 14.1 |
| Llava-v1.5-7B | 16.6 | 10.5 | 7.3 | 19.5 | 6.5 | 8.2 | 32.3 | 17.5 | 20.2 | 10.8 | 18.9 | 13.3 | 11.7 |
| Human | |||||||||||||
| Human performance | 75.8 | 80.5 | 60.0 | 83.5 | 78.4 | 76.5 | 64.6 | 74.4 | 77.8 | 61.5 | 74.6 | 78.3 | 72.0 |
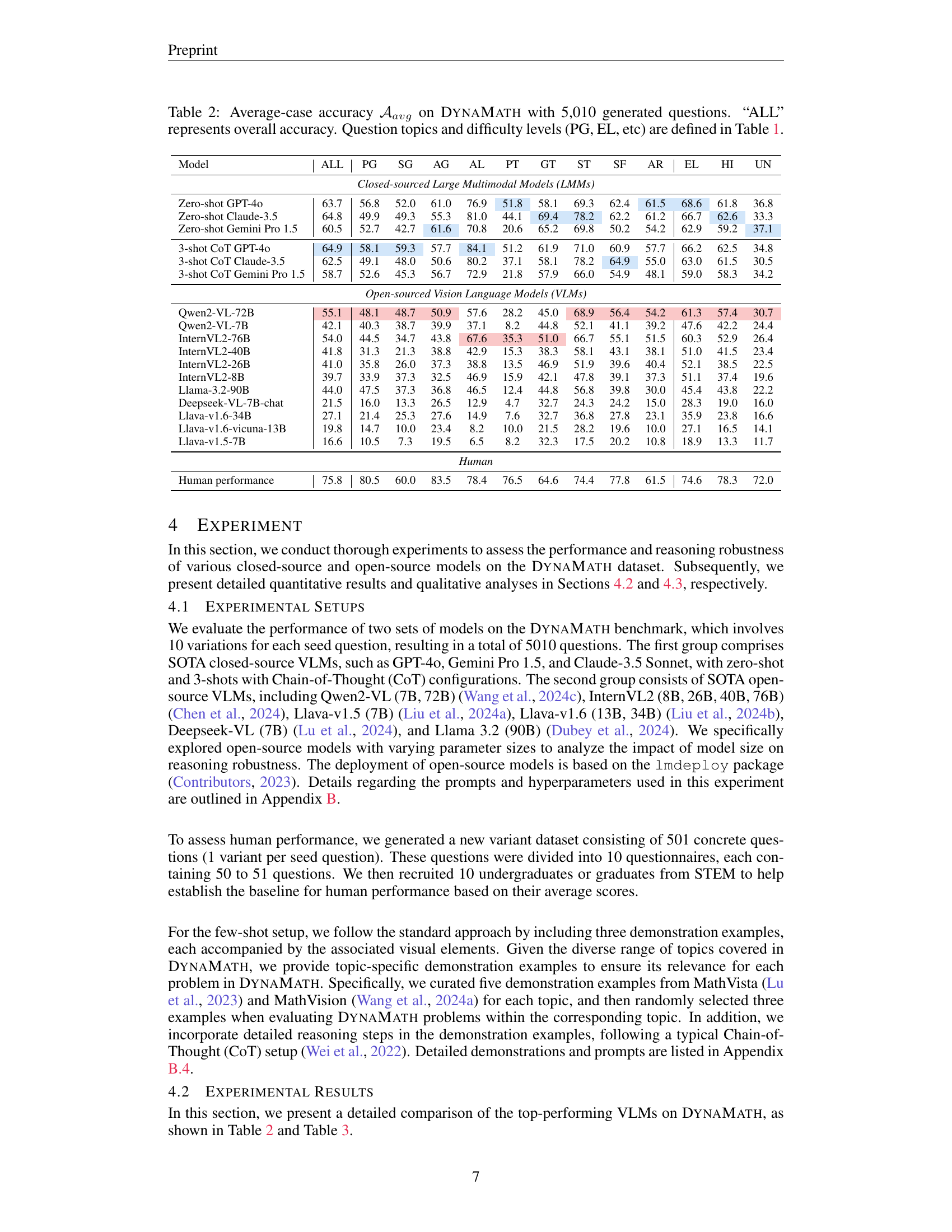
🔼 Table 2 presents the average-case accuracy of various vision-language models (VLMs) on the DynaMath benchmark. DynaMath consists of 5,010 dynamically generated visual math questions, derived from 501 seed questions. The table shows the performance of each model across different question topics (Plane Geometry (PG), Solid Geometry (SG), Analytic Geometry (AG), Algebra (AL), Puzzle Tests (PT), Graph Theory (GT), Statistics (ST), Scientific Figures (SF), Arithmetic (AR)), and difficulty levels (Elementary school (EL), High school (HI), Undergraduate (UN)). The ‘ALL’ column shows the overall average accuracy across all questions. The results are useful for comparing the performance of different models on various types of visual mathematical reasoning tasks and assessing their strengths and weaknesses.
read the caption
Table 2: Average-case accuracy 𝒜avgsubscript𝒜𝑎𝑣𝑔\mathcal{A}_{avg}caligraphic_A start_POSTSUBSCRIPT italic_a italic_v italic_g end_POSTSUBSCRIPT on DynaMath with 5,010 generated questions. “ALL” represents overall accuracy. Question topics and difficulty levels (PG, EL, etc) are defined in Table 1.
| Model | ALL | PG | SG | AG | AL | PT | GT | ST | SF | AR | EL | HI | UN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Closed-sourced Large Multimodal Models (LMMs) | |||||||||||||
| Zero-shot GPT-4o | 34.7 | 37.7 | 33.3 | 25.8 | 54.9 | 11.8 | 18.8 | 38.4 | 35.6 | 46.2 | 46.0 | 34.3 | 31.1 |
| Zero-shot Claude-3.5 | 35.3 | 22.1 | 26.7 | 18.6 | 62.7 | 23.5 | 27.1 | 53.6 | 24.4 | 42.3 | 49.2 | 33.2 | 33.5 |
| Zero-shot Gemini Pro 1.5 | 26.9 | 28.6 | 20.0 | 19.6 | 39.2 | 5.9 | 22.9 | 35.2 | 15.6 | 30.8 | 41.3 | 26.7 | 21.7 |
| 3-shot CoT GPT-4o | 32.3 | 31.2 | 40.0 | 21.6 | 54.9 | 17.6 | 20.8 | 36.8 | 26.7 | 46.2 | 47.6 | 30.7 | 29.2 |
| 3-shot CoT Claude-3.5 | 32.1 | 27.3 | 26.7 | 11.3 | 54.9 | 0.0 | 10.4 | 56.0 | 31.1 | 30.8 | 39.7 | 32.9 | 28.0 |
| 3-shot CoT Gemini Pro 1.5 | 23.6 | 27.3 | 26.7 | 14.4 | 39.2 | 5.9 | 18.8 | 27.2 | 17.8 | 26.9 | 33.3 | 23.1 | 20.5 |
| Open-sourced Vision Language Models (VLMs) | |||||||||||||
| Qwen2-VL-72B | 28.3 | 27.3 | 33.3 | 15.5 | 31.4 | 0.0 | 16.7 | 43.2 | 26.7 | 42.3 | 41.3 | 30.3 | 19.9 |
| Qwen2-VL-7B | 13.8 | 22.1 | 6.7 | 7.2 | 13.7 | 0.0 | 12.5 | 16.8 | 11.1 | 19.2 | 25.4 | 12.3 | 11.8 |
| InternVL2-76B | 24.6 | 24.7 | 20.0 | 15.5 | 37.3 | 5.9 | 12.5 | 32.8 | 20.0 | 38.5 | 39.7 | 23.1 | 21.1 |
| InternVL2-40B | 14.2 | 14.3 | 6.7 | 9.3 | 13.7 | 0.0 | 10.4 | 21.6 | 13.3 | 19.2 | 28.6 | 14.1 | 8.7 |
| InternVL2-26B | 14.4 | 19.5 | 0.0 | 6.2 | 9.8 | 0.0 | 18.8 | 20.0 | 11.1 | 26.9 | 34.9 | 12.3 | 9.9 |
| InternVL2-8B | 10.4 | 13.0 | 20.0 | 5.2 | 15.7 | 0.0 | 10.4 | 9.6 | 11.1 | 15.4 | 23.8 | 9.4 | 6.8 |
| Llama-3.2-90B | 13.0 | 22.1 | 20.0 | 7.2 | 7.8 | 0.0 | 12.5 | 16.8 | 13.3 | 3.8 | 15.9 | 14.1 | 9.9 |
| Deepseek-VL-7B-chat | 4.2 | 7.8 | 0.0 | 3.1 | 0.0 | 0.0 | 10.4 | 4.0 | 2.2 | 3.8 | 7.9 | 2.9 | 5.0 |
| Llava-v1.6-34B | 6.0 | 10.4 | 13.3 | 4.1 | 2.0 | 0.0 | 4.2 | 6.4 | 6.7 | 7.7 | 15.9 | 5.1 | 3.7 |
| Llava-v1.6-vicuna-13B | 2.8 | 7.8 | 0.0 | 4.1 | 0.0 | 0.0 | 2.1 | 2.4 | 0.0 | 0.0 | 6.3 | 2.9 | 1.2 |
| Llava-v1.5-7B | 1.8 | 3.9 | 0.0 | 2.1 | 0.0 | 0.0 | 4.2 | 0.8 | 0.0 | 3.8 | 3.2 | 1.8 | 1.2 |
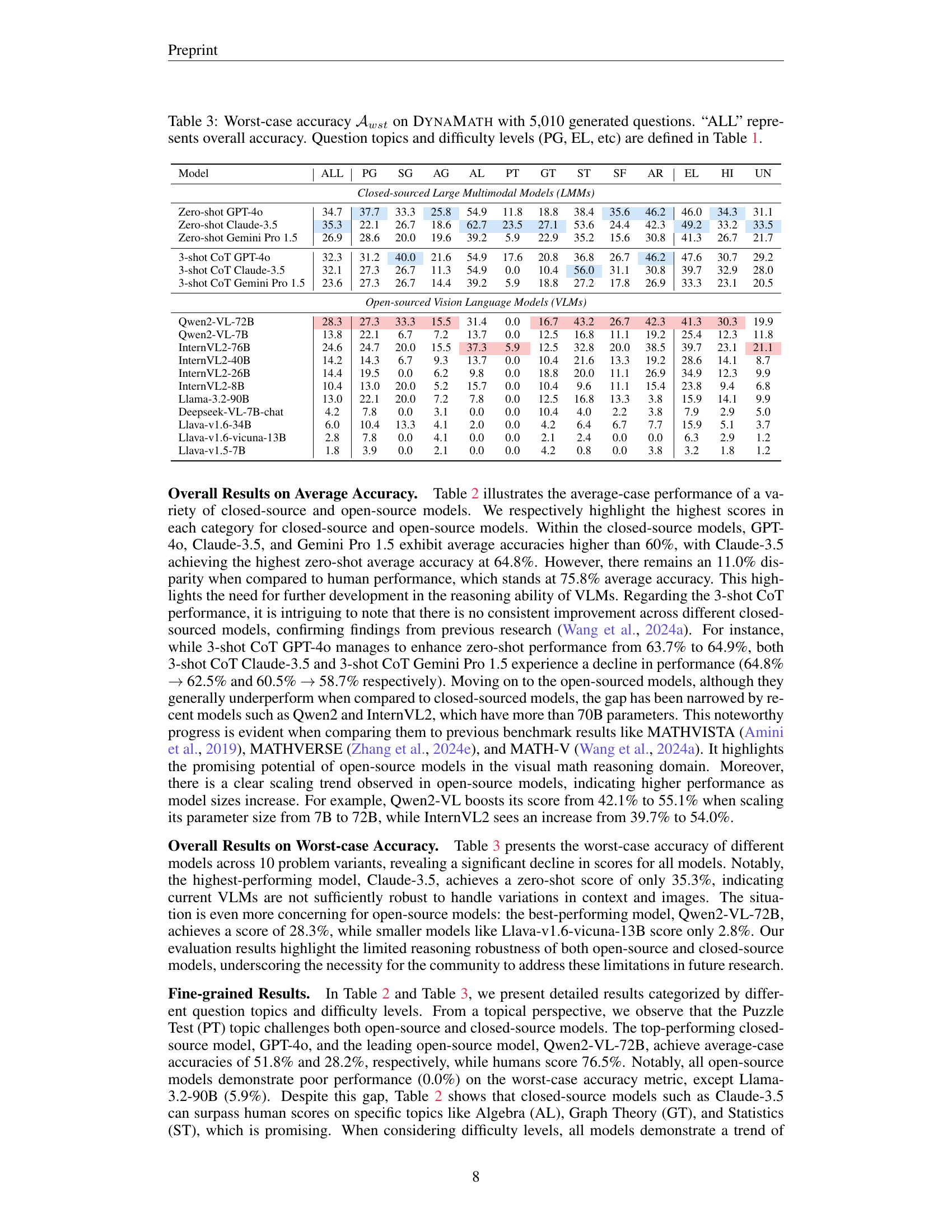
🔼 Table 3 presents the worst-case accuracy (the lowest accuracy across 10 variations of each question) of various vision-language models (VLMs) on the DynaMath benchmark. It shows the performance of each model on different mathematical question types and difficulty levels (Elementary, High School, Undergraduate) as well as an overall worst-case accuracy. The table helps assess how robust each model is to variations in question presentation, emphasizing its ability to generalize. The question types and difficulty levels are defined in Table 1 of the paper.
read the caption
Table 3: Worst-case accuracy 𝒜wstsubscript𝒜𝑤𝑠𝑡\mathcal{A}_{wst}caligraphic_A start_POSTSUBSCRIPT italic_w italic_s italic_t end_POSTSUBSCRIPT on DynaMath with 5,010 generated questions. “ALL” represents overall accuracy. Question topics and difficulty levels (PG, EL, etc) are defined in Table 1.
| Model name | GPT-4o | Gemini | Qwen2-72B | InternVL2-76B |
|---|---|---|---|---|
| Repetition Consistency (%) | 94.1 | 92.5 | 98.9 | 99.0 |
🔼 This table presents the repetition consistency (RC) scores for various vision-language models. Repetition consistency measures the consistency of a model’s responses to the same question across multiple repetitions. A higher RC indicates greater confidence and less inherent randomness in the model’s answers. The results are calculated from 5 repetitions for each question in the dataset. The table helps assess the reliability of each model, identifying those that provide consistent answers even when facing the same prompt multiple times.
read the caption
Table 4: The Repetition Consistency (RC𝑅𝐶RCitalic_R italic_C) for different models over 5 repetitions.
| Answer type | prompt |
|---|---|
| multiple choice | If the problem is a multiple choice problem, just provide the corresponing choice option, such as ’A’, ’B’, ’C’, or ’D’. |
| float | If the answer is a numerical value, format it as a three-digit floating-point number. |
| text | Please answer the question in the following form: (specific requirement in question). |
🔼 This table presents the different prompts used for generating answers based on the question type. The prompt engineering approach is tailored to guide the model to produce responses in specific formats, depending on whether the question is multiple-choice, requires a numerical (floating-point) answer, or needs a text-based response. This ensures consistency and facilitates accurate evaluation of the model’s performance.
read the caption
Table 5: The prompt for different questions and answer types in answer generation.
| Model | Hyperparameters |
|---|---|
| GPT-4o | model = gpt-4o-0806, temperature = 0.0, max_tokens = 4096 |
| Claude-3.5 | model = claude-3-5-sonnet-20240620, temperature = 0.0, max_tokens = 8192 |
| Gemini Pro 1.5 | model = gemini-1.5-pro, temperature = 0.0, max_tokens = 8192 |
| Qwen2-VL-72B | model = Qwen/Qwen2-VL-72B-Instruct, temperature = 0.0, max_tokens = 2048 |
| QWen2-VL-7B | model = Qwen/Qwen2-VL-7B-Instruct, temperature = 0.0, max_tokens = 2048 |
| InternVL2-76B | model = OpenGVLab/InternVL2-Llama3-76B, temperature = 0.0, max_tokens = 2048 |
| InternVL2-40B | model = OpenGVLab/InternVL2-40B, temperature = 0.0, max_tokens = 2048 |
| InternVL2-26B | model = OpenGVLab/InternVL2-26B, temperature = 0.0, max_tokens = 2048 |
| InternVL2-8B | model = OpenGVLab/InternVL2-8B, temperature = 0.0, max_tokens = 2048 |
| Deepseek-VL-7B-chat | model = deepseek-ai/deepseek-vl-7b-chat, temperature = 0.0, max_tokens = 2048 |
| Llama-3.2-90B | model = meta-llama/Llama-3.2-90B-Vision-Instruct, temperature = 0.0, max_tokens = 2048 |
| Llava-v1.6-34B | model = liuhaotian/llava-v1.6-34b, temperature = 0.0, max_tokens = 2048 |
| Llava-v1.6-vicuna-13B | model = liuhaotian/llava-v1.6-vicuna-13b, temperature = 0.0, max_tokens = 2048 |
| Llava-v1.5-7B | model = liuhaotian/llava-v1.5-7b, temperature = 0.0, max_tokens = 2048 |
🔼 This table lists the hyperparameters used for different Vision-Language Models (VLMs) during the experiments in the paper. For each model, it specifies the model name, the specific model version used (e.g., model size), the temperature setting, which controls the randomness of the model’s outputs, and the maximum number of tokens allowed in the model’s response.
read the caption
Table 6: Hyperparameters for various VLMs.
Full paper#