↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large diffusion models, while effective for generating high-quality images, suffer from high memory usage and slow inference speeds, limiting their deployment. Quantizing model parameters to 4-bits is a promising solution for efficiency, but it introduces significant challenges due to the sensitivity of weights and activations to such aggressive quantization.
SVDQuant tackles this issue with a novel approach. It leverages low-rank decomposition to absorb outliers in weights and activations, easing the burden on quantization. Further, it uses a co-designed inference engine called Nunchaku to fuse kernels and optimize memory access, dramatically increasing speed without sacrificing image quality. Experiments demonstrate the effectiveness of SVDQuant, showing significant memory reduction (3.5x) and latency improvement (3x) compared to state-of-the-art methods on various diffusion models. The open-sourced nature of the accompanying library and engine makes SVDQuant readily accessible for wider adoption.
Key Takeaways#
Why does it matter?#
This paper is important because it presents SVDQuant, a novel technique that significantly improves the efficiency of 4-bit diffusion models. This addresses a critical challenge in deploying these models, as they require significant memory and computational resources. The results demonstrate substantial speedup and memory reduction, opening avenues for wider deployment of these powerful generative models on resource-constrained devices. The open-source nature of the project further enhances its impact on the AI community.
Visual Insights#

🔼 Figure 1 showcases the effectiveness of SVDQuant, a post-training quantization method for 4-bit weights and activations in diffusion models. The figure presents a comparison of SVDQuant’s performance against other quantization techniques and the original 16-bit model across various metrics. Specifically, it highlights SVDQuant’s ability to maintain visual fidelity while achieving significant memory reduction (3.6x on the 12B FLUX.1-dev model) and speed improvements (8.7x speedup on a 16GB laptop with a 4090 GPU, and 3x faster than the NF4 W4A16 baseline). The results for PixArt-Σ demonstrate that SVDQuant yields superior visual quality compared to other 4-bit (W4A4 and W4A8) baselines. The end-to-end (E2E) latency includes the time taken by the text encoder and VAE decoder.
read the caption
Figure 1: SVDQuant is a post-training quantization technique for 4-bit weights and activations that well maintains visual fidelity. On 12B FLUX.1-dev, it achieves 3.6× memory reduction compared to the BF16 model. By eliminating CPU offloading, it offers 8.7× speedup over the 16-bit model when on a 16GB laptop 4090 GPU, 3× faster than the NF4 W4A16 baseline. On PixArt-ΣΣ\Sigmaroman_Σ, it demonstrates significantly superior visual quality over other W4A4 or even W4A8 baselines. “E2E” means the end-to-end latency including the text encoder and VAE decoder.
| MJHQ | sDCI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Backbone | Model | Precision | Method | Quality (FID ↓) | Similarity (IR ↑) | Quality (LPIPS ↓) | Similarity (PSNR ↑) | Quality (FID ↓) | Similarity (IR ↑) | Quality (LPIPS ↓) |
| — | — | — | — | — | — | — | — | — | — | — |
| FLUX.1-dev (50 Steps) | BF16 | – | 20.3 | 0.953 | – | – | 24.8 | 1.02 | – | – |
| INT W8A8 | Ours | 20.4 | 0.948 | 0.089 | 27.0 | 24.7 | 1.02 | 0.106 | 24.9 | |
| W4A16 | NF4 | 20.6 | 0.910 | 0.272 | 19.5 | 24.9 | 0.986 | 0.292 | 18.2 | |
| INT W4A4 | Ours | 19.9 | 0.932 | 0.254 | 20.1 | 24.7 | 0.992 | 0.273 | 18.8 | |
| FP W4A4 | Ours | 21.0 | 0.933 | 0.247 | 20.2 | 25.7 | 0.995 | 0.267 | 18.7 | |
| FLUX.1-schnell (4 Steps) | BF16 | – | 19.2 | 0.938 | – | – | 20.8 | 0.932 | – | – |
| INT W8A8 | Ours | 19.2 | 0.966 | 0.120 | 22.9 | 20.7 | 0.975 | 0.133 | 21.3 | |
| DiT | W4A16 | NF4 | 18.9 | 0.943 | 0.257 | 18.2 | 20.7 | 0.953 | 0.263 | 17.1 |
| INT W4A4 | Ours | 18.4 | 0.969 | 0.292 | 17.5 | 20.1 | 0.988 | 0.299 | 16.3 | |
| FP W4A4 | Ours | 19.9 | 0.956 | 0.279 | 17.5 | 21.5 | 0.967 | 0.278 | 16.6 | |
| PixArt-Σ (20 Steps) | FP16 | – | 16.6 | 0.944 | – | – | 24.8 | 0.966 | ||
| INT W8A8 | ViDiT-Q | 15.7 | 0.944 | 0.137 | 22.5 | 23.5 | 0.974 | 0.163 | 20.4 | |
| INT W8A8 | Ours | 16.3 | 0.955 | 0.109 | 23.7 | 24.2 | 0.969 | 0.129 | 21.8 | |
| INT W4A8 | ViDiT-Q | 37.3 | 0.573 | 0.611 | 12.0 | 40.6 | 0.600 | 0.629 | 11.2 | |
| INT W4A4 | ViDiT-Q | 412 | -2.27 | 0.854 | 6.44 | 425 | -2.28 | 0.838 | 6.70 | |
| INT W4A4 | Ours | 20.1 | 0.898 | 0.394 | 16.2 | 25.1 | 0.922 | 0.434 | 14.9 | |
| FP W4A4 | Ours | 18.3 | 0.946 | 0.326 | 17.4 | 23.7 | 0.978 | 0.357 | 16.1 | |
| UNet | SDXL-Turbo (4 Steps) | FP16 | – | 24.3 | 0.845 | – | – | 24.7 | 0.705 | – |
| INT W8A8 | MixDQ | 24.1 | 0.834 | 0.147 | 21.7 | 25.0 | 0.690 | 0.157 | 21.6 | |
| INT W8A8 | Ours | 24.3 | 0.845 | 0.100 | 24.0 | 24.8 | 0.701 | 0.110 | 23.7 | |
| INT W4A8 | MixDQ | 27.7 | 0.708 | 0.402 | 15.7 | 25.9 | 0.610 | 0.415 | 15.7 | |
| INT W4A4 | MixDQ | 353 | -2.26 | 0.685 | 11.0 | 373 | -2.28 | 0.686 | 11.3 | |
| INT W4A4 | Ours | 24.5 | 0.816 | 0.265 | 17.9 | 25.7 | 0.667 | 0.278 | 17.8 | |
| FP W4A4 | Ours | 24.1 | 0.822 | 0.250 | 18.5 | 24.7 | 0.699 | 0.261 | 18.4 | |
| SDXL (30 Steps) | FP16 | – | 16.6 | 0.729 | – | – | 22.5 | 0.573 | – | – |
| INT W8A8 | TensorRT | 20.2 | 0.591 | 0.247 | 22.0 | 25.4 | 0.453 | 0.265 | 21.7 | |
| INT W8A8 | Ours | 16.6 | 0.718 | 0.119 | 26.4 | 22.4 | 0.574 | 0.129 | 25.9 | |
| INT W4A4 | Ours | 20.7 | 0.609 | 0.298 | 20.6 | 26.3 | 0.494 | 0.314 | 20.4 | |
| FP W4A4 | Ours | 19.0 | 0.607 | 0.294 | 21.0 | 25.4 | 0.480 | 0.312 | 20.7 |
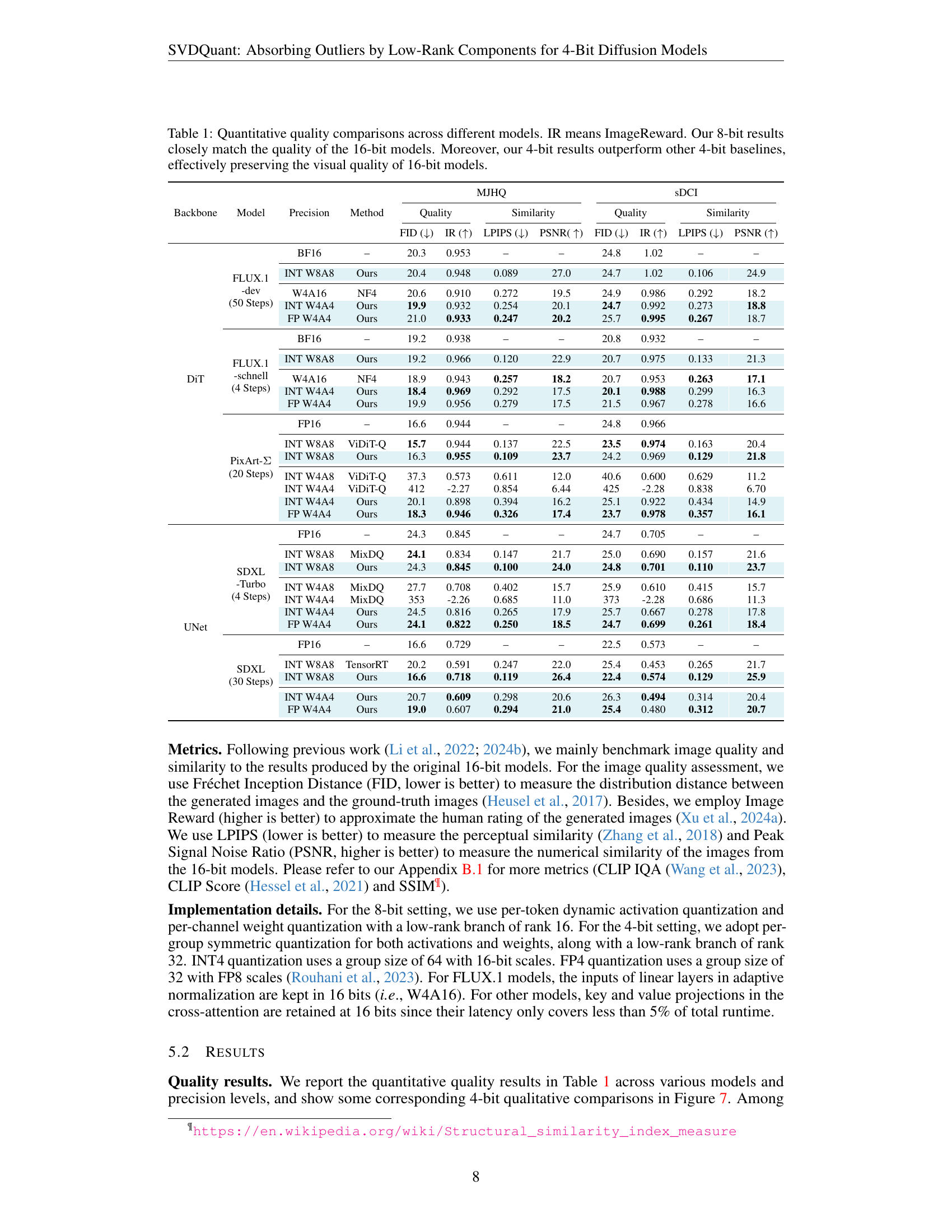
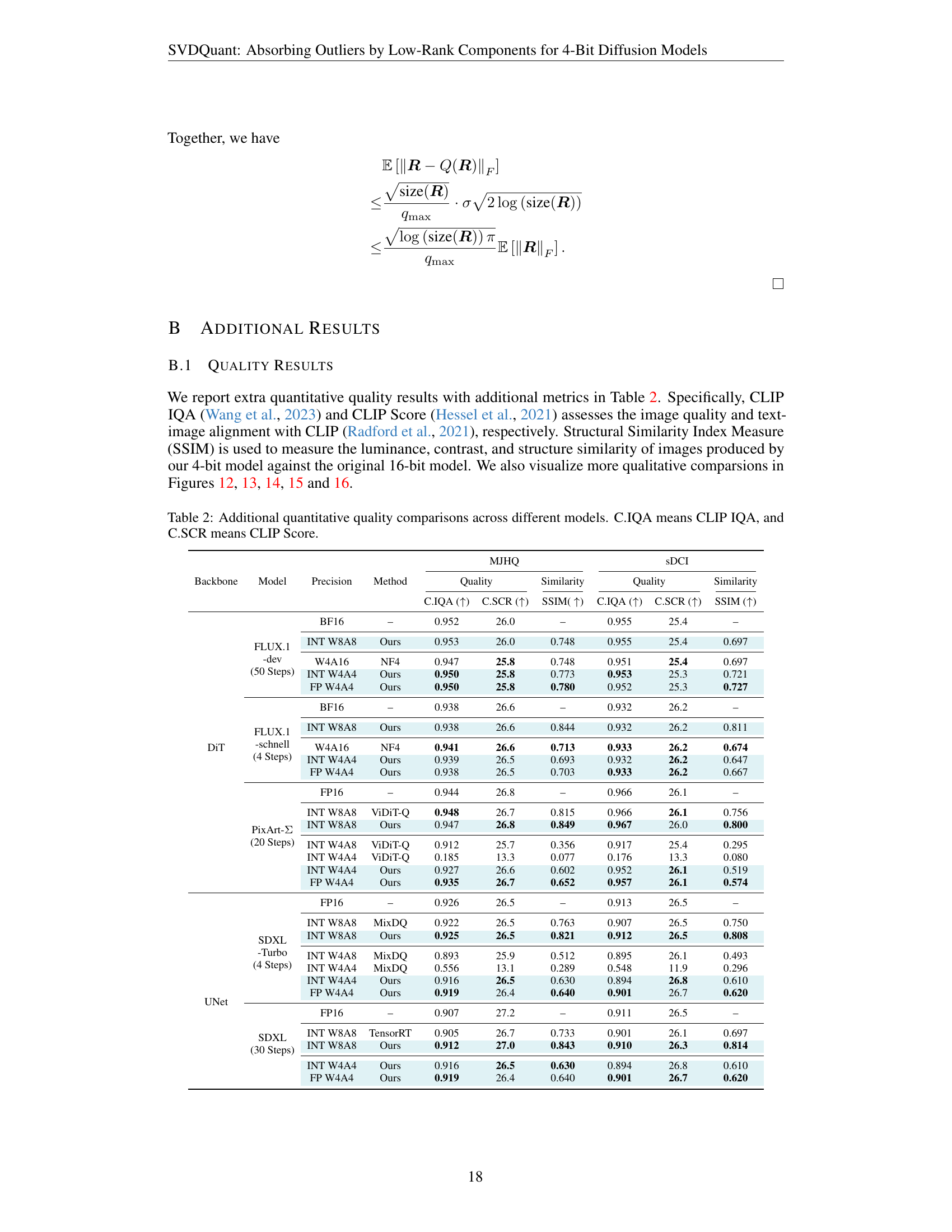
🔼 This table presents a quantitative comparison of image quality across various diffusion models and different bit-depths (8-bit and 4-bit) of weight and activation quantization. It uses several metrics, including FID (Fréchet Inception Distance), IR (ImageReward), LPIPS (Learned Perceptual Image Patch Similarity), and PSNR (Peak Signal-to-Noise Ratio), to assess the visual quality of the generated images. The results demonstrate that the 8-bit quantized models achieve similar image quality to the original 16-bit models. Furthermore, the 4-bit quantized models using the proposed SVDQuant method significantly outperform other existing 4-bit quantization baselines, indicating that SVDQuant effectively preserves image quality even at a very aggressive quantization level.
read the caption
Table 1: Quantitative quality comparisons across different models. IR means ImageReward. Our 8-bit results closely match the quality of the 16-bit models. Moreover, our 4-bit results outperform other 4-bit baselines, effectively preserving the visual quality of 16-bit models.
In-depth insights#
4-bit Diffusion#
The concept of “4-bit Diffusion” in the context of generative AI models signifies a significant advancement in model efficiency. By quantizing both weights and activations to 4 bits, the approach drastically reduces the memory footprint and computational demands of large diffusion models. This is crucial for deploying these models on resource-constrained devices like PCs or mobile platforms. The core challenge lies in maintaining high-quality image generation despite the significant reduction in numerical precision. The paper likely explores various techniques to overcome this, such as novel quantization methods (potentially leveraging low-rank decompositions to absorb outliers that would otherwise cause significant distortion). The results would showcase a compelling trade-off between model size, inference speed, and generated image fidelity. Successful implementation would represent a remarkable step towards making advanced generative AI more accessible and practical for wider use cases.
SVDQuant Method#
The SVDQuant method introduces a novel 4-bit quantization paradigm for diffusion models, addressing the limitations of existing techniques when applied to such aggressive quantization levels. The core innovation lies in absorbing outliers, which are values significantly deviating from the norm, using a low-rank branch. This branch processes a subset of weights and activations with higher precision (16-bit), thereby mitigating the negative effects of quantization on visual quality. This outlier migration strategy involves intelligently shifting outliers from activations to weights via smoothing, making the activations easier to quantize with less information loss. The low-rank decomposition, done via SVD (Singular Value Decomposition), further reduces computational cost and enhances image quality. Crucially, the method co-designs an inference engine, Nunchaku, which fuses the kernels of the low-rank branch into the low-bit branch, thereby eliminating redundant memory access and avoiding performance degradation from extra data movement. This fusion is critical for achieving speedup rather than simply trading memory for speed. Overall, SVDQuant effectively balances quality preservation with reduced memory and computational cost, demonstrating a promising solution for deploying high-quality diffusion models on resource-constrained devices.
Nunchaku Engine#
The Nunchaku engine, as described in the context of the research paper, is a crucial component designed to address the computational overhead introduced by the low-rank branch within the SVDQuant framework. The low-rank branch, while improving the accuracy of 4-bit quantization, can significantly increase latency if implemented naively. Nunchaku’s key innovation lies in its fusion of kernels, integrating the computations of the low-rank branch into the 4-bit branch. This clever co-design minimizes redundant memory access, a major source of slowdown in the low-rank branch. By fusing the kernels, Nunchaku dramatically cuts down on the extra data movement, reducing the computational burden associated with the low-rank branch. This results in a significant speed-up, effectively mitigating the performance penalty of the low-rank operation, and making the 4-bit quantization with SVDQuant significantly faster. The seamless integration of the low-rank adapters (LoRA) highlights its adaptability and broad applicability, improving the efficiency of diffusion models while maintaining image quality. This design is particularly effective for models where the activation data doesn’t entirely fit within the GPU cache, a common scenario impacting performance.
Ablation Study#
An ablation study systematically removes components of a model to understand their individual contributions. In the context of a 4-bit diffusion model, this would involve removing elements like the low-rank branch, smoothing techniques, or the specialized inference engine (Nunchaku) one at a time. By comparing the performance of the model with and without each component, researchers can determine the effectiveness of each part in maintaining image quality and speed. A key insight would be whether the low-rank branch effectively absorbs quantization outliers, improving performance compared to simpler strategies like smoothing alone. The ablation study should also demonstrate the importance of Nunchaku in mitigating the computational overhead that could otherwise negate the benefits of the low-rank approach. The results likely show a gradual decrease in performance as essential components are removed, highlighting the synergy between these techniques in achieving efficient and high-quality 4-bit diffusion model inference.
Future Works#
Future work could explore extending SVDQuant’s applicability to other model architectures and modalities beyond image generation, such as video or 3D models. Investigating the impact of different low-rank decomposition methods beyond SVD, like randomized SVD or CUR decomposition, could further optimize performance and efficiency. A more in-depth analysis of the interaction between quantization and low-rank approximation is needed to better understand how these techniques affect outlier distribution and model accuracy. The Nunchaku inference engine could also be improved through architectural optimizations, such as exploring different fusion strategies or hardware-specific optimizations for various platforms. Finally, research on adaptive rank selection for SVDQuant, determining the optimal rank based on the model and task, could significantly improve both the speedup and image quality.
More visual insights#
More on figures

🔼 This figure illustrates the relationship between computational cost and model size for both Large Language Models (LLMs) and diffusion models. For LLMs, the computation is measured using a context length of 512 tokens and generating 256 output tokens. In contrast, for diffusion models, the computation is calculated for a single step in the generation process. The graph visually represents the rapid increase in computational cost as the model size (measured in billions of parameters) grows. The dashed lines indicate trends, offering insights into the scaling characteristics of these two model types. This helps to visualize the significantly higher computational intensity of diffusion models compared to LLMs of similar parameter counts.
read the caption
Figure 2: Computation vs. parameters for LLMs and diffusion models. LLMs’ computation is measured with 512 context and 256 output tokens, and diffusion models’ computation is for a single step. Dashed lines show trends.

🔼 Figure 3 illustrates the core idea of SVDQuant, a novel 4-bit quantization method for diffusion models. It addresses the challenge of quantizing both activations and weights to 4 bits, which usually leads to significant quality degradation. The figure shows three steps: (a) The initial state, where both activations (X) and weights (W) have outliers, making direct 4-bit quantization difficult. (b) A smoothing technique is applied to shift outliers from activations to weights. This makes the activations easier to quantize, but creates more severe outliers in the weights. (c) SVDQuant decomposes the outlier-rich weights into a low-rank component (L1L2) and a residual. The low-rank component is processed in higher precision (16-bit), while the residual is quantized to 4 bits. This approach significantly reduces quantization errors and maintains image quality.
read the caption
Figure 3: Overview of SVDQuant. (a) Originally, both the activation 𝑿𝑿{\bm{X}}bold_italic_X and weight 𝑾𝑾{\bm{W}}bold_italic_W contain outliers, making 4-bit quantization challenging. (b) We migrate the outliers from the activation to weight, resulting in the updated activation 𝑿^^𝑿\hat{{\bm{X}}}over^ start_ARG bold_italic_X end_ARG and weight 𝑾^^𝑾\hat{{\bm{W}}}over^ start_ARG bold_italic_W end_ARG. While 𝑿^^𝑿\hat{{\bm{X}}}over^ start_ARG bold_italic_X end_ARG becomes easier to quantize, 𝑾^^𝑾\hat{{\bm{W}}}over^ start_ARG bold_italic_W end_ARG now becomes more difficult. (c) SVDQuant further decomposes 𝑾^^𝑾\hat{{\bm{W}}}over^ start_ARG bold_italic_W end_ARG into a low-rank component 𝑳1𝑳2subscript𝑳1subscript𝑳2{\bm{L}}_{1}{\bm{L}}_{2}bold_italic_L start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT bold_italic_L start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT and a residual 𝑾^−𝑳1𝑳2^𝑾subscript𝑳1subscript𝑳2\hat{{\bm{W}}}-{\bm{L}}_{1}{\bm{L}}_{2}over^ start_ARG bold_italic_W end_ARG - bold_italic_L start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT bold_italic_L start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT with SVD. Thus, the quantization difficulty is alleviated by the low-rank branch, which runs at 16-bit precision.

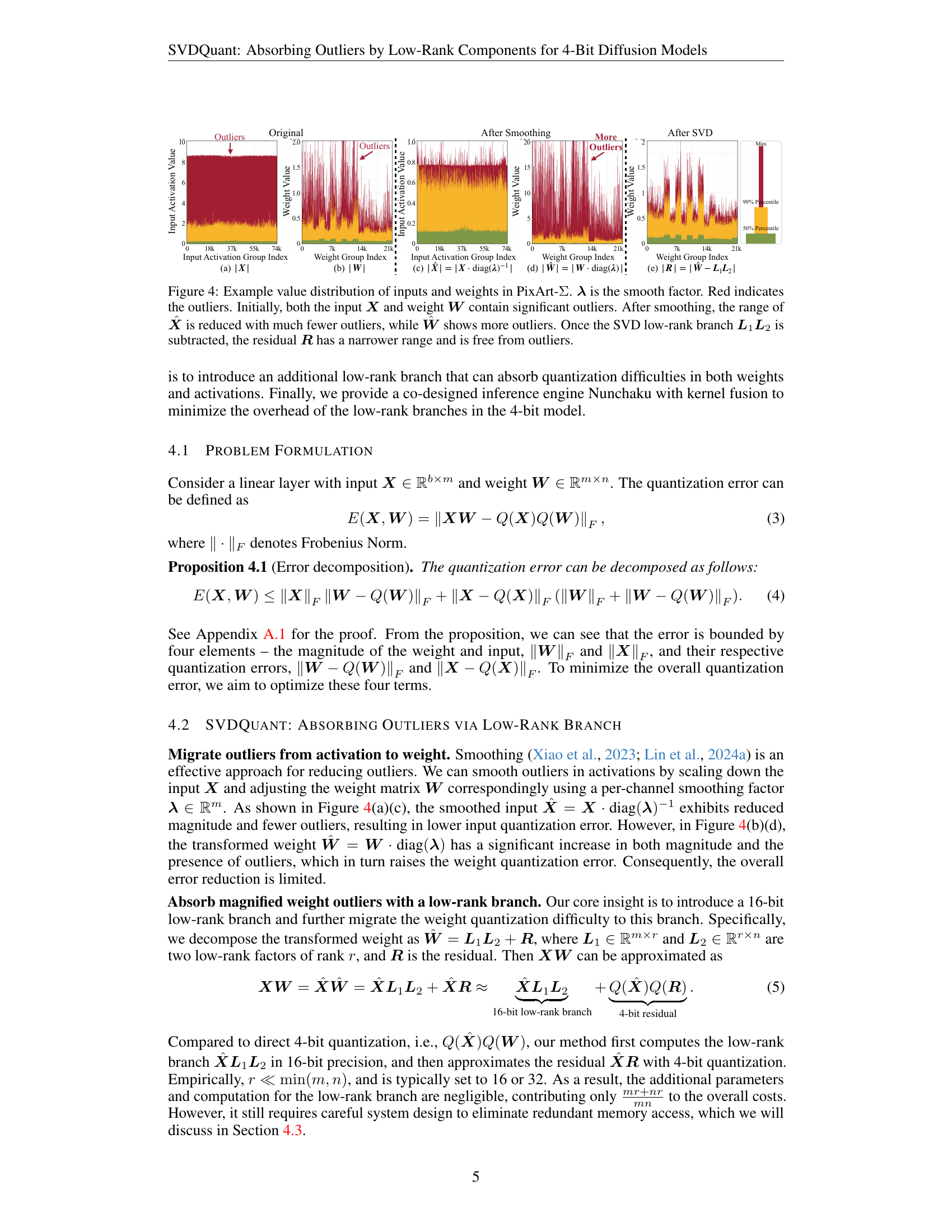
🔼 Figure 4 illustrates the effects of SVDQuant’s outlier mitigation process on the weight and activation tensors of the PixArt-Σ model. The figure shows histograms visualizing the distribution of values in the input activation tensor (X), weight tensor (W), and the tensors after applying smoothing (X^, W^) and SVD decomposition (R). Initially, both X and W have significant outliers (represented in red). Smoothing shifts outliers from the activations to the weights, reducing the range of values in X^ but increasing the range and outliers in W^. Finally, the SVD low-rank branch separates the outliers into a low-rank component (L1L2), leaving the residual (R) with a significantly reduced range and no outliers, making it easier to quantize using 4-bit precision.
read the caption
Figure 4: Example value distribution of inputs and weights in PixArt-ΣΣ\Sigmaroman_Σ. 𝝀𝝀{\bm{\lambda}}bold_italic_λ is the smooth factor. Red indicates the outliers. Initially, both the input 𝑿𝑿{\bm{X}}bold_italic_X and weight 𝑾𝑾{\bm{W}}bold_italic_W contain significant outliers. After smoothing, the range of 𝑿^^𝑿\hat{{\bm{X}}}over^ start_ARG bold_italic_X end_ARG is reduced with much fewer outliers, while 𝑾^^𝑾\hat{{\bm{W}}}over^ start_ARG bold_italic_W end_ARG shows more outliers. Once the SVD low-rank branch 𝑳1𝑳2subscript𝑳1subscript𝑳2{\bm{L}}_{1}{\bm{L}}_{2}bold_italic_L start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT bold_italic_L start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT is subtracted, the residual 𝑹𝑹{\bm{R}}bold_italic_R has a narrower range and is free from outliers.

🔼 Figure 5 illustrates the distribution of the first 64 singular values obtained through Singular Value Decomposition (SVD) for three different weight matrices: the original weight matrix 𝑾 (bold_italic_W), the transformed weight matrix 𝑾̂ (over^ start_ARG bold_italic_W end_ARG), and the residual matrix 𝑹 (bold_italic_R). The plot shows that the transformed weight matrix 𝑾̂ (over^ start_ARG bold_italic_W end_ARG) has a significantly different distribution than the original weight matrix 𝑾 (bold_italic_W). Specifically, the transformed weight matrix has a steeper drop-off in its singular values, where the first 32 values are much larger than the others. The residual matrix 𝑹 (bold_italic_R), on the other hand, exhibits a much more gradual decrease in singular values. This visual representation highlights the effectiveness of the SVD in separating the dominant components from the less significant ones, which forms the basis for the low-rank branch used in the SVDQuant method. The figure directly supports the method’s claim of mitigating outlier effects and reducing the magnitude of values requiring quantization.
read the caption
Figure 5: First 64 singular values of 𝑾𝑾{\bm{W}}bold_italic_W, 𝑾^^𝑾\hat{{\bm{W}}}over^ start_ARG bold_italic_W end_ARG, and 𝑹𝑹{\bm{R}}bold_italic_R. The first 32 singular values of 𝑾^^𝑾\hat{{\bm{W}}}over^ start_ARG bold_italic_W end_ARG exhibit a steep drop, while the remaining values are much more gradual.

🔼 Figure 6 illustrates the performance optimization achieved by Nunchaku, the co-designed inference engine. (a) shows that a naive implementation of the low-rank branch (rank 32) incurs a significant 57% latency overhead due to redundant memory access for both input and output data. Nunchaku addresses this by fusing kernels. (b) details Nunchaku’s kernel fusion strategy: it merges the Down Projection and Quantization kernels because they share the same input data and merges the Up Projection and 4-bit compute kernels as they share the same output data. This fusion significantly reduces data movement and improves efficiency.
read the caption
Figure 6: (a) Naïvely running low-rank branch with rank 32 will introduce 57% latency overhead due to extra read of 16-bit inputs in Down Projection and extra write of 16-bit outputs in Up Projection. Our Nunchaku engine optimizes this overhead with kernel fusion. (b) Down Projection and Quantize kernels use the same input, while Up Projection and 4-Bit Compute kernels share the same output. To reduce data movement overhead, we fuse the first two and the latter two kernels together.

🔼 Figure 7 presents a qualitative comparison of image generation results across different models and quantization methods using the MJHQ dataset. The ‘Image Reward’ metric, calculated across the entire dataset, quantifies the overall quality. For the FLUX.1 model, the 4-bit models (using SVDQuant) outperformed the NF4 W4A16 baseline, showing better text alignment and higher similarity to the 16-bit results. A notable example is the NF4 model’s misinterpretation of the prompt ‘dinosaur style,’ which resulted in an image of a real dinosaur rather than a stylized one. In PixArt-Σ and SDXL-Turbo, the 4-bit models from this work also yielded noticeably better visual quality compared to other state-of-the-art 4-bit methods (ViDiT-Q and MixDQ).
read the caption
Figure 7: Qualitative visual results on MJHQ. Image Reward is calculated over the entire dataset. On FLUX.1 models, our 4-bit models outperform the NF4 W4A16 baselines, demonstrating superior text alignment and closer similarity to the 16-bit models. For instance, NF4 misinterprets “dinosaur style,” generating a real dinosaur. On PixArt-ΣΣ\Sigmaroman_Σ and SDXL-Turbo, our 4-bit results demonstrate noticeably better visual quality than ViDiT-Q’s and MixDQ’s W4A8 results.

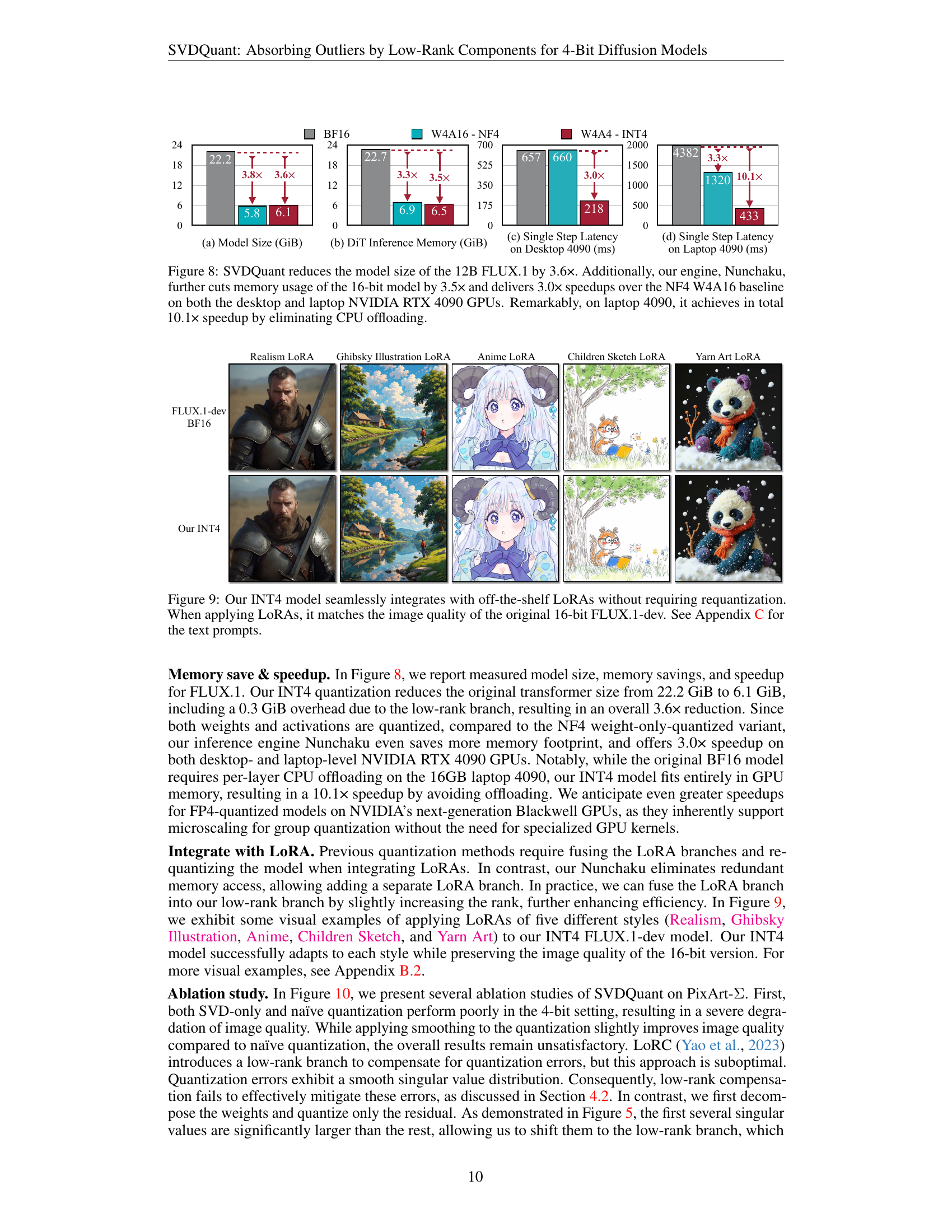
🔼 This figure presents a comparison of model size, memory usage, and inference speed between different quantization methods applied to the 12B parameter FLUX.1 diffusion model. It shows that SVDQuant, combined with the Nunchaku inference engine, significantly reduces the model size (by 3.6x compared to the original 16-bit model), memory usage (by 3.5x), and inference time (by 3.0x on desktop GPU and 10.1x on a laptop GPU). The 10.1x speedup on the laptop is attributed to eliminating the need for CPU offloading, a crucial factor in improving the performance of large models on resource-constrained hardware.
read the caption
Figure 8: SVDQuant reduces the model size of the 12B FLUX.1 by 3.6×. Additionally, our engine, Nunchaku, further cuts memory usage of the 16-bit model by 3.5× and delivers 3.0× speedups over the NF4 W4A16 baseline on both the desktop and laptop NVIDIA RTX 4090 GPUs. Remarkably, on laptop 4090, it achieves in total 10.1× speedup by eliminating CPU offloading.

🔼 Figure 9 demonstrates the seamless integration of SVDQuant with off-the-shelf Low-Rank Adapters (LoRAs) without the need for re-quantization. The figure showcases several examples of images generated using the INT4 quantized model with various LoRAs applied. The results show that the INT4 model, even with the LoRAs, maintains the image quality of the original 16-bit FLUX.1-dev model, highlighting the effectiveness of SVDQuant in preserving image quality across different model configurations. Specific prompts used to generate these images can be found in Appendix C.
read the caption
Figure 9: Our INT4 model seamlessly integrates with off-the-shelf LoRAs without requiring requantization. When applying LoRAs, it matches the image quality of the original 16-bit FLUX.1-dev. See Appendix C for the text prompts.

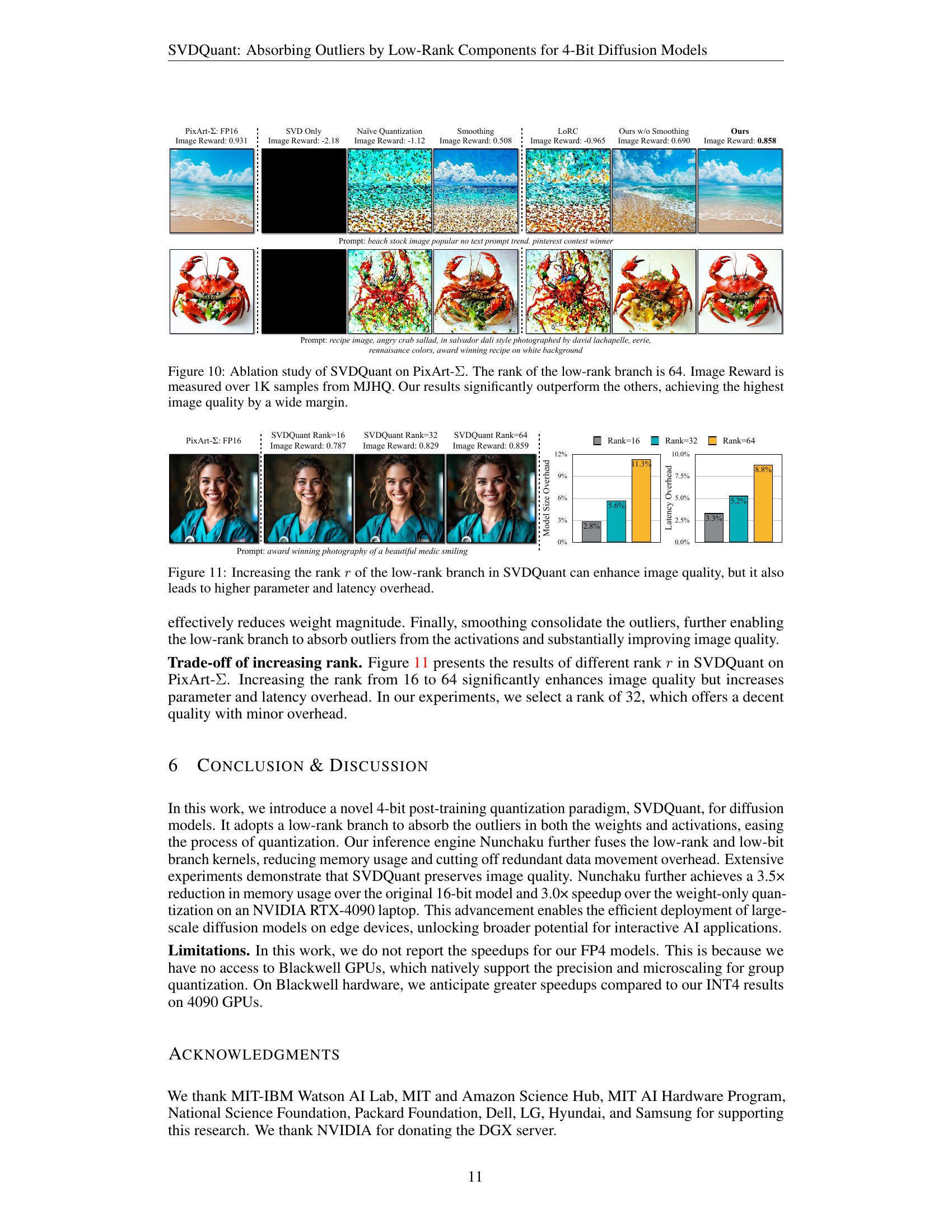
🔼 This ablation study investigates the impact of different quantization methods on the PixArt-Σ image generation model. The experiment uses a low-rank branch with a rank of 64. The performance metric is Image Reward, calculated from 1000 samples of the MJHQ dataset. The results show that SVDQuant significantly outperforms other techniques, such as simple SVD, naïve quantization, smoothing, and LoRC, in terms of image quality. This highlights the effectiveness of SVDQuant’s approach in handling outliers and achieving high-quality results in 4-bit quantization.
read the caption
Figure 10: Ablation study of SVDQuant on PixArt-ΣΣ\Sigmaroman_Σ. The rank of the low-rank branch is 64. Image Reward is measured over 1K samples from MJHQ. Our results significantly outperform the others, achieving the highest image quality by a wide margin.

🔼 This figure shows the trade-off between increasing the rank (r) of the low-rank branch within the SVDQuant model and the resulting impact on image quality, model size, and inference latency. Higher ranks generally lead to better image quality because the low-rank branch can absorb more outliers. However, this improvement comes at the cost of increased model size and latency, making it important to find the optimal balance between image quality and efficiency.
read the caption
Figure 11: Increasing the rank r𝑟ritalic_r of the low-rank branch in SVDQuant can enhance image quality, but it also leads to higher parameter and latency overhead.

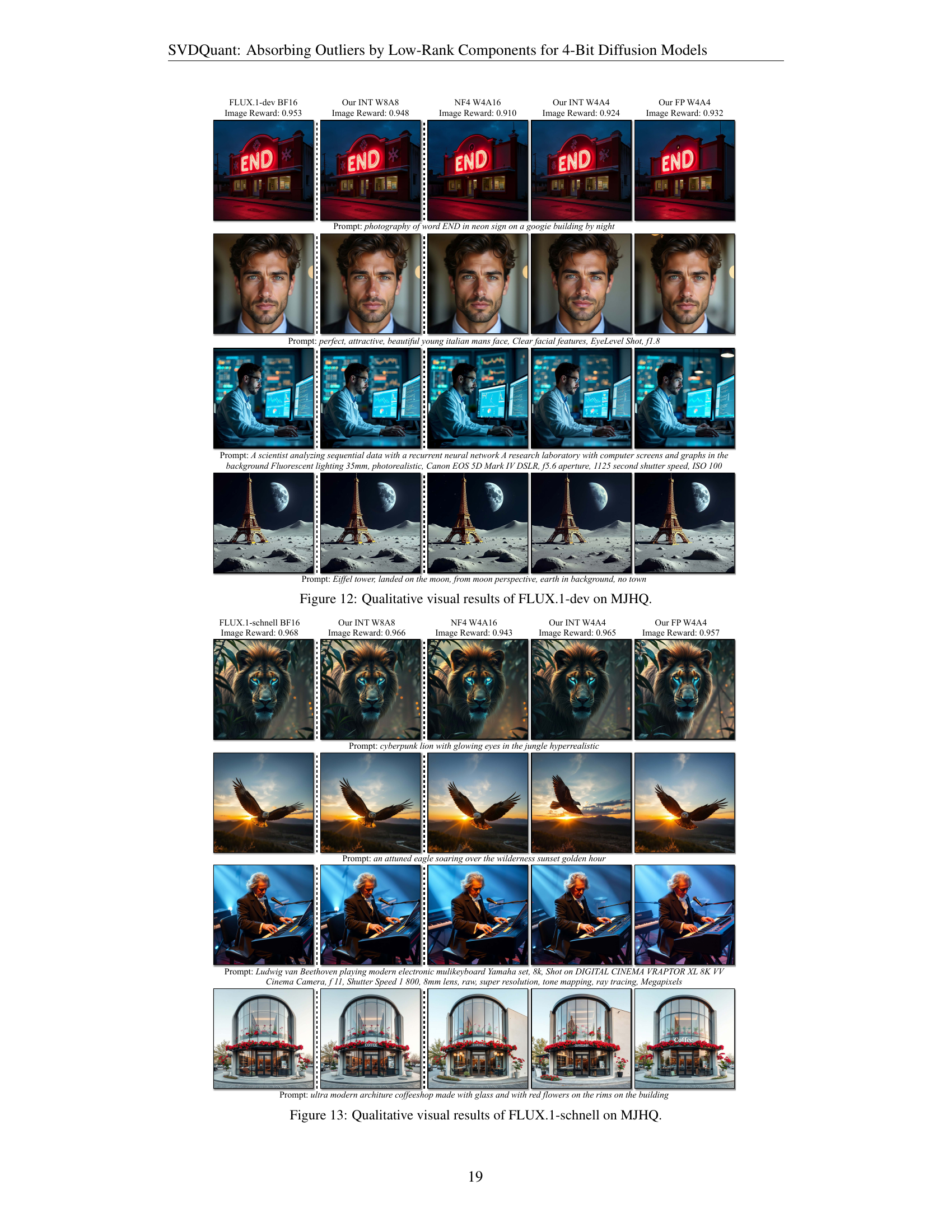
🔼 This figure showcases a qualitative comparison of image generation results from the 12B parameter FLUX.1-dev diffusion model using different quantization methods. Specifically, it visually demonstrates the impact of various methods (BF16, NF4 W4A16, SVDQuant INT4, and SVDQuant FP4) on the visual quality of generated images. Each row displays a prompt and the resulting image generated using each method, allowing for direct visual assessment of the quality differences. The prompts and images are selected from the MJHQ dataset, and the goal is to visually demonstrate how well each quantization method preserves the image quality compared to the original, unquantized model.
read the caption
Figure 12: Qualitative visual results of FLUX.1-dev on MJHQ.

🔼 This figure shows a qualitative comparison of image generation results from different models on the MJHQ dataset. Specifically, it compares the quality of images generated by the original 16-bit FLUX.1-schnell model, a weight-only quantized 4-bit version (NF4 W4A16), and the proposed SVDQuant model at 4-bit precision (INT and FP). The prompts used to generate the images are also displayed. The purpose is to visually demonstrate the effectiveness of the proposed method in maintaining image quality despite significant memory and speed improvements.
read the caption
Figure 13: Qualitative visual results of FLUX.1-schnell on MJHQ.

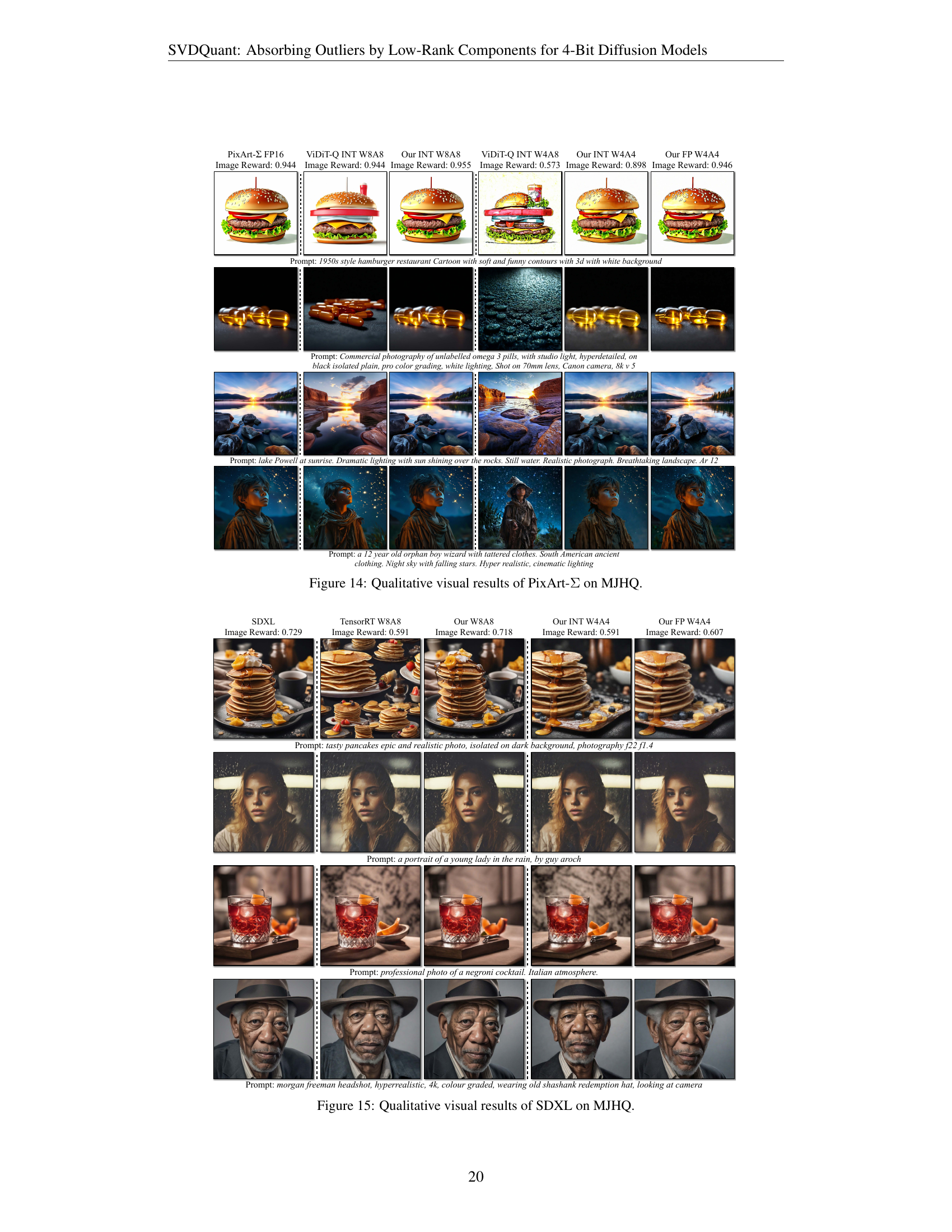
🔼 This figure showcases a qualitative comparison of image generation results using different quantization methods on the PixArt-Σ model. It displays several image prompts and compares the outputs generated using the original FP16 precision model against various 4-bit quantization techniques including ViDiT-Q (INT8 and INT4), and the authors’ SVDQuant method (INT4 and FP4). The goal is to visually demonstrate the effectiveness of SVDQuant in preserving image quality while using significantly reduced precision for weights and activations. The images allow a visual assessment of the fidelity and detail maintained across different quantization methods.
read the caption
Figure 14: Qualitative visual results of PixArt-ΣΣ\Sigmaroman_Σ on MJHQ.

🔼 This figure displays a qualitative comparison of image generation results from the SDXL model using different quantization methods. It showcases several example prompts and their corresponding generated images using the original 16-bit SDXL model and several 4-bit quantized versions, including SVDQuant (ours), TensorRT, and MixDQ. The goal is to visually demonstrate the effectiveness of SVDQuant in maintaining image quality despite aggressive quantization.
read the caption
Figure 15: Qualitative visual results of SDXL on MJHQ.

🔼 This figure displays a qualitative comparison of image generation results from the SDXL-Turbo model (Stable Diffusion XL - Turbo) using different quantization methods on the MJHQ dataset (Midjourney High-Quality dataset). It visually showcases the impact of various 4-bit and 8-bit quantization techniques on the quality of images generated from several prompts. Each row represents a different prompt, and columns show the results for the original FP16 (full precision), the 8-bit quantized versions (MixDQ and SVDQuant), and the 4-bit quantized versions (MixDQ and SVDQuant). The goal is to demonstrate the visual fidelity maintained by the SVDQuant method, even at the aggressive 4-bit quantization level.
read the caption
Figure 16: Qualitative visual results of SDXL-Turbo on MJHQ.

🔼 This figure displays the results of applying five different LoRA (Low-Rank Adaptation) styles to both the original 16-bit FLUX.1-dev model and the INT4 (4-bit integer) quantized version of the model created by SVDQuant. The LoRA styles are Realism, Ghibsky Illustration, Anime, Children’s Sketch, and Yarn Art. The purpose of the figure is to demonstrate that SVDQuant’s 4-bit quantization does not negatively impact image quality when using LoRAs. The visual similarity between the 16-bit and INT4 model outputs across all five LoRA styles supports this conclusion. More detailed text prompts used for image generation are available in Appendix C.
read the caption
Figure 17: Additional LoRA results on FLUX.1-dev. When applying LoRAs, our INT4 model matches the image quality of the original BF16 model. See Appendix C for the detailed used text prompts.
Full paper#