↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large language models (LLMs) show promise in various applications, but their rationality in strategic decision-making, particularly in game-theoretic settings, remains questionable. This paper investigates the rationality of several LLMs in a range of games, revealing frequent deviations from rational strategies, especially in complex scenarios. This unreliability stems from LLMs’ susceptibility to noise and uncertainty, leading to suboptimal choices.
To address these shortcomings, the researchers designed game-theoretic workflows to guide LLM reasoning and decision-making. These workflows incorporate established game theory principles such as Dominant Strategy Search and Backward Induction to enhance the models’ ability to identify optimal strategies. Experiments demonstrated that incorporating these workflows significantly improves LLMs’ rationality and performance in various game-theoretic scenarios. The paper also explores the meta-strategic question of whether LLMs should rationally adopt such workflows, highlighting the complexity and importance of strategic considerations in developing efficient and reliable AI agents.
Key Takeaways#
Why does it matter?#
This paper is crucial for AI researchers because it addresses the limitations of LLMs in strategic decision-making, a significant challenge in developing robust and reliable AI agents. It provides novel game-theoretic workflows that significantly improve LLM rationality, opening avenues for future research in meta-strategies and enhancing AI agent capabilities in complex interactive environments. This research is directly relevant to the rapidly evolving field of multi-agent LLMs and addresses crucial issues of robustness and rationality.
Visual Insights#

🔼 This figure illustrates the various game-theoretic scenarios explored in the paper, categorized by information completeness (complete or incomplete) and game structure (simultaneous or sequential). Each category contains specific games used in the experiments: Complete information games include Prisoner’s Dilemma, Stag Hunt, Battle of the Sexes, Wait-Go Game, Duopolistic Competition, Escalation Game, Monopoly Game, Hot-cold Game, Draco Game, and TriGame. Incomplete information games include Deal or No Deal and a common resource allocation game.
read the caption
Figure 1: Game-theoretic Landscape Investigated in this Paper.
| Cooperate | Defect | |
|---|---|---|
| Cooperate | 3,3 | 0,5 |
| Defect | 5,0 | 1,1 |
🔼 This table lists ten classic complete-information games used in the paper’s experiments to evaluate the rationality of large language models (LLMs) in strategic decision-making. It indicates whether each game requires coordination between players to achieve a Pareto optimal Nash Equilibrium, and categorizes each game as either simultaneous-move or sequential-move.
read the caption
Table 1: Landscape of classic complete-information games for analysis
In-depth insights#
LLM Rationality#
The study delves into the rationality of Large Language Models (LLMs) in strategic decision-making, particularly within game-theoretic frameworks. LLMs frequently deviate from rational strategies, especially in complex games. This irrationality is evident in scenarios with extensive payoff matrices or deep decision trees. The research explores game-theoretic workflows designed to enhance LLMs’ ability to compute Nash Equilibria and make rational choices, improving their performance and robustness in strategic tasks. However, even with workflows, negotiation can undermine rationality as LLMs may be unduly influenced by persuasive language or display an overreliance on trusting opponents’ statements. The paper also investigates the effects of prompt engineering and personality variations on LLM rationality, finding significant impacts on the consistency of choices and optimal strategy selection. Overall, the study highlights the complex interplay between rationality, negotiation, and other factors in LLM decision-making, underscoring the need for more robust and strategically sound AI agents.
Workflow Design#
The research paper section on “Workflow Design” likely details the algorithmic processes guiding Large Language Model (LLM) agents in strategic games. This likely involves a step-by-step breakdown of how the LLMs process game information, formulate strategies, and make decisions. It would probably cover different workflows for various game types (complete vs. incomplete information) and discuss techniques like backward induction or best response analysis. A crucial aspect is how these workflows aim to improve LLM rationality, moving them closer to optimal game-theoretic solutions like Nash Equilibria. The design choices likely reflect considerations of computational cost, efficiency, and the potential for exploitation by less rational opponents. The paper likely compares and contrasts different workflow strategies, analyzing their effectiveness in maximizing utility and achieving Pareto optimal or envy-free outcomes, in both simultaneous and sequential game settings. Fairness considerations such as envy-freeness are probably incorporated into the workflows for incomplete information games where resource allocation is central. The evaluation likely involves metrics measuring Nash equilibrium attainment, efficiency, Pareto optimality, and fairness, comparing agent performance with and without these structured workflows. Negotiation strategies are likely integrated into the workflow, especially for incomplete-information games, allowing for belief updates and strategic communication to improve outcomes.
Negotiation Effects#
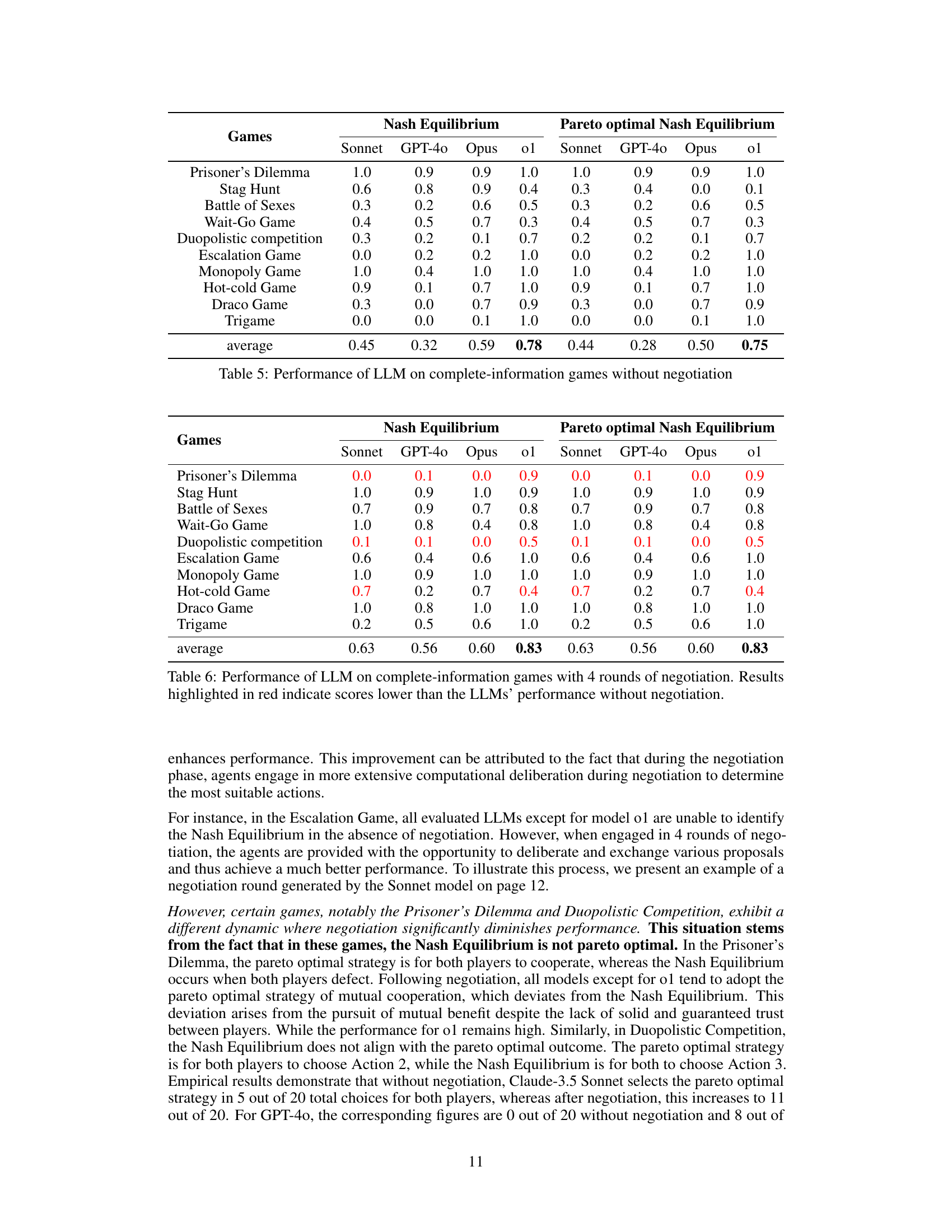
Negotiation significantly impacts the rationality and efficiency of large language models (LLMs) in game-theoretic settings. In complete-information games, negotiation sometimes improves outcomes by facilitating coordination and Pareto optimality (e.g., Stag Hunt), but it can also lead to deviations from Nash Equilibrium in games like Prisoner’s Dilemma, where cooperation is not the dominant strategy. In incomplete-information games, negotiation becomes crucial for resource allocation, but LLMs may struggle with strategic reasoning and belief updating, potentially hindering optimal outcomes. Workflows designed to guide LLM decision-making can enhance performance, but LLMs without workflows may still achieve better results due to exploiting vulnerabilities in the strategies of workflow-guided agents. Prompt engineering techniques can partially mitigate the influence of negotiation, especially when emphasizing independent decision-making, but the effect diminishes with increased rounds of negotiation.
Incomplete Info Games#
In the realm of incomplete information games, the research explores the challenges LLMs face when negotiating resource allocation with hidden valuations. The absence of complete knowledge about other players’ preferences significantly impacts the LLM’s ability to make rational decisions. The study introduces a novel workflow incorporating Bayesian belief updates to guide the negotiation process. This workflow aims to address the uncertainty by allowing agents to iteratively refine their valuation estimates of other players based on observed actions and communication. The workflow is crucial in achieving near-optimal and envy-free outcomes. Experimental results demonstrate that while the workflow significantly improves performance, negotiation still introduces complexities. LLMs show some susceptibility to exploitation, particularly when negotiating with agents not using the workflow, underscoring the importance of a meta-strategy to determine when to deploy the workflow.
Future Research#
The paper’s “Future Directions” section points toward crucial areas needing further investigation. Exploiting workflow vulnerabilities is key; understanding how deceptive strategies can undermine the proposed game-theoretic workflows is critical for developing robust, secure AI agents. Expanding to multi-stage games presents a significant challenge, requiring the development of LLM strategies that can effectively adapt across multiple decision points and anticipate opponent’s moves. This necessitates creating a meta-strategy – a higher-level framework to determine optimal workflow adoption based on context and opponent behavior. Finally, the authors suggest work on aligning LLMs with specific agent interests and stances, moving beyond helpfulness to incorporate the capacity for strategic self-advocacy and negotiation within complex interactions. This area of research focuses on imbuing LLMs with the ability to convincingly represent and pursue their defined objectives, which enhances their overall negotiation success, and it also highlights the importance of addressing potential vulnerabilities in the design of workflows used in strategic settings.
More visual insights#
More on figures

🔼 Figure 2 illustrates the workflow design for simultaneous games, specifically the Prisoner’s Dilemma. Part (a) shows the payoff matrix of the Prisoner’s Dilemma, illustrating the strategic interaction between two players who must simultaneously choose to cooperate or defect. Part (b) presents a detailed workflow diagram. This diagram breaks down the process into sequential steps: game introduction, thinking chain generation (where the model evaluates potential actions and opponent’s responses), decision-making (choosing an action based on the expected payoffs), and finally checking for Nash Equilibrium. This workflow guides the LLM in strategic decision-making for simultaneous games by providing a structured approach to analyzing payoffs and predicting opponent behavior.
read the caption
Figure 2: An illustration of workflow design for simultaneous game. (a) Illustration of prisoner’s dilemma. (b) Workflow design for prisoner’s dilemma.

🔼 Figure 3 illustrates the workflow design for sequential games, using the escalation game as an example. Part (a) shows the escalation game’s structure as a decision tree. Part (b) details the workflow’s steps: game setup (defining actions and payoffs), the backward induction process to determine the optimal strategies (predicting subsequent actions and calculating expected payoffs), and the final decision based on the Nash Equilibrium (comparing the expected payoffs of different action choices). This workflow guides LLMs to make rational decisions in sequential games.
read the caption
Figure 3: An illustration of workflow design for sequential game. (a) Illustration of escalation game. (b) Workflow design for escalation game.

🔼 Figure 4 illustrates the workflow designed for incomplete-information games involving negotiation, specifically focusing on the ‘Deal or No Deal’ game. Part (a) provides a visual representation of a simplified ‘Deal or No Deal’ game, showcasing the allocation of resources among players with varying valuations. Part (b) details the workflow’s steps: 1) Game initialization, where agents receive private resource valuations; 2) a multi-round negotiation process, where agents propose and evaluate allocations; 3) an envy-freeness check; and 4) Belief updating (using Bayesian methods), adjusting probabilities based on negotiation outcomes. The workflow aims to guide agents towards achieving a final allocation that is both envy-free (no agent prefers another’s allocation) and Pareto-optimal (no alternative allocation improves any agent’s utility without harming another).
read the caption
Figure 4: An illustration of workflow design for incomplete-information game with negotiation. (a) Illustration of deal/no-deal game. (b) Workflow design for deal/no-deal game.

🔼 This figure displays the results of experiments conducted to evaluate the robustness of Large Language Models (LLMs) in the context of the Prisoner’s Dilemma game. The experiments systematically varied the payoff matrix while maintaining the same Nash equilibrium, to assess whether the LLMs would consistently make rational decisions. The figure presents a heatmap visualization of the LLM agents’ action choices across three different payoff matrix variations and the classic version. Each heatmap represents a specific payoff matrix variation, showing the probability distribution of the actions (Cooperate or Defect) chosen by the two agents. This visualization allows for a direct comparison of LLM performance across different reward structures, providing insights into their rationality and consistency in strategic decision-making.
read the caption
Figure 5: Agents’ performance under different payoff matrix for Prisoner’s Dilemma

🔼 This figure displays the results of experiments conducted to evaluate the rationality of LLMs in the Stag Hunt game under various payoff matrix conditions. The results demonstrate the distribution of actions (Stag vs. Hare) taken by the agents (LLMs) in different scenarios. These scenarios varied in the magnitude of payoff values assigned to each action combination, but maintained the original game’s structure and Nash equilibria. The goal was to determine whether the LLM’s strategy selection remained consistent across such variations or if it was influenced by changes in the numerical payoff values.
read the caption
Figure 6: Agents’ performance under different payoff matrix for Stag Hunt

🔼 This figure shows the performance of different personalities on two games: Prisoner’s Dilemma and Stag Hunt. Six different personality types (compassionate, friendly, helpful, pragmatic, rational, witty) were tested by prompting the LLM agents. Each bar represents the average probability of choosing a particular action (e.g., cooperate or defect) across multiple trials. The results demonstrate that the agents’ performance varies significantly depending on the assigned personality. The ‘witty’ personality yields the most game-theoretically rational results, while the ‘rational’ personality performs slightly worse. Other personalities exhibit decreased rationality.
read the caption
Figure 7: Agents’ performance under different system prompt with personality

🔼 This figure visualizes the impact of different negotiation rounds (0, 1, 2, and 3) on the strategic choices made by agents in four distinct games: Prisoner’s Dilemma, Stag Hunt, Battle of the Sexes, and Rock-Paper-Scissors. Each sub-figure represents a specific game, and the heatmaps within each sub-figure show the probability distribution of the agents’ actions (e.g., cooperate/defect, stag/hare, opera/football) across various negotiation rounds. This allows for an analysis of how communication and negotiation influence the strategic decision-making of the agents in each game.
read the caption
Figure 8: Agents’ performance under different numbers of negotiation: 0-round, 1-round, 2-round, and 3-round from left to right for the four games

🔼 This figure visualizes the impact of six different prompts on the rationality of LLMs in a Prisoner’s Dilemma game. Each prompt aims to influence the LLM’s decision-making process, either by encouraging critical thinking and skepticism towards the other player’s statements, or by promoting independent decision-making without considering the other player’s influence. The results are displayed as heatmaps across three rows, each row representing a different number of negotiation rounds (one, two, and three rounds). The heatmaps for each round show how the distribution of actions by the two LLMs changes under each of the six prompts. Analyzing these heatmaps reveals how the prompts affect the balance between cooperation and defection in the Prisoner’s Dilemma game across different numbers of negotiation rounds.
read the caption
Figure 9: The effect of the 6 engineered prompts on Prisoner’s Dilemma game with different rounds of negotiation: 1-round, 2-round, and 3-round for the three rows

🔼 This figure displays the results of an experiment investigating how different prompts affect the outcome of a Stag Hunt game under varying negotiation rounds (1, 2, and 3 rounds). Six distinct prompts were tested, each designed to influence the agents’ decision-making process, ranging from cautious analysis of the other player’s statements to independent decision-making without regard for negotiation. The heatmaps show the distribution of actions (Stag/Hare choices) selected by the LLM agents for each prompt and negotiation scenario.
read the caption
Figure 10: The effect of the 6 engineered prompts on Stag Hunt game with different rounds of negotiation: 1-round, 2-round, and 3-round for the three rows

🔼 This figure displays the results of an experiment investigating whether the order of negotiation impacts the outcome in the Battle of the Sexes game. The experiment manipulated which player initiated the negotiation (Player 1 or Player 2) across different numbers of negotiation rounds (0, 1, 2, 3 rounds). Each heatmap cell shows the probability distribution of the chosen actions for the two players based on experimental outcomes. The figure aims to determine if the order of negotiation influences player choices and whether there is any bias towards players who start the dialogue.
read the caption
Figure 11: Will the fact that who starts the negotiation affect the result?
More on tables
| Stag | Hare | |
|---|---|---|
| Stag | 3,3 | 0,1 |
| Hare | 1,0 | 1,1 |
🔼 This table presents the payoff matrix for the Prisoner’s Dilemma game. The Prisoner’s Dilemma is a classic game theory example illustrating the tension between individual rationality and collective benefit. Two players independently choose to either cooperate or defect. The table shows the resulting payoffs for each player depending on the choices of both players. Higher numbers indicate better outcomes for a given player.
read the caption
(a) Table 2a: Payoff matrix for Prisoner’s Dilemma
| Opera | Football | |
|---|---|---|
| Opera | 2,1 | 0,0 |
| Football | 0,0 | 1,2 |
🔼 This table shows the payoff matrix for the Stag Hunt game. The Stag Hunt is a coordination game where two players must cooperate to achieve a high payoff, but risk a lower payoff if they act independently. The matrix shows the payoffs for each player depending on whether they choose to hunt a stag (S) or a hare (H). For example, if both players choose to hunt a stag (S,S), they both receive a payoff of 3. If one player hunts a stag and the other hunts a hare (S,H) or (H,S), the player hunting the stag receives a payoff of 0 and the other player receives a payoff of 1. If both players hunt hares (H,H), they both receive a payoff of 1.
read the caption
(b) Table 2b: Payoff matrix for Stag Hunt
| Wait | Go | |
|---|---|---|
| Wait | 0,0 | 0,2 |
| Go | 2,0 | -4,-4 |
🔼 This table shows the payoff matrix for the Battle of the Sexes game. The Battle of the Sexes is a coordination game where two players, Alice and Bob, have different preferences for two possible activities but both prefer to do the activity together. The matrix displays the payoff (utility) for each player given their choice and the other player’s choice. Understanding this payoff matrix is crucial for analyzing the game’s Nash Equilibria and predicting rational player behavior.
read the caption
(a) Table 3a: Payoff matrix for Battle of Sexes
| action 1 | action 2 | action 3 | action 4 | action 5 | action 6 | |
|---|---|---|---|---|---|---|
| action 1 | 0,0 | 0,9 | 0,14 | 0,15 | 0,12 | 0,5 |
| action 2 | 9,0 | 7,7 | 5,10 | 3,9 | 1,4 | -1,-5 |
| action 3 | 14,0 | 10,5 | 6,6 | 2,3 | -2,-4 | -2,-5 |
| action 4 | 15,0 | 9,3 | 3,2 | -3,-3 | -3,-4 | -3,-5 |
| action 5 | 12,0 | 4,1 | -4,-2 | -4,-3 | -4-4, | -4,-5 |
| action 6 | 5,0 | -5,-1 | -5,-2 | -5,-3 | -5,-4 | -5,-5 |
🔼 This table displays the payoff matrix for the Wait-Go game, a classic game theory example illustrating strategic interaction between two drivers at an intersection. Each driver must decide to either wait or go, resulting in four possible outcomes (both wait, both go, driver 1 waits while driver 2 goes, and driver 2 waits while driver 1 goes). The matrix shows the associated payoffs (rewards or costs) for each driver for each of these four outcomes. The payoffs represent the consequences of the choices such as the time spent waiting or the potential cost of a collision.
read the caption
(b) Table 3b: Payoff matrix for Wait-Go Game
| Difficulty(d) | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 |
|---|---|---|---|---|---|---|---|---|---|---|
| total number of datapoints | 13 | 27 | 57 | 85 | 108 | 133 | 177 | 189 | 210 | 217 |
| Agreement rate | 0.5385 | 0.5556 | 0.5614 | 0.6235 | 0.6574 | 0.6917 | 0.7119 | 0.7249 | 0.7381 | 0.7373 |
| envy free rate | 0.3077 | 0.4074 | 0.4035 | 0.4824 | 0.5463 | 0.6015 | 0.6441 | 0.6614 | 0.6810 | 0.6820 |
| Pareto optimal rate | 0.5384 | 0.4444 | 0.4385 | 0.4823 | 0.5277 | 0.5413 | 0.5310 | 0.5396 | 0.5523 | 0.5529 |
| envy free and Pareto optimal rate | 0.3077 | 0.3333 | 0.3333 | 0.3882 | 0.4537 | 0.4812 | 0.4858 | 0.4973 | 0.5142 | 0.5161 |
🔼 This table shows the payoff matrix for a duopolistic competition game between two firms, Firm A and Firm B. Each firm independently chooses a quantity of output to produce. The payoff to each firm depends on the quantity of output chosen by both firms, which determines the market price and resulting profits. The table shows the payoff (profit) for each firm (Firm A, Firm B) for all possible combinations of output levels from both firms (action 1 through action 6). Note: The payoff is represented as a pair of numbers where the first value is Firm A’s payoff and the second value is Firm B’s payoff.
read the caption
Table 4: A payoff matrix for Duopolistic Competition
| Model | Negotiation Round | Agreement | Alice score | Bob score | PO | EF | total reward |
|---|---|---|---|---|---|---|---|
| Best | – | 1.0000 | 5.82 | 6.66 | 1.0000 | 1.0000 | 12.48 |
| Human | 2.86 | 0.6817 | 3.32 | 3.39 | 0.4317 | 0.4545 | 6.64 |
| Sonnet | 7.07 | 0.9545 | 5.55 | 5.57 | 0.7045 | 0.7045 | 11.11 |
| o1 | 3.86 | 0.7500 | 4.39 | 4.43 | 0.4545 | 0.4772 | 8.82 |
| GPT-4o | 18.45 | 0.6363 | 2.80 | 4.38 | 0.4091 | 0.3864 | 7.14 |
| Opus | 4.37 | 0.4772 | 2.68 | 3.02 | 0.3636 | 0.2727 | 5.70 |
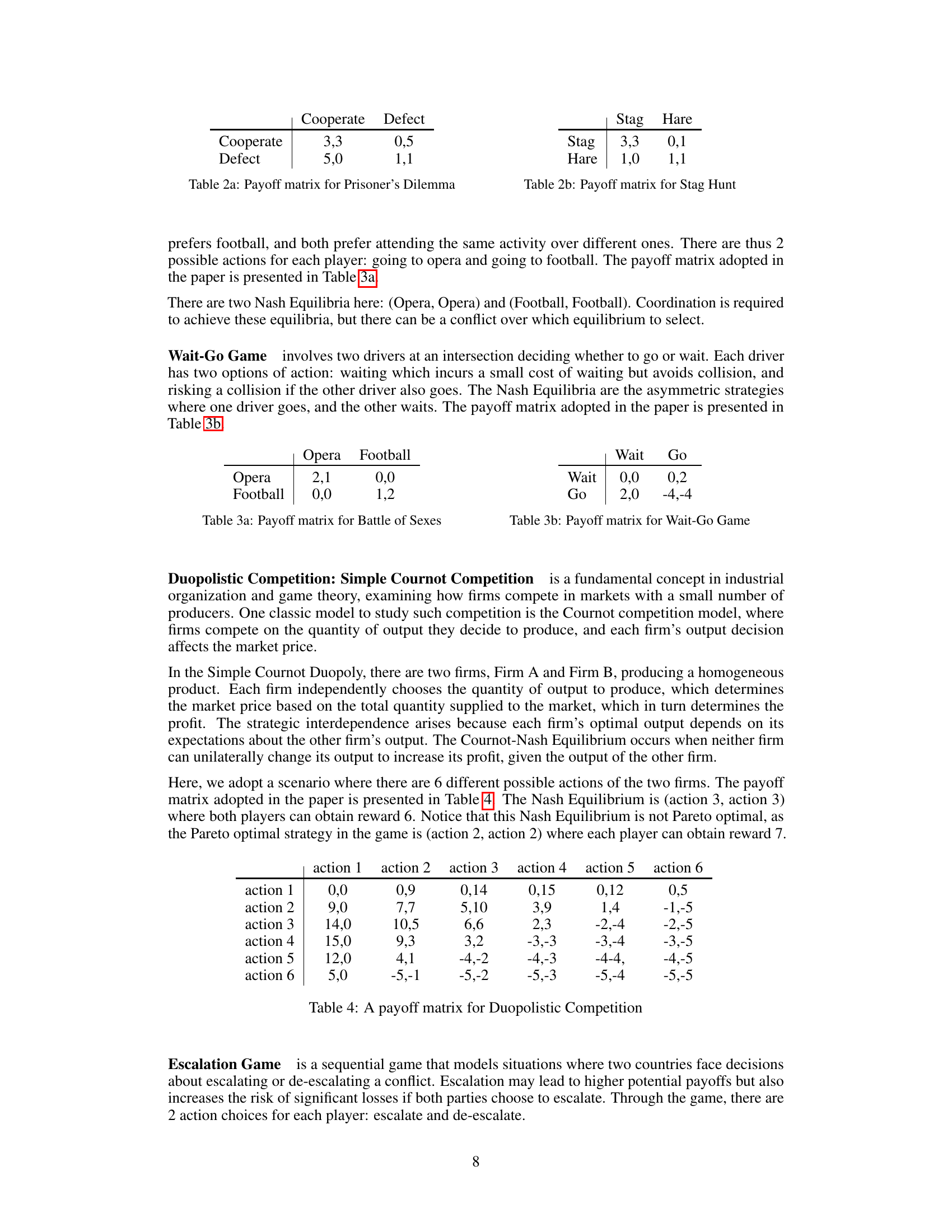
🔼 This table presents the performance of four different Large Language Models (LLMs) on ten complete-information games without any negotiation. The LLMs tested are Claude-3.5 Sonnet, Claude-3 Opus, GPT-40, and o1. For each game, the table shows the percentage of times each LLM achieved a Nash Equilibrium and a Pareto optimal Nash Equilibrium across multiple trials. This data provides insights into the ability of LLMs to make rational decisions in strategic settings without the aid of negotiation.
read the caption
Table 5: Performance of LLM on complete-information games without negotiation
| Model | Negotiation Round | Agreement | Alice score | Bob score | PO | EF | total reward |
|---|---|---|---|---|---|---|---|
| temp=0.0 | 19.36 | 0.5681 | 2.98 | 3.47 | 0.4091 | 0.3260 | 6.44 |
| temp=1.0 | 18.45 | 0.6364 | 2.80 | 4.38 | 0.4090 | 0.3864 | 7.14 |
🔼 This table presents the performance of four Large Language Models (LLMs) across ten complete-information games, after four rounds of negotiation between the agents. The performance is measured by the percentage of times the agents reached the Nash Equilibrium and the Pareto Optimal Nash Equilibrium. The table allows for comparison with the results of the same LLMs without negotiation (Table 5), identifying cases where negotiation, even with a structured approach, hurt performance. Results that are worse than the no-negotiation condition are highlighted in red, indicating that the negotiation process was not always beneficial for achieving optimal outcomes.
read the caption
Table 6: Performance of LLM on complete-information games with 4 rounds of negotiation. Results highlighted in red indicate scores lower than the LLMs’ performance without negotiation.
| Model | Negotiation Round | Agreement | Alice score | Bob score | PO | EF | total reward |
|---|---|---|---|---|---|---|---|
| Best | - | 1.0000 | 5.82 | 6.66 | 1.0000 | 1.0000 | 12.48 |
| Opus | 4.05 | 1.0000 | 5.82 | 6.50 | 0.9091 | 0.9318 | 12.31 |
| GPT-4o | 4.91 | 1.0000 | 5.93 | 6.25 | 0.8636 | 1.0000 | 12.18 |
| Sonnet | 4.45 | 1.0000 | 5.93 | 6.16 | 0.7953 | 0.9772 | 12.11 |
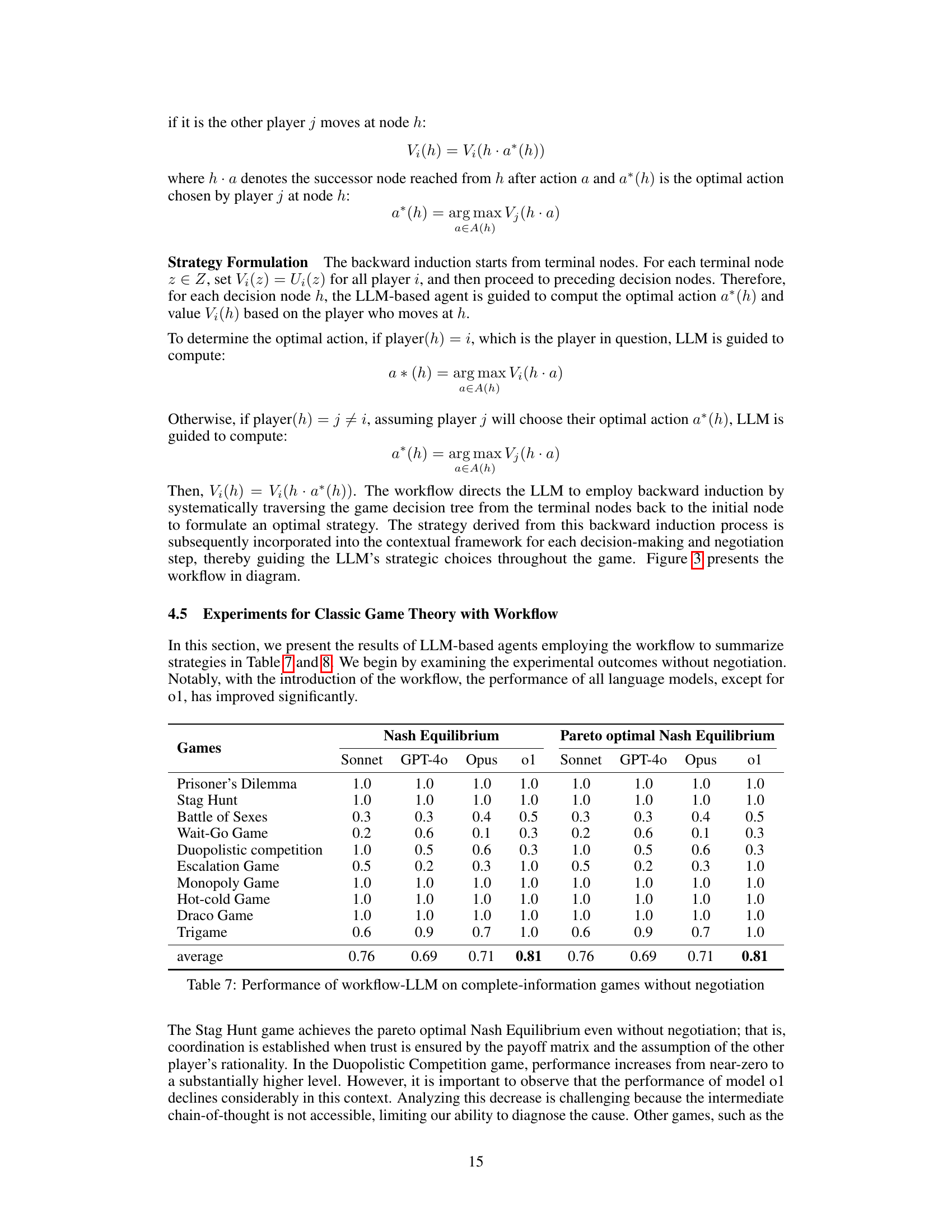
🔼 This table presents the performance of Large Language Models (LLMs) enhanced with a game-theoretic workflow in 10 complete-information games without any negotiation involved. The performance is measured by the percentage of trials where the LLMs reached a Nash Equilibrium (a stable state where no player can improve their outcome by changing their strategy alone), and also by the percentage of trials reaching the Pareto optimal Nash Equilibrium (a state where no one can be made better off without making someone worse off). The games included represent various game types including simultaneous and sequential games requiring differing levels of strategic reasoning and coordination. The results highlight how the workflow impacts the LLM’s ability to find optimal and rational solutions in these games.
read the caption
Table 7: Performance of workflow-LLM on complete-information games without negotiation
| Model | Negotiation Round | Agreement | Alice score | Bob score | PO | EF | total reward |
|---|---|---|---|---|---|---|---|
| temp=0.0 | 4.80 | 1.0000 | 5.53 | 6.67 | 0.8695 | 1.0000 | 12.20 |
| temp=1.0 | 4.91 | 1.0000 | 5.93 | 6.16 | 0.8636 | 1.0000 | 12.18 |
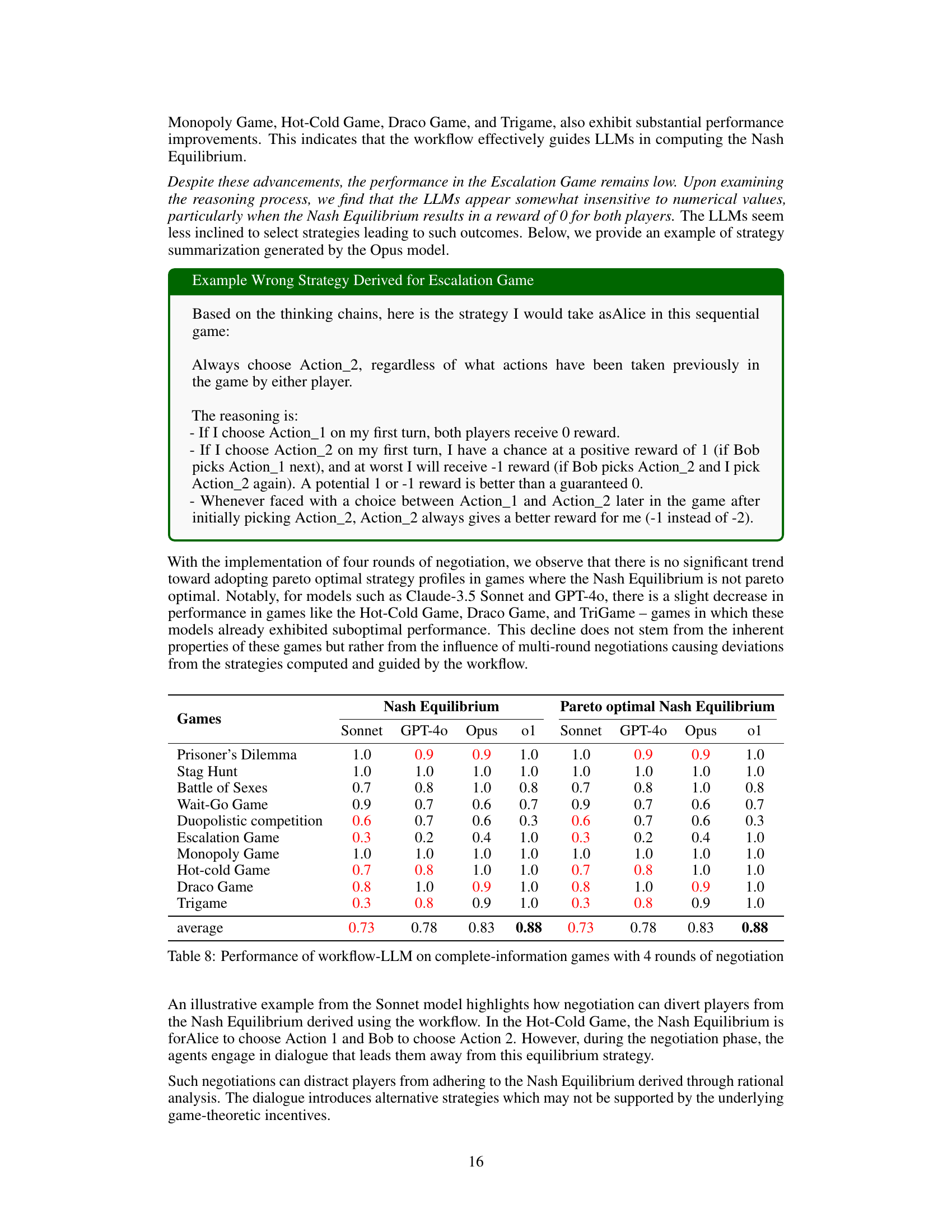
🔼 This table presents the performance of Large Language Models (LLMs) enhanced with a game-theoretic workflow in complete-information games. It shows the percentage of times each LLM reached the Nash Equilibrium and Pareto Optimal Nash Equilibrium across ten different games after four rounds of negotiation. This data illustrates the impact of integrating a structured workflow based on classic game theory on the LLMs’ ability to arrive at optimal strategies in different game scenarios.
read the caption
Table 8: Performance of workflow-LLM on complete-information games with 4 rounds of negotiation
| Model | Precision | Recall | Reduction Percentage |
|---|---|---|---|
| Sonnet | 0.9545 | 0.3766 | 0.7033 |
| GPT-4o | 0.9545 | 0.3515 | 0.6980 |
| Opus | 0.7954 | 0.2737 | 0.6947 |
🔼 This table presents the results of human negotiations across various difficulty levels, showing the percentages of successful agreements reached, envy-free allocations, Pareto-optimal allocations, and allocations that satisfy both criteria. The difficulty levels are determined by calculating the L1 distance (sum of absolute differences) between the players’ valuation vectors; larger distances represent greater differences in valuation preferences. The data reveals trends in negotiation success rates across different levels of difficulty. It demonstrates how the challenges of negotiation and achieving fairness change when players have similar (difficult scenarios) vs. differing (easier scenarios) preferences.
read the caption
Table 9: Percentage of datapoints where humans achieve agreement, envy free allocations, pareto optimal allocations, and allocations that are both envy free and pareto optimal with different levels of difficulty.
| Metric | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Precision | 0.9545 | 0.9318 | 0.7500 | 0.8636 | 0.9318 | 0.9432 | 0.9545 |
| Recall | 0.2381 | 0.3099 | 0.2958 | 0.3079 | 0.3655 | 0.3652 | 0.3766 |
| Reduction Percentage | 0.5997 | 0.6825 | 0.7397 | 0.7011 | 0.7025 | 0.7033 | 0.7033 |
🔼 This table presents a comparison of the negotiation performance between four different LLMs (Claude-3.5 Sonnet, Claude-3 Opus, GPT-40, and o1) and human performance in a common resource allocation game without using any workflow. It shows the average results across 50 difficult data points selected based on the l1 distance between player’s valuations. The metrics included are the average number of negotiation rounds to reach an agreement, the percentage of successful agreements, the average utility scores for each agent, and the percentages of allocations satisfying pareto optimality and envy freeness. The table also displays the total rewards (the sum of individual rewards) and the best possible total rewards for these data points.
read the caption
Table 10: Raw-LLM vs. Raw-LLM
| Model | precision w.r.t \mathcal{I}(\mathbf{v}) | recall w.r.t \mathcal{I}(\mathbf{v}) |
|---|---|---|
| Sonnet | 1.0 | 0.6022 |
| GPT-4o | 1.0 | 0.5633 |
| Opus | 1.0 | 0.5399 |
🔼 This table presents the results of experiments conducted using the GPT-40 language model with temperature parameters set to 0.0 and 1.0. The experiments involved a negotiation task in a game-theoretic setting and measured several key metrics: the number of negotiation rounds, the percentage of agreements reached, the average scores obtained by Alice and Bob (two agents), the percentage of Pareto optimal outcomes, the percentage of envy-free allocations, and the total reward achieved. By comparing the results across different temperatures, the table assesses the impact of temperature on the performance of GPT-40 in negotiation scenarios.
read the caption
Table 11: GPT-4o with temperature 0.0 and 1.0
| Model | Negotiation Round | Agreement | Alice score | Bob score | PO | EF | total reward |
|---|---|---|---|---|---|---|---|
| Sonnet | 6.91 | 0.9773 | 4.88 | 6.57 | 0.6136 | 0.5909 | 11.45 |
| GPT-4o | 11.84 | 0.8182 | 3.66 | 6.18 | 0.5909 | 0.3636 | 9.84 |
| Opus | 3.86 | 0.9091 | 5.09 | 5.53 | 0.6136 | 0.5909 | 10.52 |
🔼 This table presents the results of experiments where two LLMs, both using the proposed negotiation workflow, engage in a negotiation game. It shows the average number of negotiation rounds needed to reach an agreement, the average utility (score) achieved by each LLM (Alice and Bob), the percentage of agreements that are Pareto optimal (meaning no agent could improve their outcome without harming another), the percentage of agreements that are envy-free (meaning no agent prefers another’s allocation to their own), and the combined total utility achieved by both agents.
read the caption
Table 12: Workflow-LLM vs. Workflow-LLM
| Model | Negotiation Round | Agreement | Alice score | Bob score | PO | EF | total reward |
|---|---|---|---|---|---|---|---|
| Sonnet | 6.45 | 1.0000 | 6.39 | 5.70 | 0.7727 | 0.5909 | 12.09 |
| GPT-4o | 11.36 | 0.8181 | 5.75 | 4.14 | 0.6136 | 0.5227 | 9.89 |
| Opus | 3.89 | 0.7955 | 4.86 | 4.57 | 0.4318 | 0.5455 | 9.43 |
🔼 This table presents the results of experiments conducted using the GPT-40 language model with different temperature settings (0.0 and 1.0) while employing a negotiation workflow. The metrics presented include the number of negotiation rounds, whether an agreement was reached, individual agent scores, Pareto optimality, envy-freeness, and the total reward. The table showcases the impact of temperature on the model’s negotiation performance when using the structured workflow, providing insights into the model’s stability and consistency under different temperature conditions.
read the caption
Table 13: Workflow-GPT-4o with temperature 0.0 and 1.0
| Models | Sonnet | GPT-4o | Opus | |||
|---|---|---|---|---|---|---|
| Actions | use | not use | use | not use | use | not use |
| use | 5.82, 6.16 | 4.88, 6.57 | 5.93, 6.25 | 3.66, 6.18 | 5.82, 6.50 | 5.09,5.53 |
| not use | 6.39, 5.07 | 5.55, 5.57 | 5.75, 4.14 | 2.80, 4.38 | 4.86,4.57 | 2.80,4.38 |
🔼 This table presents the performance of different LLMs in estimating the valuation of the other player during a negotiation game. The metrics used to evaluate the performance are Precision (whether the true valuation is included in the estimated set of valuations), Recall (how many incorrect valuations are included along with the true valuation), and Reduction Percentage (how much the estimated valuation set has been reduced from the initial prior distribution). The results are shown for three different LLMs: Sonnet, GPT-40, and Opus.
read the caption
Table 14: Performance of Estimation of Valuation of the Other Player
| action 1 | action 2 | |
|---|---|---|
| action 1 | 300,300 | 0,301 |
| action 2 | 301,0 | 1,1 |
🔼 This table presents the performance of the Sonnet model in estimating the opponent’s valuation across multiple negotiation rounds in the Deal or No Deal game. It shows how the model’s precision (how often the true valuation is included in the estimated set), recall (how many incorrect valuations are included along with the true one), and reduction percentage (how much the estimated valuation space has been narrowed) evolve as the number of rounds increases.
read the caption
Table 15: Performance of Sonnet’s Estimation of Opponent’s Valuation Across Negotiations
| action 1 | action 2 | |
|---|---|---|
| action 1 | 3,3 | -300, 5 |
| action 2 | 5,-300 | -299,-299 |
🔼 This table presents the performance of the LLM in estimating the opponent’s valuation during the negotiation process of the Deal or No Deal game. Specifically, it shows how accurately the model’s estimated valuations align with the set of valuations that lead to the same optimal allocations (envy-free and maximizing total utility). The metrics used to evaluate the performance are precision (whether at least one estimated valuation is indistinguishable from the true valuation) and recall (the proportion of estimated valuations that are indistinguishable from the true valuation). Results are presented for three different LLMs: Sonnet, GPT-40, and Opus.
read the caption
Table 16: Performance of estimated valuations with respect to indistinguishable of the true valuation.
| action 1 | action 2 | |
|---|---|---|
| action 1 | 300,300 | 0,1 |
| action 2 | 1,0 | 1,1 |
🔼 This table presents a comparison of negotiation outcomes when one agent employs a game-theoretic workflow and the other agent does not. It shows the average number of negotiation rounds, agreement rate, individual agent scores, Pareto optimality rate, envy-freeness rate, and the total reward for both agents across multiple negotiation scenarios. This helps to understand the impact of the workflow on negotiation outcomes, comparing the performance of a workflow-guided agent against an agent using direct prompting without strategic guidance.
read the caption
Table 17: Workflow-LLM vs. Raw-LLM
| action 1 | action 2 | |
|---|---|---|
| action 1 | 3,3 | -100,-99 |
| action 2 | -99,-100 | -99,-99 |
🔼 This table presents a comparison of the performance of Large Language Models (LLMs) in negotiation games, specifically focusing on a scenario where one LLM utilizes a proposed negotiation workflow while the other does not. The metrics compared include the number of negotiation rounds, whether an agreement was reached, the individual utilities obtained by each LLM, the percentage of allocations that are Pareto optimal and envy-free, and the total combined utility of both LLMs. The results reveal insights into the effectiveness and potential limitations of the proposed negotiation workflow in enhancing the rationality and efficiency of LLM-based agents in a strategic interaction setting.
read the caption
Table 18: Raw-LLM vs. Workflow-LLM
Full paper#