↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Instruction tuning, crucial for aligning LLMs with user instructions, relies heavily on the quality of instruction datasets. Creating these datasets is expensive and time-consuming. Current methods often assume larger models are better response generators for creating synthetic datasets, using them as “teachers” for smaller models. However, this approach hasn’t been rigorously evaluated.
This research investigates whether stronger models truly make better teachers for instruction tuning. The authors challenge the existing assumption and find that larger models are not always superior. They introduce a novel metric called Compatibility-Adjusted Reward (CAR) to assess the effectiveness of different response generators (teacher models) in instruction tuning. The experiments reveal that CAR outperforms existing metrics in accurately predicting the effectiveness of teachers, thus providing a more effective and cost-efficient method to select them.
Key Takeaways#
Why does it matter?#
This paper challenges the common assumption that larger language models are better teachers for instruction tuning. It introduces a novel metric, Compatibility-Adjusted Reward (CAR), to assess the effectiveness of different models as teachers, potentially improving the efficiency and cost-effectiveness of instruction tuning. This has significant implications for researchers and practitioners working with LLMs, guiding more informed choices in model selection for synthetic data generation.
Visual Insights#

🔼 This figure illustrates the instruction tuning process. Instruction tuning adapts a pre-trained large language model (LLM) to better follow user instructions. It involves creating an instruction dataset (pairs of instructions and corresponding responses) and fine-tuning the LLM on this dataset. The figure highlights that this paper focuses on the generation of high-quality responses using various response generators (different LLMs). These responses are paired with instructions to build the instruction dataset. The resulting fine-tuned model’s ability to follow instructions is then evaluated.
read the caption
Figure 1: This figure demonstrates the process of instruction tuning and the scope of this paper.
| Model Family | Release Date | Model ID | Size |
|---|---|---|---|
| Qwen2 Yang et al. (2024) | Jun, 2024 | Qwen2-1.5B-Instruct | 1.5B |
| Qwen2-7B-Instruct | 7B | ||
| Qwen2-72B-Instruct | 72B | ||
| Qwen2.5 Team (2024) | Sept, 2024 | Qwen2.5-3B-Instruct | 3B |
| Qwen2.5-7B-Instruct | 7B | ||
| Qwen2.5-14B-Instruct | 14B | ||
| Qwen2.5-32B-Instruct | 32B | ||
| Qwen2.5-72B-Instruct | 72B | ||
| Llama 3 (Meta, 2024c) | Apr, 2024 | Llama-3-8B-Instruct | 8B |
| Llama-3-70B-Instruct | 70B | ||
| Llama 3.1 (Meta, 2024c) | Jul, 2024 | Llama-3.1-8B-Instruct | 8B |
| Llama-3.1-70B-Instruct | 70B | ||
| Llama-3.1-405B-Instruct | 405B | ||
| Gemma 2 Team et al. (2024) | Jun, 2024 | Gemma-2-2b-it | 2B |
| Gemma-2-9b-it | 9B | ||
| Gemma-2-27b-it | 27B | ||
| Phi-3 Abdin et al. (2024) | Jun, 2024 | Phi-3-mini-128k-instruct | 3.8B |
| Phi-3-small-128k-instruct | 7B | ||
| Phi-3-medium-128k-instruct | 14B | ||
| GPT-4 Achiam et al. (2023) | Since Mar, 2023 | GPT-4 & GPT-4 Turbo | - |
🔼 This table lists the twenty different large language models (LLMs) used to generate responses for synthetic instruction datasets. For each LLM, it specifies the model family it belongs to, the model’s size (in parameters), and its release date. These LLMs serve as response generators, and the resulting responses are paired with instructions to create the instruction-following datasets used in training various base models.
read the caption
Table 1: Overview of 20 response generators used in our study.
In-depth insights#
Instruction Tuning#
Instruction tuning, a crucial technique for aligning large language models (LLMs) with user intentions, heavily relies on the quality of instruction datasets. Synthetic datasets, generated by LLMs themselves, offer a cost-effective alternative to human-curated data. However, the paper challenges the common assumption that larger, more powerful models always serve as better ’teachers’ for this process. The Larger Models’ Paradox reveals that stronger models aren’t necessarily superior at generating suitable responses for instruction tuning, highlighting the importance of compatibility between the teacher and student models. This necessitates a more nuanced approach to dataset creation, moving beyond simply using the strongest available model. The paper introduces a novel metric, Compatibility-Adjusted Reward (CAR), to better predict the effectiveness of response generators without extensive fine-tuning, thus improving the efficiency of instruction tuning.
Model Paradox#
The “Model Paradox” highlights a surprising finding: larger language models (LLMs) aren’t always better teachers for instruction tuning. Intuitively, one might expect that stronger models, with their superior capabilities, would generate higher-quality instruction-response pairs for training smaller models. However, the research reveals that this isn’t necessarily true. Smaller or mid-sized models sometimes produce training data that leads to better performance in the smaller models being trained, suggesting that compatibility between teacher and student models is crucial. This paradox challenges the common assumption that simply using the largest available model is optimal for synthetic dataset creation in instruction tuning, and underscores the need for more nuanced metrics beyond simple model size or benchmark performance when selecting teacher models.
CAR Metric#
The research paper introduces a novel metric, Compatibility-Adjusted Reward (CAR), to assess the effectiveness of response generators in instruction tuning for large language models (LLMs). Existing metrics fail to capture the compatibility between the response generator and the base LLM being fine-tuned, leading to inaccurate predictions of performance. CAR addresses this limitation by incorporating both the reward (quality) and the compatibility (risk) of responses. Higher compatibility, indicated by lower loss on the base model, reduces the risk, while higher reward signifies better quality. The authors demonstrate that CAR significantly outperforms existing metrics in predicting the effectiveness of response generators, offering a more reliable method for selecting optimal teachers in the instruction tuning process. This is particularly important because using the right response generator can drastically improve the efficiency and effectiveness of the instruction tuning process, avoiding costly trial-and-error experiments with various models.
Future Work#
The paper’s ‘Future Work’ section presents exciting avenues for extending this research. Investigating the theoretical underpinnings of compatibility between response generators and base models is crucial. This could involve exploring the latent representations learned by these models and identifying factors that influence their alignment. Analyzing the impact of different response generators on preference tuning is another key area. This could lead to better alignment of LLMs with human values. Finally, efficiently transforming existing datasets to enhance compatibility would significantly improve instruction tuning. The authors also acknowledge the need for broader application of the findings to specialized domains, such as complex reasoning and mathematics, while acknowledging potential ethical considerations.
Study Limits#
This study’s limitations center on its focus on general instruction-following tasks, neglecting specialized domains like mathematics or complex reasoning. The generalizability of findings to such areas remains uncertain. Furthermore, the research primarily analyzes the impact of response generators on instruction-following capabilities, without a comprehensive exploration of the entire dataset creation process, including instruction generation. The absence of an analysis for different response generation methods (like temperature, top-p) may limit the broader applicability. Finally, the ethical implications of findings, particularly concerning the potential misuse of the proposed CAR metric, require further investigation.
More visual insights#
More on figures

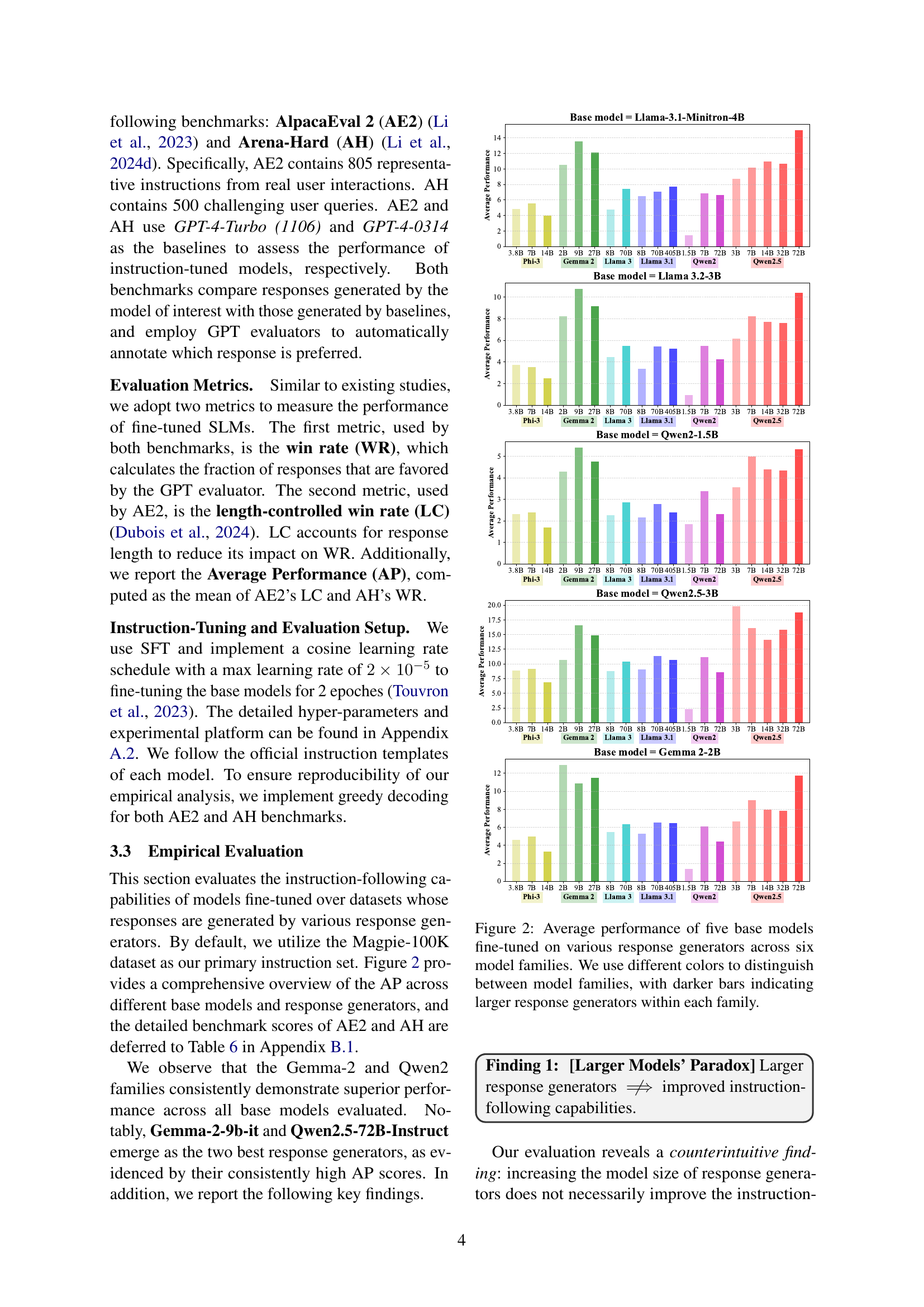
🔼 This figure displays the average performance results for five base language models that have been fine-tuned using instruction datasets generated by 20 different response generators. The response generators represent seven distinct model families. The x-axis categorizes the response generators by their family and size, while the y-axis represents the average performance score. The color-coding helps differentiate the various model families, with darker shades indicating larger models within each family. The figure visually demonstrates the effect that different response generators have on the performance of the fine-tuned base models.
read the caption
Figure 2: Average performance of five base models fine-tuned on various response generators across six model families. We use different colors to distinguish between model families, with darker bars indicating larger response generators within each family.

🔼 This figure displays the results of an experiment investigating how different sampling methods affect the quality of responses generated by a large language model (LLM). The experiment uses Gemma-2-9b-it as the response generator, which creates responses to a set of instructions. These responses are then used to fine-tune a smaller base model, Llama-3.1-Minitron-4B, via supervised fine-tuning. The figure shows the average performance of the fine-tuned model across various temperature and top-p settings, which are hyperparameters controlling the randomness of the LLM’s output. Higher temperature and top-p values generally lead to more diverse and creative, but potentially less coherent, responses. The experiment aims to determine the optimal sampling strategy for generating high-quality training data for instruction tuning.
read the caption
Figure 3: This figure demonstrates the impact of different sampling hyper-parameters when generating responses. We use Gemma-2-9b-it as the response generator. All models are supervised-fine-tuned on the Llama-3.1-Minitron-4B base model.

🔼 Figure 4 presents the average reward scores obtained from three different reward models (ArmoRM-Llama3-8B-v0.1, Skywork-Reward-Llama-3.1-8B, and Skywork-Reward-Gemma-2-27B) for responses generated by various LLMs. The x-axis displays the response generators, categorized by model family and size, while the y-axis shows the average reward. This visualization helps in assessing the quality of responses produced by different LLMs when used as response generators in instruction tuning. The figure highlights the varying performance of different models as response generators in terms of the quality of their generated responses as evaluated by human preferences via reward models.
read the caption
Figure 4: This figures demonstrates the response quality measured by three reward models.

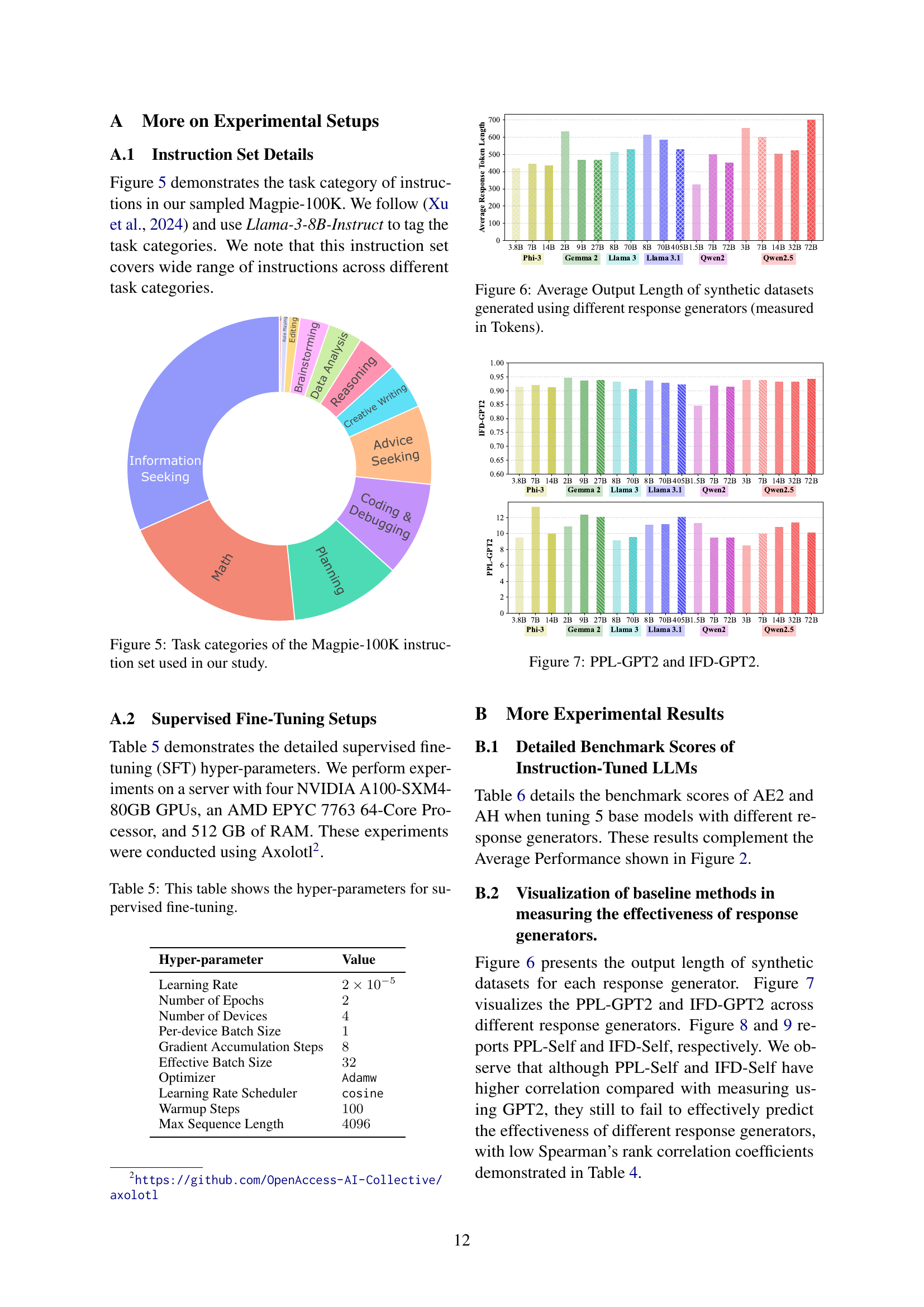
🔼 This pie chart visualizes the distribution of instruction types within the Magpie-100K dataset, a subset of 100,000 high-quality instructions used in the study. The dataset is categorized into several task types, illustrating the variety of instructions included. This breakdown helps to understand the diversity of the data used to train and evaluate the instruction-tuned language models.
read the caption
Figure 5: Task categories of the Magpie-100K instruction set used in our study.

🔼 Figure 6 presents a bar chart illustrating the average length, measured in tokens, of responses generated by various Large Language Models (LLMs) used as response generators in the creation of synthetic instruction datasets. The x-axis categorizes the different LLMs, while the y-axis represents the average response length. The chart allows for a comparison of the output lengths produced by different models, highlighting variations in response brevity and verbosity.
read the caption
Figure 6: Average Output Length of synthetic datasets generated using different response generators (measured in Tokens).

🔼 This figure shows the average response perplexity (PPL) and instruction following difficulty (IFD), both calculated using GPT-2, across different response generators. The x-axis represents the various response generators used, categorized by model family. The y-axis shows the average PPL and IFD scores. This visualization helps to understand how the quality and difficulty of responses generated by different models vary. Lower PPL indicates higher response quality, while lower IFD suggests less difficulty in following the instructions.
read the caption
Figure 7: PPL-GPT2 and IFD-GPT2.

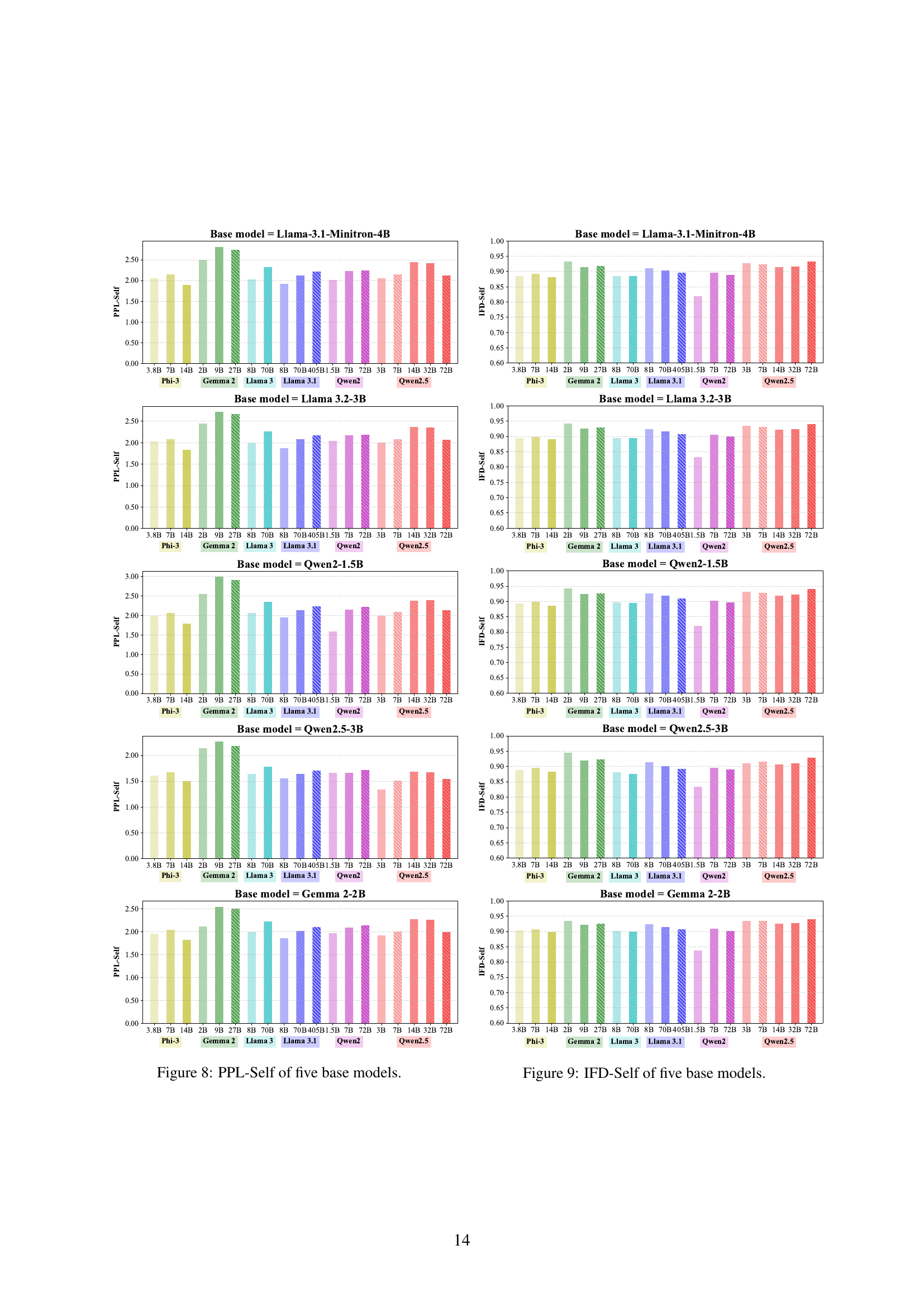
🔼 This figure displays the perplexity scores (PPL-Self) calculated using each of the five base language models. The perplexity measures how well each base model predicts the responses generated by different response generators across six model families (Phi-3, Gemma 2, Llama 3, Llama 3.1, Qwen2, and Qwen2.5). The x-axis represents the various response generators within the model families, while the y-axis shows the perplexity values. Lower perplexity indicates better prediction of the generated responses by the corresponding base model.
read the caption
Figure 8: PPL-Self of five base models.

🔼 This figure displays the Instruction Following Difficulty (IFD) scores, calculated using each base model itself (IFD-Self), for five different base language models. Each base model was evaluated using instruction-response pairs generated by twenty different response generators spanning across seven model families: Qwen2, Qwen2.5, Llama 3, Llama 3.1, Gemma 2, Phi-3, and GPT-4. The x-axis represents the different response generators, grouped by model family, and ordered by increasing size. The y-axis represents the IFD-Self score. Lower IFD-Self scores indicate that the responses generated by the model were easier for the corresponding base model to process, suggesting better compatibility. The purpose of the figure is to show the compatibility between response generators and different base models, in the context of instruction tuning, thereby helping to explain the Larger Models’ Paradox.
read the caption
Figure 9: IFD-Self of five base models.
More on tables
| Response | AlpacaEval 2 | AlpacaEval 2 | Arena-Hard | AP |
|---|---|---|---|---|
| Generator Model | LC (%) | WR (%) | WR (%) | (%) |
| Gemma-2-9b-it | 16.09 | 13.70 | 13.7 | 14.90 |
| Gemma-2-27b-it | 13.93 | 13.31 | 12.4 | 13.17 |
| Llama-3-70b-Instruct | 10.55 | 10.68 | 6.7 | 8.62 |
| Llama-3.1-70b-Instruct | 9.52 | 10.10 | 8.3 | 8.91 |
| Qwen2.5-7B-Instruct | 13.50 | 14.33 | 10.6 | 12.05 |
| Qwen2.5-72B-Instruct | 19.20 | 21.01 | 13.1 | 16.15 |
| GPT-4 | 6.63 | 5.70 | 4.8 | 5.72 |
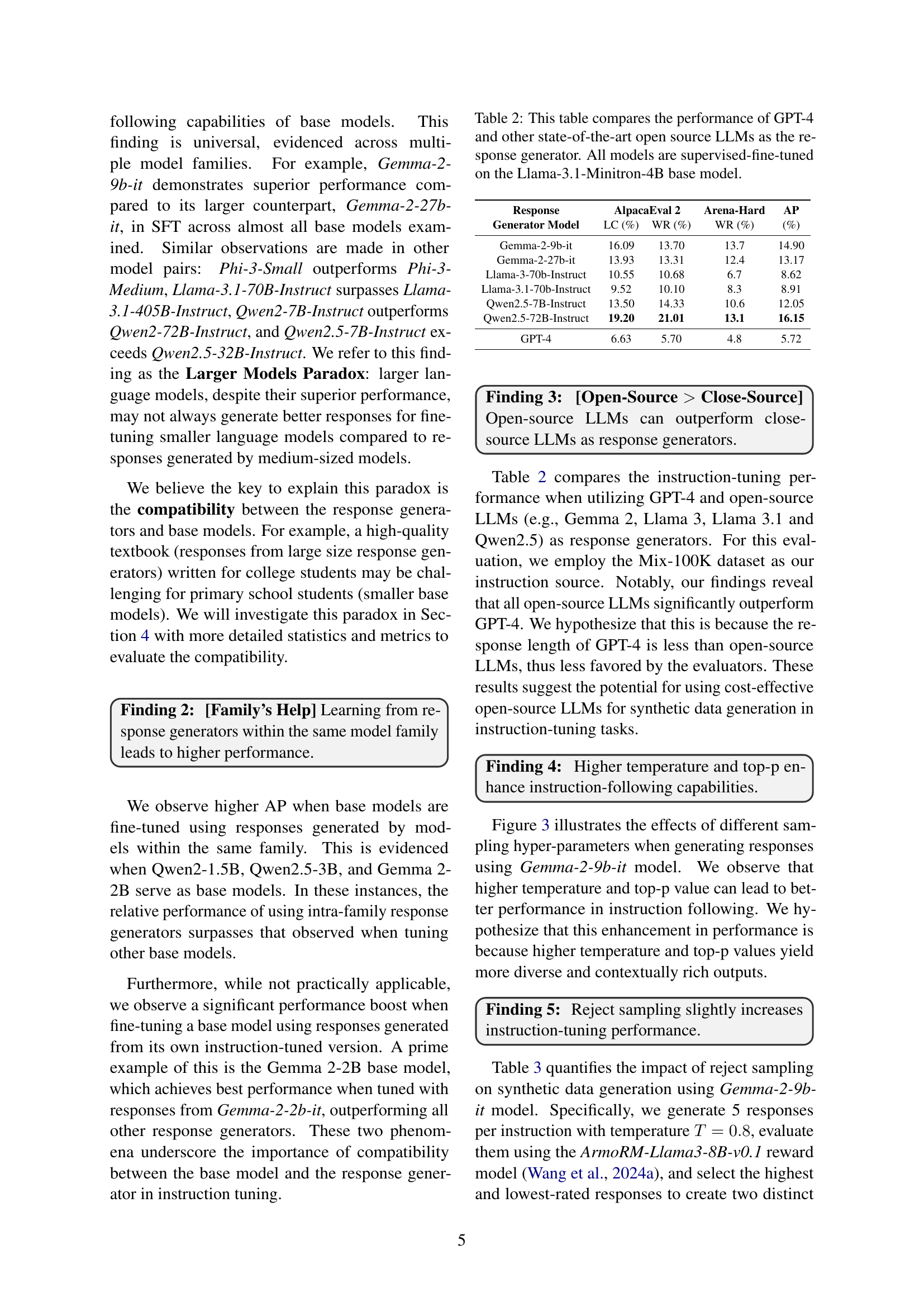
🔼 This table presents a comparison of the performance of various Large Language Models (LLMs) when used as response generators in instruction tuning. Specifically, it focuses on GPT-4 (a closed-source model) and several state-of-the-art open-source LLMs. The performance is evaluated by fine-tuning a Llama-3.1-Minitron-4B base model using instruction datasets generated by each of these LLMs as response generators. The table shows the AlpacaEval 2 LC (Length-Controlled Win Rate), AlpacaEval 2 WR (Win Rate), Arena-Hard WR, and the average performance (AP) across these metrics for each LLM, allowing for a direct comparison of their effectiveness in this role.
read the caption
Table 2: This table compares the performance of GPT-4 and other state-of-the-art open source LLMs as the response generator. All models are supervised-fine-tuned on the Llama-3.1-Minitron-4B base model.
| Base Model | Method | AlpacaEval 2 LC (%) | AlpacaEval 2 WR (%) | Arena-Hard WR (%) | AP (%) | |
|---|---|---|---|---|---|---|
| Llama-3.1-Minitron-4B | Best-of-N | 15.94 | 15.14 | 11.9 | 13.92 | |
| Worst-of-N | 13.02 | 12.66 | 11.0 | 12.01 | ||
| Sampling | 15.71 | 14.81 | 11.8 | 13.755 | ||
| Greedy | 16.13 | 14.51 | 11.0 | 13.565 | ||
| Qwen2.5-3B-Instruct | Best-of-N | 13.83 | 13.57 | 21.0 | 17.415 | |
| Worst-of-N | 12.37 | 12.54 | 17.9 | 15.135 | ||
| Sampling | 13.43 | 13.29 | 20.1 | 16.765 | ||
| Greedy | 13.78 | 13.57 | 19.4 | 16.59 |
🔼 This table presents the results of an experiment evaluating the effect of reject sampling on the performance of instruction-tuned language models. Reject sampling is a technique used to improve the quality of generated responses by discarding samples below a certain quality threshold. The table shows the average performance across various evaluation metrics for models trained using both reject sampling and greedy sampling (without rejection). The models were fine-tuned on a synthetic dataset using a specific response generator, Gemma-2-9b-it, for different base models. Performance is measured across the AlpacaEval 2 benchmark (using Length Controlled Win Rate and Win Rate) and the Arena-Hard benchmark (using Win Rate). The metrics show how reject sampling impacts the instruction-following capabilities of models trained on synthetic datasets generated under different sampling approaches.
read the caption
Table 3: This table investigates the impact of reject sampling on model performance.
| Base Models | Reward | Difficulty | Response Length | CAR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Base Models | Reward | Difficulty | Response Length | CAR | ||||||
| ℛℳ₁ | ℛℳ₂ | ℛℳ₃ | IFD-GPT2 | IFD-Self | PPL-GPT2 | PPL-Self | ||||
| Qwen2-1.5B | 0.5526 | 0.7895 | 0.8754 | 0.7088 | 0.7719 | 0.1473 | 0.5596 | 0.5404 | 0.8842 | |
| Gemma 2-2B | 0.5526 | 0.7982 | 0.8842 | 0.8281 | 0.8930 | 0.1614 | 0.4351 | 0.6298 | 0.9000 | |
| Qwen2.5-3B | 0.4526 | 0.7351 | 0.7456 | 0.7386 | 0.8088 | 0.0456 | -0.0614 | 0.6088 | 0.8105 | |
| Llama 3.2-3B | 0.6088 | 0.8105 | 0.9088 | 0.7632 | 0.8579 | 0.0456 | 0.6018 | 0.5877 | 0.9053 | |
| Llama-3.1-Minitron-4B | 0.6632 | 0.8860 | 0.9386 | 0.7491 | 0.8555 | 0.1579 | 0.6263 | 0.5807 | 0.9439 | |
| Average | 0.5660 | 0.8039 | 0.8705 | 0.7575 | 0.8374 | 0.1116 | 0.4323 | 0.5895 | 0.8888 |
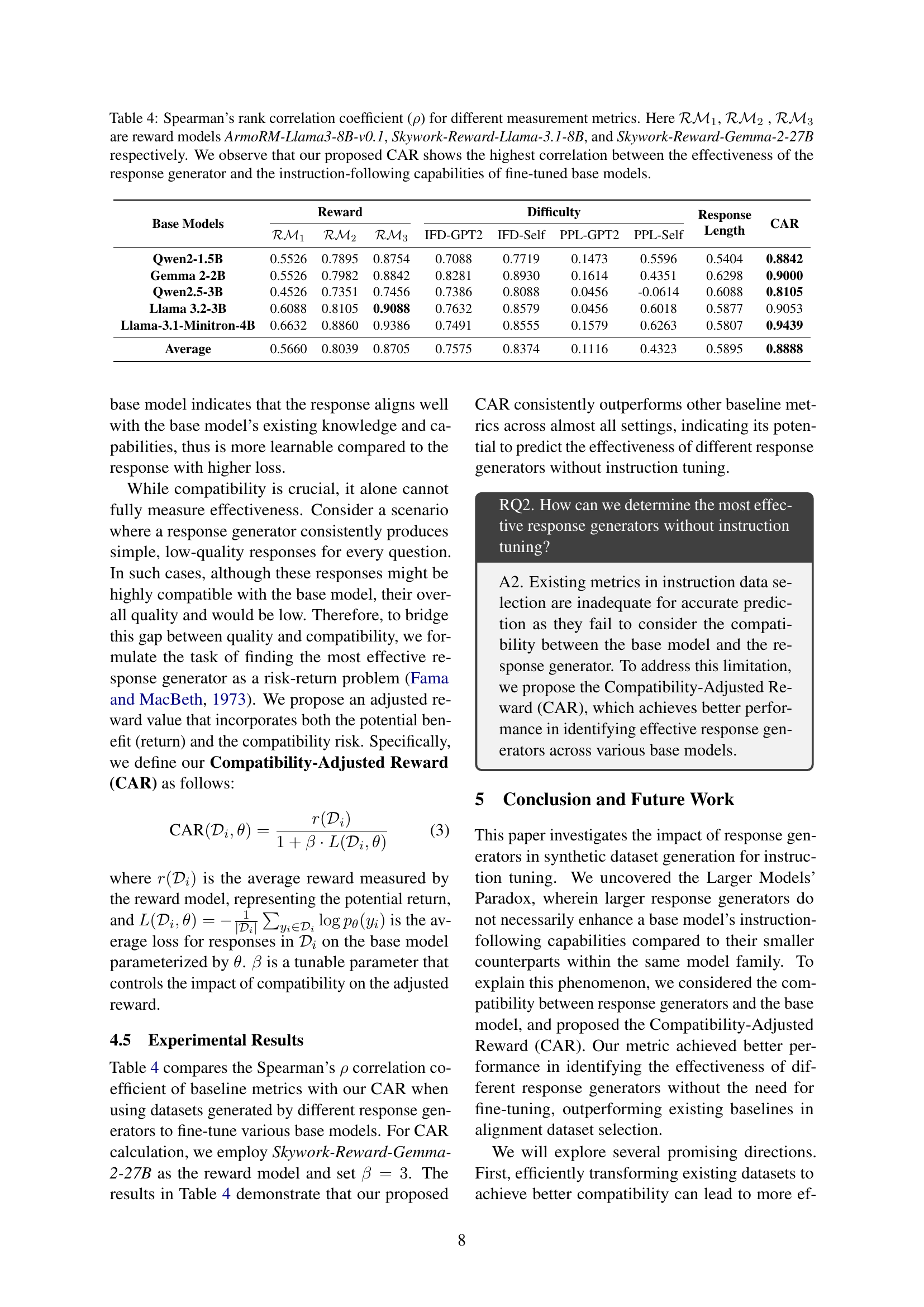
🔼 Table 4 presents Spearman’s rank correlation coefficients (ρ) to compare different metrics for evaluating response generators. The metrics include three reward models (ArmoRM-Llama3-8B-v0.1, Skywork-Reward-Llama-3.1-8B, and Skywork-Reward-Gemma-2-27B), instruction-following difficulty metrics (IFD-GPT2, IFD-Self, PPL-GPT2, PPL-Self), and response length. The table shows the correlation between each metric’s ranking of response generators and the actual average performance (AP) achieved after fine-tuning five different base models using instruction datasets generated by those response generators. The key finding is that the proposed Compatibility-Adjusted Reward (CAR) metric exhibits the strongest correlation, indicating its superior ability to predict the effectiveness of a response generator based on its compatibility with the base model.
read the caption
Table 4: Spearman’s rank correlation coefficient (ρ𝜌\rhoitalic_ρ) for different measurement metrics. Here ℛℳ1ℛsubscriptℳ1\mathcal{RM}_{1}caligraphic_R caligraphic_M start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT, ℛℳ2ℛsubscriptℳ2\mathcal{RM}_{2}caligraphic_R caligraphic_M start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT , ℛℳ3ℛsubscriptℳ3\mathcal{RM}_{3}caligraphic_R caligraphic_M start_POSTSUBSCRIPT 3 end_POSTSUBSCRIPT are reward models ArmoRM-Llama3-8B-v0.1, Skywork-Reward-Llama-3.1-8B, and Skywork-Reward-Gemma-2-27B respectively. We observe that our proposed CAR shows the highest correlation between the effectiveness of the response generator and the instruction-following capabilities of fine-tuned base models.
| Hyper-parameter | Value |
|---|---|
| Learning Rate | 2e-05 |
| Number of Epochs | 2 |
| Number of Devices | 4 |
| Per-device Batch Size | 1 |
| Gradient Accumulation Steps | 8 |
| Effective Batch Size | 32 |
| Optimizer | Adamw |
| Learning Rate Scheduler | cosine |
| Warmup Steps | 100 |
| Max Sequence Length | 4096 |
🔼 This table details the hyperparameters used in the supervised fine-tuning process of the language models. It includes the learning rate, number of epochs, batch size, optimizer, learning rate scheduler, and other parameters relevant to the training process.
read the caption
Table 5: This table shows the hyper-parameters for supervised fine-tuning.
| Base Model | Metric | Phi-3 Mini | Phi-3 Small | Phi-3 Medium | Phi-3 2B | Gemma 2 2B | Gemma 2 9B | Gemma 2 27B | Llama 3 8B | Llama 3 70B | Llama 3.1 405B | Llama 3.1 1.5B | Llama 3.1 7B | Llama 3.1 72B | Qwen2 3B | Qwen2 7B | Qwen2 14B | Qwen2 32B | Qwen2 72B | Qwen2.5 3B | Qwen2.5 7B | Qwen2.5 14B | Qwen2.5 32B | Qwen2.5 72B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Qwen2-1.5B | AE 2 WR | 3.65 | 3.64 | 2.80 | 5.34 | 6.13 | 5.49 | 3.39 | 3.74 | 2.76 | 3.49 | 3.09 | 2.83 | 4.09 | 3.35 | 5.60 | 6.84 | 5.13 | 5.65 | 7.03 | ||||
| AE 2 LC | 2.85 | 2.98 | 2.18 | 4.16 | 5.60 | 4.99 | 2.64 | 3.10 | 2.10 | 2.74 | 2.36 | 2.68 | 3.47 | 2.82 | 4.50 | 5.66 | 4.38 | 4.96 | 5.83 | |||||
| AH | 1.8 | 1.8 | 1.2 | 4.4 | 5.2 | 4.5 | 1.9 | 2.6 | 2.2 | 2.8 | 2.4 | 1.0 | 3.3 | 1.8 | 2.6 | 4.3 | 4.4 | 3.7 | 4.8 | |||||
| Gemma 2-2B | AE 2 WR | 6.60 | 6.54 | 4.54 | 16.88 | 11.83 | 12.09 | 7.09 | 8.49 | 7.20 | 9.45 | 8.92 | 2.14 | 7.11 | 6.07 | 7.91 | 12.00 | 8.07 | 9.19 | 16.68 | ||||
| AE 2 LC | 5.90 | 5.89 | 3.99 | 12.93 | 12.51 | 13.09 | 5.70 | 7.13 | 5.63 | 7.32 | 7.11 | 1.91 | 6.45 | 5.46 | 6.84 | 10.94 | 7.53 | 8.77 | 13.85 | |||||
| AH | 3.3 | 4.1 | 2.6 | 12.9 | 9.3 | 9.9 | 5.2 | 5.6 | 4.9 | 5.8 | 5.8 | 0.9 | 5.7 | 3.4 | 6.5 | 7.1 | 8.4 | 6.9 | 9.6 | |||||
| Qwen2.5-3B | AE 2 WR | 8.19 | 7.79 | 5.97 | 10.52 | 13.57 | 10.01 | 8.07 | 10.17 | 7.91 | 9.68 | 9.12 | 2.98 | 8.54 | 6.86 | 16.22 | 12.76 | 10.32 | 11.71 | 18.42 | ||||
| AE 2 LC | 7.22 | 7.29 | 5.49 | 9.58 | 13.78 | 10.18 | 7.85 | 9.37 | 7.22 | 8.94 | 8.59 | 2.54 | 7.98 | 6.59 | 14.79 | 11.89 | 10.28 | 11.65 | 16.41 | |||||
| AH | 10.5 | 11.0 | 8.3 | 11.8 | 19.4 | 19.6 | 9.7 | 11.4 | 10.9 | 13.8 | 12.7 | 2.1 | 14.4 | 10.6 | 24.8 | 20.4 | 17.9 | 19.9 | 21.2 | |||||
| Llama-3.2-3B | AE 2 WR | 4.88 | 3.54 | 3.05 | 8.89 | 11.45 | 10.58 | 4.67 | 5.45 | 4.26 | 6.68 | 6.44 | 1.72 | 6.23 | 5.13 | 6.09 | 7.72 | 6.82 | 7.10 | 12.12 | ||||
| AE 2 LC | 4.11 | 2.95 | 2.37 | 7.49 | 10.60 | 9.79 | 3.79 | 4.52 | 3.17 | 5.19 | 5.17 | 1.28 | 5.41 | 4.49 | 5.11 | 6.63 | 5.92 | 6.32 | 9.99 | |||||
| AH | 3.3 | 4.1 | 2.6 | 9.0 | 10.9 | 8.5 | 5.1 | 6.5 | 3.6 | 5.7 | 5.3 | 0.6 | 5.6 | 4.0 | 7.2 | 9.8 | 9.5 | 8.9 | 10.8 | |||||
| Llama-3.1-Minitron-4B | AE 2 WR | 6.35 | 7.11 | 4.83 | 11.80 | 14.50 | 11.90 | 6.11 | 9.87 | 8.24 | 9.61 | 10.03 | 2.30 | 7.84 | 8.45 | 10.27 | 12.05 | 11.30 | 11.65 | 19.58 | ||||
| AE 2 LC | 5.74 | 6.61 | 4.31 | 10.37 | 16.13 | 12.34 | 4.80 | 8.93 | 6.96 | 8.52 | 9.23 | 2.03 | 7.31 | 8.11 | 9.17 | 11.12 | 10.89 | 11.13 | 17.77 | |||||
| AH | 3.9 | 4.5 | 3.6 | 10.7 | 11.0 | 11.9 | 4.7 | 6.0 | 6.0 | 5.6 | 6.2 | 0.9 | 6.4 | 5.1 | 8.3 | 9.2 | 11.1 | 10.2 | 12.2 |
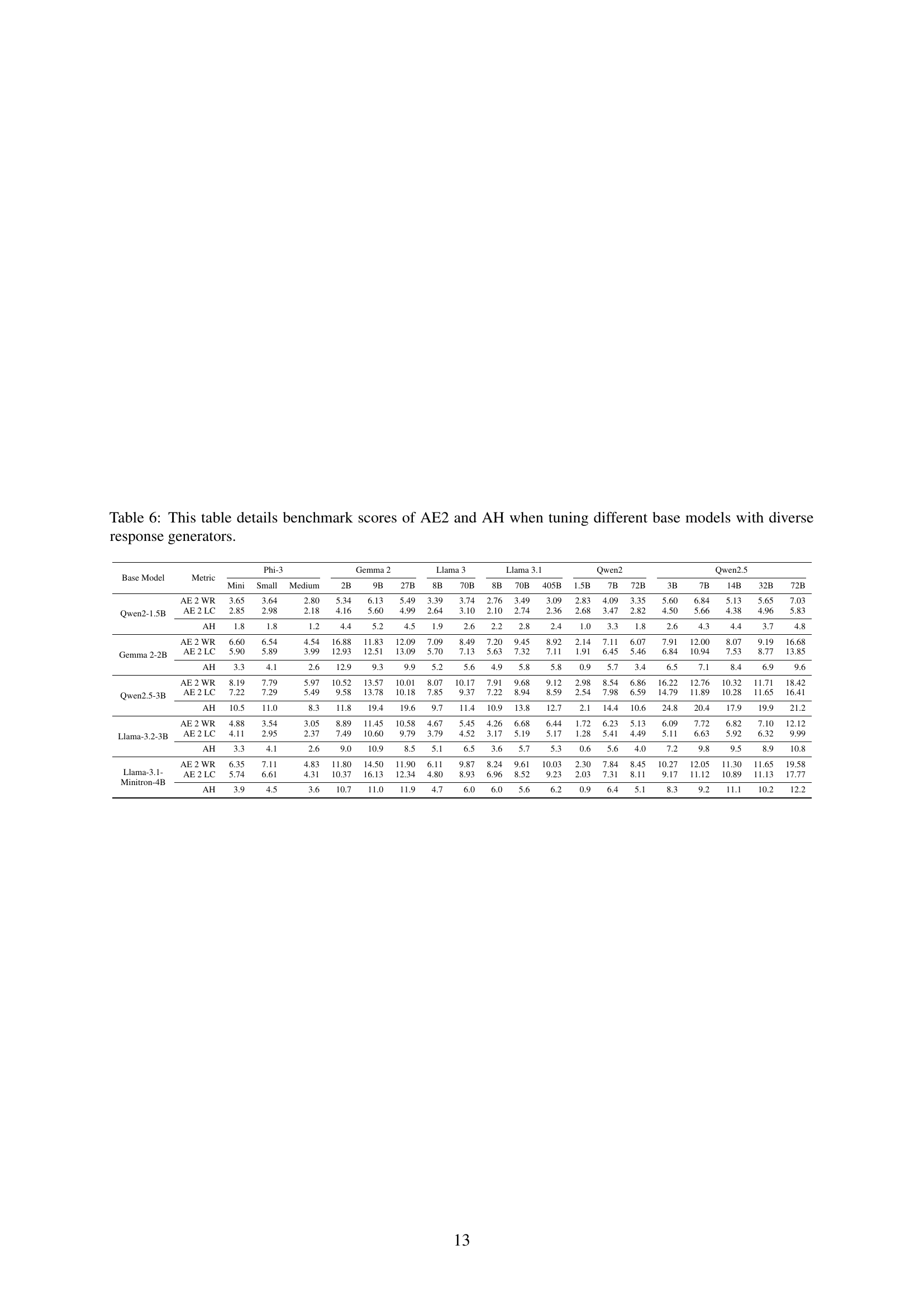
🔼 Table 6 presents a detailed breakdown of the performance of various base language models after being fine-tuned using instruction datasets generated by a diverse set of response generators. The performance is evaluated using two benchmark metrics: AlpacaEval 2 (AE2) and Arena-Hard (AH). AE2 and AH each provide a win rate (WR) and, in the case of AE2, a length-controlled win rate (LC) score for each model and response generator combination. This allows for a comprehensive comparison of different model and generator pairings across the two benchmarks.
read the caption
Table 6: This table details benchmark scores of AE2 and AH when tuning different base models with diverse response generators.
Full paper#