↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large Language Models (LLMs) often struggle with balancing factual accuracy and creative output because a single, fixed decoding temperature is used. Lower temperatures lead to factual but less creative text, while higher temperatures yield creative but sometimes inaccurate results. This is problematic for tasks requiring a mix of both. Existing approaches using manual tuning are time-consuming and task-specific.
This research introduces Adaptive Decoding, a method that adds a learnable layer to the LLM to dynamically select the decoding temperature at either the token or sequence level. To train this layer, the authors developed Latent Preference Optimization (LPO), a general approach for training discrete latent variables. The results demonstrate that Adaptive Decoding significantly outperforms fixed-temperature methods across various tasks, showing that adapting to task-specific needs with dynamic temperature improves LLM performance.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel method for improving the performance of large language models (LLMs) by dynamically adjusting the decoding temperature. This has significant implications for a wide range of applications involving LLMs, including creative writing, factual question answering, and general instruction following. The approach is general and applicable to other hyperparameters beyond temperature, opening up new avenues of research in LLM optimization. The proposed method shows significant performance improvements over existing fixed-temperature approaches across various tasks, underscoring the value of adaptive decoding strategies.
Visual Insights#

🔼 The figure illustrates the Adaptive Decoder module, a learnable layer added to a standard transformer-based language model to dynamically select decoding temperatures. The Adaptive Decoder consists of a new decoder head that takes the last hidden state as input and outputs a probability distribution over different temperature choices. These choices can be made at either the token or sequence level. At the token level, the model selects a unique temperature for each generated token, enabling fine-grained control over the output’s diversity and accuracy. At the sequence level, a single temperature is chosen for the entire sequence. This dynamic temperature selection allows the model to generate more factually consistent responses when needed (low temperature) and more creative outputs when appropriate (high temperature).
read the caption
Figure 1: The AdaptiveDecoder. This learned module is added to the standard transformer in order to select decoding hyperparameters. It consists of a new decoder head attached to the last hidden state which assigns probabilities to different hyperparameter choices per token (right) or sequence (left), and the highest probability choice is selected in each case. This allows the LLM to select low temperatures for tokens requiring factual consistency, and higher temperatures for tasks requiring creativity and diversity. For the token level adaptive decoder, a different temperature can be selected for different parts of the response given a single instruction.
| Method | 3-gram-repeats ↓ | % of non-greedy |
|---|---|---|
| Greedy Decoding | 0.36% | 0% |
| AdaptiveDecodertok | 0.22% | 94% |
🔼 This table presents the results of an experiment designed to evaluate the effectiveness of the AdaptiveDecodertok in reducing n-gram repetitions during text generation. The experiment involved feeding text from the Wikitext-2 dataset to a language model equipped with the AdaptiveDecodertok and measuring the frequency of n-gram repetitions in the generated text. The table shows that the AdaptiveDecodertok successfully learned to reduce these repetitions, and it achieved this by selecting non-greedy temperatures (higher temperatures produce more diverse and creative text, reducing the likelihood of repetition) in 94% of the samples.
read the caption
Table 1: Reducing Repeats using the AdaptiveDecoder. We feed text from Wikitext-2 to the model and ask it to complete it. When completing a text, AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT learns to avoid greedy decoding in order to reduce repeats. In 94% of samples, AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT learns to pick a non-greedy temperature.
In-depth insights#
Adaptive Decoding#
Adaptive decoding methods represent a significant advancement in natural language processing by dynamically adjusting decoding parameters during text generation. Instead of relying on a fixed temperature or sampling strategy, these methods learn to select optimal parameters (like temperature) based on the context of the input and the desired output. This adaptability allows models to balance creativity and accuracy, generating diverse and original text when appropriate, while maintaining factual correctness for tasks requiring precision. Latent Preference Optimization (LPO) is a particularly effective training method for adaptive decoders, allowing the model to learn to choose optimal parameters based on the rewards associated with different outputs. The benefits are substantial, leading to improved performance across various tasks and reducing the need for manual parameter tuning. The flexibility offered by adaptive decoding methods makes them a powerful tool for many NLP applications.
Latent Preference#
The concept of “Latent Preference” in the context of this research paper likely refers to the implicit, unobserved preferences that a language model exhibits when generating text. These preferences aren’t explicitly programmed but rather emerge from the model’s training data and architecture. The paper likely argues that these latent preferences influence the model’s choice of decoding temperature during text generation. By introducing a new layer (Adaptive Decoder) and a training method (Latent Preference Optimization), the authors aim to learn and control these latent preferences, allowing the model to dynamically adjust its output diversity and accuracy depending on the task. This approach is significant because it suggests that a model’s ability to generate high-quality text isn’t solely determined by its training but also by its ability to effectively manage these latent preferences, thus improving performance across a range of tasks requiring varying degrees of creativity and factuality.
LPO Optimization#
The proposed Latent Preference Optimization (LPO) method is a novel approach for training discrete latent variables, unlike traditional methods focusing on word tokens. LPO leverages the inherent preference signals within multiple model responses, ranking them according to a reward model or task-specific metric. This ranking generates preference pairs, forming the basis of training. The method’s generality extends beyond temperature selection, making it applicable to other discrete hyperparameters. Its key strength lies in its ability to learn optimal settings for diverse tasks by implicitly considering the tradeoff between exploration and exploitation, resulting in improved performance and task adaptability. A major advantage is its simplicity and efficiency, eliminating the need for complex reinforcement learning setups.
Empirical Results#
An ‘Empirical Results’ section in a research paper would ideally present a thorough and nuanced evaluation of the proposed method. It should go beyond simply stating performance metrics; instead, it would demonstrate a deep understanding of the results, addressing both strengths and limitations. The presentation should be clear, using tables and figures effectively to showcase key findings. A strong emphasis should be placed on comparing the new method’s performance against existing state-of-the-art approaches using appropriate benchmark datasets. Crucially, the discussion should interpret the results in the context of the research question, explaining their implications and suggesting avenues for future work. Statistical significance, if applicable, needs to be carefully considered and reported. Finally, any unexpected or counter-intuitive results should be discussed, and potential explanations offered.
Future Work#
Future research could explore several promising avenues. Extending LPO to other hyperparameters beyond temperature, such as top-k or top-p, would broaden the applicability and impact of adaptive decoding. Investigating the interaction between adaptive decoding and other LLM training techniques like RLHF warrants further study. Analyzing the effect of different neural architectures for the ADAPTIVEDECODER is crucial to optimize performance and efficiency. Moreover, a thorough exploration of the trade-off between accuracy and diversity with varying task types and prompt structures is needed. Finally, evaluating the model’s robustness and generalizability across diverse datasets and languages will help determine its practical implications. Benchmarking against other adaptive decoding methods can further highlight the advantages and limitations of LPO. The scalability and computational cost of the proposed approach also need careful consideration for real-world deployment.
More visual insights#
More on figures

🔼 This figure illustrates the Latent Preference Optimization (LPO) training process. Two different responses are generated for the same input prompt using the Adaptive Decoder module. A reward model (RM) evaluates the responses and assigns a higher score to one. The temperature used to generate the higher-scoring response (τ=0.6) is considered the ‘chosen’ temperature, while the temperature used for the lower-scoring response (τ=0.2) is the ‘rejected’ temperature. The LPO loss function is then used to train the model to favor the ‘chosen’ temperature over the ‘rejected’ temperature for similar inputs.
read the caption
Figure 2: Latent Preference Optimization (LPO) Training Mechanism. We demonstrate how preference pairs are constructed for training the LPO loss (we show a Sequence-Level AdaptiveDecoder, but the procedure remains the same for Token-Level). Here we have N=2 generated response samples for a single prompt, and the Reward Model (RM) scores Response1 better than Response2. Therefore, we use τ=0.6𝜏0.6\tau=0.6italic_τ = 0.6 as the chosen temperature, and τ=0.2𝜏0.2\tau=0.2italic_τ = 0.2 as the rejected temperature, and then apply the loss to prefer the chosen temperature over the rejected one for the given context (prompt).

🔼 Figure 3 presents the results of experiments conducted on the UltraMathStories dataset, which combines UltraFeedback, GSM8K, and Stories datasets. Adaptive decoding models (both sequence-level and token-level) were trained on all three subtasks simultaneously. The figure displays win-rates, averaged across the three test sets, comparing the adaptive decoding models to multiple models using fixed decoding temperatures. The left panel shows the comparison using the sequence-level adaptive decoder, and the right panel illustrates the results for the token-level adaptive decoder. In both cases, the adaptive decoding approach demonstrates superior performance compared to all fixed temperature baselines.
read the caption
Figure 3: UltraMathStories Results. UltraMathStories is a superset of UltraFeedback, GSM8K, and Stories. The Adaptive Decoding models are trained on all 3 subtasks simultaneously. Winrates are shown as the average winrate across the test sets of the 3 subtasks in UltraMathStories. (left) AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT vs Fixed Temperature Winrates. (right) AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT vs Fixed Temperature Winrates. In both cases, Adaptive Decoding outperforms all fixed temperatures.

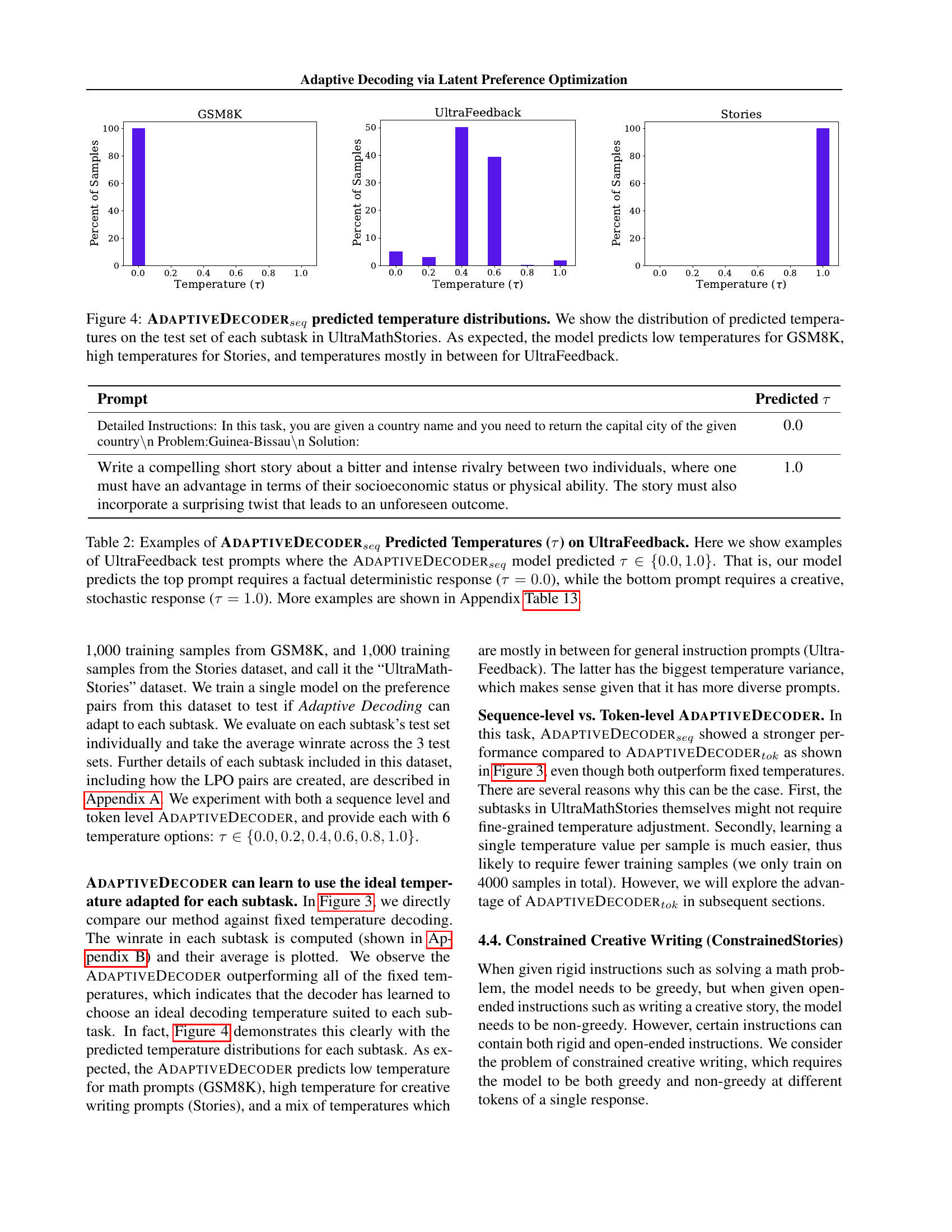
🔼 Figure 4 presents the distributions of predicted temperatures generated by the ADAPTIVEDECODERseq model on three different subtasks within the UltraMathStories dataset: GSM8K (mathematical reasoning), Stories (creative writing), and UltraFeedback (general instructions). The x-axis represents the temperature values, and the y-axis shows the percentage of samples with a given temperature. As expected, the model demonstrates task-appropriate temperature selection: lower temperatures are predicted for the GSM8K task (requiring factual accuracy), higher temperatures are used for the Stories task (emphasizing creativity), and intermediate temperatures are prevalent in UltraFeedback (a mix of creative and factual tasks). This visualization highlights the model’s ability to adapt its decoding temperature dynamically according to task demands.
read the caption
Figure 4: AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT predicted temperature distributions. We show the distribution of predicted temperatures on the test set of each subtask in UltraMathStories. As expected, the model predicts low temperatures for GSM8K, high temperatures for Stories, and temperatures mostly in between for UltraFeedback.

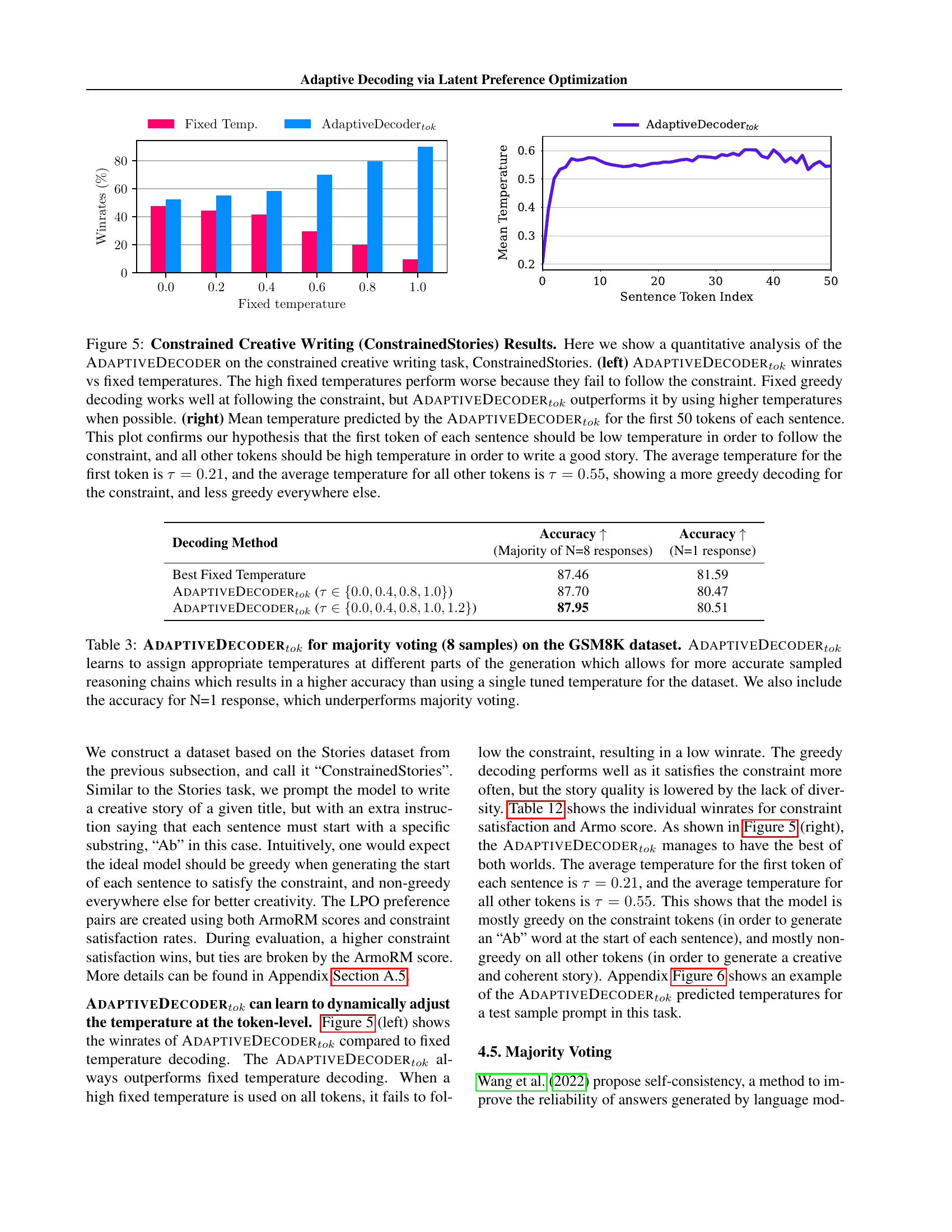
🔼 Figure 5 presents a comparative analysis of the Adaptive Decoder’s performance on a constrained creative writing task. The left panel displays win rates for the Adaptive Decoder (token-level) against various fixed temperature settings. It demonstrates that while fixed greedy decoding excels at constraint adherence, the Adaptive Decoder achieves superior performance by strategically employing higher temperatures whenever feasible. The right panel shows the average predicted temperature across the first 50 tokens of each sentence. This visualization confirms the hypothesis that lower temperatures are optimal for initial tokens (to maintain constraint compliance), while higher temperatures are preferable for subsequent tokens (to foster narrative creativity). The average temperature for the first token is 0.21, indicating a preference for greedy decoding in this context, whereas the average temperature for subsequent tokens is 0.55, showing a less greedy approach, allowing for more creative output.
read the caption
Figure 5: Constrained Creative Writing (ConstrainedStories) Results. Here we show a quantitative analysis of the AdaptiveDecoder on the constrained creative writing task, ConstrainedStories. (left) AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT winrates vs fixed temperatures. The high fixed temperatures perform worse because they fail to follow the constraint. Fixed greedy decoding works well at following the constraint, but AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT outperforms it by using higher temperatures when possible. (right) Mean temperature predicted by the AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT for the first 50 tokens of each sentence. This plot confirms our hypothesis that the first token of each sentence should be low temperature in order to follow the constraint, and all other tokens should be high temperature in order to write a good story. The average temperature for the first token is τ=0.21𝜏0.21\tau=0.21italic_τ = 0.21, and the average temperature for all other tokens is τ=0.55𝜏0.55\tau=0.55italic_τ = 0.55, showing a more greedy decoding for the constraint, and less greedy everywhere else.

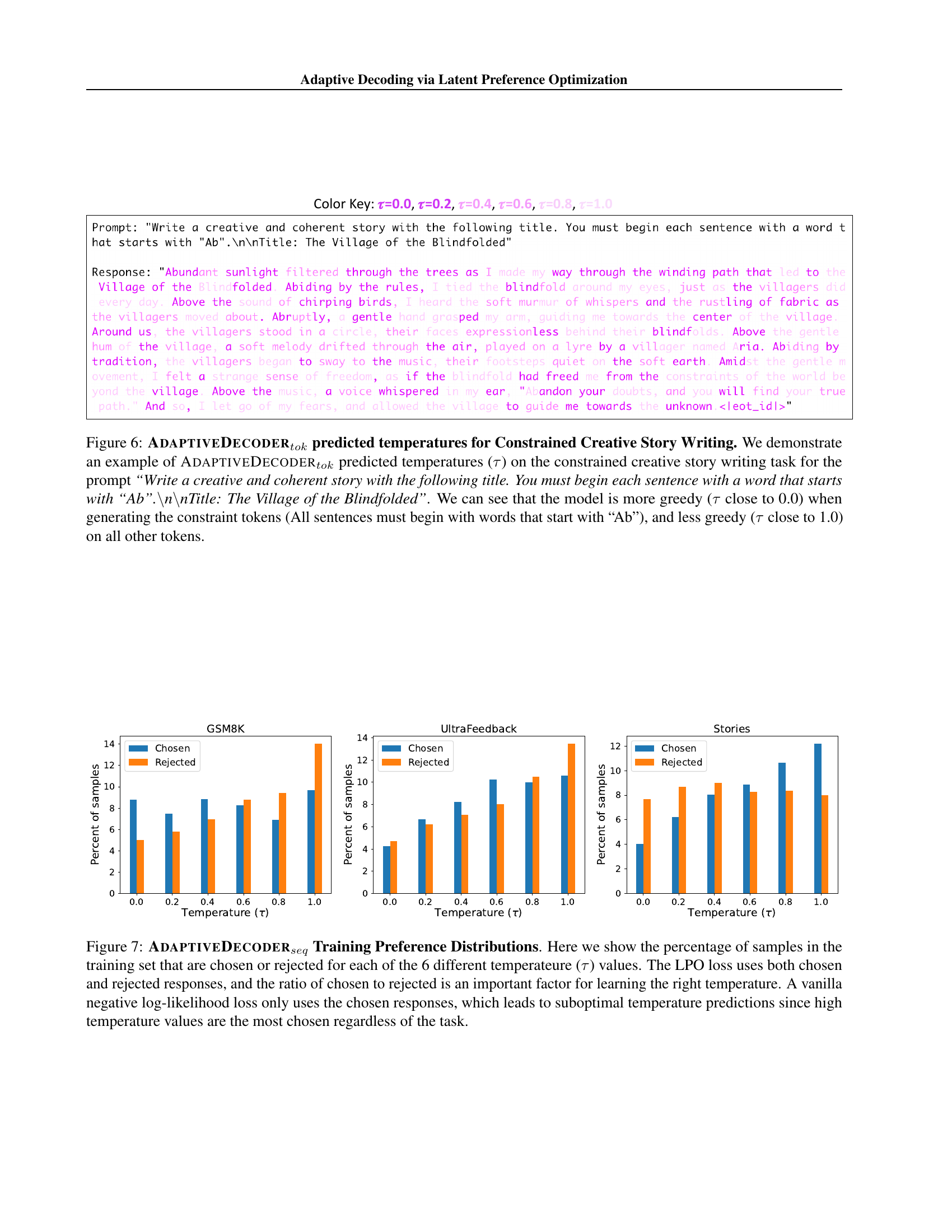
🔼 Figure 6 presents the AdaptiveDecodertok’s predicted temperature values for a constrained creative story-writing task. The model is tasked with writing a coherent story, but each sentence must begin with a word starting with ‘Ab’. The figure shows the model’s temperature selection for each token in the generated text. Low temperatures (closer to 0.0) indicate greedy decoding, favoring high-probability words, which is necessary for meeting the constraint of starting each sentence with ‘Ab’. High temperatures (closer to 1.0) correspond to less greedy decoding, allowing for more diverse and creative word choices. As expected, the model uses low temperatures for the constraint-satisfying tokens at the beginning of each sentence and then higher temperatures for other tokens, demonstrating that it learns to adapt its temperature choices depending on the specific requirements of the task.
read the caption
Figure 6: AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT predicted temperatures for Constrained Creative Story Writing. We demonstrate an example of AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT predicted temperatures (τ𝜏\tauitalic_τ) on the constrained creative story writing task for the prompt “Write a creative and coherent story with the following title. You must begin each sentence with a word that starts with “Ab”.\n\nTitle: The Village of the Blindfolded”. We can see that the model is more greedy (τ𝜏\tauitalic_τ close to 0.0) when generating the constraint tokens (All sentences must begin with words that start with “Ab”), and less greedy (τ𝜏\tauitalic_τ close to 1.0) on all other tokens.

🔼 Figure 7 illustrates the training data distribution for the Latent Preference Optimization (LPO) method used to train the ADAPTIVEDECODER model. It shows, for each of six temperature values (τ), the percentage of training samples that were labeled as ‘chosen’ (preferred) versus ‘rejected’ (less preferred) by the reward model. The ratio of chosen to rejected samples is crucial for the LPO loss function to learn effective temperature selection. In contrast, a standard negative log-likelihood loss, which only considers chosen samples, would lead to suboptimal temperature choices, as high temperatures tend to be more frequently chosen, irrespective of their actual effectiveness on different tasks.
read the caption
Figure 7: AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT Training Preference Distributions. Here we show the percentage of samples in the training set that are chosen or rejected for each of the 6 different temperateure (τ𝜏\tauitalic_τ) values. The LPO loss uses both chosen and rejected responses, and the ratio of chosen to rejected is an important factor for learning the right temperature. A vanilla negative log-likelihood loss only uses the chosen responses, which leads to suboptimal temperature predictions since high temperature values are the most chosen regardless of the task.
More on tables
| Prompt | Predicted τ |
|---|---|
| Detailed Instructions: In this task, you are given a country name and you need to return the capital city of the given country. Problem:Guinea-Bissau Solution: | 0.0 |
| Write a compelling short story about a bitter and intense rivalry between two individuals, where one must have an advantage in terms of their socioeconomic status or physical ability. The story must also incorporate a surprising twist that leads to an unforeseen outcome. | 1.0 |
🔼 Table 2 shows examples from the UltraFeedback test set where the model’s Adaptive Decoder chose either a very low temperature (0.0, for deterministic, factual responses) or a very high temperature (1.0, for creative, stochastic responses). This illustrates the model’s ability to dynamically select appropriate temperatures based on the task’s requirements. Additional examples are provided in Appendix Table 13.
read the caption
Table 2: Examples of AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT Predicted Temperatures (τ𝜏\tauitalic_τ) on UltraFeedback. Here we show examples of UltraFeedback test prompts where the AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT model predicted τ∈{0.0,1.0}𝜏0.01.0\tau\in\{0.0,1.0\}italic_τ ∈ { 0.0 , 1.0 }. That is, our model predicts the top prompt requires a factual deterministic response (τ=0.0𝜏0.0\tau=0.0italic_τ = 0.0), while the bottom prompt requires a creative, stochastic response (τ=1.0𝜏1.0\tau=1.0italic_τ = 1.0). More examples are shown in Appendix Table 13.
| Decoding Method | Accuracy ↑ (Majority of N=8 responses) | Accuracy ↑ (N=1 response) |
|---|---|---|
| Best Fixed Temperature | 87.46 | 81.59 |
| \textsc{AdaptiveDecoder}_{tok} ($\tau\in{0.0,0.4,0.8,1.0}$) | 87.70 | 80.47 |
| \textsc{AdaptiveDecoder}_{tok} ($\tau\in{0.0,0.4,0.8,1.0,1.2}$) | 87.95 | 80.51 |
🔼 This table presents the results of using the AdaptiveDecodertok model for majority voting on the GSM8K dataset. The AdaptiveDecodertok model dynamically adjusts the decoding temperature during generation, leading to more accurate reasoning chains compared to using a single, fixed temperature. The table shows accuracy improvements when using majority voting (averaging results from 8 samples) and highlights the lower accuracy of using a single response, demonstrating the benefits of the AdaptiveDecodertok’s adaptive approach.
read the caption
Table 3: AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT for majority voting (8 samples) on the GSM8K dataset. AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT learns to assign appropriate temperatures at different parts of the generation which allows for more accurate sampled reasoning chains which results in a higher accuracy than using a single tuned temperature for the dataset. We also include the accuracy for N=1 response, which underperforms majority voting.
| Fixed Temperature | AdaptiveDecoderseq | τ=0 | τ=0.6 | τ=1.0 | |||
|---|---|---|---|---|---|---|---|
| 81.59 | 81.59 | 81.59 | 79.15 | 78.32 | ℒLPO | ℒLPO | ℒNLL |
🔼 This table presents a comparison of different loss functions used to train a sequence-level Adaptive Decoder model on the GSM8K dataset. The goal is to determine which loss function yields the best accuracy. Three loss functions are compared: two variants of the Latent Preference Optimization (LPO) loss (detailed in section 3.3) and the standard negative log-likelihood (NLL) loss. The NLL loss is trained only on the chosen responses from the preference pairs, while the LPO loss functions utilize both chosen and rejected responses to learn the optimal parameters for selecting temperatures. The table shows the accuracy achieved by each loss function on the GSM8K dataset, allowing for a direct comparison of their performance.
read the caption
Table 4: GSM8K Accuracy comparing different loss functions for training a sequence-leval AdaptiveDecoder (ADseqsubscriptAD𝑠𝑒𝑞\textsc{AD}_{seq}AD start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT). We compare two different ℒLPOsubscriptℒLPO\mathcal{L}_{\text{LPO{}}}caligraphic_L start_POSTSUBSCRIPT LPO end_POSTSUBSCRIPT loss functions, as outlined in Section 3.3, as well as negative log likelihood loss, ℒNLLsubscriptℒNLL\mathcal{L}_{\text{NLL}}caligraphic_L start_POSTSUBSCRIPT NLL end_POSTSUBSCRIPT, trained on the chosen responses from the preference pairs.
🔼 This table compares two methods for selecting temperatures (a hyperparameter controlling randomness in text generation) within the AdaptiveDecoder model. The AdaptiveDecoder model dynamically chooses the temperature for each token generated, balancing creativity and accuracy. The first method involves sampling a temperature from a probability distribution. The second method greedily selects the temperature with the highest probability. The table shows the win rates (percentage of correct predictions) for each temperature selection method against fixed temperature methods for UltraFeedback. UltraFeedback represents a diverse set of tasks requiring varying levels of randomness in the outputs. Results show the AdaptiveDecoder consistently outperforms the fixed temperature baselines across different temperatures, irrespective of the temperature selection method used.
read the caption
Table 5: AdaptiveDecoder Temperature Selection Methods on UltraFeedback. The AdaptiveDecoder outputs a distribution over temperature values τ𝜏\tauitalic_τ, so we can either sample τ𝜏\tauitalic_τ from that distribution or greedily select the highest probability τ𝜏\tauitalic_τ. Here we show winrates against the fixed temperature decoding in the left column, using the AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT model trained on UltraMathStories (Section 4.3). All the winrates are above 50%, which means the AdaptiveDecoder always outperforms the fixed temperature. Also, we do not observe a significant difference between the two temperature selection methods.
| Fixed Temp | AdaptiveDecoderseq Winrate | Fixed Temp Winrate |
|---|---|---|
| τ=0.0 | 53.10 | 46.90 |
| τ=0.2 | 53.35 | 46.65 |
| τ=0.4 | 50.80 | 49.20 |
| τ=0.6 | 52.15 | 47.85 |
| τ=0.8 | 52.78 | 47.22 |
| τ=1.0 | 54.89 | 45.11 |
🔼 This table presents a comparison of the win rates achieved by the ADAPTIVEDECODERseq model against various fixed temperatures on the UltraFeedback task. The ADAPTIVEDECODERseq model dynamically adjusts the decoding temperature, offering a potential improvement over static temperature approaches. The win rate, a common metric for evaluating model performance, is presented for different fixed temperatures to highlight the impact of temperature on performance.
read the caption
Table 6: AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT vs Fixed Temperatures Winrates on the UltraFeedback Task.
| Fixed Temp | AdaptiveDecoderseq Winrate | Fixed Temp Winrate |
|---|---|---|
| τ=0.0 | 58.75 | 41.25 |
| τ=0.2 | 57.25 | 42.75 |
| τ=0.4 | 57.05 | 42.95 |
| τ=0.6 | 56.65 | 43.35 |
| τ=0.8 | 54.55 | 45.45 |
| τ=1.0 | 52.10 | 47.90 |
🔼 This table presents the results of comparing the performance of the sequence-level adaptive decoder (ADseq) against fixed-temperature decoding methods on a creative story writing task. Winrates are calculated by comparing the ADseq model’s outputs to outputs generated using various fixed temperatures. Higher winrates indicate superior performance. This comparison helps to demonstrate the effectiveness of the adaptive decoding approach in achieving higher accuracy compared to a single, fixed temperature setting.
read the caption
Table 7: AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT vs Fixed Temperatures Winrates on the Stories Task.
| Fixed Temp | AdaptiveDecoderseq Winrate | Fixed Temp Winrate |
|---|---|---|
| τ=0.0 | 50.68 | 49.32 |
| τ=0.2 | 51.10 | 48.90 |
| τ=0.4 | 51.14 | 48.86 |
| τ=0.6 | 51.40 | 48.60 |
| τ=0.8 | 51.42 | 48.58 |
| τ=1.0 | 51.82 | 48.18 |
🔼 This table presents the win rates achieved by the ADAPTIVEDECODERseq model, compared to models using fixed temperatures, on the GSM8K (Grade School Math 8K) task. The GSM8K task involves solving math word problems, and the win rate represents the percentage of problems where the ADAPTIVEDECODERseq model’s solution was more accurate than the model using a fixed temperature. The table helps demonstrate the ADAPTIVEDECODERseq model’s ability to adapt its temperature dynamically to improve accuracy on a specific task.
read the caption
Table 8: AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT vs Fixed Temperatures Winrates on the GSM8K Task.
| Fixed Temp | AdaptiveDecodertok Winrate | Fixed Temp Winrate |
|---|---|---|
| τ=0.0 | 49.60 | 50.40 |
| τ=0.2 | 50.70 | 49.30 |
| τ=0.4 | 48.75 | 51.25 |
| τ=0.6 | 49.60 | 50.40 |
| τ=0.8 | 49.25 | 50.75 |
| τ=1.0 | 52.75 | 47.25 |
🔼 This table presents a comparison of the win rates achieved by the AdaptiveDecodertok model and those obtained using fixed temperature decoding strategies on the UltraFeedback task. It shows the performance of AdaptiveDecodertok (a model that dynamically adjusts decoding temperature) against several fixed-temperature baselines (0.0, 0.2, 0.4, 0.6, 0.8, and 1.0). Each row represents a different fixed temperature, and the win rate is a measure of the model’s success relative to the baselines on the UltraFeedback task.
read the caption
Table 9: AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT vs Fixed Temperatures Winrates on the UltraFeedback Task.
| Fixed Temp | AdaptiveDecodertok Winrate | Fixed Temp Winrate |
|---|---|---|
| τ=0.0 | 54.40 | 45.60 |
| τ=0.2 | 53.40 | 46.60 |
| τ=0.4 | 54.20 | 45.80 |
| τ=0.6 | 52.30 | 47.70 |
| τ=0.8 | 51.10 | 48.90 |
| τ=1.0 | 47.25 | 52.75 |
🔼 This table presents a comparison of the win rates achieved by using the token-level adaptive decoder (AdaptiveDecodertok) against those obtained using various fixed temperatures for text generation in a creative story writing task. The win rate is a measure of the model’s success in generating high-quality responses compared to a baseline. The table helps to illustrate the effectiveness of dynamically adjusting the temperature during decoding compared to employing a fixed temperature across all text generations.
read the caption
Table 10: AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT vs Fixed Temperatures Winrates on the Stories Task.
| Fixed Temp | AdaptiveDecodertok Winrate | Fixed Temp Winrate |
|---|---|---|
| (\tau=0.0) | 49.66 | 50.34 |
| (\tau=0.2) | 50.08 | 49.92 |
| (\tau=0.4) | 50.11 | 49.89 |
| (\tau=0.6) | 50.38 | 49.62 |
| (\tau=0.8) | 50.49 | 49.51 |
| (\tau=1.0) | 51.55 | 48.45 |
🔼 This table presents the win rates achieved by the AdaptiveDecodertok model compared to models using fixed temperatures on the GSM8K math reasoning task. The AdaptiveDecodertok model dynamically adjusts the decoding temperature at the token level, while the fixed-temperature models use a single temperature throughout the entire decoding process. Win rate is a metric representing the percentage of times a model’s answer to a question was correct compared to another method.
read the caption
Table 11: AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT vs Fixed Temperatures Winrates on the GSM8K Task.
| Fixed Temp | AdaptiveDecodertok Constraint Winrate | AdaptiveDecodertok ArmoRM Winrate | AdaptiveDecodertok Avg Winrate |
|---|---|---|---|
| τ=0.0 | 50.95 | 52.55 | 51.75 |
| τ=0.2 | 53.70 | 49.50 | 51.60 |
| τ=0.4 | 58.05 | 48.25 | 53.15 |
| τ=0.6 | 68.05 | 41.05 | 54.55 |
| τ=0.8 | 77.85 | 36.45 | 57.15 |
| τ=1.0 | 87.80 | 31.50 | 59.65 |
🔼 This table presents a detailed breakdown of the performance of the AdaptiveDecodertok model on a constrained creative writing task. It shows the individual win rates for two separate evaluation metrics: constraint satisfaction (how well the model followed the rule of starting each sentence with ‘Ab’) and ArmoRM score (a measure of the quality of the generated story). The results are compared against using various fixed temperatures during decoding. The AdaptiveDecodertok model demonstrates an ability to balance constraint satisfaction with story quality, outperforming fixed temperature approaches. However, as fixed temperatures increase, the constraint satisfaction rate improves at the cost of lower story quality, highlighting the model’s ability to dynamically adjust temperature during generation.
read the caption
Table 12: AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT Constrained Creative Writing Individual Winrates. Here we show the individual winrates of the AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT for both constraint following and ArmoRM score. The AdaptiveDecodertoksubscriptAdaptiveDecoder𝑡𝑜𝑘\textsc{AdaptiveDecoder}_{tok}AdaptiveDecoder start_POSTSUBSCRIPT italic_t italic_o italic_k end_POSTSUBSCRIPT learns to follow the constraint better than all fixed temperatures, but as we compare to higher fixed temperatures, the story winrate goes down because it follows the constraint better.
| Predicted τ=0.0 | |
|---|---|
| In this task, given a sentence in the English language, your task is to convert it into the Thai language. | |
| Problem:The secondary principals’ association head, Graham Young, said: T̈he NCEA system put pressure on schools to accumulate credits - and the easiest way to do that was to encourage students into internally assessed unit standards. | |
| Solution: | |
| You are given a math word problem and you are supposed to apply multiple mathematical operators like addition, subtraction, multiplication, or division on the numbers embedded in the text to answer the following question and then only report the final numerical answer. | |
| Input: Consider Input: debby makes 67 pancakes . she adds blueberries to 20 of them and bananas to 24 of them . the rest are plain . how many plain pancakes are there ? | |
| You have been tasked with arranging a group of travelers, each with different preferences and needs, onto various modes of transportation. There are four modes of transportation available: A, B, C, and D. Each mode has its own unique features and limitations. The travelers and their preferences are as follows: | |
| 1. Alice: Is afraid of flying and prefers to take mode C or D | |
| 2. Bob: Can only travel by mode A due to motion sickness | |
| 3. Charlie: Wants to take mode B because it has the shortest travel time | |
| 4. Dave: Needs to take mode D because he has a lot of luggage | |
| 5. Ellie: Wants to take mode A because she enjoys the scenic route | |
| Your task is to assign each traveler to the mode of transportation that best suits their needs and preferences. Keep in mind that each mode of transportation can only accommodate a certain number of people, and some modes may have already reached their capacity. Can you solve this puzzle and successfully group the travelers onto their preferred modes of transportation? | |
| Predicted τ=1.0 | |
| Write a 70,000 word fantasy novel about a hidden world of magic and mythical creatures. The main character must be a human who discovers this world and becomes involved in a conflict between the magical creatures. The novel should have a fast-paced plot with plenty of action and suspense. The style should be descriptive and immersive, with detailed descriptions of the magical world and its inhabitants. The novel should also explore themes such as the nature of power and the importance of loyalty and friendship. | |
| Write me a 1000 word ghost story in a campfire setting | |
| Write a story about Ego Must, a prominent innovator with technology who leverages his vast wealth to communicate his views. However, despite being exceptionally smart he seems to not understand the basics when it comes to the ’us and them’ problem that is at the root of a lot of human conflict. |
🔼 Table 13 presents examples from the UltraFeedback test set where the AdaptiveDecoder model predicted temperatures of either 0.0 or 1.0. The examples demonstrate the model’s ability to adapt its decoding strategy: prompts with a predicted temperature of 0.0 require factual, deterministic answers, while those with a predicted temperature of 1.0 call for creative, stochastic responses. This showcases the model’s capacity to generalize beyond the specific tasks (GSM8K and Stories) used in its initial training.
read the caption
Table 13: Examples of AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT Predicted Temperatures (τ𝜏\tauitalic_τ) on UltraFeedback. Here we show examples of UltraFeedback test prompts where the AdaptiveDecoderseqsubscriptAdaptiveDecoder𝑠𝑒𝑞\textsc{AdaptiveDecoder}_{seq}AdaptiveDecoder start_POSTSUBSCRIPT italic_s italic_e italic_q end_POSTSUBSCRIPT model predicted τ∈{0.0,1.0}𝜏0.01.0\tau\in\{0.0,1.0\}italic_τ ∈ { 0.0 , 1.0 }. We can see that the τ=0.0𝜏0.0\tau=0.0italic_τ = 0.0 prompts require factual, deterministic responses, and the τ=1.0𝜏1.0\tau=1.0italic_τ = 1.0 prompts require creative, stochastic responses. This shows generalization outside of the GSM8K and Stories subtasks to specific prompts within UltraFeedback.
Full paper#