↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Deep learning models heavily rely on attention mechanisms, but these are computationally expensive. Existing methods, like FlashAttention, aim to improve efficiency but still face limitations. The high computational cost of attention significantly restricts the scalability and speed of models, particularly for long sequences. Current quantization techniques mostly target linear layers; efficient quantization for attention remains challenging, often sacrificing accuracy.
SageAttention2 tackles this challenge by using a novel 4-bit quantization strategy. It employs a mix of precision techniques, including 4-bit quantization for query (Q) and key (K) matrices, and 8-bit for value (V) matrices. Key innovations include warp-level granularity quantization, smoothing techniques to enhance accuracy, and an adaptive quantization approach to handle variability across different layers and timesteps. This approach results in a significant speed improvement (3x-5x faster than existing methods like FlashAttention2 and xformers) with negligible impact on overall accuracy across various deep learning models.
Key Takeaways#
Why does it matter?#
This paper is important because it presents SageAttention2, a novel method for accelerating attention mechanisms in deep learning models. This is crucial because attention is computationally expensive, limiting the size and speed of models. The method’s plug-and-play nature and minimal accuracy loss make it highly practical for researchers, and its speed improvements are significant. It opens avenues for research into efficient quantization techniques and high-performance attention implementations.
Visual Insights#

🔼 This figure is a composite of two sub-figures. The left sub-figure presents a bar chart illustrating the kernel speedup achieved by SageAttention2 compared to FlashAttention2 on an RTX 4090 GPU. It showcases the significant performance improvement of SageAttention2. The right sub-figure displays the end-to-end inference speedup and performance metrics for the same models, but this time focusing on the ’needle-in-a-haystack’ task using the LLaMA-3-8B model. The task is performed with a sequence length of 100K tokens, providing a comparison of the inference speed across the two attention mechanisms.
read the caption
Figure 1: The left figure shows the kernel speedup on RTX4090 GPU. The right figure shows the end-to-end inference speedup of generating the first token and performance metrics for the needle-in-a-haystack task (gkamradt, 2023) with a sequence length of 100K on Llama3.1 on L20 GPU.
| Method | Smoothing (Q+K) | Llama 3.1 (Lambda) ↑ | Llama 3.1 (WikiText) ↓ | CogVideo (vqa-a) ↑ | CogVideo (vqa-t) ↑ |
|---|---|---|---|---|---|
| Full-Precision | - | 81.5% | 6.013 | 77.605 | 75.360 |
| INT4 Quantization | ✗ | 72.6% | 11.698 | 27.114 | 24.670 |
| ✓ | 80.8% | 6.219 | 77.276 | 75.147 |
🔼 This table presents a comparison of end-to-end performance metrics across various quantization methods. The focus is on the impact of quantizing the Q and K matrices to 4-bit integers (INT4), while keeping the P and V matrices at full precision. The metrics used allow for evaluation of the accuracy loss introduced by the quantization process. The table helps to assess whether quantizing Q and K to INT4 while maintaining P and V at full precision leads to significant performance degradation.
read the caption
Table 1: End-to-end metrics comparison of different quantization methods, where Q,K are quantized into INT4, while P,V stay in full precision.
In-depth insights#
4-bit Attention#
The concept of “4-bit Attention” signifies a significant advancement in efficient deep learning, particularly concerning the computationally intensive attention mechanism. Reducing the precision of attention calculations from the typical 8-bit or 16-bit to just 4-bit dramatically reduces memory bandwidth and computational costs. This is crucial for deploying large language models and other resource-demanding AI applications on devices with limited resources. However, such drastic quantization introduces challenges in maintaining accuracy. The research likely explores novel techniques to mitigate the loss of precision inherent in 4-bit quantization, potentially involving innovative quantization methods, advanced precision-enhancing techniques, or adaptive precision strategies. These techniques may focus on minimizing quantization error, preserving important information, or dynamically adjusting precision based on the context or the layers of the neural network. The successful implementation of 4-bit attention would be a major breakthrough, enabling faster and more efficient inference, particularly on edge devices and resource-constrained environments. The trade-off between speed and accuracy is a key focus, aiming for a balance where the considerable gains in speed do not come at the expense of unacceptable accuracy degradation.
Quantization Methods#
The research paper explores various quantization methods to accelerate attention mechanisms in deep learning models. A core challenge is balancing computational efficiency with accuracy loss during quantization. The authors investigate different quantization granularities (per-tensor, per-channel, per-block, per-warp) for quantizing the query (Q) and key (K) matrices, highlighting the trade-offs involved. Per-warp quantization emerges as a superior approach, offering a balance between accuracy and efficiency. They also explore quantization strategies for the product (P) and value (V) matrices, using lower precision formats like FP8 to leverage hardware acceleration. Innovative smoothing techniques for Q, K, and V matrices are introduced to mitigate accuracy loss associated with quantization. Adaptive quantization, which selectively applies different quantization levels across different model layers or time steps, is a key contribution to maintaining end-to-end performance. The study demonstrates that the chosen quantization methods significantly enhance computational speed while only minimally affecting accuracy across diverse model architectures.
Adaptive Precision#
Adaptive precision in deep learning models, particularly in attention mechanisms, aims to dynamically adjust the numerical precision of computations based on the characteristics of the data or the specific layer/timestep. This contrasts with fixed-precision methods, offering potential benefits in terms of accuracy and efficiency. A model might employ higher precision (e.g., FP16 or FP32) in computationally critical areas or layers where accuracy is paramount. Conversely, lower precision (e.g., INT4 or INT8) could be used in less sensitive parts to reduce memory footprint and accelerate computation. Identifying which parts of the network benefit from adaptive precision is a crucial aspect, requiring careful analysis of the model’s sensitivity to quantization error across different layers and data characteristics. Effective strategies for adaptive precision typically involve monitoring metrics during training or inference and then adjusting precision levels accordingly. The trade-off between accuracy and speed needs to be carefully considered, necessitating thorough experimentation to determine the optimal balance for a specific application.
Speed and Accuracy#
The research paper’s findings on speed and accuracy reveal a significant advancement in attention mechanisms. SageAttention2 demonstrates a substantial speedup, exceeding FlashAttention2 and xformers by a considerable margin. This acceleration is achieved without compromising accuracy, as demonstrated by the negligible loss in end-to-end metrics across diverse models. The use of 4-bit quantization for Q and K matrices and 8-bit quantization for P and V matrices is key to this performance improvement. The introduction of precision-enhancing techniques, such as smoothing Q and V, further minimizes accuracy loss during quantization. The adaptive precision method dynamically adjusts the bit precision depending on the layer and timestep, ensuring optimal balance between speed and accuracy. Overall, the results highlight the success of SageAttention2 in achieving both high speed and accuracy in attention computations, paving the way for efficient and effective large-scale language modeling.
Future Work#
The authors of the SageAttention2 paper outline several promising avenues for future research. Extending the work to the Hopper architecture is a key goal, leveraging its specialized hardware to further boost performance, particularly with FP16 accumulators for the PV matrix multiplication. They also highlight the need to investigate alternative quantization methods beyond INT4 and FP8 for Q, K, P, and V, potentially uncovering more accurate and efficient representations. Exploring the impact of different smoothing techniques on overall accuracy and efficiency is another area for future investigation. The adaptive quantization strategy employed in SageAttention2 represents a significant contribution; however, further optimization and refinement of this strategy would likely enhance its efficacy and broaden its applicability. Finally, they suggest exploring the benefits of incorporating the SageAttention2 approach into more sophisticated attention mechanisms beyond the standard self-attention framework.
More visual insights#
More on figures

🔼 This figure demonstrates the consequences of directly quantizing the query (Q) and key (K) matrices to 4-bit integers (INT4) during the attention mechanism of the CogvideoX model. Direct quantization without additional techniques leads to significant information loss, resulting in a drastic reduction in the quality of the generated video. It visually showcases the difference between using a naive INT4 quantization and the proposed SageAttention2 method.
read the caption
Figure 2: An example of quantizing Q, K to INT4 from CogvideoX.

🔼 This figure illustrates the workflow of the SageAttention2 algorithm, a novel method for accelerating attention mechanisms in deep learning models. The process begins by smoothing the Q, K, and V matrices to improve accuracy (Step 1). A general matrix-vector multiplication (GEMV) is then performed to obtain ΔS (Step 2). Subsequently, the Q and K matrices are quantized using a per-warp approach, while V is quantized per-channel (Step 3). This is followed by execution of the core SageAttention2 kernel (Step 4). Finally, the output is corrected to ensure accuracy (Step 5). This detailed breakdown clarifies each step involved in the algorithm’s operation.
read the caption
Figure 3: Workflow of SageAttention2. 1 Smooth Q,K,V. 2 A GEMV to obtain ΔSΔ𝑆\Delta Sroman_Δ italic_S. 3 Per-warp quantize Q,K and per-channel quantize V. 4 Perform the SageAttention2 kernel. 5 Correct the output.

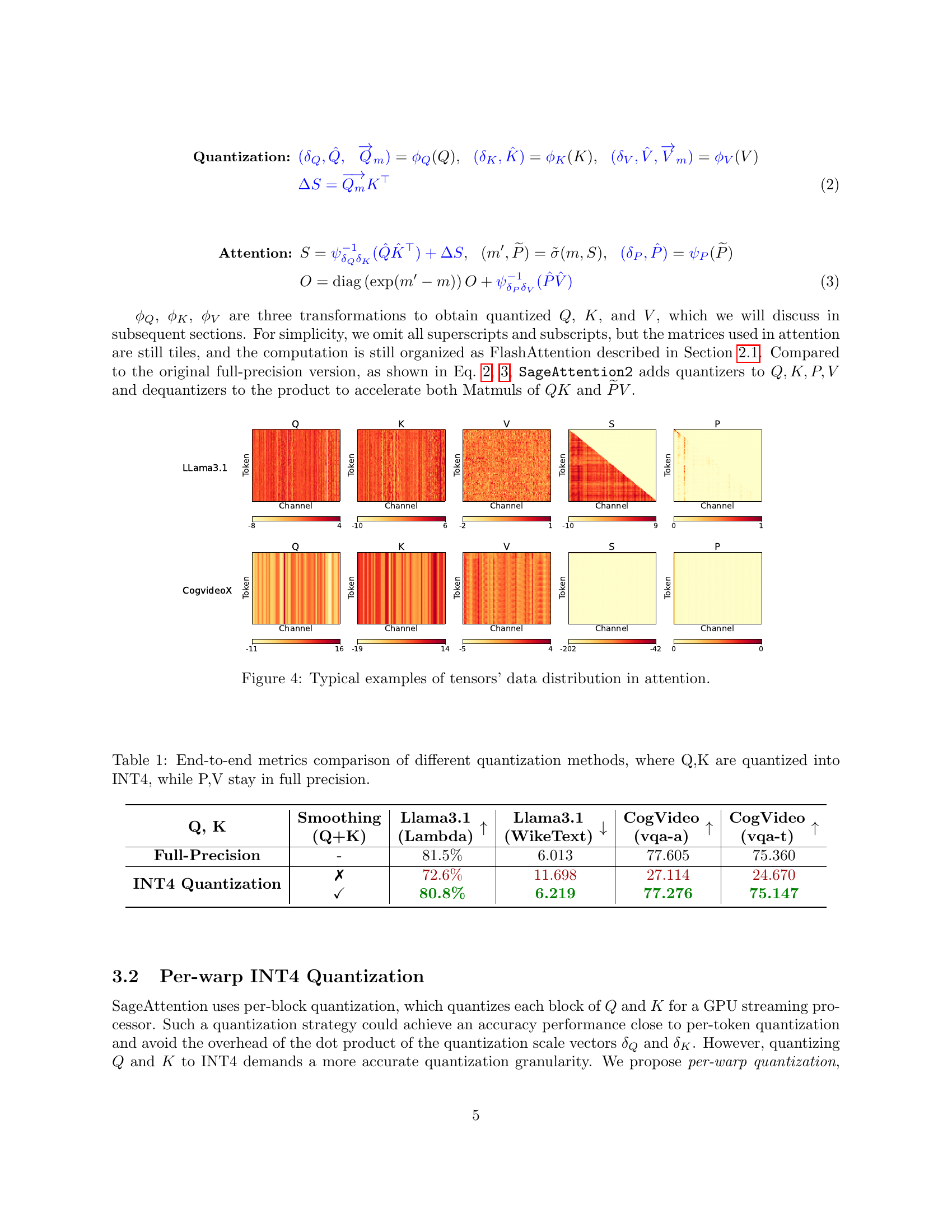
🔼 This figure visualizes the distribution of data within various tensors used in the attention mechanism. It showcases examples from different models and highlights the range and distribution of values for the Q, K, V, and S tensors, illustrating how their data characteristics vary across tokens and channels. This visualization is important to understanding the challenges of quantization, as uneven or extreme value distributions can make effective quantization difficult.
read the caption
Figure 4: Typical examples of tensors’ data distribution in attention.

🔼 This table presents a comparison of the average accuracy achieved across all layers of a model when different quantization granularities are used for the Q and K matrices in the attention mechanism. It compares the cosine similarity, relative L1 distance, and RMSE across four different quantization methods: per-token, per-warp, per-block, and per-tensor. The table helps illustrate the trade-off between quantization granularity and accuracy.
read the caption
Table 2: Average accuracy across all layers using different quantization granularities.

🔼 This table presents the worst-case accuracy metrics across all layers of a model when different quantization granularities are used for the Q and K matrices in the attention mechanism. The metrics shown are Cosine Similarity (Cos Sim), Relative L1 distance, and Root Mean Squared Error (RMSE). Lower values for Relative L1 and RMSE indicate better accuracy. The table helps to illustrate the impact of the choice of quantization granularity on the accuracy of the model’s attention mechanism.
read the caption
Table 3: Worst accuracy across all layers using different quantization granularities.

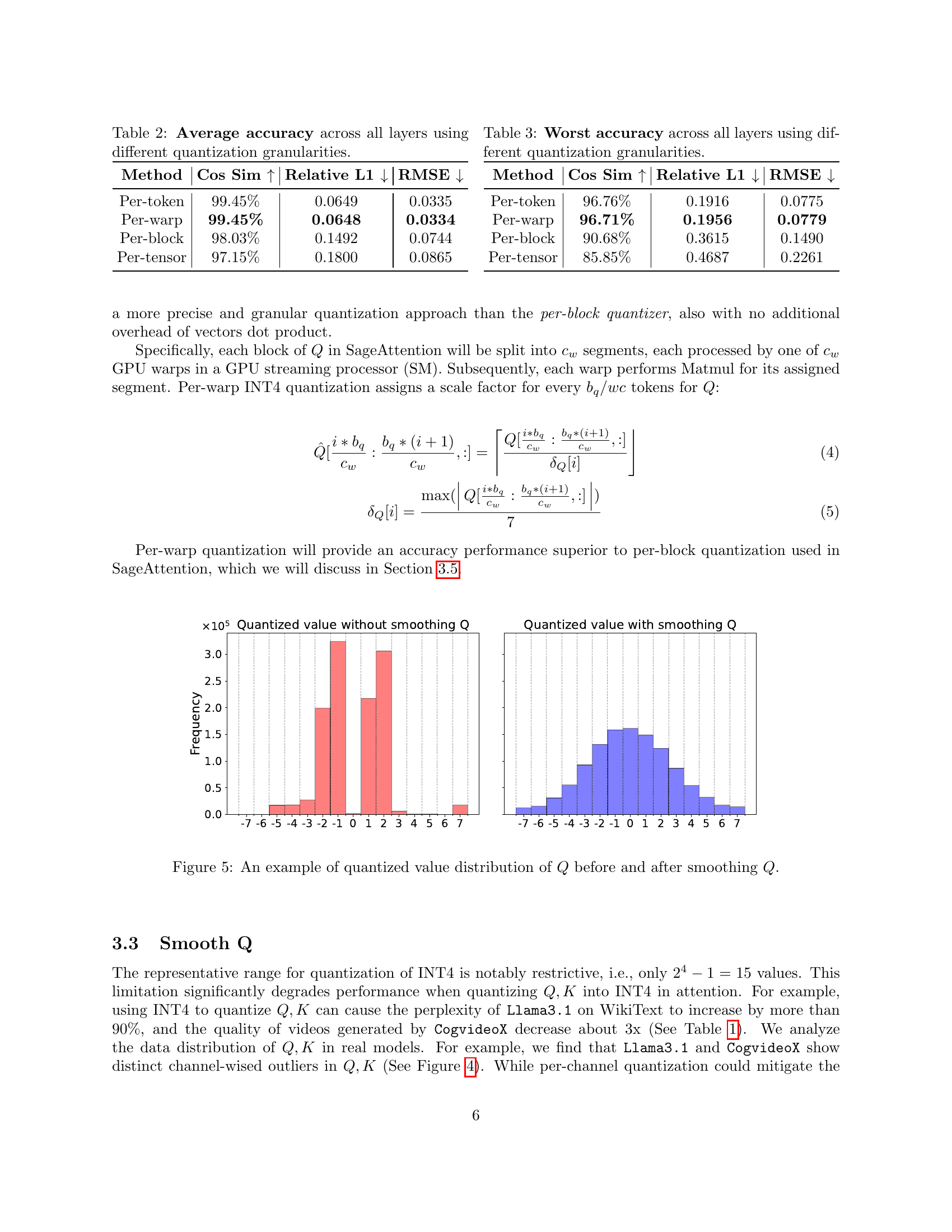
🔼 Figure 5 displays histograms illustrating the distribution of quantized values for the Q matrix before and after applying a smoothing technique. The x-axis represents the quantized values, while the y-axis indicates frequency. The before-smoothing histogram shows a less uniform distribution, concentrated towards the extremes of the quantized range. The after-smoothing histogram demonstrates a more uniform distribution of quantized values, suggesting that smoothing successfully mitigated the effect of outliers and improved the overall quantization accuracy.
read the caption
Figure 5: An example of quantized value distribution of Q𝑄Qitalic_Q before and after smoothing Q𝑄Qitalic_Q.

🔼 This table presents a comparison of the average accuracy achieved across all layers of the CogvideoX model when using different data types for matrices P and V in the attention mechanism. The accuracy is measured using various metrics. Notably, matrices Q and K are smoothed before being used in the attention calculations. The different data types explored include INT8, FP16, and INT4 for (P, V) to compare the performance of using various levels of precision for these matrices. This allows for evaluating the trade-off between computational efficiency and accuracy.
read the caption
Table 4: Average accuracy using different data types of (P~,V)~𝑃𝑉(\widetilde{P},V)( over~ start_ARG italic_P end_ARG , italic_V ) across all layers of a CogvideoX model, where (Q,K)𝑄𝐾(Q,K)( italic_Q , italic_K ) are smoothed.

🔼 This table presents the worst-case accuracy metrics across all layers of the CogvideoX model when using different data types for matrices P and V in the attention mechanism. The accuracy is evaluated using several metrics, such as cosine similarity, relative L1 distance, and root mean square error. The Q and K matrices are pre-processed using a smoothing technique to improve accuracy. The different data types tested include INT8, E5M2, INT4, and FP16, allowing for comparison of performance with various quantization methods.
read the caption
Table 5: Worst accuracy using different data types of (P~,V)~𝑃𝑉(\widetilde{P},V)( over~ start_ARG italic_P end_ARG , italic_V ) across all layers of a CogvideoX model, where (Q,K)𝑄𝐾(Q,K)( italic_Q , italic_K ) are smoothed.

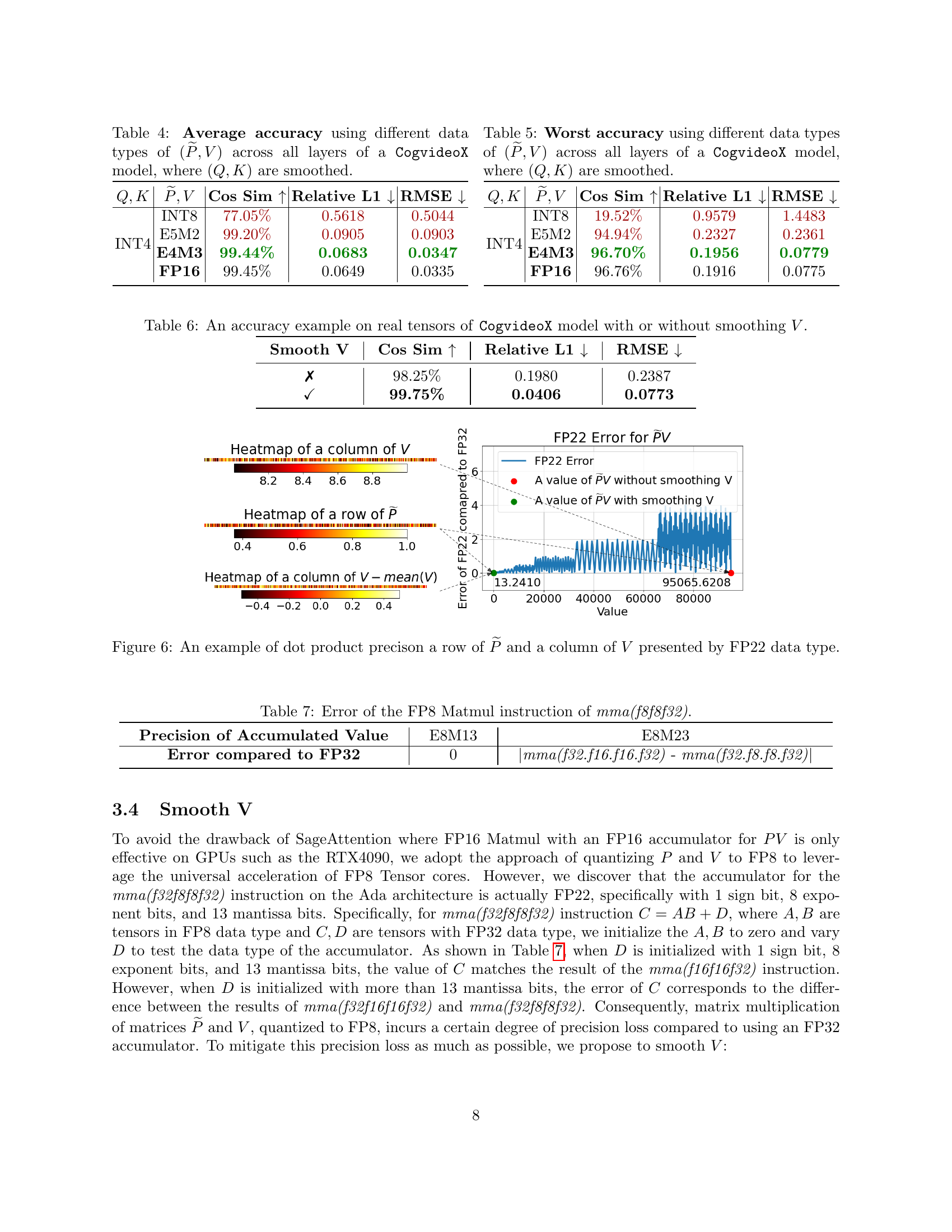
🔼 This figure visualizes the impact of using a 22-bit accumulator (FP22) instead of a 32-bit accumulator (FP32) during the matrix multiplication of P and V in the attention mechanism. It compares the dot product precision of a row from matrix P and a column from matrix V when using FP22. The heatmaps show the distribution of values before and after applying the smoothing technique to V. The graph illustrates the error introduced by using FP22 compared to the higher precision FP32.
read the caption
Figure 6: An example of dot product precison a row of P~~𝑃\widetilde{P}over~ start_ARG italic_P end_ARG and a column of V𝑉Vitalic_V presented by FP22 data type.

🔼 Figure 7 shows the performance of the SageAttn-4b model (a 4-bit attention mechanism) across different layers and timesteps of the Llama3.1 and CogvideoX models. It plots the mean and standard deviation of a combined accuracy metric, calculated as cossim * (1 - L1), which balances cosine similarity (cossim) and relative L1 distance (L1). Higher values indicate better performance. The figure aims to illustrate whether the accuracy of SageAttn-4b is consistent across different parts of the network and with different inputs, highlighting potential areas where it may underperform.
read the caption
Figure 7: Mean and standard deviation of cossim∗(1−L1)𝑐𝑜𝑠𝑠𝑖𝑚1𝐿1cossim*(1-L1)italic_c italic_o italic_s italic_s italic_i italic_m ∗ ( 1 - italic_L 1 )) of SageAttn-4b in different layers and timesteps for different inputs in Llama3.1 and CogvideoX.

🔼 This figure displays a speed comparison of SageAttention2 against several baselines using the RTX4090 GPU with a hidden dimension of 64. The x-axis represents the sequence length, and the y-axis represents the speed in TOPS (Trillions of Operations Per Second). Different colored bars show the performance for each method: Torch, xformers, FlashAttention2, SageAttention, SageAttention2-8b, and SageAttention2-4b. The graph visually demonstrates how SageAttention2 achieves faster performance than other approaches, especially at longer sequence lengths.
read the caption
Figure 8: Speed comparison between SageAttention2 and baselines (RTX4090, headdim=64).

🔼 This figure compares the speed of SageAttention2 with several baselines (Torch, xformers, and FlashAttention2) on an RTX4090 GPU. The experiment is performed with a hidden dimension size of 128 and for both causal and non-causal attention mechanisms. The x-axis represents the sequence length, while the y-axis shows the speed in TOPS (Tera Operations Per Second). The different lines represent different methods, allowing a direct comparison of their performance across varying sequence lengths. It helps to visualize the efficiency gains of SageAttention2 over existing attention mechanisms.
read the caption
Figure 9: Speed comparison between SageAttention2 and baselines (RTX4090, headdim=128).

🔼 This figure showcases a performance comparison between SageAttention2 and other baseline methods for attention mechanisms. The comparison is based on the speed (measured in TOPS - Tera Operations Per Second) achieved by each method while processing sequences of varying lengths on an RTX 4090 GPU. The different settings include causal and non-causal attention, with head dimensions of 256. The graph likely shows SageAttention2’s speed advantage over other methods, especially as sequence length increases.
read the caption
Figure 10: Speed comparison between SageAttention2 and baselines (RTX4090, headdim=256).

🔼 This figure presents a comparison of the inference speed among four different attention mechanisms: SageAttention2 (with 4-bit and 8-bit implementations), FlashAttention2, and xformers. The comparison is performed on an L20 GPU with a head dimension of 64. The x-axis represents the sequence length, and the y-axis shows the inference speed measured in TOPS (Tera Operations Per Second). The figure allows for a direct visual assessment of the relative performance gains of SageAttention2 compared to existing state-of-the-art methods across different sequence lengths. Separate graphs are provided for both causal and non-causal attention.
read the caption
Figure 11: Speed comparison between SageAttention2 and baselines (L20, headdim=64).
More on tables
| Method | Cos Sim ↑ | Relative L1 ↓ | RMSE ↓ |
|---|---|---|---|
| Per-token | 99.45% | 0.0649 | 0.0335 |
| Per-warp | 99.45% | 0.0648 | 0.0334 |
| Per-block | 98.03% | 0.1492 | 0.0744 |
| Per-tensor | 97.15% | 0.1800 | 0.0865 |
🔼 This table presents a comparison of the accuracy of dot product operations using FP22 data type in the CogvideoX model, with and without applying a smoothing technique to matrix V. It demonstrates the impact of smoothing V on mitigating precision loss inherent in the FP22 accumulator used for the FP8 matrix multiplication. The table visually shows heatmaps to illustrate the data distribution in matrices V and P, and a graph showing the error of FP22 compared to FP32.
read the caption
Table 6: An accuracy example on real tensors of CogvideoX model with or without smoothing V𝑉Vitalic_V.
| Method | Cos Sim ↑ | Relative L1 ↓ | RMSE ↓ |
|---|---|---|---|
| Per-token | 96.76% | 0.1916 | 0.0775 |
| Per-warp | 96.71% | 0.1956 | 0.0779 |
| Per-block | 90.68% | 0.3615 | 0.1490 |
| Per-tensor | 85.85% | 0.4687 | 0.2261 |
🔼 This table shows the errors in the FP8 matrix multiplication instruction, mma(f32.f8.f8.f32), compared to the results obtained using the FP32 instruction. It illustrates the precision loss incurred when using the FP8 accumulator in FP8 matrix multiplications. The table displays the accumulated value errors for different precision levels, highlighting the discrepancies between FP8 and FP32 calculations.
read the caption
Table 7: Error of the FP8 Matmul instruction of mma(f8f8f32).
| Q,K | \widetilde{P},V | Cos Sim ↑ | Relative L1 ↓ | RMSE ↓ |
|---|---|---|---|---|
| INT4 | INT8 | 77.05% | 0.5618 | 0.5044 |
| INT4 | E5M2 | 99.20% | 0.0905 | 0.0903 |
| INT4 | E4M3 | 99.44% | 0.0683 | 0.0347 |
| INT4 | FP16 | 99.45% | 0.0649 | 0.0335 |
🔼 This table presents two different kernel implementations of the SageAttention2 algorithm. The key difference lies in the quantization granularity used for the Q and K matrices, and the speed/accuracy trade-off involved. SageAttn2-4b uses 4-bit quantization per-warp, while SageAttn2-8b uses 8-bit quantization per-warp, for both Q and K. Both implementations employ FP8 for P and V, with a per-block and per-channel quantization strategy, respectively.
read the caption
Table 8: Two kernel implementations of SageAttention2.
| Q,K | \widetilde{P},V | Cos Sim ↑ | Relative L1 ↓ | RMSE ↓ |
|---|---|---|---|---|
| INT4 | INT8 | 19.52% | 0.9579 | 1.4483 |
| E5M2 | 94.94% | 0.2327 | 0.2361 | |
| E4M3 | 96.70% | 0.1956 | 0.0779 | |
| FP16 | 96.76% | 0.1916 | 0.0775 |
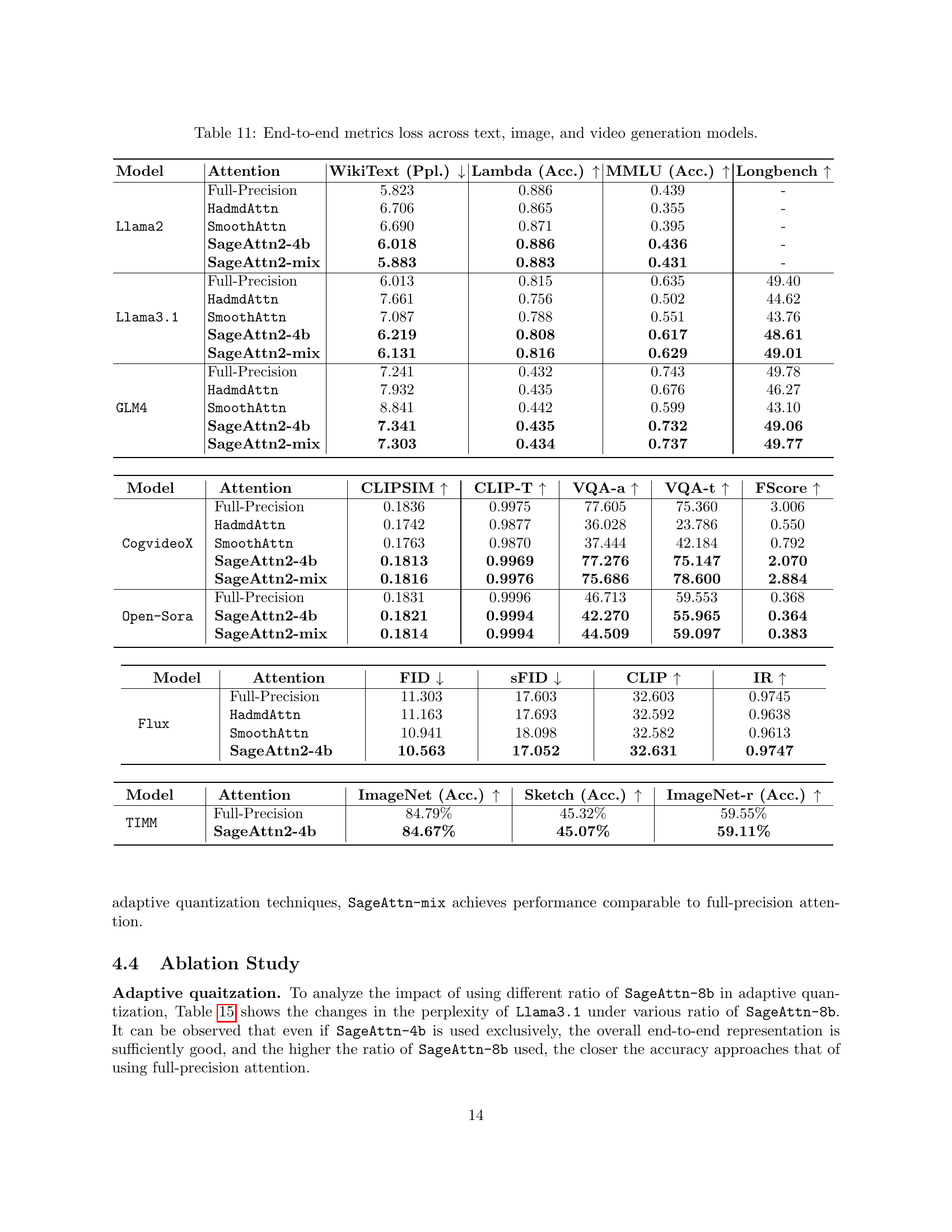
🔼 This table presents a comprehensive evaluation of the end-to-end performance of the proposed SageAttention2 model across various tasks involving text, image, and video generation. For each model (Llama2, Llama3.1, GLM4, CogvideoX, Open-Sora, Flux, and TIMM), it compares the performance of the full-precision attention mechanism with various quantization methods. Metrics reported include perplexity (for text), accuracy (for text and image classification), and specific metrics relevant to video generation and image quality (CLIPSim, CLIP-Temp, VQA-a, VQA-t, FScore, FID, sFID, CLIP score, and ImageReward). It demonstrates the impact of different quantization approaches on the overall model performance.
read the caption
Table 11: End-to-end metrics loss across text, image, and video generation models.
Full paper#