↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
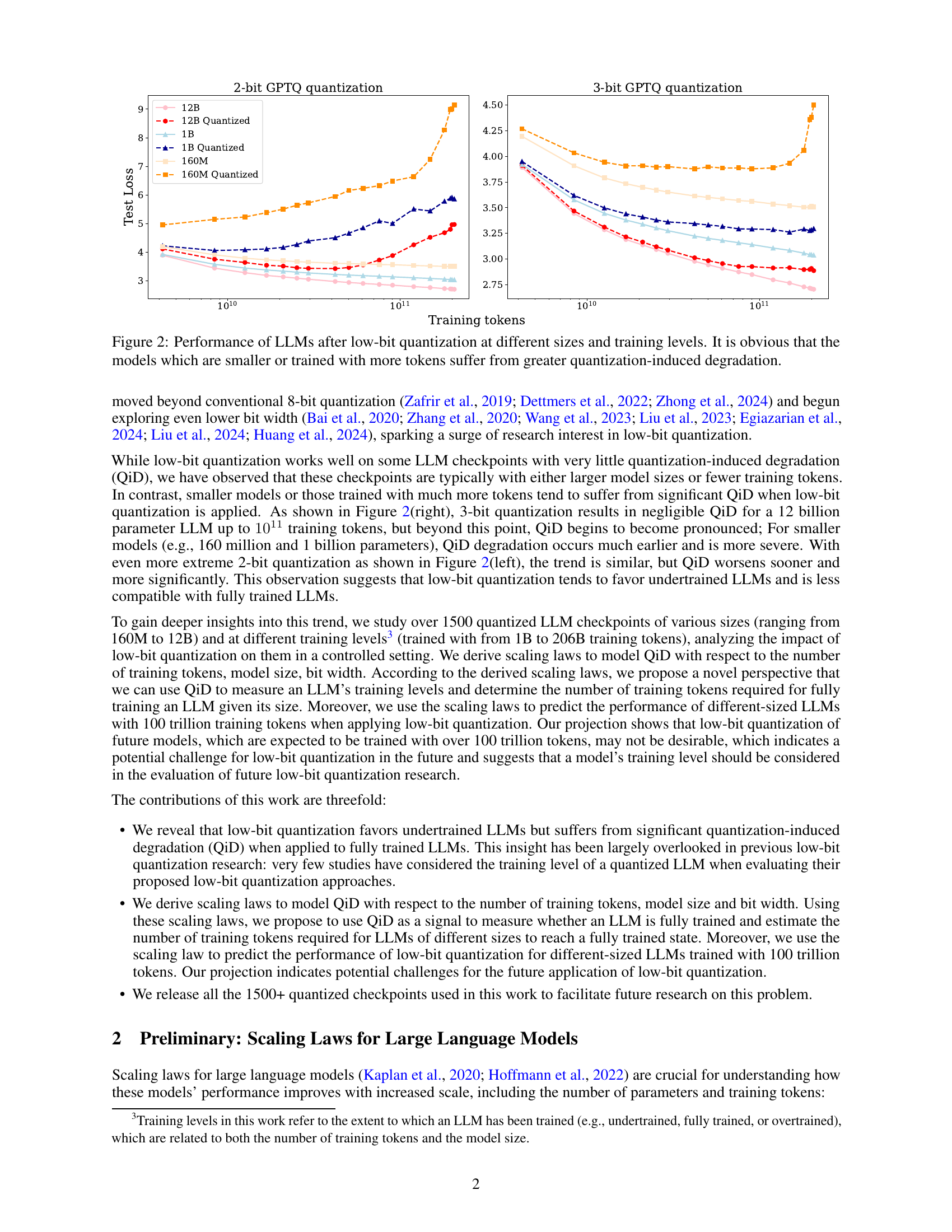
Current low-bit quantization techniques primarily focus on optimizing resource efficiency in large language models (LLMs) without considering the impact of model training stage. This research reveals that low-bit quantization performs exceptionally well on undertrained LLMs but shows significant degradation on fully-trained models. This study identified this issue, explored the scaling laws that govern this phenomena, and predicted the effect on future LLMs.
This paper addresses this gap by conducting experiments on over 1500 quantized LLMs checkpoints, deriving scaling laws to predict quantization-induced degradation (QiD) based on training tokens, model size, and bit-width. These laws reveal that QiD increases with the number of training tokens and decreases with model size and bit-width, indicating a preference for undertrained LLMs. The researchers also predict that the trend will continue with future LLMs, highlighting a potential limitation of low-bit quantization techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the prevailing assumptions about low-bit quantization in LLMs. By revealing that this technique is more effective for undertrained models and establishing scaling laws for quantization-induced degradation, it redirects future research towards a more nuanced understanding of model training and resource efficiency. This opens up new investigation avenues in optimizing quantization strategies for various training levels, ultimately improving LLM deployment and reducing resource costs.
Visual Insights#

🔼 This figure presents scaling laws that predict the impact of quantization on large language models (LLMs). The x-axis represents the number of training tokens used to train the model. The y-axis represents the quantization-induced degradation (QiD), measured as the increase in loss after applying low-bit quantization. Three different model sizes (7B, 70B, and 405B parameters) are shown. The figure demonstrates that low-bit quantization is acceptable for undertrained LLMs (trained on fewer tokens), but that the QiD increases significantly as the number of training tokens increases, especially for smaller models. The gray shaded regions highlight QiD levels that result in performance worse than random guessing.
read the caption
Figure 1: Scaling laws for predicting Quantization-induced Degradation (QiD, denoted as ΔqLosssubscriptΔ𝑞𝐿𝑜𝑠𝑠\Delta_{q}Lossroman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s) in 7B, 70B, and 405B models trained on up to 100 trillion (1014superscript101410^{14}10 start_POSTSUPERSCRIPT 14 end_POSTSUPERSCRIPT) tokens. While low-bit quantization yields acceptable QiD for undertrained LLMs (trained with ≤1012absentsuperscript1012\leq 10^{12}≤ 10 start_POSTSUPERSCRIPT 12 end_POSTSUPERSCRIPT tokens), it becomes undesirable when applied to fully trained LLMs (e.g., trained with 100 trillion tokens, a milestone expected to be reached in the next few years), particularly for smaller models. Note that the gray areas in this figure indicate levels of QiD that degrade the model’s predictions to a level worse than random guessing.
| $Loss = 0.5 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 bits | 3 bits | 4 bits | 2 bits | 3 bits | 4 bits | 2 bits | 3 bits | 4 bits | 2 bits | 3 bits | 4 bits | |
| — | — | — | — | — | — | — | — | — | — | — | — | — |
| 1B | 0.0011 | 0.1089 | 1.4424 | 0.0025 | 0.1990 | 2.6786 | 0.0043 | 0.3051 | 4.1556 | 0.0066 | 0.4251 | 5.8422 |
| 7B | 0.0026 | 0.3038 | 4.5066 | 0.0057 | 0.5550 | 8.3689 | 0.0099 | 0.8512 | 12.9836 | 0.0152 | 1.1860 | 18.2531 |
| 70B | 0.0071 | 1.0228 | 17.3499 | 0.0154 | 1.8687 | 32.2192 | 0.0267 | 2.8659 | 49.9854 | 0.0409 | 3.9932 | 70.2723 |
| 405B | 0.0151 | 2.5807 | 48.4861 | 0.0328 | 4.7151 | 90.0398 | 0.0567 | 7.2311 | 139.6892 | 0.0868 | 10.0754 | 196.3829 |
🔼 This table presents estimations of the number of training tokens (in trillions) needed to reach specific training levels for different model sizes and bit-widths using low-bit quantization. The training level is measured by the quantization-induced degradation (QiD), denoted as ΔqLoss. A ΔqLoss of 0.2 signifies an 80% reduction in likelihood (e⁻⁰·² ≈ 0.8), while a ΔqLoss of 0.5 indicates a 60% reduction (e⁻⁰·⁵ ≈ 0.6). The table shows these token estimations for four different QiD values (0.2, 0.3, 0.4, 0.5) across various model sizes (1B, 7B, 70B, 405B parameters) and bit-widths (2, 3, and 4 bits).
read the caption
Table 1: Prediction of the number of training tokens (in trillion) needed to achieve a given training level measured by ΔqLosssubscriptΔ𝑞𝐿𝑜𝑠𝑠\Delta_{q}Lossroman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s for different model sizes and bit widths. Note that ΔqLoss=0.2subscriptΔ𝑞𝐿𝑜𝑠𝑠0.2\Delta_{q}Loss=0.2roman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s = 0.2 means the likelihood is reduced to 80% of its original value (e−0.2≈0.8superscript𝑒0.20.8e^{-0.2}\approx 0.8italic_e start_POSTSUPERSCRIPT - 0.2 end_POSTSUPERSCRIPT ≈ 0.8), while ΔqLoss=0.5subscriptΔ𝑞𝐿𝑜𝑠𝑠0.5\Delta_{q}Loss=0.5roman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s = 0.5 means the likelihood is reduced to 60% (e−0.5≈0.6superscript𝑒0.50.6e^{-0.5}\approx 0.6italic_e start_POSTSUPERSCRIPT - 0.5 end_POSTSUPERSCRIPT ≈ 0.6).
In-depth insights#
Quantization Limits#
The concept of “Quantization Limits” in the context of large language models (LLMs) centers on the inherent trade-offs between model compression and performance degradation. Lower-bit quantization, while effective in reducing model size and improving inference speed, inevitably introduces information loss. This loss manifests as quantization-induced degradation (QiD), impacting the model’s accuracy and overall effectiveness. The paper investigates how different factors, such as model size, training data, and quantization bit-width, influence QiD. A key finding is that undertrained models are more resilient to quantization, exhibiting less degradation compared to their fully-trained counterparts. This suggests a fundamental limit to the effectiveness of aggressive quantization on highly-trained, large LLMs, hinting at the need for alternative compression techniques or a re-evaluation of training strategies for future, massive LLMs.
Training Level Impact#
The research reveals a crucial, previously overlooked aspect of low-bit quantization: its strong dependence on the model’s training level. Undertrained LLMs exhibit significantly less quantization-induced degradation (QiD) compared to their fully trained counterparts. This is because undertrained models have weights that fluctuate significantly during training; hence, small weight changes caused by quantization have a minimal impact. Conversely, fully trained models show minimal weight variation, making them highly susceptible to QiD as low-bit quantization pushes weights beyond their established narrow range. This finding introduces a new perspective on evaluating low-bit quantization techniques, highlighting the necessity of considering the training level when assessing their effectiveness. The study’s scaling laws provide a tool to predict the performance of future models, suggesting potential challenges for low-bit quantization as models scale to 100 trillion training tokens.
Scaling Laws QiD#
The concept of “Scaling Laws for Quantization-Induced Degradation (QiD)” explores how the amount of performance loss from quantization changes with key model attributes. The research likely investigates scaling relationships between QiD and factors like model size, number of training tokens, and bit-width. A key finding might show that smaller models or those extensively trained suffer more from quantization, while larger, less-trained models are more robust. This suggests a crucial tradeoff: while larger models offer better performance, their sensitivity to quantization could hinder efficient deployment. The study could further propose a unified scaling law that combines these factors, enabling predictions of QiD for future, larger models. Ultimately, these findings highlight the importance of considering training levels when evaluating quantization techniques and offer valuable insights for future model design and deployment strategies.
Unified Scaling Law#
The concept of a Unified Scaling Law in the context of low-bit quantization for LLMs attempts to create a single, comprehensive mathematical model that captures how quantization-induced degradation (QiD) changes based on three key factors: model size, number of training tokens, and bit-width. It builds upon existing scaling laws for LLM performance, extending them to account for the effects of quantization. This unified approach is crucial for predicting the performance of future, extremely large language models (LLMs) under low-bit quantization, helping researchers anticipate potential challenges and guide the design of more efficient quantization techniques. The successful development and validation of a Unified Scaling Law would represent a significant advancement in the field, providing a powerful predictive tool for evaluating and optimizing the trade-offs between model size, training data, precision, and quantization performance. Its accuracy depends heavily on the range and quality of the datasets used for training and validation, as well as the generalizability of the underlying model across different architectures and quantization methods. Further work should focus on testing its limits and refining it to be more robust and widely applicable.
Future of Quant#
The research paper explores the challenges and opportunities in low-bit quantization for large language models (LLMs). A key finding is that low-bit quantization performs well on undertrained LLMs but struggles with fully trained models. This implies that as LLMs continue to grow in size and training data, the effectiveness of this widely used efficiency technique might diminish. The paper suggests a need for a paradigm shift, perhaps towards methods that are less sensitive to the model’s training level, or designing LLMs inherently suited for low-bit precision. Future research should consider the interplay of model size, training data, and quantization bit width, to better predict performance and develop more robust quantization strategies. Furthermore, exploring alternative quantization methods beyond GPTQ, or focusing on techniques suited to specific model architectures, could yield valuable improvements. Ultimately, the future of quantization for LLMs hinges on addressing this critical limitation and moving beyond simplistic scaling laws to develop more sophisticated and effective solutions.
More visual insights#
More on figures

🔼 This figure displays the performance of Large Language Models (LLMs) after applying low-bit quantization. It compares LLMs of different sizes (160M, 1B, and 12B parameters) and training levels (varying number of training tokens). The results show a clear trend: smaller models and those trained on larger datasets exhibit significantly more performance degradation due to quantization compared to larger models trained on smaller datasets. This suggests that low-bit quantization is more effective for undertrained LLMs.
read the caption
Figure 2: Performance of LLMs after low-bit quantization at different sizes and training levels. It is obvious that the models which are smaller or trained with more tokens suffer from greater quantization-induced degradation.

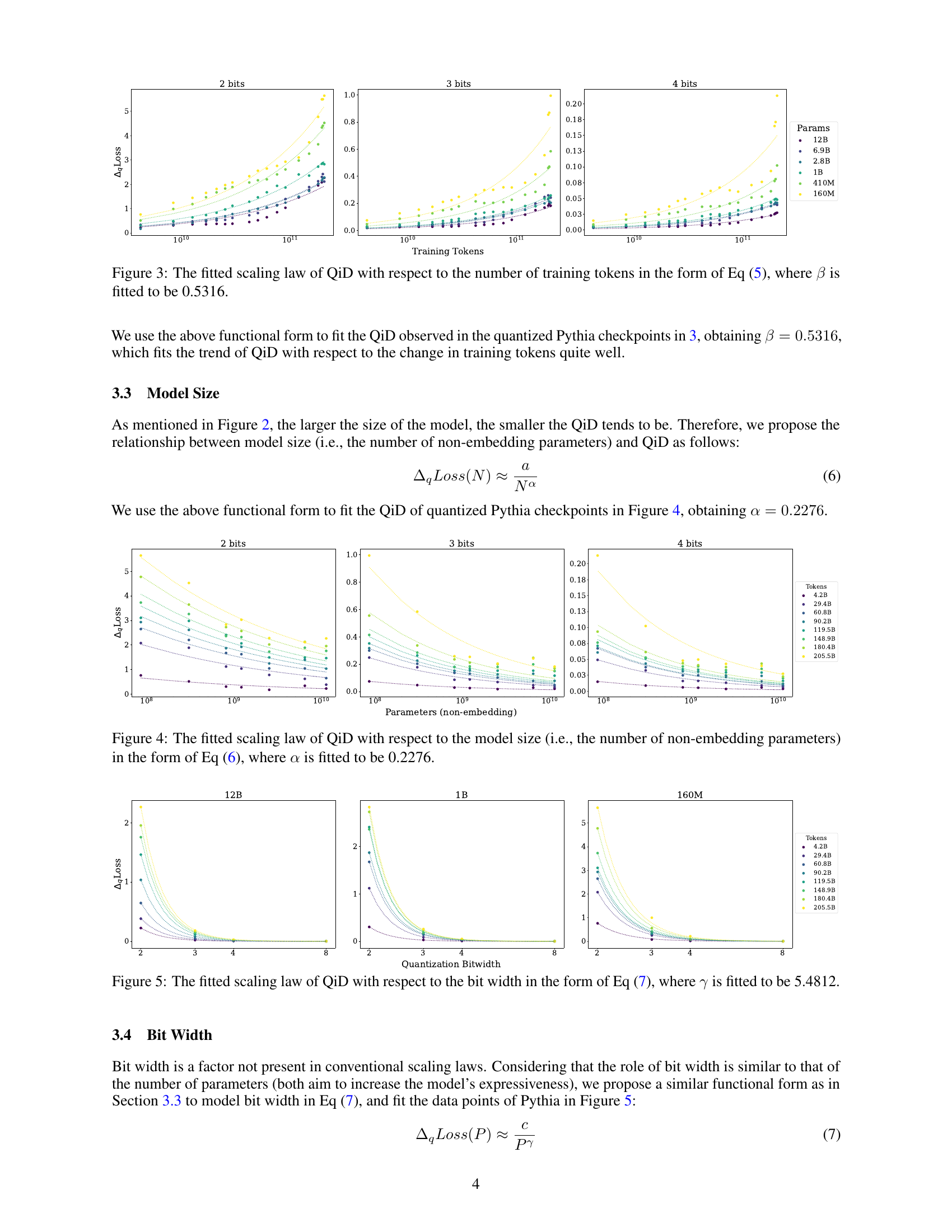
🔼 Figure 3 shows the relationship between quantization-induced degradation (QiD) and the number of training tokens. The graph displays fitted curves for 2-bit, 3-bit, and 4-bit quantization, illustrating how QiD increases with the number of training tokens. The equation used to fit the curves is specified as Eq (5), with the scaling exponent (β) calculated to be 0.5316. This indicates that QiD grows sublinearly with respect to the number of training tokens. Different curves represent different model sizes, demonstrating that smaller models exhibit more significant QiD.
read the caption
Figure 3: The fitted scaling law of QiD with respect to the number of training tokens in the form of Eq (5), where β𝛽\betaitalic_β is fitted to be 0.5316.

🔼 Figure 4 presents the relationship between quantization-induced degradation (QiD) and model size in the context of low-bit quantization. It shows how the amount of QiD decreases as the number of non-embedding parameters in the model increases. The figure displays fitted curves derived from experimental data, illustrating the scaling law formulated in Equation (6). The fitted scaling parameter α is found to be 0.2276. This indicates that larger models exhibit less QiD than smaller models under low-bit quantization.
read the caption
Figure 4: The fitted scaling law of QiD with respect to the model size (i.e., the number of non-embedding parameters) in the form of Eq (6), where α𝛼\alphaitalic_α is fitted to be 0.2276.

🔼 Figure 5 presents the relationship between quantization-induced degradation (QiD) and the bit-width used for quantization. The figure shows that as the bit-width decreases, the QiD increases. Specifically, it shows how the fitted scaling law, represented by the equation AqLoss(P) ≈ Pγ, effectively models this relationship. The exponent γ (gamma) in the equation is determined through a fitting process and is found to be 5.4812. This implies that the degradation in performance due to quantization increases significantly with decreasing bit width.
read the caption
Figure 5: The fitted scaling law of QiD with respect to the bit width in the form of Eq (7), where γ𝛾\gammaitalic_γ is fitted to be 5.4812.

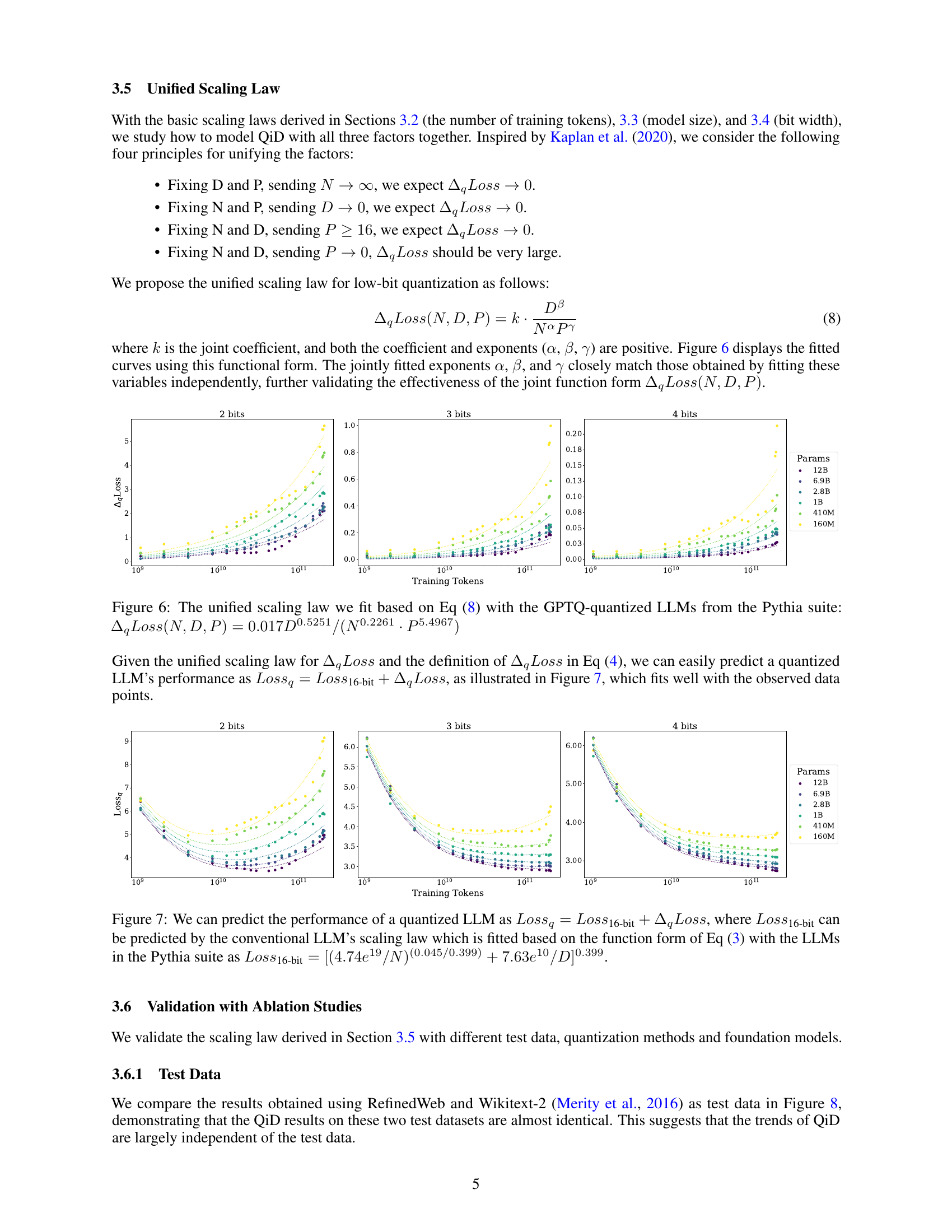
🔼 Figure 6 presents a unified scaling law that combines three factors—model size (N), number of training tokens (D), and bit width (P)—to predict quantization-induced degradation (ΔqLoss) in low-bit quantized LLMs. The formula ΔqLoss(N,D,P) = 0.017D^0.5251/(N^0.2261⋅P^5.4967) shows that QiD decreases as model size (N) increases and as bit-width (P) increases. Conversely, it increases with the number of training tokens (D). The figure visually represents this relationship using fitted curves for different bit widths, illustrating how ΔqLoss changes with model size and training tokens for each bit width.
read the caption
Figure 6: The unified scaling law we fit based on Eq (8) with the GPTQ-quantized LLMs from the Pythia suite: ΔqLoss(N,D,P)=0.017D0.5251/(N0.2261⋅P5.4967)subscriptΔ𝑞𝐿𝑜𝑠𝑠𝑁𝐷𝑃0.017superscript𝐷0.5251⋅superscript𝑁0.2261superscript𝑃5.4967\Delta_{q}Loss(N,D,P)=0.017D^{0.5251}/(N^{0.2261}\cdot P^{5.4967})roman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s ( italic_N , italic_D , italic_P ) = 0.017 italic_D start_POSTSUPERSCRIPT 0.5251 end_POSTSUPERSCRIPT / ( italic_N start_POSTSUPERSCRIPT 0.2261 end_POSTSUPERSCRIPT ⋅ italic_P start_POSTSUPERSCRIPT 5.4967 end_POSTSUPERSCRIPT )

🔼 Figure 7 illustrates how to predict the performance of a quantized large language model (LLM). It uses the equation Lossq = Loss16-bit + ΔqLoss, where Lossq represents the cross-entropy loss of the quantized LLM, Loss16-bit represents the cross-entropy loss of the original LLM (16-bit precision), and ΔqLoss represents the quantization-induced degradation. The figure shows that Loss16-bit can be predicted using a conventional LLM scaling law, specifically the one fitted using the LLMs from the Pythia suite with the formula: [ (4.74e^19/N)^(0.045/0.399) + 7.63e^10/D]^0.399. The plot visually demonstrates the agreement between the predicted and observed loss values for different LLM sizes and training tokens.
read the caption
Figure 7: We can predict the performance of a quantized LLM as Lossq=Loss16-bit+ΔqLoss𝐿𝑜𝑠subscript𝑠𝑞𝐿𝑜𝑠subscript𝑠16-bitsubscriptΔ𝑞𝐿𝑜𝑠𝑠Loss_{q}=Loss_{\textrm{16-bit}}+\Delta_{q}Lossitalic_L italic_o italic_s italic_s start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT = italic_L italic_o italic_s italic_s start_POSTSUBSCRIPT 16-bit end_POSTSUBSCRIPT + roman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s, where Loss16-bit𝐿𝑜𝑠subscript𝑠16-bitLoss_{\textrm{16-bit}}italic_L italic_o italic_s italic_s start_POSTSUBSCRIPT 16-bit end_POSTSUBSCRIPT can be predicted by the conventional LLM’s scaling law which is fitted based on the function form of Eq (3) with the LLMs in the Pythia suite as Loss16-bit=[(4.74e19/N)(0.045/0.399)+7.63e10/D]0.399𝐿𝑜𝑠subscript𝑠16-bitsuperscriptdelimited-[]superscript4.74superscript𝑒19𝑁0.0450.3997.63superscript𝑒10𝐷0.399Loss_{\textrm{16-bit}}=[(4.74e^{19}/N)^{(0.045/0.399)}+7.63e^{10}/D]^{0.399}italic_L italic_o italic_s italic_s start_POSTSUBSCRIPT 16-bit end_POSTSUBSCRIPT = [ ( 4.74 italic_e start_POSTSUPERSCRIPT 19 end_POSTSUPERSCRIPT / italic_N ) start_POSTSUPERSCRIPT ( 0.045 / 0.399 ) end_POSTSUPERSCRIPT + 7.63 italic_e start_POSTSUPERSCRIPT 10 end_POSTSUPERSCRIPT / italic_D ] start_POSTSUPERSCRIPT 0.399 end_POSTSUPERSCRIPT.

🔼 This figure compares the quantization-induced degradation (QiD) results obtained using two different test datasets, RefinedWeb and Wikitext-2, with the 12B parameter Pythia language model. It shows that the QiD trends are largely independent of the test dataset used, indicating a robustness and generalizability of the results.
read the caption
Figure 8: QiD results evaluated on RefinedWeb and Wikitext-2 with the 12B Pythia model.

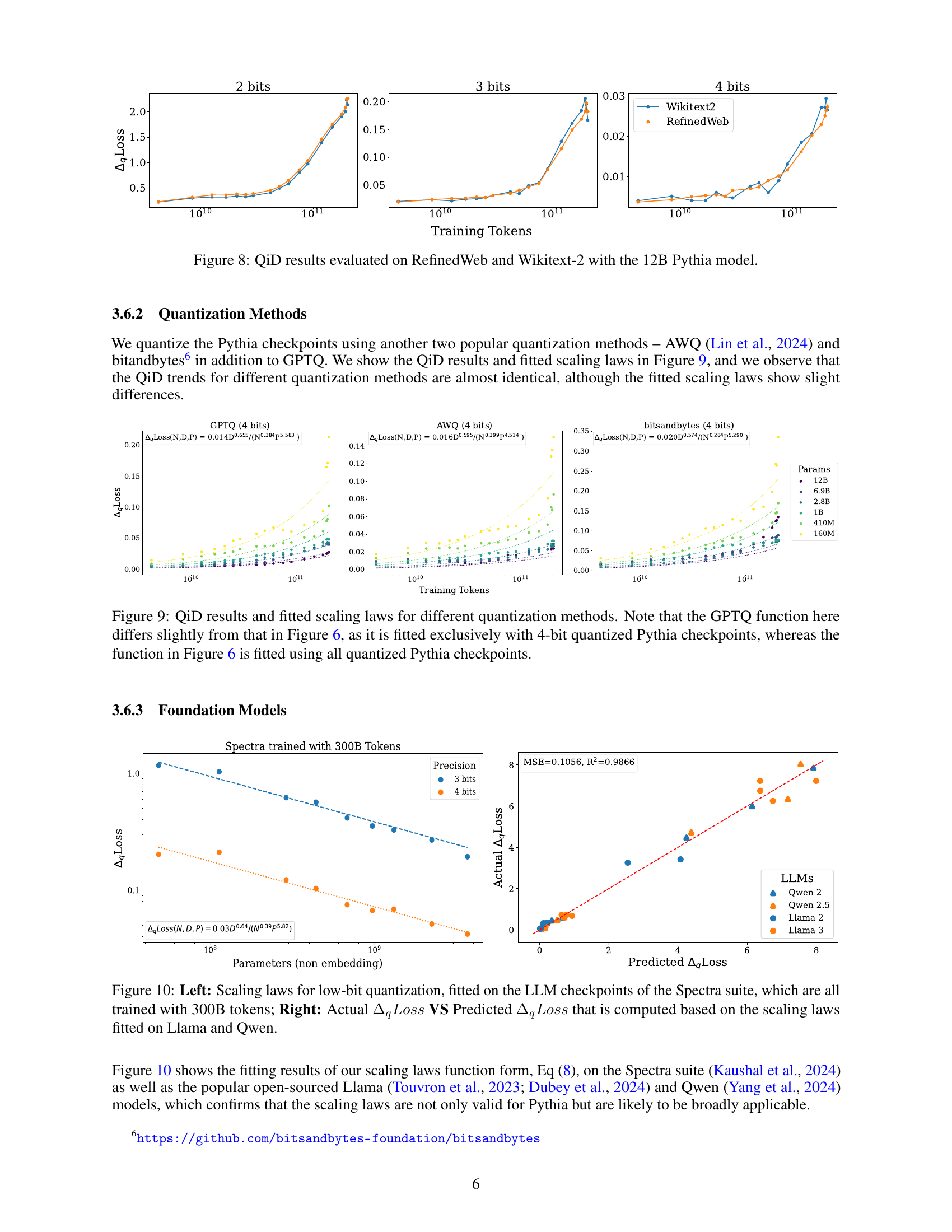
🔼 Figure 9 presents a comparison of Quantization-Induced Degradation (QiD) across three different quantization methods: GPTQ, AWQ, and bitsandbytes. The results are shown for 4-bit quantization applied to Pythia language models of various sizes and training levels. Importantly, the GPTQ results in Figure 9 are specifically fitted using only the 4-bit quantized data, unlike Figure 6 where all bit-width data for GPTQ was used. This distinction highlights how the choice of data used to fit the scaling laws impacts the resulting curves. The figure demonstrates that while the QiD trends are similar across the three quantization methods, the precise scaling laws (formulas describing the relationship between QiD and various factors) differ slightly depending on the chosen method.
read the caption
Figure 9: QiD results and fitted scaling laws for different quantization methods. Note that the GPTQ function here differs slightly from that in Figure 6, as it is fitted exclusively with 4-bit quantized Pythia checkpoints, whereas the function in Figure 6 is fitted using all quantized Pythia checkpoints.

🔼 Figure 10 presents a two-part visualization evaluating the accuracy of the proposed scaling laws for low-bit quantization. The left panel displays the fitted scaling laws on the Spectra suite of LLMs, which share a consistent training size of 300 billion tokens. This demonstrates the application of the scaling laws to a different set of LLMs than the primary dataset used for deriving the laws. The right panel shows a comparison between the actual and predicted quantization-induced degradation (ΔqLoss) for various LLMs (Llama and Qwen). This scatter plot visually assesses the predictive power of the scaling laws by comparing predicted ΔqLoss values to the observed ΔqLoss values for these models, providing a validation of their generalizability across different LLM architectures.
read the caption
Figure 10: Left: Scaling laws for low-bit quantization, fitted on the LLM checkpoints of the Spectra suite, which are all trained with 300B tokens; Right: Actual ΔqLosssubscriptΔ𝑞𝐿𝑜𝑠𝑠\Delta_{q}Lossroman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s VS Predicted ΔqLosssubscriptΔ𝑞𝐿𝑜𝑠𝑠\Delta_{q}Lossroman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s that is computed based on the scaling laws fitted on Llama and Qwen.

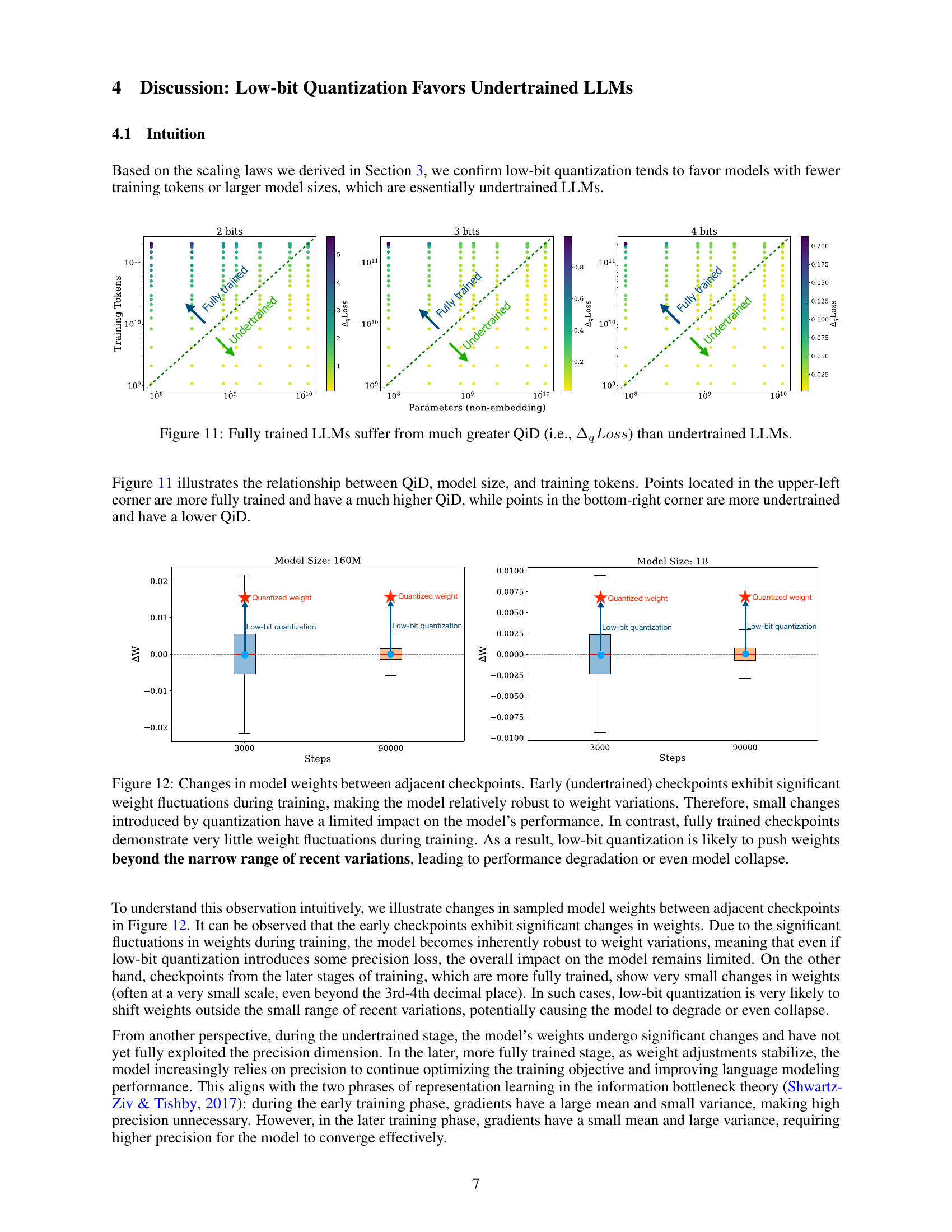
🔼 This figure visualizes the relationship between quantization-induced degradation (QiD), model size, and the number of training tokens for large language models (LLMs). The x and y axes represent model size (number of parameters) and number of training tokens, respectively. Each point represents a specific LLM checkpoint, colored according to the bit-width used for quantization (2, 3, or 4 bits). The color intensity of the points represents the magnitude of QiD (ΔqLoss), with darker colors indicating higher QiD values. The plot shows a clear trend: smaller models trained with more tokens (fully trained) exhibit significantly higher QiD than larger models trained with fewer tokens (undertrained). This visual supports the paper’s claim that low-bit quantization is more effective for undertrained LLMs.
read the caption
Figure 11: Fully trained LLMs suffer from much greater QiD (i.e., ΔqLosssubscriptΔ𝑞𝐿𝑜𝑠𝑠\Delta_{q}Lossroman_Δ start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT italic_L italic_o italic_s italic_s) than undertrained LLMs.
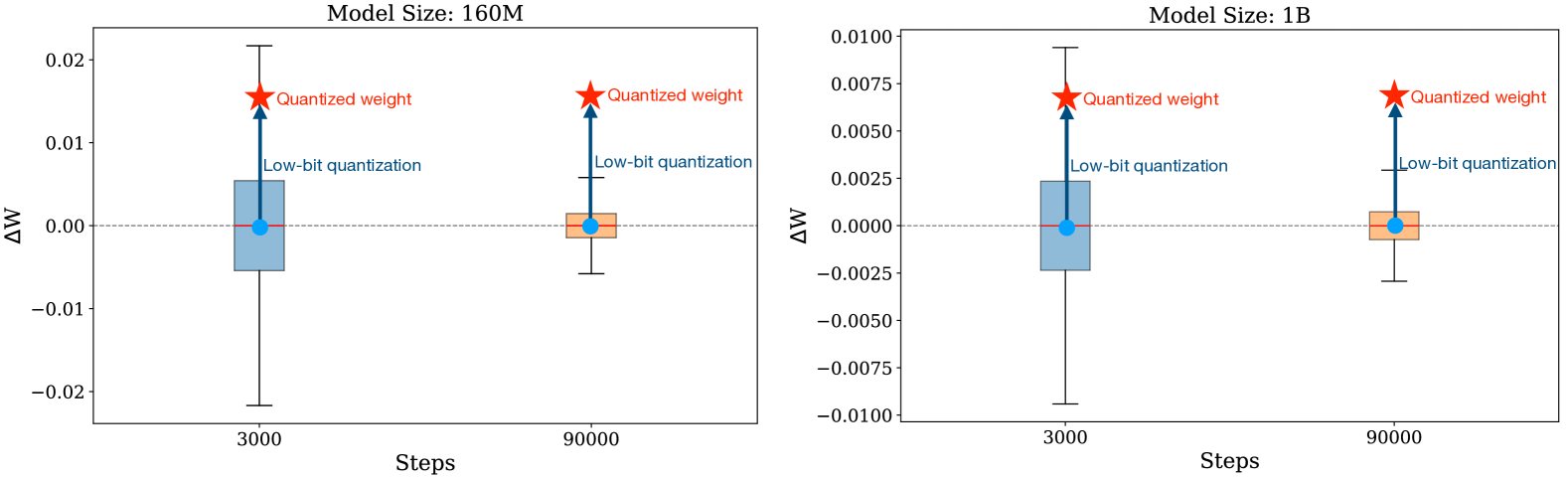
🔼 This figure displays boxplots visualizing the change in model weights between consecutive checkpoints during training for both undertrained and fully trained LLMs. The boxplots show that undertrained models exhibit significant weight fluctuations throughout training, meaning the model is tolerant of variations in weight values. Consequently, the small weight changes introduced by low-bit quantization have minimal impact on performance. In contrast, fully-trained models display very little weight fluctuation during the later stages of training. Low-bit quantization is more likely to shift weights outside this narrow range of recent variations, causing potential performance degradation or even model failure. The figure provides visual evidence supporting the paper’s claim that low-bit quantization is more effective for undertrained LLMs.
read the caption
Figure 12: Changes in model weights between adjacent checkpoints. Early (undertrained) checkpoints exhibit significant weight fluctuations during training, making the model relatively robust to weight variations. Therefore, small changes introduced by quantization have a limited impact on the model’s performance. In contrast, fully trained checkpoints demonstrate very little weight fluctuations during training. As a result, low-bit quantization is likely to push weights beyond the narrow range of recent variations, leading to performance degradation or even model collapse.

🔼 Figure 13 illustrates the rapid growth in the number of training tokens used for training state-of-the-art 7B parameter Large Language Models (LLMs) over the past four years. The figure shows a nearly 50-fold increase in training tokens. The x-axis represents the year (2020-2024), and the y-axis represents the number of training tokens in trillions. Each bar represents a specific LLM and its corresponding training tokens. This trend strongly suggests that future LLMs will utilize significantly larger amounts of training data.
read the caption
Figure 13: The number of training tokens for the state-of-the-art 7B-scale LLMs increase by nearly 50×50\times50 × over the past 4 years. According to this trend, it is expected that the future models will have much more training tokens.

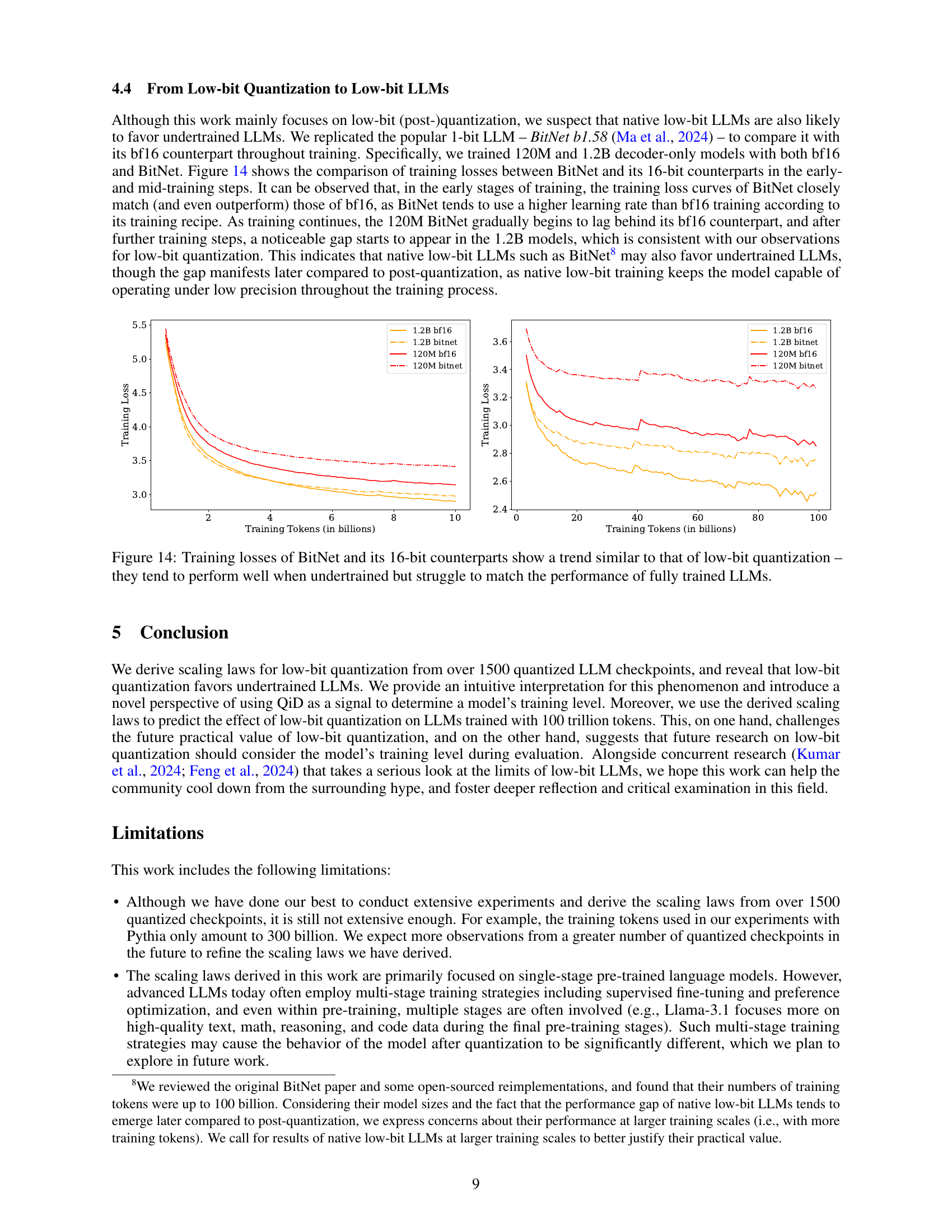
🔼 Figure 14 presents a comparison of training loss curves for 120M and 1.2B parameter decoder-only language models trained using both standard 16-bit precision (bf16) and the 1-bit BitNet method. The plot shows that in the early stages of training, BitNet’s performance is comparable or even superior to the 16-bit models, primarily due to BitNet employing a higher learning rate. However, as training progresses, the 16-bit models pull ahead, demonstrating the performance gap that widens further with larger models. This divergence highlights the limitations of low-bit, 1-bit training, particularly in later training stages, where the benefit of higher precision becomes increasingly crucial for achieving optimal model performance. It provides visual evidence supporting the claim that native low-bit LLMs also favor undertrained models in a manner similar to post-training quantization.
read the caption
Figure 14: Training losses of BitNet and its 16-bit counterparts show a trend similar to that of low-bit quantization – they tend to perform well when undertrained but struggle to match the performance of fully trained LLMs.
Full paper#