↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Speculative decoding accelerates large language model inference by using a smaller, faster model to generate draft sequences, which are then verified by a larger model. However, current methods use a fixed draft length, which is inefficient as token generation difficulty varies greatly. This paper introduces SVIP, a new method that dynamically adjusts the draft sequence length based on the predicted difficulty of each token.
SVIP determines this difficulty using a lower bound of the acceptance rate, approximating it with the draft model’s entropy, which is readily available during inference. Experimental results show that SVIP significantly improves speed across several benchmarks and is compatible with various existing methods, resulting in substantial improvements in wall-time.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves the speed of large language model inference by addressing a key limitation of existing speculative decoding methods. Its novel self-verification length policy (SVIP) is training-free and easily adaptable to various models and frameworks, making it highly relevant to the broader NLP community. The findings open avenues for developing more efficient and faster LLM inference systems, particularly beneficial for resource-intensive applications.
Visual Insights#

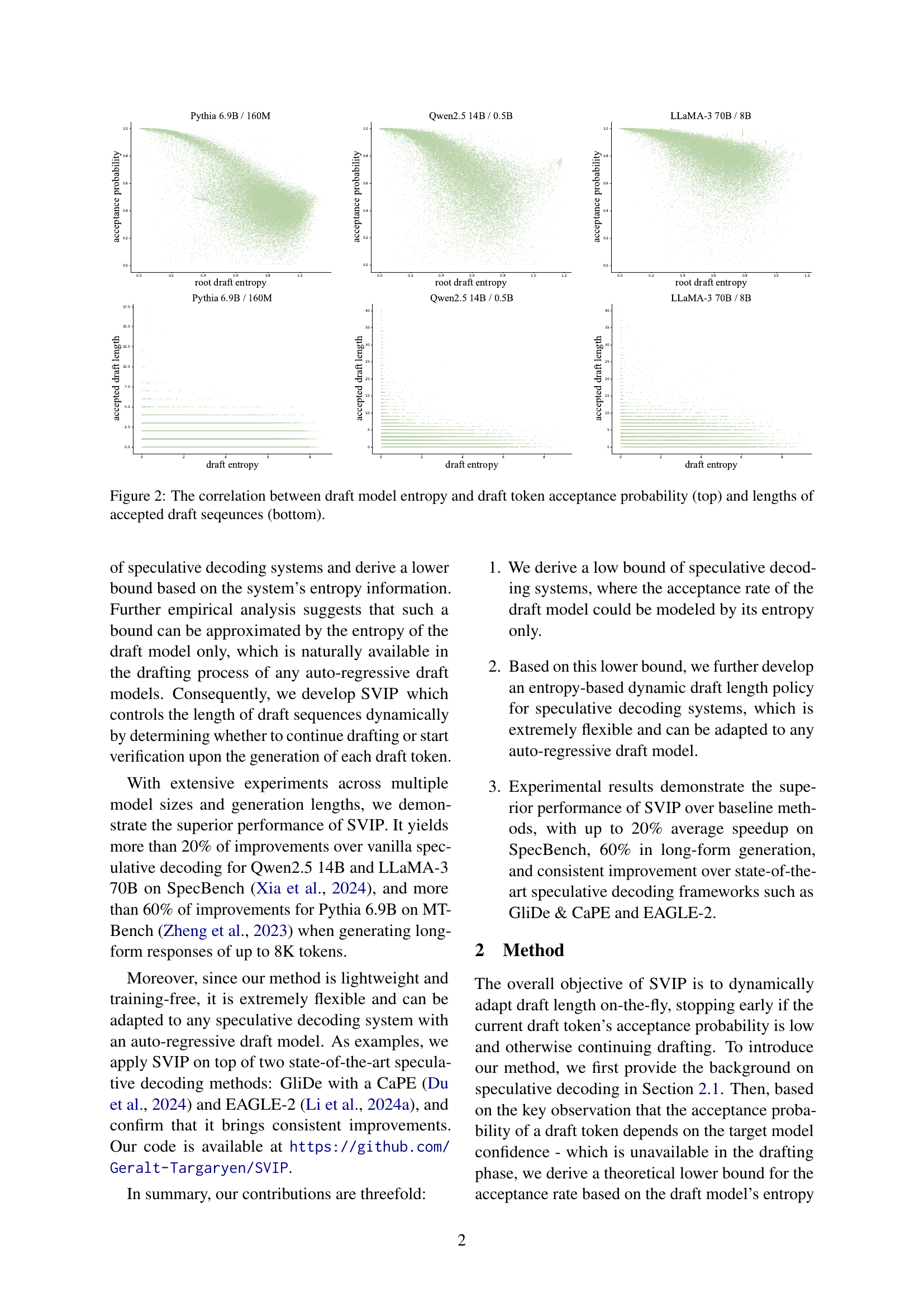
🔼 The figure illustrates how the difficulty of generating tokens varies within a sequence. A draft model is used to predict tokens which are then verified by a more powerful target model. Some tokens, like common greetings, are easy for the draft model to predict and thus have high acceptance rates (many draft tokens are accepted and verified). Other tokens, such as those requiring complex reasoning or domain-specific knowledge, are much harder for the draft model to accurately predict. This results in a lower acceptance rate, with fewer draft tokens being accepted for these more difficult parts of the sentence.
read the caption
Figure 1: The “difficulty” of tokens varies in a sequence, resulting in different numbers of accepted draft tokens at different positions.
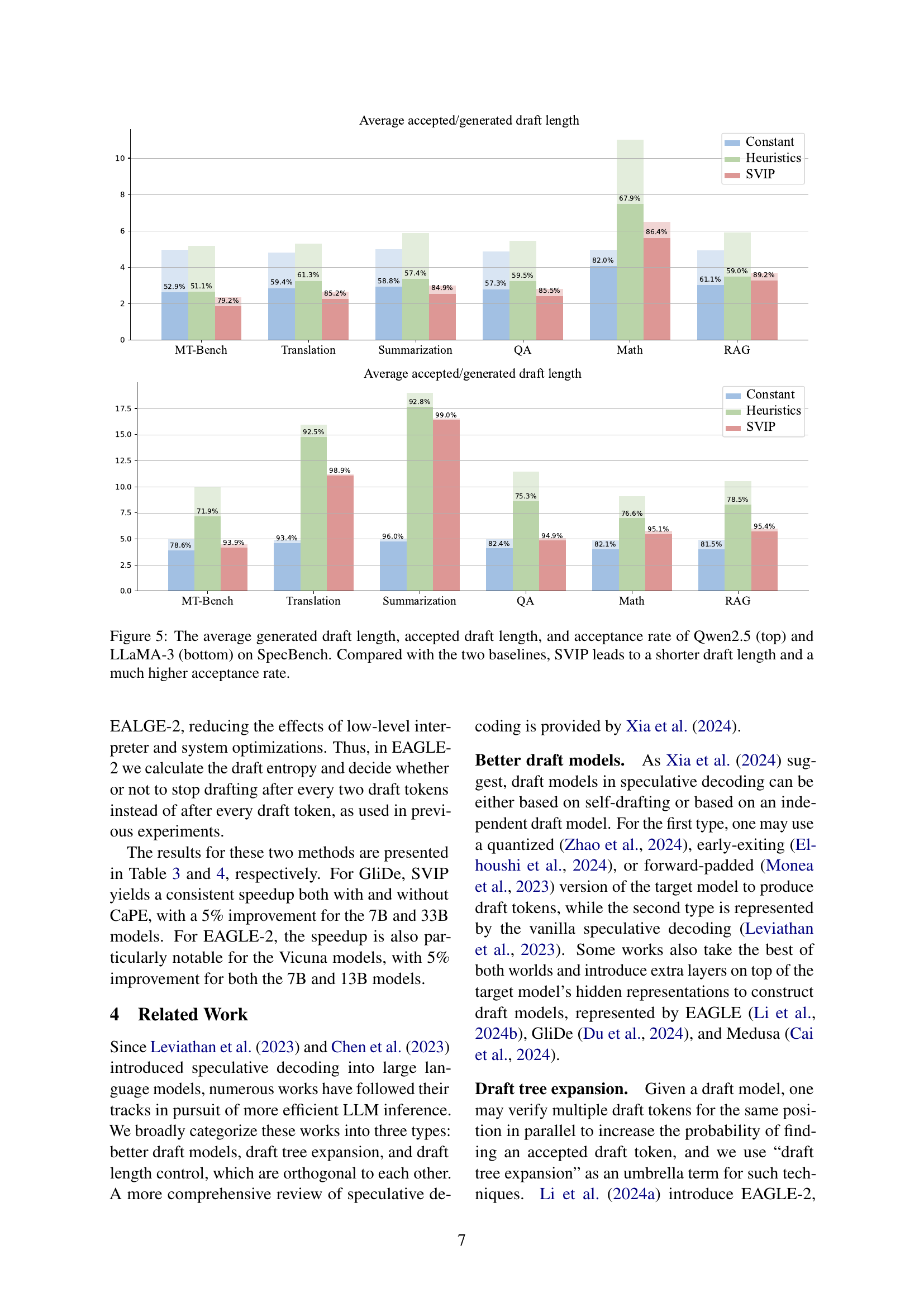
| Methods | MT-Bench | Trans. | Sum. | QA | Math | RAG | Avg. |
|---|---|---|---|---|---|---|---|
| Pythia(6.9B, 160M) Const. | 1.45 | 1.47 | 1.24 | 1.43 | 1.52 | 1.42 | 1.42 |
| Heuristics | 1.51 | 1.58 | 1.34 | 1.58 | 1.64 | 1.51 | 1.53 |
| SVIP | 1.63 | 1.62 | 1.45 | 1.67 | 1.72 | 1.66 | 1.63(+14.8%) |
| Qwen2.5(14B, 0.5B) Const. | 1.08 | 0.87 | 1.11 | 0.92 | 1.43 | 0.99 | 1.07 |
| Heuristics | 1.10 | 0.91 | 1.10 | 0.92 | 1.34 | 1.03 | 1.07 |
| SVIP | 1.33 | 1.12 | 1.37 | 1.14 | 1.57 | 1.23 | 1.29(+20.6%) |
| LLaMA-3(70B, 8B) Const. | 2.04 | 2.48 | 2.56 | 2.34 | 2.32 | 2.28 | 2.34 |
| Heuristics | 2.30 | 3.13 | 3.33 | 2.61 | 2.52 | 2.63 | 2.76 |
| SVIP | 2.31 | 3.04 | 3.48 | 2.63 | 2.89 | 2.59 | 2.83(+20.9%) |
🔼 This table presents the speedup achieved by using the Self-Verification length Policy (SVIP) for speculative decoding compared to a baseline approach of using only the target language model for autoregressive decoding. The speedup is calculated across six different tasks within the SpecBench benchmark, using three different large language models (Pythia, Qwen, and LLaMA) with their corresponding smaller draft models. Results are shown for two baseline methods (‘Const’ for constant draft length and ‘Heuristics’ for a heuristic-based draft length) and SVIP. The percentage improvement of SVIP over the target-model-only approach is indicated in parentheses.
read the caption
Table 1: Speedup over target-model-only autoregressive decoding on SpecBench.
In-depth insights#
SVIP: Core Algorithm#
The core algorithm of SVIP revolves around dynamically adjusting the length of draft sequences in speculative decoding. Instead of a fixed draft length, SVIP leverages the entropy of the draft model’s token distribution to determine when to stop drafting and begin verification. A lower bound on the system’s acceptance rate, approximated by the draft model’s entropy, guides this decision. High entropy indicates difficult tokens, prompting earlier termination of the draft sequence, while low entropy signals easier tokens, allowing for longer drafts. This adaptive approach aims to optimize speed without sacrificing accuracy, achieving significant wall-clock time improvements over baseline methods. SVIP is inherently training-free, requiring only the draft model’s probability distribution. The algorithm’s simplicity and compatibility with various existing speculative decoding frameworks highlight its practical value for enhancing LLM inference efficiency.
Entropy-Based Policy#
An entropy-based policy for speculative decoding offers a novel approach to optimizing the efficiency of large language models. The core idea revolves around dynamically adjusting the length of draft sequences generated by a lightweight model based on the inherent uncertainty, or entropy, of the predicted token distributions. By analyzing the entropy of each draft token, the policy can intelligently decide when to continue drafting or to verify the draft with a more powerful model. This avoids the limitations of fixed-length draft policies, which often fail to account for the varying difficulty of token generation across different tasks and contexts. A low entropy signifies high confidence, thus justifying longer drafts to enhance efficiency. Conversely, high entropy signals uncertainty, prompting early verification to minimize wasted computation on uncertain predictions. The policy’s adaptability improves both speed and acceptance rates compared to fixed-length counterparts, yielding substantial wall-clock speedups across various benchmarks and model sizes. The training-free nature further enhances its practicality and compatibility with existing speculative decoding frameworks.
Speculative Decoding#
Speculative decoding is a crucial technique accelerating large language model (LLM) inference. It leverages a faster, lightweight draft model to predict token sequences, which are subsequently verified by a more powerful, but slower, target model. This approach avoids the computationally expensive autoregressive generation of every token by the target model. The efficiency gains are significant, especially for longer sequences. However, traditional methods employ a fixed draft length, failing to account for varying levels of difficulty in generating different tokens. This limitation can reduce efficiency, as some tokens are easily predicted, while others may require significant computation. Dynamic draft length policies address this by adjusting the length of the draft sequence based on the difficulty of the tokens. Such policies offer a self-verifying approach, adapting based on the probability of acceptance by the target model. This adaptability leads to substantial speed improvements over methods with fixed draft lengths, maximizing the advantages of speculative decoding without compromising generation quality. The use of entropy, as an indicator of draft token uncertainty, is particularly insightful for controlling the length of draft sequences. It provides a practical, training-free method for optimizing efficiency. The research demonstrates consistent improvements across multiple LLMs and speculative decoding frameworks, proving the effectiveness and general applicability of dynamic draft length policies.
Dynamic Draft Length#
The concept of “Dynamic Draft Length” in speculative decoding addresses a critical limitation of traditional methods. Fixed-length draft sequences ignore the inherent variability in token generation difficulty. Some tokens are easier for the draft model to predict (e.g., common words, simple phrases), while others are significantly more complex (e.g., knowledge-intensive, reasoning-heavy). A dynamic approach, therefore, allows the model to adapt its draft length based on this difficulty. By considering factors like token entropy or acceptance probability, the model can generate longer drafts for simpler tokens (improving efficiency) and shorter drafts for complex tokens (reducing unnecessary computation). This results in significant improvements in speed and efficiency without compromising the quality of the generated text. The key benefit is a system that is more robust and adapts to different generation tasks, offering better wall-clock speedups compared to approaches relying on fixed-length drafting.
Long-Form Generation#
The section on “Long-Form Generation” in this research paper is crucial because it tests the scalability and generalizability of the proposed Self-Verification Interval Policy (SVIP) beyond the typical short-sequence tasks. By evaluating SVIP on the generation of sequences up to 8K tokens, the authors move beyond the limitations of previous speculative decoding methods that mostly focus on shorter outputs. This is important because long-form generation poses unique challenges due to increased computational cost and the potential for cumulative errors in draft sequences. The results demonstrate that SVIP not only maintains its effectiveness but also shows an even greater speedup in this scenario, particularly highlighting the advantage of dynamically adapting the draft length according to the inherent difficulty of the tokens. This validates the robustness of SVIP and suggests its wider applicability in various practical applications dealing with the generation of longer text, such as document summarization, story writing, or code generation, where the ability to efficiently produce high-quality long-form content is crucial.
More visual insights#
More on figures

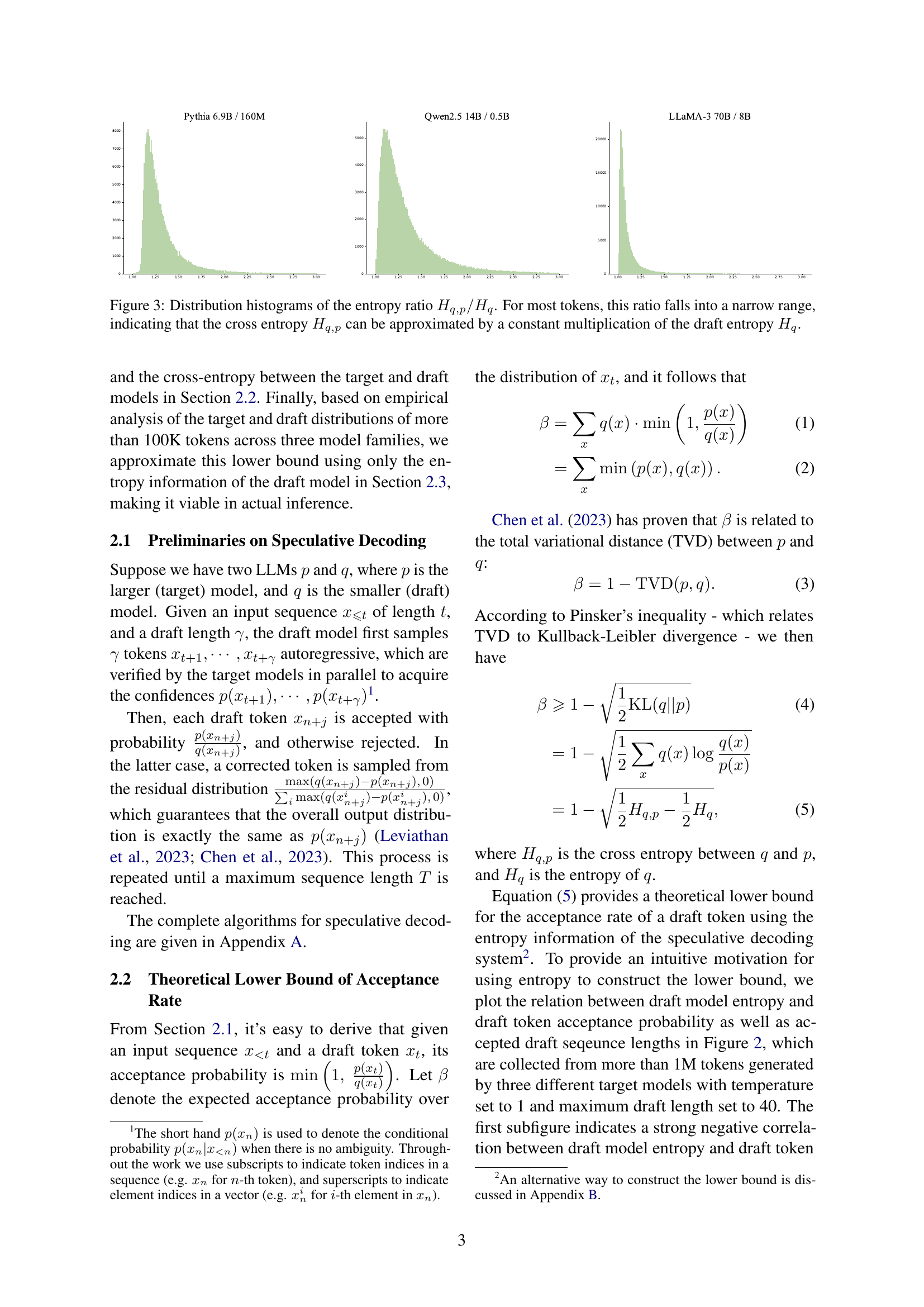
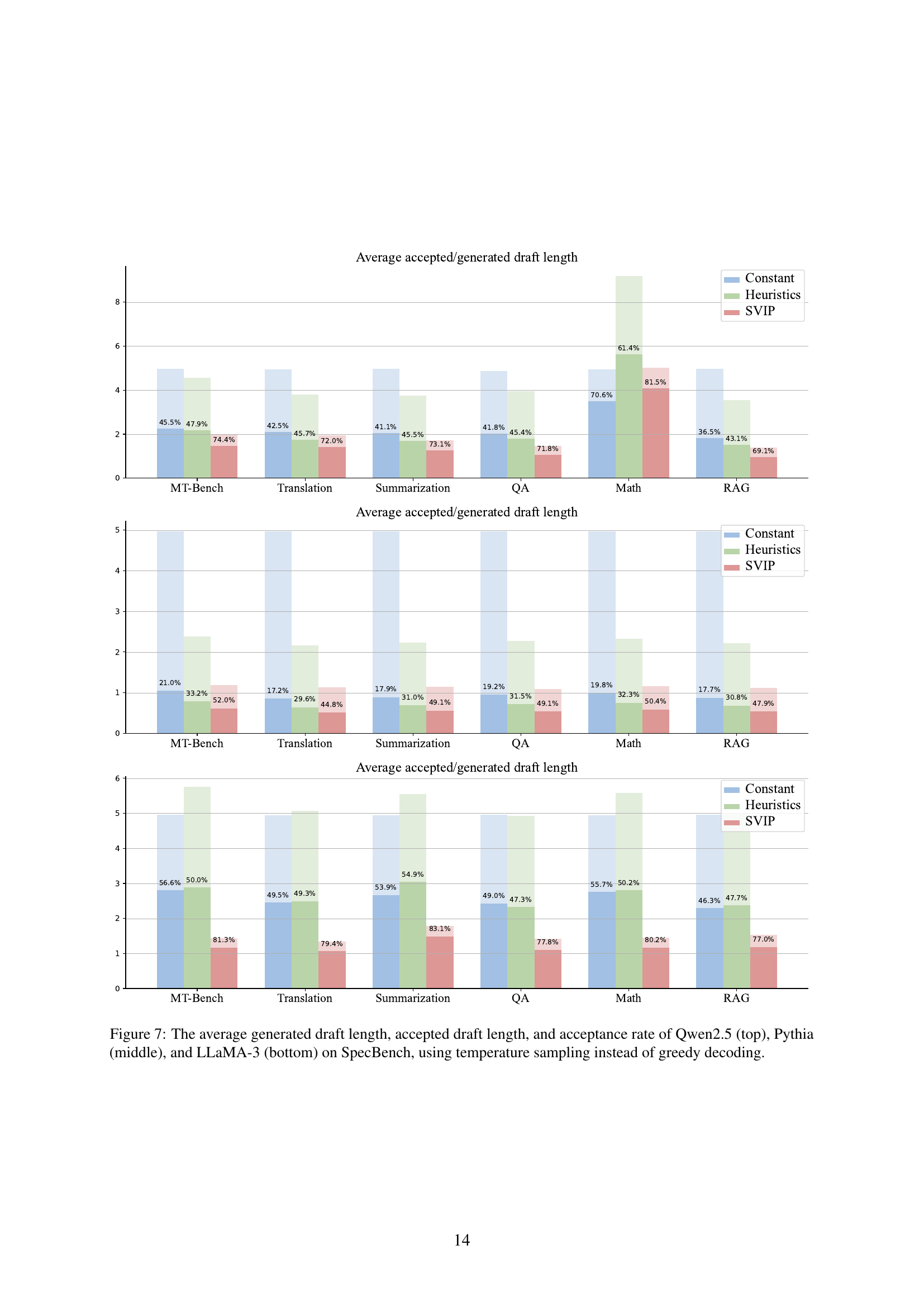
🔼 This figure displays the relationship between draft model entropy and two key aspects of speculative decoding: the probability of draft tokens being accepted by the target model, and the lengths of accepted draft sequences. The top row shows that lower draft model entropy correlates with higher acceptance probabilities, while the bottom row reveals that lower entropy also corresponds to longer sequences of accepted draft tokens. This visualization underscores the variability in drafting difficulty and motivates the need for a dynamic draft length policy that adapts to varying levels of prediction uncertainty.
read the caption
Figure 2: The correlation between draft model entropy and draft token acceptance probability (top) and lengths of accepted draft seqeunces (bottom).

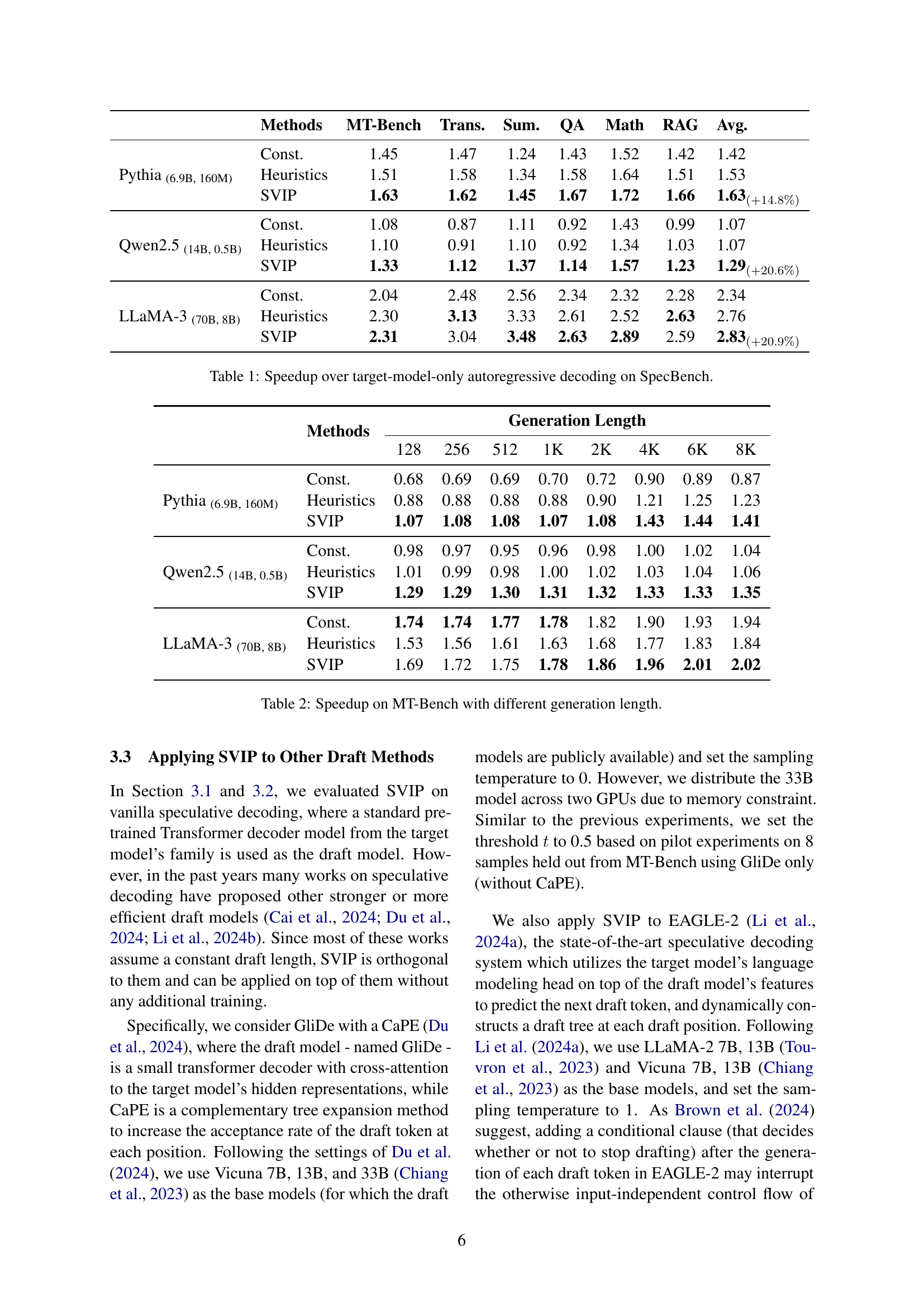
🔼 Figure 3 presents histograms showing the distribution of the ratio between the cross-entropy (Hq,p) and the draft entropy (Hq) for three different large language models. The cross-entropy measures the dissimilarity between the probability distributions generated by the draft and target language models. The draft entropy quantifies the uncertainty in the draft model’s predictions. The histograms reveal that for the vast majority of tokens, this ratio remains within a narrow range. This key observation supports the paper’s approximation that the cross-entropy (Hq,p) can be estimated efficiently using only the draft entropy (Hq) multiplied by a constant value. This simplification is crucial for the algorithm’s efficiency.
read the caption
Figure 3: Distribution histograms of the entropy ratio Hq,p/Hqsubscript𝐻𝑞𝑝subscript𝐻𝑞H_{q,p}/H_{q}italic_H start_POSTSUBSCRIPT italic_q , italic_p end_POSTSUBSCRIPT / italic_H start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT. For most tokens, this ratio falls into a narrow range, indicating that the cross entropy Hq,psubscript𝐻𝑞𝑝H_{q,p}italic_H start_POSTSUBSCRIPT italic_q , italic_p end_POSTSUBSCRIPT can be approximated by a constant multiplication of the draft entropy Hqsubscript𝐻𝑞H_{q}italic_H start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT.

🔼 Figure 4 illustrates the relationship between the theoretical acceptance probability of draft tokens and their entropy. The figure compares three values: the actual acceptance probability calculated using Equation (2) from the paper; a lower bound on this probability derived from Equation (5), which uses the cross-entropy between the draft and target language models; and an estimated lower bound that simplifies Equation (5) by approximating cross-entropy as a constant multiple of draft model entropy. The tokens are ordered on the x-axis according to their actual acceptance probability, enabling a visual comparison of the actual and estimated probabilities.
read the caption
Figure 4: Comparison between the actual acceptance probability from Equation (2), the acceptance probability lower bound from Equation (5), and the estimated lower bound after approximating the cross entropy Hq,psubscript𝐻𝑞𝑝H_{q,p}italic_H start_POSTSUBSCRIPT italic_q , italic_p end_POSTSUBSCRIPT with a constant multiplication of Hqsubscript𝐻𝑞H_{q}italic_H start_POSTSUBSCRIPT italic_q end_POSTSUBSCRIPT. Each position on the x-axis corresponds to a token, which has been sorted according to the actual acceptance probability.

🔼 Figure 5 presents a comparison of the performance of three different draft length policies (Constant, Heuristics, and SVIP) on the SpecBench benchmark using Qwen-2.5 and LLaMA-3 language models. The top half shows results for Qwen-2.5, while the bottom half shows results for LLaMA-3. For each model and policy, the figure displays three key metrics: the average generated draft length (the average number of tokens generated by the draft model before verification), the average accepted draft length (the average number of tokens accepted by the target model after verification), and the overall acceptance rate (the percentage of draft tokens accepted by the target model). The figure clearly demonstrates that SVIP consistently leads to shorter generated draft lengths and significantly higher acceptance rates compared to both the Constant and Heuristics baselines, thereby indicating its superior efficiency in speculative decoding.
read the caption
Figure 5: The average generated draft length, accepted draft length, and acceptance rate of Qwen2.5 (top) and LLaMA-3 (bottom) on SpecBench. Compared with the two baselines, SVIP leads to a shorter draft length and a much higher acceptance rate.
More on tables
| Methods | 128 | 256 | 512 | 1K | 2K | 4K | 6K | 8K | |
|---|---|---|---|---|---|---|---|---|---|
| Pythia (6.9B, 160M) | Const. | 0.68 | 0.69 | 0.69 | 0.70 | 0.72 | 0.90 | 0.89 | 0.87 |
| Heuristics | 0.88 | 0.88 | 0.88 | 0.88 | 0.90 | 1.21 | 1.25 | 1.23 | |
| SVIP | 1.07 | 1.08 | 1.08 | 1.07 | 1.08 | 1.43 | 1.44 | 1.41 | |
| Qwen2.5 (14B, 0.5B) | Const. | 0.98 | 0.97 | 0.95 | 0.96 | 0.98 | 1.00 | 1.02 | 1.04 |
| Heuristics | 1.01 | 0.99 | 0.98 | 1.00 | 1.02 | 1.03 | 1.04 | 1.06 | |
| SVIP | 1.29 | 1.29 | 1.30 | 1.31 | 1.32 | 1.33 | 1.33 | 1.35 | |
| LLaMA-3 (70B, 8B) | Const. | 1.74 | 1.74 | 1.77 | 1.78 | 1.82 | 1.90 | 1.93 | 1.94 |
| Heuristics | 1.53 | 1.56 | 1.61 | 1.63 | 1.68 | 1.77 | 1.83 | 1.84 | |
| SVIP | 1.69 | 1.72 | 1.75 | 1.78 | 1.86 | 1.96 | 2.01 | 2.02 |
🔼 This table presents the speedup achieved by different methods (Const, Heuristics, SVIP) on the MT-Bench benchmark for various text generation lengths (128, 256, 512, 1K, 2K, 4K, 6K, 8K tokens). It shows how the performance of each method changes as the length of the generated text increases, allowing for a comparison of their efficiency in long-form text generation. The speedup is calculated relative to a baseline of using only the target model for autoregressive decoding.
read the caption
Table 2: Speedup on MT-Bench with different generation length.
| Methods | MT-Bench | Code | Finance | GSM | Spider | Avg. | |
|---|---|---|---|---|---|---|---|
| 7B | GliDe | 1.95 | 2.04 | 1.91 | 1.98 | 1.69 | 1.95 |
| +SVIP | 2.00 | 2.12 | 2.03 | 2.01 | 1.63 | 2.02 | |
| GliDe + CaPE | 2.36 | 2.57 | 2.29 | 2.51 | 1.97 | 2.40 | |
| +SVIP | 2.56 | 2.65 | 2.49 | 2.54 | 2.08 | 2.52 | |
| 13B | GliDe | 2.22 | 2.41 | 2.15 | 2.31 | 1.85 | 2.24 |
| +SVIP | 2.31 | 2.43 | 2.17 | 2.35 | 1.85 | 2.28 | |
| GliDe + CaPE | 2.73 | 2.86 | 2.66 | 2.80 | 2.24 | 2.73 | |
| +SVIP | 2.72 | 2.93 | 2.66 | 2.85 | 2.27 | 2.76 | |
| 33B | GliDe | 2.12 | 2.25 | 2.09 | 2.29 | 1.99 | 2.18 |
| +SVIP | 2.29 | 2.40 | 2.20 | 2.42 | 2.03 | 2.30 | |
| GliDe + CaPE | 2.08 | 1.98 | 2.10 | 2.13 | 1.76 | 2.03 | |
| +SVIP | 2.13 | 2.02 | 2.15 | 2.16 | 1.82 | 2.08 |
🔼 This table presents the speedup achieved by using SVIP in conjunction with GliDe and CaPE models. It compares the performance of using these methods with and without SVIP across various tasks in the MT-Bench benchmark. Vicuna models of various sizes (7B, 13B, and 33B parameters) are used as base models for the experiments. The speedup is calculated relative to the performance of GliDe and CaPE alone.
read the caption
Table 3: Speedup comparison with GliDe & CaPE, using Vicuna as the base model.
| Methods | MT-Bench | H-Eval | GSM8K | Alpaca | CNN/DM | QA | Avg. | |
|---|---|---|---|---|---|---|---|---|
| LLaMA-2 7B | EAGLE-2 | 3.10 | 3.61 | 3.15 | 3.10 | 2.76 | 2.84 | 3.10 |
| + SVIP | 3.16 | 3.66 | 3.18 | 3.13 | 2.82 | 3.02 | 3.16 | |
| LLaMA-2 13B | EAGLE-2 | 3.38 | 4.12 | 3.41 | 3.25 | 3.01 | 2.98 | 3.41 |
| + SVIP | 3.41 | 4.09 | 3.45 | 3.34 | 3.05 | 3.17 | 3.46 | |
| Vicuna 7B | EAGLE-2 | 2.66 | 2.84 | 2.77 | 2.48 | 2.31 | 2.13 | 2.58 |
| + SVIP | 2.84 | 2.97 | 2.75 | 2.66 | 2.42 | 2.30 | 2.73 | |
| Vicuna 13B | EAGLE-2 | 2.85 | 3.31 | 2.93 | 2.74 | 2.48 | 2.30 | 2.83 |
| + SVIP | 2.94 | 3.49 | 3.19 | 2.89 | 2.60 | 2.53 | 2.98 |
🔼 This table presents the speedup achieved by using the SVIP method on top of the EAGLE-2 speculative decoding framework. Two sets of base language models are used: LLaMA-2-Chat and Vicuna, each tested in 7B and 13B parameter variants. The speedup is calculated relative to using only the target model without any speculative decoding. The speedup is shown across multiple benchmark tasks (MT-Bench, H-Eval, GSM8K, Alpaca, CNN/DM, QA) and provides a comparison of the performance gain using SVIP.
read the caption
Table 4: Speedup comparison with EAGLE-2, using LLaMA-2-Chat and Vicuna as the base models.
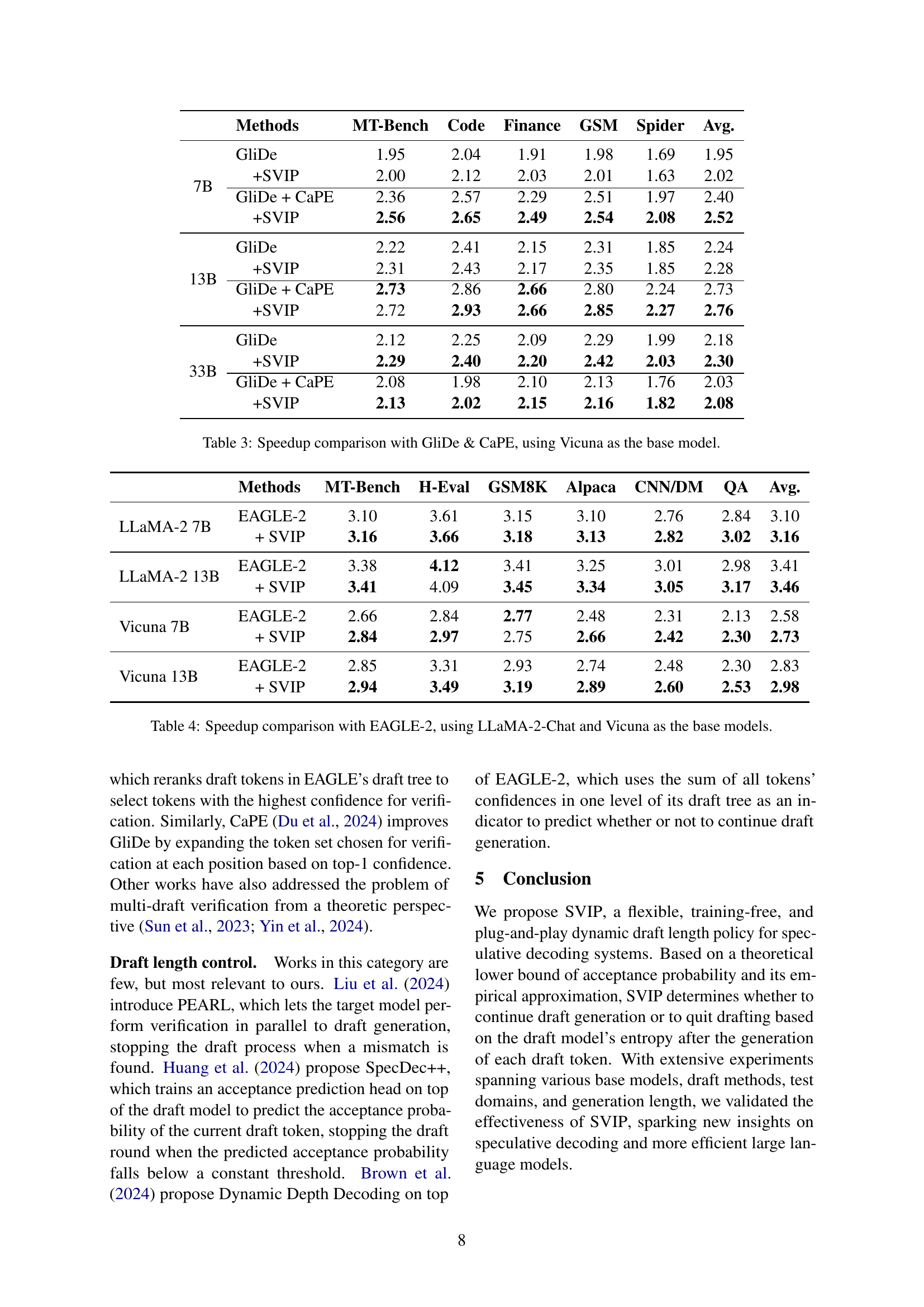
| Methods | MT-Bench | Trans. | Sum. | QA | Math | RAG | Avg. | |
|---|---|---|---|---|---|---|---|---|
| Pythia | Const. | 0.65 | 0.63 | 0.65 | 0.66 | 0.65 | 0.64 | 0.65 |
| Heuristics | 0.82 | 0.83 | 0.85 | 0.83 | 0.83 | 0.83 | 0.83 | |
| SVIP | 1.05 | 1.02 | 1.03 | 1.01 | 1.03 | 1.00 | 1.02(+56.9%) | |
| Qwen2.5 | Const. | 1.01 | 0.85 | 0.87 | 0.85 | 1.32 | 0.86 | 0.96 |
| Heuristics | 1.02 | 0.94 | 0.93 | 0.88 | 1.22 | 0.91 | 0.99 | |
| SVIP | 1.24 | 1.08 | 1.19 | 1.11 | 1.47 | 1.10 | 1.20(+25.0%) | |
| LLaMA-3 | Const. | 1.62 | 1.56 | 1.65 | 1.53 | 1.73 | 1.54 | 1.60 |
| Heuristics | 1.56 | 1.55 | 1.76 | 1.49 | 1.61 | 1.55 | 1.58 | |
| SVIP | 1.53 | 1.53 | 1.69 | 1.51 | 1.71 | 1.56 | 1.58(-1.3%) |
🔼 This table presents the speedup achieved by the SVIP method compared to baseline methods (constant and heuristic draft length policies) on the SpecBench benchmark. The speedup is calculated relative to using only the target language model without speculative decoding. Importantly, this table’s results utilize temperature sampling during token generation, a different approach than used in other tables of the paper.
read the caption
Table 5: Speedup on SpecBench using temperature sampling.
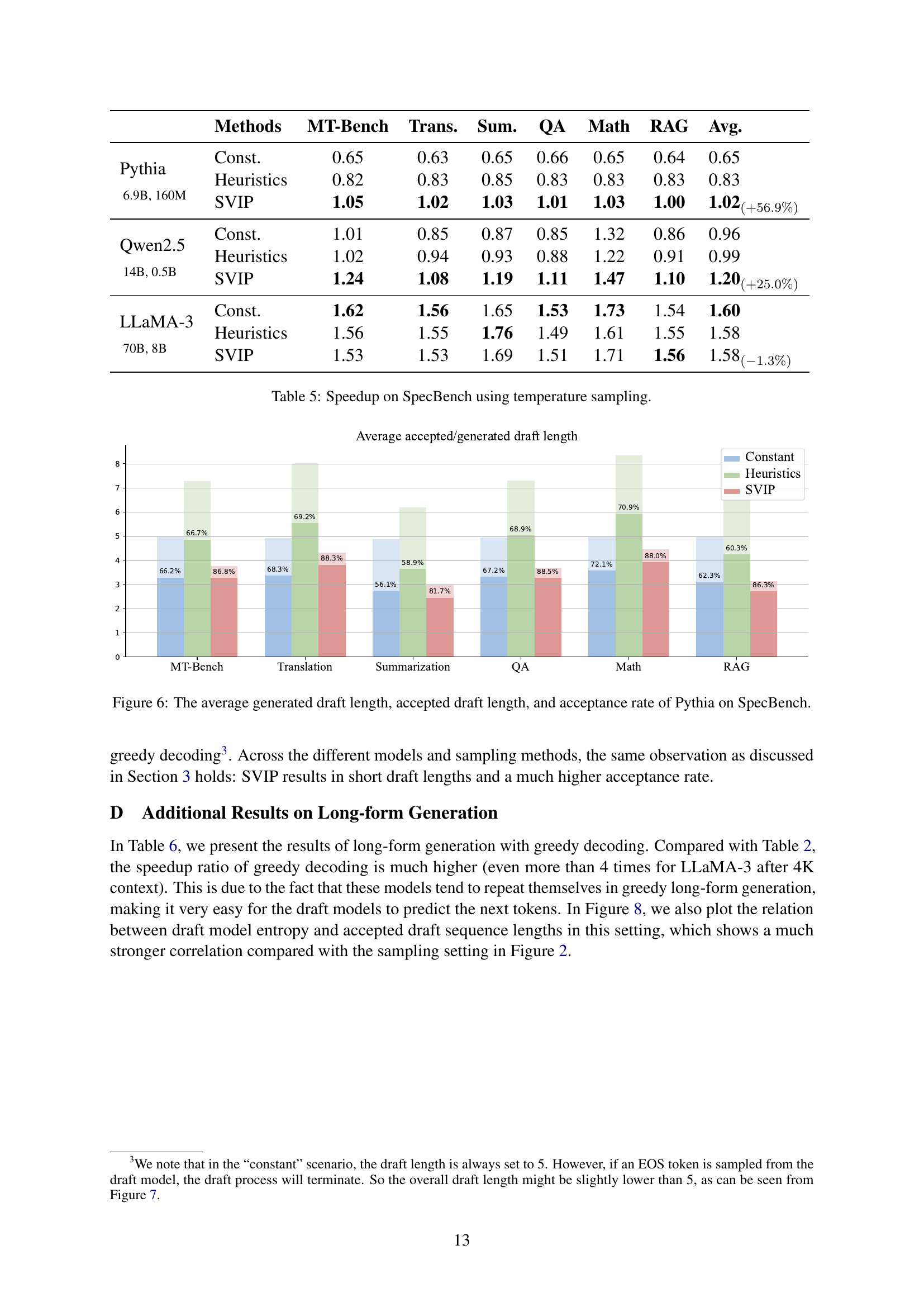
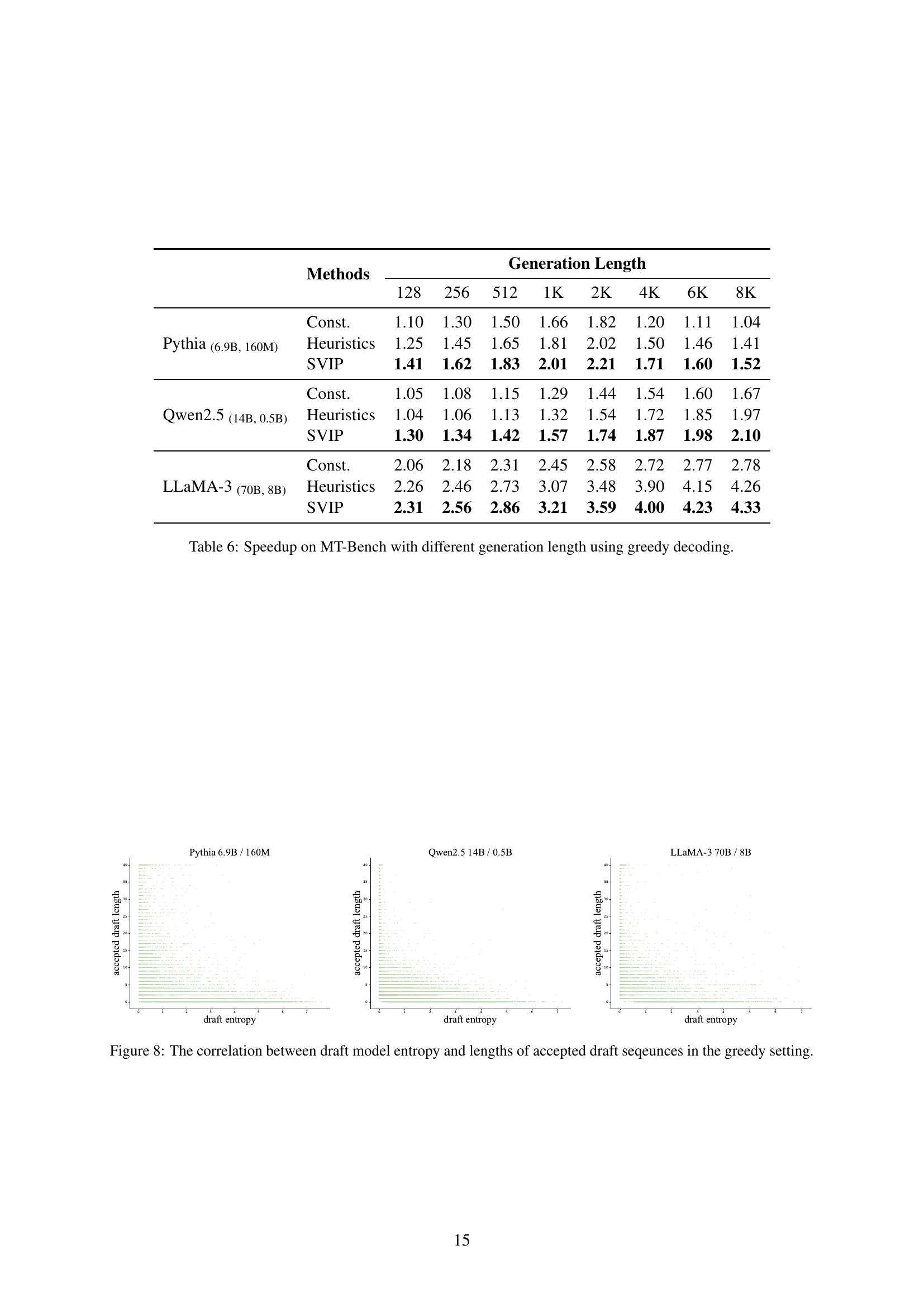
| Model | Methods | 128 | 256 | 512 | 1K | 2K | 4K | 6K | 8K |
|---|---|---|---|---|---|---|---|---|---|
| Pythia(6.9B, 160M) | Const. | 1.10 | 1.30 | 1.50 | 1.66 | 1.82 | 1.20 | 1.11 | 1.04 |
| Heuristics | 1.25 | 1.45 | 1.65 | 1.81 | 2.02 | 1.50 | 1.46 | 1.41 | |
| SVIP | 1.41 | 1.62 | 1.83 | 2.01 | 2.21 | 1.71 | 1.60 | 1.52 | |
| Qwen2.5(14B, 0.5B) | Const. | 1.05 | 1.08 | 1.15 | 1.29 | 1.44 | 1.54 | 1.60 | 1.67 |
| Heuristics | 1.04 | 1.06 | 1.13 | 1.32 | 1.54 | 1.72 | 1.85 | 1.97 | |
| SVIP | 1.30 | 1.34 | 1.42 | 1.57 | 1.74 | 1.87 | 1.98 | 2.10 | |
| LLaMA-3(70B, 8B) | Const. | 2.06 | 2.18 | 2.31 | 2.45 | 2.58 | 2.72 | 2.77 | 2.78 |
| Heuristics | 2.26 | 2.46 | 2.73 | 3.07 | 3.48 | 3.90 | 4.15 | 4.26 | |
| SVIP | 2.31 | 2.56 | 2.86 | 3.21 | 3.59 | 4.00 | 4.23 | 4.33 |
🔼 This table presents the speedup achieved by using the SVIP method compared to baseline methods (constant and heuristics) on the MT-Bench dataset for various generation lengths when greedy decoding is employed. The results are broken down by model (Pythia, Qwen, LLaMA) and show the speedup factor for different output sequence lengths ranging from 128 to 8192 tokens. This demonstrates SVIP’s performance on long-form text generation.
read the caption
Table 6: Speedup on MT-Bench with different generation length using greedy decoding.
Full paper#