↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Traditional in-context learning (ICL) for large language models (LLMs) struggles with complex reasoning tasks due to its heavy reliance on high-quality example demonstrations and human intervention. This dependence limits its generalization ability and efficiency. Furthermore, creating these demonstrations often requires substantial human expertise, making it a time-consuming and labor-intensive process.
This paper introduces HiAR-ICL, a novel high-level automated reasoning paradigm. HiAR-ICL utilizes Monte Carlo Tree Search (MCTS) to explore reasoning paths and construct “thought cards,” representing abstract thinking patterns. These cards guide the reasoning process, reducing the need for specific examples and human intervention. The results show that HiAR-ICL significantly outperforms existing methods in complex mathematical reasoning, achieving state-of-the-art accuracy and demonstrating improved efficiency.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses limitations of traditional in-context learning (ICL) in complex reasoning tasks. By introducing HiAR-ICL, a novel automated reasoning paradigm, it offers a solution to improve ICL’s generalization ability and reduce dependence on human expertise in demonstration creation. This opens new avenues for improving LLMs’ reasoning capabilities, particularly in domains requiring advanced cognitive skills. The findings have significant implications for the field and researchers working on improving LLMs’ performance in complex reasoning tasks, making this a timely and relevant piece of research.
Visual Insights#
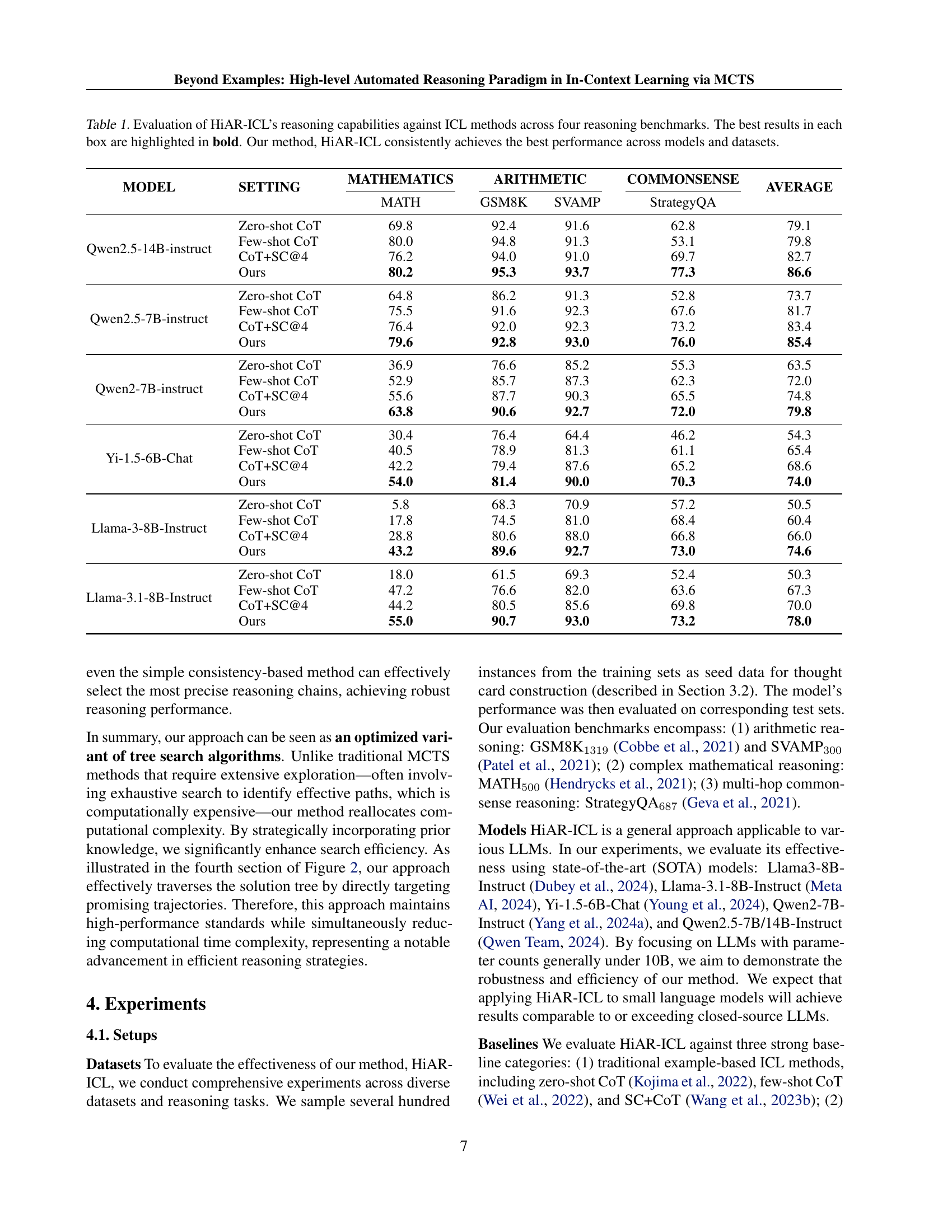
| MODEL | SETTING | MATHEMATICS | ARITHMETIC | ARITHMETIC | COMMONSENSE | AVERAGE |
|---|---|---|---|---|---|---|
| MATH | GSM8K | SVAMP | StrategyQA | |||
| Qwen2.5-14B-instruct | Zero-shot CoT | 69.8 | 92.4 | 91.6 | 62.8 | 79.1 |
| Few-shot CoT | 80.0 | 94.8 | 91.3 | 53.1 | 79.8 | |
| CoT+SC@4 | 76.2 | 94.0 | 91.0 | 69.7 | 82.7 | |
| Ours | 80.2 | 95.3 | 93.7 | 77.3 | 86.6 | |
| Qwen2.5-7B-instruct | Zero-shot CoT | 64.8 | 86.2 | 91.3 | 52.8 | 73.7 |
| Few-shot CoT | 75.5 | 91.6 | 92.3 | 67.6 | 81.7 | |
| CoT+SC@4 | 76.4 | 92.0 | 92.3 | 73.2 | 83.4 | |
| Ours | 79.6 | 92.8 | 93.0 | 76.0 | 85.4 | |
| Qwen2-7B-instruct | Zero-shot CoT | 36.9 | 76.6 | 85.2 | 55.3 | 63.5 |
| Few-shot CoT | 52.9 | 85.7 | 87.3 | 62.3 | 72.0 | |
| CoT+SC@4 | 55.6 | 87.7 | 90.3 | 65.5 | 74.8 | |
| Ours | 63.8 | 90.6 | 92.7 | 72.0 | 79.8 | |
| Yi-1.5-6B-Chat | Zero-shot CoT | 30.4 | 76.4 | 64.4 | 46.2 | 54.3 |
| Few-shot CoT | 40.5 | 78.9 | 81.3 | 61.1 | 65.4 | |
| CoT+SC@4 | 42.2 | 79.4 | 87.6 | 65.2 | 68.6 | |
| Ours | 54.0 | 81.4 | 90.0 | 70.3 | 74.0 | |
| Llama-3-8B-Instruct | Zero-shot CoT | 5.8 | 68.3 | 70.9 | 57.2 | 50.5 |
| Few-shot CoT | 17.8 | 74.5 | 81.0 | 68.4 | 60.4 | |
| CoT+SC@4 | 28.8 | 80.6 | 88.0 | 66.8 | 66.0 | |
| Ours | 43.2 | 89.6 | 92.7 | 73.0 | 74.6 | |
| Llama-3.1-8B-Instruct | Zero-shot CoT | 18.0 | 61.5 | 69.3 | 52.4 | 50.3 |
| Few-shot CoT | 47.2 | 76.6 | 82.0 | 63.6 | 67.3 | |
| CoT+SC@4 | 44.2 | 80.5 | 85.6 | 69.8 | 70.0 | |
| Ours | 55.0 | 90.7 | 93.0 | 73.2 | 78.0 |
🔼 This table presents a comprehensive evaluation of the HiAR-ICL method’s reasoning capabilities. It compares HiAR-ICL’s performance against several state-of-the-art In-Context Learning (ICL) techniques across four distinct reasoning benchmarks: MATH, GSM8K, SVAMP, and StrategyQA. The comparison includes both zero-shot and few-shot Chain-of-Thought (CoT) prompting methods, as well as CoT enhanced with a Self-Consistency (SC) approach. Results are shown for various large language models (LLMs), highlighting the consistent superior performance of HiAR-ICL across different models and datasets. The best performance in each category is indicated in bold.
read the caption
Table 1: Evaluation of HiAR-ICL’s reasoning capabilities against ICL methods across four reasoning benchmarks. The best results in each box are highlighted in bold. Our method, HiAR-ICL consistently achieves the best performance across models and datasets.
In-depth insights#
HiAR-ICL Framework#
The HiAR-ICL framework represents a novel approach to in-context learning (ICL), addressing limitations of traditional ICL in complex reasoning tasks. Instead of relying heavily on example-based learning, HiAR-ICL focuses on higher-level, abstract reasoning patterns. This shift is crucial, as it moves beyond simple imitation to a more sophisticated understanding of problem-solving strategies. The framework leverages Monte Carlo Tree Search (MCTS) to explore various reasoning paths and construct ’thought cards’—templates encapsulating these patterns. These thought cards are then dynamically matched to problems based on a cognitive complexity metric, ensuring the selection of appropriate reasoning strategies. Finally, a multi-faceted verification process helps ensure accuracy, integrating output and process reward models alongside consistency checks. This framework thus integrates high-level reasoning pattern identification with a powerful search mechanism and a robust verification system, leading to improved performance and generalizability in complex problem-solving scenarios. The automated nature eliminates the need for human intervention in designing demonstrations, significantly improving efficiency and reducing reliance on high-quality example datasets.
MCTS Reasoning#
The core of the proposed HiAR-ICL framework lies in its MCTS-based reasoning paradigm. Instead of relying solely on example demonstrations, HiAR-ICL leverages MCTS to explore a tree of reasoning paths, dynamically constructing and selecting optimal sequences of atomic reasoning actions (SA, OST, CoT, DC, SRR) tailored to the problem’s cognitive complexity. This approach moves beyond simplistic linear reasoning chains to embrace a more nuanced and human-like problem-solving process. The use of MCTS enables HiAR-ICL to overcome the limitations of traditional ICL, which heavily depend on the quality and relevance of example demonstrations. This method not only improves accuracy, especially on complex reasoning tasks, but also addresses the issue of generalization, allowing the model to efficiently tackle unseen problems with similar logical structures. The thought cards, generated through the MCTS process, act as high-level reasoning templates, providing reusable patterns for tackling various problems. Consequently, HiAR-ICL presents a novel approach to ICL that surpasses traditional methods in both accuracy and generalization ability.
Cognitive Complexity#
The concept of Cognitive Complexity, while not explicitly a heading in the provided text, is central to the paper’s methodology. It’s used to dynamically match problems with appropriate reasoning patterns, or ’thought cards.’ The authors define complexity using three key metrics: subquestion count, problem condition complexity, and semantic similarity. This framework moves beyond simple example-based learning, acknowledging that different problem structures require different levels of cognitive processing. By using the cognitive complexity metric, the system efficiently chooses the right reasoning strategy without relying heavily on the quality or quantity of training examples. This approach suggests that a deeper understanding of a problem’s inherent difficulty is crucial for effective reasoning, and that a well-designed complexity metric can help LLMs leverage more appropriate reasoning pathways, thereby improving accuracy and efficiency. The authors’ success highlights the potential of incorporating cognitive factors into machine learning models for improved performance in complex tasks.
Benchmark Results#
Benchmark results are crucial for evaluating the effectiveness of any proposed methodology. In this context, a thorough analysis of benchmark results would involve examining the model’s performance across various datasets, comparing it to existing state-of-the-art models, and investigating the impact of different parameters. Key aspects to consider include accuracy metrics, such as precision, recall, and F1-score, for diverse tasks. Furthermore, analyzing computational efficiency is vital, particularly concerning resource usage and time complexity. A detailed breakdown of performance across diverse datasets, highlighting strengths and weaknesses, can reveal potential biases or limitations. Direct comparison with existing methods and commercially available models (like GPT-4) provides context and enables a clear demonstration of the proposed method’s advantages. Statistical significance testing of results and error analysis would strengthen the credibility of the findings. The overall discussion should highlight both the achievements and limitations of the approach, paving the way for future improvements and research directions.
Future of ICL#
The future of In-Context Learning (ICL) hinges on addressing its current limitations. Moving beyond reliance on high-quality, human-crafted examples is crucial. This requires developing automated methods for generating diverse and effective prompts and demonstrations, potentially leveraging techniques like Monte Carlo Tree Search (MCTS) to explore the reasoning space more efficiently. Integrating higher-level cognitive reasoning patterns, rather than solely relying on surface-level example imitation, will unlock LLMs’ true potential for complex problem-solving. Further research should focus on developing more robust evaluation metrics that go beyond simple accuracy, and explore methods for improving generalization and reducing sensitivity to specific example characteristics. Ultimately, the future of ICL likely involves a hybrid approach that combines data-driven methods with symbolic reasoning, enabling LLMs to learn abstract principles and apply them effectively to novel situations.
More visual insights#
More on tables
| MODEL | SETTING | MATH | GSM8K |
|---|---|---|---|
| Claude-3-Opus | CS | 60.1 | 95.0 |
| Claude-3.5-Sonnet | CS | 71.1 | 96.4 |
| GPT-3.5 | CS | 43.1 | 81.6 |
| GPT-4 | CS | 64.5 | 94.2 |
| GPT-4o | CS | 76.6 | 96.1 |
| GPT-4o mini | CS | 70.2 | 93.2 |
| Gemini-1.5-Pro | CS | 67.7 | 90.8 |
| Llama-3.1-405B-Instruct | OS 405B | 73.8 | 96.8 |
| Llama-3.1-70B-Instruct | OS 70B | 68.0 | 95.1 |
| Llama-3-70B-Instruct | OS 70B | 50.4 | 93.0 |
| Nemotron4-340B-Instruct | OS 340B | 41.1 | 92.3 |
| Mixtral-large2-Instruct | OS 123B | 69.9 | 92.7 |
| Mixtral-8x22B-Instruct | OS 141B | 54.1 | 88.2 |
| NuminaMath-72B CoT | OS 72B | 66.7 | 90.8 |
| Qwen2-72B-Instruct | OS 72B | 69.0 | 93.2 |
| Yi-1.5-34B-Chat | OS 34B | 50.1 | 90.2 |
| Qwen2.5-14B-instruct | Ours | 80.2 | 95.3 |
| Qwen2.5-7B-instruct | Ours | 79.6 | 92.8 |
| Qwen2-7B-instruct | Ours | 63.8 | 90.6 |
| Yi-1.5-6B-Chat | Ours | 54.0 | 81.4 |
| Llama-3-8B-Instruct | Ours | 43.2 | 89.6 |
| Llama-3.1-8B-Instruct | Ours | 55.0 | 90.7 |
🔼 Table 2 compares the performance of the proposed HiAR-ICL method with several leading closed-source Large Language Models (LLMs) and open-source LLMs on two benchmark datasets: MATH and GSM8K. The table highlights the accuracy achieved by each model on each dataset. ‘CS’ denotes closed-source models and ‘OS’ denotes open-source models. The best performance for each model/dataset combination is shown in bold. Importantly, the table demonstrates that the 7B parameter Qwen2.5-7B-Instruct model, enhanced with HiAR-ICL, surpasses all the closed-source LLMs in performance, achieving state-of-the-art (SOTA) results.
read the caption
Table 2: Comparison with leading closed-source LLMs. The best results in each box are highlighted in bold. Results for closed-source models are sourced from corresponding official websites. ‘CS’ and ‘OS’ represent closed-source and open-source LLMs, respectively. Notably, the 7B model, Qwen2.5-7b-instruct, surpasses all closed-source models, achieving SOTA performance.
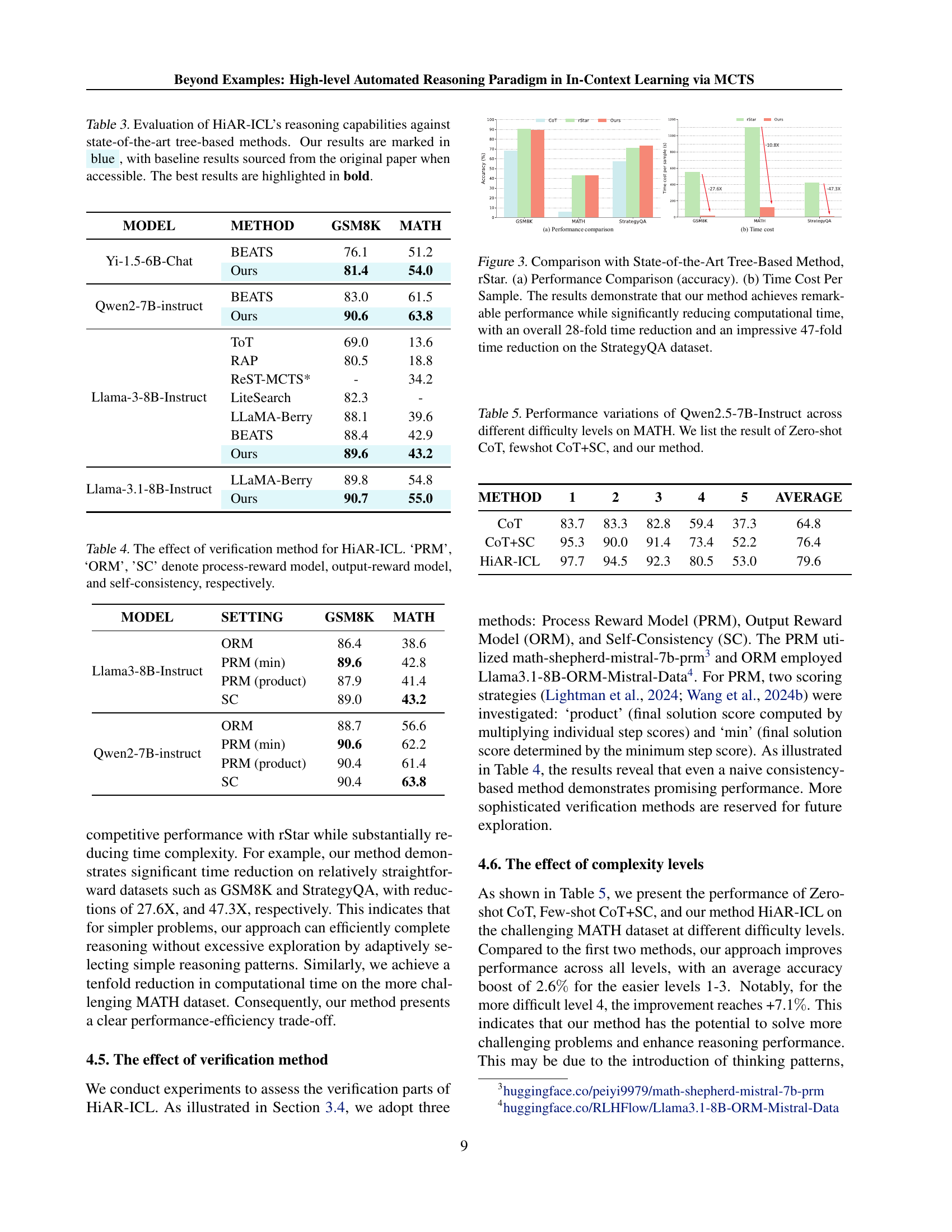
| MODEL | METHOD | GSM8K | MATH |
|---|---|---|---|
| Yi-1.5-6B-Chat | BEATS | 76.1 | 51.2 |
| Ours | 81.4 | 54.0 | |
| Qwen2-7B-instruct | BEATS | 83.0 | 61.5 |
| Ours | 90.6 | 63.8 | |
| Llama-3-8B-Instruct | ToT | 69.0 | 13.6 |
| RAP | 80.5 | 18.8 | |
| ReST-MCTS* | - | 34.2 | |
| LiteSearch | 82.3 | - | |
| LLaMA-Berry | 88.1 | 39.6 | |
| BEATS | 88.4 | 42.9 | |
| Ours | 89.6 | 43.2 | |
| Llama-3.1-8B-Instruct | LLaMA-Berry | 89.8 | 54.8 |
| Ours | 90.7 | 55.0 |
🔼 This table presents a comparison of HiAR-ICL’s performance against other state-of-the-art tree-based reasoning methods on several benchmark datasets (GSM8K, MATH, and StrategyQA). It highlights HiAR-ICL’s accuracy and efficiency in solving complex reasoning problems compared to existing approaches such as ToT, RAP, ReST-MCTS*, LiteSearch, LLaMA-Berry, and rStar. The best performance for each model and dataset is shown in bold. HiAR-ICL results are shown in blue, while the baseline results are taken from the original papers where accessible.
read the caption
Table 3: Evaluation of HiAR-ICL’s reasoning capabilities against state-of-the-art tree-based methods. Our results are marked in blue, with baseline results sourced from the original paper when accessible. The best results are highlighted in bold.
| MODEL | SETTING | GSM8K | MATH |
|---|---|---|---|
| Llama3-8B-Instruct | ORM | 86.4 | 38.6 |
| PRM (min) | 89.6 | 42.8 | |
| PRM (product) | 87.9 | 41.4 | |
| SC | 89.0 | 43.2 | |
| Qwen2-7B-instruct | ORM | 88.7 | 56.6 |
| PRM (min) | 90.6 | 62.2 | |
| PRM (product) | 90.4 | 61.4 | |
| SC | 90.4 | 63.8 |
🔼 This table presents the results of an ablation study on the HiAR-ICL model, evaluating the impact of different verification methods on its performance. The model uses three verification methods: Process Reward Model (PRM), Output Reward Model (ORM), and self-consistency (SC). PRM assesses the quality of the reasoning steps, ORM assesses the final solution, and SC checks for consistency in the reasoning process. The table compares the performance of HiAR-ICL across different datasets (GSM8K and MATH) with each verification method used individually. This analysis helps understand which method, or combination of methods, contributes most to the model’s accuracy and overall effectiveness.
read the caption
Table 4: The effect of verification method for HiAR-ICL. ‘PRM’, ‘ORM’, ’SC’ denote process-reward model, output-reward model, and self-consistency, respectively.
| METHOD | 1 | 2 | 3 | 4 | 5 | AVERAGE |
|---|---|---|---|---|---|---|
| CoT | 83.7 | 83.3 | 82.8 | 59.4 | 37.3 | 64.8 |
| CoT+SC | 95.3 | 90.0 | 91.4 | 73.4 | 52.2 | 76.4 |
| HiAR-ICL | 97.7 | 94.5 | 92.3 | 80.5 | 53.0 | 79.6 |
🔼 This table presents a detailed breakdown of the performance of the Qwen2.5-7B-Instruct model on the MATH benchmark dataset across various difficulty levels. It compares the results obtained using three different approaches: Zero-shot Chain-of-Thought (CoT), Few-shot CoT with Self-Consistency (CoT+SC), and the authors’ proposed HiAR-ICL method. The table allows for a direct comparison of these three approaches, highlighting the impact of different prompting strategies and the effectiveness of the novel HiAR-ICL method in addressing the challenges posed by varying problem complexities.
read the caption
Table 5: Performance variations of Qwen2.5-7B-Instruct across different difficulty levels on MATH. We list the result of Zero-shot CoT, fewshot CoT+SC, and our method.
Full paper#