↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large Language Models (LLMs) are powerful but prone to errors, especially in high-stakes applications needing near perfect reliability. Existing methods often rely on complex techniques or external verifiers that limit scalability. This paper tackles the problem of improving LLM reliability by focusing on test-time computation, which means making the LLM think longer or perform more computations to enhance its accuracy during inference.
The researchers propose a simple yet powerful two-stage algorithm: first, generate several candidate solutions using the LLM, then select the best one through a series of pairwise comparisons (a knockout tournament). They prove that this approach demonstrates a scaling law – the accuracy improves exponentially with the number of computations done. Experiments using a challenging benchmark confirm the approach and its gains in accuracy when scaled up. This offers a more practical and theoretically grounded method for enhancing LLM performance in critical scenarios.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel, provable scaling law for improving the reliability of LLMs. It offers a practical, efficient two-stage algorithm easily implemented using only a black-box LLM. This opens avenues for research into more reliable and efficient LLM applications in high-stakes scenarios and boosts the overall field of LLM reliability and efficiency. The provable scaling law adds theoretical rigor to existing work and provides a solid foundation for future advancements.
Visual Insights#

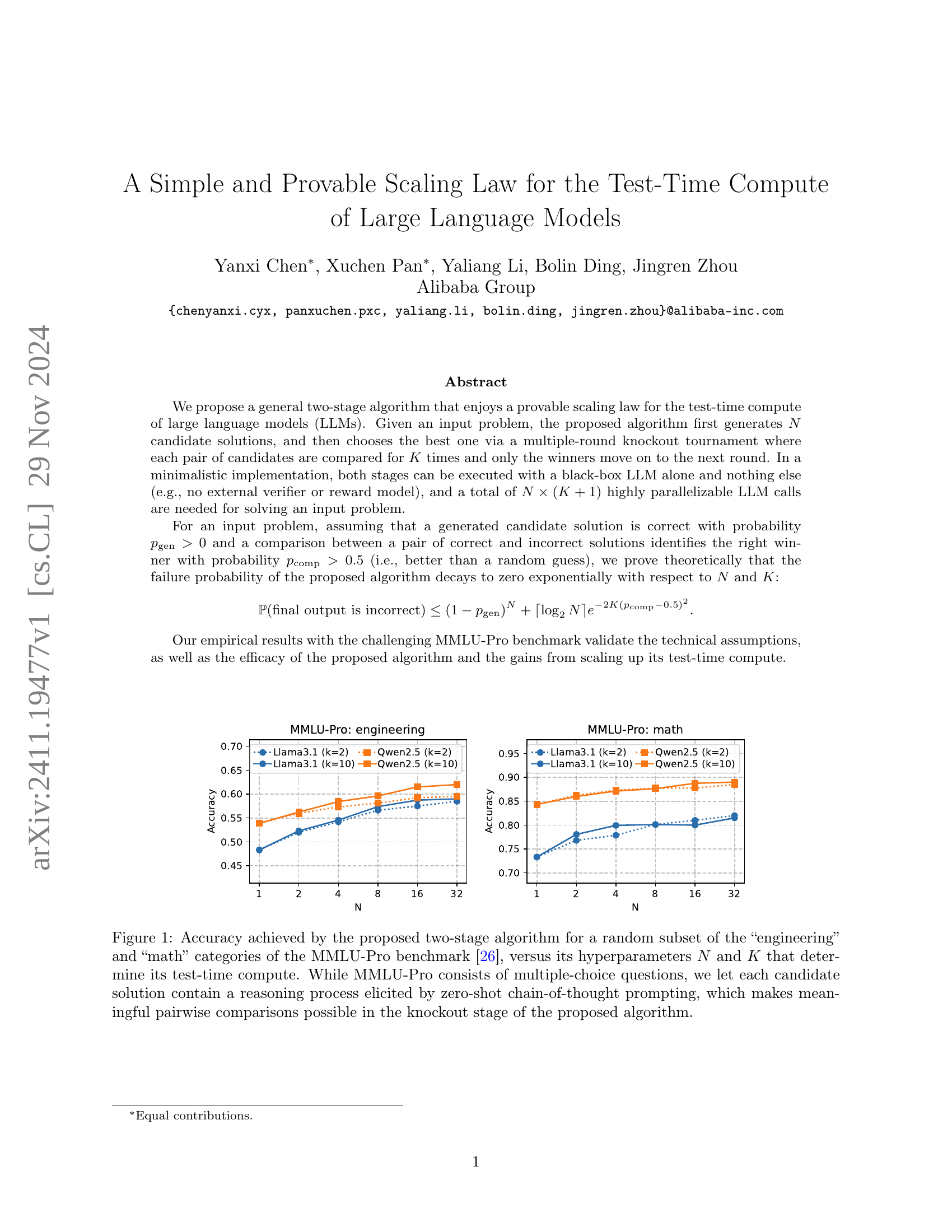
🔼 This figure displays the performance of a two-stage algorithm for solving problems in the ’engineering’ and ‘math’ categories of the MMLU-Pro benchmark. The algorithm first generates multiple candidate solutions (N) and then uses a knockout tournament approach to select the best one. In each round of the tournament, pairs of solutions are compared K times, and only the winners proceed. The x-axis represents the number of initial candidate solutions (N), while the y-axis represents the accuracy of the algorithm. Separate lines show the results for different comparison counts (K). The chart demonstrates how accuracy increases with both N and K, illustrating the algorithm’s scalability and improved performance with increased computational resources.
read the caption
Figure 1: Accuracy achieved by the proposed two-stage algorithm for a random subset of the “engineering” and “math” categories of the MMLU-Pro benchmark [26], versus its hyperparameters N𝑁Nitalic_N and K𝐾Kitalic_K that determine its test-time compute. While MMLU-Pro consists of multiple-choice questions, we let each candidate solution contain a reasoning process elicited by zero-shot chain-of-thought prompting, which makes meaningful pairwise comparisons possible in the knockout stage of the proposed algorithm.
| Download | Code |
|---|---|
| ⬇ | ```% System prompt |
| Your task is to answer the question provided by the user via step-by-step reasoning. |
% User prompt
Question#
{question}
Output Format#
<reason>your step-by-step reasoning proecss</reason>
<answer>final answer: **The answer is [X]**</answer>
```|
🔼 This table presents the prompt template used to instruct the large language model (LLM) to generate candidate solutions for a given problem. The template includes placeholders for the system’s instructions, the user’s question, and the expected output format, which requires the LLM to provide both a step-by-step reasoning process and the final answer.
read the caption
Table 1: The adopted prompt template for generating a candidate solution.
In-depth insights#
LLM Reliability Boost#
LLM reliability is a critical concern, especially in high-stakes applications. Boosting LLM reliability often involves increasing computational cost at test time. This trade-off is a key focus of research. Strategies commonly involve generating multiple candidate solutions and using various comparison mechanisms to select the best one. This can leverage techniques like majority voting or pairwise comparisons, potentially involving external verifiers or reward models. However, these methods lack a provable scaling law to guarantee improved reliability with increased compute. The proposed two-stage algorithm offers a provable scaling law, showing that the failure probability decreases exponentially with the number of candidate solutions and comparisons, making it a significant contribution towards reliable and scalable LLM inference. Minimalistic implementation using only a black-box LLM further enhances the practical value of the proposed method. The approach demonstrates a powerful way to tackle the inherent unreliability of LLMs, paving the way for more robust and dependable LLM applications in mission-critical contexts.
2-Stage Algorithm#
The core of the proposed approach is a two-stage algorithm designed for enhancing the reliability of large language model (LLM) solutions. The first stage involves generating multiple candidate solutions in parallel, leveraging the LLM’s capacity for diverse outputs. This diversification is crucial for mitigating the inherent uncertainty associated with individual LLM responses. The second stage employs a knockout tournament, where candidate solutions are compared pairwise multiple times, with the winners advancing to subsequent rounds. This competitive evaluation mechanism leverages the LLM’s ability to discriminate between better and worse solutions, and iteratively refines the selection process to converge on a high-quality solution. The algorithmic design is theoretically grounded, featuring provable scaling laws that demonstrate an exponential decrease in error probability with increased computation. This theoretical framework is empirically validated using the challenging MMLU-Pro benchmark, showcasing the practical efficacy and scalability of the proposed two-stage approach. Minimalistic implementation, requiring only a black-box LLM, makes the algorithm readily adaptable and deployable.
Provable Scaling Law#
The concept of a ‘Provable Scaling Law’ in the context of large language models (LLMs) is significant because it offers a theoretical guarantee of improved performance with increased computational resources. Unlike empirical scaling laws, which are observed through experimentation, a provable law provides a mathematical foundation, demonstrating that the model’s error rate decreases exponentially as more computational power is invested. This is particularly valuable for high-stakes applications where a very high success rate is crucial, as it allows for quantifiable predictions of the resources needed to achieve a specific performance target. However, the assumptions underlying such a law are critical. The validity of these assumptions (e.g., the ability of the LLM to generate correct solutions with non-zero probability, and to perform better than random guess in comparing solutions) must be rigorously evaluated and verified. The practical implications rely heavily on these assumptions holding true, and a provable scaling law doesn’t automatically equate to practical feasibility. Further research needs to focus on exploring the boundaries of these assumptions and expanding the scope of problems for which such provable scaling laws can realistically be established.
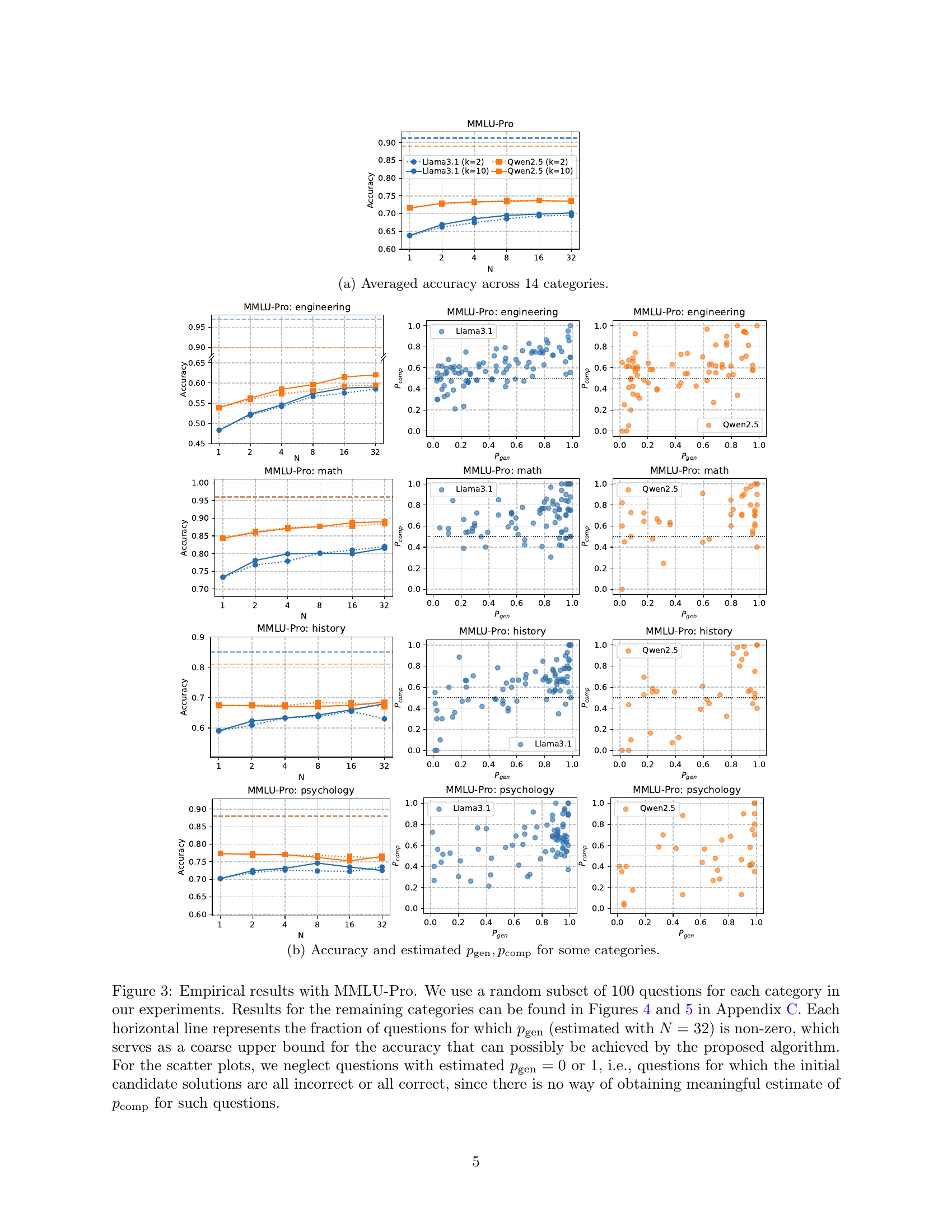
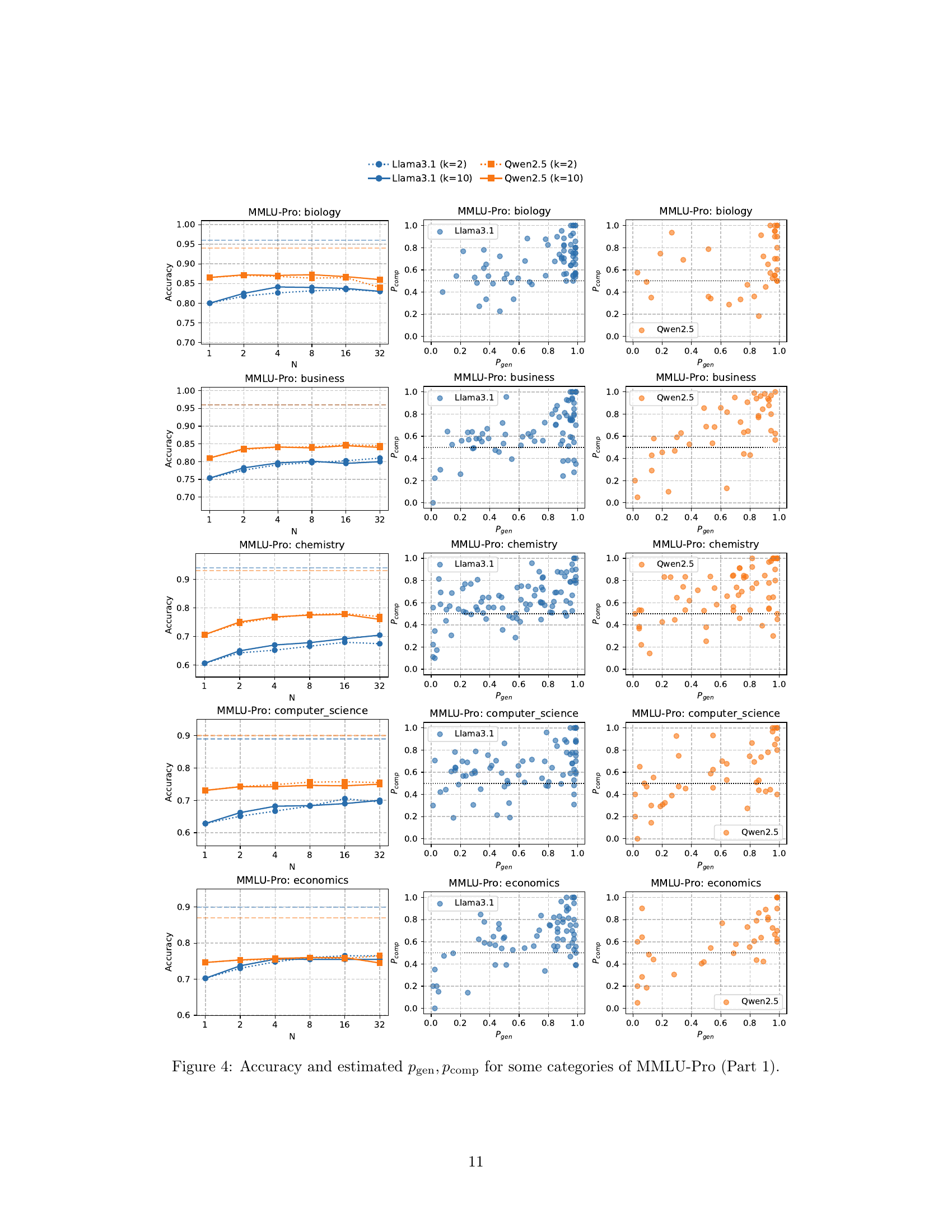
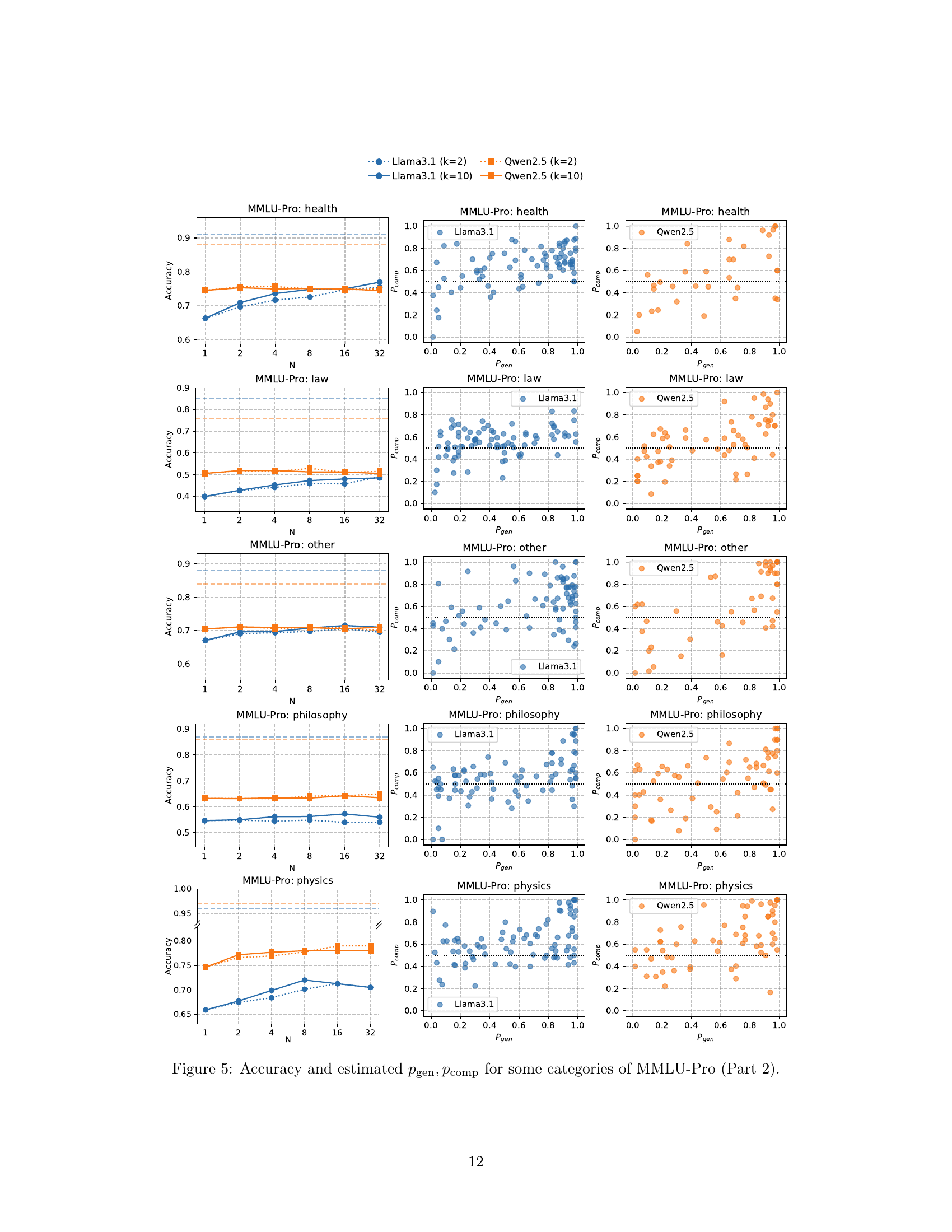
MMLU-Pro Results#
The MMLU-Pro results section likely presents empirical evidence supporting the proposed two-stage algorithm’s efficacy. It probably showcases accuracy improvements across various MMLU-Pro categories as test-time compute scales. Key insights would include whether the observed scaling aligns with the theoretical scaling law, demonstrating the algorithm’s ability to reliably boost accuracy through increased LLM calls. The results likely also explore the impact of hyperparameters (N and K) on performance, revealing optimal configurations. Comparisons across different LLMs would be crucial, highlighting the algorithm’s robustness and performance variations. A thoughtful analysis should also examine whether assumptions made in the theoretical analysis hold empirically, such as the LLM’s ability to generate correct solutions and outperform random guesses in pairwise comparisons. Finally, a deeper dive might analyze variations in performance across MMLU-Pro categories, identifying potential links between problem types and the effectiveness of the proposed method. Overall, this section would serve to validate the claims made in the paper, and potentially uncover valuable insights on how to improve the reliability of LLMs in real-world applications.
Future Directions#
Future research should focus on relaxing the assumptions of the proposed two-stage algorithm, particularly the assumption that the LLM performs better than random guessing when comparing correct and incorrect solutions. Investigating alternative algorithms that achieve similar performance with fewer assumptions is crucial. Exploring different comparison methods beyond simple pairwise comparisons, such as incorporating more sophisticated ranking or scoring mechanisms, could enhance the effectiveness and robustness of the algorithm. Another promising area is to study task decomposition strategies. Applying this algorithm to sub-problems within a complex task, instead of the whole task directly, could unlock significant improvements in solving intricate problems. Finally, it’s crucial to empirically test the algorithm on a wider array of benchmarks beyond MMLU-Pro to better understand its generalizability and limitations across various tasks and domains. Further development should also concentrate on scalability and efficiency, especially when dealing with high-dimensional data.
More visual insights#
More on tables
| Download | System prompt | |
|---|---|---|
| ⬇ | % System prompt | |
| You are a fair Judge. Given a question and two candidate solutions, your task is to figure out which solution is better. Your judgment should be unbiased, without favoring either Solution 1 or 2. | ||
| % User prompt | ||
| —- QUESTION —- | ||
| {question} | ||
| —- Solution 1 —- | ||
| {solution 1} | ||
| —- Solution 2 —- | ||
| {solution 2} | ||
| —- OUTPUT FORMAT —- | ||
| “‘ | ||
| “‘ |
🔼 This table presents the prompt template used for pairwise comparison in the knockout stage of the two-stage algorithm. The prompt instructs the LLM to act as a judge, evaluating two candidate solutions to a given question and selecting the better one based on unbiased, thorough step-by-step comparison and error checking.
read the caption
Table 2: The adopted prompt template for pairwise comparison.
| Question | Solution | |
|---|---|---|
| In a 2 pole lap winding dc machine , the resistance of one conductor is 2Ω and total number of conductors is 100. Find the total resistance | A) 50Ω | |
| B) 1Ω | ||
| C) 25Ω | ||
| D) 200Ω | ||
| E) 10Ω | ||
| F) 100Ω | ||
| G) 500Ω | ||
| H) 150Ω | ||
| I) 75Ω | ||
| J) 20Ω |
🔼 This table presents a case study demonstrating the capability of a large language model (LLM) to perform pairwise comparisons even when the probability of generating a correct solution (p_gen) is low and most initial solutions are incorrect. The example problem, sourced from the MMLU-Pro ’engineering’ category’s validation set, showcases the LLM’s ability to identify the superior solution between two flawed options through comparison and reasoning, thereby highlighting its capacity for improved performance with increased computation, even under challenging circumstances.
read the caption
Table 3: Case study: the LLM is capable of conducting pairwise comparison for a question where pgensubscript𝑝genp_{\text{gen}}italic_p start_POSTSUBSCRIPT gen end_POSTSUBSCRIPT is small and the majority of the initial candidate solutions are incorrect. This question is sampled from the validation set for the “engineering” category of MMLU-Pro.
Full paper#