TL;DR#
Large diffusion transformer models excel at image generation but demand extensive computational resources. Existing depth-pruning methods struggle to balance model efficiency and accuracy after removing layers. The difficulty arises from the high cost of fine-tuning pruned models and finding a balance between immediate loss and future performance.
This paper introduces TinyFusion, a new technique that overcomes these issues. By incorporating a differentiable sampling process for layer masks and a co-optimized weight update, TinyFusion effectively learns to identify and preserve critical layers. This learnable approach directly models and optimizes the post-fine-tuning performance, enabling superior recovery after pruning. The results show that TinyFusion is efficient and generalizable, creating high-performing shallow transformers across different architectures with dramatically improved speed and substantially reduced training costs.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel, efficient method for compressing large diffusion transformer models, a significant challenge in deploying these powerful models for real-world applications. It offers a solution to the computational cost problem by focusing on depth pruning while ensuring performance, directly impacting researchers in AI, computer vision, and related fields seeking to improve model efficiency.
Visual Insights#

🔼 The figure illustrates TinyFusion, a novel method for pruning pre-trained diffusion transformers. Instead of solely focusing on minimizing immediate loss after pruning, TinyFusion optimizes both a differentiable sampling process for selecting layers to remove (represented by layer masks) and a weight update mechanism to simulate and improve the model’s performance after subsequent fine-tuning. This dual optimization strategy aims to find a pruned model that is highly ‘recoverable,’ meaning it can regain strong performance after retraining with minimal computational cost. The figure visually depicts how layer masks are sampled and refined iteratively using the differentiable sampling approach and how weights are updated to estimate post-fine-tuning performance.
read the caption
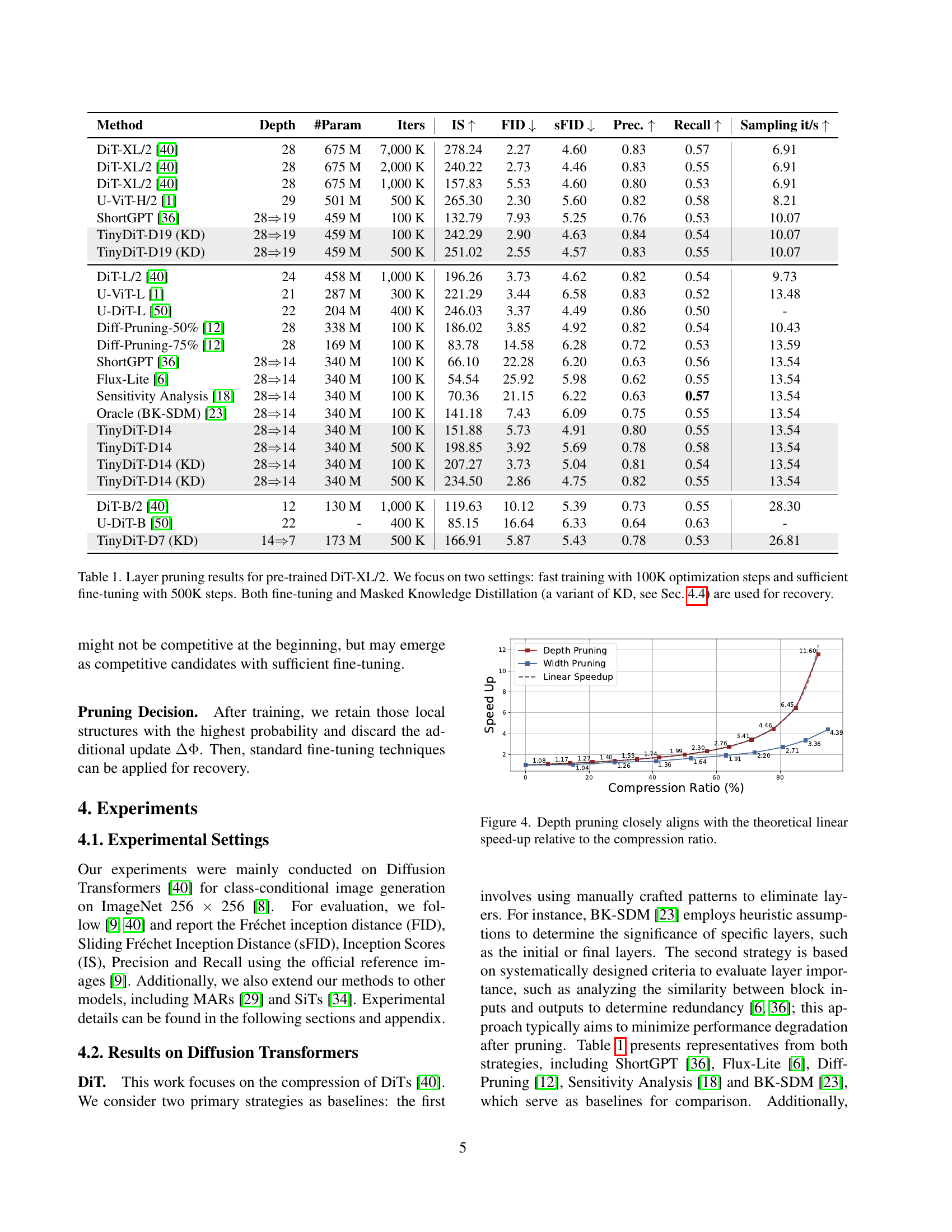
Figure 1: This work presents a learnable approach for pruning the depth of pre-trained diffusion transformers. Our method simultaneously optimizes a differentiable sampling process of layer masks and a weight update to identify a highly recoverable solution, ensuring that the pruned model maintains competitive performance after fine-tuning.
| Method | Depth | #Param | Iters | IS ↑ | FID ↓ | sFID ↓ | Prec. ↑ | Recall ↑ | Sampling it/s ↑ |
|---|---|---|---|---|---|---|---|---|---|
| DiT-XL/2 [40] | 28 | 675 M | 7,000 K | 278.24 | 2.27 | 4.60 | 0.83 | 0.57 | 6.91 |
| DiT-XL/2 [40] | 28 | 675 M | 2,000 K | 240.22 | 2.73 | 4.46 | 0.83 | 0.55 | 6.91 |
| DiT-XL/2 [40] | 28 | 675 M | 1,000 K | 157.83 | 5.53 | 4.60 | 0.80 | 0.53 | 6.91 |
| U-ViT-H/2 [1] | 29 | 501 M | 500 K | 265.30 | 2.30 | 5.60 | 0.82 | 0.58 | 8.21 |
| ShortGPT [36] | 28 ⇒ 19 | 459 M | 100 K | 132.79 | 7.93 | 5.25 | 0.76 | 0.53 | 10.07 |
| TinyDiT-D19 (KD) | 28 ⇒ 19 | 459 M | 100 K | 242.29 | 2.90 | 4.63 | 0.84 | 0.54 | 10.07 |
| TinyDiT-D19 (KD) | 28 ⇒ 19 | 459 M | 500 K | 251.02 | 2.55 | 4.57 | 0.83 | 0.55 | 10.07 |
| DiT-L/2 [40] | 24 | 458 M | 1,000 K | 196.26 | 3.73 | 4.62 | 0.82 | 0.54 | 9.73 |
| U-ViT-L [1] | 21 | 287 M | 300 K | 221.29 | 3.44 | 6.58 | 0.83 | 0.52 | 13.48 |
| U-DiT-L [50] | 22 | 204 M | 400 K | 246.03 | 3.37 | 4.49 | 0.86 | 0.50 | - |
| Diff-Pruning-50% [12] | 28 | 338 M | 100 K | 186.02 | 3.85 | 4.92 | 0.82 | 0.54 | 10.43 |
| Diff-Pruning-75% [12] | 28 | 169 M | 100 K | 83.78 | 14.58 | 6.28 | 0.72 | 0.53 | 13.59 |
| ShortGPT [36] | 28 ⇒ 14 | 340 M | 100 K | 66.10 | 22.28 | 6.20 | 0.63 | 0.56 | 13.54 |
| Flux-Lite [6] | 28 ⇒ 14 | 340 M | 100 K | 54.54 | 25.92 | 5.98 | 0.62 | 0.55 | 13.54 |
| Sensitivity Analysis [18] | 28 ⇒ 14 | 340 M | 100 K | 70.36 | 21.15 | 6.22 | 0.63 | 0.57 | 13.54 |
| Oracle (BK-SDM) [23] | 28 ⇒ 14 | 340 M | 100 K | 141.18 | 7.43 | 6.09 | 0.75 | 0.55 | 13.54 |
| TinyDiT-D14 | 28 ⇒ 14 | 340 M | 100 K | 151.88 | 5.73 | 4.91 | 0.80 | 0.55 | 13.54 |
| TinyDiT-D14 | 28 ⇒ 14 | 340 M | 500 K | 198.85 | 3.92 | 5.69 | 0.78 | 0.58 | 13.54 |
| TinyDiT-D14 (KD) | 28 ⇒ 14 | 340 M | 100 K | 207.27 | 3.73 | 5.04 | 0.81 | 0.54 | 13.54 |
| TinyDiT-D14 (KD) | 28 ⇒ 14 | 340 M | 500 K | 234.50 | 2.86 | 4.75 | 0.82 | 0.55 | 13.54 |
| DiT-B/2 [40] | 12 | 130 M | 1,000 K | 119.63 | 10.12 | 5.39 | 0.73 | 0.55 | 28.30 |
| U-DiT-B [50] | 22 | - | 400 K | 85.15 | 16.64 | 6.33 | 0.64 | 0.63 | - |
| TinyDiT-D7 (KD) | 14 ⇒ 7 | 173 M | 500 K | 166.91 | 5.87 | 5.43 | 0.78 | 0.53 | 26.81 |
🔼 This table presents the results of depth pruning experiments performed on a pre-trained DiT-XL/2 model. The experiments compare different depth pruning methods and explore the impact of fine-tuning duration (100K vs. 500K optimization steps). Metrics evaluated include Inception Score (IS), Fréchet Inception Distance (FID), and Sliding FID (sFID), along with Precision and Recall. The table also shows the effect of applying Masked Knowledge Distillation (a variant of knowledge distillation) during the recovery phase after pruning. The number of parameters, sampling speed (iterations per second), and the depth of the pruned model are also included. The table highlights the trade-off between model efficiency and performance.
read the caption
Table 1: Layer pruning results for pre-trained DiT-XL/2. We focus on two settings: fast training with 100K optimization steps and sufficient fine-tuning with 500K steps. Both fine-tuning and Masked Knowledge Distillation (a variant of KD, see Sec. 4.4) are used for recovery.
In-depth insights#
Learnable Pruning#
The concept of “learnable pruning” offers a significant advancement in model compression. Instead of relying on heuristic methods to identify less important layers for removal, this approach frames pruning as a learnable optimization problem. This allows the model itself to determine which layers are most expendable, directly impacting performance. The key innovation is the integration of a differentiable sampling mechanism to select layers for removal. This clever technique enables the use of gradient-based optimization, guiding the process towards solutions that yield high post-pruning performance after subsequent fine-tuning. Unlike traditional pruning methods that focus solely on minimizing immediate loss, this method explicitly models and optimizes the recoverability of the pruned network. This recoverability is crucial because it acknowledges that some initial performance degradation post-pruning is acceptable, provided the model can be efficiently restored through fine-tuning. The framework’s probabilistic approach further enhances efficiency by directing the exploration towards promising pruning patterns. This ultimately produces compact, lightweight models, while reducing the computational cost of both the pruning and the fine-tuning phases.
Recoverability Focus#
The “Recoverability Focus” in this paper represents a paradigm shift in the approach to model pruning. Traditional methods primarily minimize loss after pruning, often neglecting the model’s ability to regain performance after fine-tuning. This paper argues that recoverability, the ability of a pruned model to achieve high performance post-fine-tuning, is a more crucial metric. The authors highlight that focusing solely on immediate loss minimization can be misleading, as it might fail to capture the long-term impact of pruning decisions. By explicitly modeling and optimizing recoverability, the approach aims to identify models that, while showing initially high calibration losses, can effectively recover to a competitive state after subsequent fine-tuning. This novel focus allows for significantly more efficient pruning, as it directly targets the model’s capacity for performance restoration, rather than relying on heuristic or indirect measures.
Efficient Compression#
Efficient compression of large language models is crucial for deploying them on resource-constrained devices. This paper explores depth pruning as a compression technique, focusing on diffusion transformers. Existing methods often prioritize minimizing immediate loss after pruning, neglecting the importance of post-fine-tuning performance. The authors introduce TinyFusion, a novel method that directly optimizes for recoverability after pruning by using a differentiable sampling technique combined with a weight update to simulate fine-tuning. This learnable approach surpasses traditional importance-based and error-based pruning methods. The effectiveness of TinyFusion is demonstrated across various transformer architectures, achieving significant speedups with competitive FID scores, showcasing its potential for creating efficient and high-performing compressed models. The probabilistic perspective and joint optimization of pruning and recoverability are key innovations. The results highlight the limitations of solely relying on calibration loss minimization for depth pruning in diffusion transformers and demonstrate the superiority of directly targeting post-fine-tuning performance.
KD Enhancements#
The concept of “KD Enhancements” within the context of a diffusion model compression paper suggests exploring improvements to knowledge distillation (KD) for better performance recovery after pruning. Standard KD might struggle to effectively transfer knowledge when significant model architecture changes occur, such as aggressive layer removal in depth pruning. The authors likely investigated modifications to standard KD techniques to address this. This could involve focusing on specific parts of the model or employing advanced distillation methods. For instance, they might have explored masked KD, selectively transferring knowledge from the teacher model to avoid the negative impact of outlier activations. The ultimate goal would be to improve the student model’s ability to recover after the pruning process, achieving FID scores comparable to the original unpruned model while maintaining computational efficiency. The results section would then demonstrate whether these KD enhancements successfully improved the FID score or other metrics after fine-tuning, showcasing their effectiveness in addressing the challenges of depth pruning.
Future Directions#
Future research could explore several promising avenues. Improving the differentiable sampling process is crucial; more sophisticated methods could lead to more efficient exploration of the vast search space during pruning. Investigating alternative recoverability estimation techniques beyond LoRA and full fine-tuning, such as other parameter-efficient methods, is vital to enhance efficiency and potentially achieve even better results. Extending the framework to handle different architectures beyond DiTs, MARs, and SiTs would broaden its applicability. Analyzing the impact of various hyperparameters in greater detail, particularly concerning the temperature parameter in Gumbel-Softmax sampling and the knowledge distillation parameters, is needed to optimize performance. Finally, a thorough investigation into the theoretical foundations of the approach is needed to better understand why it outperforms existing loss-minimization techniques. This work opens the door to efficient model compression for various generative tasks, impacting resource-constrained applications.
More visual insights#
More on figures

🔼 The figure illustrates TinyFusion, a method for learning shallow diffusion transformers. It shows how the method learns a probability distribution over possible ways to prune layers (removing layers from the model). This is done by jointly optimizing both the probability distribution (which layers are removed) and a weight update that simulates the effects of subsequent fine-tuning. The goal is to bias the distribution toward pruning choices that result in good performance after fine-tuning, ensuring the smaller model retains strong performance. The figure highlights the differentiable sampling of layer masks and the co-optimized weight update. After training, TinyFusion retains only the network structures that showed the highest probability of success during training, effectively creating a shallower, faster model.
read the caption
Figure 2: The proposed TinyFusion method learns to perform a differentiable sampling of candidate solutions, jointly optimized with a weight update to estimate recoverability. This approach aims to increase the likelihood of favorable solutions that ensure strong post-fine-tuning performance. After training, local structures with the highest sampling probabilities are retained.

🔼 This figure illustrates the forward propagation process within a diffusion transformer model that incorporates a differentiable pruning mask and LoRA for recoverability estimation. The diagram shows how the pruning mask (mᵢ) acts as a gate, selectively allowing or blocking the passage of information through layers. LoRA (Low-Rank Adaptation) is employed to simulate and estimate the model’s recoverability after pruning. This process involves a weight update (ΔΦ) to adjust model weights, improving its performance after the pruned layers have been fine-tuned. The figure visually demonstrates how the combined application of a learnable pruning mask and LoRA enables a differentiable calculation of recoverability, facilitating effective layer pruning within the diffusion transformer.
read the caption
Figure 3: An example of forward propagation with differentiable pruning mask misubscript𝑚𝑖m_{i}italic_m start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT and LoRA for recoverability estimation.

🔼 This figure shows a graph comparing the speed-up achieved by depth pruning against the theoretical linear speed-up. The x-axis represents the compression ratio (percentage of layers removed), and the y-axis represents the speed-up factor. The graph demonstrates that depth pruning achieves a speed-up closely matching the expected linear increase as the compression ratio grows. This suggests that removing layers in this manner is an efficient way to compress diffusion transformer models.
read the caption
Figure 4: Depth pruning closely aligns with the theoretical linear speed-up relative to the compression ratio.

🔼 This figure shows the distribution of calibration loss across 100,000 randomly sampled candidate models created by pruning a diffusion transformer at 50% depth. Each model represents a different pruning configuration. The x-axis represents the calibration loss, which is the loss of the model after pruning but before fine-tuning. The y-axis represents the frequency or count of models with that specific calibration loss. The figure demonstrates that models with lower initial calibration loss do not necessarily lead to better performance (lower FID) after fine-tuning. The proposed TinyFusion method, despite having a higher initial calibration loss, achieves the lowest FID score after fine-tuning, indicating it is effective in selecting models with high recoverability.
read the caption
Figure 5: Distribution of calibration loss through random sampling of candidate models. The proposed learnable method achieves the best post-fine-tuning FID yet has a relatively high initial loss compared to other baselines.

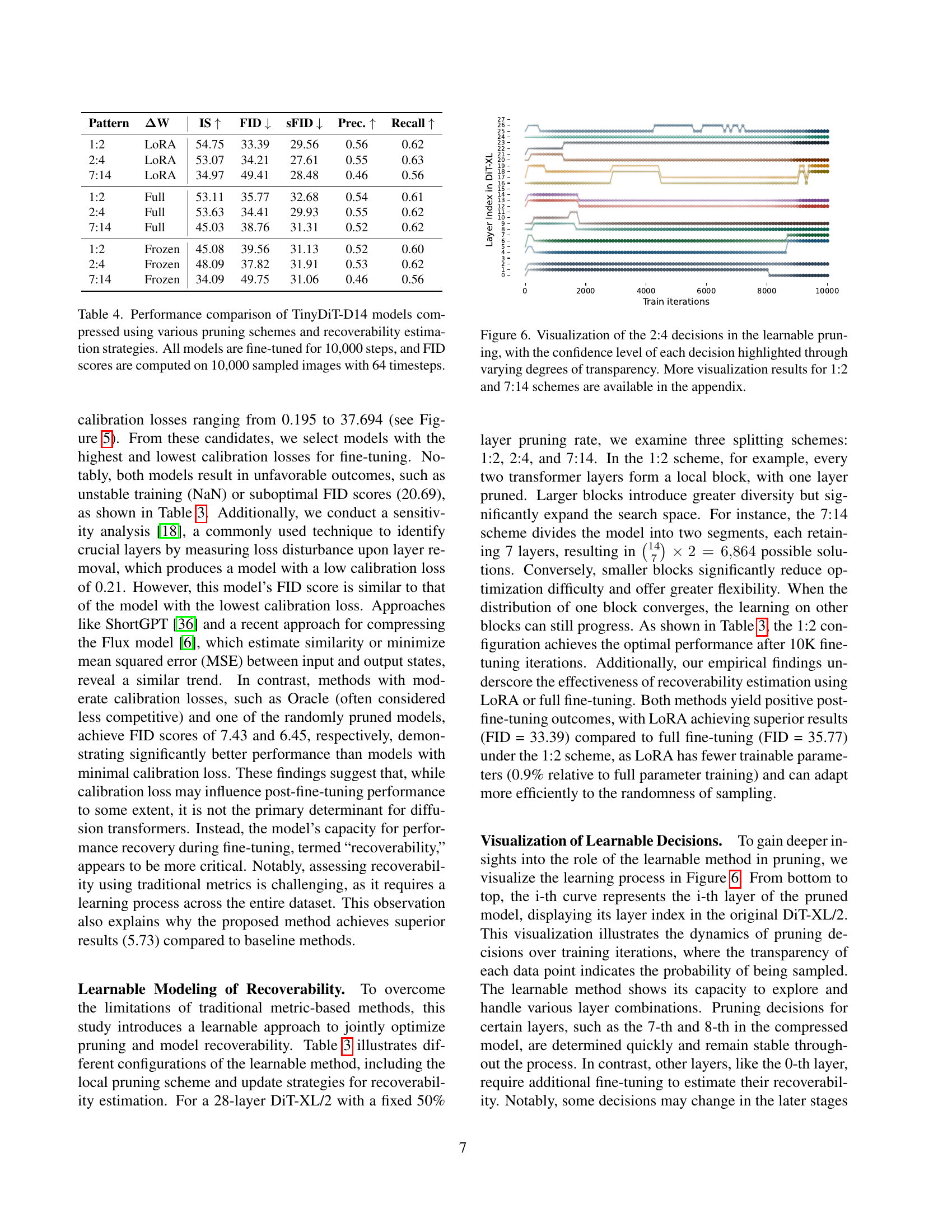
🔼 This figure visualizes the decisions made during the learnable pruning process, specifically focusing on the 2:4 pruning scheme. Each line represents a layer in the DiT-XL model, and the color intensity (transparency) of the data points along each line indicates the probability of that layer being pruned at each training iteration. Lighter colors signify a lower probability of pruning. This visualization helps demonstrate how the model learns to identify and retain important layers during training, ultimately leading to the selection of a final pruned model. The appendix includes similar visualizations for the 1:2 and 7:14 pruning schemes.
read the caption
Figure 6: Visualization of the 2:4 decisions in the learnable pruning, with the confidence level of each decision highlighted through varying degrees of transparency. More visualization results for 1:2 and 7:14 schemes are available in the appendix.

🔼 This figure displays images generated using the TinyDiT-D14 model. TinyDiT-D14 is a smaller, more efficient version of the DiT-XL/2 model, created through a process of pruning (removing less important layers) and knowledge distillation (transferring knowledge from the larger model to the smaller one). The images showcase the model’s ability to generate images on the ImageNet dataset, demonstrating its performance despite its reduced size and computational cost.
read the caption
Figure 7: Images generated by TinyDiT-D14 on ImageNet 224×\times×224, pruned and distilled from a DiT-XL/2.

🔼 This figure shows the distribution of activation values in the hidden states of the DiT-XL/2 model (teacher model). The x-axis represents the activation value (on a logarithmic scale), and the y-axis shows the density of the activation values. The distribution is shown as a histogram. It highlights that there are a significant number of large activation values (positive and negative) in the teacher model. This is relevant to the discussion in section 4.4, knowledge distillation for recovery, which explains how these extreme activations can affect the distillation process between the teacher and student (pruned) models.
read the caption
(a) DiT-XL/2 (Teacher)

🔼 This figure is a histogram showing the distribution of activation values in the hidden states of the TinyDiT-D14 model. The x-axis represents the activation values (on a logarithmic scale), and the y-axis represents the frequency of those values. It is used to illustrate the presence of large or ‘massive’ activation values within the model, which is a common issue that can negatively affect the model’s performance and stability during fine-tuning, especially when performing knowledge distillation. Comparing this to the distribution in the teacher model (Figure 8a) helps explain the challenges and the need for a technique like MaskedKD, which mitigates the effects of these outliers.
read the caption
(b) TinyDiT-D14 (Student)

🔼 Figure 8 shows a comparison of activation distributions in the hidden states of a teacher (DiT-XL/2) and student (TinyDiT-D14) diffusion transformer model. The histograms illustrate the presence of many large magnitude activations (both positive and negative) in both models. Directly using knowledge distillation to transfer these activations from teacher to student is problematic; it can lead to excessively large losses during training and instability in the training process. This highlights the need for a method to handle or mitigate these massive activations to improve the effectiveness of knowledge distillation.
read the caption
Figure 8: Visualization of massive activations [47] in DiTs. Both teacher and student models display large activation values in their hidden states. Directly distilling these massive activations may result in excessively large losses and unstable training.

🔼 This figure visualizes the learning process of the 1:2 pruning scheme during training. The x-axis represents the training iterations, and the y-axis represents the layer index in the DiT-XL model. Each curve shows the probability of a layer being pruned at each iteration. The transparency of the data points indicates the probability of the layer being selected for pruning. Darker points signify higher probabilities. This visualization illustrates how the model learns to make pruning decisions over time, and how different layers are selected at different stages of training.
read the caption
Figure 9: 1:2 Pruning Decisions

🔼 This figure visualizes the learning dynamics of pruning decisions during training, specifically focusing on the 2:4 pruning scheme. In this scheme, the model is divided into blocks of four layers, with two layers retained. Each curve represents a layer in the original DiT-XL model, and the transparency of the data points reflects their probability of being selected during pruning across training iterations. The visualization shows how the learnable method progressively identifies and retains important layers while discarding less crucial ones, showcasing the iterative optimization process.
read the caption
Figure 10: 2:4 Pruning Decisions
More on tables
| Method | Depth | Params | Epochs | FID | IS |
|---|---|---|---|---|---|
| MAR-Large | 32 | 479 M | 400 | 1.78 | 296.0 |
| MAR-Base | 24 | 208 M | 400 | 2.31 | 281.7 |
| TinyMAR-D16 | 32 => 16 | 277 M | 40 | 2.28 | 283.4 |
| SiT-XL/2 | 28 | 675 M | 1,400 | 2.06 | 277.5 |
| TinySiT-D14 | 28 => 14 | 340 M | 100 | 3.02 | 220.1 |
🔼 This table presents the results of applying depth pruning techniques to two different types of diffusion transformer models: Masked Autoregressive models (MARs) and Scalable Interpolant Transformers (SiTs). It shows the depth of the original and pruned models, the number of parameters, the number of training epochs used, and the resulting Fréchet Inception Distance (FID) and Inception Score (IS) after pruning. The FID and IS scores are commonly used metrics to evaluate the quality of images generated by these models; lower FID and higher IS scores generally indicate better image quality.
read the caption
Table 2: Depth pruning results on MARs [29] and SiTs [34].
| Strategy | Loss | IS | FID | Prec. | Recall |
|---|---|---|---|---|---|
| Max. Loss | 37.69 | NaN | NaN | NaN | NaN |
| Med. Loss | 0.99 | 149.51 | 6.45 | 0.78 | 0.53 |
| Min. Loss | 0.20 | 73.10 | 20.69 | 0.63 | 0.58 |
| Sensitivity | 0.21 | 70.36 | 21.15 | 0.63 | 0.57 |
| ShortGPT [36] | 0.20 | 66.10 | 22.28 | 0.63 | 0.56 |
| Flux-Lite [6] | 0.85 | 54.54 | 25.92 | 0.62 | 0.55 |
| Oracle (BK-SDM) | 1.28 | 141.18 | 7.43 | 0.75 | 0.55 |
| Learnable | 0.98 | 151.88 | 5.73 | 0.80 | 0.55 |
🔼 This table compares different depth pruning methods for diffusion transformers, focusing on the impact of minimizing calibration loss versus maximizing post-fine-tuning performance. It shows that simply minimizing calibration loss doesn’t guarantee optimal results after fine-tuning. The methods compared are: (1) Random pruning with varying calibration losses, demonstrating the lack of correlation between initial loss and final performance. (2) Metric-based methods (Sensitivity Analysis and ShortGPT) which are based on heuristics and importance scores to identify layers to remove, which also underperform. (3) An oracle method (retaining first and last layers while uniformly pruning the rest), which provides a reasonably good baseline. (4) The proposed ‘Learnable’ method which aims to directly optimize for post-fine-tuning performance. All methods are fine-tuned for 100,000 steps without knowledge distillation.
read the caption
Table 3: Directly minimizing the calibration loss may lead to non-optimal solutions. All pruned models are fine-tuned without knowledge distillation (KD) for 100K steps. We evaluate the following baselines: (1) Loss – We randomly prune a DiT-XL model to generate 100,000 models and select models with different calibration losses for fine-tuning; (2) Metric-based Methods – such as Sensitivity Analysis and ShortGPT; (3) Oracle – We retain the first and last layers while uniformly pruning the intermediate layers following [23]; (4) Learnable – The proposed learnable method.
| Pattern | ΔW | IS ↑ | FID ↓ | sFID ↓ | Prec. ↑ | Recall ↑ |
|---|---|---|---|---|---|---|
| 1:2 | LoRA | 54.75 | 33.39 | 29.56 | 0.56 | 0.62 |
| 2:4 | LoRA | 53.07 | 34.21 | 27.61 | 0.55 | 0.63 |
| 7:14 | LoRA | 34.97 | 49.41 | 28.48 | 0.46 | 0.56 |
| 1:2 | Full | 53.11 | 35.77 | 32.68 | 0.54 | 0.61 |
| 2:4 | Full | 53.63 | 34.41 | 29.93 | 0.55 | 0.62 |
| 7:14 | Full | 45.03 | 38.76 | 31.31 | 0.52 | 0.62 |
| 1:2 | Frozen | 45.08 | 39.56 | 31.13 | 0.52 | 0.60 |
| 2:4 | Frozen | 48.09 | 37.82 | 31.91 | 0.53 | 0.62 |
| 7:14 | Frozen | 34.09 | 49.75 | 31.06 | 0.46 | 0.56 |
🔼 This table compares the performance of different TinyDiT-D14 models created using various pruning techniques and recoverability estimation strategies. The performance is measured by FID score (Frechet Inception Distance), IS (Inception Score), SFID (Sliding Fréchet Inception Distance), Precision and Recall. Each model was fine-tuned for 10,000 steps using 10,000 samples generated with 64 timesteps. The comparison allows us to assess the impact of different pruning methods and strategies on the overall quality and efficiency of the model.
read the caption
Table 4: Performance comparison of TinyDiT-D14 models compressed using various pruning schemes and recoverability estimation strategies. All models are fine-tuned for 10,000 steps, and FID scores are computed on 10,000 sampled images with 64 timesteps.
| fine-tuning Strategy | Init. Distill. Loss | FID @ 100K |
|---|---|---|
| fine-tuning | - | 5.79 |
| Logits KD | - | 4.66 |
| RepKD | 2840.1 | NaN |
| Masked KD (0.1σ) | 15.4 | NaN |
| Masked KD (2σ) | 387.1 | 3.73 |
| Masked KD (4σ) | 391.4 | 3.75 |
🔼 This table presents the results of different fine-tuning strategies used for recovering the performance of pruned diffusion transformer models. The strategies compared include standard fine-tuning, logits KD (knowledge distillation), RepKD (representation distillation), and a novel Masked KD. Masked KD is a variation of RepKD designed to mitigate the negative effects of extremely large activation values in the hidden layers of both teacher and student networks by ignoring the loss associated with these values above a certain threshold (k*σx, where k is a hyperparameter and σx is the standard deviation of the activations). The table shows that Masked KD significantly improves the final FID (Fréchet Inception Distance) score, indicating better performance recovery compared to the other methods, likely due to the more effective transfer of knowledge between models. The FID score is a lower-is-better metric for evaluating the quality of generated images. Lower FID scores indicate that the generated images are more similar to real images.
read the caption
Table 5: Evaluation of different fine-tuning strategies for recovery. Masked RepKD ignores those massive activations (|x|>kσx𝑥𝑘subscript𝜎𝑥|x|>k\sigma_{x}| italic_x | > italic_k italic_σ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT) in both teacher and student, which enables effective knowledge transfer between diffusion transformers.
| Model | Optimizer | Cosine Sched. | Teacher | αKD | αGT | β | Grad. Clip | Pruning Configs |
|---|---|---|---|---|---|---|---|---|
| DiT-D19 | AdamW(lr=2e-4, wd=0.0) | ηmin=1e-4 | DiT-XL | 0.9 | 0.1 | 1e-2 → 0 | 1.0 | LoRA-1:2 |
| DiT-D14 | AdamW(lr=2e-4, wd=0.0 | ηmin=1e-4 | DiT-XL | 0.9 | 0.1 | 1e-2 → 0 | 1.0 | LoRA-1:2 |
| DiT-D7 | AdamW(lr=2e-4, wd=0.0) | ηmin=1e-4 | DiT-D14 | 0.9 | 0.1 | 1e-2 → 0 | 1.0 | LoRA-1:2 |
| SiT-D14 | AdamW(lr=2e-4, wd=0.0) | ηmin=1e-4 | SiT-XL | 0.9 | 0.1 | 2e-4 → 0 | 1.0 | LoRA-1:2 |
| MAR-D16 | AdamW(lr=2e-4, wd=0.0) | ηmin=1e-4 | MAR-Large | 0.9 | 0.1 | 1e-2 → 0 | 1.0 | LoRA-1:2 |
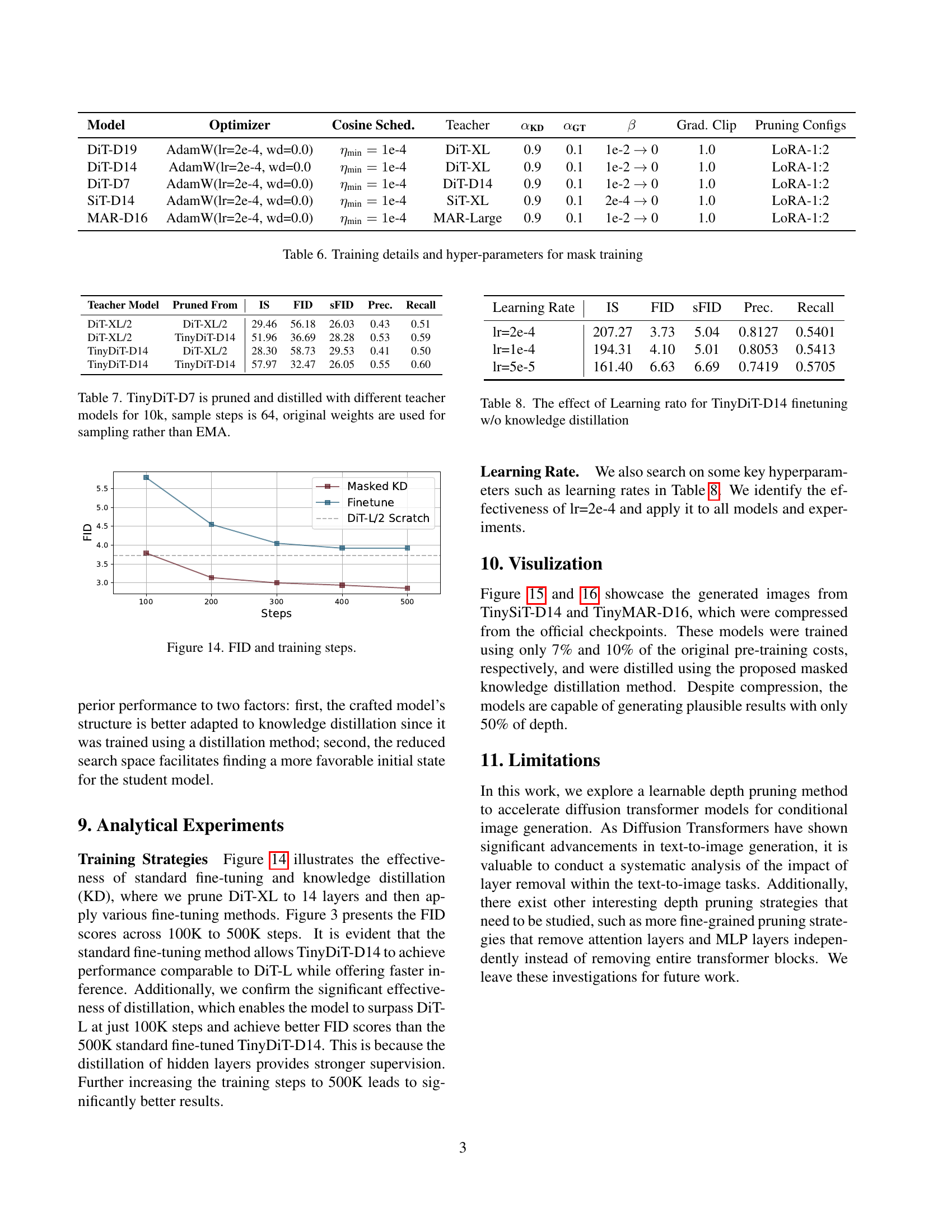
🔼 This table details the training configurations used for the learnable depth pruning method in the TinyFusion model. It lists the model variations (DiT-D19, DiT-D14, DiT-D7, SiT-D14, MAR-D16), the optimizer used (AdamW), the cosine scheduler parameters (minimum learning rate), the teacher model used for knowledge distillation (DiT-XL, SiT-XL, MAR-Large), the hyperparameters for the loss function (αKD, αGT, β), gradient clipping parameters, and the pruning configuration (LORA-1:2). These parameters dictate how the model learns to effectively prune layers while maintaining performance.
read the caption
Table 6: Training details and hyper-parameters for mask training
| Teacher Model | Pruned From | IS | FID | sFID | Prec. | Recall |
|---|---|---|---|---|---|---|
| DiT-XL/2 | DiT-XL/2 | 29.46 | 56.18 | 26.03 | 0.43 | 0.51 |
| DiT-XL/2 | TinyDiT-D14 | 51.96 | 36.69 | 28.28 | 0.53 | 0.59 |
| TinyDiT-D14 | DiT-XL/2 | 28.30 | 58.73 | 29.53 | 0.41 | 0.50 |
| TinyDiT-D14 | TinyDiT-D14 | 57.97 | 32.47 | 26.05 | 0.55 | 0.60 |
🔼 This table presents the results of experiments evaluating different approaches to training a smaller, more efficient diffusion transformer model (TinyDiT-D7). The model is created by pruning a larger pre-trained model (DiT-XL/2), and then fine-tuned using knowledge distillation from different teacher models. The table shows the Inception Score (IS), Fréchet Inception Distance (FID), and Sliding FID (SFID), along with precision and recall metrics. These metrics help evaluate the quality and efficiency of the generated images from the pruned and fine-tuned model. Note that the sampling uses the original weights instead of the Exponential Moving Average (EMA).
read the caption
Table 7: TinyDiT-D7 is pruned and distilled with different teacher models for 10k, sample steps is 64, original weights are used for sampling rather than EMA.
| Learning Rate | IS | FID | sFID | Prec. | Recall | |
|---|---|---|---|---|---|---|
| lr=2e-4 | 207.27 | 3.73 | 5.04 | 0.8127 | 0.5401 | |
| lr=1e-4 | 194.31 | 4.10 | 5.01 | 0.8053 | 0.5413 | |
| lr=5e-5 | 161.40 | 6.63 | 6.69 | 0.7419 | 0.5705 |
🔼 This table shows the impact of different learning rates on the performance of the TinyDiT-D14 model when fine-tuned without knowledge distillation. It presents the Inception Score (IS), Fréchet Inception Distance (FID), and Sliding FID (SFID) along with Precision and Recall metrics for three different learning rates (2e-4, 1e-4, and 5e-5). The results demonstrate how the choice of learning rate affects the model’s performance after fine-tuning.
read the caption
Table 8: The effect of Learning rato for TinyDiT-D14 finetuning w/o knowledge distillation
Full paper#