↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Current LLM fusion methods face challenges like vocabulary alignment and merging distribution matrices, which are complex and error-prone. The Mixture-of-Experts (MoE) approach reduces activation costs but still incurs significant memory overhead, while model merging is restricted to models with identical architectures. Knowledge distillation methods, such as explicit model fusion (EMF), also have limitations in vocabulary alignment and matrix merging. These issues lead to complex procedures that may introduce noise and errors.
This paper proposes a novel implicit fusion method called Weighted-Reward Preference Optimization (WRPO). WRPO leverages preference optimization between source and target LLMs, eliminating the need for vocabulary alignment and matrix fusion. A progressive adaptation strategy is introduced to address distributional deviations, and experiments show that WRPO outperforms existing methods and baselines across different benchmarks, achieving length-controlled win rates of up to 55.9% against GPT-4 on AlpacaEval-2.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and efficient method for implicit model fusion of large language models (LLMs). It addresses the challenges of existing fusion methods and opens up new avenues for research in LLM enhancement and efficiency. The proposed method, WRPO, has the potential to significantly improve the capabilities of smaller LLMs by leveraging the strengths of larger models without excessive computational costs. This is particularly relevant in the current research trends of efficient LLM development and deployment.
Visual Insights#

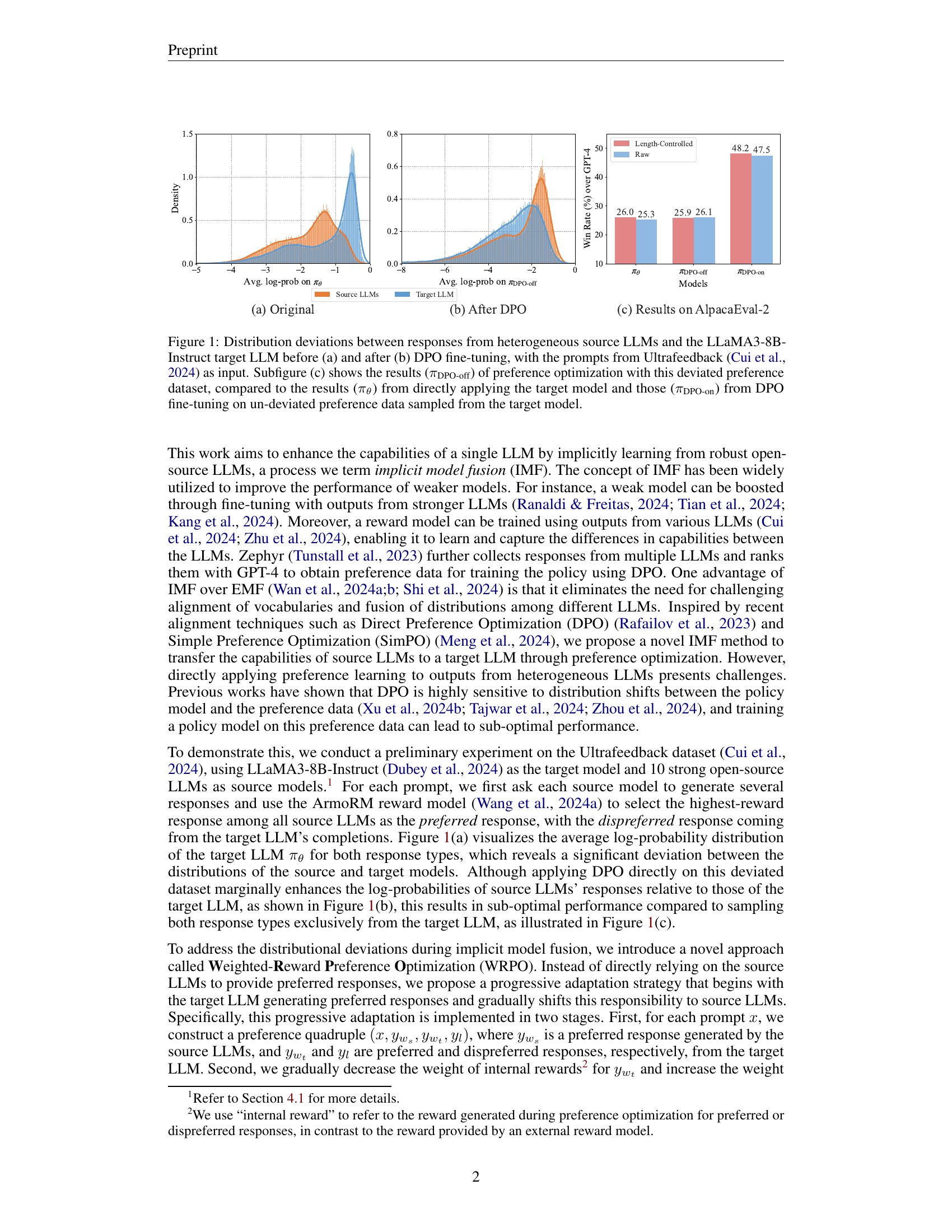
🔼 Figure 1 illustrates the distribution differences between responses generated by source LLMs and the target LLM (LLaMA3-8B-Instruct) before and after DPO fine-tuning. Subfigure (a) shows the distributions before fine-tuning, highlighting the significant differences. Subfigure (b) demonstrates how DPO fine-tuning reduces these differences. Finally, subfigure (c) compares the performance of preference optimization using the deviated preference dataset (πDPO-off) against using only the target model (πθ) and using DPO fine-tuned on a non-deviated dataset (πDPO-on). This comparison highlights the impact of the distribution shift on the effectiveness of DPO.
read the caption
Figure 1: Distribution deviations between responses from heterogeneous source LLMs and the LLaMA3-8B-Instruct target LLM before (a) and after (b) DPO fine-tuning, with the prompts from Ultrafeedback (Cui et al., 2024) as input. Subfigure (c) shows the results (πDPO-offsubscript𝜋DPO-off\pi_{\text{DPO-off}}italic_π start_POSTSUBSCRIPT DPO-off end_POSTSUBSCRIPT) of preference optimization with this deviated preference dataset, compared to the results (πθsubscript𝜋𝜃\pi_{\theta}italic_π start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT) from directly applying the target model and those (πDPO-onsubscript𝜋DPO-on\pi_{\text{DPO-on}}italic_π start_POSTSUBSCRIPT DPO-on end_POSTSUBSCRIPT) from DPO fine-tuning on un-deviated preference data sampled from the target model.
| Source LLMs | Percentage |
|---|---|
| Mistral-Large-Instruct-2407 (Jiang et al., 2023a) | 28.24% |
| Gemma2-27B-IT (Riviere et al., 2024) | 15.45% |
| Qwen2-72B-Instruct (Yang et al., 2024) | 12.38% |
| LLaMA3-70B-Instruct (Dubey et al., 2024) | 9.92% |
| Gemma2-9B-IT (Riviere et al., 2024) | 9.91% |
| InternLM2.5-20B-Chat (Cai et al., 2024) | 7.54% |
| DeepSeek-V2-Chat (DeepSeek-AI et al., 2024) | 6.20% |
| DeepSeek-Coder-V2-Instruct (Shao et al., 2024) | 4.01% |
| Yi-1.5-34B-Chat (Young et al., 2024) | 3.86% |
| Phi-3-medium-4k-instruct (Abdin et al., 2024) | 2.50% |
🔼 This table lists the ten open-source Large Language Models (LLMs) used as source models in the experiments. For each LLM, its name, parameter size (in billions), and the percentage of times it produced the highest-scoring response (as determined by the reward model) across all source LLMs are provided. This shows the relative contribution of each LLM to the overall fusion process.
read the caption
Table 1: Details of the source LLMs used in our experiments along with the percentage of the highest-scoring responses from each source LLM.
In-depth insights#
Implicit LLM Fusion#
Implicit LLM fusion presents a novel approach to combining the strengths of multiple Large Language Models (LLMs) without explicitly merging their parameters or aligning vocabularies. This contrasts with explicit methods, which can be complex and error-prone. Implicit fusion leverages techniques like preference learning or reward modeling to indirectly transfer knowledge and capabilities between LLMs, often requiring less computational resources and avoiding the potential noise introduced by explicit merging. The core idea is to implicitly guide a target LLM toward the behavior of more capable source LLMs using a training strategy that focuses on preferred outputs. This approach offers the advantage of scalability and flexibility, enabling the combination of LLMs with diverse architectures and sizes. However, challenges such as distributional shifts between LLMs need to be addressed. Effective implicit fusion strategies generally incorporate mechanisms to mitigate these shifts, often through progressive adaptation or careful sampling techniques. The effectiveness of implicit fusion hinges on the quality of the preference data or reward model, and the choice of optimization technique plays a crucial role in successful knowledge transfer.
WRPO Optimization#
The core of the research paper revolves around Weighted-Reward Preference Optimization (WRPO), a novel implicit model fusion method. Unlike explicit methods that struggle with vocabulary alignment and distribution merging, WRPO cleverly leverages preference optimization between source and target LLMs, effectively transferring capabilities without these complexities. A key innovation is its progressive adaptation strategy, gradually shifting reliance from the target LLM to the source LLMs, thereby mitigating distributional deviations that often hinder preference optimization. This progressive approach proves highly effective, as demonstrated by consistent outperformance of various fine-tuning baselines and knowledge fusion methods across multiple benchmarks. WRPO’s efficiency is another strength, eliminating the need for resource-intensive pre-processing steps, making it scalable for diverse LLMs.
Progressive Adaptation#
Progressive adaptation, in the context of the research paper, is a crucial strategy for mitigating distributional shifts between source and target LLMs during implicit model fusion. It elegantly addresses the challenge of aligning models with vastly different training data and architectures. The core idea is to gradually transition the reliance on preferred examples from solely the target LLM to a combination of both target and source LLMs. This controlled shift prevents abrupt changes in the training distribution, which can hinder optimization and result in suboptimal performance. This gradual integration of source LLM knowledge allows for smoother adaptation and better knowledge transfer. The progressive nature of the adaptation not only enhances stability but also enables the target LLM to effectively learn from the strengths of diverse source models. The effectiveness of this strategy is particularly noteworthy in handling heterogeneous LLMs, demonstrating the robustness and adaptability of the proposed method.
Empirical Evaluation#
An empirical evaluation section in a research paper would typically present the results of experiments designed to test the paper’s hypotheses or claims. A strong empirical evaluation would include a clear description of the experimental setup, datasets used, and evaluation metrics. The choice of datasets is crucial; using well-established benchmarks allows for easy comparison with prior work, while novel datasets could demonstrate the method’s capability in new domains. Detailed results should be presented, potentially with tables and figures to visualize key findings. Statistical significance tests should be used to determine whether observed improvements are meaningful and not just due to chance. The discussion of results should be detailed, comparing the performance of the proposed method to baselines and alternative approaches, and explaining any unexpected or surprising findings. A limitation analysis acknowledging the method’s shortcomings is also essential for a balanced evaluation. Overall, a well-crafted empirical evaluation strengthens the paper’s credibility by providing concrete evidence to support the claims.
Future Directions#
Future research could explore more sophisticated reward models to better capture nuanced aspects of language quality. Investigating the use of diverse evaluation metrics beyond those currently used would provide a more comprehensive assessment of model performance. Furthermore, the development of more efficient training techniques is crucial for scaling the model fusion approach to larger and more diverse sets of LLMs. Research into robust methods for handling distributional shifts between source and target LLMs would be vital, perhaps through the use of domain adaptation techniques or advanced regularization methods. Finally, exploring applications beyond instruction following would unlock the potential of implicit model fusion for a wider range of NLP tasks, such as text summarization, question answering, and machine translation.
More visual insights#
More on figures

🔼 This figure illustrates the architecture of the Weighted-Reward Preference Optimization (WRPO) method for implicit model fusion. It shows how multiple source LLMs provide responses to a given prompt. A reward model ranks these responses, and the highest-ranked response is selected as the preferred response. The target LLM also generates responses, and the best and worst are identified. A progressive adaptation strategy adjusts the weighting of the preferred responses from the source LLMs and the target LLM during training to minimize distribution discrepancies. The training objective aims to maximize the reward margin between preferred and dispreferred responses, leading to the implicit fusion of knowledge from the source LLMs into the target LLM.
read the caption
Figure 2: Overview of our proposed WRPO for implicit model fusion.

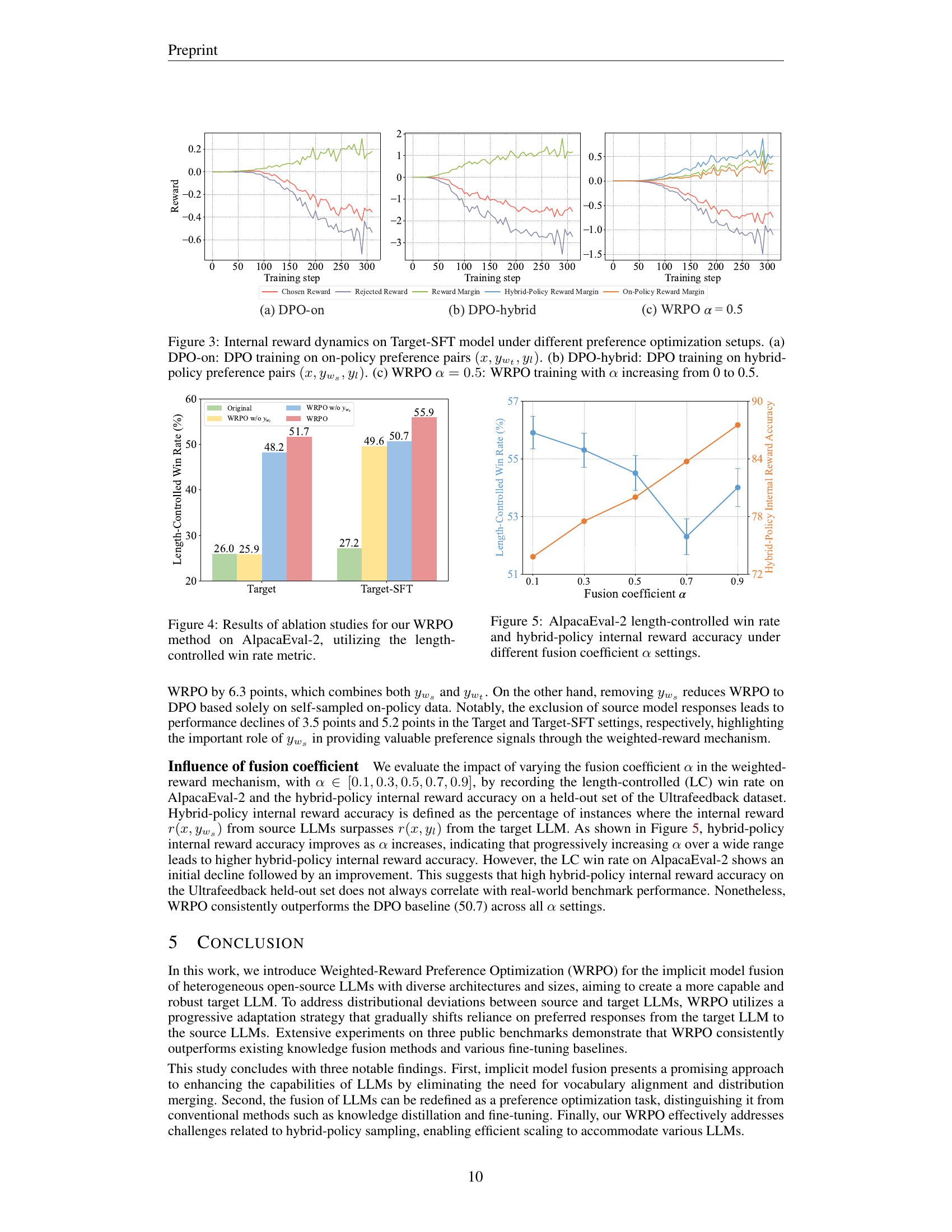
🔼 Figure 3 visualizes the changes in internal reward dynamics observed during the training of the Target-SFT model under three different preference optimization methods. Each method uses different combinations of preferred and dispreferred response pairs. Panel (a) shows DPO training using only preferred and dispreferred responses generated from the target LLM (on-policy data). Panel (b) demonstrates DPO training with preferred responses sourced from both target and source models (hybrid-policy data). Finally, Panel (c) showcases the WRPO method, where the influence of source model responses is progressively increased during training via a dynamic fusion coefficient (α) that starts at 0 and increases to 0.5. The figure illustrates how the different methods affect the reward dynamics over time, showing the internal rewards for both the chosen and rejected responses, as well as the resulting reward margin.
read the caption
Figure 3: Internal reward dynamics on Target-SFT model under different preference optimization setups. (a) DPO-on: DPO training on on-policy preference pairs (x,ywt,yl)𝑥subscript𝑦subscript𝑤𝑡subscript𝑦𝑙(x,y_{w_{t}},y_{l})( italic_x , italic_y start_POSTSUBSCRIPT italic_w start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT end_POSTSUBSCRIPT , italic_y start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ). (b) DPO-hybrid: DPO training on hybrid-policy preference pairs (x,yws,yl)𝑥subscript𝑦subscript𝑤𝑠subscript𝑦𝑙(x,y_{w_{s}},y_{l})( italic_x , italic_y start_POSTSUBSCRIPT italic_w start_POSTSUBSCRIPT italic_s end_POSTSUBSCRIPT end_POSTSUBSCRIPT , italic_y start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ). (c) WRPO α=0.5𝛼0.5\alpha=0.5italic_α = 0.5: WRPO training with α𝛼\alphaitalic_α increasing from 0 to 0.5.

🔼 This figure displays the results of ablation studies conducted to evaluate the effectiveness of different components within the Weighted-Reward Preference Optimization (WRPO) method. The study specifically focuses on the AlpacaEval-2 benchmark, using the length-controlled win rate as the evaluation metric. It likely shows the performance when certain aspects of the WRPO are removed or modified (ablated), such as removing the influence of the source LLMs or the target LLMs, demonstrating the contribution of each part of the overall WRPO model to its final performance.
read the caption
Figure 4: Results of ablation studies for our WRPO method on AlpacaEval-2, utilizing the length-controlled win rate metric.

🔼 This figure shows the results of an experiment on the AlpacaEval-2 benchmark, where the fusion coefficient α (alpha) was varied. The experiment tested a model’s ability to implicitly learn from multiple language models (LLMs), using a technique that progressively incorporates LLM responses. The graph displays two key metrics: the length-controlled win rate (a measure of the model’s performance against a baseline model) and the hybrid-policy internal reward accuracy (reflecting the model’s confidence in its own predictions when combining its own generated responses with those from other LLMs). The x-axis represents the different values of α, showing how the balance between the model’s own responses and the other LLMs’ responses influences the performance. The plot allows for assessing the optimal α setting that maximizes both the win rate and the hybrid-policy accuracy.
read the caption
Figure 5: AlpacaEval-2 length-controlled win rate and hybrid-policy internal reward accuracy under different fusion coefficient α𝛼\alphaitalic_α settings.
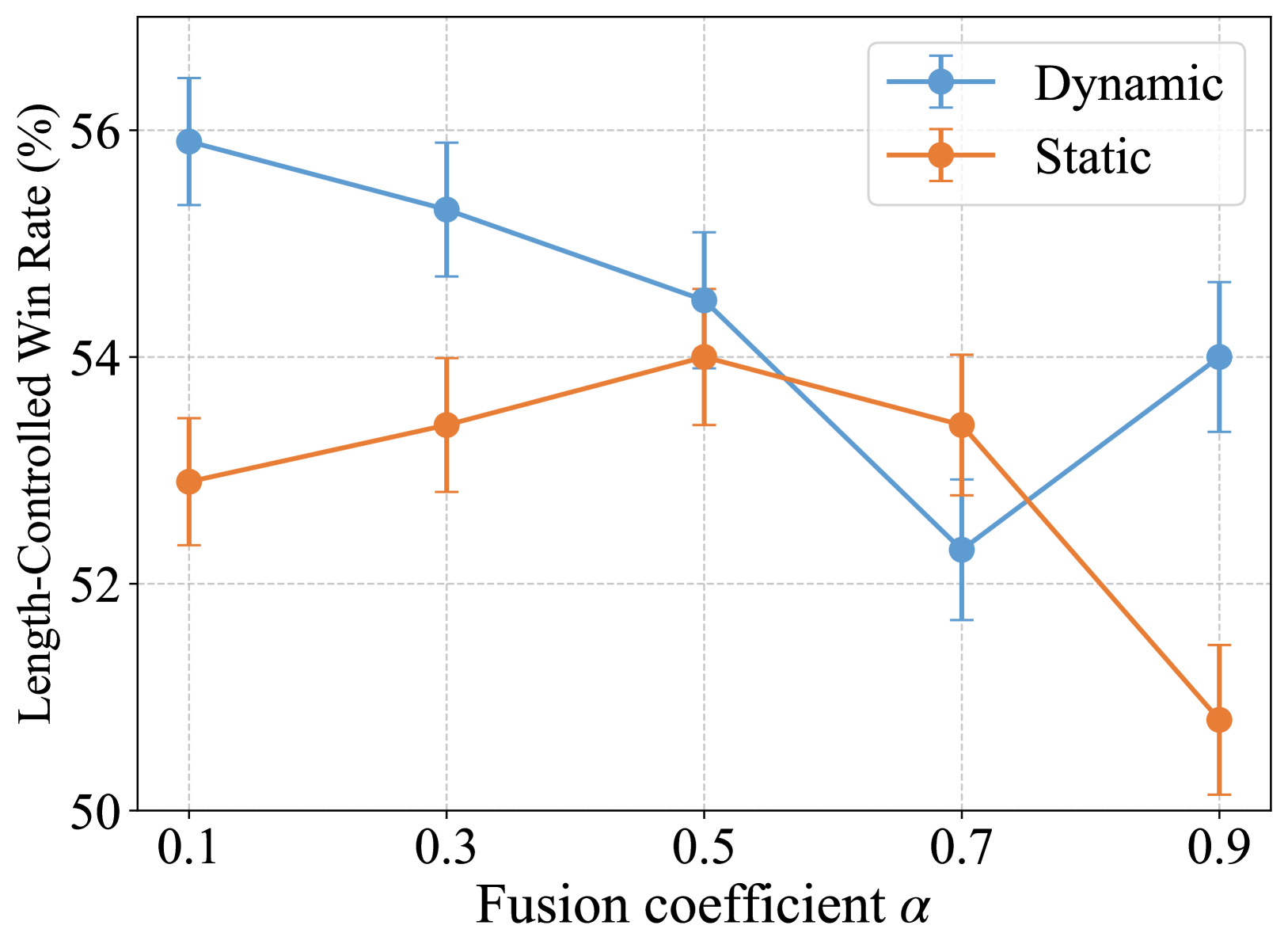
🔼 Figure 6 shows the results of an ablation study comparing two strategies for adjusting the fusion coefficient (α) in the Weighted-Reward Preference Optimization (WRPO) method. The fusion coefficient controls the balance between using preferred responses from the source LLMs and the target LLM during training. The x-axis represents different values of α, ranging from 0.1 to 0.9. The y-axis shows the length-controlled win rate on the AlpacaEval-2 benchmark. The figure compares a dynamic strategy (where α increases linearly during training) and a static strategy (where α is fixed at a particular value throughout training). The results indicate that the dynamic strategy generally performs better than the static strategy across various α values, highlighting the benefits of progressively adapting the model’s reliance on preferred responses from source LLMs during training. Error bars might be present but are not described in the caption.
read the caption
Figure 6: Comparisons of dynamic and static tuning strategies for the fusion coefficient on AlpacaEval-2, utilizing the length-controlled win rate metric.
More on tables
| Model | Size | AlpacaEval-2 (GPT-4-1106-Preview) | Arena-Hard (GPT-4-1106-Preview) | MT-Bench (GPT-4-0125-Preview) | |||
|---|---|---|---|---|---|---|---|
| LC(%) | WR(%) | WR(%) | T1 | T2 | Overall | ||
| — | — | — | — | — | — | — | — |
| Source&Target LLMs | |||||||
| Target | 8B | 26.0 | 25.3 | 20.6 | 7.41 | 7.04 | 7.23 |
| Mistral-Large-Instruct-2407 | 123B | 54.3 | 46.8 | 70.4 | 8.83 | 8.31 | 8.57 |
| Gemma2-27B-IT | 27B | 55.5 | 41.0 | 57.5 | 8.34 | 8.03 | 8.19 |
| Qwen2-72B-Instruct | 72B | 38.1 | 29.9 | 46.9 | 8.44 | 7.84 | 8.15 |
| LLaMA3-70B-Instruct | 70B | 34.4 | 33.2 | 46.6 | 8.61 | 7.77 | 8.19 |
| Gemma2-9B-IT | 9B | 51.1 | 38.1 | 40.8 | 8.27 | 7.44 | 7.86 |
| InternLM2.5-20B-Chat | 20B | 37.4 | 45.3 | 31.2 | 8.03 | 7.23 | 7.64 |
| DeepSeek-V2-Chat | 236B | 51.4 | 51.3 | 68.3 | 8.65 | 7.96 | 8.31 |
| DeepSeek-Coder-V2-Instruct | 236B | 50.7 | 54.0 | 66.3 | 8.80 | 7.42 | 8.13 |
| Yi-1.5-34B-Chat | 34B | 37.5 | 44.5 | 42.6 | 7.99 | 7.64 | 7.81 |
| Phi-3-Medium-4K-Instruct | 14B | 29.8 | 24.2 | 33.4 | 8.63 | 7.46 | 8.04 |
| Collective LLMs | |||||||
| PackLLM-Top1-PPL | 849B | 49.1 | 48.0 | 64.8 | 8.29 | 8.20 | 8.25 |
| LLM-Blender-Top1 | 849B | 46.2 | 44.3 | 58.2 | 8.69 | 8.06 | 8.38 |
| MOA | 849B | 61.3 | 77.2 | 83.1 | 9.04 | 8.03 | 8.54 |
| Target-FuseLLM | 8B | 36.0 | 33.8 | 32.1 | 7.53 | 7.13 | 7.33 |
| Target-FuseChat | 8B | 38.1 | 35.2 | 32.7 | 7.68 | 7.07 | 7.38 |
| Preference Optimization Methods | |||||||
| Target-DPO | 8B | 48.2 | 47.5 | 35.2 | 7.68 | 7.23 | 7.46 |
| Target-SimPO | 8B | 53.7 | 47.5 | 36.5 | 7.73 | 7.00 | 7.38 |
| Target-IPO | 8B | 46.8 | 42.4 | 36.6 | 7.89 | 7.19 | 7.54 |
| Our Methods | |||||||
| Target-SFT | 8B | 27.2 | 26.0 | 24.7 | 7.69 | 7.03 | 7.36 |
| Target-SFT-DPO | 8B | 50.7 | 53.1 | 40.2 | 7.98 | 7.23 | 7.61 |
| Target-SFT-WRPO-Medium | 8B | 53.5 | 53.8 | 41.6 | 7.80 | 7.03 | 7.42 |
| Target-SFT-WRPO | 8B | 55.9 | 57.6 | 46.2 | 7.95 | 7.31 | 7.63 |
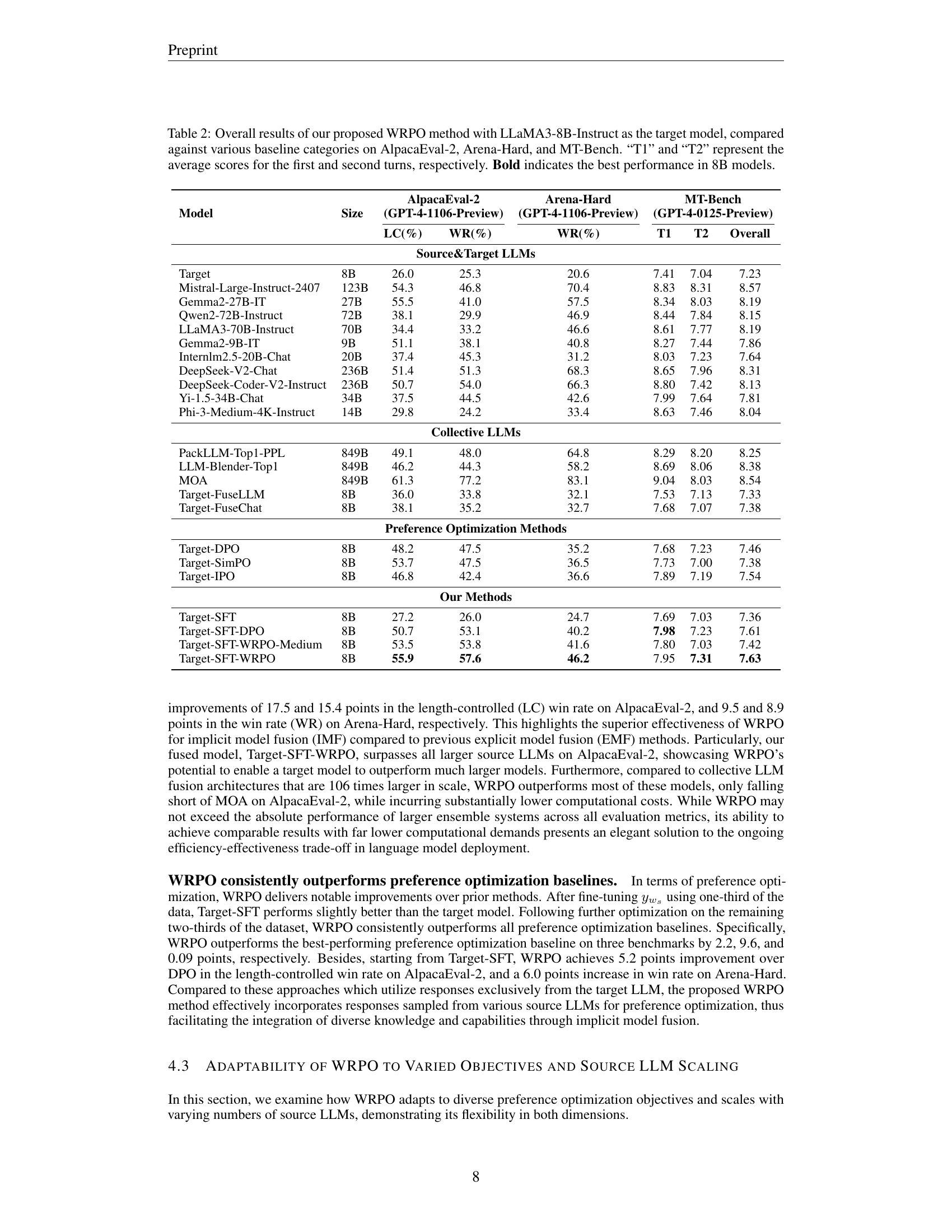
🔼 This table presents a comprehensive comparison of different Large Language Models (LLMs) on three benchmark datasets: AlpacaEval-2, Arena-Hard, and MT-Bench. The models are evaluated based on their performance in instruction-following tasks. The key model being evaluated is LLaMA3-8B-Instruct, which has been enhanced using the Weighted-Reward Preference Optimization (WRPO) method. The table includes various baseline models for comparison, categorized as source & target LLMs (individual models and their performance), collective LLMs (ensemble methods), and preference optimization methods. The results are presented as win rates (AlpacaEval-2 and Arena-Hard) and average scores (MT-Bench, across two turns of dialogue, T1 and T2). The best performing 8B parameter model is highlighted in bold.
read the caption
Table 2: Overall results of our proposed WRPO method with LLaMA3-8B-Instruct as the target model, compared against various baseline categories on AlpacaEval-2, Arena-Hard, and MT-Bench. “T1” and “T2” represent the average scores for the first and second turns, respectively. Bold indicates the best performance in 8B models.
| Method | AlpacaEval-2 LC(%) | AlpacaEval-2 WR(%) | MT-Bench Overall |
|---|---|---|---|
| SimPO | 53.9 | 49.9 | 7.39 |
| IPO | 51.1 | 52.4 | 7.67 |
| WRPOSimPO | 55.8 | 51.8 | 7.42 |
| WRPOIPO | 53.3 | 57.7 | 7.72 |
🔼 This table presents the results of applying the Weighted-Reward Preference Optimization (WRPO) method in combination with three different preference optimization objectives: Direct Preference Optimization (DPO), Inverse Preference Optimization (IPO), and Simple Preference Optimization (SimPO). It shows how WRPO’s performance varies when integrated with these different optimization strategies. The metrics used to evaluate performance are likely related to the instruction-following capabilities of the language model.
read the caption
Table 3: Results of WRPO combined with different preference optimization objectives.
| Num | AlpacaEval-2 | MT-Bench | |
|---|---|---|---|
| LC(%) | WR(%) | Overall | |
| 1 | 48.9 | 50.3 | 7.29 |
| 2 | 52.3 | 50.4 | 7.54 |
| 5 | 53.5 | 53.8 | 7.42 |
| 10 | 55.9 | 58.0 | 7.63 |
🔼 This table presents the performance of the Weighted-Reward Preference Optimization (WRPO) model on two benchmark datasets, AlpacaEval-2 and MT-Bench, using different numbers of source Large Language Models (LLMs). It demonstrates how the model’s performance changes as the number of source LLMs increases, showing the impact of adding more diverse knowledge sources on the model’s ability to generate high-quality responses. The results are likely presented as metrics such as accuracy or win rate, indicating the effectiveness of the model under varying conditions.
read the caption
Table 4: Results of our WRPO implemented with varying numbers of source LLMs on AlpacaEval-2 and MT-Bench.
| Method | Objective | Hyperparameter |
|---|---|---|
| DPO [2023] | −logσ(βlogπθ(yw | x)πref(yw |
| IPO [2023] | (logπθ(yw | x)πref(yw |
| SimPO [2024] | −logσ(β | yw |
| γ∈[0,1.0,2.0] | ||
| WRPO_DPO | −logσ(α⋅βlogπθ(yws∣x)πref(yws∣x)+(1−α)⋅βlogπθ(jwt∣x)πref(jwt∣x)−βlogπθ(yl∣x)πref(yl∣x)) | β=0.01 |
| α∈[0.1,0.3,0.5,0.7,0.9] | ||
| WRPO_SimPO | −logσ(α⋅β | yws |
| α∈[0.1,0.3,0.5] | ||
| WRPO_IPO | (α⋅logπθ(yws∣x)πref(yws∣x)+(1−α)⋅logπθ(jwt∣x)πref(jwt∣x)−logπθ(yl∣x)πref(yl∣x)−12τ)2 | τ∈[0.01,0.1] |
| α∈[0.1,0.3,0.5] |
🔼 This table presents a comparison of different preference optimization objectives and their associated hyperparameter ranges. It lists the objective function for each method (DPO, IPO, SimPO, and WRPO variants) along with the hyperparameters used and their respective search ranges during the optimization process. This information is crucial for understanding the experimental setup and for reproducibility.
read the caption
Table 5: Various preference optimization objectives and hyperparameter search range.
| Method | β | γ | α | LR |
|---|---|---|---|---|
| DPO | 0.01 | - | - | 3e-7 |
| IPO | - | - | 0.01 | 1e-6 |
| SimPO | 10 | 1.0 | - | 6e-7 |
| WRPODPO | 0.01 | - | 0.1 | 3e-7 |
| WRPOIPO | - | 0.01 | 0.1 | 1e-6 |
| WRPOSimPO | 10 | 0 | 0.5 | 6e-7 |
🔼 This table presents the hyperparameter settings used for various preference optimization methods. The methods include Direct Preference Optimization (DPO), Implicit Preference Optimization (IPO), and Simple Preference Optimization (SimPO). The Target-SFT model serves as the policy model for all these methods. The table shows the hyperparameters β, τ, γ, and the learning rate (LR) used for each method and highlights the specific values selected after tuning for optimal performance.
read the caption
Table 6: Hyperparameter settings for preference optimization methods using Target-SFT as the policy model. “LR” denotes the learning rate.
| Model | ARC | HellaSwag | MMLU | TruthfulQA | Winogrande | GSM8K | Avg. |
|---|---|---|---|---|---|---|---|
| Target | 61.43 | 78.48 | 65.71 | 51.64 | 75.61 | 75.21 | 68.01 |
| Target-SFT | 51.19 | 79.83 | 64.56 | 45.93 | 76.87 | 62.77 | 63.53 |
| Target-SFT-DPO | 60.67 | 81.7 | 64.98 | 50.3 | 76.95 | 68.76 | 67.23 |
| Target-SFT-IPO | 60.58 | 81.68 | 65.5 | 53.93 | 77.9 | 69.67 | 68.21 |
| Target-SFT-SimPO | 61.77 | 82.23 | 65.13 | 54.76 | 78.45 | 69.6 | 68.66 |
| Target-SFT-WRPO | 62.63 | 82.38 | 64.91 | 54.72 | 78.53 | 71.57 | 69.12 |
| Target-SFT-WRPOIPO | 59.98 | 81.53 | 65.35 | 53.48 | 78.14 | 69.83 | 68.05 |
| Target-SFT-WRPOSimPO | 61.69 | 81.95 | 65.08 | 57.11 | 78.69 | 68.69 | 68.87 |
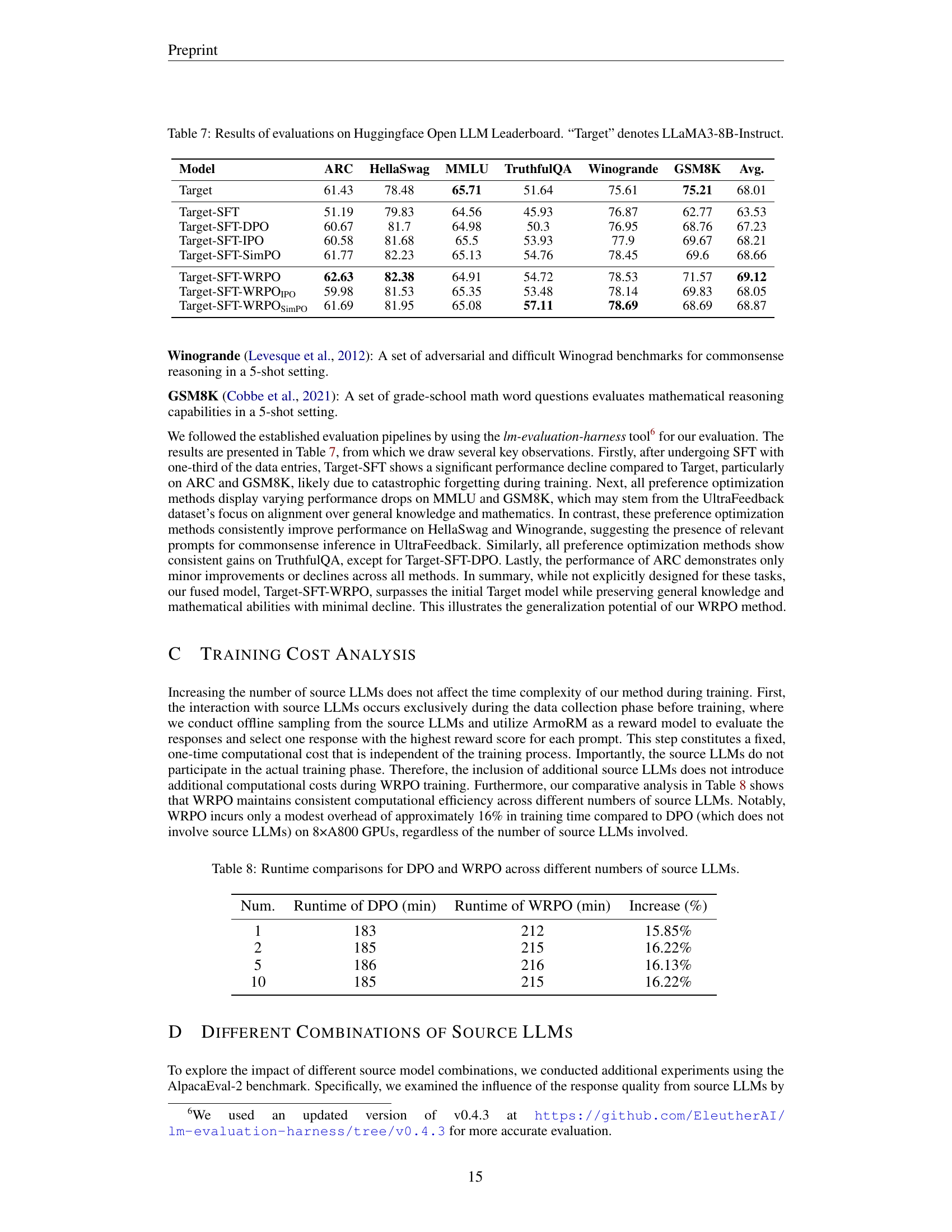
🔼 This table presents the results of evaluating different language models on the HuggingFace Open LLM Leaderboard. The models evaluated include the base LLaMA3-8B-Instruct model (denoted as ‘Target’), a supervised fine-tuned version of this model (‘Target-SFT’), and several variations incorporating different preference optimization techniques (DPO, IPO, SimPO, and WRPO). The evaluation covers seven diverse benchmarks assessing various aspects of language model capabilities, including commonsense reasoning, mathematical reasoning, and instruction following. Each model’s performance is quantified by its score on each benchmark.
read the caption
Table 7: Results of evaluations on Huggingface Open LLM Leaderboard. “Target” denotes LLaMA3-8B-Instruct.
| Num. | Runtime of DPO (min) | Runtime of WRPO (min) | Increase (%) |
|---|---|---|---|
| 1 | 183 | 212 | 15.85% |
| 2 | 185 | 215 | 16.22% |
| 5 | 186 | 216 | 16.13% |
| 10 | 185 | 215 | 16.22% |
🔼 This table presents a comparison of the training times for Direct Preference Optimization (DPO) and Weighted-Reward Preference Optimization (WRPO), highlighting the impact of varying the number of source Large Language Models (LLMs) used in the WRPO method. It shows the runtime in minutes for DPO and WRPO with 1, 2, 5, and 10 source LLMs and calculates the percentage increase in WRPO runtime compared to DPO for each scenario. This helps assess the computational efficiency and scalability of WRPO, especially when using multiple source LLMs.
read the caption
Table 8: Runtime comparisons for DPO and WRPO across different numbers of source LLMs.
| Method | AlpacaEval-2 | ||
|---|---|---|---|
| LC(%) | WR(%) | Length | |
| — | — | — | — |
| Rank1 | 55.9 | 57.6 | 2159 |
| Rank2 | 53.7 | 55.4 | 2143 |
| Group1 | 53.5 | 53.8 | 2098 |
| Group2 | 53.7 | 60.7 | 2440 |
🔼 This table presents the results of the Weighted-Reward Preference Optimization (WRPO) method on the AlpacaEval-2 benchmark using different combinations of source Large Language Models (LLMs). It shows how the performance of the WRPO method changes when using different sets of source LLMs. Specifically, it compares the length-controlled win rate (LC), raw win rate (WR), and the average length of generated responses for various scenarios. The scenarios include using only the highest-ranked response from source LLMs, only the second-highest, and using groups of five LLMs (Group1 and Group2) with different characteristics.
read the caption
Table 9: Results of our WRPO implemented with varying combinations of source LLMs on AlpacaEval-2.
| Method | AlpacaEval-2 LC(%) | AlpacaEval-2 WR(%) | MT-Bench Overall |
|---|---|---|---|
| WRPO | 55.9 | 57.6 | 7.63 |
| WRPOw/yls | 54.0 | 56.0 | 7.52 |
🔼 This table presents the results of an experiment evaluating the impact of incorporating additional dispreferred responses from source models into the WRPO framework. It shows the performance metrics (length-controlled win rate (LC) and raw win rate (WR) on AlpacaEval-2, and the overall score on MT-Bench) for different model configurations. Specifically, it compares the standard WRPO method against a modified version that includes dispreferred responses from both the target and source LLMs. This allows for an assessment of whether adding these extra dispreferred responses improves or harms the overall model performance.
read the caption
Table 10: Results of WRPO combined with additional dispreferred responses from source models.
| Model | Huggingface ID |
|---|---|
| Target | meta-llama/Meta-Llama-3-8B-Instruct |
| Mistral-Large-Instruct-2407 | Mistral-Large-Instruct-2407 |
| Gemma2-27B-IT | google/gemma-2-27b-it |
| Qwen2-72B-Instruct | Qwen/Qwen2-72B-Instruct |
| LLaMA3-70B-Instruct | meta-llama/Meta-Llama-3-70B-Instruct |
| Gemma2-9B-IT | google/gemma-2-9b-it |
| Internlm2.5-20B-Chat | internlm/internlm2_5-20b-chat |
| DeepSeek-V2-Chat | deepseek-ai/DeepSeek-V2-Chat-0628 |
| DeepSeek-Coder-V2-Instruct | deepseek-ai/DeepSeek-Coder-V2-Instruct-0724 |
| Yi-1.5-34B-Chat | 01-ai/Yi-1.5-34B-Chat |
| Phi-3-medium-4k-instruct | microsoft/Phi-3-medium-4k-instruct |
| ArmoRM-LLaMA3-8B-v0.1 | RLHFlow/ArmoRM-Llama3-8B-v0.1 |
| Target-DPO | princeton-nlp/Llama-3-Instruct-8B-DPO-v0.2 |
| Target-SimPO | princeton-nlp/Llama-3-Instruct-8B-SimPO-v0.2 |
| Target-IPO | princeton-nlp/Llama-3-Instruct-8B-IPO-v0.2 |
🔼 This table lists the details of the open-source large language models (LLMs) used in the experiments described in the paper. It includes the name of each model, its size (in billions of parameters), and its HuggingFace ID (a unique identifier for models hosted on the HuggingFace platform). A row is also dedicated to the target model used in the fusion process: LLaMA3-8B-Instruct. The table also specifies the HuggingFace IDs for the reward model and preference optimization baseline checkpoints.
read the caption
Table 11: Details of open-source models in our experiments. “Target” denotes LLaMA3-8B-Instruct.
| Topic | Instruction | GPT-4-0314 Reference Answer | Target-SFT Answer | Target-SFT-DPO Answer | Target-SFT-WRPO Answer |
|---|---|---|---|---|---|
| Situation Puzzle Challenges | Help me find out how to solve a math puzzle. It’s: “How many dots you can joint down on a page while drawing lines between them, without three of them ever forming a straight line?” | This math puzzle is related to the concept of “no three points being collinear.” In this case, you want to find the maximum number of points you can place on a page such that no three of them are in a straight line. The answer to this puzzle is that you can place an infinite number of points without having three of them form a straight line. One way to achieve this is by placing the points in a non-linear pattern, such as arranging them in a spiral or a circle. However, if you are looking for a more specific answer, you can consider placing the points in a triangular grid pattern. In this arrangement, you can place as many points as you want without having three of them form a straight line. Each new point added will be connected to the existing points without creating a straight line with any other two points. | This is a classic puzzle known as the “Three Dots Puzzle” or “No Straight Lines Puzzle.” The answer is 3. Here’s why: If you draw lines between 3 dots, you can’t avoid creating at least one straight line. If you draw lines between 4 dots, you can create a triangle with two straight sides, which means three dots are forming a straight line. If you draw lines between 5 dots, you can create a pentagon with three straight sides, which means three dots are forming a straight line. Therefore, the maximum number of dots you can connect without three of them forming a straight line is 3. | This puzzle is a classic example of a graph theory problem, specifically a planar graph challenge. Here’s a breakdown and solution: Understanding the Problem: Graph: Think of each dot as a node, and the lines connecting them as edges. Planarity: The key constraint is that no three nodes (dots) can be connected by straight lines, forming a triangle. This ensures no three edges intersect at a single point. Goal: Find the maximum number of dots you can connect without violating this planarity condition. Solution: The maximum number of dots you can connect while maintaining planarity is 5. Why 5? Proof: Imagine arranging the dots in a pentagon (a five-sided shape). Each edge of the pentagon connects two dots, and no three dots form a straight line within the pentagon. Generalization: For any number of dots greater than 5, it’s impossible to draw a planar graph without three dots forming a straight line. This is because as you add more dots, the likelihood of forming triangles increases, eventually leading to intersections. Key Takeaway: For any planar graph, the maximum number of nodes (dots) without three forming a straight line is 5. This fundamental limit arises from the inherent geometry of planar graphs. I hope this explanation helps you solve your math puzzle! | Unraveling the Puzzle: This problem is a classic example of “Non-Collinear Point Arrangement” with a twist. Let’s break it down step by step: Key Insights: 1. No Straight Triangles: The core constraint is that no three dots (points) should ever form a straight line. 2. Geometric Considerations: - A straight line requires three points in a specific arrangement (collinear). - We need to avoid this configuration. Strategies for Solving: 1. The Fundamental Approach: Inductive Reasoning: Start with two dots. Adding a third dot that doesn’t create a straight line is always possible (e.g., forming a triangle with slightly obtuse or acute angles). Generalization: If you can place three dots without a straight line, you can always add more dots, ensuring each new addition maintains this property. 2. Mathematical Proof (for the curious): Proof by Contradiction: Assume, for the sake of contradiction, that you’ve found a set of dots where three form a straight line. Analysis: This implies a triangle with all angles equal (180°), which is impossible in a non-degenerate triangle (no sides are zero-length). Conclusion: Therefore, it’s impossible to construct a set of dots where three always form a straight line. Practical Implications: Infinite Solutions: There are infinitely many ways to arrange dots without creating straight lines between any three. Page Limitation: While theoretically infinite, the practical limitation is your page size. You can draw as many dots as your paper allows, ensuring no three forms a straight line. Solving on Paper: Start with two dots: This sets the foundation. Add dots gradually: Choose each new dot carefully to avoid creating a straight line with the existing ones. Visual Inspection: Continuously check that no three dots form a straight line as you add more. Remember: The beauty of this puzzle lies in its simplicity and the creative process of finding arrangements that satisfy the constraint. Happy dot-connecting! |
🔼 This table presents a case study demonstrating the capabilities of the Weighted-Reward Preference Optimization (WRPO) model in solving a complex mathematical puzzle from the Arena Hard benchmark. It compares the performance of three different models: the base model (Target-SFT), a model enhanced with direct preference optimization (Target-SFT-DPO), and the WRPO model (Target-SFT-WRPO). The responses from each model are shown, along with an analysis of their respective approaches and outcomes. This case study highlights WRPO’s ability to produce a mathematically sound and user-friendly solution by combining logical reasoning, detailed explanations, and insights not captured by the base model or the model using only direct preference optimization. The inclusion of the GPT-4 response offers a comparison to a state-of-the-art model.
read the caption
Table 12: Case study of a math puzzle on Situation Puzzle Challenges from Arena Hard. Our Target-SFT-WRPO model delivers a mathematically sound and user-oriented response, highlighting the efficacy of WRPO in enhancing model performance in challenging problem-solving scenarios.
Full paper#