↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Many recent studies leverage synthetic data generated by large language models (LLMs) for post-training tasks, improving their performance. However, these studies lack systematic comparisons of different LLMs’ capabilities in a unified setting. This makes it difficult to assess which LMs are best suited for synthetic data generation and how to improve the process.
To address this gap, the authors propose AGORABENCH, a benchmark with standardized settings and metrics. They use AGORABENCH to evaluate 6 LLMs, uncovering that LMs’ data generation ability doesn’t necessarily correlate with their problem-solving ability, multiple intrinsic features of data quality are more important. Also, the benchmark demonstrates that output format and cost-conscious model selection significantly impact data generation effectiveness.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical need for a standardized benchmark to evaluate language models’ abilities as synthetic data generators. This significantly impacts the development and application of post-training methods relying on synthetic data, a growing trend in the field. The findings highlight cost-effective strategies, offering valuable insights for researchers with limited resources. The work also opens up new avenues for investigating the intrinsic qualities that make an effective data generator.
Visual Insights#

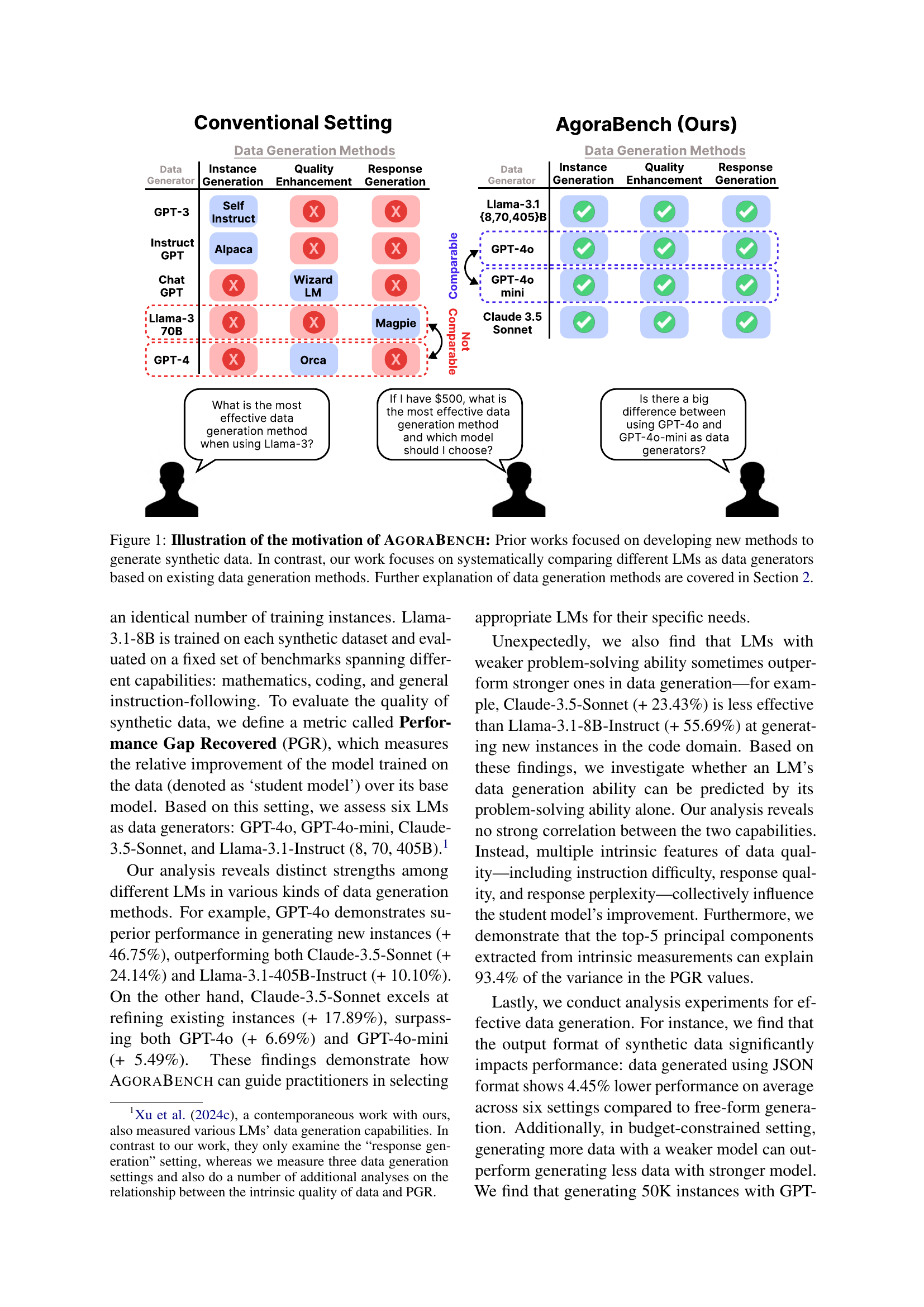
🔼 Figure 1 illustrates the core difference between AgoraBench and previous research in using large language models (LLMs) to generate synthetic data. Prior studies primarily concentrated on creating new data generation techniques, often showcasing their effectiveness through case studies with varying experimental setups. In contrast, AgoraBench systematically compares the data generation capabilities of six different LLMs, using pre-existing data generation methods. This controlled approach allows for a direct comparison of the LLMs’ performance, providing valuable insights into their relative strengths and weaknesses as synthetic data generators. Details on the data generation methods are provided in Section 2 of the paper.
read the caption
Figure 1: Illustration of the motivation of AgoraBench: Prior works focused on developing new methods to generate synthetic data. In contrast, our work focuses on systematically comparing different LMs as data generators based on existing data generation methods. Further explanation of data generation methods are covered in Section 2.
| Domain | Data Generation Method | Seed Data | Seed Data Size | Benchmark |
|---|---|---|---|---|
| Math | Instance Generation | GSM8K, MATH (train set) | 14,856 | GSM8K, MATH (test set) |
| Response Generation | Magpie-Reasoning (math) | 10,000 | GSM8K, MATH (test set) | |
| Quality Enhancement | WebInstruct (math) | 10,000 | GSM8K, MATH (test set) | |
| Code | Instance Generation | MBPP (train set), xP3x | 874 | MBPP, HumanEval (test set) |
| Response Generation | Magpie-Reasoning (code) | 10,000 | MBPP, HumanEval (test set) | |
| Quality Enhancement | CoNaLa | 10,000 | MBPP, HumanEval (test set) | |
| Inst. Follow | Instance Generation | LIMA | 503 | AlpacaEval 2.0, Arena-Hard |
| Response Generation | Magpie-Pro | 10,000 | AlpacaEval 2.0, Arena-Hard | |
| Quality Enhancement | WebInstruct (code) | 10,000 | AlpacaEval 2.0, Arena-Hard |
🔼 The table details the experimental setup of AGORABENCH, a benchmark designed to evaluate language models as synthetic data generators. Each of the nine settings involves a specific domain (math, code, or instruction following), a data generation method (instance generation, response generation, or quality enhancement), a corresponding seed dataset, and a benchmark for evaluating the generated data. For each setting, the same meta-prompt is used, and each language model (LM) generates 10,000 instances. Crucially, for instance generation, the seed dataset is also used as the training data for the student model. This controlled setup allows for a fair comparison of different LMs’ data generation capabilities.
read the caption
Table 1: AgoraBench Settings: For each of the nine settings, an LM being evaluated generates 10K instances with the same meta-prompt and seed data. Note that the seed dataset is also used for training in instance generation.
In-depth insights#
LM Data Gen#
The heading ‘LM Data Gen,’ likely short for “Large Language Model Data Generation,” encapsulates a critical area of research focusing on the capabilities of LMs to produce synthetic datasets. A thoughtful analysis would explore the methodologies used for data generation (e.g., instruction-following, response generation, or data augmentation), the quality metrics employed to assess the generated data (e.g., accuracy, fluency, relevance, and diversity), and the impact of these synthetic datasets when used to fine-tune or train other LMs. Furthermore, a comprehensive discussion should consider the different LMs’ strengths and weaknesses as data generators and the factors influencing their performance, such as model size, architecture, training data, and prompting strategies. Cost-effectiveness is another crucial aspect; comparing the cost of using various LMs for data generation is essential for practical application. Finally, examining whether an LM’s problem-solving ability correlates with its data generation capabilities is vital, as is the exploration of intrinsic data properties that contribute to effective synthetic datasets. A thorough analysis of these factors provides valuable insights into the capabilities and limitations of current LMs as synthetic data generators and how this technology can be further advanced.
AgoraBench Eval#
The hypothetical “AgoraBench Eval” section would likely present a detailed analysis of the benchmark’s performance. It would likely include quantitative results showing the performance of various language models (LMs) across different data generation tasks and metrics. Key aspects would be comparing the models’ abilities to generate high-quality, diverse data, perhaps measuring performance differences across various domains and generation methods. The analysis might involve comparing performance against human-generated baselines, investigating the correlation between model size/cost and data quality, and examining the impact of different generation strategies and model choices. A crucial aspect would be the assessment of the resulting student models trained on the synthetic data, perhaps using downstream task performance as a metric. The section should also discuss the limitations of AgoraBench, for instance, potential biases in the benchmark datasets or the generalizability of its findings to real-world applications. Finally, the analysis would likely include a discussion of future research directions, such as exploring new data generation techniques, improving the evaluation metrics, or expanding the benchmark to cover a wider range of LMs and tasks.
Data Quality#
Evaluating the quality of synthetic data generated by large language models (LLMs) is crucial for their effective use in post-training. A key aspect is the alignment between the synthetic data and the characteristics of real-world data used in downstream tasks. Intrinsic data quality metrics, such as response quality, perplexity, and instruction difficulty, can provide valuable insights but don’t fully capture the impact on downstream task performance. The study highlights that higher problem-solving ability in an LLM doesn’t guarantee higher quality synthetic data generation. Therefore, a multifaceted approach involving both intrinsic metrics and downstream task evaluation is necessary for a comprehensive assessment of data quality, with an emphasis on how well the synthetic data mimics the distribution and properties of real-world data to achieve optimal post-training results. Cost-effectiveness should also be a factor, and trade-offs between cost and quality, like using large volumes of data from cheaper models vs smaller datasets from more expensive models, warrant careful consideration.
Cost-Perf Tradeoff#
The cost-performance tradeoff in large language model (LLM) based synthetic data generation is a crucial consideration. Cost-effective models like Llama-3.1-8B-Instruct, despite having lower problem-solving capabilities, surprisingly outperform more powerful, expensive models like GPT-4 in certain data generation scenarios. This highlights the importance of selecting the right model based on the specific task and budget rather than solely focusing on the LLM’s inherent performance on established benchmarks. Generating larger volumes of synthetic data with cheaper models can be more effective and cost efficient than using fewer samples from higher-performing, more expensive models. This finding emphasizes a shift from prioritizing peak performance to optimizing the overall cost-effectiveness of data synthesis for training student models. There is no direct correlation between an LLM’s problem-solving ability and its data generation effectiveness. This suggests that other intrinsic data quality metrics, like response quality and instruction difficulty, are more strongly predictive of a model’s success as a synthetic data generator. Therefore, a careful analysis of these metrics is crucial in choosing cost-effective LLMs for synthetic data generation.
Future Work#
The authors of this research paper on evaluating language models as synthetic data generators acknowledge several avenues for future work. Improving the prediction of data generation capability is a primary goal. While the PCA analysis uncovered valuable insights into intrinsic data features, the model’s predictive power (R-squared of 0.325) suggests that more sophisticated metrics, or a deeper understanding of the underlying relationships between these metrics, could significantly enhance predictive accuracy. Further investigation is needed to understand how different model architectures and training methodologies impact data generation effectiveness, especially concerning the trade-off between cost and performance when scaling up data generation. Exploring diverse data generation methods beyond the three explored (instance generation, response generation, quality enhancement) is critical. Investigating the effect of different prompt designs and formats, such as the influence of JSON structuring on generation quality, and further exploring the effects of instruction and response diversity on model performance would offer valuable insights. Finally, the authors propose exploring the development and evaluation of specialized language models optimized specifically for synthetic data generation; a task that would further validate and deepen the insights gained by this work.
More visual insights#
More on figures

🔼 The figure illustrates the three data generation methods used in AgoraBench. The left panel shows instance generation, where a small number of human-written instruction-response pairs are used as seed data to generate many more new pairs. The middle panel depicts response generation, which starts with many instructions without responses and generates responses for each one. The right panel shows quality enhancement, taking a large set of existing instruction-response pairs and improving the quality of either the instructions or responses.
read the caption
Figure 2: AgoraBench tests three data generation methods: generating new instruction and response pairs (left), generating responses (middle), and enhancing the quality of the instruction and/or the response (right).

🔼 The figure illustrates the Performance Gap Recovered (PGR) metric. PGR measures the relative improvement in performance of a student model (SDG) trained on synthetic data generated by a language model (LM), compared to a reference model (Sref) trained on a different dataset. Both SDG and Sref are derived from the same base model (SØ). The formula highlights how much improvement SDG gains relative to Sref, demonstrating the effectiveness of the LM as a synthetic data generator.
read the caption
Figure 3: Illustration of Performance Gap Recovered metric: The performance gap recovered metric captures the relative improvement of SDGsubscript𝑆subscript𝐷𝐺S_{D_{G}}italic_S start_POSTSUBSCRIPT italic_D start_POSTSUBSCRIPT italic_G end_POSTSUBSCRIPT end_POSTSUBSCRIPT with respect to Srefsubscript𝑆𝑟𝑒𝑓S_{ref}italic_S start_POSTSUBSCRIPT italic_r italic_e italic_f end_POSTSUBSCRIPT where SDGsubscript𝑆subscript𝐷𝐺S_{D_{G}}italic_S start_POSTSUBSCRIPT italic_D start_POSTSUBSCRIPT italic_G end_POSTSUBSCRIPT end_POSTSUBSCRIPT and Srefsubscript𝑆𝑟𝑒𝑓S_{ref}italic_S start_POSTSUBSCRIPT italic_r italic_e italic_f end_POSTSUBSCRIPT is both trained from SØsubscript𝑆ØS_{\text{\O}}italic_S start_POSTSUBSCRIPT Ø end_POSTSUBSCRIPT.

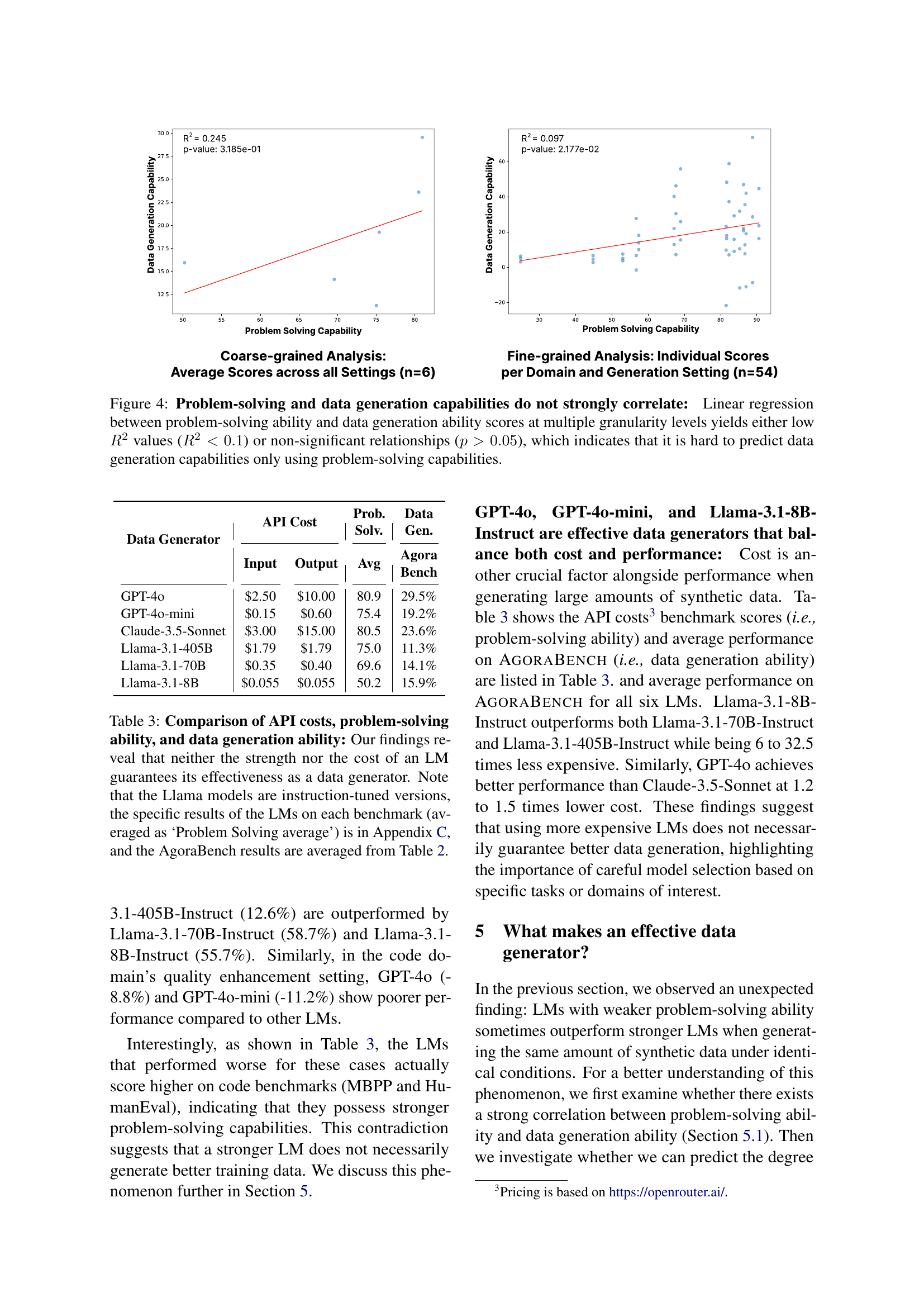
🔼 This figure displays the results of a correlation analysis between a language model’s problem-solving ability and its data generation capability. Two types of analyses were performed: a coarse-grained analysis using average scores across all settings, and a fine-grained analysis using individual scores per domain and generation setting. The results show weak correlations (low R-squared values) and lack statistical significance (p-values > 0.05). This suggests that a model’s problem-solving ability is a poor predictor of its data generation performance.
read the caption
Figure 4: Problem-solving and data generation capabilities do not strongly correlate: Linear regression between problem-solving ability and data generation ability scores at multiple granularity levels yields either low R2superscript𝑅2R^{2}italic_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT values (R2<0.1superscript𝑅20.1R^{2}<0.1italic_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT < 0.1) or non-significant relationships (p>0.05𝑝0.05p>0.05italic_p > 0.05), which indicates that it is hard to predict data generation capabilities only using problem-solving capabilities.

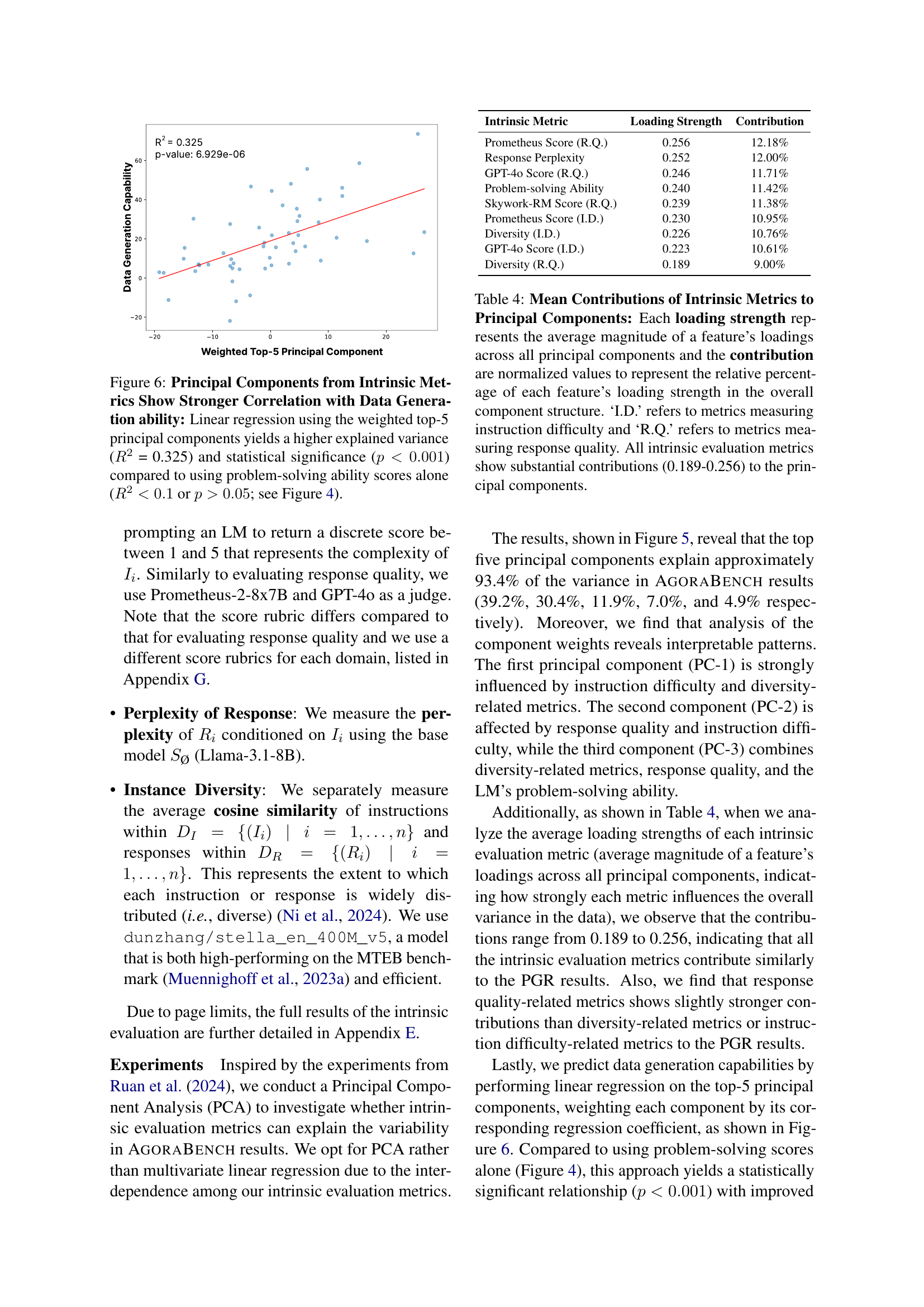
🔼 Principal Component Analysis (PCA) was performed on several intrinsic metrics to analyze the data generated by different large language models (LLMs). The PCA revealed that the top five principal components account for 93.4% of the variance in data generation capabilities. These components are interpretable and capture aspects like instruction difficulty, response quality, and diversity. This analysis indicates that a small number of key factors determine the effectiveness of an LLM for synthetic data generation.
read the caption
Figure 5: Through a PCA analysis on multiple intrinsic evaluation metrics, we find that there exists interpretable low-dimension principal components that explain the variance of data generation capabilities up to 93.4%.

🔼 This figure demonstrates that a linear regression model using the top five principal components derived from intrinsic data metrics achieves a significantly higher explained variance (R-squared = 0.325) and statistical significance (p<0.001) in predicting data generation capabilities compared to using problem-solving ability scores alone. The use of problem-solving ability scores alone resulted in either low R-squared values (less than 0.1) or insignificant results (p>0.05), highlighting the stronger predictive power of the intrinsic metrics. This suggests that analyzing intrinsic properties of generated data provides better insights into a language model’s effectiveness as a data generator.
read the caption
Figure 6: Principal Components from Intrinsic Metrics Show Stronger Correlation with Data Generation ability: Linear regression using the weighted top-5 principal components yields a higher explained variance (R2superscript𝑅2R^{2}italic_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT = 0.325) and statistical significance (p<0.001𝑝0.001p<0.001italic_p < 0.001) compared to using problem-solving ability scores alone (R2<0.1superscript𝑅20.1R^{2}<0.1italic_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT < 0.1 or p>0.05𝑝0.05p>0.05italic_p > 0.05; see Figure 4).

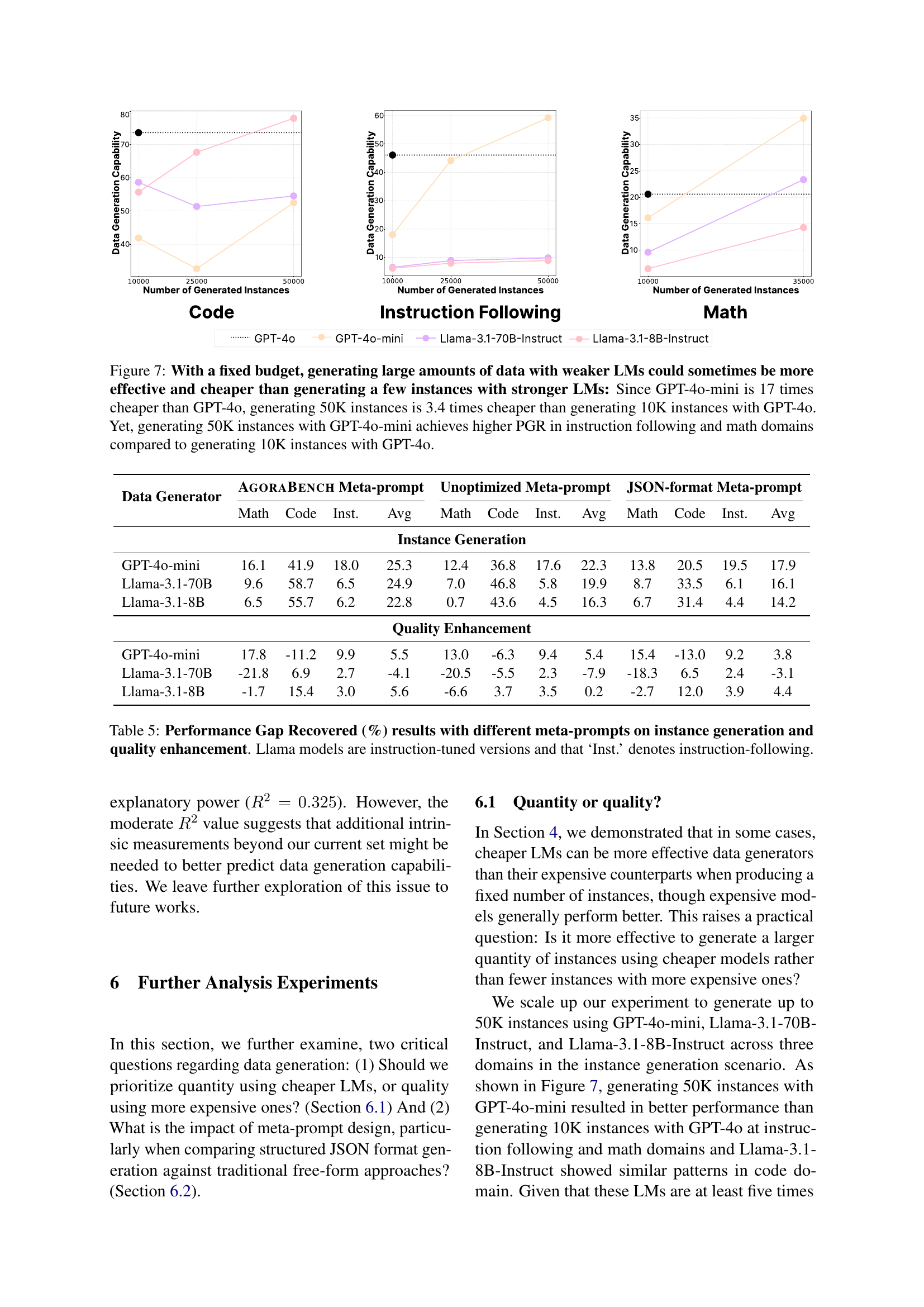
🔼 This figure compares the cost-effectiveness of using different language models (LMs) to generate synthetic training data. It shows that, while stronger models like GPT-4 might produce higher-quality data with fewer instances, weaker but cheaper models like GPT-4-mini can achieve comparable performance improvements (measured by Performance Gap Recovered or PGR) when generating a much larger dataset. The cost savings from using GPT-4-mini are substantial (17x cheaper than GPT-4), making it a more practical choice for certain scenarios, especially when considering the gains in instruction following and mathematical problem-solving tasks demonstrated in the graph. The x-axis shows the number of instances generated, and the y-axis displays the performance gain (PGR).
read the caption
Figure 7: With a fixed budget, generating large amounts of data with weaker LMs could sometimes be more effective and cheaper than generating a few instances with stronger LMs: Since GPT-4o-mini is 17 times cheaper than GPT-4o, generating 50K instances is 3.4 times cheaper than generating 10K instances with GPT-4o. Yet, generating 50K instances with GPT-4o-mini achieves higher PGR in instruction following and math domains compared to generating 10K instances with GPT-4o.
More on tables
| Data Generator | Math | Code | Inst. | Avg | Math | Code | Inst. | Avg | Math | Code | Inst. | Avg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
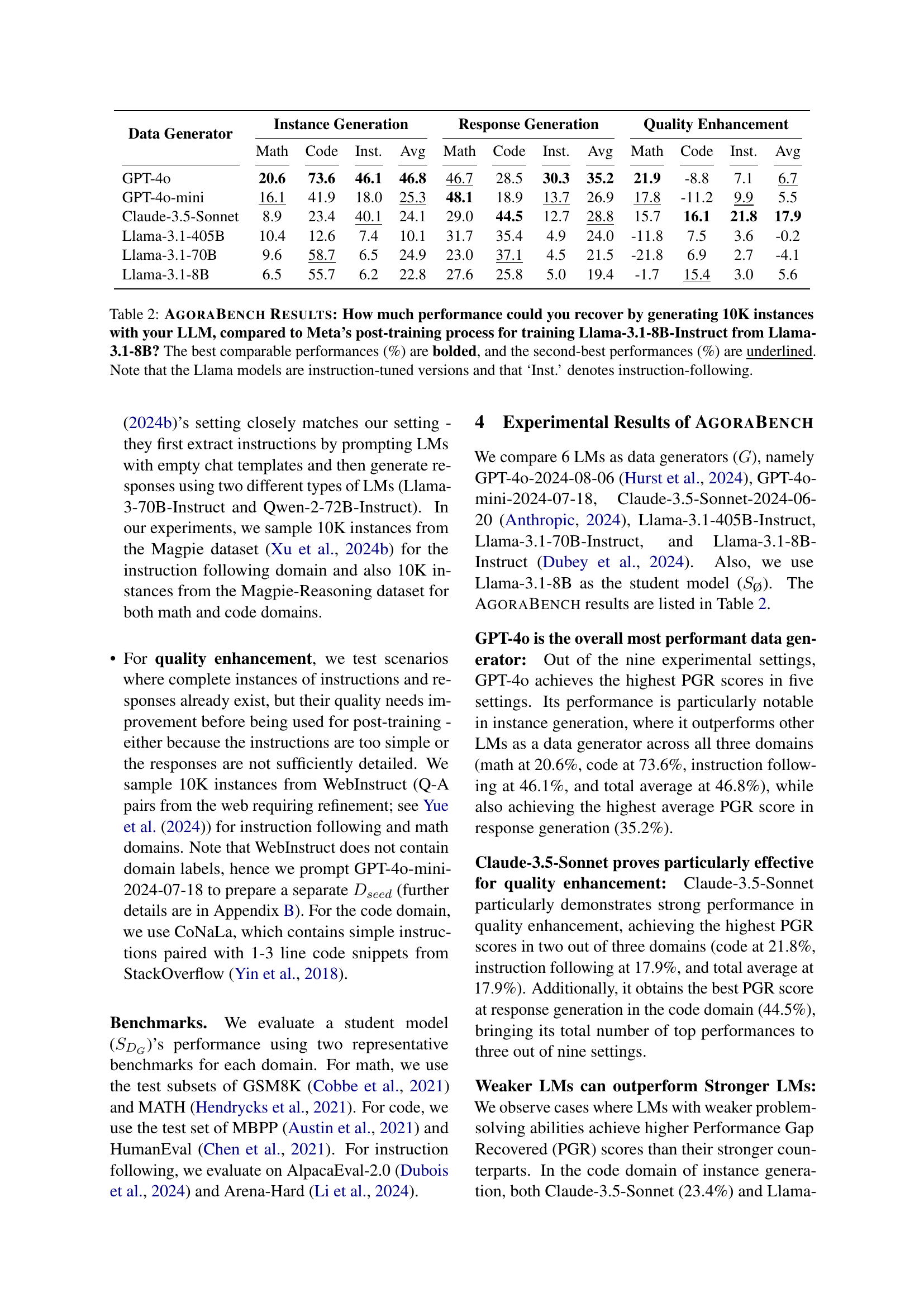
| GPT-4o | 20.6 | 73.6 | 46.1 | 46.8 | 46.7 | 28.5 | 30.3 | 35.2 | 21.9 | -8.8 | 7.1 | 6.7 |
| GPT-4o-mini | 16.1 | 41.9 | 18.0 | 25.3 | 48.1 | 18.9 | 13.7 | 26.9 | 17.8 | -11.2 | 9.9 | 5.5 |
| Claude-3.5-Sonnet | 8.9 | 23.4 | 40.1 | 24.1 | 29.0 | 44.5 | 12.7 | 28.8 | 15.7 | 16.1 | 21.8 | 17.9 |
| Llama-3.1-405B | 10.4 | 12.6 | 7.4 | 10.1 | 31.7 | 35.4 | 4.9 | 24.0 | -11.8 | 7.5 | 3.6 | -0.2 |
| Llama-3.1-70B | 9.6 | 58.7 | 6.5 | 24.9 | 23.0 | 37.1 | 4.5 | 21.5 | -21.8 | 6.9 | 2.7 | -4.1 |
| Llama-3.1-8B | 6.5 | 55.7 | 6.2 | 22.8 | 27.6 | 25.8 | 5.0 | 19.4 | -1.7 | 15.4 | 3.0 | 5.6 |
🔼 This table presents the results of the AGORABENCH benchmark, which evaluates the effectiveness of different Language Models (LLMs) in generating synthetic data for post-training. It shows the percentage improvement (Performance Gap Recovered or PGR) achieved by a student model (Llama-3.1-8B) trained on synthetic data generated by six different LLMs (GPT-40, GPT-40-mini, Claude-3.5-Sonnet, Llama-3.1-405B-Instruct, Llama-3.1-70B-Instruct, Llama-3.1-8B-Instruct) compared to the same model trained without synthetic data. The results are broken down by three data generation methods (instance generation, response generation, quality enhancement) and three domains (math, code, instruction following). The best and second-best performance for each LLM in each category are highlighted. Note that the Llama models used are instruction-tuned versions.
read the caption
Table 2: AgoraBench Results: How much performance could you recover by generating 10K instances with your LLM, compared to Meta’s post-training process for training Llama-3.1-8B-Instruct from Llama-3.1-8B? The best comparable performances (%) are bolded, and the second-best performances (%) are underlined. Note that the Llama models are instruction-tuned versions and that ‘Inst.’ denotes instruction-following.
| Data Generator | API Cost | Prob. | Data | |
|---|---|---|---|---|
| Solv. | Gen. | |||
| — | — | — | — | — |
| GPT-4o | $2.50 | $10.00 | 80.9 | 29.5% |
| GPT-4o-mini | $0.15 | $0.60 | 75.4 | 19.2% |
| Claude-3.5-Sonnet | $3.00 | $15.00 | 80.5 | 23.6% |
| Llama-3.1-405B | $1.79 | $1.79 | 75.0 | 11.3% |
| Llama-3.1-70B | $0.35 | $0.40 | 69.6 | 14.1% |
| Llama-3.1-8B | $0.055 | $0.055 | 50.2 | 15.9% |
🔼 This table compares the API costs, problem-solving abilities, and data generation capabilities of six different Language Models (LMs). It highlights that a more powerful or expensive LM does not automatically translate to better performance as a data generator. The table shows the average API cost (for generating data) for each LM, its average problem-solving score across various benchmarks (detailed in Appendix C), and its average data generation score from the AgoraBench benchmark (averaged from Table 2). This demonstrates the need to consider multiple factors when selecting an LM for data generation purposes and shows that even less expensive, less powerful models can be surprisingly effective at the task.
read the caption
Table 3: Comparison of API costs, problem-solving ability, and data generation ability: Our findings reveal that neither the strength nor the cost of an LM guarantees its effectiveness as a data generator. Note that the Llama models are instruction-tuned versions, the specific results of the LMs on each benchmark (averaged as ‘Problem Solving average’) is in Appendix C, and the AgoraBench results are averaged from Table 2.
| Intrinsic Metric | Loading Strength | Contribution |
|---|---|---|
| Prometheus Score (R.Q.) | 0.256 | 12.18% |
| Response Perplexity | 0.252 | 12.00% |
| GPT-4o Score (R.Q.) | 0.246 | 11.71% |
| Problem-solving Ability | 0.240 | 11.42% |
| Skywork-RM Score (R.Q.) | 0.239 | 11.38% |
| Prometheus Score (I.D.) | 0.230 | 10.95% |
| Diversity (I.D.) | 0.226 | 10.76% |
| GPT-4o Score (I.D.) | 0.223 | 10.61% |
| Diversity (R.Q.) | 0.189 | 9.00% |
🔼 Table 4 shows the contribution of different intrinsic evaluation metrics to the principal components derived from a principal component analysis (PCA). The ’loading strength’ represents the average magnitude of each metric’s influence across all principal components. The ‘contribution’ is the normalized percentage of each metric’s loading strength within the total variance explained by the principal components. Metrics related to instruction difficulty (I.D.) and response quality (R.Q.) are both significant contributors to the principal components, as indicated by the substantial loading strengths (0.189-0.256). This suggests that the combination of instruction difficulty and response quality are important factors in determining data generation capability.
read the caption
Table 4: Mean Contributions of Intrinsic Metrics to Principal Components: Each loading strength represents the average magnitude of a feature’s loadings across all principal components and the contribution are normalized values to represent the relative percentage of each feature’s loading strength in the overall component structure. ‘I.D.’ refers to metrics measuring instruction difficulty and ‘R.Q.’ refers to metrics measuring response quality. All intrinsic evaluation metrics show substantial contributions (0.189-0.256) to the principal components.
| Data Generator | AgoraBench Meta-prompt Math | AgoraBench Meta-prompt Code | AgoraBench Meta-prompt Inst. | AgoraBench Meta-prompt Avg | Unoptimized Meta-prompt Math | Unoptimized Meta-prompt Code | Unoptimized Meta-prompt Inst. | Unoptimized Meta-prompt Avg | JSON-format Meta-prompt Math | JSON-format Meta-prompt Code | JSON-format Meta-prompt Inst. | JSON-format Meta-prompt Avg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Instance Generation | ||||||||||||
| GPT-4o-mini | 16.1 | 41.9 | 18.0 | 25.3 | 12.4 | 36.8 | 17.6 | 22.3 | 13.8 | 20.5 | 19.5 | 17.9 |
| Llama-3.1-70B | 9.6 | 58.7 | 6.5 | 24.9 | 7.0 | 46.8 | 5.8 | 19.9 | 8.7 | 33.5 | 6.1 | 16.1 |
| Llama-3.1-8B | 6.5 | 55.7 | 6.2 | 22.8 | 0.7 | 43.6 | 4.5 | 16.3 | 6.7 | 31.4 | 4.4 | 14.2 |
| Quality Enhancement | ||||||||||||
| GPT-4o-mini | 17.8 | -11.2 | 9.9 | 5.5 | 13.0 | -6.3 | 9.4 | 5.4 | 15.4 | -13.0 | 9.2 | 3.8 |
| Llama-3.1-70B | -21.8 | 6.9 | 2.7 | -4.1 | -20.5 | -5.5 | 2.3 | -7.9 | -18.3 | 6.5 | 2.4 | -3.1 |
| Llama-3.1-8B | -1.7 | 15.4 | 3.0 | 5.6 | -6.6 | 3.7 | 3.5 | 0.2 | -2.7 | 12.0 | 3.9 | 4.4 |
🔼 This table presents the results of an experiment comparing the effectiveness of different meta-prompts when using language models to generate synthetic training data. The experiment focuses on two data generation methods: instance generation (creating new training examples) and quality enhancement (improving existing examples). The table shows the ‘Performance Gap Recovered (PGR)’ for each method, indicating how much the performance of a model trained on the synthetic data improved compared to a baseline model. Three different Language Models (LLMs), all instruction-tuned versions of Llama, are compared. Results are presented for three domains: math, code and instruction following. The performance is evaluated by calculating the percentage of the performance improvement (PGR).
read the caption
Table 5: Performance Gap Recovered (%) results with different meta-prompts on instance generation and quality enhancement. Llama models are instruction-tuned versions and that ‘Inst.’ denotes instruction-following.
| Inference Hyper-parameter | |
|---|---|
| Temperature | 0.2 (math) & 0.0 (other domains) |
| Top_p | 0.95 |
| Max New Tokens | 1024 |
| Repetition Penalty | 1.03 |
| Training Hyper-parameter | |
| — | — |
| Base Model | meta-llama/Llama-3.1-8B |
| Torch dtype | bfloat16 |
| Epoch | 5 |
| Max Seq Length | 4096 |
| Learning Rate | 1e-5 |
| Train Batch Size | 4 |
| Gradient Accumulation | 8 |
| GPU | H100 (80GB) x 4 |
| Random Seed | 42 |
| Training Method | Supervised Fine-tuning |
🔼 This table details the hyperparameters employed during the inference stage of the AGORABENCH experiments. It lists values for parameters such as temperature, top_p, maximum new tokens, and repetition penalty, offering a clear view of the settings used for generating predictions from the language models.
read the caption
Table 6: Hyper-parameters used for inference.
| Data Generator | GSM8K | MATH | MBPP | Human | Alpaca | Arena | Average |
|---|---|---|---|---|---|---|---|
| GPT-4o | 96.1 | 76.6 | 86.2 | 91.5 | 57.5 | 77.9 | 80.9 |
| GPT-4o-mini | 93.2 | 70.2 | 85.7 | 88.4 | 50.7 | 64.2 | 75.4 |
| Claude-3.5-Sonnet | 96.4 | 71.1 | 89.2 | 92.0 | 52.4 | 82.0 | 80.5 |
| Llama-3.1-405B | 96.8 | 73.8 | 84.5 | 89.0 | 39.3 | 66.8 | 75.0 |
| Llama-3.1-70B | 95.1 | 68.0 | 84.2 | 80.5 | 38.1 | 51.6 | 69.6 |
| Llama-3.1-8B | 78.9 | 34.6 | 68.5 | 69.5 | 24.2 | 25.5 | 50.2 |
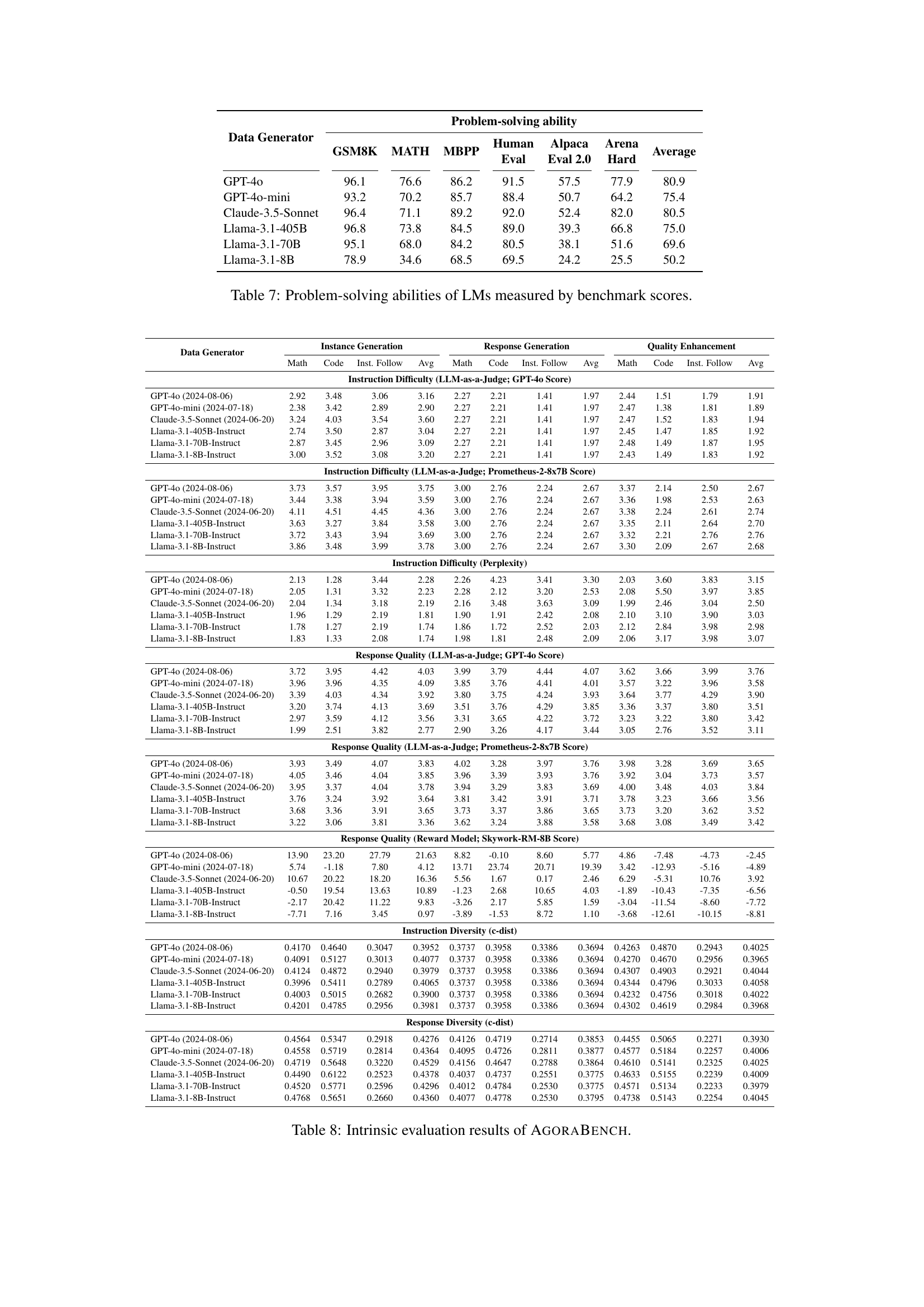
🔼 This table presents the problem-solving capabilities of six different Large Language Models (LLMs) across six benchmark datasets. The benchmarks cover three domains: mathematics (GSM8K, MATH), code (MBPP, HumanEval), and instruction following (AlpacaEval 2.0, Arena-Hard). The scores represent the percentage of correct answers each LLM achieved on each benchmark, providing a comprehensive assessment of their problem-solving abilities across various tasks and complexities.
read the caption
Table 7: Problem-solving abilities of LMs measured by benchmark scores.
| Data Generator | Math | Code | Inst. Follow | Avg | Math | Code | Inst. Follow | Avg | Math | Code | Inst. Follow | Avg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Instruction Difficulty (LLM-as-a-Judge; GPT-4o Score) | |||||||||||||
| GPT-4o (2024-08-06) | 2.92 | 3.48 | 3.06 | 3.16 | 2.27 | 2.21 | 1.41 | 1.97 | 2.44 | 1.51 | 1.79 | 1.91 | |
| GPT-4o-mini (2024-07-18) | 2.38 | 3.42 | 2.89 | 2.90 | 2.27 | 2.21 | 1.41 | 1.97 | 2.47 | 1.38 | 1.81 | 1.89 | |
| Claude-3.5-Sonnet (2024-06-20) | 3.24 | 4.03 | 3.54 | 3.60 | 2.27 | 2.21 | 1.41 | 1.97 | 2.47 | 1.52 | 1.83 | 1.94 | |
| Llama-3.1-405B-Instruct | 2.74 | 3.50 | 2.87 | 3.04 | 2.27 | 2.21 | 1.41 | 1.97 | 2.45 | 1.47 | 1.85 | 1.92 | |
| Llama-3.1-70B-Instruct | 2.87 | 3.45 | 2.96 | 3.09 | 2.27 | 2.21 | 1.41 | 1.97 | 2.48 | 1.49 | 1.87 | 1.95 | |
| Llama-3.1-8B-Instruct | 3.00 | 3.52 | 3.08 | 3.20 | 2.27 | 2.21 | 1.41 | 1.97 | 2.43 | 1.49 | 1.83 | 1.92 | |
| Instruction Difficulty (LLM-as-a-Judge; Prometheus-2-8x7B Score) | |||||||||||||
| GPT-4o (2024-08-06) | 3.73 | 3.57 | 3.95 | 3.75 | 3.00 | 2.76 | 2.24 | 2.67 | 3.37 | 2.14 | 2.50 | 2.67 | |
| GPT-4o-mini (2024-07-18) | 3.44 | 3.38 | 3.94 | 3.59 | 3.00 | 2.76 | 2.24 | 2.67 | 3.36 | 1.98 | 2.53 | 2.63 | |
| Claude-3.5-Sonnet (2024-06-20) | 4.11 | 4.51 | 4.45 | 4.36 | 3.00 | 2.76 | 2.24 | 2.67 | 3.38 | 2.24 | 2.61 | 2.74 | |
| Llama-3.1-405B-Instruct | 3.63 | 3.27 | 3.84 | 3.58 | 3.00 | 2.76 | 2.24 | 2.67 | 3.35 | 2.11 | 2.64 | 2.70 | |
| Llama-3.1-70B-Instruct | 3.72 | 3.43 | 3.94 | 3.69 | 3.00 | 2.76 | 2.24 | 2.67 | 3.32 | 2.21 | 2.76 | 2.76 | |
| Llama-3.1-8B-Instruct | 3.86 | 3.48 | 3.99 | 3.78 | 3.00 | 2.76 | 2.24 | 2.67 | 3.30 | 2.09 | 2.67 | 2.68 | |
| Instruction Difficulty (Perplexity) | |||||||||||||
| GPT-4o (2024-08-06) | 2.13 | 1.28 | 3.44 | 2.28 | 2.26 | 4.23 | 3.41 | 3.30 | 2.03 | 3.60 | 3.83 | 3.15 | |
| GPT-4o-mini (2024-07-18) | 2.05 | 1.31 | 3.32 | 2.23 | 2.28 | 2.12 | 3.20 | 2.53 | 2.08 | 5.50 | 3.97 | 3.85 | |
| Claude-3.5-Sonnet (2024-06-20) | 2.04 | 1.34 | 3.18 | 2.19 | 2.16 | 3.48 | 3.63 | 3.09 | 1.99 | 2.46 | 3.04 | 2.50 | |
| Llama-3.1-405B-Instruct | 1.96 | 1.29 | 2.19 | 1.81 | 1.90 | 1.91 | 2.42 | 2.08 | 2.10 | 3.10 | 3.90 | 3.03 | |
| Llama-3.1-70B-Instruct | 1.78 | 1.27 | 2.19 | 1.74 | 1.86 | 1.72 | 2.52 | 2.03 | 2.12 | 2.84 | 3.98 | 2.98 | |
| Llama-3.1-8B-Instruct | 1.83 | 1.33 | 2.08 | 1.74 | 1.98 | 1.81 | 2.48 | 2.09 | 2.06 | 3.17 | 3.98 | 3.07 | |
| Response Quality (LLM-as-a-Judge; GPT-4o Score) | |||||||||||||
| GPT-4o (2024-08-06) | 3.72 | 3.95 | 4.42 | 4.03 | 3.99 | 3.79 | 4.44 | 4.07 | 3.62 | 3.66 | 3.99 | 3.76 | |
| GPT-4o-mini (2024-07-18) | 3.96 | 3.96 | 4.35 | 4.09 | 3.85 | 3.76 | 4.41 | 4.01 | 3.57 | 3.22 | 3.96 | 3.58 | |
| Claude-3.5-Sonnet (2024-06-20) | 3.39 | 4.03 | 4.34 | 3.92 | 3.80 | 3.75 | 4.24 | 3.93 | 3.64 | 3.77 | 4.29 | 3.90 | |
| Llama-3.1-405B-Instruct | 3.20 | 3.74 | 4.13 | 3.69 | 3.51 | 3.76 | 4.29 | 3.85 | 3.36 | 3.37 | 3.80 | 3.51 | |
| Llama-3.1-70B-Instruct | 2.97 | 3.59 | 4.12 | 3.56 | 3.31 | 3.65 | 4.22 | 3.72 | 3.23 | 3.22 | 3.80 | 3.42 | |
| Llama-3.1-8B-Instruct | 1.99 | 2.51 | 3.82 | 2.77 | 2.90 | 3.26 | 4.17 | 3.44 | 3.05 | 2.76 | 3.52 | 3.11 | |
| Response Quality (LLM-as-a-Judge; Prometheus-2-8x7B Score) | |||||||||||||
| GPT-4o (2024-08-06) | 3.93 | 3.49 | 4.07 | 3.83 | 4.02 | 3.28 | 3.97 | 3.76 | 3.98 | 3.28 | 3.69 | 3.65 | |
| GPT-4o-mini (2024-07-18) | 4.05 | 3.46 | 4.04 | 3.85 | 3.96 | 3.39 | 3.93 | 3.76 | 3.92 | 3.04 | 3.73 | 3.57 | |
| Claude-3.5-Sonnet (2024-06-20) | 3.95 | 3.37 | 4.04 | 3.78 | 3.94 | 3.29 | 3.83 | 3.69 | 4.00 | 3.48 | 4.03 | 3.84 | |
| Llama-3.1-405B-Instruct | 3.76 | 3.24 | 3.92 | 3.64 | 3.81 | 3.42 | 3.91 | 3.71 | 3.78 | 3.23 | 3.66 | 3.56 | |
| Llama-3.1-70B-Instruct | 3.68 | 3.36 | 3.91 | 3.65 | 3.73 | 3.37 | 3.86 | 3.65 | 3.73 | 3.20 | 3.62 | 3.52 | |
| Llama-3.1-8B-Instruct | 3.22 | 3.06 | 3.81 | 3.36 | 3.62 | 3.24 | 3.88 | 3.58 | 3.68 | 3.08 | 3.49 | 3.42 | |
| Response Quality (Reward Model; Skywork-RM-8B Score) | |||||||||||||
| GPT-4o (2024-08-06) | 13.90 | 23.20 | 27.79 | 21.63 | 8.82 | -0.10 | 8.60 | 5.77 | 4.86 | -7.48 | -4.73 | -2.45 | |
| GPT-4o-mini (2024-07-18) | 5.74 | -1.18 | 7.80 | 4.12 | 13.71 | 23.74 | 20.71 | 19.39 | 3.42 | -12.93 | -5.16 | -4.89 | |
| Claude-3.5-Sonnet (2024-06-20) | 10.67 | 20.22 | 18.20 | 16.36 | 5.56 | 1.67 | 0.17 | 2.46 | 6.29 | -5.31 | 10.76 | 3.92 | |
| Llama-3.1-405B-Instruct | -0.50 | 19.54 | 13.63 | 10.89 | -1.23 | 2.68 | 10.65 | 4.03 | -1.89 | -10.43 | -7.35 | -6.56 | |
| Llama-3.1-70B-Instruct | -2.17 | 20.42 | 11.22 | 9.83 | -3.26 | 2.17 | 5.85 | 1.59 | -3.04 | -11.54 | -8.60 | -7.72 | |
| Llama-3.1-8B-Instruct | -7.71 | 7.16 | 3.45 | 0.97 | -3.89 | -1.53 | 8.72 | 1.10 | -3.68 | -12.61 | -10.15 | -8.81 | |
| Instruction Diversity (c-dist) | |||||||||||||
| GPT-4o (2024-08-06) | 0.4170 | 0.4640 | 0.3047 | 0.3952 | 0.3737 | 0.3958 | 0.3386 | 0.3694 | 0.4263 | 0.4870 | 0.2943 | 0.4025 | |
| GPT-4o-mini (2024-07-18) | 0.4091 | 0.5127 | 0.3013 | 0.4077 | 0.3737 | 0.3958 | 0.3386 | 0.3694 | 0.4270 | 0.4670 | 0.2956 | 0.3965 | |
| Claude-3.5-Sonnet (2024-06-20) | 0.4124 | 0.4872 | 0.2940 | 0.3979 | 0.3737 | 0.3958 | 0.3386 | 0.3694 | 0.4307 | 0.4903 | 0.2921 | 0.4044 | |
| Llama-3.1-405B-Instruct | 0.3996 | 0.5411 | 0.2789 | 0.4065 | 0.3737 | 0.3958 | 0.3386 | 0.3694 | 0.4344 | 0.4796 | 0.3033 | 0.4058 | |
| Llama-3.1-70B-Instruct | 0.4003 | 0.5015 | 0.2682 | 0.3900 | 0.3737 | 0.3958 | 0.3386 | 0.3694 | 0.4232 | 0.4756 | 0.3018 | 0.4022 | |
| Llama-3.1-8B-Instruct | 0.4201 | 0.4785 | 0.2956 | 0.3981 | 0.3737 | 0.3958 | 0.3386 | 0.3694 | 0.4302 | 0.4619 | 0.2984 | 0.3968 | |
| Response Diversity (c-dist) | |||||||||||||
| GPT-4o (2024-08-06) | 0.4564 | 0.5347 | 0.2918 | 0.4276 | 0.4126 | 0.4719 | 0.2714 | 0.3853 | 0.4455 | 0.5065 | 0.2271 | 0.3930 | |
| GPT-4o-mini (2024-07-18) | 0.4558 | 0.5719 | 0.2814 | 0.4364 | 0.4095 | 0.4726 | 0.2811 | 0.3877 | 0.4577 | 0.5184 | 0.2257 | 0.4006 | |
| Claude-3.5-Sonnet (2024-06-20) | 0.4719 | 0.5648 | 0.3220 | 0.4529 | 0.4156 | 0.4647 | 0.2788 | 0.3864 | 0.4610 | 0.5141 | 0.2325 | 0.4025 | |
| Llama-3.1-405B-Instruct | 0.4490 | 0.6122 | 0.2523 | 0.4378 | 0.4037 | 0.4737 | 0.2551 | 0.3775 | 0.4633 | 0.5155 | 0.2239 | 0.4009 | |
| Llama-3.1-70B-Instruct | 0.4520 | 0.5771 | 0.2596 | 0.4296 | 0.4012 | 0.4784 | 0.2530 | 0.3775 | 0.4571 | 0.5134 | 0.2233 | 0.3979 | |
| Llama-3.1-8B-Instruct | 0.4768 | 0.5651 | 0.2660 | 0.4360 | 0.4077 | 0.4778 | 0.2530 | 0.3795 | 0.4738 | 0.5143 | 0.2254 | 0.4045 |
🔼 Table 8 presents the detailed results of the intrinsic evaluation conducted as part of the AgoraBench benchmark. It shows the values for several metrics across different large language models (LLMs) and for three data generation methods (instance generation, response generation, quality enhancement). The metrics include those assessing instruction difficulty (using LLM-as-a-judge scores from both GPT-40 and Prometheus-2-8x7B, and perplexity) and response quality (LLM-as-a-judge scores from GPT-40 and Prometheus-2-8x7B, and Skywork-RM score), as well as instruction and response diversity (using cosine distance). The table offers a granular view of the data quality generated by each LLM, facilitating a deeper understanding of their strengths and weaknesses in various data generation tasks.
read the caption
Table 8: Intrinsic evaluation results of AgoraBench.
Full paper#