↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large Language Models (LLMs) are rapidly advancing, but scaling up model size to enhance performance poses significant challenges in efficiency and deployment. Current scaling laws primarily focus on the relationship between model size and performance, often overlooking the critical aspect of cost-effectiveness. This results in unsustainable scaling trends and hinders the adoption of LLMs in resource-constrained environments.
This research introduces a new metric called ‘capacity density’ to evaluate LLMs more comprehensively. Capacity density considers both the actual parameter size and the effective parameter size needed to achieve comparable performance. The study reveals a novel empirical law, the ‘Densing Law,’ which shows an exponential increase in maximum capacity density. This Densing Law provides valuable insights into the development of more efficient LLMs by emphasizing the importance of improving model density rather than simply increasing parameter size. The findings suggest that inference costs can be significantly reduced through efficient model design, leading to cost-effective large language models.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces a novel metric, ‘capacity density,’ to evaluate LLMs, addressing the limitations of solely focusing on parameter size. It reveals the exponential growth of LLM capacity density, leading to exponentially decreasing inference costs and providing valuable guidance for future LLM development. This is highly relevant to the current research trends in efficient LLM design and deployment.
Visual Insights#

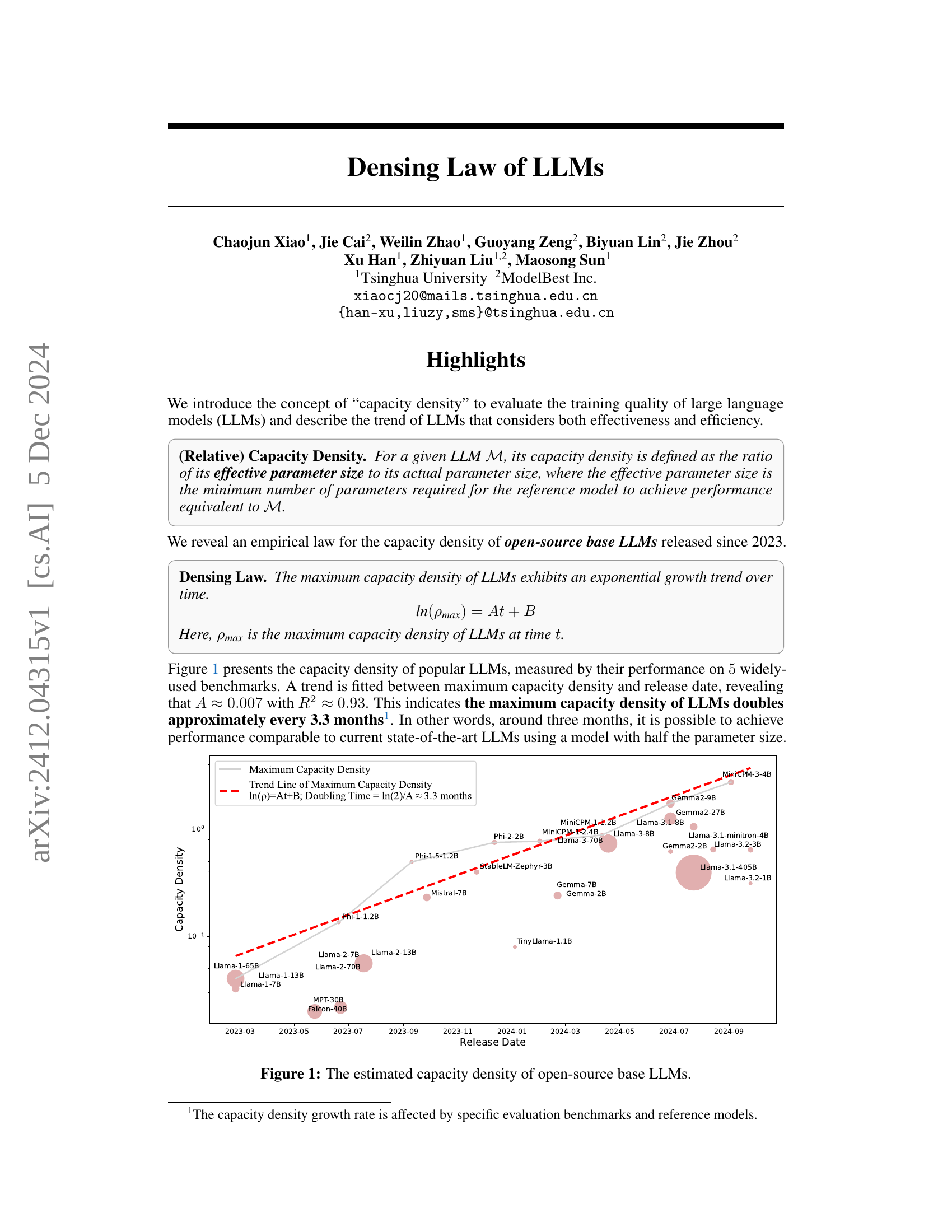
🔼 This figure shows the estimated capacity density of various open-source base Large Language Models (LLMs) released since early 2023. Capacity density is a new metric introduced in the paper to evaluate the training quality of LLMs by considering both effectiveness and efficiency. It’s calculated as the ratio of a model’s effective parameter size (the minimum number of parameters needed to achieve the same performance as the model) to its actual parameter size. The figure plots the capacity density against the release date of each LLM, revealing an exponential growth trend which the authors call the ‘Densing Law’. This trend indicates a doubling of maximum capacity density roughly every 3.3 months. Different LLMs are represented by different colored circles, with their sizes possibly corresponding to parameter size or another relevant model characteristic. A trendline is fitted to the data points to visually demonstrate the exponential growth.
read the caption
Figure 1: The estimated capacity density of open-source base LLMs.
| Name | # Para | BS | nlayer | d | dffn | dhead | nhead | nkv |
|---|---|---|---|---|---|---|---|---|
| 0.005B | 5,247,232 | 32 | 8 | 256 | 640 | 64 | 4 | 1 |
| 0.03B | 31,470,080 | 32 | 12 | 512 | 1,280 | 64 | 8 | 2 |
| 0.1B | 106,196,736 | 64 | 18 | 768 | 1,920 | 64 | 12 | 3 |
| 0.2B | 245,416,960 | 128 | 24 | 1,024 | 2,560 | 64 | 16 | 2 |
| 0.4B | 476,852,480 | 256 | 30 | 1,280 | 3,200 | 64 | 20 | 2 |
| 0.8B | 828,225,024 | 512 | 36 | 1,536 | 3,840 | 64 | 24 | 3 |
🔼 This table details the hyperparameters used in training the smaller language models that were used to estimate the loss function in the paper’s experiments. These smaller models served as a basis for calculating the effective parameter size of larger LLMs, a key part of the paper’s capacity density metric. The hyperparameters listed include the number of parameters, batch size, number of layers, dimension of the hidden layer, inner dimension of the feedforward network, number of attention heads, and other model details.
read the caption
Table 1: The detailed hyper-parameters of small models trained for loss estimation.
In-depth insights#
LLM Capacity Density#
The concept of “LLM Capacity Density” introduces a crucial metric for evaluating the efficiency and effectiveness of large language models (LLMs). It moves beyond simply focusing on parameter size, instead measuring the ratio of a model’s effective parameter size (the minimum parameters needed to achieve comparable performance) to its actual parameter size. Higher capacity density signifies better training quality, indicating more efficient use of resources. The authors propose a novel “Densing Law,” suggesting an exponential growth in maximum capacity density over time. This implies that future LLMs can achieve state-of-the-art performance with significantly fewer parameters, leading to exponentially decreasing inference costs. The Densing Law, therefore, offers valuable insights for guiding future LLM research and development, encouraging a shift towards density-optimal training, prioritizing cost-effective models and enabling deployment on resource-constrained devices. This contrasts with the historical emphasis on solely scaling model size to increase performance, and offers a more sustainable and environmentally friendly approach to LLM development.
Densing Law Trend#
The “Densing Law Trend” in the research paper reveals a rapid increase in the capacity density of Large Language Models (LLMs). Capacity density, a key metric introduced in the paper, represents the ratio of a model’s effective parameter size (minimum parameters needed for equivalent performance) to its actual parameter size. The exponential growth observed suggests a significant shift in LLM development, prioritizing efficiency and effectiveness simultaneously. This trend isn’t merely about scaling up model size, but rather about achieving superior performance with fewer parameters. This is substantiated by the doubling of capacity density approximately every three months. The paper highlights implications like exponentially decreasing inference costs, making LLMs more accessible and cost-effective. The accelerated growth rate after ChatGPT’s release is also notable, attributed to increased investment and the availability of high-quality open-source models. However, the paper cautions that simply compressing models doesn’t always improve density; efficient training methodologies are crucial. Therefore, the “Densing Law” emphasizes a paradigm shift towards density-optimal training, where minimizing computational costs is paramount, leading to a more sustainable and environmentally friendly approach to LLM development.
Inference Cost Drop#
The research paper reveals a significant drop in inference costs for large language models (LLMs), a trend linked to the exponential growth in model density. This ‘Densing Law’ shows that the ratio of a model’s effective parameter size to its actual size doubles approximately every three months. As a result, equivalent performance can be achieved with significantly fewer parameters, thus reducing the computational resources needed for inference. This decrease is further amplified by concurrent advancements in hardware, as Moore’s Law continues to increase computing power, resulting in a faster-than-expected drop in inference costs. The paper underscores the importance of prioritizing density improvement in LLM development, shifting focus from simply increasing model size to achieving optimal performance with minimal computational overhead. The cost decrease is not solely attributed to improved algorithms; it’s also a product of advancements in computing hardware and infrastructure, emphasizing the interplay between software and hardware advancements. This synergy of efficiency gains from both areas creates a synergistic effect leading to substantially reduced inference costs, making LLMs more accessible and sustainable for diverse applications.
Density Evaluation#
Density evaluation in the context of large language models (LLMs) is crucial for assessing the effectiveness and efficiency of training. A key challenge is the multifaceted nature of LLM capabilities, making a singular metric insufficient. A comprehensive approach involves multiple benchmarks to evaluate various aspects of LLM performance, such as reasoning, knowledge, and code generation. However, benchmark selection significantly impacts results, necessitating a diverse set and a cautious interpretation. Another critical aspect is the evaluation of both effectiveness and efficiency. While achieving high performance is desirable, it is equally important to do so with minimal computational resources. Capacity density, which balances both aspects, emerges as a key metric. The development of appropriate evaluation datasets and metrics continues to evolve with LLMs. Future directions include improving the robustness and fairness of evaluations, addressing data biases, and encompassing multimodal LLMs.
Future of LLMs#
The future of LLMs is bright but multifaceted. Densing Law, as introduced in the research, suggests an exponential increase in model efficiency, implying that future LLMs will achieve comparable performance with significantly fewer parameters. This trend is driven by algorithmic improvements, improved training techniques, and advancements in hardware. However, challenges remain. Accurate capacity measurement currently relies on benchmarks which might not comprehensively capture the capabilities of LLMs, especially as they advance. Moreover, the field needs to move beyond solely focusing on language models and explore multi-modal LLMs. Finally, the economic aspects, specifically the shift towards density-optimal training, will drive the focus from mere performance improvement to cost-effective solutions, impacting both research and deployment strategies, leading to sustainable scaling.
More visual insights#
More on figures

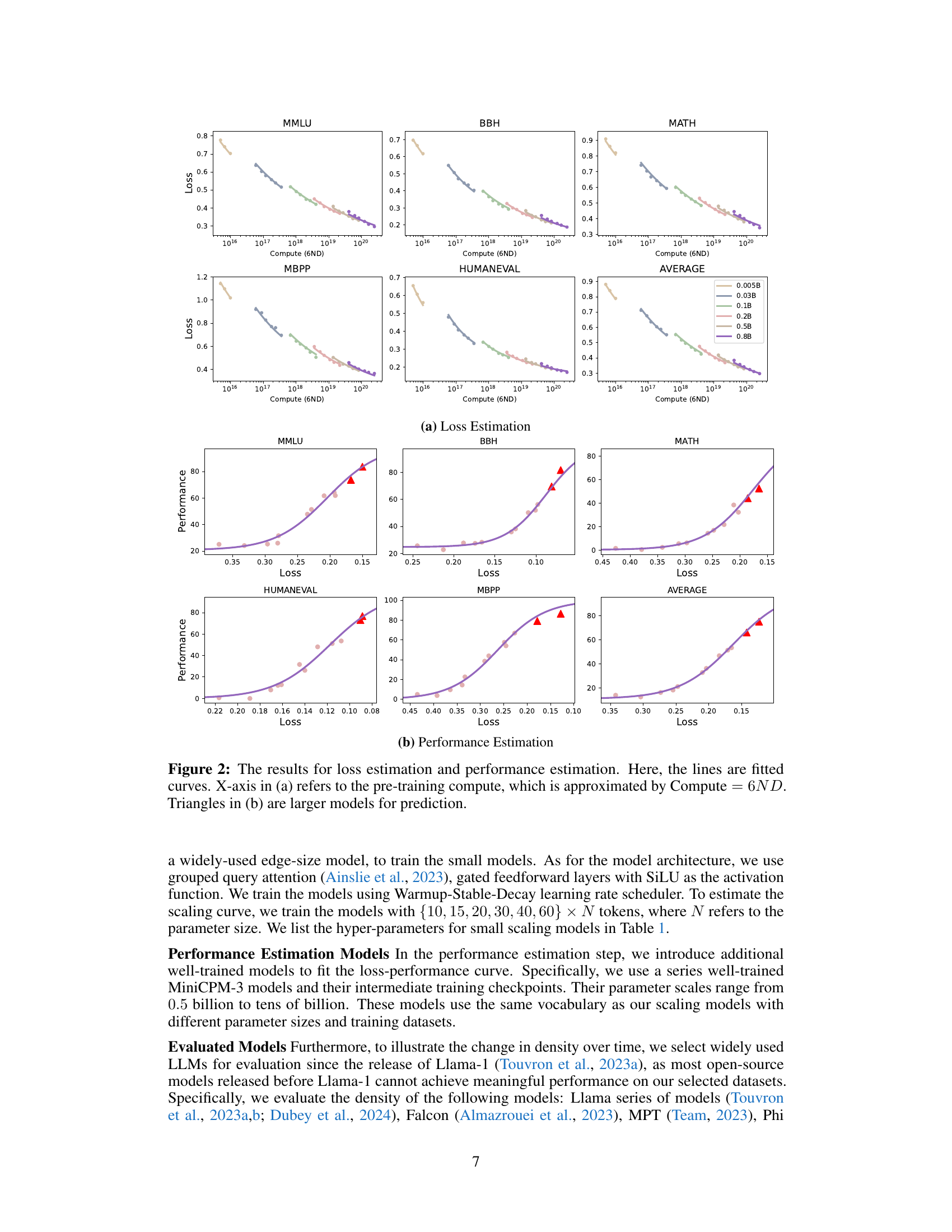
🔼 This figure shows the results of the loss estimation step in the two-step estimation approach used to calculate LLM density. The left panel (a) displays the relationship between the language model loss and the pre-training compute (represented as 6ND), which is fitted using a power-law function (L = aN^α + bD^-β). Separate curves are shown for different downstream tasks (MMLU, BBH, MATH, HumanEval, MBPP, and the average across all tasks). The x-axis represents the pre-training compute and the y-axis shows the language modeling loss. Each curve depicts how the language model loss changes with increasing compute for the specific task.
read the caption
(a) Loss Estimation

🔼 Figure 2(b) displays the results of the performance estimation step in a two-step process for predicting downstream task performance. The first step uses scaling laws to estimate language modeling loss, and the second step uses this loss to predict actual performance. The plot shows the fitted curves for multiple downstream tasks (MMLU, BBH, MATH, HumanEval, MBPP, and their average). Triangles represent the performance of larger models (those with more than 4 billion parameters) that were used for prediction, demonstrating the effectiveness of the two-step estimation approach for predicting the performance of significantly larger models based on smaller ones.
read the caption
(b) Performance Estimation

🔼 Figure 2 presents the results of a two-step estimation process used to predict the performance of downstream tasks based on the pre-training loss. Panel (a) shows the loss estimation, plotting the relationship between pre-training computational cost (approximated by Compute = 6ND, where N is the number of parameters and D is the number of training tokens) and the pre-training loss for several smaller models. The lines represent fitted curves for this relationship. Panel (b) displays the performance estimation, showing the relationship between pre-training loss and downstream task performance. The lines are fitted curves based on the smaller models. The triangles represent larger models used for prediction, demonstrating the effectiveness of the model in predicting performance based on pre-training loss. These plots showcase the process of using scaling laws to estimate the effective parameter size and the density of LLMs.
read the caption
Figure 2: The results for loss estimation and performance estimation. Here, the lines are fitted curves. X-axis in (a) refers to the pre-training compute, which is approximated by Compute=6NDCompute6𝑁𝐷\text{Compute}=6NDCompute = 6 italic_N italic_D. Triangles in (b) are larger models for prediction.

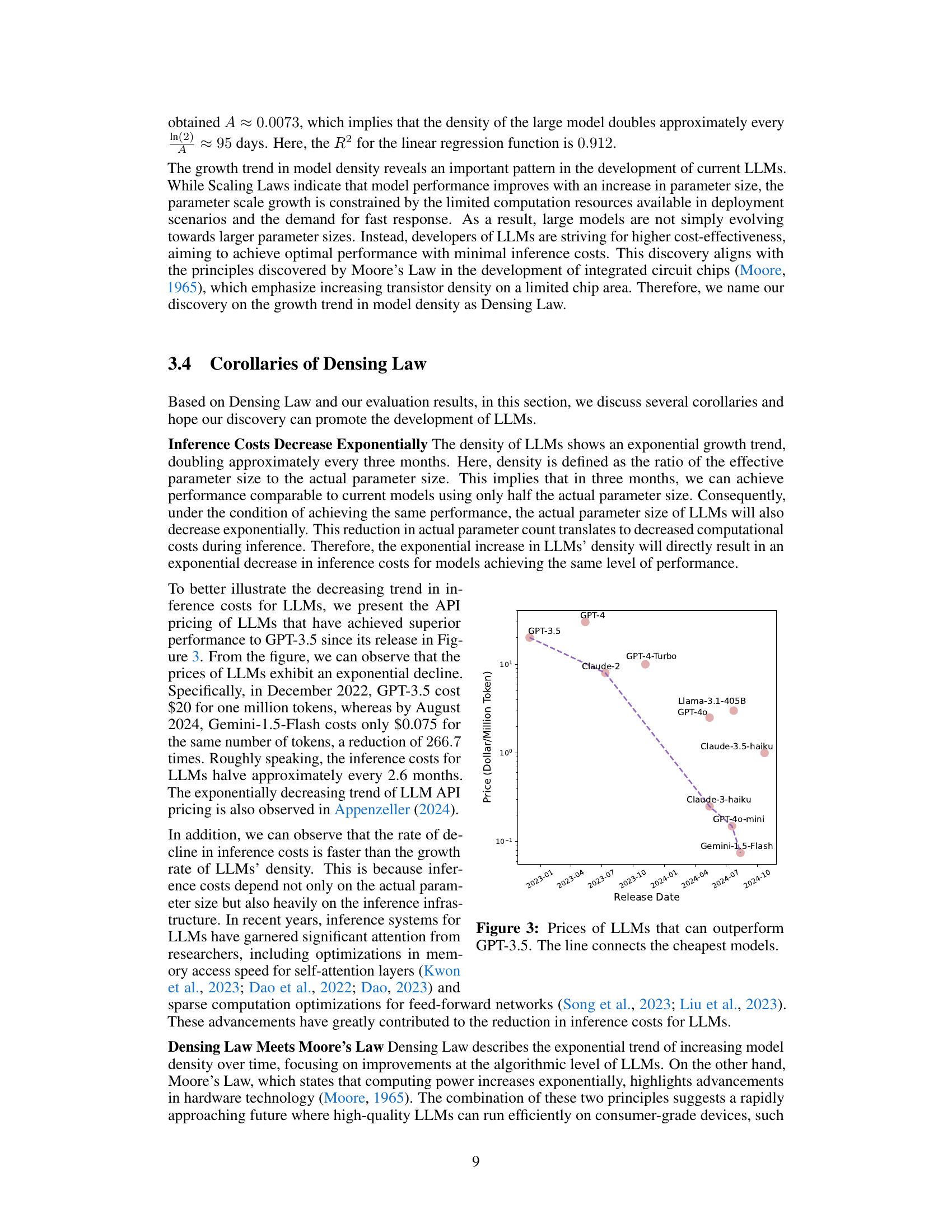
🔼 This figure shows the price trend of Large Language Models (LLMs) that surpass the performance of GPT-3.5. The y-axis represents the price per million tokens, and the x-axis denotes the release date. The data points represent various models, and a line is drawn to connect the lowest price point at each time interval. This visually demonstrates how the cost of accessing high-performance LLMs has decreased over time.
read the caption
Figure 3: Prices of LLMs that can outperform GPT-3.5. The line connects the cheapest models.

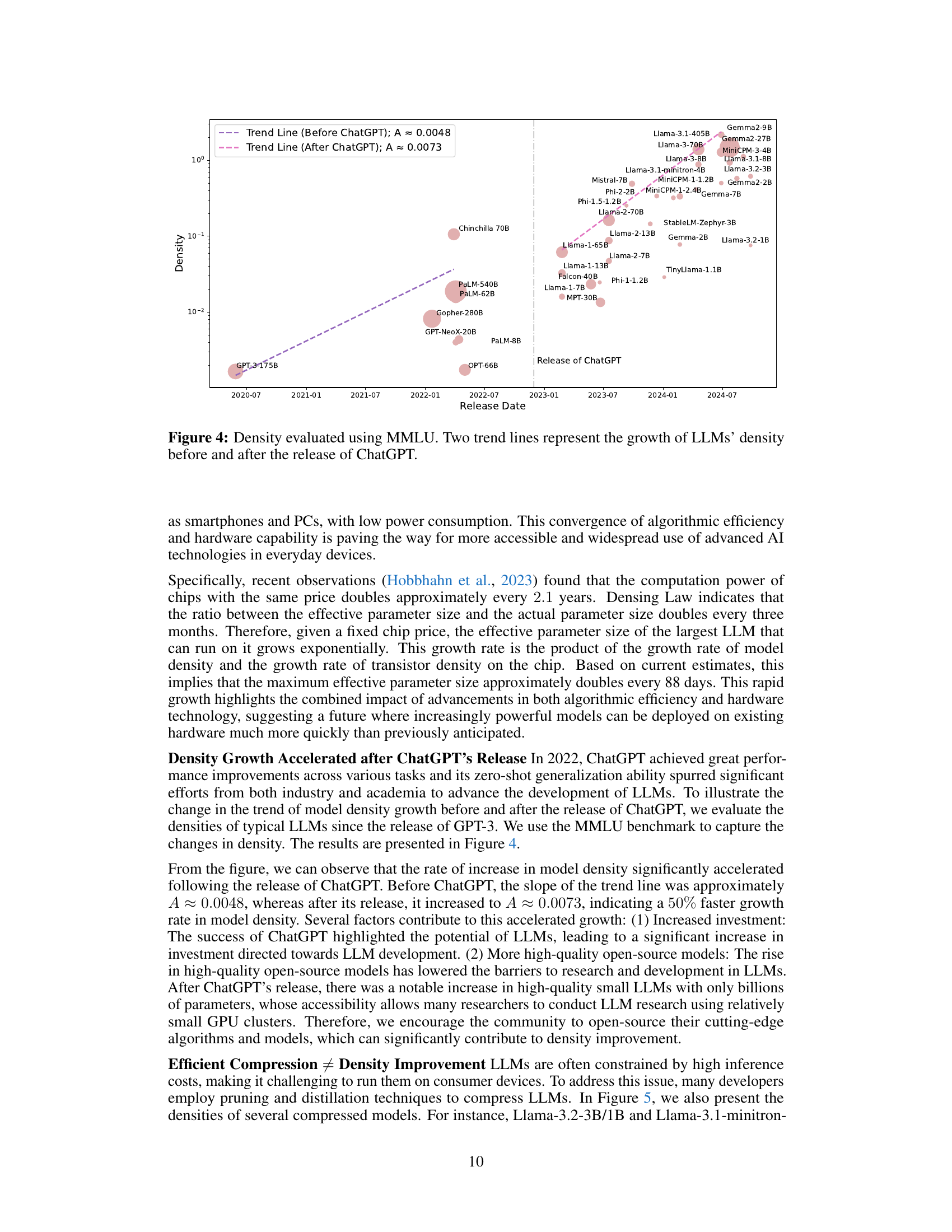
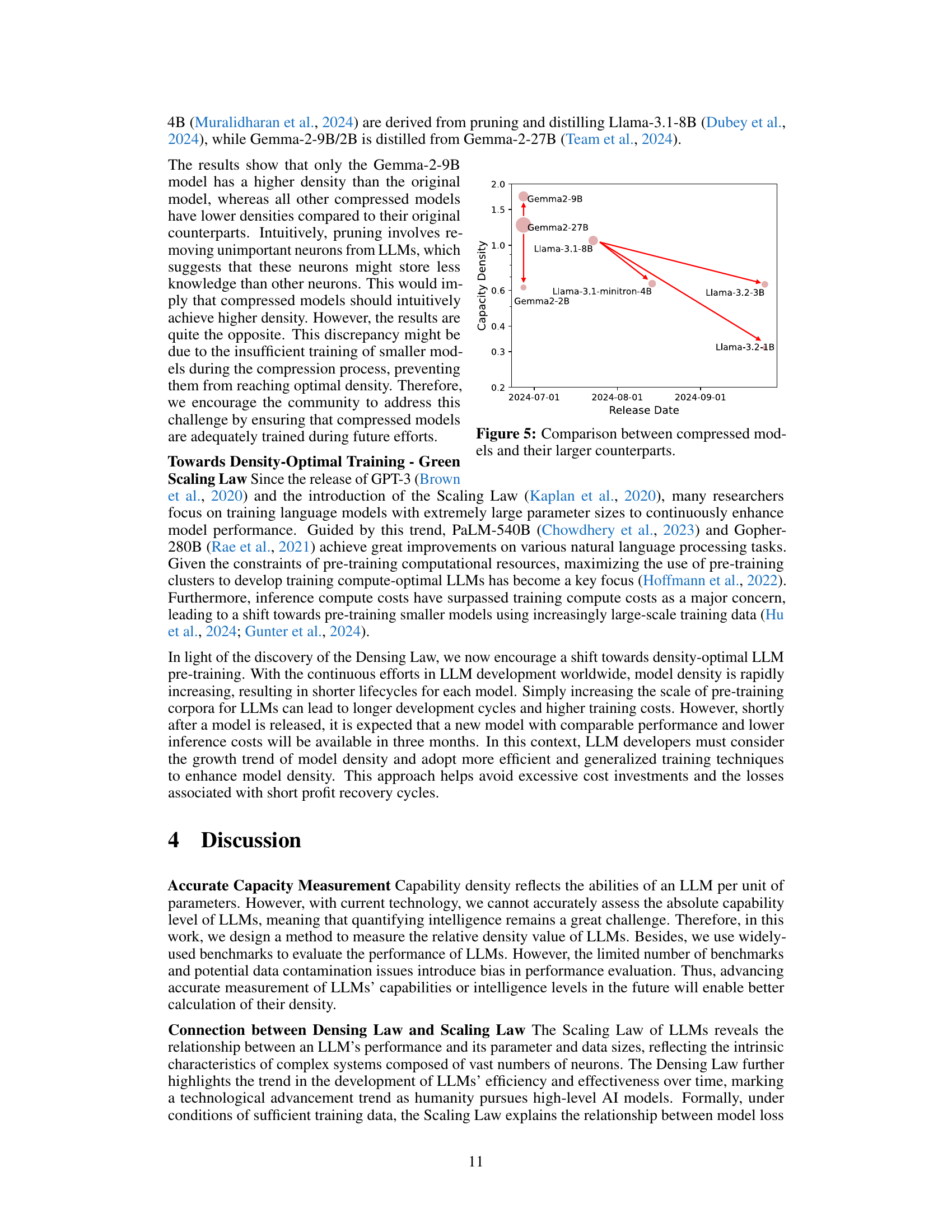
🔼 Figure 4 presents the capacity density of various LLMs evaluated using the MMLU benchmark. The x-axis represents the release date of the models, and the y-axis shows the capacity density. Two trend lines are included: one showing the density growth rate before the release of ChatGPT, and another showing the growth rate after its release. This visualization demonstrates that the growth of LLM capacity density accelerated significantly after ChatGPT’s release, highlighting the impact of this model on subsequent LLM development.
read the caption
Figure 4: Density evaluated using MMLU. Two trend lines represent the growth of LLMs’ density before and after the release of ChatGPT.
Full paper#