↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large Language Models (LLMs) typically reason by generating a chain-of-thought (CoT) in natural language, but this approach is not always optimal. The language-based approach has limitations, such as the need for complex planning that poses challenges for LLMs. Neuroimaging studies also suggest that human reasoning does not heavily rely on language networks. This paper argues that reasoning within the language space is suboptimal for LLMs.
To address these issues, the paper proposes COCONUT (Chain of Continuous Thought), a novel paradigm that enables LLMs to reason directly in a continuous latent space. Instead of generating a sequence of words, COCONUT uses the LLM’s hidden state (continuous thought) as input for the next step. This allows the model to explore multiple reasoning paths simultaneously, similar to a breadth-first search, enhancing its ability to solve complex problems efficiently. Experiments demonstrate that COCONUT outperforms traditional CoT methods in tasks requiring complex planning and backtracking. The results show COCONUT’s superior performance in tasks requiring advanced reasoning patterns.
Key Takeaways#
Why does it matter?#
This paper is important because it challenges the conventional wisdom of LLMs reasoning solely within the language space. By introducing COCONUT, a novel latent reasoning paradigm, it opens exciting avenues for enhancing LLMs’ reasoning capabilities, particularly in complex problem-solving scenarios. The findings underscore the potential of latent reasoning and provide valuable insights for developing more advanced machine reasoning systems, pushing the boundaries of current AI research.
Visual Insights#

🔼 Figure 1 illustrates the core difference between the Chain-of-Thought (CoT) and Chain of Continuous Thought (CoCoNut) methods. CoT generates reasoning steps as a sequence of words, which are processed sequentially by the language model. In contrast, CoCoNut leverages the LLM’s hidden state (the ‘continuous thought’) as a representation of the reasoning process. This hidden state, rather than being decoded into words, is directly fed back into the model as input for the next step, enabling reasoning in a continuous latent space instead of relying on discrete word tokens. This allows for more flexible and potentially more efficient reasoning paths.
read the caption
Figure 1: A comparison of Chain of Continuous Thought (Coconut) with Chain-of-Thought (CoT). In CoT, the model generates the reasoning process as a word token sequence (e.g., [xi,xi+1,…,xi+j]subscript𝑥𝑖subscript𝑥𝑖1…subscript𝑥𝑖𝑗[x_{i},x_{i+1},...,x_{i+j}][ italic_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT , italic_x start_POSTSUBSCRIPT italic_i + 1 end_POSTSUBSCRIPT , … , italic_x start_POSTSUBSCRIPT italic_i + italic_j end_POSTSUBSCRIPT ] in the figure). Coconut regards the last hidden state as a representation of the reasoning state (termed “continuous thought”), and directly uses it as the next input embedding. This allows the LLM to reason in an unrestricted latent space instead of a language space.
| Method | GSM8k Acc. (%) | GSM8k # Tokens | ProntoQA Acc. (%) | ProntoQA # Tokens | ProsQA Acc. (%) | ProsQA # Tokens |
|---|---|---|---|---|---|---|
| CoT | 42.9 ± 0.2 | 25.0 | 98.8 ± 0.8 | 92.5 | 77.5 ± 1.9 | 49.4 |
| No-CoT | 16.5 ± 0.5 | 2.2 | 93.8 ± 0.7 | 3.0 | 76.7 ± 1.0 | 8.2 |
| iCoT | 30.0* | 2.2 | 99.8 ± 0.3 | 3.0 | 98.2 ± 0.3 | 8.2 |
| Pause Token | 16.4 ± 1.8 | 2.2 | 77.7 ± 21.0 | 3.0 | 75.9 ± 0.7 | 8.2 |
| Coconut (Ours) | 34.1 ± 1.5 | 8.2 | 99.8 ± 0.2 | 9.0 | 97.0 ± 0.3 | 14.2 |
| - w/o curriculum | 14.4 ± 0.8 | 8.2 | 52.4 ± 0.4 | 9.0 | 76.1 ± 0.2 | 14.2 |
| - w/o thought | 21.6 ± 0.5 | 2.3 | 99.9 ± 0.1 | 3.0 | 95.5 ± 1.1 | 8.2 |
| - pause as thought | 24.1 ± 0.7 | 2.2 | 100.0 ± 0.1 | 3.0 | 96.6 ± 0.8 | 8.2 |
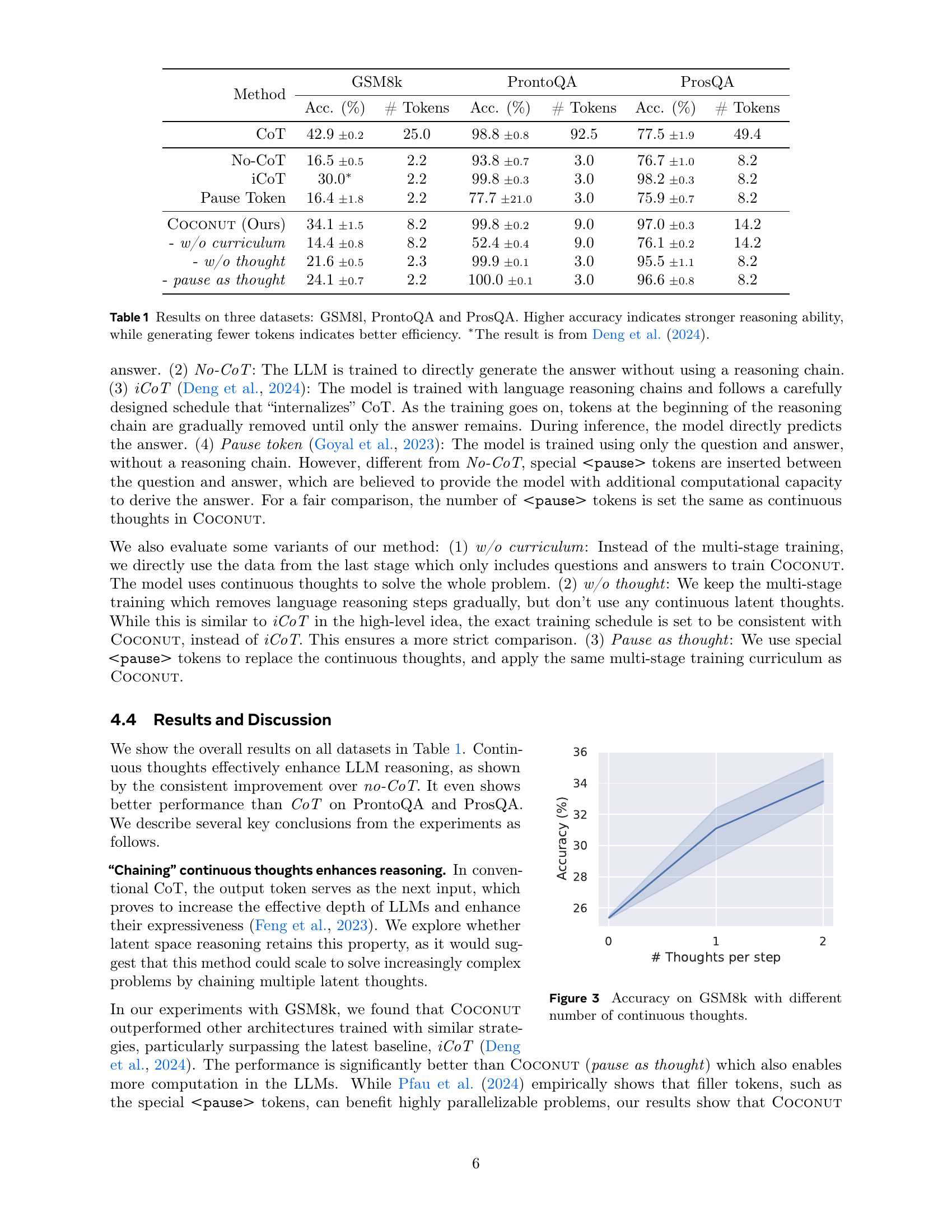
🔼 This table presents the results of three different reasoning tasks: GSM8k (grade-school level math problems), ProntoQA (5-hop logical reasoning problems), and ProsQA (a new logical reasoning dataset requiring stronger planning). For each dataset and method, the table shows the accuracy and the number of tokens generated by the model. Higher accuracy indicates stronger reasoning ability, while a lower number of tokens indicates better efficiency. The results are compared across several methods: CoT (Chain-of-Thought), No-CoT (no chain of thought), iCoT (internalized chain of thought), Pause Token (using pause tokens), and COCONUT (the proposed method). One result marked with an asterisk (*) is taken from a previous study by Deng et al. (2024) for comparison purposes.
read the caption
Table 1: Results on three datasets: GSM8l, ProntoQA and ProsQA. Higher accuracy indicates stronger reasoning ability, while generating fewer tokens indicates better efficiency. ∗The result is from Deng et al. (2024).
In-depth insights#
Latent Reasoning#
Latent reasoning, as explored in the context of large language models (LLMs), represents a significant departure from traditional language-based reasoning. Instead of relying on explicit chains of thought expressed in natural language, latent reasoning leverages the internal hidden states of the LLM to perform inferential processes. This approach offers several key advantages. Firstly, it bypasses the limitations imposed by the inherent constraints of natural language, allowing for more flexible and efficient reasoning. The use of continuous latent spaces allows the model to maintain and explore multiple potential reasoning paths concurrently, enabling a breadth-first search-like approach rather than a strictly linear, deterministic path commonly found in chain-of-thought methods. Secondly, latent reasoning can lead to more compact and efficient representations of the reasoning process, reducing the number of tokens needed for inference and thus potentially improving efficiency. The ability to encode multiple alternative steps within a latent state is a major advantage over typical autoregressive methods that are restricted to a single path. However, effective latent reasoning requires careful consideration of training methodologies. The study demonstrates that multi-stage training strategies and carefully designed curricula are crucial for enabling LLMs to leverage the full potential of latent representations. Further research should investigate how to optimize training and inference within latent spaces to enhance both accuracy and efficiency of the reasoning process.
COCONUT Model#
The COCONUT model presents a novel approach to large language model (LLM) reasoning by shifting from a reliance on the traditional chain-of-thought (CoT) method in the language space to a continuous latent space. Instead of generating reasoning steps as a sequence of words, COCONUT leverages the LLM’s last hidden state as a representation of the reasoning process (‘continuous thought’), feeding this directly back into the LLM as the next input embedding. This allows for more flexible and efficient reasoning, potentially enabling exploration of multiple pathways simultaneously (akin to breadth-first search) rather than committing to a single deterministic path. The model’s ability to encode multiple potential next steps is a key advantage, particularly in tasks demanding substantial backtracking during planning. Furthermore, COCONUT’s use of latent space reasoning reduces the computational cost associated with generating unnecessary words for textual coherence, focusing resources on the core reasoning steps. Experimental results show that COCONUT outperforms CoT on tasks requiring complex planning, demonstrating the potential of latent reasoning for enhanced LLM capabilities. The multi-stage training strategy further enhances the model’s performance by gradually transitioning from language-based reasoning to continuous thought reasoning, which helps the model learn more effective representations of reasoning steps.
Multi-Stage Training#
Multi-stage training, as presented in the research paper, is a crucial technique for effectively training the model to reason using continuous thoughts. This approach gradually transitions the model from a reliance on traditional language-based reasoning (like chain-of-thought) to a more advanced latent reasoning process. Starting with the model trained on standard language CoT instances, the multi-stage process systematically replaces language steps with continuous thoughts. This is done incrementally, enhancing the model’s proficiency in latent reasoning across various stages. The stage-wise training allows for a smoother transition, enabling the model to learn and adapt to the complexities of latent space representations without sudden performance disruptions. By carefully controlling the number of latent thoughts substituted for language reasoning steps at each stage, the model progressively internalizes continuous thought reasoning, thereby improving efficiency. This method effectively addresses challenges in directly training LLMs for latent reasoning, which is often problematic. The methodology facilitates a more robust and efficient latent reasoning process by gradually increasing the model’s dependence on latent representations. Therefore, multi-stage training proves essential for successfully leveraging the advantages of continuous thoughts in enhancing LLM reasoning.
Reasoning Efficiency#
Reasoning efficiency in large language models (LLMs) is a crucial aspect of their practical applicability. The paper explores this concept through a novel approach called COCONUT, which shifts reasoning from the traditional language space to a continuous latent space. COCONUT demonstrates improved efficiency by reducing the number of tokens generated during inference, compared to the Chain-of-Thought (CoT) method. This enhancement is particularly notable in tasks requiring complex planning, where COCONUT’s latent reasoning capabilities effectively prune less promising paths. The latent space allows for a more efficient representation of the reasoning process, encoding multiple potential next steps simultaneously, mimicking a breadth-first search. While CoT’s autoregressive nature limits its ability to explore multiple paths concurrently, COCONUT’s inherent parallelism is a significant factor in improving efficiency. Although the model isn’t explicitly trained to search efficiently, the results suggest an emergent property, where the continuous thoughts act as an implicit value function, guiding the model towards the most promising solution paths. The trade-off between accuracy and efficiency is also relevant: fewer tokens might slightly compromise accuracy in some cases, but the overall benefits of reduced computational cost make the efficiency gains worthwhile. Furthermore, the study explores the impact of the number of continuous thoughts on both accuracy and speed, revealing an optimal balance that maximizes performance.
Future Research#
Future research directions stemming from this work on latent reasoning in LLMs are plentiful. Improving the training efficiency of COCONUT is crucial, potentially through exploration of parallel training techniques or more sophisticated curriculum designs that smoothly transition between language and latent modes. Investigating alternative methods for determining when to switch between latent and language modes during inference could lead to more robust and adaptable models. A deeper investigation into the implicit value function guiding the model’s latent search is needed. Understanding how this function emerges and how it can be shaped or improved is key to unlocking even greater reasoning capabilities. Finally, applying this latent reasoning approach to other complex tasks and datasets beyond those studied here will help establish its generalizability and impact. Exploring its application in areas like program synthesis, robotics, or scientific discovery could yield significant breakthroughs in artificial intelligence.
More visual insights#
More on figures

🔼 The figure illustrates the multi-stage training process for the COCONUT model. It starts with standard Chain-of-Thought (CoT) data, where reasoning is explicitly expressed in natural language. In each subsequent training stage, a number (c) of continuous thoughts (latent representations of the reasoning process) are substituted for language-based reasoning steps. This substitution is gradually increased across training stages, ultimately leading to a model that reasons primarily in the latent space, relying on continuous thoughts to generate the final answer rather than using a language-based step-by-step process. The cross-entropy loss is calculated using the remaining tokens and continuous thoughts after the substitution.
read the caption
Figure 2: Training procedure of Chain of Continuous Thought (Coconut). Given training data with language reasoning steps, at each training stage we integrate c𝑐citalic_c additional continuous thoughts (c=1𝑐1c=1italic_c = 1 in this example), and remove one language reasoning step. The cross-entropy loss is then used on the remaining tokens after continuous thoughts.

🔼 This figure shows the relationship between the accuracy of the GSM8k dataset and the number of continuous thoughts used in the COCONUT model. It demonstrates how increasing the number of continuous thoughts, which represent the model’s internal reasoning steps in a latent space, affects its ability to correctly solve mathematical problems. The graph likely plots accuracy on the y-axis and the number of continuous thoughts per reasoning step on the x-axis. It visualizes the performance gain achieved by using the COCONUT method.
read the caption
Figure 3: Accuracy on GSM8k with different number of continuous thoughts.

🔼 This figure demonstrates how the model’s continuous thoughts, which are internal representations of the reasoning process, can be translated into human-understandable language tokens. The example shows a simple math word problem where the model uses continuous thoughts to arrive at the solution. The decoded tokens reveal intermediate steps in the computation, indicating the model’s internal reasoning process. The figure highlights the potential of decoding continuous thoughts to gain insights into the model’s internal decision-making and reasoning strategy.
read the caption
Figure 4: A case study where we decode the continuous thought into language tokens.

🔼 Figure 5 presents a detailed analysis of the performance of various COCONUT models and baseline methods on the ProsQA dataset. The left panel shows the accuracy of the final answer generated by each method. The right panel provides a more nuanced breakdown, displaying the frequency of different reasoning outcomes such as correct labels, correct paths, and various types of errors (incorrect label, longer path, wrong target, hallucination). This dual view allows for a comprehensive assessment of model efficacy not only in terms of correct answer generation but also in terms of the quality and soundness of the reasoning process itself.
read the caption
Figure 5: The accuracy of final answer (left) and reasoning process (right) of multiple variants of Coconut and baselines on ProsQA.

🔼 This figure showcases a specific example from the ProsQA dataset, highlighting the different reasoning approaches of Chain-of-Thought (CoT), COCONUT (k=1), and COCONUT (k=2). The problem involves determining if a statement is true or false based on a set of logical rules. CoT, operating within the language space, makes an incorrect deduction, generating a path that includes a nonexistent relationship (Every yumpus is a rempus). This showcases CoT’s tendency to hallucinate information and get stuck. COCONUT (k=1), allowing for one step of latent reasoning, also produces an incorrect result due to selecting an irrelevant node. Finally, COCONUT (k=2), with two steps of latent reasoning, successfully navigates the problem and reaches the correct conclusion, demonstrating its effectiveness for complex planning tasks.
read the caption
Figure 6: A case study of ProsQA. The model trained with CoT hallucinates an edge (Every yumpus is a rempus) after getting stuck in a dead end. Coconut (k=1) outputs a path that ends with an irrelevant node. Coconut (k=2) solves the problem correctly.

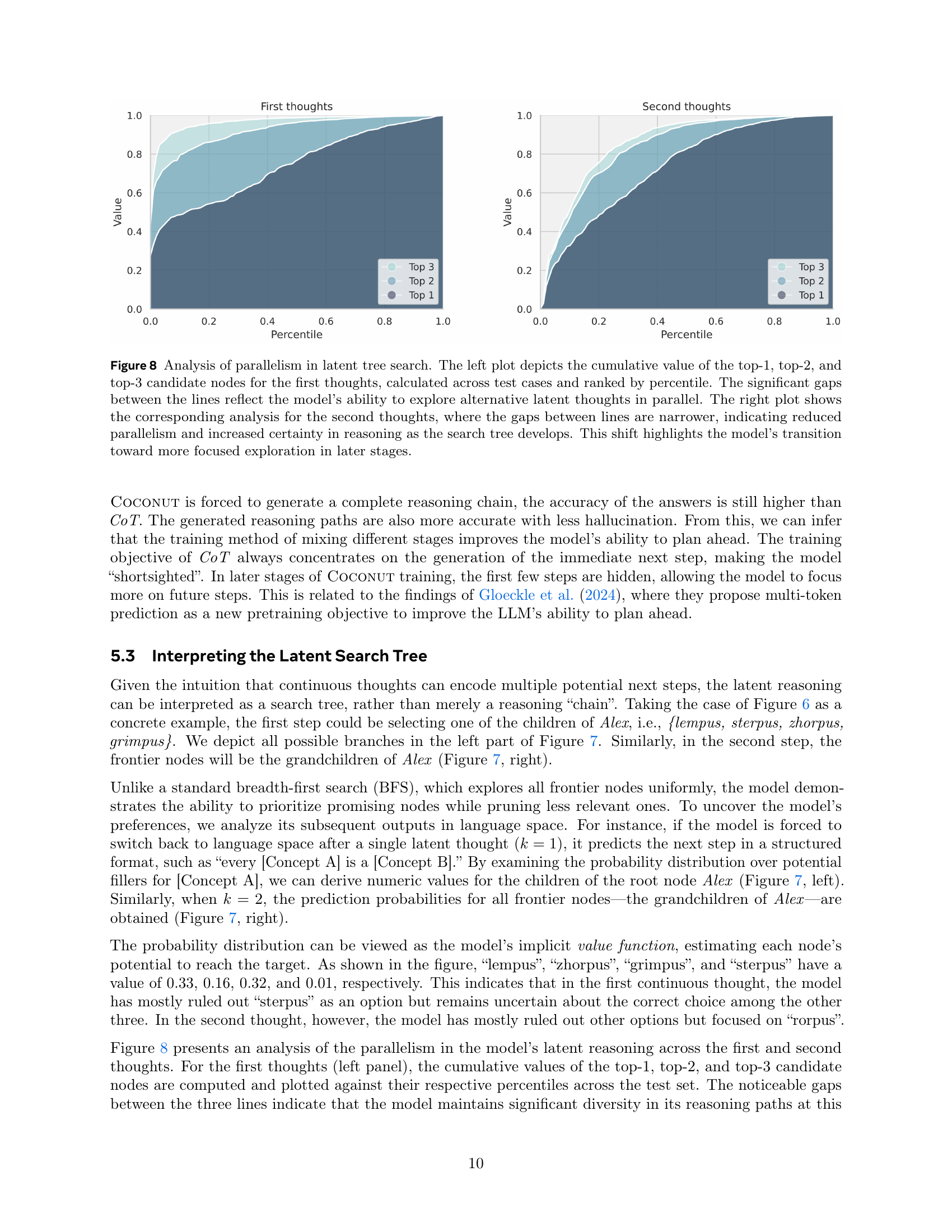
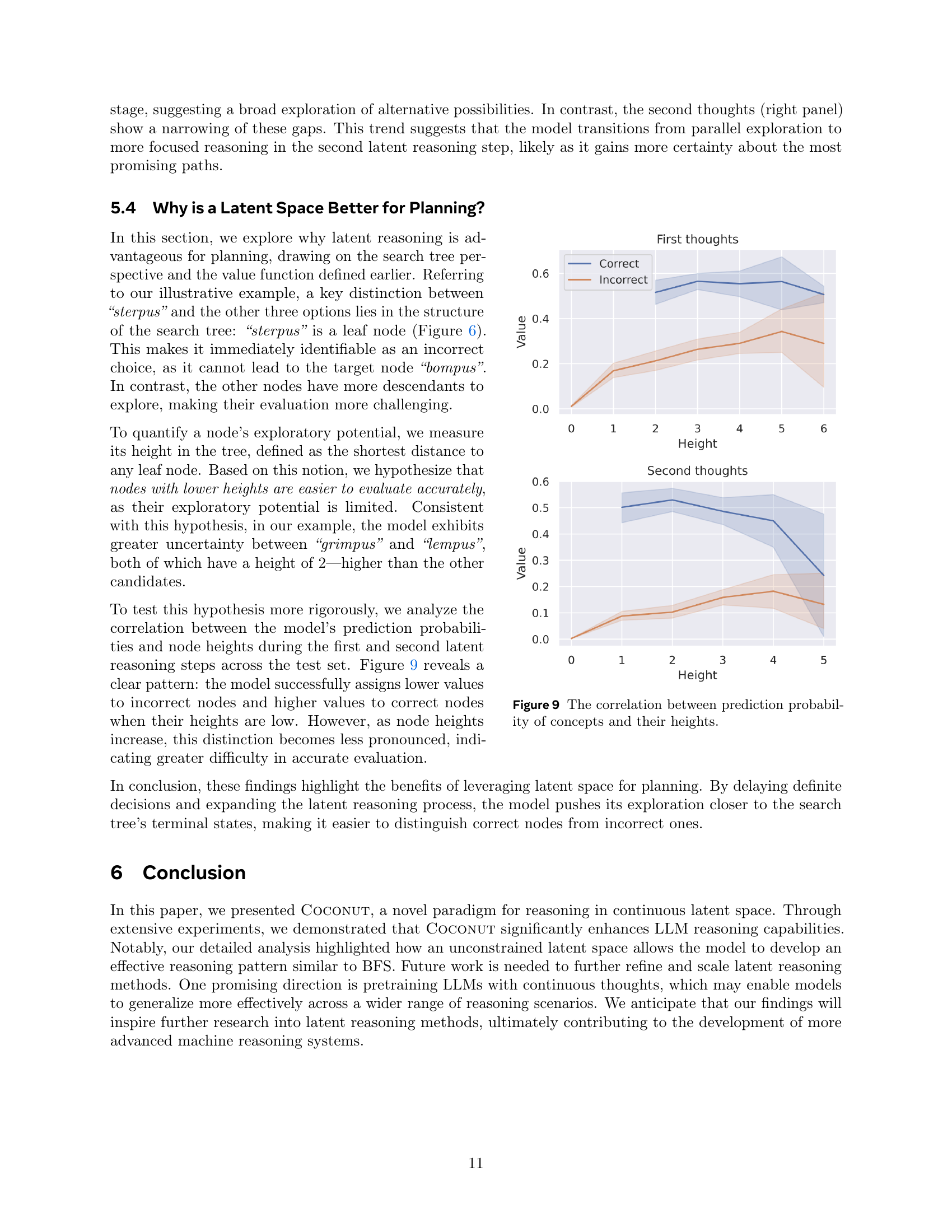
🔼 Figure 7 illustrates the latent search tree used by the COCONUT model. The example shown is the same as in Figure 6. Node height (h) represents the longest path to a leaf node. The figure displays the probability of the model predicting a specific concept (e.g., ’lempus’) as the first step in the latent reasoning process. This probability is calculated as the product of individual token probabilities within that concept, given the preceding context. The omitted context for brevity does not affect the meaning. Essentially, the probability acts as an implicit value function, estimated by the model, which indicates the likelihood of a particular path leading to the correct answer.
read the caption
Figure 7: An illustration of the latent search trees. The example is the same test case as in Figure 7. The height of a node (denoted as hℎhitalic_h in the figure) is defined as the longest distance to any leaf nodes in the graph. We show the probability of the first concept predicted by the model following latent thoughts (e.g., “lempus” in the left figure). It is calculated as the multiplication of the probability of all tokens within the concept conditioned on previous context (omitted in the figure for brevity). This metric can be interpreted as an implicit value function estimated by the model, assessing the potential of each node leading to the correct answer.
More on tables
| # Nodes | # Edges | Len. of Shortest Path | # Shortest Paths |
|---|---|---|---|
| 23.0 | 36.0 | 3.8 | 1.6 |
🔼 Table 2 presents a statistical overview of the graph structures used in the ProsQA dataset. It shows the average number of nodes and edges in the graphs, along with the average length of the shortest path between nodes and the average number of shortest paths. These statistics provide insights into the complexity and structure of the logical reasoning problems within the ProsQA dataset, indicating the challenges involved in navigating and finding solutions within these graphs.
read the caption
Table 2: Statistics of the graph structure in ProsQA.
| Dataset | Training | Validation | Test |
|---|---|---|---|
| GSM8k | 385,620 | 500 | 1319 |
| ProntoQA | 9,000 | 200 | 800 |
| ProsQA | 17,886 | 300 | 500 |
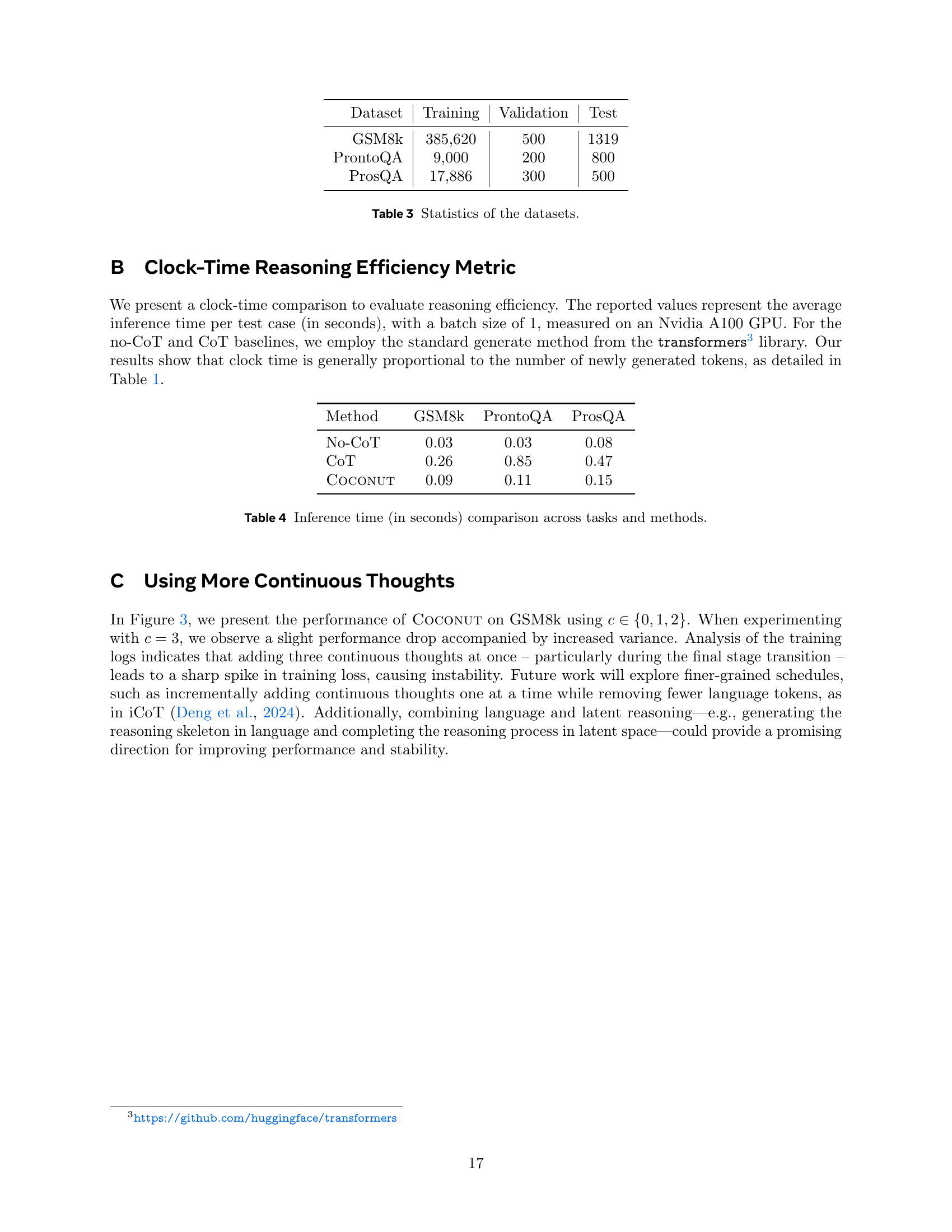
🔼 This table presents a statistical overview of the three datasets used in the paper’s experiments: GSM8k, ProntoQA, and ProsQA. For each dataset, it shows the number of instances in the training, validation, and test sets.
read the caption
Table 3: Statistics of the datasets.
| Method | GSM8k | ProntoQA | ProsQA |
|---|---|---|---|
| No-CoT | 0.03 | 0.03 | 0.08 |
| CoT | 0.26 | 0.85 | 0.47 |
| Coconut | 0.09 | 0.11 | 0.15 |
🔼 This table presents a comparison of the inference time, measured in seconds, for different reasoning methods across three tasks: GSM8k, ProntoQA, and ProsQA. It shows the average time taken to generate an answer for each method, providing insights into the computational efficiency of various approaches. The methods compared include No-CoT (no chain-of-thought), CoT (chain-of-thought), and COCONUT.
read the caption
Table 4: Inference time (in seconds) comparison across tasks and methods.
Full paper#