↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Generating high-quality images quickly is a core challenge in AI. ReFlows, an alternative to popular diffusion models, offer faster image generation by using simpler mathematical equations. However, precisely inverting and editing images with ReFlows was slow, hindering their wider use. This problem limits real-time high-fidelity applications like image editing and latent space manipulation. Existing methods either sacrificed accuracy or computational resources.
FireFlow tackles this issue by introducing a novel numerical solver for ReFlows. This innovative solver dramatically speeds up image inversion while improving accuracy. It reuses previously calculated data, avoiding redundant calculations. This allows ReFlow models to invert and edit images in only 8 steps, achieving a 3x speedup compared to state-of-the-art methods, all without additional training. This breakthrough opens up exciting possibilities for real-time, high-fidelity image editing applications.
Key Takeaways#
Why does it matter?#
Faster and more accurate image editing. This research introduces FireFlow, a new method for inverting Rectified Flows (ReFlows) used in image generation. It’s vital for researchers exploring image editing, reconstruction, and latent space manipulation as it offers a more efficient way to edit images while preserving details, which is a crucial step towards real-time, high-fidelity image editing applications and can influence future development of efficient numerical methods.
Visual Insights#

🔼 Figure 1 showcases the application of FireFlow for image inversion and editing within 8 steps. The examples demonstrate semantic image editing and stylizations using prompts while preserving the original image content, covering various modifications like adding or removing content ([+]/[-]), changing visual attributes ([C]), and replacing existing content or gestures ([R]).
read the caption
Figure 1: FireFlow for Image Inversion and Editing in 8 Steps. Our approach achieves outstanding results in semantic image editing and stylization guided by prompts, while maintaining the integrity of the reference content image and avoiding undesired alterations. [+]/[-] means adding or removing contents, [C] indicates changes in visual attributes (style, material, or texture), and [R] denotes content or gesture replacements.
| Methods | Add-it | RF-Solver | RF-Inv. | Ours |
|---|---|---|---|---|
| Steps | 30 | 15 | 28 | 8 |
| NFE | 60 | 60 | 56 | 18 |
| Aux. Model | ✓ | w/o | w/o | w/o |
| Local Error | (O(Δt^2)) | (O(Δt^3)) | (O(Δt^2)) | (O(Δt^3)) |
🔼 This table compares training-free inversion and editing methods using FLUX, a ReFlow-based model. It considers factors like the number of steps, function evaluations (NFEs), error order of the ODE solver, and the need for a pre-trained auxiliary model. The comparison highlights the efficiency and effectiveness of the proposed ‘FireFlow’ method.
read the caption
Table 1: Comparison of recent training-free inversion and editing methods based on FLUX, including inversion/denoising steps, NFEs (Number of Function Evaluations) for both inversion and editing, local truncation error orders for solving ODE, and the need for a pre-trained auxiliary model for editing. Our approach offers a simple yet effective solution to address the challenges.
In-depth insights#
Fast ReFlow Inversion#
Fast ReFlow inversion tackles the challenge of efficiently reversing ReFlows for image editing. Existing methods struggle with slow speeds or inaccuracies. This new approach proposes a novel second-order numerical solver, which reuses intermediate velocity calculations, reducing redundant computations. It achieves a 3x speedup compared to other methods while maintaining smaller reconstruction errors. This efficiency unlocks real-time, high-fidelity inversion, making ReFlow a more practical tool for semantic image editing and stylization.
Solver for Editing#
A novel solver for image editing is introduced, enabling real-time, high-fidelity results. It deviates from traditional diffusion models by employing a deterministic approach, leading to faster and more efficient transformations. The solver’s core strength lies in its ability to maintain second-order precision while retaining the computational cost of a first-order solver. This efficiency stems from reusing intermediate velocity approximations, thus minimizing redundant computations. This approach is particularly well-suited for ReFlow based generative models, enhancing their utility in various image editing applications.
8-Step Editing#
While the paper doesn’t explicitly mention “8-Step Editing” as a heading, its core contribution revolves around efficient and accurate image editing using Rectified Flows (ReFlows) within a few steps. The proposed FireFlow method achieves second-order precision for ReFlow inversion, similar to more computationally expensive methods, but at the cost of a first-order solver, making it significantly faster. This is achieved by cleverly reusing intermediate velocity approximations, which reduces redundant calculations. Consequently, FireFlow enables high-fidelity image editing in just 8 steps, a remarkable improvement over existing techniques. This efficiency is crucial for real-time applications and resource-constrained environments. Furthermore, FireFlow demonstrates superior reconstruction quality and edit fidelity compared to diffusion-based and other ReFlow methods, as shown through qualitative and quantitative evaluations. This advancement unlocks the potential of ReFlows for broader adoption in image editing tasks.
ReFlow vs. Diffusion#
ReFlow models, using ODEs, offer a compelling alternative to diffusion models, which rely on SDEs, for image editing. ReFlows, exemplified by FLUX, achieve competitive generative performance and particularly excel in fast sampling. However, efficiently inverting these models for editing remains a challenge. Existing ReFlow inversion techniques often compromise accuracy for speed or incur high computational costs. This highlights a key difference: while diffusion models have well-established inversion methods, ReFlow inversion requires specialized solvers. The core trade-off lies in balancing speed and accuracy during inversion, with ReFlows potentially offering faster generation but requiring careful solver design for accurate reconstruction. This suggests that the choice between ReFlow and diffusion depends on the specific application, prioritizing either generation speed or ease of inversion.
Editing Limits#
While FireFlow excels in many image editing tasks, it struggles with object color changes and uncommon scenarios. For instance, altering a cat’s color or editing images with obscured subjects yields subpar results. Complex prompts also pose a challenge. This limitation stems from the editing strategy’s reliance on replacing “V” features in the self-attention module. While supplementing “K” features improves results, it compromises background preservation. This highlights the need for more robust editing approaches that better handle these challenges.
More visual insights#
More on figures

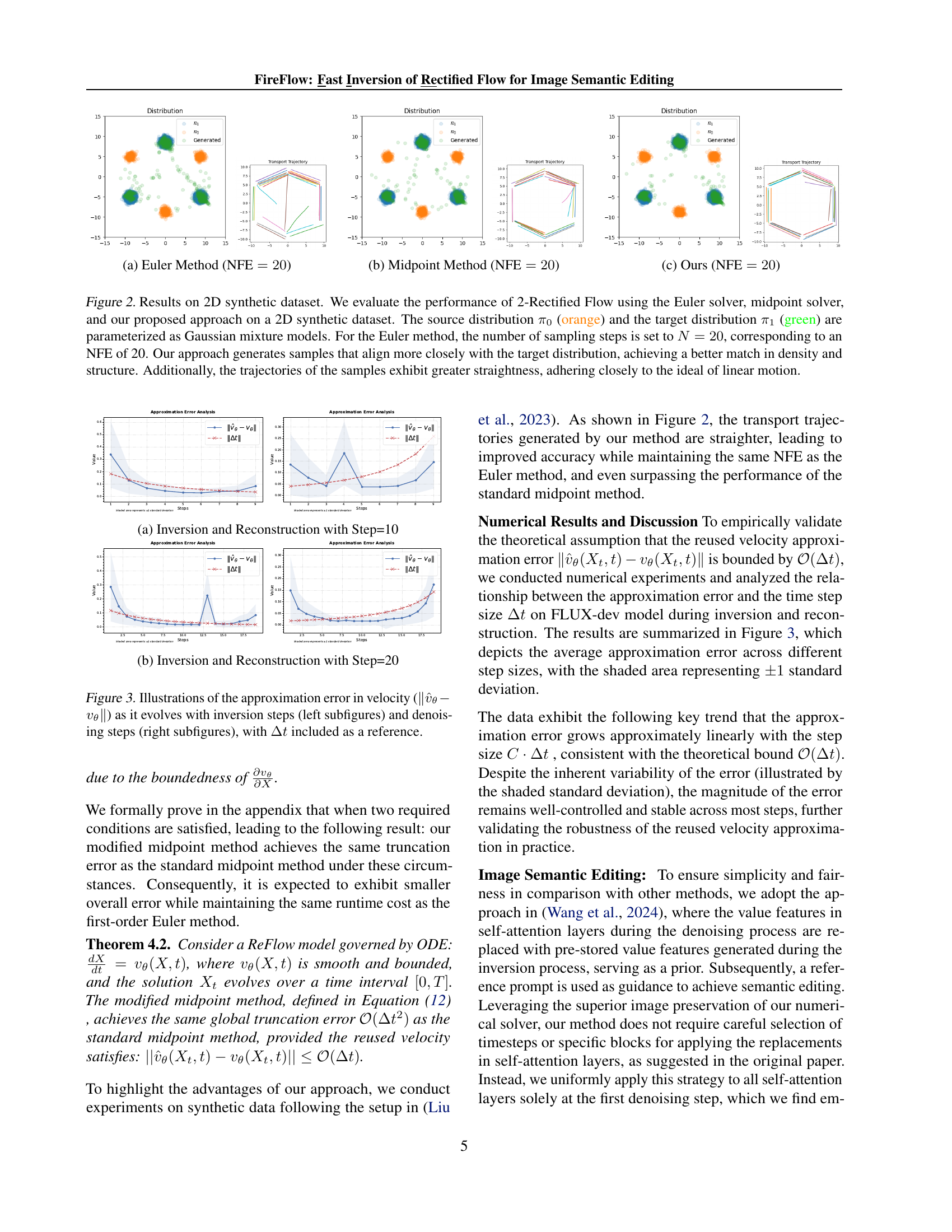
🔼 This figure presents a comparison of different numerical solvers for 2-Rectified Flow on a 2D synthetic dataset. The dataset consists of two distributions: a source distribution (orange) and a target distribution (green), both parameterized as Gaussian mixture models. The Euler Method, Midpoint Method, and the proposed method are compared, all using 20 NFEs (Number of Function Evaluations). The trajectories of samples during the transformation are visualized. The purpose is to demonstrate that the proposed method generates samples that better align with the target distribution in terms of density and structure, and the trajectories are straighter, indicating closer adherence to the ideal linear motion.
read the caption
(a) Euler Method (NFE=20NFE20\text{NFE}=20NFE = 20)

🔼 Figure 2(b) depicts the behavior of a 2D Rectified Flow model when using the standard midpoint method for numerical integration. The midpoint method enhances accuracy over simpler first-order methods by evaluating the flow’s velocity at the midpoint of each time step. The visualization demonstrates the trajectories of samples as they transition between two distributions. Orange represents the source distribution, green the target, and blue the flow’s estimate after transformation. Notably, the trajectories exhibit a degree of curvature, reflecting the second-order nature of the midpoint method. The NFE = 20 specifies that the velocity function was evaluated 20 times during the sampling process, influencing both the computational cost and accuracy of the result.
read the caption
(b) Midpoint Method (NFE=20NFE20\text{NFE}=20NFE = 20)

🔼 This subfigure shows the results on a 2D synthetic dataset using the proposed FireFlow approach with NFE=20. The proposed approach generates samples that better align with the target distribution compared to Euler Method and Midpoint Method, both visually and in terms of density and structure. The trajectories of the samples generated by FireFlow are straighter, closely adhering to the ideal linear motion principle.
read the caption
(c) Ours (NFE=20NFE20\text{NFE}=20NFE = 20)

🔼 This figure visualizes the results of applying three different numerical solvers (Euler, Midpoint, and the proposed method) to a 2D synthetic dataset using 2-Rectified Flow. The goal is to transform samples from a source distribution (orange) to a target distribution (green), both parameterized as Gaussian mixture models. The figure demonstrates that the proposed method achieves a better match in density and structure with the target distribution, and generates straighter trajectories, indicating closer adherence to the ideal of linear motion, all while using the same number of function evaluations (NFE) as the Euler method and fewer NFEs than the midpoint method.
read the caption
Figure 2: Results on 2D synthetic dataset. We evaluate the performance of 2-Rectified Flow using the Euler solver, midpoint solver, and our proposed approach on a 2D synthetic dataset. The source distribution π0subscript𝜋0\pi_{0}italic_π start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT (orange) and the target distribution π1subscript𝜋1\pi_{1}italic_π start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT (green) are parameterized as Gaussian mixture models. For the Euler method, the number of sampling steps is set to N=20𝑁20N=20italic_N = 20, corresponding to an NFE of 20. Our approach generates samples that align more closely with the target distribution, achieving a better match in density and structure. Additionally, the trajectories of the samples exhibit greater straightness, adhering closely to the ideal of linear motion.

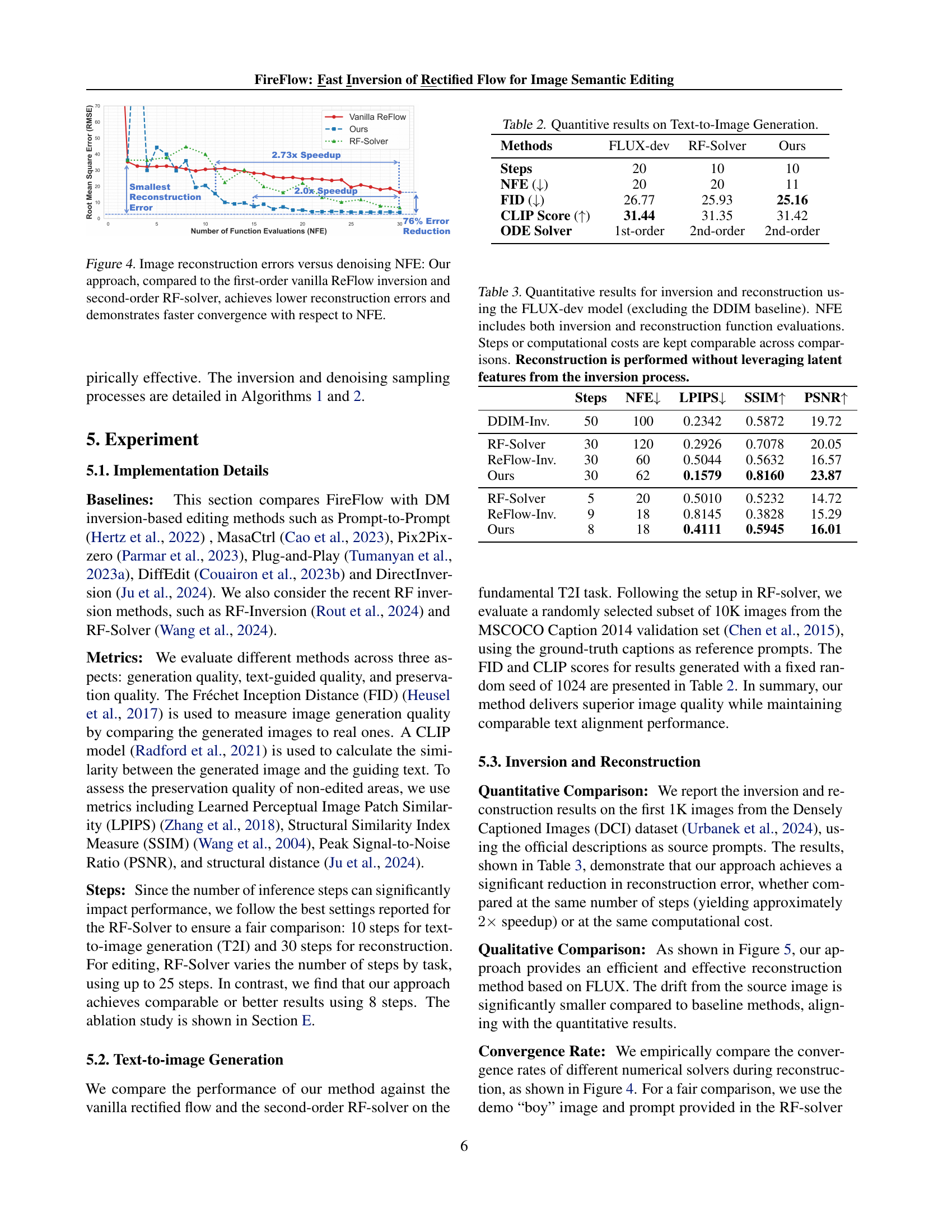
🔼 This subfigure presents an analysis of the approximation error in velocity (represented as ||v_hat - v||) during the inversion and reconstruction process with 10 steps. The graph showcases how this error changes with respect to the inversion and denoising steps. The value of delta_t is also displayed for reference, allowing for a comparison between the approximation error and the step size used in the numerical integration.
read the caption
(a) Inversion and Reconstruction with Step=10

🔼 This subfigure shows the relationship between the approximation error in velocity and the number of inversion (left) and denoising (right) steps with 20 steps settings. The x-axis represents the steps, while the y-axis shows the magnitude of the error. Notably, the error magnitude remains relatively stable and under control. This figure helps to confirm the robustness of the proposed velocity approximation method during the inversion and reconstruction processes.
read the caption
(b) Inversion and Reconstruction with Step=20

🔼 This figure illustrates the approximation error in velocity (the difference between the approximated velocity and the true velocity) during both the inversion and denoising steps of a rectified flow model. The error is plotted against the step number, and the time step size (Δt) is included as a reference. The left subfigures show the error during inversion (mapping from image to noise), while the right subfigures show the error during denoising/reconstruction (mapping from noise back to image). The purpose is to demonstrate that the approximation error is well-controlled and scales proportionally with the time step, supporting the theoretical analysis.
read the caption
Figure 3: Illustrations of the approximation error in velocity (‖v^θ−vθ‖normsubscript^𝑣𝜃subscript𝑣𝜃\|\hat{v}_{\theta}-v_{\theta}\|∥ over^ start_ARG italic_v end_ARG start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT - italic_v start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT ∥) as it evolves with inversion steps (left subfigures) and denoising steps (right subfigures), with ΔtΔ𝑡\Delta troman_Δ italic_t included as a reference.

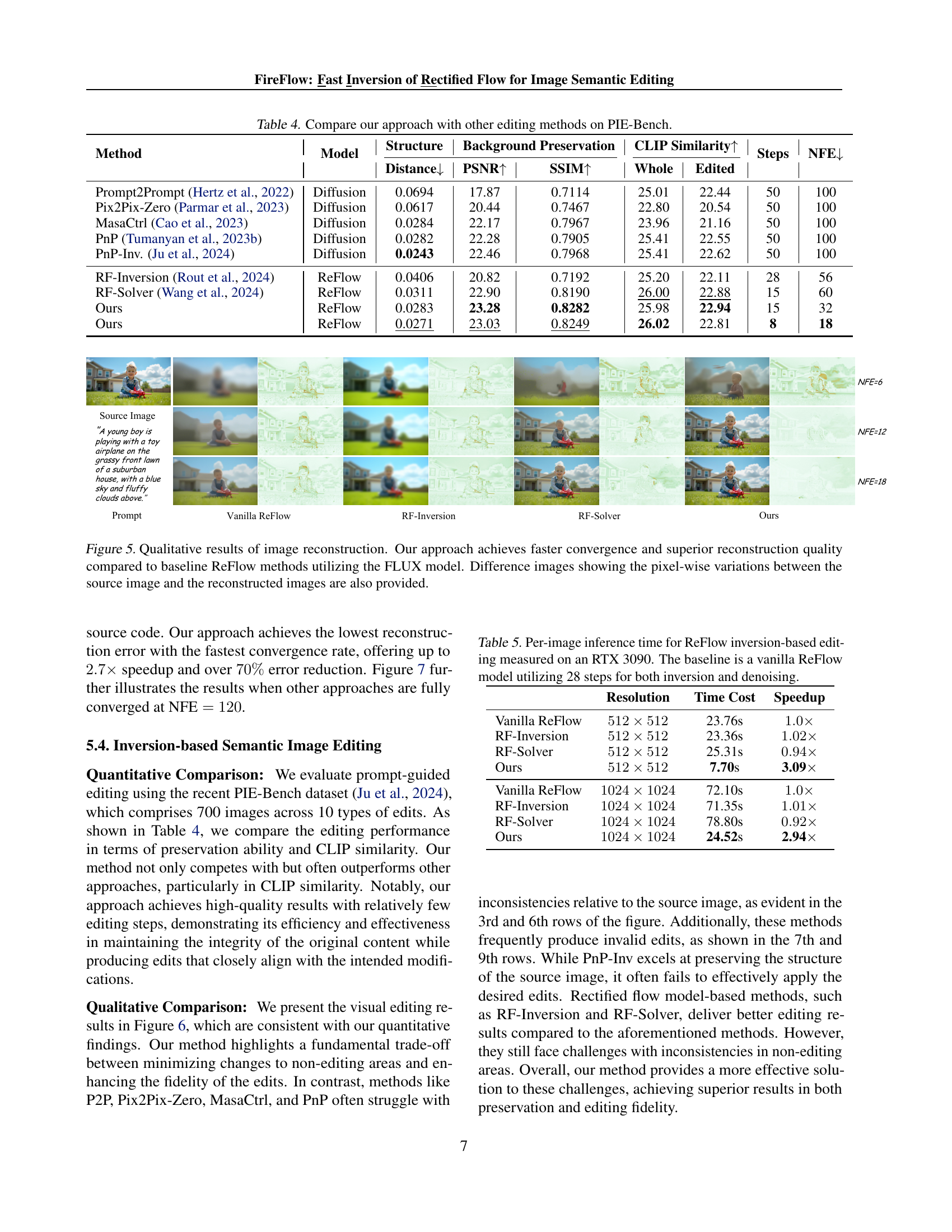
🔼 This figure compares the reconstruction error of different ReFlow inversion methods as a function of the number of Neural Function Evaluations (NFEs). The plot shows that the proposed method achieves significantly lower reconstruction errors compared to both the first-order vanilla ReFlow inversion and the second-order RF-Solver. Furthermore, the proposed method converges much faster to the minimal reconstruction error requiring fewer NFE for a given error tolerance.
read the caption
Figure 4: Image reconstruction errors versus denoising NFE: Our approach, compared to the first-order vanilla ReFlow inversion and second-order RF-solver, achieves lower reconstruction errors and demonstrates faster convergence with respect to NFE.

🔼 This figure presents a qualitative comparison of image reconstruction results using different ReFlow-based methods with the FLUX model. The first column displays the original source image and its corresponding text prompt. Subsequent columns showcase the reconstructed images generated by Vanilla ReFlow, RF-Inversion, RF-Solver, and our proposed FireFlow method. The last row provides difference images (pixel-wise variations) between the source and reconstructed images for each method, highlighting the reconstruction fidelity. The comparison demonstrates our method’s superior reconstruction quality and faster convergence compared to the baselines.
read the caption
Figure 5: Qualitative results of image reconstruction. Our approach achieves faster convergence and superior reconstruction quality compared to baseline ReFlow methods utilizing the FLUX model. Difference images showing the pixel-wise variations between the source image and the reconstructed images are also provided.

🔼 This figure presents a qualitative comparison of our proposed FireFlow method with other state-of-the-art image editing techniques. Examples are shown for several different input images and editing prompts, and the results of each method are displayed side-by-side for comparison. The baseline methods include both diffusion-based methods (Prompt-to-Prompt, Pix2Pix-Zero, MasaCtrl, Plug-and-Play, PnP-Inv, and DiffEdit) and ReFlow-based methods (RF-Inversion and RF-Solver).
read the caption
Figure 6: Comparison with State-of-the-art editing methods.

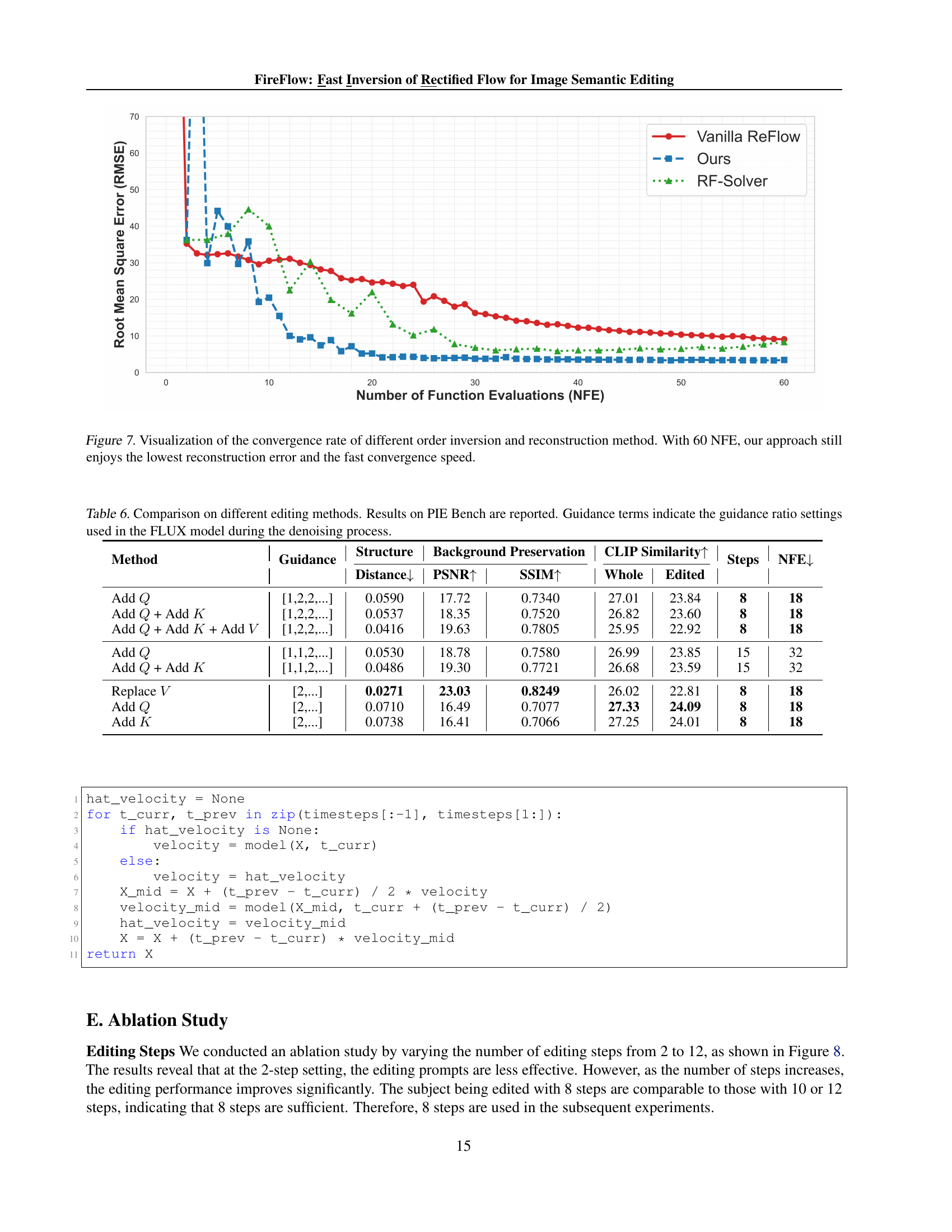
🔼 This figure visualizes the convergence speed during image reconstruction across different numerical solvers using a fixed random seed. The x-axis represents the Number of Function Evaluations (NFEs), which serves as a proxy for computational cost. The y-axis represents the Root Mean Square Error (RMSE) between the reconstructed image and the original image. Lower RMSE values indicate better reconstruction quality. Three solvers are compared: first-order ‘Vanilla ReFlow,’ the proposed second-order method (‘Ours’), and another second-order method ‘RF-Solver.’ The results demonstrate that the proposed method converges faster to a lower RMSE than the other methods, indicating more accurate and efficient image reconstruction.
read the caption
Figure 7: Visualization of the convergence rate of different order inversion and reconstruction method. With 60 NFE, our approach still enjoys the lowest reconstruction error and the fast convergence speed.

🔼 This figure presents an ablation study showcasing the impact of varying the number of denoising steps during image editing with FireFlow. A source image of a cake is edited to include cherries on top. Results for 2, 4, 6, 8, 10, and 12 steps are visualized. The study demonstrates that while fewer steps (e.g., 2) hinder effective prompt incorporation, increasing the steps progressively enhances editing performance. A point of diminishing returns is observed, with 8 steps offering comparable results to higher step counts, indicating sufficient prompt integration is achieved at this point.
read the caption
Figure 8: Ablation Study on the Number of Editing Steps.

🔼 The original image before any edits or transformations are applied, serving as the starting point for subsequent steps in the image manipulation process. It depicts a cat sitting on a wall.
read the caption
(a) Source Image

🔼 Edited Image: An edited image of the original cat where it becomes black.
read the caption
(b) Black Cat

🔼 An example image from the PIE-Bench dataset in its original state. The girl has brown hair and a neutral expression. This serves as the ‘before’ image for demonstrating semantic editing using ReFlow and FireFlow. The goal of editing would be to change aspects of the image according to a text prompt while minimizing distortion in non-edited regions.
read the caption
(c) Source Image

🔼 The figure shows the result of applying the ‘raising hands’ edit to an image of a man in a black shirt using FireFlow. The original image features the man with his arms at his sides, while the edited image shows him with both arms raised above his head.
read the caption
(d) Raising Hands
More on tables
| Tewel et al. (2024) for Add-it, Wang et al. (2024) for RF-Solver, Rout et al. (2024) for RF-Inv. |
🔼 This table compares three different Rectified Flow models using image generation metrics. The metrics include the number of function evaluations, Fréchet Inception Distance (FID), and CLIP Score. It appears in the paper to show that the proposed model can generate high-quality images with few function evaluations.
read the caption
Table 2: Quantitive results on Text-to-Image Generation.
| Methods | FLUX-dev | RF-Solver | Ours |
|---|---|---|---|
| Steps | 20 | 10 | 10 |
| NFE (↓) | 20 | 20 | 11 |
| FID (↓) | 26.77 | 25.93 | 25.16 |
| CLIP Score (↑) | 31.44 | 31.35 | 31.42 |
| ODE Solver | 1st-order | 2nd-order | 2nd-order |
🔼 This table presents quantitative results for image inversion and reconstruction using the FLUX-dev model, comparing different methods based on varying steps and NFE (Number of Function Evaluations). Metrics used for evaluation include LPIPS, SSIM, and PSNR. The table showcases the effectiveness of FireFlow. It demonstrates that the FireFlow can outperform baseline models in reconstruction quality while using fewer steps, hence offering a better speed and computation efficiency.
read the caption
Table 3: Quantitative results for inversion and reconstruction using the FLUX-dev model (excluding the DDIM baseline). NFE includes both inversion and reconstruction function evaluations. Steps or computational costs are kept comparable across comparisons. Reconstruction is performed without leveraging latent features from the inversion process.
| Steps | NFE↓ | LPIPS↓ | SSIM↑ | PSNR↑ | |
|---|---|---|---|---|---|
| DDIM-Inv. | 50 | 100 | 0.2342 | 0.5872 | 19.72 |
| RF-Solver | 30 | 120 | 0.2926 | 0.7078 | 20.05 |
| ReFlow-Inv. | 30 | 60 | 0.5044 | 0.5632 | 16.57 |
| Ours | 30 | 62 | 0.1579 | 0.8160 | 23.87 |
| RF-Solver | 5 | 20 | 0.5010 | 0.5232 | 14.72 |
| ReFlow-Inv. | 9 | 18 | 0.8145 | 0.3828 | 15.29 |
| Ours | 8 | 18 | 0.4111 | 0.5945 | 16.01 |
🔼 Comparison of our approach with state-of-the-art image editing methods on PIE-Bench dataset, evaluating structure preservation, background preservation, CLIP similarity, inference steps, and number of function evaluations (NFE).
read the caption
Table 4: Compare our approach with other editing methods on PIE-Bench.
| Method | Model | Structure ↓ | Background Preservation | CLIP Similarity ↑ | Steps | NFE ↓ |
|---|---|---|---|---|---|---|
| Prompt2Prompt (Hertz et al., 2022) | Diffusion | 0.0694 | PSNR ↑: 17.87 SSIM ↑: 0.7114 | Whole: 25.01 Edited: 22.44 | 50 | 100 |
| Pix2Pix-Zero (Parmar et al., 2023) | Diffusion | 0.0617 | PSNR ↑: 20.44 SSIM ↑: 0.7467 | Whole: 22.80 Edited: 20.54 | 50 | 100 |
| MasaCtrl (Cao et al., 2023) | Diffusion | 0.0284 | PSNR ↑: 22.17 SSIM ↑: 0.7967 | Whole: 23.96 Edited: 21.16 | 50 | 100 |
| PnP (Tumanyan et al., 2023b) | Diffusion | 0.0282 | PSNR ↑: 22.28 SSIM ↑: 0.7905 | Whole: 25.41 Edited: 22.55 | 50 | 100 |
| PnP-Inv. (Ju et al., 2024) | Diffusion | 0.0243 | PSNR ↑: 22.46 SSIM ↑: 0.7968 | Whole: 25.41 Edited: 22.62 | 50 | 100 |
| RF-Inversion (Rout et al., 2024) | ReFlow | 0.0406 | PSNR ↑: 20.82 SSIM ↑: 0.7192 | Whole: 25.20 Edited: 22.11 | 28 | 56 |
| RF-Solver (Wang et al., 2024) | ReFlow | 0.0311 | PSNR ↑: 22.90 SSIM ↑: 0.8190 | Whole: 26.00 Edited: 22.88 | 15 | 60 |
| Ours | ReFlow | 0.0283 | PSNR ↑: 23.28 SSIM ↑: 0.8282 | Whole: 25.98 Edited: 22.94 | 15 | 32 |
| Ours | ReFlow | 0.0271 | PSNR ↑: 23.03 SSIM ↑: 0.8249 | Whole: 26.02 Edited: 22.81 | 8 | 18 |
🔼 This table presents the per-image inference time for different ReFlow inversion-based editing methods, including Vanilla ReFlow, RF-Inversion, RF-Solver, and the proposed method (Ours), measured on an RTX 3090. The baseline is Vanilla ReFlow with 28 steps for both inversion and denoising. The table compares these methods at two different image resolutions (512x512 and 1024x1024) and shows the speedup achieved by each method compared to the baseline.
read the caption
Table 5: Per-image inference time for ReFlow inversion-based editing measured on an RTX 3090. The baseline is a vanilla ReFlow model utilizing 28 steps for both inversion and denoising.
| Resolution | Time Cost | Speedup | |
|---|---|---|---|
| Vanilla ReFlow | 512x512 | 23.76s | 1.0x |
| RF-Inversion | 512x512 | 23.36s | 1.02x |
| RF-Solver | 512x512 | 25.31s | 0.94x |
| Ours | 512x512 | 7.70s | 3.09x |
| Vanilla ReFlow | 1024x1024 | 72.10s | 1.0x |
| RF-Inversion | 1024x1024 | 71.35s | 1.01x |
| RF-Solver | 1024x1024 | 78.80s | 0.92x |
| Ours | 1024x1024 | 24.52s | 2.94x |
🔼 This table presents a comparison of various image editing methods evaluated on the PIE Bench dataset. The methods differ in their guidance ratio settings within the FLUX model during the denoising phase of image generation. Specifically, it examines the impact of adding query (Q), key (K), and value (V) features from the inversion process to the self-attention mechanism during the denoising process. The table reports metrics for structure preservation, background preservation, and CLIP similarity, alongside the number of steps and NFEs (Number of Function Evaluations) used during the editing process. This allows for a comparison of the editing performance and computational cost of the different guidance strategies.
read the caption
Table 6: Comparison on different editing methods. Results on PIE Bench are reported. Guidance terms indicate the guidance ratio settings used in the FLUX model during the denoising process.
Full paper#