↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Many machine learning models struggle with high-resolution data due to computational constraints. Existing compression techniques either don’t sufficiently reduce dimensionality or result in significant information loss. This paper addresses these issues.
The proposed method, WaLLOC, combines linear wavelet transforms with a novel autoencoder architecture to achieve both high compression ratios and uniform dimensionality reduction. WaLLOC outperforms existing methods in various benchmarks across different modalities (images, audio) and tasks (classification, colorization). Its computationally efficient design and modality-agnostic nature make it suitable for resource-constrained environments and a wide range of applications.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and efficient compression method, WaLLOC, specifically designed for compressed-domain learning. WaLLOC addresses the limitations of existing methods by combining linear transforms with non-linear dimensionality reduction, resulting in high compression ratios with minimal computational overhead. This is highly relevant to researchers working with high-resolution data and resource-constrained devices. The modality-agnostic nature of WaLLOC opens doors for applications beyond image processing and expands the potential of compressed-domain learning across various fields.
Visual Insights#

🔼 The figure demonstrates a comparison of model performance using resolution reduction versus WaLLoC for both discriminative and generative tasks. The left side shows that in discriminative models, reducing resolution improves training and inference speed but drastically reduces accuracy. Using WaLLoC maintains the speed gains of reduced resolution but significantly improves accuracy, essentially achieving higher effective resolution for the same computational cost. The right side illustrates that in signal enhancement tasks (image colorization and audio source separation), WaLLoC achieves better quality at higher resolutions compared to standard methods.
read the caption
Figure 1: In discriminative models (left), resolution reduction increases training and inference efficiency, but significantly degrades accuracy. Replacing resolution reduction with WaLLoC leads to significantly higher accuracy, while providing the same degree of acceleration. For signal enhancement (right), WaLLoC provides better quality when scaling to high resolutions compared to directly operating on image pixels or audio samples.
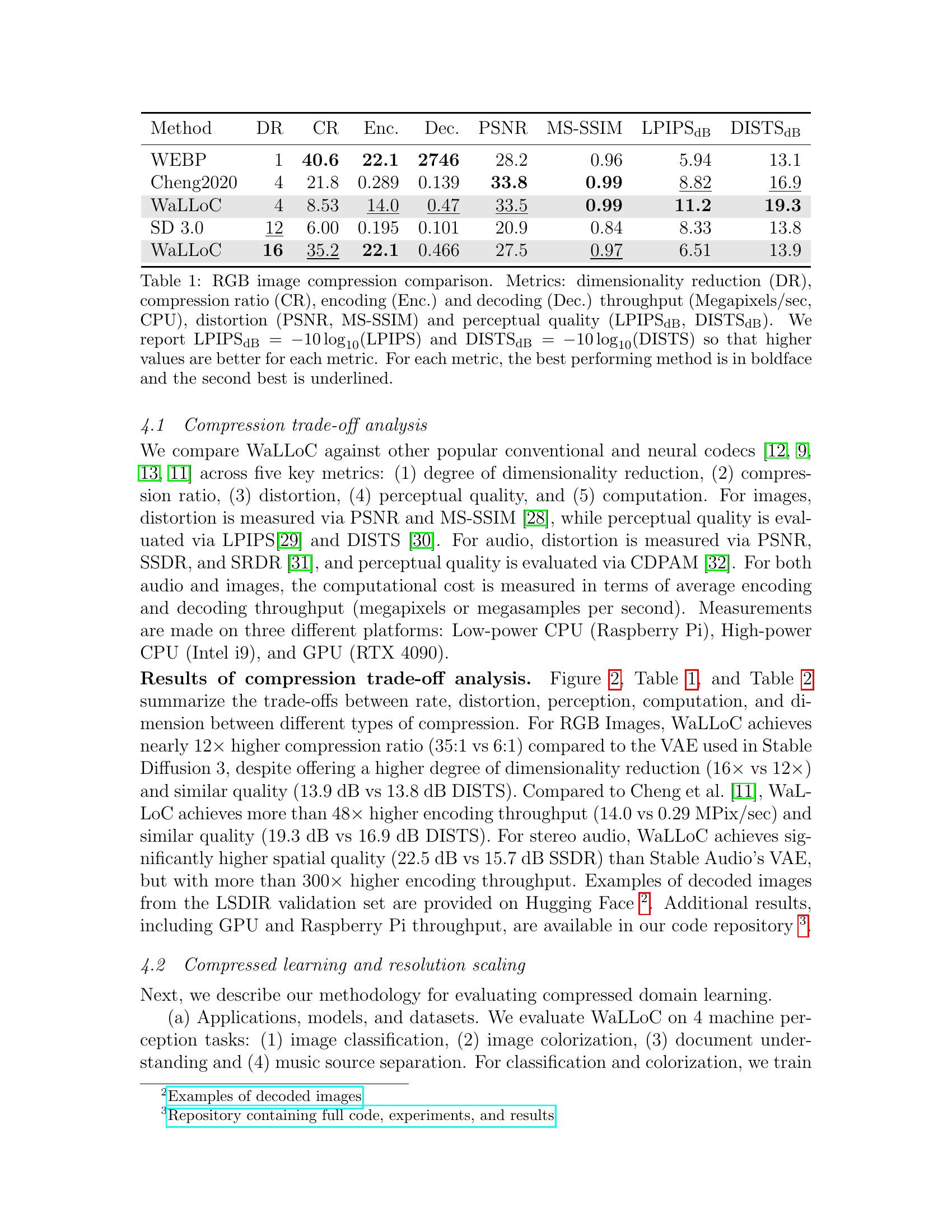
| Method | DR | CR | Enc. | Dec. | PSNR | MS-SSIM | LPIPSdB | DISTSdB |
|---|---|---|---|---|---|---|---|---|
| WEBP | 1 | 40.6 | 22.1 | 2746 | 28.2 | 0.96 | 5.94 | 13.1 |
| Cheng2020 | 4 | 21.8 | 0.289 | 0.139 | 33.8 | 0.99 | 8.82 | 16.9 |
| WaLLoC | 4 | 8.53 | 14.0 | 0.47 | 33.5 | 0.99 | 11.2 | 19.3 |
| SD 3.0 | 12 | 6.00 | 0.195 | 0.101 | 20.9 | 0.84 | 8.33 | 13.8 |
| WaLLoC | 16 | 35.2 | 22.1 | 0.466 | 27.5 | 0.97 | 6.51 | 13.9 |
🔼 This table compares the performance of different RGB image compression methods, including WaLLoC and existing techniques like WEBP and Cheng2020. It evaluates them across several key metrics: dimensionality reduction (how much smaller the compressed representation is), compression ratio (how much smaller the compressed file is compared to the original), encoding and decoding speed (in megapixels per second on a CPU), distortion (measured by PSNR and MS-SSIM), and perceptual quality (using LPIPS and DISTS). Higher values generally indicate better performance for PSNR, MS-SSIM, LPIPS, and DISTS, while lower values are better for encoding and decoding time. The best performing method for each metric is shown in bold, with the second best underlined.
read the caption
Table 1: RGB image compression comparison. Metrics: dimensionality reduction (DR), compression ratio (CR), encoding (Enc.) and decoding (Dec.) throughput (Megapixels/sec, CPU), distortion (PSNR, MS-SSIM) and perceptual quality (LPIPSdB_subscriptdB_{}_{\_}{\text{dB}}start_FLOATSUBSCRIPT _ end_FLOATSUBSCRIPT dB, DISTSdB_subscriptdB_{}_{\_}{\text{dB}}start_FLOATSUBSCRIPT _ end_FLOATSUBSCRIPT dB). We report LPIPSdB_=−10log_10(LPIPS)subscriptdB_10subscript_10LPIPS{}_{\_}{\text{dB}}=-10\log_{\_}{10}(\text{LPIPS})start_FLOATSUBSCRIPT _ end_FLOATSUBSCRIPT dB = - 10 roman_log start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT 10 ( LPIPS ) and DISTSdB_=−10log_10(DISTS)subscriptdB_10subscript_10DISTS{}_{\_}{\text{dB}}=-10\log_{\_}{10}(\text{DISTS})start_FLOATSUBSCRIPT _ end_FLOATSUBSCRIPT dB = - 10 roman_log start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT 10 ( DISTS ) so that higher values are better for each metric. For each metric, the best performing method is in boldface and the second best is underlined.
In-depth insights#
WaLLOC’s Design#
WaLLOC’s design is a novel approach to lossy compression for compressed-domain learning that addresses the shortcomings of existing methods. It cleverly combines linear transform coding (using the computationally efficient wavelet packet transform) with nonlinear dimensionality-reducing autoencoders. This hybrid approach allows for significant dimensionality reduction while maintaining computational efficiency and achieving high compression ratios. The use of an asymmetric autoencoder further enhances efficiency, with a simple linear encoder and a more complex, deep neural network decoder to handle the complexity of signal reconstruction. The incorporation of an entropy bottleneck provides robustness to quantization errors, improving compression performance. WaLLOC’s design is modality-agnostic, meaning it is applicable to various data types beyond RGB images and stereo audio, expanding its potential applications across a wider range of machine learning tasks.
Compression Tradeoffs#
The concept of “Compression Tradeoffs” in lossy compression algorithms is a critical area of research. The core challenge lies in balancing compression ratio (how much the data is reduced) with distortion (how much information is lost). Linear transform coding methods offer computational efficiency but often achieve limited compression and introduce noticeable distortion. End-to-end learned codecs generally perform better in terms of rate-distortion, but the increased computational cost can negate their benefits, especially for resource-constrained devices. Generative autoencoders excel at dimensionality reduction, but they often struggle to preserve crucial details leading to significant perceptual distortions. Therefore, the optimal approach hinges on finding a sweet spot, carefully evaluating the cost-benefit ratio of various compression techniques for a given application. This necessitates considering not only the quantitative metrics (e.g., PSNR, MS-SSIM) but also the qualitative perceptual impact of the distortion. Designing a compression method that effectively handles the tradeoff is essential for enabling efficient compressed-domain learning. The ideal system would provide high compression, minimal distortion, and low computational overhead simultaneously, making the technology applicable to a wider range of hardware platforms and computational budgets.
Resolution Scaling#
The concept of “Resolution Scaling” in the context of compressed domain learning is crucial. It explores how models trained on lower-resolution data, compressed using techniques like WaLLOC, perform when presented with higher-resolution inputs. The effectiveness of WaLLOC is particularly highlighted, demonstrating its ability to maintain or even improve accuracy at higher resolutions compared to traditional resolution reduction methods. This suggests that WaLLOC’s uniform dimensionality reduction is superior to simple downsampling, which often leads to significant information loss and accuracy degradation. The results highlight the potential of compressed domain learning to address the computational challenges associated with high-resolution data, allowing for efficient processing while preserving or enhancing model performance. Careful analysis of resolution scaling experiments is essential to fully understand the trade-offs between computational efficiency, compression ratio, and accuracy, especially when dealing with diverse modalities like images and audio.
Future Research#
Future research directions stemming from this WaLLOC paper could explore extending its applicability to diverse high-resolution data types beyond RGB images and stereo audio, such as hyperspectral images or whole-slide microscopy. Addressing the unique challenges presented by these data modalities, including higher dimensionality and specialized processing needs, would be crucial. Further investigation into optimizing the WaLLOC architecture for specific hardware platforms, particularly resource-constrained mobile devices, holds significant promise. A key area for exploration is developing a more comprehensive theoretical understanding of the interplay between lossy compression and downstream model performance. This includes analyzing the impact of different compression parameters and exploring alternative entropy coding strategies. Finally, in-depth comparative studies against emerging compression techniques, especially those tailored for specific model architectures, would provide valuable insights into WaLLOC’s strengths and limitations, facilitating further improvements and refinement of its design.
Limitations of WaLLOC#
While WaLLOC offers significant advancements in compressed-domain learning, several limitations warrant consideration. Computational efficiency, a key advantage, relies on the wavelet transform’s speed; however, extremely high-resolution inputs might still pose challenges. The asymmetric autoencoder design, while contributing to efficiency, might limit the model’s ability to reconstruct intricate details. The reliance on an additive noise bottleneck for quantization resilience introduces a trade-off: it improves robustness but might also slightly increase distortion. The generalizability across diverse modalities needs further evaluation, and while initial results are promising, specific performance may vary significantly depending on data characteristics and task complexity. Finally, the hyperparameter selection (e.g., latent dimension) is crucial for optimal performance and requires careful tuning, potentially necessitating additional computational cost for hyperparameter optimization. Therefore, a more robust and adaptive mechanism for selecting optimal hyperparameters would enhance the technique’s practical usability and overall efficacy.
More visual insights#
More on figures

🔼 Figure 2 is a 3D visualization comparing WaLLoC’s performance to other autoencoder methods (Cheng2020, Stable Diffusion 3, EnCodec, Stable Audio) across key metrics for both RGB images and stereo audio. Each point represents a different method, and the three axes show dimensionality reduction, compression ratio, and distortion. WaLLoC outperforms other methods across multiple metrics, showing better trade-offs between compression ratio and distortion. Tables 1 and 2 provide additional quantitative details.
read the caption
Figure 2: Comparison of our proposed method (WaLLoC) with other autoencoder designs for RGB Images (Cheng2020 [11], Stable Diffusion 3 [12]) and stereo audio (EnCodec [13], Stable Audio [9]). Additional metrics are reported in Tables 1 and 2.
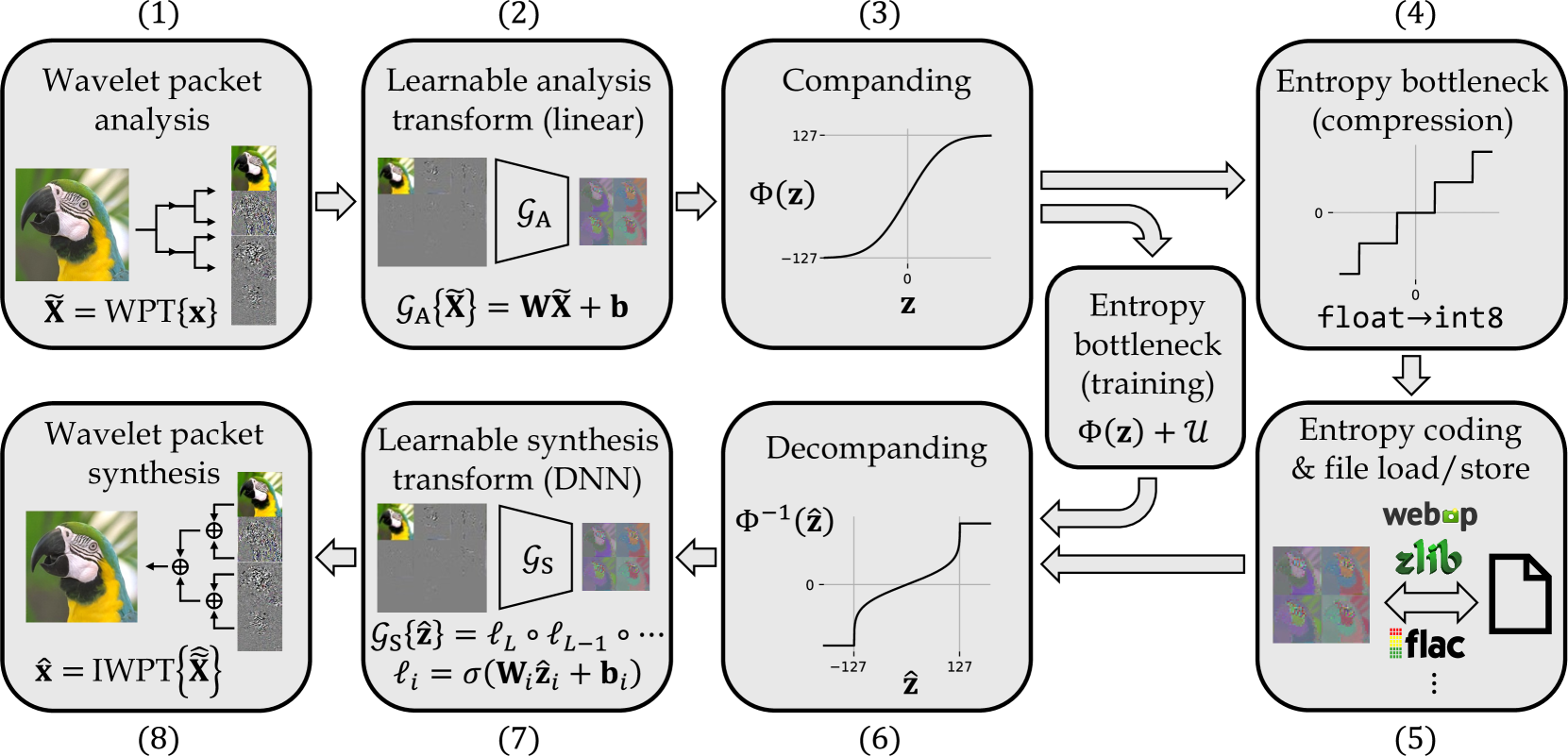
🔼 WaLLoC’s encode-decode pipeline consists of eight stages. The input signal undergoes wavelet packet analysis (WPT) to decompose it into frequency subbands, reducing redundancy. A learnable analysis transform then projects this data to a lower-dimensional latent representation. A companding function and an entropy bottleneck (added noise during training) further enhance the compression ratio. Entropy coding can be applied for storage and transmission. The decoder reverses these steps, performing inverse entropy coding, decompanding, a learnable synthesis transform, and finally inverse wavelet packet synthesis (IWPT) to reconstruct the output. Importantly, for compressed-domain learning, the entropy bottleneck and coding stages are optional, improving efficiency by eliminating CPU-GPU transfers.
read the caption
Figure 3: WaLLoC’s encode-decode pipeline. The entropy bottleneck and entropy coding steps are only required to achieve high compression ratios for storage and transmission. For compressed-domain learning where dimensionality reduction is the primary goal, these steps can be skipped to reduce overhead and completely eliminate CPU-GPU transfers.

🔼 This figure illustrates the forward and inverse wavelet packet transform (WPT) with two levels (J=2). Each level involves applying high-pass (HA) and low-pass (LA) filters independently to each signal channel. After filtering, a downsampling operation reduces the signal’s spatial or temporal resolution by a factor of two. The inverse process is depicted, starting with upsampling and applying low-pass (LS) and high-pass (HS) filters, followed by summation of the resultant two channels to reconstruct the original signal. The figure shows that the full WPT of a signal comprises J levels of this process.
read the caption
Figure 4: Example of forward and inverse WPT with J=2𝐽2J=2italic_J = 2 levels. Each level applies filters L_AsubscriptL_A\text{L}_{\_}{\text{A}}L start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT A and H_AsubscriptH_A\text{H}_{\_}{\text{A}}H start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT A independently to each of the signal channels, followed by downsampling by a factor of two (↓2)↓absent2\left(\downarrow 2\right)( ↓ 2 ). An inverse level consists of upsampling (↑2)↑absent2\left(\uparrow 2\right)( ↑ 2 ) followed by L_SsubscriptL_S\text{L}_{\_}{\text{S}}L start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT S and H_SsubscriptH_S\text{H}_{\_}{\text{S}}H start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT S, then summing the two channels. The full WPT X∼superscriptXsimilar-to\stackrel{{\scriptstyle\sim}}{{\smash{\textbf{X}}\rule{0.0pt}{4.73611pt}}}start_RELOP SUPERSCRIPTOP start_ARG bold_X end_ARG start_ARG ∼ end_ARG end_RELOP of consists of J𝐽Jitalic_J levels.

🔼 Figure 5 shows a comparison of image reconstruction quality between the method proposed by Cheng et al. in 2020 and the method used in Stable Diffusion 3. The image shows a photograph of a coffee shop at night. The top image displays the reconstruction using the method from Cheng et al. [11]. The bottom image displays the result from Stable Diffusion 3 [12], illustrating the visual differences in quality achieved by the two methods. This visual comparison helps to demonstrate one aspect of the performance and capabilities of different image compression approaches.
read the caption
Figure 5: Cheng et al. 2020 [11]

🔼 The figure shows an image of the Monkey Nest Coffee shop reconstructed using the Stable Diffusion 3 VAE. This illustrates the output quality of a generative autoencoder approach to image compression. The image shows some level of detail loss and artifacts, commonly seen in lossy compression techniques where image details are sacrificed to reduce the file size. The level of quality is relatively good considering the high compression ratio achieved by VAEs, but not as detailed as the original image. This visualization supports the discussion in the paper of how different image compression methods affect the quality and detail of compressed images and the impact on compressed-domain learning.
read the caption
Figure 6: Stable Diffusion 3 VAE [12]

🔼 This figure shows the result of compressing an image using WaLLoC with a compression ratio of 4x. It visually compares the reconstructed image to the original, demonstrating the effectiveness of WaLLoC in maintaining image quality at a reduced bitrate.
read the caption
Figure 7: WaLLoC 4×\times×

🔼 This figure shows the result of applying WaLLOC with a compression ratio of 16x to an image. WaLLOC, or Wavelet Learned Lossy Compression, is a neural codec architecture designed for efficient and high-quality compression, particularly suited for compressed-domain learning. The figure likely demonstrates the visual quality of the compressed image compared to the original (not shown) or other compression methods. The details preserved in the image after 16x compression highlight the efficacy of WaLLOC in reducing dimensionality while maintaining high fidelity.
read the caption
Figure 8: WaLLoC 16×\times×

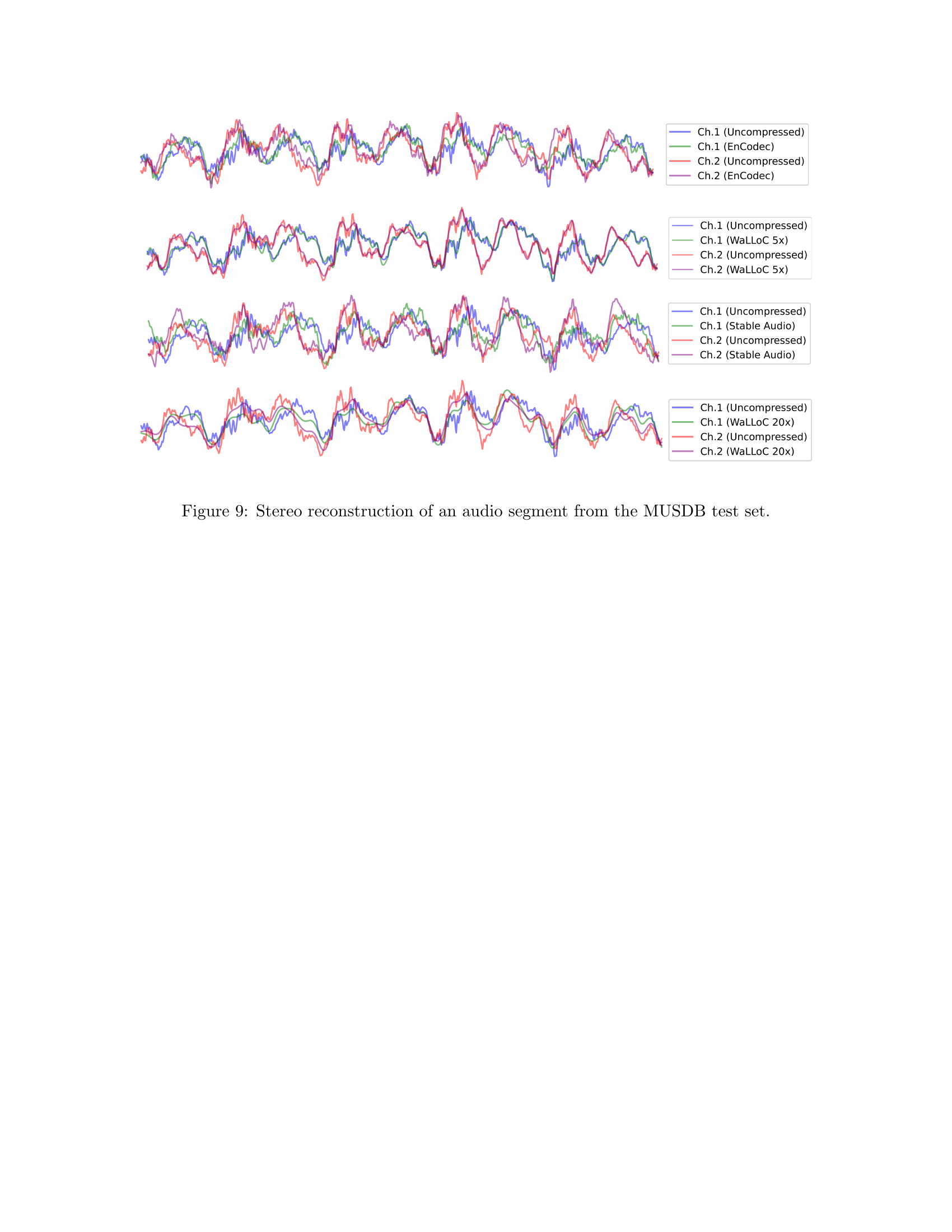
🔼 This figure displays the stereo reconstruction of an audio segment from the MUSDB test set, comparing the original uncompressed audio with the reconstructions generated by different compression methods: EnCodec, WaLLOC at 5x compression, Stable Audio, and WaLLOC at 20x compression. Each method’s reconstruction is shown as separate waveforms for each stereo channel (Ch.1 and Ch.2), allowing for a visual comparison of the fidelity and accuracy of each compression algorithm in preserving the original audio signal.
read the caption
Figure 9: Stereo reconstruction of an audio segment from the MUSDB test set.

🔼 This figure visualizes the result of decoding a 12x3x3 latent tensor using the WaLLoC 16x RGB codec. The latent tensor is mostly zeros except for a single channel, where a value of 31 is inserted in the middle element. The image shows the reconstructed images from this latent data, highlighting how the codec interprets and reconstructs the image information based on this specific input. It demonstrates the effect of a single non-zero channel on the output, showing the model’s behavior when processing sparse or low-information latent representations.
read the caption
Figure 10: Result of using the C_z=12subscript𝐶_z12C_{\_}{\textbf{z}}=12italic_C start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT z = 12 RGB codec (WaLLoC 16×\times×) to decode a 12×3×3123312\times 3\times 312 × 3 × 3 latent with all elements equal to zero except except for channel i𝑖iitalic_i, which is set to [0000310000]matrix0000310000\begin{bmatrix}0&0&0\\ 0&31&0\\ 0&0&0\end{bmatrix}[ start_ARG start_ROW start_CELL 0 end_CELL start_CELL 0 end_CELL start_CELL 0 end_CELL end_ROW start_ROW start_CELL 0 end_CELL start_CELL 31 end_CELL start_CELL 0 end_CELL end_ROW start_ROW start_CELL 0 end_CELL start_CELL 0 end_CELL start_CELL 0 end_CELL end_ROW end_ARG ].

🔼 This figure visualizes the effect of activating individual latent channels in the WaLLoC 4x RGB codec’s 48-dimensional latent space. A 48x3x3 latent representation (a tensor with dimensions 48, 3, and 3) was created where all values were set to zero except for a single channel. This channel was set to a 3x3 matrix with a single non-zero value of 31 in the center. The figure then shows the corresponding image reconstruction for each of the 48 channels. This demonstrates the individual channel’s contribution to the overall image reconstruction, illustrating WaLLoC’s ability to handle high-dimensional latent spaces effectively.
read the caption
Figure 11: Result of using the C_z=48subscript𝐶_z48C_{\_}{\textbf{z}}=48italic_C start_POSTSUBSCRIPT _ end_POSTSUBSCRIPT z = 48 RGB codec (WaLLoC 4×\times×) to decode a 48×3×3483348\times 3\times 348 × 3 × 3 latent with all elements equal to zero except except for channel i𝑖iitalic_i, which is set to [0000310000]matrix0000310000\begin{bmatrix}0&0&0\\ 0&31&0\\ 0&0&0\end{bmatrix}[ start_ARG start_ROW start_CELL 0 end_CELL start_CELL 0 end_CELL start_CELL 0 end_CELL end_ROW start_ROW start_CELL 0 end_CELL start_CELL 31 end_CELL start_CELL 0 end_CELL end_ROW start_ROW start_CELL 0 end_CELL start_CELL 0 end_CELL start_CELL 0 end_CELL end_ROW end_ARG ].
More on tables
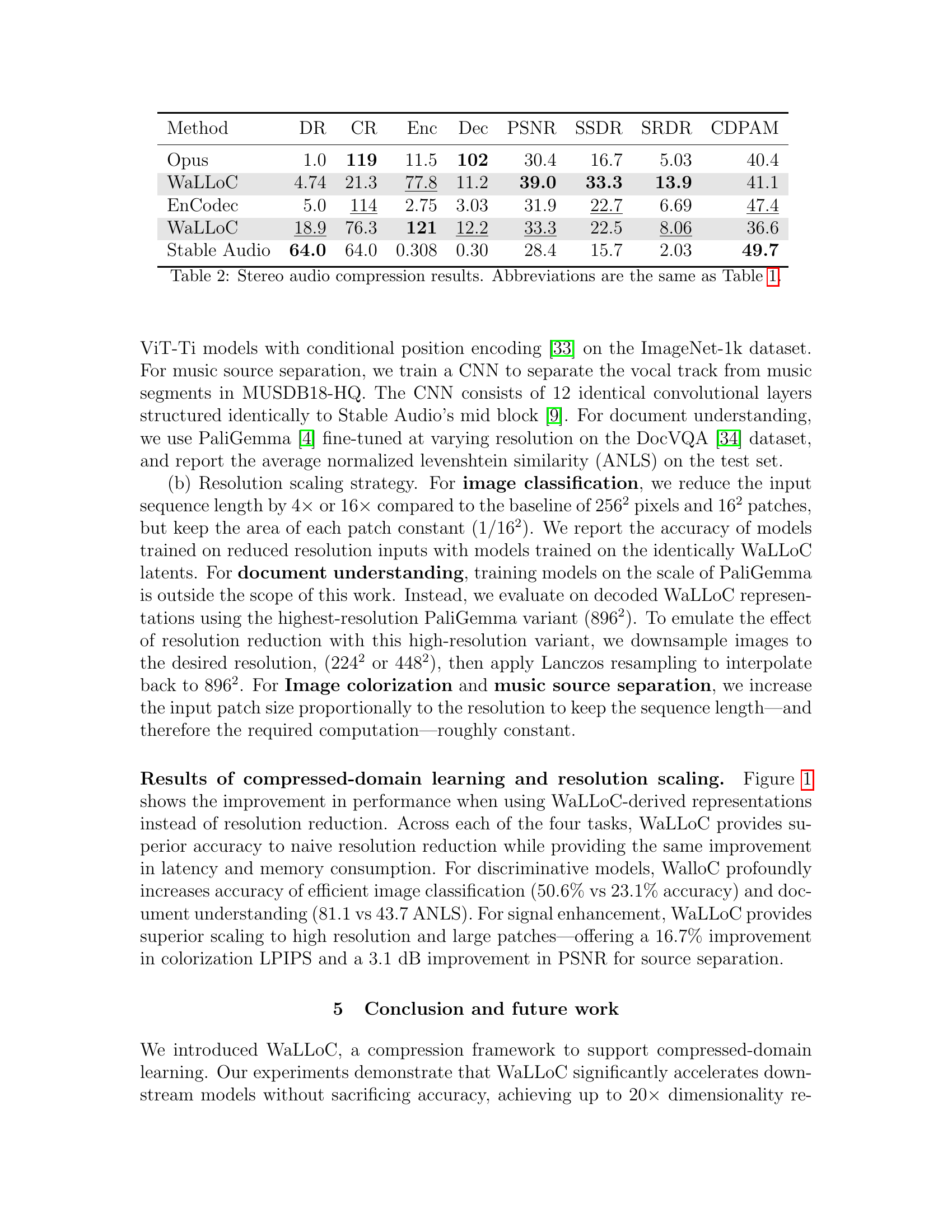
| Method | DR | CR | Enc | Dec | PSNR | SSDR | SRDR | CDaPM |
|---|---|---|---|---|---|---|---|---|
| Opus | 1.0 | 119 | 11.5 | 102 | 30.4 | 16.7 | 5.03 | 40.4 |
| WaLLoC | 4.74 | 21.3 | 77.8 | 11.2 | 39.0 | 33.3 | 13.9 | 41.1 |
| EnCodec | 5.0 | 114 | 2.75 | 3.03 | 31.9 | 22.7 | 6.69 | 47.4 |
| WaLLoC | 18.9 | 76.3 | 121 | 12.2 | 33.3 | 22.5 | 8.06 | 36.6 |
| Stable Audio | 64.0 | 64.0 | 0.308 | 0.30 | 28.4 | 15.7 | 2.03 | 49.7 |
🔼 This table presents a comparison of different stereo audio compression methods, including their dimensionality reduction (DR), compression ratio (CR), encoding and decoding throughput, and perceptual quality metrics (PSNR, SSDR, SRDR, CDPAM). The results show how WaLLoC (the proposed method) compares to other state-of-the-art techniques in terms of efficiency and fidelity. Abbreviations for the metrics are consistent with Table 1.
read the caption
Table 2: Stereo audio compression results. Abbreviations are the same as Table 1.
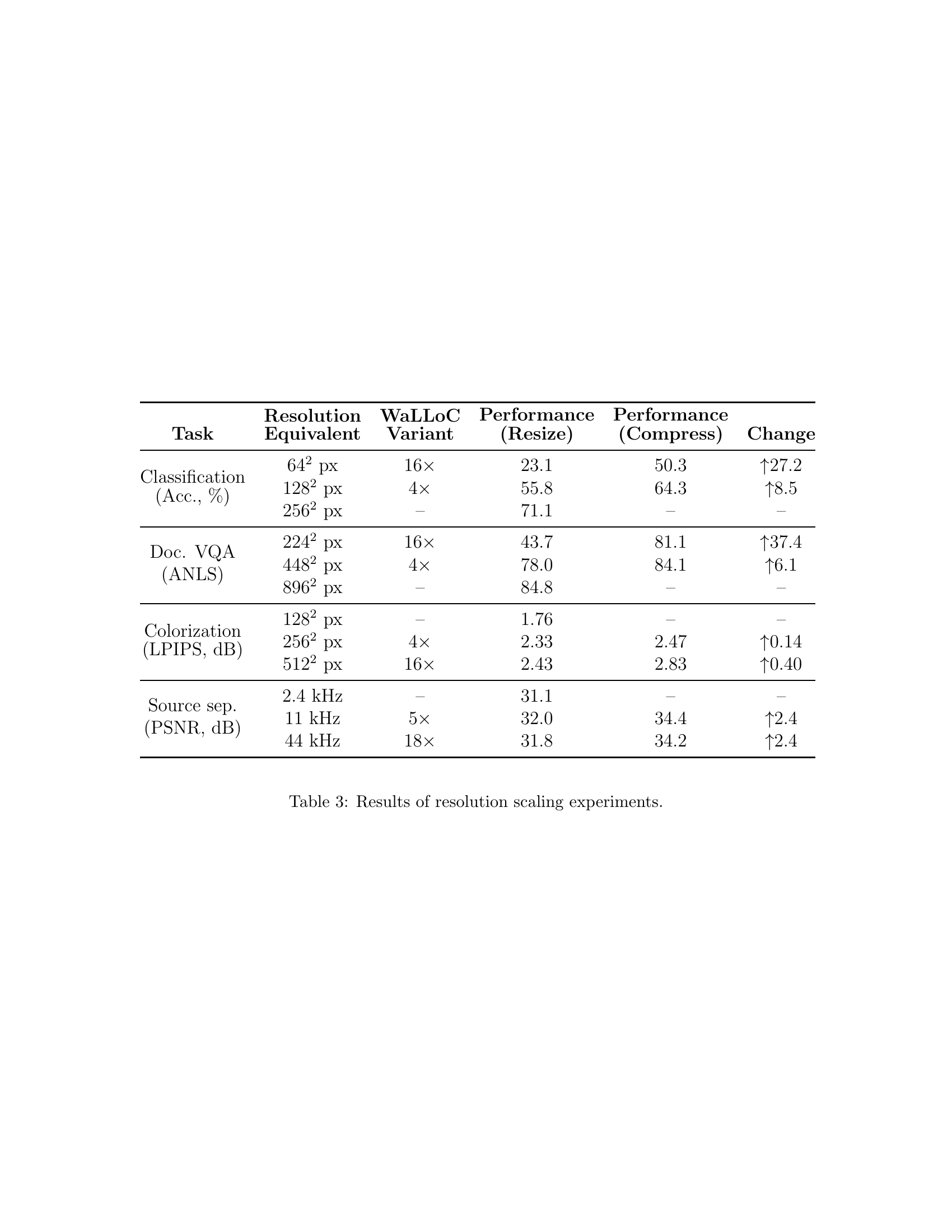
| Task | Resolution Equivalent | WaLLoC Variant | Performance (Resize) | Performance (Compress) | Change |
|---|---|---|---|---|---|
| Classification (Acc., %) | 642 px | 16x | 23.1 | 50.3 | ↑27.2 |
| 1282 px | 4x | 55.8 | 64.3 | ↑8.5 | |
| 2562 px | - | 71.1 | - | - | |
| Doc. VQA (ANLS) | 2242 px | 16x | 43.7 | 81.1 | ↑37.4 |
| 4482 px | 4x | 78.0 | 84.1 | ↑6.1 | |
| 8962 px | - | 84.8 | - | - | |
| Colorization (LPIPS, dB) | 1282 px | - | 1.76 | - | - |
| 2562 px | 4x | 2.33 | 2.47 | ↑0.14 | |
| 5122 px | 16x | 2.43 | 2.83 | ↑0.40 | |
| Source sep. (PSNR, dB) | 2.4 kHz | - | 31.1 | - | - |
| 11 kHz | 5x | 32.0 | 34.4 | ↑2.4 | |
| 44 kHz | 18x | 31.8 | 34.2 | ↑2.4 |
🔼 This table presents the results of experiments evaluating the impact of using WaLLoC for compressed-domain learning across different tasks and resolutions. It compares the performance of models trained on images/audio at various resolutions using standard resolution reduction techniques against models trained on data compressed using WaLLoC. The metrics shown reflect the changes in performance observed when using WaLLoC compared to resizing. This allows an assessment of WaLLoC’s effectiveness in maintaining or improving model performance while reducing computational costs associated with high-resolution data.
read the caption
Table 3: Results of resolution scaling experiments.
Full paper#