↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large Language Models (LLMs) are powerful but require significant computational resources. Quantization, reducing the precision of model parameters, is a common method for compression but often leads to accuracy loss or system inefficiencies. Existing solutions struggle to balance accuracy, memory usage, and speed.
MixLLM tackles this issue with a novel approach. It uses mixed-precision quantization, assigning different precision levels to different output features based on their global importance to the model’s accuracy. This is combined with a co-designed system optimization that includes a two-step dequantization process and a software pipeline to maximize the use of hardware and reduce computational overhead. Experiments show MixLLM significantly improves both accuracy and efficiency compared to state-of-the-art methods across several large language models.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical challenge in large language model (LLM) deployment: the trade-off between model size, accuracy, and efficiency. By introducing a novel mixed-precision quantization method and a highly efficient system design, this research offers a practical solution to compress LLMs without significant accuracy loss. This is particularly relevant given the increasing demand for deploying LLMs on resource-constrained devices and the growing interest in efficient model compression techniques. The findings open up new avenues for research into mixed-precision quantization, algorithm-system co-design, and improving the efficiency of LLM inference.
Visual Insights#

🔼 This figure illustrates MixLLM’s quantization method. It shows how a global mixed-precision strategy is applied to output features before kernel execution. Low-salience output features are quantized with 4-bit precision, while high-salience features use 8-bit precision. The process is designed to balance accuracy and efficiency by focusing higher precision on the most important parts of the model’s output. This is followed by a parallel execution of the matrix multiplications for the different bit-widths, resulting in optimized computation, and finally a fused scatter operation to combine the results.
read the caption
Figure 1: Illustration of the quantization with mixed-precision between output features and kernel execution.
| Llama 3.1/3.2 | Qwen2.5 | Mistral | |
|---|---|---|---|
| baselines | 1B 8B 70B | 0.5B 1.5B 7B 32B | 7B v0.3 |
| float16 | 9.75/12.72 6.24/8.95 2.81/6.68 | 13.07/17.55 9.26/13.11 6.85/10.44 | 5.02/8.95 5.32/7.84 |
| W4A16 | 11.72/15.56 6.82/9.72 3.55/7.43 | 15.54/20.55 10.35/14.35 7.23/10.88 | 5.27/9.14 5.51/8.04 |
| RTN W5A16 | 10.15/13.25 6.40/9.15 3.16/9.52 | 13.61/18.17 9.52/13.38 6.95/10.53 | 5.09/8.99 5.38/7.91 |
| GPTQ W4A16 | 10.38/14.15 6.52/9.55 Abn/Abn | 14.01/19.04 9.64/13.75 7.09/10.75 | 5.20/9.08 5.49/8.19 |
| AWQ W4A16 | 10.81/14.12 6.65/9.48 3.28/6.96 | 15.04/19.75 9.95/13.85 7.10/10.71 | 5.23/9.08 5.44/7.98 |
| SmoothQuant W8A8 | 9.89/12.91 6.34/9.08 2.92/6.77 | 13.84/18.40 9.63/13.49 7.17/10.85 | 5.12/9.04 5.35/7.88 |
| QoQ W4A8 | Abn/Abn 6.64/9.49 3.49/7.07 | Abn/Abn Abn/Abn 7.39/11.06 | 5.55/9.31 5.44/7.98 |
| W4A4 | Abn/Abn 8.34/11.95 6.16/9.91 | NA/NA Abn/Abn 8.15/12.05 | 6.26/9.98 5.83/8.50 |
| QuaRot W4A8 | Abn/Abn 6.60/9.67 3.43/7.10 | NA/NA Abn/Abn 7.03/10.68 | 5.23/9.10 5.40/7.99 |
| W4A8 (p0) | 10.36/14.09 6.54/9.62 3.30/7.24 | 14.43/19.61 9.66/13.79 7.03/10.75 | 5.21/9.08 5.42/8.02 |
| W4.4A8 (p10) | 10.05/13.51 6.42/9.33 3.02/6.83 | 13.42/18.13 9.44/13.43 6.92/10.57 | 5.12/9.01 5.36/7.93 |
| W4.8A8 (p20) | 9.95/13.25 6.37/9.22 2.97/6.79 | 13.32/17.99 9.40/13.35 6.90/10.53 | 5.09/9.00 5.35/7.90 |
| W6A8 (p50) | 9.85/12.98 6.30/9.09 2.86/6.73 | 13.21/17.78 9.33/13.25 6.88/10.49 | 5.05/8.98 5.33/7.87 |
| MixLLM W8A8 (p100) | 9.76/12.75 6.25/8.97 2.81/6.68 | 13.12/17.60 9.28/13.14 6.86/10.45 | 5.02/8.96 5.32/7.84 |
🔼 Table 1 presents perplexity scores, a measure of how well a language model predicts a text sequence, for several LLMs (Large Language Models) on the Wikitext2 and C4 datasets. Lower perplexity indicates better performance. The table compares different quantization methods (techniques to reduce the size and computational cost of the models), including various bit-widths (the number of bits used to represent model weights and activations). Different methods are compared, including weight-only quantization and weight-activation quantization. The results are shown for different model sizes. Values marked as ‘NA’ signify that the method is not applicable to that model size, while ‘Abn’ indicates perplexity scores exceeding 105. For MixLLM, the ‘pn’ notation signifies the percentage of 8-bit precision used.
read the caption
Table 1: Perplexity evaluation (↓↓\downarrow↓) on wikitext2/c4 (gray for c4), sequence length 2048. NA means no support. Abn means the value is too large (>105absentsuperscript105>10^{5}> 10 start_POSTSUPERSCRIPT 5 end_POSTSUPERSCRIPT). For MixLLM, pn means n%percent𝑛n\%italic_n % 8-bit.
In-depth insights#
Mixed-Precision Quant#
Mixed-precision quantization is a powerful technique that offers a compelling compromise between accuracy and efficiency in large language model (LLM) compression. By selectively applying different bit-widths to various parts of the model, it avoids the significant accuracy drop often associated with uniform low-bit quantization. The key lies in strategically choosing which parts of the model are more sensitive to precision reduction and assigning them higher bit-widths. This might involve using higher precision for weights of crucial layers or highly influential output features while employing lower precision for less critical components. The success of mixed-precision quantization hinges on effective identification of these sensitive areas, often requiring careful analysis of model performance and potentially incorporating techniques like gradient-based salience estimation. The approach represents a significant advance over uniform quantization, allowing for substantial compression while mitigating accuracy loss, and thus enabling efficient deployment on resource-constrained platforms.
Global Salience ID#
The concept of “Global Salience ID” in the context of large language model (LLM) quantization presents a novel approach to mixed-precision quantization. Instead of locally assessing the importance of individual neurons within each layer, a global perspective is adopted. This means evaluating each neuron’s contribution to the overall model’s output loss, assigning higher precision (e.g., 8-bit) to those with high global salience and lower precision (e.g., 4-bit) to those with less impact. This is a significant departure from existing methods that often focus on local salience identification, potentially leading to suboptimal accuracy and efficiency. The global approach allows for a more effective allocation of bitwidths, maximizing accuracy while minimizing memory consumption. Furthermore, the design’s consideration for the interplay of algorithm and system efficiency suggests a thoughtful approach to practical implementation, addressing the challenge of balancing model accuracy and computational cost. The method’s effectiveness in improving accuracy, while maintaining high system efficiency, is further substantiated by its superior performance in downstream tasks compared to the state-of-the-art methods.
Efficient Quant System#
The research paper section on ‘Efficient Quant System’ would likely detail optimizations for efficient quantization. This likely includes two-step dequantization to leverage int8 Tensor Cores effectively, mitigating the overhead of converting low-bit representations to higher-precision formats before matrix multiplications. A crucial aspect would be software pipeline design, carefully orchestrating memory access, dequantization, and matrix multiplication to maximize hardware utilization and minimize latency. The discussion would also cover fast integer-to-float conversion techniques, perhaps employing range-dependent methods to speed up the transformation process. Furthermore, GPU kernel optimization, tailored for specific quantization configurations (e.g., mixed-precision between output features), would be a focal point, aiming to enhance throughput and reduce computational costs. The system design likely accounts for minimizing latency from memory access to arithmetic operations, possibly through techniques such as memory interleaving and optimized data layouts. Overall, the efficient quant system design aims to achieve a balance between accuracy, memory consumption, and computational efficiency, allowing for faster and more memory-efficient LLM inference.
System Co-design#
System co-design in MixLLM centers on optimizing the quantization process for both accuracy and efficiency. The two-step dequantization method cleverly leverages int8 Tensor Cores, accelerating computation while mitigating the overhead of converting low-precision data back to higher precision. This is coupled with a software pipeline designed to overlap memory access, dequantization, and matrix multiplication (MatMul), maximizing GPU utilization. The choice of symmetric quantization for 8-bit activation and asymmetric quantization for 4-bit weights, along with the group-wise approach, represents a carefully considered trade-off between accuracy and computational efficiency. The overall design highlights the importance of holistic optimization, moving beyond algorithm-level improvements to encompass architectural considerations for a significantly enhanced performance.
Future Work#
Future research directions stemming from this work on MixLLM could explore several promising avenues. Extending the global salience identification method to other quantization schemes beyond the current weight-only approach would broaden the applicability and impact of MixLLM. Investigating the optimal group size for both weight and activation quantization is crucial for balancing accuracy and efficiency. Further study on the interaction between the two-step dequantization and the GPU kernel optimization would lead to improved system efficiency. The current global precision search algorithm could be improved by exploring more efficient methods, or by integrating it into the training process for a truly end-to-end solution. A comprehensive comparison against a wider array of state-of-the-art quantization methods across various LLM architectures and sizes is vital to establishing MixLLM’s overall position. Finally, research into deploying MixLLM on diverse hardware platforms would assess its robustness and potential benefits beyond the A100 GPU, paving the way for wider adoption.
More visual insights#
More on figures

🔼 This figure visualizes the distribution of high-saliency output features across different layers of the Llama 3.1 8B model after 4-bit quantization. The analysis focuses on the top 10% of features globally identified as having the most significant impact on the final loss. The x-axis represents the decoder layer indices, and the y-axis shows the percentage of high-saliency output features in each layer. Each decoder layer is composed of seven sub-layers (q_proj, k_proj, v_proj, o_proj, gate_proj, up_proj, and down_proj), and the figure shows the aggregate high-saliency percentage for the entire layer. This illustrates that the importance of various features differs significantly across different layers.
read the caption
Figure 2: The percentage of high-salient out features within each linear layer of Llama 3.1 8B model according to each feature’s contribution to the final loss after quantizing to 4-bit, with 10% high-salient features globally. Each decoder layer contains q_proj, k_proj, v_proj, o_proj, gate_proj, up_proj, and down_proj in order.

🔼 This figure illustrates how a two-step dequantization method allows efficient use of the int8 Tensor Cores on GPUs. It shows that a float32 number can be represented as a 9-bit fixed integer part and a 23-bit variable fractional part. The figure demonstrates that there’s a range where the binary representation of an integer and its corresponding float are the same (for example, ‘010010110xx…x’ where ‘x’ can be any bit). This range allows for fast integer-to-float conversion by adding and subtracting a bias, without explicitly using computationally expensive instructions. This method helps avoid performance drops that are typically associated with directly converting integers to floating point numbers for low-bit quantization.
read the caption
Figure 3: The float and integer value of binary (010010110xx...x), each within a consecutive range.
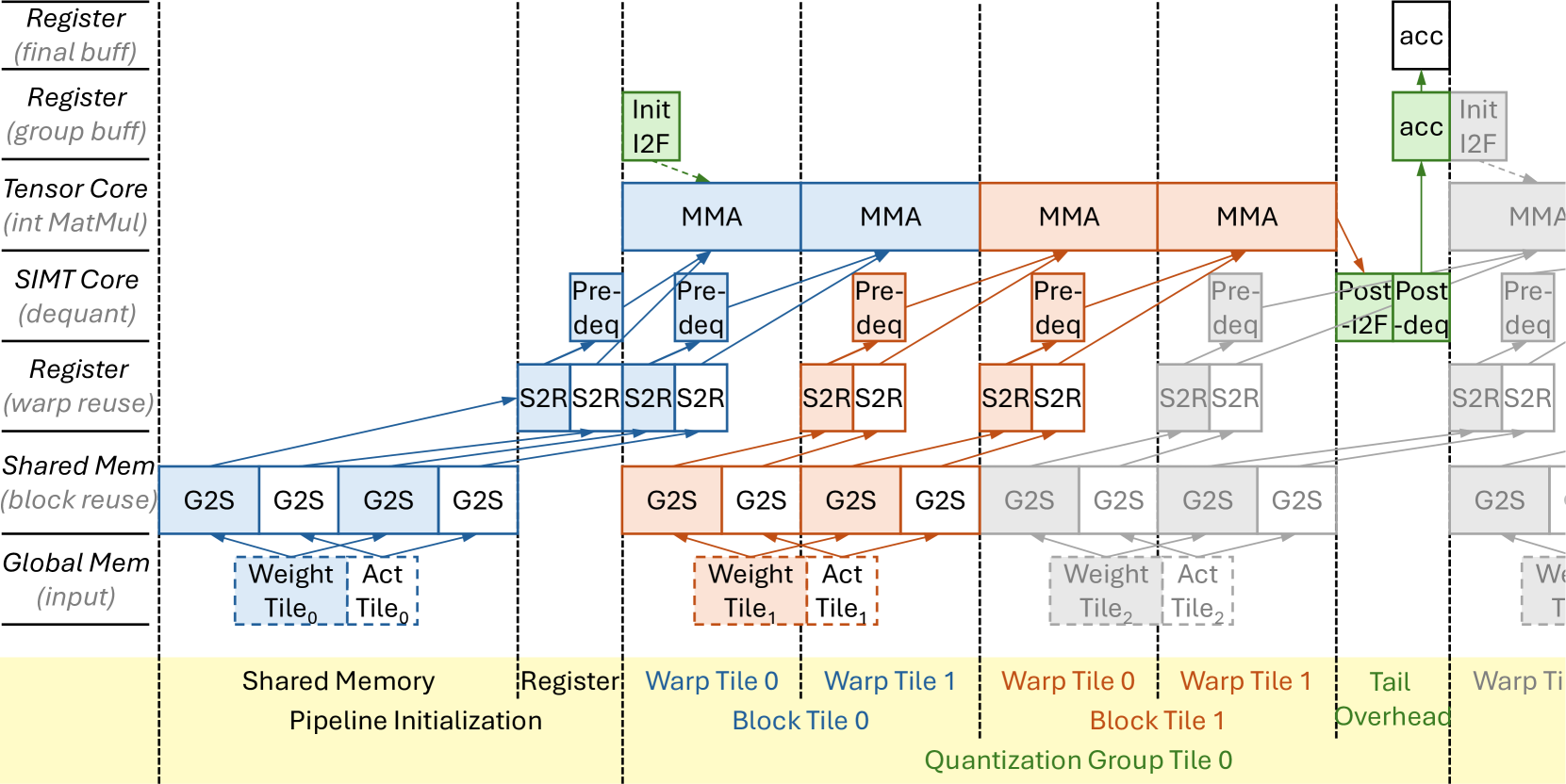
🔼 Figure 4 illustrates the optimized GPU kernel execution pipeline for performing group-wise quantized matrix multiplications (MatMul). It showcases the parallel processing stages involved in handling both 4-bit (W4A8) and 8-bit (W8A8) quantized weights and activations. The pipeline is designed for optimal performance by maximizing resource utilization and minimizing overhead. Key stages include loading data from global memory to shared memory (G2S), transferring data from shared memory to registers (S2R), performing the matrix multiply-accumulate operation (MMA) using Tensor Cores, converting integers to floating-point numbers (I2F), dequantization (deq), and accumulation (acc). The diagram assumes perfect overlapping between these stages for maximum efficiency.
read the caption
Figure 4: The GPU kernel software pipeline of group-wise W4A8/W8A8 quantized MatMul. It assumes perfect overlapping. G2S: load global to shared memory; S2R: load shared memory to register; MMA: matrix multiply-accumulation; I2F: integer to float conversion; deq: dequantize; acc: accumulate.

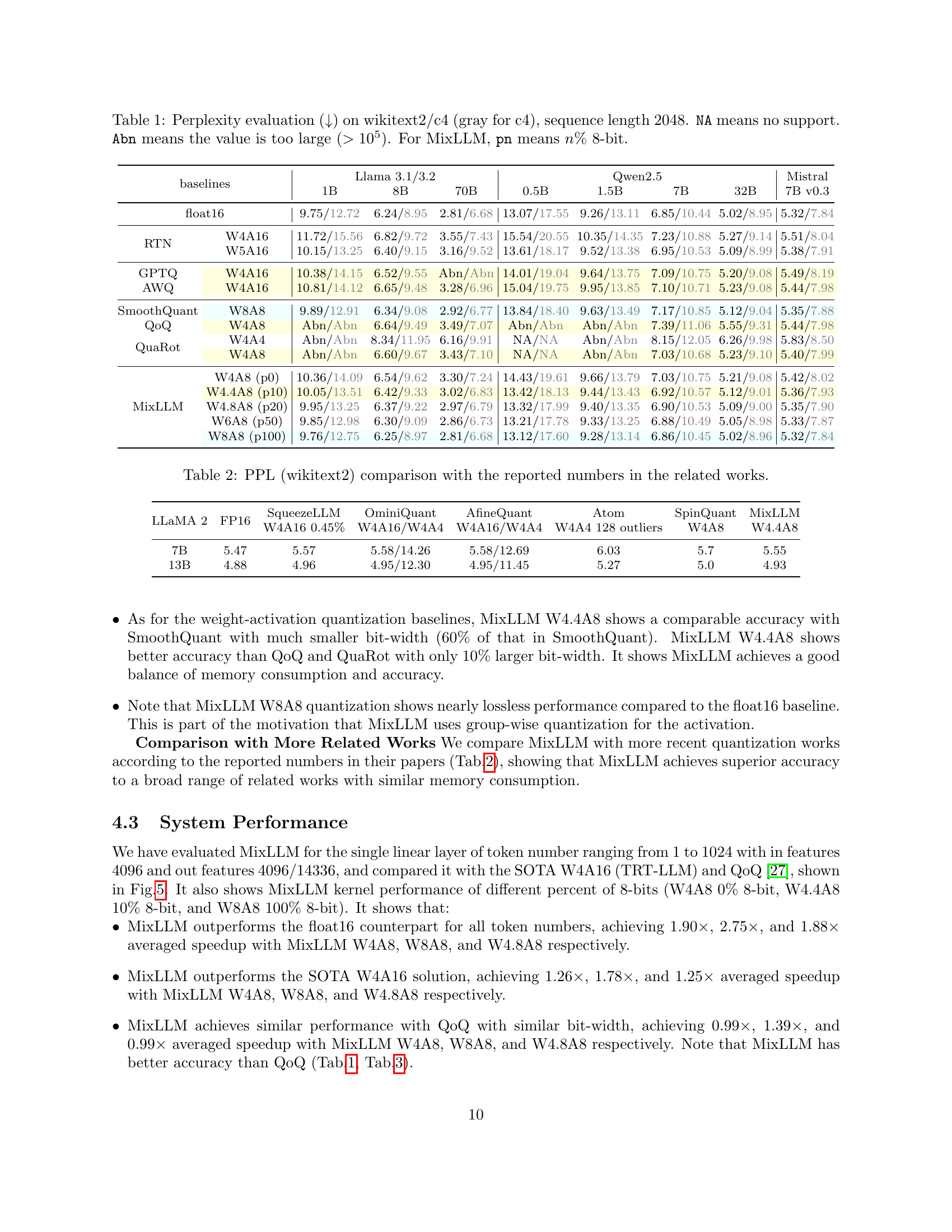
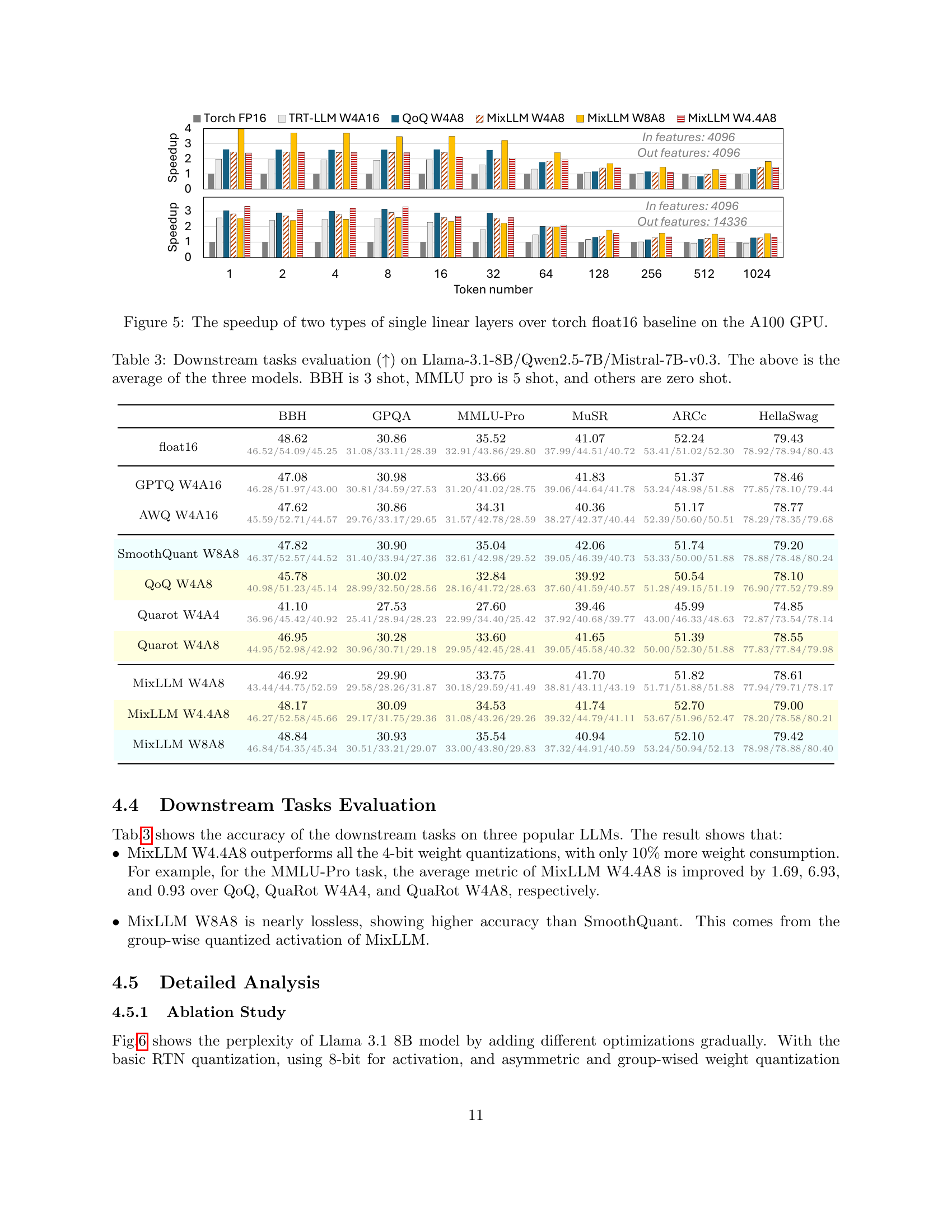
🔼 This figure showcases the performance speedup achieved by various quantization methods compared to a baseline using Torch float16 on an NVIDIA A100 GPU. Two distinct types of single linear layers are examined, each with varying numbers of tokens (input sequence length). The speedups are presented for different quantization methods with different bit-widths, offering insights into how each approach impacts the processing speed of large language models (LLMs).
read the caption
Figure 5: The speedup of two types of single linear layers over torch float16 baseline on the A100 GPU.

🔼 Figure 6 illustrates an ablation study analyzing the impact of various optimization techniques on the perplexity of the Llama 3.1 8B model when using the Wikitext2 dataset. It systematically shows the effects of adding each component: 8-bit activation quantization, asymmetric weight quantization, group-wise quantization, global 10% 8-bit feature selection using a diagonal Fisher Information matrix (with and without the first-order term), and finally GPTQ with and without the reorder technique. The baseline is 4-bit weight-only quantization with symmetric quantization per channel.
read the caption
Figure 6: The perplexity (wikitext2) of Llama 3.1 8B model with different configurations.
More on tables
| LLaMA 2 | FP16 | SqueezeLLM | OminiQuant | AfineQuant | Atom | SpinQuant | MixLLM |
|---|---|---|---|---|---|---|---|
| 7B | 5.47 | 5.57 | 5.58/14.26 | 5.58/12.69 | 6.03 | 5.7 | 5.55 |
| 13B | 4.88 | 4.96 | 4.95/12.30 | 4.95/11.45 | 5.27 | 5.0 | 4.93 |
🔼 This table compares the perplexity scores (PPL) achieved by MixLLM on the Wikitext2 dataset against various other state-of-the-art quantization methods. It specifically focuses on the results from Llama 2, showing a comparison of different quantization strategies (weight-only, mixed-precision) and bit-widths. The purpose is to demonstrate the superior performance of MixLLM, in terms of achieving a lower perplexity score indicating better performance, using either comparable or fewer bits than existing approaches.
read the caption
Table 2: PPL (wikitext2) comparison with the reported numbers in the related works.
| Model | Result |
|---|---|
| SqueezeLLM | W4A16 0.45% |
🔼 Table 3 presents the results of downstream task evaluations performed on three different large language models (LLMs): Llama-3.1-8B, Qwen2.5-7B, and Mistral-7B-v0.3. The table shows the average performance across these three models for several downstream tasks. The evaluation metrics used are not explicitly stated in the caption. Different numbers of shots were used for certain tasks: BBH used 3 shots, MMLU pro used 5 shots, while the remaining tasks employed zero shots. The table compares performance using various quantization methods.
read the caption
Table 3: Downstream tasks evaluation (↑↑\uparrow↑) on Llama-3.1-8B/Qwen2.5-7B/Mistral-7B-v0.3. The above is the average of the three models. BBH is 3 shot, MMLU pro is 5 shot, and others are zero shot.
| Model | Architecture |
|---|---|
| OminiQuant | W4A16/W4A4 |
🔼 This table shows the distribution of 8-bit output features across different linear layer types within the Llama 3.1 8B model when using MixLLM with a global 10% 8-bit output feature setting. It breaks down the proportion of high-precision (8-bit) channels within each of the seven categories of linear layers (q_proj, k_proj, v_proj, o_proj, gate_proj, up_proj, down_proj) to illustrate the non-uniform distribution of high-salience features across different parts of the model. This highlights MixLLM’s approach of selectively applying higher precision to more important features rather than uniformly.
read the caption
Table 4: The average percentage of 8-bit out features in the seven classes of linear layers in Llama 3.1 8B, with 10% global 8-bit out features in MixLLM.
| AfineQuant | |
|---|---|
| W4A16/W4A4 |
🔼 This table presents the computational time required for the global precision search algorithm used in MixLLM to determine the optimal bit-width for each output feature. The search is performed once for each model during the quantization process. The models vary in size, ranging from 1.5B to 70B parameters. The results show the trade-off between model size and search time.
read the caption
Table 5: The overhead of global precision search in MixLLM.
Full paper#