↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Multimodal reasoning poses a significant challenge for large language models, as they often struggle with complex, multi-step problems. Existing methods like outcome reward models provide sparse feedback, while manual annotation for process reward models is costly and limits scalability. Beam search, commonly used for sampling reasoning paths, often lacks diversity and reliability, especially in the multimodal context where input misalignment frequently occurs.
The proposed AR-MCTS framework leverages active retrieval to dynamically gather relevant information for each reasoning step, addressing the limitations of beam search. By integrating Monte Carlo Tree Search (MCTS), AR-MCTS automatically generates step-wise annotations and uses a process reward model for verification. Experimental results on various benchmarks show that AR-MCTS significantly enhances the performance of different MLLMs, improving both the accuracy and diversity of reasoning paths. The results highlight the effectiveness of the active retrieval strategy and demonstrate the framework’s potential for reliable and efficient automated multimodal reasoning.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel framework, AR-MCTS, that significantly improves the performance of multimodal large language models (MLLMs) in complex reasoning tasks. It addresses the challenge of enhancing MLLM reasoning capabilities by combining active retrieval with Monte Carlo Tree Search (MCTS), leading to more reliable and diverse reasoning. This work is relevant to the current research trends in retrieval-augmented generation and automated reasoning verification, opening new avenues for improving the accuracy and trustworthiness of AI systems.
Visual Insights#

🔼 This figure presents a breakdown of the composition of the hybrid-modal retrieval corpus used in the study. The corpus is comprised of both multimodal and text-only data sources. The multimodal section details the number of samples and percentage from each of several datasets, highlighting the variety of mathematical sub-fields represented. The text-only section shows the size and percentage contribution from general reasoning knowledge bases (e.g., Wikipedia). This visual representation gives the reader a clear overview of the data sources and their relative proportions in building the hybrid-modal retrieval corpus, which forms the basis for the models’ reasoning capabilities.
read the caption
Figure 1: The statistics of our hybrid-modal retrieval corpus.
| Model | Method | MathVista ALL ↑ | MathVista GPS ↑ | MathVista MWP ↑ | MathVista ALG ↑ | MathVista GEO ↑ | MathVista STA ↑ | We-Math S1 ↑ | We-Math S2 ↑ | We-Math S3 ↑ | We-Math AVG ↑ | We-Math IK ↑ | We-Math IG ↑ | We-Math CM ↑ | We-Math RM ↓ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPT-4o | Zero-shot | 59.0 | 59.6 | 65.1 | 61.2 | 60.7 | 72.4 | 71.5 | 58.3 | 46.1 | 40.8 | 31.8 | 13.7 | 33.9 | 37.8 | |
| GPT-4o | Self-Consistency | 61.8 | 68.3 | 65.1 | 68.0 | 68.2 | 74.8 | 73.3 | 63.6 | 53.0 | 45.2 | 29.9 | 12.8 | 38.8 | 32.8 | |
| GPT-4o | Self-Correction | 59.9 | 61.1 | 65.6 | 61.2 | 61.1 | 72.8 | 72.8 | 58.9 | 43.6 | 42.9 | 31.2 | 15.2 | 35.2 | 34.2 | |
| GPT-4o | ORM | 61.9 | 68.3 | 66.1 | 68.0 | 68.2 | 74.8 | 73.1 | 63.3 | 50.3 | 44.3 | 26.5 | 10.9 | 38.9 | 38.0 | |
| GPT-4o | AR-MCTS | 62.6 | 68.6 | 66.4 | 68.0 | 68.8 | 75.3 | 74.7 | 65.6 | 56.4 | 46.8 | 28.0 | 12.8 | 40.4 | 31.8 | |
| LLaVA-OneVision-72B | Zero-shot | 64.2 | 80.8 | 69.4 | 73.3 | 77.0 | 66.8 | 58.1 | 44.7 | 40.6 | 24.6 | 42.5 | 14.1 | 17.5 | 59.7 | |
| LLaVA-OneVision-72B | Self-Consistency | 66.0 | 79.8 | 73.1 | 74.0 | 76.6 | 67.8 | 70.7 | 52.8 | 38.2 | 36.9 | 33.9 | 15.8 | 29.0 | 42.4 | |
| LLaVA-OneVision-72B | Self-Correction | 58.3 | 78.4 | 68.8 | 70.1 | 74.9 | 56.8 | 48.2 | 33.9 | 30.3 | 14.7 | 55.4 | 11.8 | 8.7 | 73.3 | |
| LLaVA-OneVision-72B | ORM | 65.9 | 80.3 | 73.1 | 74.0 | 77.0 | 67.8 | 66.6 | 48.3 | 44.2 | 30.6 | 34.9 | 18.1 | 21.5 | 54.3 | |
| LLaVA-OneVision-72B | AR-MCTS | 66.3 | 79.8 | 73.1 | 74.4 | 76.6 | 67.8 | 71.1 | 52.8 | 38.9 | 37.4 | 33.7 | 18.1 | 28.4 | 41.1 | |
| InternVL2-8B | Zero-shot | 57.3 | 62.5 | 62.4 | 61.2 | 60.7 | 59.1 | 50.0 | 36.7 | 23.6 | 17.4 | 59.8 | 10.1 | 12.4 | 58.9 | |
| InternVL2-8B | Self-Consistency | 61.8 | 77.4 | 64.0 | 73.0 | 72.8 | 62.1 | 58.4 | 47.1 | 35.1 | 26.6 | 45.5 | 13.5 | 19.8 | 51.6 | |
| InternVL2-8B | Self-Correction | 46.8 | 57.7 | 31.2 | 55.9 | 56.1 | 46.2 | 43.5 | 28.1 | 30.3 | 9.8 | 62.7 | 8.6 | 5.5 | 80.8 | |
| InternVL2-8B | ORM | 61.1 | 67.8 | 64.0 | 64.1 | 64.9 | 68.4 | 64.0 | 45.0 | 32.7 | 29.7 | 42.9 | 16.0 | 21.7 | 47.2 | |
| InternVL2-8B | AR-MCTS | 63.1 | 62.9 | 71.6 | 59.9 | 62.6 | 71.4 | 65.1 | 52.2 | 43.6 | 30.5 | 37.7 | 14.7 | 23.2 | 51.2 | |
| Qwen2-VL-7B | Zero-shot | 58.8 | 45.5 | 60.5 | 45.5 | 47.9 | 70.8 | 53.4 | 37.2 | 33.9 | 19.8 | 51.2 | 12.6 | 13.5 | 62.6 | |
| Qwen2-VL-7B | Self-Consistency | 61.2 | 54.8 | 61.8 | 56.2 | 55.2 | 72.1 | 57.6 | 41.9 | 33.9 | 23.6 | 46.9 | 13.7 | 16.8 | 57.5 | |
| Qwen2-VL-7B | Self-Correction | 50.8 | 43.3 | 53.2 | 45.9 | 43.9 | 62.1 | 52.3 | 38.6 | 26.7 | 20.0 | 54.1 | 11.1 | 14.5 | 58.5 | |
| Qwen2-VL-7B | ORM | 62.3 | 55.5 | 62.7 | 56.9 | 56.5 | 72.4 | 57.8 | 45.1 | 34.6 | 26.4 | 42.9 | 11.2 | 20.8 | 54.8 | |
| Qwen2-VL-7B | AR-MCTS | 64.1 | 63.9 | 72.6 | 60.9 | 63.6 | 72.4 | 59.9 | 48.1 | 40.6 | 28.1 | 40.0 | 14.3 | 21.0 | 54.2 |
🔼 This table presents the results of a mathematical reasoning assessment conducted on various large language models (LLMs), both proprietary and open-source. The models were evaluated on two benchmark datasets: MathVista and We-Math. MathVista’s results are categorized into six sub-categories reflecting different problem types (overall accuracy, geometry problem-solving, math word problems, algebraic reasoning, geometry reasoning, and statistical reasoning). We-Math’s results are broken down into eight sub-categories based on problem complexity and reasoning skills (one-step problems, two-step problems, three-step problems, overall average score, insufficient knowledge, inadequate generalization, complete mastery, and rote memorization). The highest accuracy score achieved by each model in each category is highlighted in bold, allowing for easy comparison across models and problem types.
read the caption
Table 1: Mathematical reasoning assessment on different MLLMs using MathVista and We-Math testmini Sets. In the case of MathVista, we picked 6 categories from the original 12: ALL (overall accuracy), GPS (geometry problem solving), MWP (math word problems), ALG (algebraic reasoning), GEO (geometry reasoning), and STA (statistical reasoning). For We-Math, we selected 8 categories: S1 (one-step problems), S2 (two-step problems), S3 (three-step problems), AVG (strict overall average scores), IK (insufficient knowledge), IG (inadequate generalization), CM (complete mastery), and RM (rote memorization). The top scores for each model are highlighted in bold.
In-depth insights#
Multimodal Reasoning#
Multimodal reasoning, as explored in this research paper, presents a significant challenge in AI, demanding models capable of effectively integrating and interpreting information from diverse modalities (e.g., text, images, audio). The core difficulty lies in the complex interactions between these modalities, which often require multi-step processes for logical inference. Current approaches, often relying on beam search or similar sampling methods, are limited in their ability to explore the vast search space of potential reasoning paths and often suffer from issues of path diversity and reliability. The paper proposes a novel framework, AR-MCTS, which leverages active retrieval to dynamically obtain relevant supporting information at each reasoning step, significantly enhancing the path exploration process. This dynamic retrieval of external knowledge allows for greater accuracy and a more robust solution generation. AR-MCTS combines this active retrieval with Monte Carlo Tree Search (MCTS) to systematically explore and verify reasoning paths, leading to improved accuracy and reliability in multimodal reasoning tasks. A key innovation is the introduction of a process reward model, which progressively aligns with the reasoning process, enabling automatic verification without manual annotation. This framework demonstrates significant improvements over baseline methods across multiple benchmarks, highlighting its potential to advance the state-of-the-art in multimodal reasoning.
AR-MCTS Framework#
The AR-MCTS framework presents a novel approach to enhance multimodal reasoning in large language models (LLMs). It leverages active retrieval (AR) to dynamically select relevant information from a hybrid-modal corpus at each reasoning step, enriching the context for more accurate and diverse decision-making. This contrasts with traditional methods that rely solely on internal model knowledge. By integrating Monte Carlo Tree Search (MCTS), AR-MCTS systematically explores the reasoning space, generating step-wise annotations. A crucial component is the process reward model (PRM), which is progressively refined using direct preference optimization (DPO) and supervised fine-tuning (SFT), enabling automatic verification of the reasoning process. This automated verification alleviates reliance on human annotation, improving scalability and reliability. The framework’s effectiveness is demonstrated across multiple benchmarks, showcasing improved accuracy and diversity in sampling, especially beneficial for complex multimodal reasoning tasks and less powerful models. The combination of AR, MCTS, and a progressively refined PRM is key to AR-MCTS’ success.
Retrieval Augmentation#
Retrieval augmentation significantly enhances large language models (LLMs) by supplementing their internal knowledge with external information. This approach is particularly valuable for complex reasoning tasks, where LLMs may lack sufficient context or expertise. Effective retrieval methods are crucial, as they directly impact the quality and relevance of the information provided. The strategy of actively retrieving context during the reasoning process, rather than retrieving all information upfront, improves efficiency and accuracy. This dynamic retrieval ensures that the model receives the most pertinent information at each step of the reasoning process, allowing for more focused and reliable solutions. Furthermore, combining retrieval with techniques like Monte Carlo Tree Search (MCTS) enables automated exploration of multiple reasoning paths, leading to more robust and diverse problem-solving capabilities. However, challenges remain, such as managing the computational cost of dynamic retrieval and ensuring the compatibility of different retrieval methods with the LLM architecture. Future research should explore more efficient retrieval techniques and further investigate the integration of retrieval augmentation with other reasoning methods to enhance the overall capabilities of LLMs in complex tasks.
Process Reward Model#
A process reward model is a crucial component in enhancing the performance of multimodal large language models (MLLMs) in multi-step reasoning tasks. Unlike outcome-based reward models that only provide sparse feedback at the end of a reasoning process, a process reward model offers finer-grained rewards at each step. This allows for more effective learning and enables the model to learn from both correct and incorrect intermediate steps. By assigning intermediate rewards, the model receives more frequent feedback and guidance, leading to improved accuracy and reliability. The design of a process reward model is crucial and should align well with the specific task and characteristics of the multimodal data. The paper leverages an active retrieval mechanism to dynamically retrieve relevant information at each reasoning step, thereby enriching the information provided to the process reward model and increasing the accuracy of the intermediate feedback. This approach significantly differs from traditional methods, such as beam search, which rely solely on the model’s internal knowledge, often resulting in limited diversity and error propagation. The active retrieval component, combined with the process reward model, enables more reliable path expansion within the MCTS algorithm, allowing the MLLM to better navigate the reasoning space and optimize sampling diversity.
Future Research#
Future research directions stemming from this work on progressive multimodal reasoning via active retrieval should prioritize efficiency improvements. The current method, while effective, is computationally expensive. Exploring alternative search algorithms or optimization techniques for Monte Carlo Tree Search (MCTS) is crucial to improve scalability and reduce runtime. Further research should focus on deeper integration of retrieval and reasoning, moving beyond a simple retrieval-then-reasoning pipeline towards a more synergistic approach where retrieval dynamically informs the reasoning process and vice-versa. This might involve developing novel multimodal reasoning models that inherently leverage external knowledge sources. Investigating different reward model designs beyond the process reward model is also warranted. Exploring reinforcement learning techniques to fine-tune the reward model with less reliance on human annotation would make the system more robust and adaptable. Finally, applying this framework to a broader range of multimodal reasoning tasks and domains beyond mathematical reasoning is essential to validate its generalizability and assess its potential for wider impact. Benchmarking against a diverse set of baselines is needed to thoroughly establish the proposed method’s superiority.
More visual insights#
More on figures

🔼 This figure illustrates the process of the unified multimodal retrieval module used in the AR-MCTS framework. The module takes as input a multimodal query (text and image). It then uses two separate retrieval methods: a text-to-text retriever to search a text-only corpus and a cross-modal retriever that searches a hybrid-modal corpus (combining text and image data). The top-K results from both retrievers are combined, and a knowledge concept filtering step is applied to select the most relevant insights (top-K knowledge) to the original query based on the query’s knowledge concept. This filtered set of key insights is then passed on for use in the next step of the AR-MCTS process.
read the caption
Figure 2: The pipeline of our unified multimodal retrieval module.

🔼 The figure illustrates the AR-MCTS framework, a method for enhancing multimodal large language model (MLLM) reasoning. AR-MCTS uses active retrieval to fetch relevant information at each step of the Monte Carlo Tree Search (MCTS) process, enriching the MCTS states and expanding the MLLM’s possible actions. Importantly, the diagram highlights that not every state in MCTS requires retrieved insights; some states are generated directly from the MLLM’s internal knowledge.
read the caption
Figure 3: The overall framework of AR-MCTS: The retrieval module actively retrieves key insights at each step of the MCTS process. Then, the states of the MCTS is enhanced with different insights to expand the possible action space of the MLLM. Notably, one state of each step, such as state S1,3superscript𝑆13S^{1,3}italic_S start_POSTSUPERSCRIPT 1 , 3 end_POSTSUPERSCRIPT and S2,3superscript𝑆23S^{2,3}italic_S start_POSTSUPERSCRIPT 2 , 3 end_POSTSUPERSCRIPT in this figure, no insights are provided, and the state is a direct output of the MLLM.
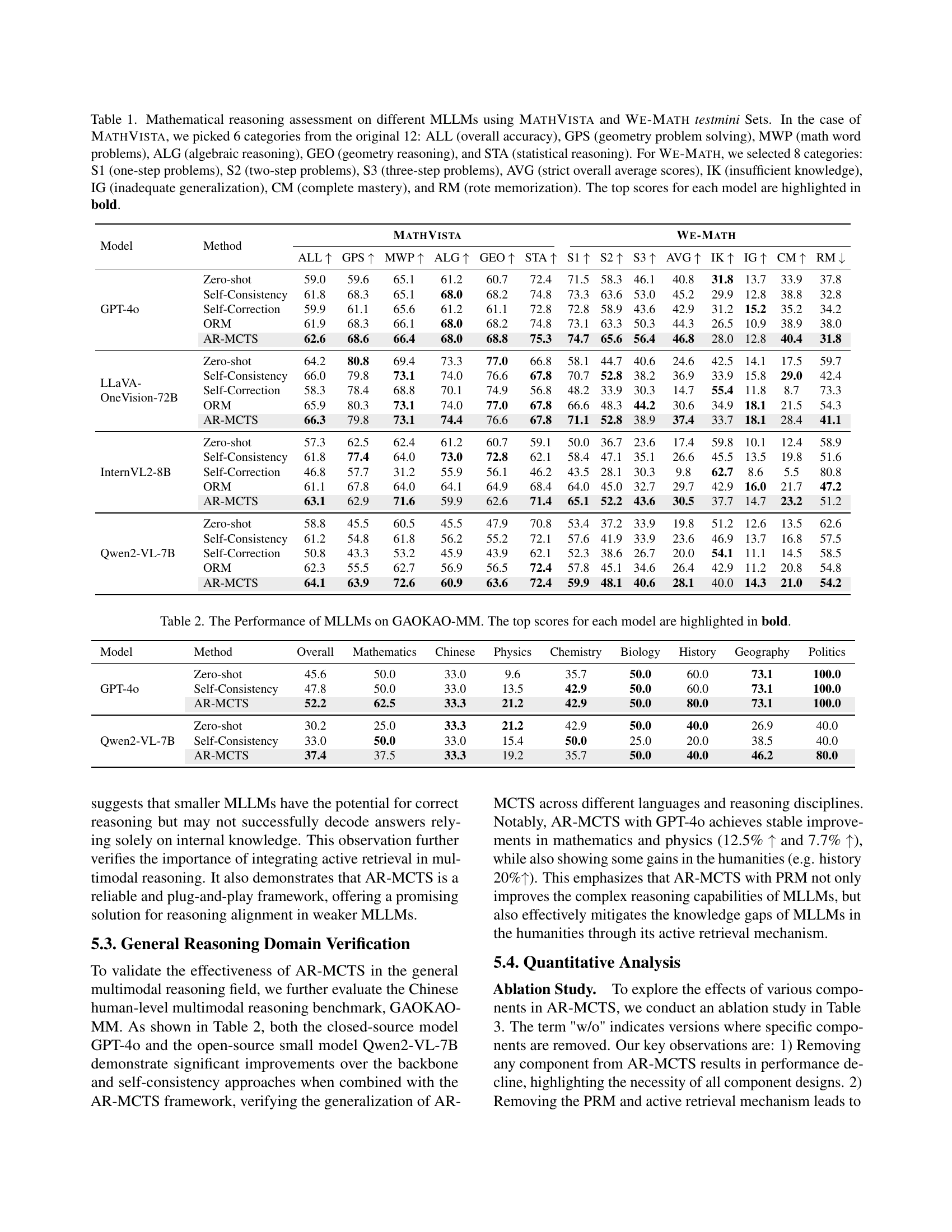
🔼 This figure presents a scaling analysis of different reasoning strategies, comparing their performance across varying numbers of sampled solutions (from 1 to 32). The x-axis represents the number of samples considered during the reasoning process. The y-axis displays the accuracy of the chosen solution. The results demonstrate how the accuracy of various methods (including AR-MCTS, Self-Consistency, and ORM) changes as the number of solution samples increases. A random sampling baseline is also included to provide a reference for comparison. The analysis is performed on two different benchmarks: MATHVISTA (ALL) and WE-MATH (S3).
read the caption
Figure 4: Scaling analysis on inference samplings. Random Choice denotes the average result of randomly sampling from 1 to 32.

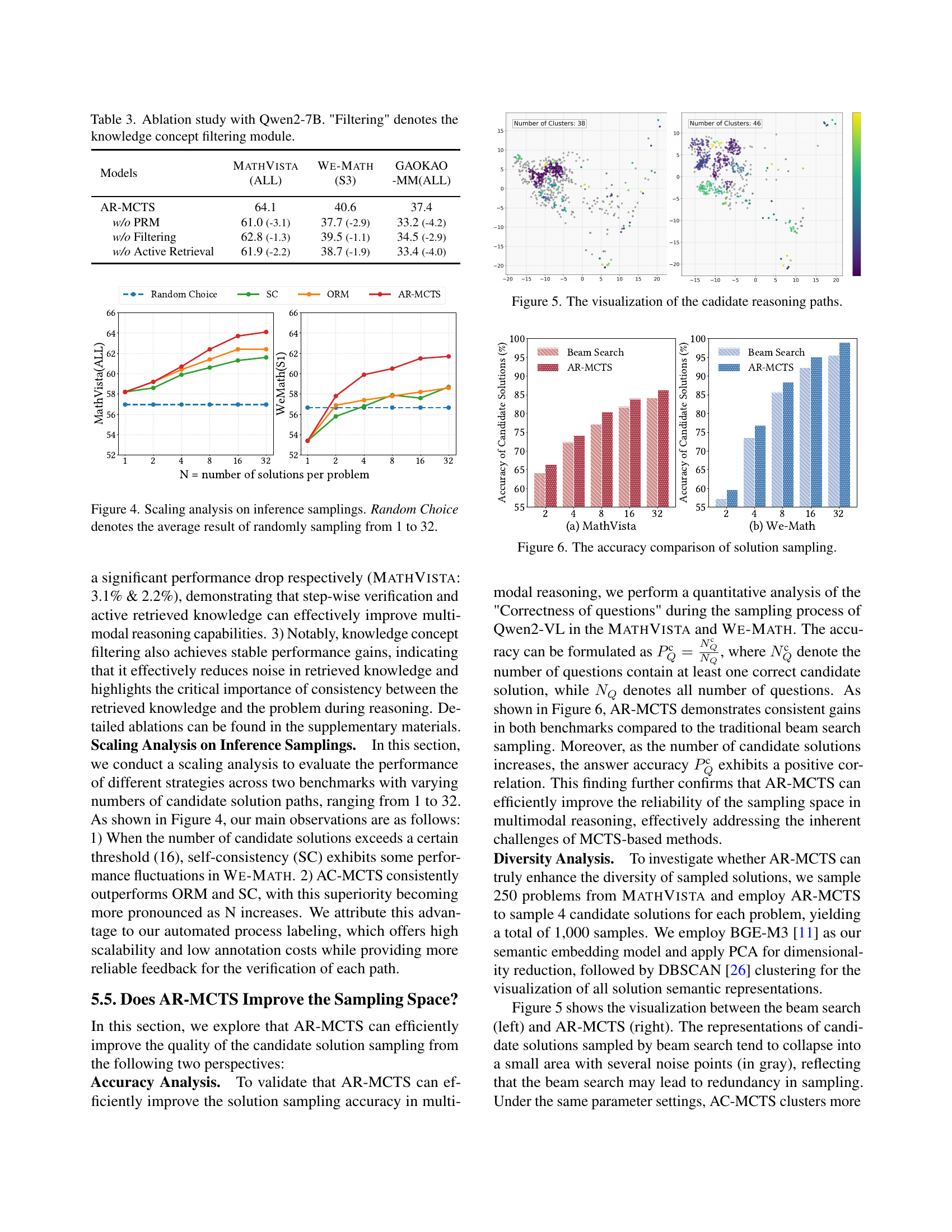
🔼 This figure visualizes the candidate reasoning paths generated by different methods: random choice, self-consistency, ORM, and AR-MCTS. Each point represents a reasoning path, and the proximity of points indicates similarity between the paths. The plots for MATHVISTA (ALL) and We-Math (S1) show the diversity and clustering of reasoning paths generated by each method. AR-MCTS demonstrates better diversity in path sampling compared to other methods.
read the caption
Figure 5: The visualization of the cadidate reasoning paths.
More on tables
| Model | Method | Overall | Mathematics | Chinese | Physics | Chemistry | Biology | History | Geography | Politics |
|---|---|---|---|---|---|---|---|---|---|---|
| GPT-4o | Zero-shot | 45.6 | 50.0 | 33.0 | 9.6 | 35.7 | 50.0 | 60.0 | 73.1 | 100.0 |
| Self-Consistency | 47.8 | 50.0 | 33.0 | 13.5 | 42.9 | 50.0 | 60.0 | 73.1 | 100.0 | |
| AR-MCTS | 52.2 | 62.5 | 33.3 | 21.2 | 42.9 | 50.0 | 80.0 | 73.1 | 100.0 | |
| Qwen2-VL-7B | Zero-shot | 30.2 | 25.0 | 33.3 | 21.2 | 42.9 | 50.0 | 40.0 | 26.9 | 40.0 |
| Self-Consistency | 33.0 | 50.0 | 33.0 | 15.4 | 50.0 | 25.0 | 20.0 | 38.5 | 40.0 | |
| AR-MCTS | 37.4 | 37.5 | 33.3 | 19.2 | 35.7 | 50.0 | 40.0 | 46.2 | 80.0 |
🔼 This table presents the performance of various Multimodal Large Language Models (MLLMs) on the GAOKAO-MM benchmark. GAOKAO-MM is a Chinese human-level multimodal reasoning benchmark, focusing on diverse subjects like mathematics, Chinese, physics, chemistry, biology, history, geography, and politics. The table shows the zero-shot performance, the performance with self-consistency, and the performance enhanced by the AR-MCTS framework. The top scores across different subjects and methods are highlighted in bold, enabling a direct comparison of MLLM capabilities across different reasoning strategies and benchmarks.
read the caption
Table 2: The Performance of MLLMs on GAOKAO-MM. The top scores for each model are highlighted in bold.
| Models | MathVista (ALL) | We-Math (S3) | GAOKAO-MM(ALL) |
|---|---|---|---|
| AR-MCTS | 64.1 | 40.6 | 37.4 |
| w/o PRM | 61.0 (-3.1) | 37.7 (-2.9) | 33.2 (-4.2) |
| w/o Filtering | 62.8 (-1.3) | 39.5 (-1.1) | 34.5 (-2.9) |
| w/o Active Retrieval | 61.9 (-2.2) | 38.7 (-1.9) | 33.4 (-4.0) |
🔼 This ablation study investigates the impact of each component of the AR-MCTS framework on the performance of the Qwen2-7B language model. Specifically, it examines the effect of removing the process reward model (PRM), the knowledge concept filtering module, and the active retrieval mechanism individually, evaluating their contributions to the overall accuracy of the model on three different benchmarks: MATHVISTA (ALL), WE-MATH (S3), and GAOKAO-MM (ALL). The results show the relative importance of each component in achieving high performance.
read the caption
Table 3: Ablation study with Qwen2-7B. 'Filtering' denotes the knowledge concept filtering module.
| Dataset | Count | Percentage |
|---|---|---|
| Wikipedia(zh-CN) | 4.7B | 23.9% |
| Wikipedia(en-US) | 15B | 73.6% |
| COIG | 178K | 0.1% |
🔼 This table presents a detailed breakdown of the general reasoning knowledge base used in the research. It shows the sources of the data, the amount of data from each source (count), and the percentage each source contributes to the overall knowledge base. The sources include two versions of Wikipedia (Chinese and English) and the COIG dataset. This information is crucial because it details the composition of the external knowledge used to augment the model’s reasoning abilities.
read the caption
Table 4: The statistics of General Reasoning Knowledge.
| Dataset | Count | Percentage |
|---|---|---|
| Text-only Datasets | ||
| GSM8K | 8,792 | 24.6% |
| MATH | 12,500 | 36.2% |
| Multimodal Datasets | ||
| MathVista | 6,141 | 17.8% |
| MathVerse | 2,612 | 7.6% |
| MathVision | 3,040 | 8.8% |
| We-Math | 1,740 | 5.0% |
🔼 This table presents a detailed breakdown of the datasets used for mathematics-specific reasoning in the research. It categorizes the datasets into text-only and multimodal categories, indicating the count and percentage contribution of each dataset to the overall corpus. This information is crucial for understanding the composition and scale of the data used for training and evaluating the proposed multimodal reasoning model.
read the caption
Table 5: The statistics of Mathematics-Specific Reasoning Knowledge.
| Model | Method | ALL | GPS | MWP | ALG | GEO | STA |
|---|---|---|---|---|---|---|---|
| GPT-4V | Zero-shot | 53.7 | 59.6 | 53.8 | 59.8 | 58.2 | 58.5 |
| Self-Consistency | 56.2 | 65.4 | 53.2 | 63.7 | 63.2 | 58.8 | |
| Self-Correction | 50.4 | 56.3 | 50.2 | 55.9 | 56.1 | 57.4 | |
| ORM | 56.6 | 65.3 | 53.1 | 65.2 | 63.2 | 59.0 | |
| AR-MCTS | 57.4 | 66.1 | 53.9 | 64.8 | 63.2 | 59.5 | |
| LLaVA-NEXT | Zero-shot | 22.5 | 22.3 | 13.4 | 24.4 | 24.7 | 22.3 |
| Self-Consistency | 23.1 | 22.6 | 16.7 | 26.0 | 24.3 | 24.3 | |
| Seld-Correction | 22.5 | 22.6 | 17.2 | 24.9 | 22.6 | 25.2 | |
| ORM | 24.4 | 22.6 | 17.5 | 27.9 | 24.3 | 29.9 | |
| AR-MCTS | 25.6 | 23.0 | 17.4 | 28.1 | 28.6 | 31.5 |
🔼 Table 6 presents the performance comparison of different methods on the MathVista testmini dataset. MathVista is a benchmark for evaluating mathematical reasoning capabilities, and the testmini set consists of 1000 problems categorized into 12 mathematical categories. This table focuses on 6 of these categories: overall accuracy (ALL), geometry problem-solving (GPS), math word problems (MWP), algebraic reasoning (ALG), geometry reasoning (GEO), and statistical reasoning (STA). Each row represents a different method, including zero-shot, self-consistency, self-correction, ORM (Outcome Reward Model), and AR-MCTS (Active Retrieval Monte Carlo Tree Search). The columns show the accuracy for each of the six categories, with the best accuracy scores for each model highlighted in bold. This table helps demonstrate the effectiveness of AR-MCTS in improving the performance of various models on complex mathematical reasoning tasks.
read the caption
Table 6: Mathematical evaluation on MathVista testmini sets. We select 6 out of the original 12 mathematical categories in MathVista: ALL (overall accuracy), GPS (geometry problem solving), MWP (math word problems), ALG (algebraic reasoning), GEO (geometry reasoning), and STA (statistical reasoning). In the results for each model, the best accuracy scores are highlighted in bold.
| Dataset | MathVista | We-Math |
|---|---|---|
| Text-only Datasets | ||
| COIG | 0.1% | 0.1% |
| Wikipedia(en-US) | 0.6% | 1.1% |
| GSM8K | 4.5% | 2.0% |
| MATH | 4.5% | 1.8% |
| Multimodal Datasets | ||
| MathVerse | 0.7% | 2.9% |
| MathVision | 0.3% | 0.9% |
| We-Math | 0.5% | - |
| MathVista-testmini | - | 4.2% |
🔼 This table presents the results of a contamination analysis performed on the hybrid-modal retrieval corpus used in the study. The analysis aims to quantify the level of overlap or contamination between the data used for training and the data used for testing, ensuring the integrity and reliability of the experimental results. The table likely shows percentages of overlap between different datasets comprising the retrieval corpus and test sets, helping to confirm the absence of data leakage, a crucial aspect of evaluating model performance.
read the caption
Table 7: The contamination analysis on hybrid-modal retrieval corpus.
| Model | ALL | GPS | MWP | ALG | GEO | STA |
|---|---|---|---|---|---|---|
| Qwen2-VL-7B | 58.8 | 45.5 | 60.5 | 45.5 | 47.9 | 70.8 |
| + BM25 | 60.2 | 54.8 | 57.9 | 53.3 | 54.6 | 72.1 |
| + Contriever | 59.9 | 53.9 | 58.5 | 53.3 | 54.1 | 72.4 |
🔼 This table presents the ablation study results focusing on the impact of different text retrieval methods on the overall performance of the AR-MCTS model. It shows the accuracy scores across various mathematical reasoning categories (ALL, GPS, MWP, ALG, GEO, STA) when using different text retrieval approaches (BM25, Contriever) with the Qwen2-VL-7B model. The goal is to determine the effectiveness of various text retrieval methods within the AR-MCTS framework, highlighting the contribution of the chosen retrieval method on the overall task performance.
read the caption
Table 8: The ablations of different text retrievers.
| Model | S1 | S2 | S3 |
|---|---|---|---|
| Qwen2-VL-7B | 53.4 | 37.2 | 33.9 |
| + CLIP-ViT-L/14 | 54.9 | 38.7 | 34.5 |
| + Jina-CLIP-v1 | 54.4 | 36.9 | 34.1 |
🔼 This table presents the ablation study results focusing on different multimodal retrieval methods used within the AR-MCTS framework. It shows the impact of using various multimodal retrieval techniques (CLIP-ViT-L/14 and Jina-CLIP-v1) on the overall performance, specifically evaluating the S1, S2, and S3 metrics of the WE-MATH benchmark. The results demonstrate the effectiveness of the chosen multimodal retrieval method in enhancing the reasoning capabilities of the model.
read the caption
Table 9: The ablations of different multimodal retrievers.
| Model | ALL | GPS | MWP | ALG | GEO | STA |
|---|---|---|---|---|---|---|
| PRM (Hard) | 62.9 | 63.3 | 71.5 | 59.4 | 62.2 | 71.0 |
| PRM (Soft) | 64.1 | 63.9 | 72.6 | 60.9 | 63.6 | 72.4 |
🔼 This table presents a comparison of the performance of two different Process Reward Model (PRM) training methods: one using hard labels and the other using soft labels. The comparison is done across various metrics on the MATHVISTA benchmark, evaluating the models’ overall accuracy and performance on specific mathematical reasoning sub-categories.
read the caption
Table 10: The comparison of different training objectives for PRMs.
Full paper#