↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Current large language models (LLMs) struggle with complex mathematical problems. Existing math-specialized LLMs often lack robustness and reliable evaluation methods. There’s a need for more effective training processes and better ways to assess the quality of generated solutions.
AceMath introduces a new suite of powerful math models, significantly outperforming existing systems. This is achieved through a two-stage fine-tuning process and a novel reward model, AceMath-RM. The project also introduces AceMath-RewardBench, a comprehensive benchmark for evaluating reward models. The models and datasets are open-sourced to facilitate further research.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language models (LLMs) and mathematical reasoning. AceMath pushes the boundaries of LLM capabilities in complex mathematical problem-solving, offering significant advancements in both instruction-tuned models and reward modeling. Its open-sourcing of models and datasets fosters collaboration and accelerates future research. The two-stage fine-tuning strategy and the novel reward model are particularly impactful, providing new avenues for improved LLM training and evaluation.
Visual Insights#

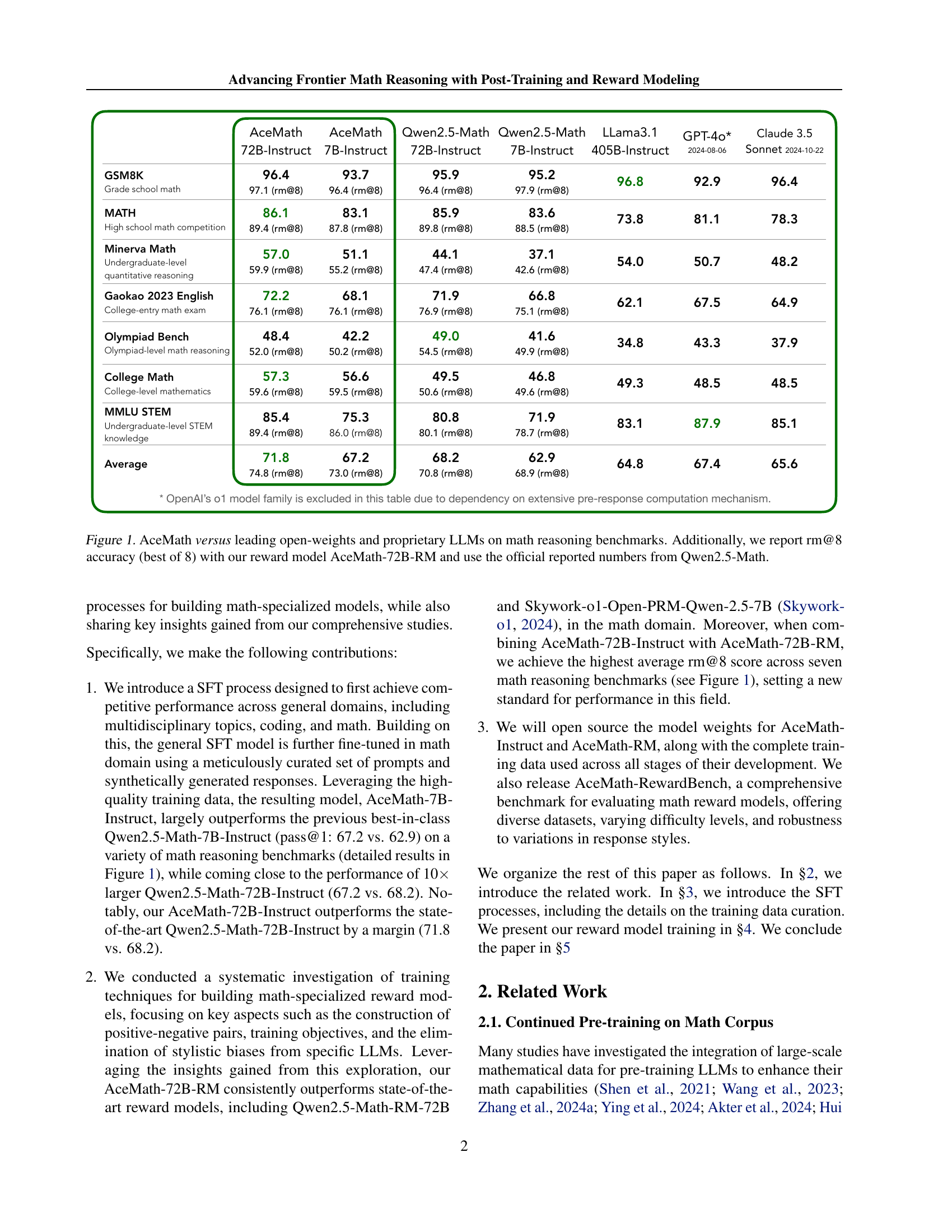
🔼 This figure compares the performance of AceMath models against other leading open-source and proprietary large language models (LLMs) on various math reasoning benchmarks. AceMath models consistently outperform the others. The chart displays the accuracy of each model on several benchmark datasets, including those focused on different grade levels and types of math problems. The results show AceMath’s superiority and the benefit of incorporating AceMath’s reward model (AceMath-72B-RM) for improved accuracy.
read the caption
Figure 1: AceMath versus leading open-weights and proprietary LLMs on math reasoning benchmarks. Additionally, we report rm@8 accuracy (best of 8) with our reward model AceMath-72B-RM and use the official reported numbers from Qwen2.5-Math.
| Models | HumanEval | MBPP | GSM8K | MATH | MMLU | MMLU Pro | Avg. |
|---|---|---|---|---|---|---|---|
| DeepSeek-Coder-7B-Instruct-v1.5 | 64.10 | 64.60 | 72.60 | 34.10 | 49.50 | - | - |
| DeepSeek-Coder-7B-Base + Two-Stage SFT (Ours) | 78.05 | 73.54 | 82.56 | 55.62 | 54.65 | 33.28 | 62.95 |
| Llama3.1-8B-Instruct | 72.60 | 69.60 | 84.50 | 51.90 | 69.40 | 48.30 | 66.05 |
| Llama3.1-8B-Base + Two-Stage SFT (Ours) | 81.10 | 74.71 | 90.45 | 64.42 | 68.31 | 43.27 | 70.38 |
| Qwen2.5-1.5B-Instruct | 61.60 | 63.20 | 73.20 | 55.20 | 58.37 | 32.40 | 57.33 |
| Qwen2.5-1.5B-Base + Two-Stage SFT (Ours) | 73.17 | 65.76 | 80.44 | 60.34 | 58.17 | 33.78 | 61.94 |
| Qwen2.5-7B-Instruct | 84.80 | 79.20 | 91.60 | 75.50 | 74.51 | 56.30 | 76.99 |
| Qwen2.5-7B-Base + Two-Stage SFT (Ours) | 85.37 | 74.32 | 93.10 | 76.40 | 74.68 | 54.50 | 76.40 |
| Qwen2.5-72B-Instruct | 86.60 | 88.20 | 95.80 | 83.10 | 84.67 | 71.10 | 84.91 |
| Qwen2.5-72B-Base + Two-Stage SFT (Ours) | 89.63 | 83.66 | 96.36 | 84.50 | 83.88 | 66.10 | 84.02 |
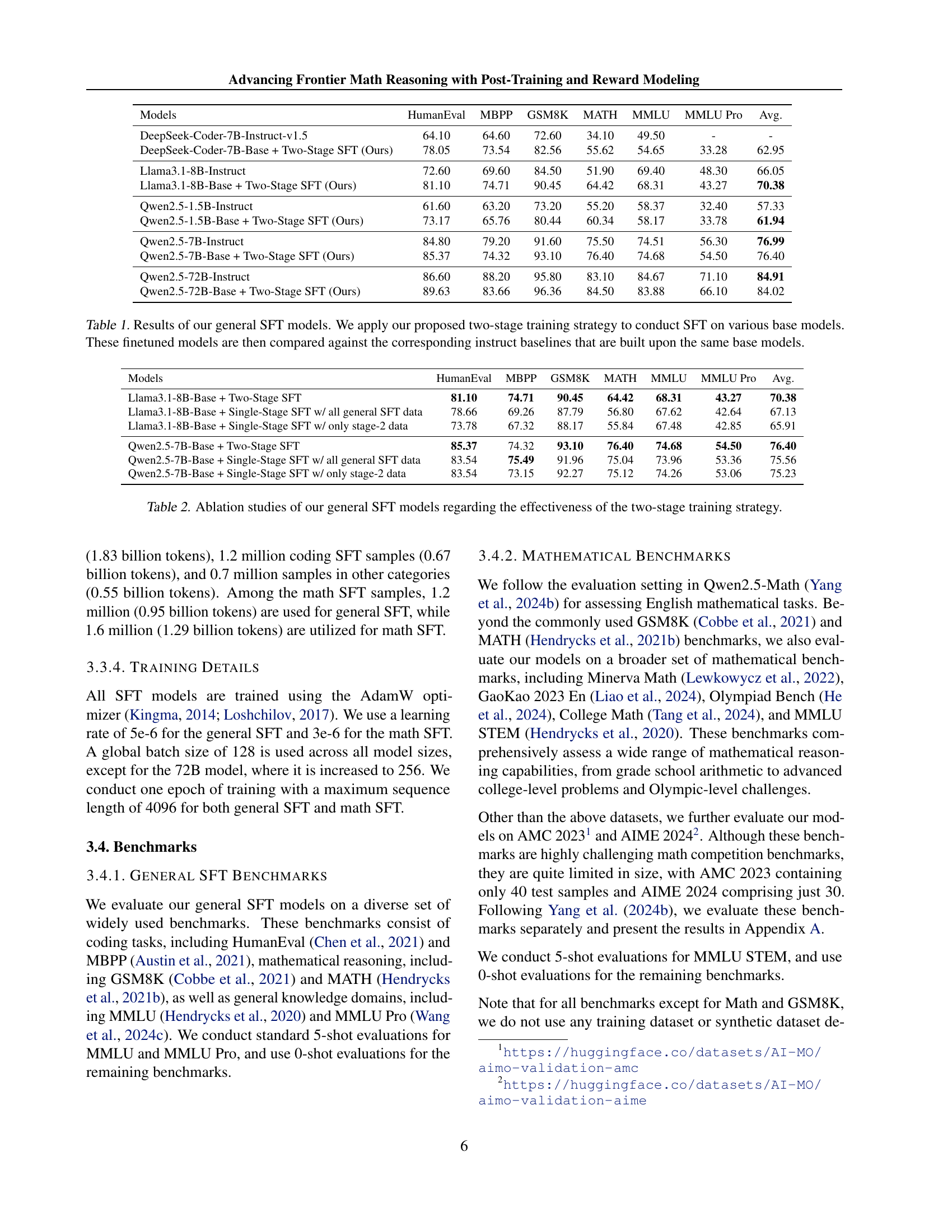
🔼 This table presents a comparison of the performance of several large language models (LLMs) after undergoing supervised fine-tuning (SFT). The models were fine-tuned using a two-stage approach: first, a general SFT was performed, followed by targeted fine-tuning for math-related tasks. The table shows the performance of these fine-tuned models, denoted as ‘Base + Two-Stage SFT (Ours)’, across various benchmarks. For comparison, the table also includes results for corresponding instruction-tuned baselines, which were not fine-tuned with the two-stage approach. These results demonstrate the effectiveness of the two-stage training strategy.
read the caption
Table 1: Results of our general SFT models. We apply our proposed two-stage training strategy to conduct SFT on various base models. These finetuned models are then compared against the corresponding instruct baselines that are built upon the same base models.
In-depth insights#
SFT for Math LLMs#
Supervised fine-tuning (SFT) plays a crucial role in enhancing the mathematical reasoning capabilities of large language models (LLMs). Effective SFT for math LLMs necessitates high-quality training data, often involving a combination of carefully curated prompts and synthetically generated responses. A two-stage SFT approach can be particularly effective: first, performing SFT on general domains to build a strong foundation of instruction-following and reasoning skills; then, conducting targeted SFT using a carefully curated math dataset to hone the LLM’s mathematical abilities. The quality of synthetic data is crucial. Data decontamination techniques are essential to mitigate bias and prevent memorization of test samples. Careful consideration of the training process, including the choice of optimizer and learning rate, are also vital factors to achieve optimal results and improve model performance on math-specific benchmarks.
Reward Model Design#
Designing effective reward models is crucial for training high-performing language models, particularly in complex domains like mathematics. The paper emphasizes a robust benchmark, AceMath-RewardBench, for comprehensive evaluation, going beyond existing limitations. The training strategy focuses on a systematic approach, addressing issues like stylistic biases and data quality. A key aspect is the use of score-sorted sampling to create balanced positive-negative pairs, enhancing the model’s ability to discriminate correctly. The choice of listwise Bradley-Terry loss shows efficiency and effectiveness for optimization. The resulting AceMath-RM consistently surpasses state-of-the-art reward models, demonstrating the success of this thoughtful design process.
AceMath Benchmarks#
AceMath Benchmarks would ideally encompass a diverse range of mathematical problems, spanning various difficulty levels and topics. Comprehensive coverage is key; including arithmetic, algebra, calculus, geometry, and potentially even more advanced areas like abstract algebra or number theory. The benchmarks should not only assess the accuracy of solutions but also the reasoning process. This could involve evaluating the clarity, completeness, and correctness of the steps taken to arrive at an answer. Diverse problem formats (multiple-choice, free-response, proof-based) would also enhance the robustness of the evaluation. Finally, scalability is crucial. The benchmark should be designed to easily accommodate future growth, enabling the assessment of ever-larger and more sophisticated models. The selection of existing datasets should be justified and the rationale clearly described. A strong AceMath Benchmark would be a valuable tool for assessing progress in the field of mathematical reasoning within large language models.
Ablation Studies#
Ablation studies systematically remove components of a model or training process to assess their individual contributions. In this context, several key ablation studies were conducted. The impact of different training strategies (e.g., two-stage vs. single-stage fine-tuning) on model performance was evaluated, revealing the effectiveness of a staged approach. The influence of various datasets and training techniques for reward model development was also analyzed. The results demonstrated the importance of careful data selection and the choice of training methodologies. Furthermore, studies investigated the influence of using different base models and the impact of synthetic data on overall model accuracy. These ablation experiments provided crucial insights into the design choices and the robustness of the proposed AceMath models, highlighting the critical role of specific components in achieving state-of-the-art performance.
Future Directions#
Future research directions for advancing frontier math reasoning with LLMs could involve exploring more sophisticated reward modeling techniques, such as incorporating step-wise reasoning or incorporating external knowledge sources into the reward function. Further improvements could be made by developing larger and more diverse training datasets, perhaps focusing on problems that require complex multi-step reasoning and problem decomposition. Investigating more advanced training strategies that better leverage synthetic data and minimize issues related to data contamination is also crucial. Additionally, research into the interpretability of the models’ reasoning processes would be valuable, as it would allow for greater insights into the models’ strengths and weaknesses, as well as providing a way to debug or improve them. Finally, it will be important to develop robust and standardized benchmarks for evaluating math reasoning capabilities, helping to compare across different models and promote fair and meaningful comparisons.
More visual insights#
More on figures

🔼 This figure shows the distribution of the total number of tokens used in the supervised fine-tuning (SFT) data for training the general SFT model. The total tokens are broken down into three categories: math, coding, and others. The math category consists of tokens from various math-related datasets, including NuminaMath, OrcaMathWordProblems, MathInstruct, MetaMathQA, and synthetically generated data. The coding category contains tokens from datasets like Magicoder, WizardCoder, GlaiveCodeAssistant, and CodeSFT. The ‘others’ category encompasses tokens from various general-purpose instruction-following datasets such as ShareGPT, SlimOrca, EvolInstruct, GPTeacher, AlpacaGPT4, and UltraInteract.
read the caption
Figure 2: The proportion of total SFT tokens for math, coding, and other categories.

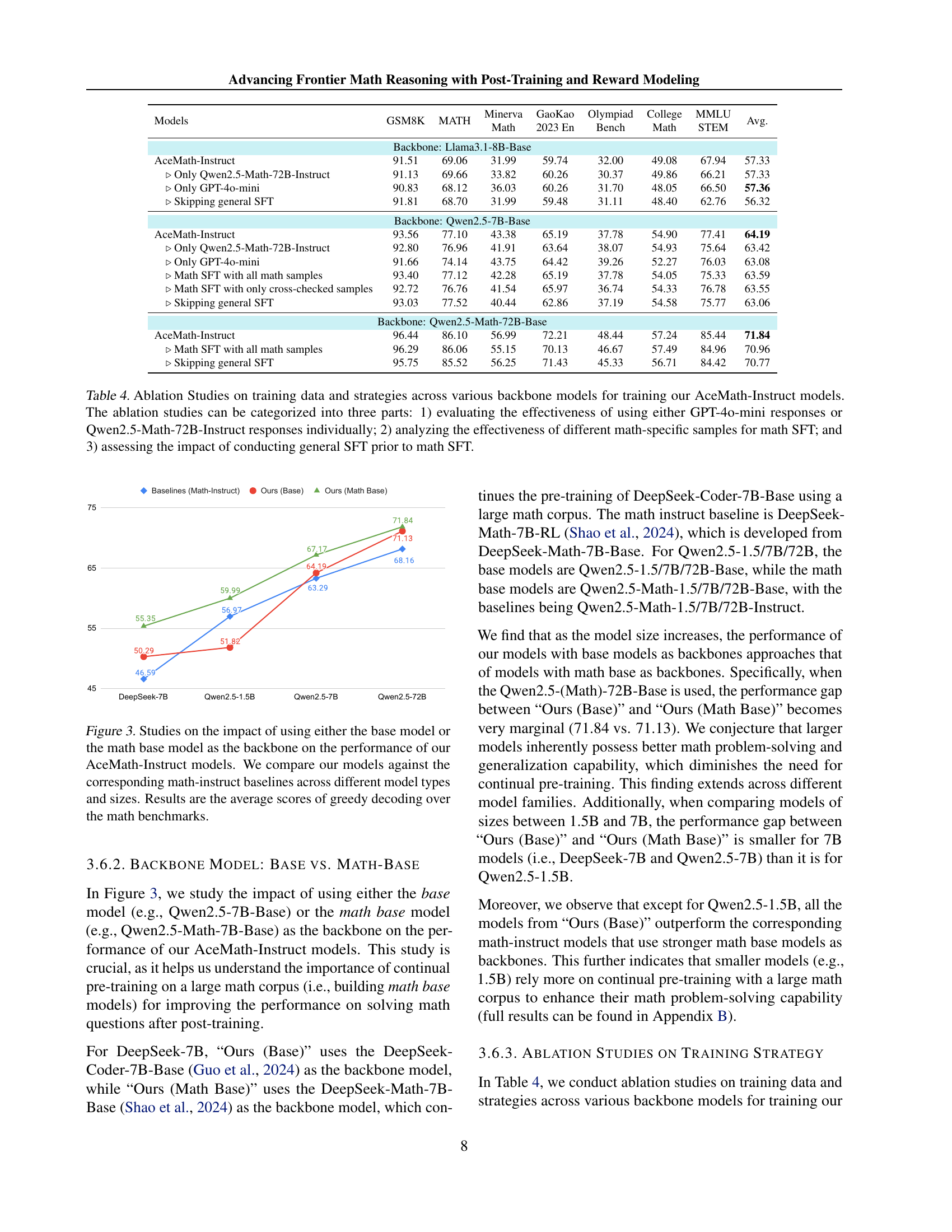
🔼 This figure compares the performance of AceMath-Instruct models, which are fine-tuned using both general and math-specific data, against their corresponding math-instruct baselines (models trained only on math data). It investigates the impact of using either a general-purpose base model or a math-specialized base model as the starting point for fine-tuning. The comparison is done across various model sizes and types, and the results are shown as average greedy decoding scores across several math reasoning benchmarks. This illustrates whether pre-training a model on a large math corpus before instruction-tuning improves its performance on math-related tasks.
read the caption
Figure 3: Studies on the impact of using either the base model or the math base model as the backbone on the performance of our AceMath-Instruct models. We compare our models against the corresponding math-instruct baselines across different model types and sizes. Results are the average scores of greedy decoding over the math benchmarks.

🔼 This figure shows the performance of the AceMath-7B-Instruct model on seven different math datasets, evaluating the model’s ability to select the correct answer from a list of k candidates. The x-axis represents the number of candidates (k) considered, while the y-axis shows the average accuracy across the seven datasets for that k value. The graph visualizes how the model’s accuracy changes as the number of considered answers increases. This allows one to evaluate the model’s performance when presented with varying degrees of uncertainty in the answer selection process.
read the caption
Figure 4: rm@k𝑘kitalic_k evaluation on average accuracy of 7 datasets for AceMath-7B-Instruct.

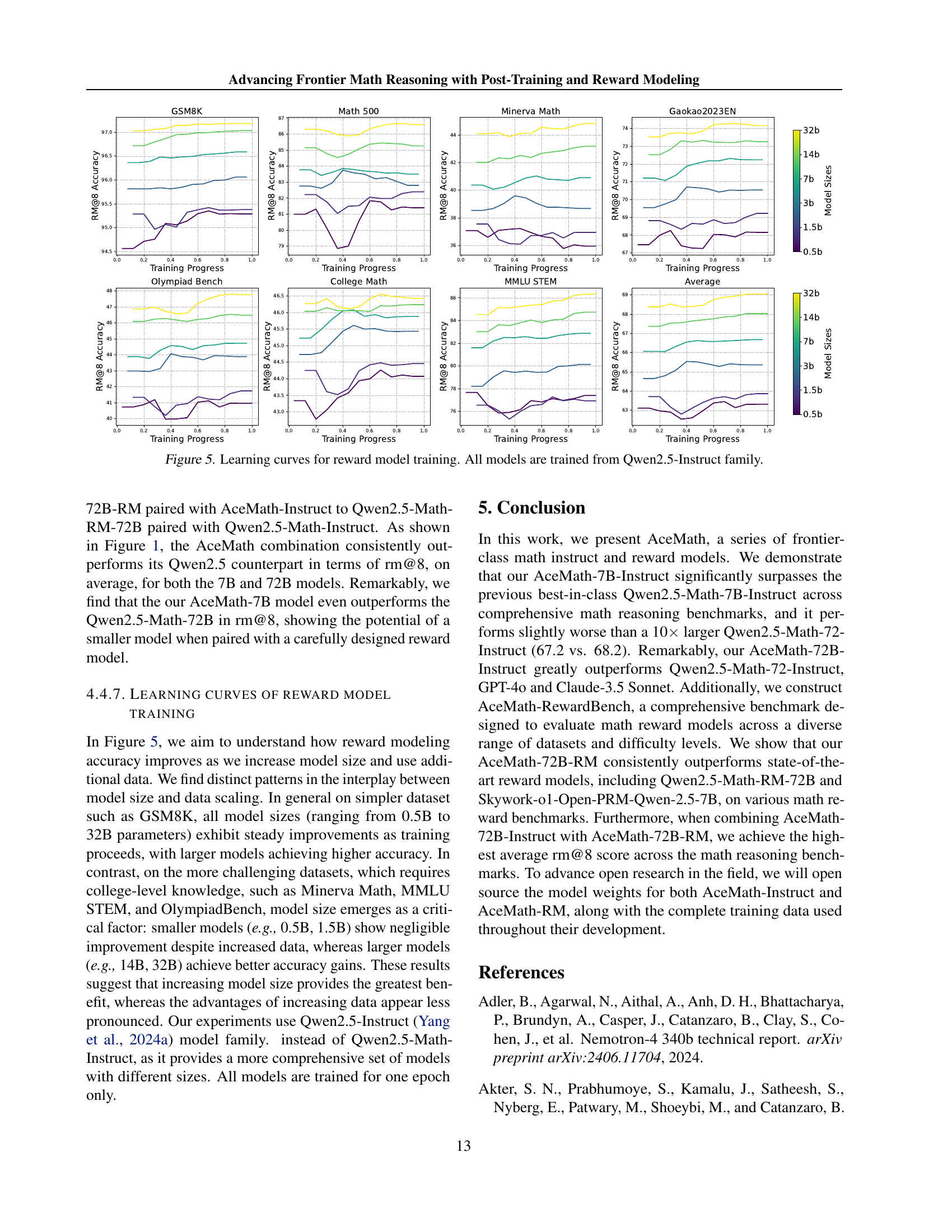
🔼 This figure presents the learning curves for reward model training, illustrating how the model’s accuracy improves as training progresses. The curves are shown for various model sizes, ranging from 0.5B to 32B parameters, across several mathematical reasoning benchmarks (GSM8K, Math500, Minerva Math, Gaokao2023EN, Olympiad Bench, College Math, MMLU STEM). This provides insights into the relationship between model size, training data, and performance on different types of mathematical problems. The data shows that larger models generally achieve better accuracy, but the rate of improvement varies depending on the complexity of the benchmark.
read the caption
Figure 5: Learning curves for reward model training. All models are trained from Qwen2.5-Instruct family.
More on tables
| Models | HumanEval | MBPP | GSM8K | MATH | MMLU | MMLU Pro | Avg. |
|---|---|---|---|---|---|---|---|
| Llama3.1-8B-Base + Two-Stage SFT | 81.10 | 74.71 | 90.45 | 64.42 | 68.31 | 43.27 | 70.38 |
| Llama3.1-8B-Base + Single-Stage SFT w/ all general SFT data | 78.66 | 69.26 | 87.79 | 56.80 | 67.62 | 42.64 | 67.13 |
| Llama3.1-8B-Base + Single-Stage SFT w/ only stage-2 data | 73.78 | 67.32 | 88.17 | 55.84 | 67.48 | 42.85 | 65.91 |
| Qwen2.5-7B-Base + Two-Stage SFT | 85.37 | 74.32 | 93.10 | 76.40 | 74.68 | 54.50 | 76.40 |
| Qwen2.5-7B-Base + Single-Stage SFT w/ all general SFT data | 83.54 | 75.49 | 91.96 | 75.04 | 73.96 | 53.36 | 75.56 |
| Qwen2.5-7B-Base + Single-Stage SFT w/ only stage-2 data | 83.54 | 73.15 | 92.27 | 75.12 | 74.26 | 53.06 | 75.23 |
🔼 This table presents an ablation study evaluating the impact of the two-stage supervised fine-tuning (SFT) strategy on the performance of general-purpose large language models (LLMs). It compares the two-stage approach (training first on a specialized subset of data, then on a broader dataset) against a single-stage approach using either all the data at once or just the broader dataset in the second stage. Results show the performance across several benchmarks (HumanEval, MBPP, GSM8K, MATH, MMLU, MMLU Pro) for different base models (Llama and Qwen) across various sizes. The goal is to understand if the two-stage training method is more effective for improving LLM performance and if this effect varies depending on model size and architecture.
read the caption
Table 2: Ablation studies of our general SFT models regarding the effectiveness of the two-stage training strategy.
| Models | GSM8K | MATH | Minerva Math | GaoKao 2023 En | Olympiad Bench | College Math | MMLU STEM | Avg. |
|---|---|---|---|---|---|---|---|---|
| GPT-4o (2024-0806) | 92.90 | 81.10 | 50.74 | 67.50 | 43.30 | 48.50 | 87.99 | 67.43 |
| Claude-3.5 Sonnet (2024-1022) | 96.40 | 75.90 | 48.16 | 64.94 | 37.93 | 48.47 | 85.06 | 65.27 |
| Llama3.1-70B-Instruct | 94.10 | 65.70 | 34.20 | 54.00 | 27.70 | 42.50 | 80.40 | 56.94 |
| Llama3.1-405B-Instruct | 96.80 | 73.80 | 54.04 | 62.08 | 34.81 | 49.25 | 83.10 | 64.84 |
| OpenMath2-Llama3.1-8B | 91.70 | 67.80 | 16.91 | 53.76 | 28.00 | 46.13 | 46.02 | 50.08 |
| Qwen2.5-Math-1.5B-Instruct | 84.80 | 75.80 | 29.40 | 65.50 | 38.10 | 47.70 | 57.50 | 56.97 |
| Qwen2.5-Math-7B-Instruct | 95.20 | 83.60 | 37.10 | 66.80 | 41.60 | 46.80 | 71.90 | 63.29 |
| Qwen2.5-Math-72B-Instruct | 95.90 | 85.90 | 44.10 | 71.90 | 49.00 | 49.50 | 80.80 | 68.16 |
| AceMath-1.5B-Instruct (Ours) | 86.95 | 76.84 | 41.54 | 64.42 | 33.78 | 54.36 | 62.04 | 59.99 |
| AceMath-7B-Instruct (Ours) | 93.71 | 83.14 | 51.11 | 68.05 | 42.22 | 56.64 | 75.32 | 67.17 |
| AceMath-72B-Instruct (Ours) | 96.44 | 86.10 | 56.99 | 72.21 | 48.44 | 57.24 | 85.44 | 71.84 |
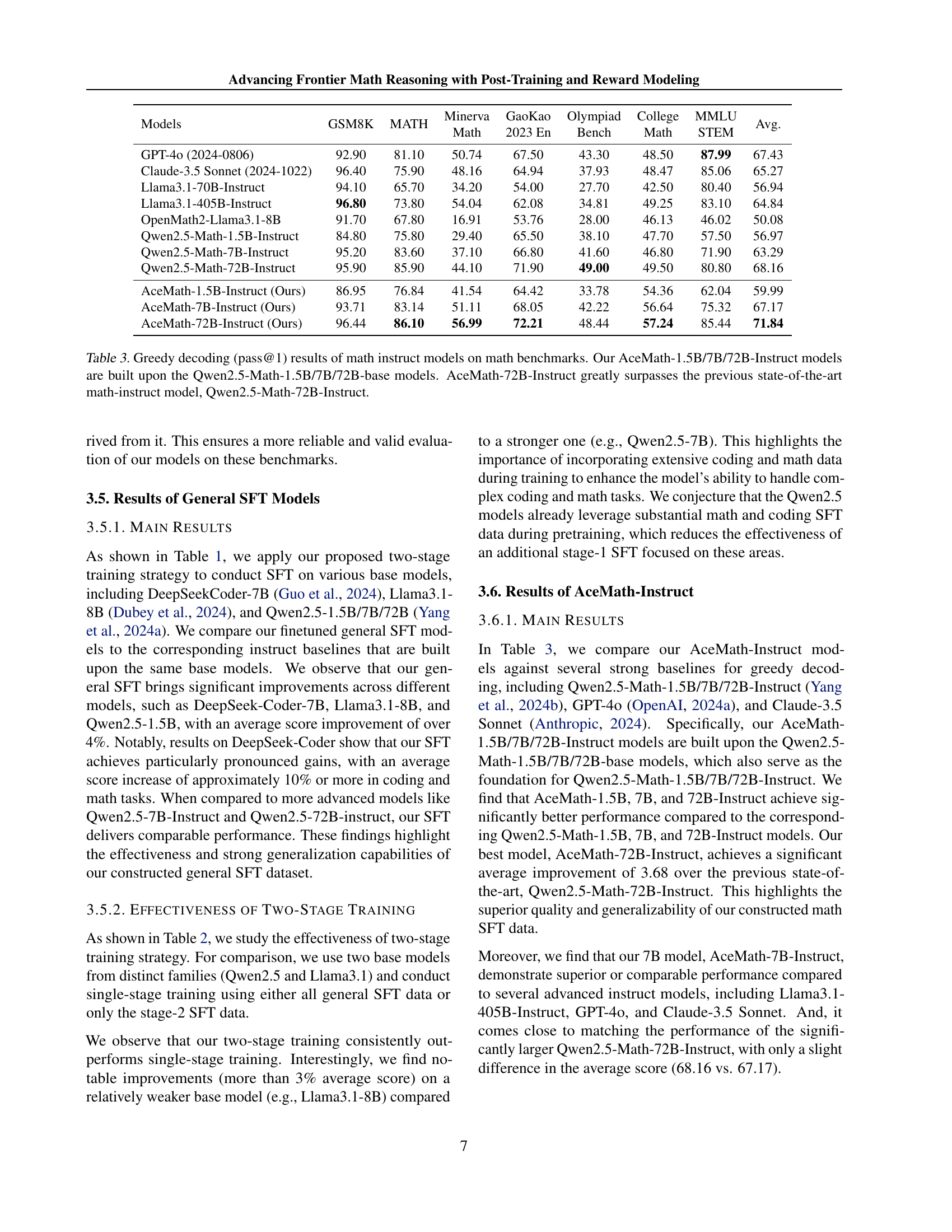
🔼 Table 3 presents a comparison of the performance of various math instruction-tuned large language models (LLMs) on several math reasoning benchmarks. The models compared include various sizes of the Qwen2.5-Math Instruct models and the AceMath-Instruct models (1.5B, 7B, and 72B parameter sizes). The AceMath models were built upon the Qwen2.5-Math base models. The table shows that AceMath-72B-Instruct significantly outperforms Qwen2.5-Math-72B-Instruct and establishes a new state-of-the-art in performance.
read the caption
Table 3: Greedy decoding (pass@1) results of math instruct models on math benchmarks. Our AceMath-1.5B/7B/72B-Instruct models are built upon the Qwen2.5-Math-1.5B/7B/72B-base models. AceMath-72B-Instruct greatly surpasses the previous state-of-the-art math-instruct model, Qwen2.5-Math-72B-Instruct.
| Minerva | |
|---|---|
| Math |
🔼 This table presents ablation studies on the training data and strategies used to train the AceMath-Instruct models. Three sets of experiments are shown: 1) comparing the use of GPT-40-mini generated responses versus Qwen-2.5-Math-72B-Instruct responses for both general and math-specific supervised fine-tuning (SFT), 2) testing the impact of different math-specific datasets (all, only high-quality or a subset) on the model’s performance during the Math SFT stage, and 3) evaluating whether performing general SFT before math SFT improves performance.
read the caption
Table 4: Ablation Studies on training data and strategies across various backbone models for training our AceMath-Instruct models. The ablation studies can be categorized into three parts: 1) evaluating the effectiveness of using either GPT-4o-mini responses or Qwen2.5-Math-72B-Instruct responses individually; 2) analyzing the effectiveness of different math-specific samples for math SFT; and 3) assessing the impact of conducting general SFT prior to math SFT.
| GaoKao | 2023 En |
|---|
🔼 This table presents ablation study results focusing on the impact of synthetic data on the AceMath-Instruct model’s performance. It compares the model’s performance under three conditions: using the full set of synthetic data, removing all synthetic data, and adding extra low-quality synthetic data. The backbone model used for all experiments is Qwen2.5-7B-Base. The average score across seven math benchmarks is reported for each condition, showing how different types and quantities of synthetic training data affect the model’s ability to solve math problems.
read the caption
Table 5: Ablation studies on the synthetic data, exploring the effects of removing all synthetic math SFT data and incorporating additional low-quality synthetic math SFT data. The backbone of AceMath-Instruct is Qwen2.5-7B-Base. Results are average across the seven math benchmark.
| Olympiad | Bench |
|---|
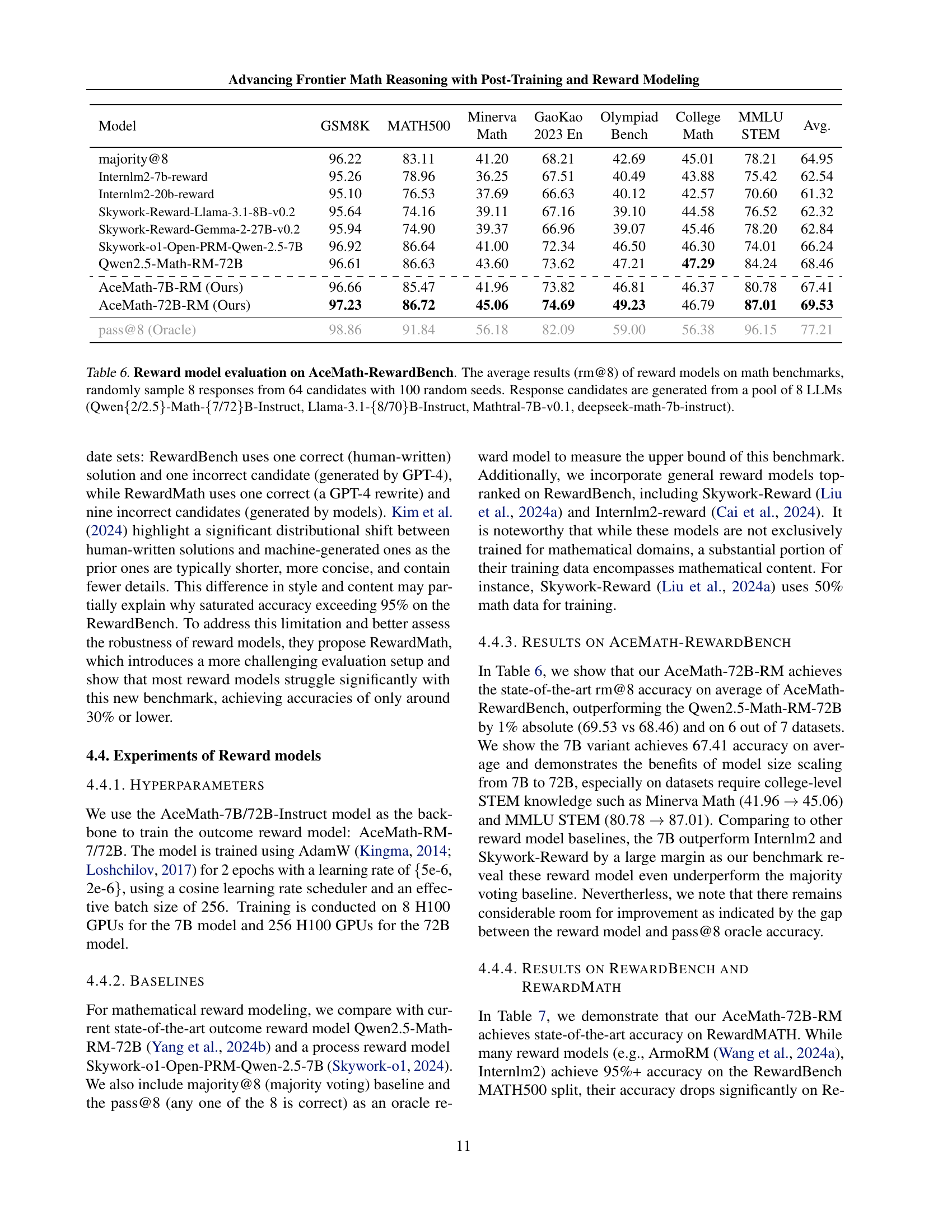
🔼 This table presents the performance of various reward models on the AceMath-RewardBench benchmark. The benchmark consists of seven math datasets, and for each problem, eight response candidates are generated from a pool of eight different large language models (LLMs). The rm@8 metric is used to evaluate each reward model’s ability to select the top eight performing responses out of sixty-four. The results reported are the average rm@8 scores across the seven datasets and 100 random seeds, providing a robust and statistically significant comparison of the different reward models.
read the caption
Table 6: Reward model evaluation on AceMath-RewardBench. The average results (rm@8) of reward models on math benchmarks, randomly sample 8 responses from 64 candidates with 100 random seeds. Response candidates are generated from a pool of 8 LLMs (Qwen{2/2.5}-Math-{7/72}B-Instruct, Llama-3.1-{8/70}B-Instruct, Mathtral-7B-v0.1, deepseek-math-7b-instruct).
| College | |
|---|---|
| Math |
🔼 This table compares the performance of various reward models on two benchmarks: RewardBench (MATH500) and RewardMATH. RewardBench (MATH500) uses one human-written correct solution and one model-generated incorrect solution, while RewardMATH uses one GPT-4-rewritten correct solution and nine model-generated incorrect solutions. The table shows the accuracy (top-1 and top-2) of each model in selecting the correct solution from the provided candidates. Results from RewardMATH are marked with a dagger. The ‘pass@8’ (oracle) indicates the maximum possible accuracy if the best of 8 responses is always selected.
read the caption
Table 7: The accuracy of reward models on RewardBench (MATH500) (Lambert et al., 2024) and RewardMATH (Kim et al., 2024). ††\dagger†: Results are copied from RewardMATH. Bold: top-1. Underline: top-2 accuracy.
| Category | |
|---|---|
| MMLU | |
| STEM |
🔼 This ablation study investigates the impact of different design choices on the performance of the AceMath reward models (AceMath-7B-RM and AceMath-72B-RM). The study focuses on three key aspects: the backbone model used for initialization (AceMath-7B-Instruct vs. AceMath-72B-Instruct), the data sampling method (reward score-sorted sampling), and the loss function employed during training (listwise Bradley-Terry). The results are evaluated using the AceMath-RewardBench benchmark, providing a comprehensive assessment of how these choices affect the final performance of the reward models.
read the caption
Table 8: Ablation study of AceMath-7/72B-RM on AceMath-RewardBench (Backbone: AceMath-7/72B-Instruct; Data: reward score-sorted sampling; Loss: listwise Bradley-Terry.
| Models | GSM8K | MATH | Minerva \ Math | GaoKao \ 2023 En | Olympiad \ Bench | College \ Math | MMLU \ STEM | Avg. | |
|---|---|---|---|---|---|---|---|---|---|
| Backbone: Llama3.1-8B-Base | |||||||||
| AceMath-Instruct | 91.51 | 69.06 | 31.99 | 59.74 | 32.00 | 49.08 | 67.94 | 57.33 | |
| ▷ Only Qwen2.5-Math-72B-Instruct | 91.13 | 69.66 | 33.82 | 60.26 | 30.37 | 49.86 | 66.21 | 57.33 | |
| ▷ Only GPT-4o-mini | 90.83 | 68.12 | 36.03 | 60.26 | 31.70 | 48.05 | 66.50 | 57.36 | |
| ▷ Skipping general SFT | 91.81 | 68.70 | 31.99 | 59.48 | 31.11 | 48.40 | 62.76 | 56.32 | |
| Backbone: Qwen2.5-7B-Base | |||||||||
| AceMath-Instruct | 93.56 | 77.10 | 43.38 | 65.19 | 37.78 | 54.90 | 77.41 | 64.19 | |
| ▷ Only Qwen2.5-Math-72B-Instruct | 92.80 | 76.96 | 41.91 | 63.64 | 38.07 | 54.93 | 75.64 | 63.42 | |
| ▷ Only GPT-4o-mini | 91.66 | 74.14 | 43.75 | 64.42 | 39.26 | 52.27 | 76.03 | 63.08 | |
| ▷ Math SFT with all math samples | 93.40 | 77.12 | 42.28 | 65.19 | 37.78 | 54.05 | 75.33 | 63.59 | |
| ▷ Math SFT with only cross-checked samples | 92.72 | 76.76 | 41.54 | 65.97 | 36.74 | 54.33 | 76.78 | 63.55 | |
| ▷ Skipping general SFT | 93.03 | 77.52 | 40.44 | 62.86 | 37.19 | 54.58 | 75.77 | 63.06 | |
| Backbone: Qwen2.5-Math-72B-Base | |||||||||
| AceMath-Instruct | 96.44 | 86.10 | 56.99 | 72.21 | 48.44 | 57.24 | 85.44 | 71.84 | |
| ▷ Math SFT with all math samples | 96.29 | 86.06 | 55.15 | 70.13 | 46.67 | 57.49 | 84.96 | 70.96 | |
| ▷ Skipping general SFT | 95.75 | 85.52 | 56.25 | 71.43 | 45.33 | 56.71 | 84.42 | 70.77 |
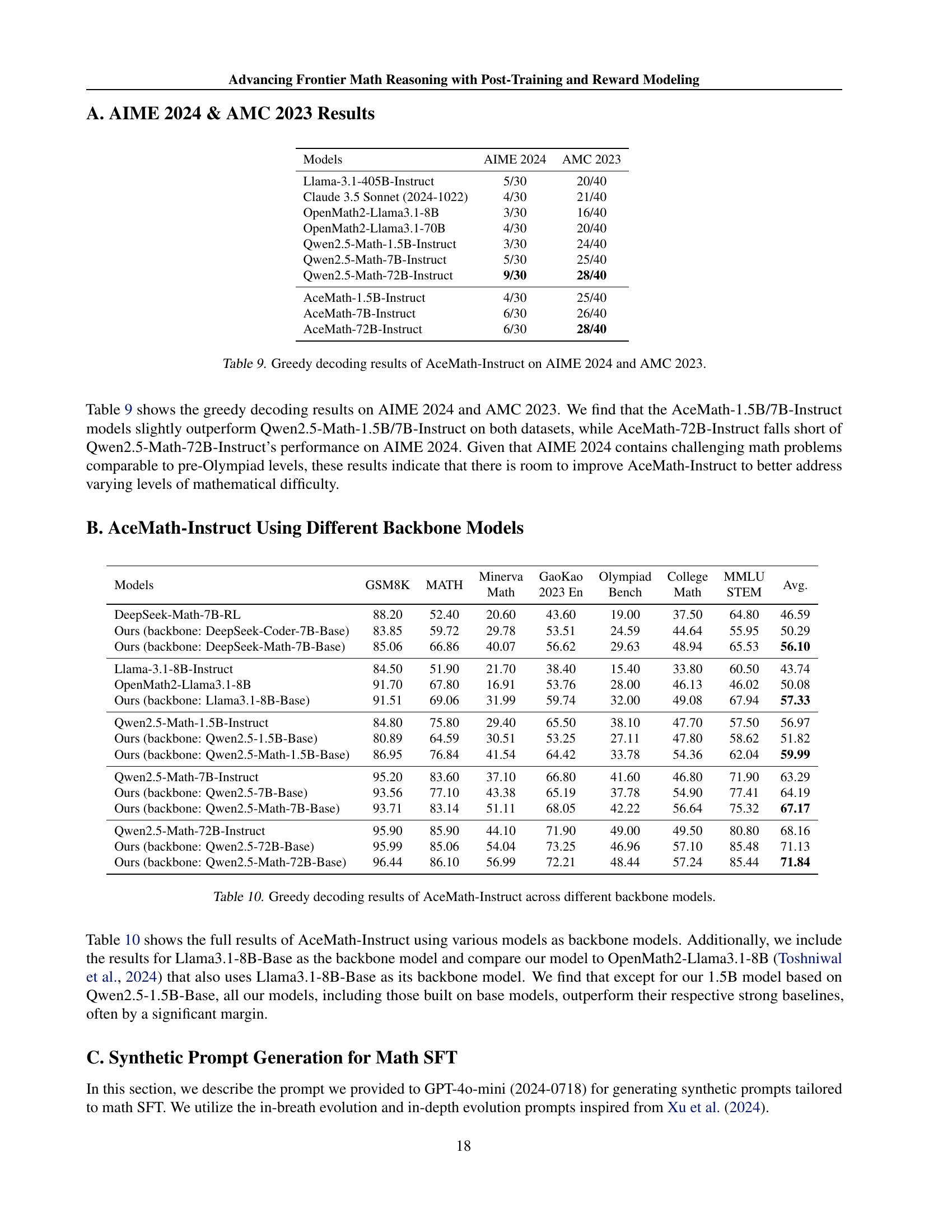
🔼 This table presents the performance of AceMath-Instruct models (AceMath-1.5B, AceMath-7B, and AceMath-72B) on two prominent math competitions: AIME 2024 (American Invitational Mathematics Examination) and AMC 2023 (American Mathematics Competitions). The results are shown as the number of problems correctly solved out of the total number of problems for each model. This allows for a comparison of the AceMath models against each other and provides insight into their capabilities on challenging mathematical problems with varying difficulty levels.
read the caption
Table 9: Greedy decoding results of AceMath-Instruct on AIME 2024 and AMC 2023.
| Minerva | |
|---|---|
| Math |
🔼 This table presents the performance of AceMath-Instruct models trained on various base models. It compares AceMath-Instruct’s performance with that of several strong baselines on a variety of math benchmarks, allowing for an assessment of the model’s effectiveness across different backbone models. Results are based on greedy decoding (pass@1).
read the caption
Table 10: Greedy decoding results of AceMath-Instruct across different backbone models.
Full paper#