↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large language models (LLMs) struggle with processing long contexts due to computational and memory constraints. This research explores gist token-based context compression, a promising approach to mitigate these limitations by condensing long sequences into a smaller set of ‘gist tokens’. However, the study finds that this method, while effective for some tasks, suffers from critical failure patterns.
The authors address these challenges by proposing two new strategies: fine-grained autoencoding, which improves the reconstruction of original token information, and segment-wise token importance estimation, which adjusts optimization based on token dependencies. Experiments demonstrate that these techniques significantly enhance compression performance, offering valuable insights into how to improve context compression strategies for LLMs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on long-context processing in large language models (LLMs). It addresses the critical challenge of computational and memory limitations in handling long sequences, providing valuable insights and practical strategies for improving context compression. The identified failure patterns and proposed mitigation techniques open new avenues for research in efficient LLM design and optimization. This work is relevant to the broader field of AI and will help advance the development of more capable and efficient LLMs for various applications.
Visual Insights#

🔼 This figure illustrates various gist token-based context compression architectures. These architectures all begin by segmenting long input texts into smaller, more manageable chunks. However, they differ in two key ways: (1) Memory Location – some store the compressed context as the last hidden state of the gist tokens (recurrent memory), while others store it in the key-value (KV) cache. (2) Gist Granularity – gist tokens can be inserted either coarsely (appended at the end of a segment) or finely (evenly dispersed within the segment). The figure visually represents these different memory location and granularity combinations, showing how the gist tokens and their interactions with the original tokens (or previous outputs) contribute to the compression process within each architecture.
read the caption
Figure 1: Overview of gist token-based context compression architectures. Long texts are segmented for compression, enabling diverse architectures through different memory locations and gist granularity.
| Ratio | Type | MMLU-Pro | BBH | GSM8K | HellaSwag |
|---|---|---|---|---|---|
| - | Full Attention | 34.1 | 64.8 | 51.2 | 82.8 |
| 4 | Coarse-Rec | 34.1 | 53.8 | 50.3 | 81.9 |
| Coarse-KV | 35.3 | 58.1 | 48.7 | 82.3 | |
| Fine-KV | 33.9 | 59.2 | 52.2 | 82.5 | |
| 8 | Coarse-Rec | 34.1 | 54.6 | 51.9 | 82.0 |
| Coarse-KV | 35.6 | 56.1 | 49.0 | 82.2 | |
| Fine-KV | 34.6 | 56.8 | 51.9 | 82.5 | |
| 16 | Coarse-Rec | 34.1 | 53.2 | 50.0 | 81.9 |
| Coarse-KV | 35.6 | 55.7 | 50.1 | 82.2 | |
| Fine-KV | 34.3 | 56.0 | 51.7 | 82.2 | |
| 32 | Coarse-Rec | 34.1 | 54.8 | 50.8 | 81.9 |
| Coarse-KV | 35.6 | 50.6 | 50.5 | 82.2 | |
| Fine-KV | 33.6 | 55.0 | 50.6 | 82.2 |
🔼 This table presents the performance of different context compression methods on four weak context-dependent tasks: MMLU-Pro, BBH, GSM8K, and HellaSwag. These tasks assess various aspects of language understanding, including knowledge, common sense reasoning, and mathematical abilities, but are not inherently dependent on long context. The table shows the performance of full attention models and three different gist-token based compression architectures (coarse-grained recurrent, coarse-grained KV cache, and fine-grained KV cache) at different compression ratios (4, 8, 16, 32). The results help determine how well gist token compression performs on tasks that aren’t highly reliant on extended contexts.
read the caption
Table 1: Performance on weak context-dependent tasks.
In-depth insights#
Gist Token Contexts#
Gist token-based context compression offers a promising approach to address the computational challenges of handling long sequences in large language models (LLMs). By representing extended contexts with a reduced set of gist tokens, this method aims to improve efficiency while maintaining acceptable performance. However, a comprehensive analysis reveals both strengths and weaknesses. While gist tokens show potential for near-lossless performance on certain tasks, like retrieval-augmented generation, their effectiveness is significantly impacted by specific failure modes. These include information loss at segment boundaries, failure to capture surprising information, and gradual degradation of accuracy across longer sequences. Fine-grained autoencoding and segment-wise token importance estimation are proposed as strategies to mitigate these limitations, showing improvement in experiments. The overall success of this compression method depends heavily on careful design considerations and appropriate task selection. Further research into the underlying mechanisms of information loss and improved compression strategies is necessary to fully unlock the potential of gist token contexts for LLMs.
Compression Failures#
The section on ‘Compression Failures’ would delve into the limitations of gist-based context compression in LLMs. It would likely identify specific failure modes, such as information loss near segment boundaries (’lost by the boundary’), where the model struggles to maintain coherence at the transitions between compressed segments. Another likely failure mode is the inability to handle unexpected or surprising information (’lost if surprise’), showcasing the model’s tendency to prioritize information consistent with the established context. A third failure mode might be gradual degradation of accuracy within longer segments (’lost along the way’), indicating a difficulty in maintaining precise recall over extended spans of compressed text. The analysis would likely show how these failures impact different downstream tasks, with more complex or nuanced tasks being disproportionately affected. The discussion could conclude by highlighting the need for more robust compression techniques and suggesting potential strategies to mitigate these failure patterns, perhaps relating it to decoder architecture or specific loss functions.
Autoencoding Gains#
The concept of ‘Autoencoding Gains’ in the context of a research paper on context compression within large language models (LLMs) refers to the potential improvements achieved by incorporating autoencoding techniques. Autoencoders are neural networks designed to learn compressed representations of input data, and subsequently reconstruct the original input from this compressed representation. In LLMs, this can be applied to compress the contextual information, thereby reducing computational costs and memory requirements associated with long sequences. The ‘gains’ would be measured by improvements in downstream tasks, such as question answering or text generation, while simultaneously maintaining efficiency. A successful autoencoding approach would learn a compressed representation that effectively captures the essential information needed for a task while discarding less relevant details. The gains are likely context and task-dependent, meaning the improvements might be substantial for certain tasks but minimal for others. The effectiveness would hinge on the ability of the autoencoder to learn a sufficiently informative and compact representation, striking a balance between compression and information preservation. Furthermore, a significant challenge is identifying and mitigating the failure modes that arise from information loss during compression. This loss could stem from various factors such as boundary effects (information at the beginning or end of a sequence is lost), unexpected events, or gradual information decay during processing. The paper likely investigates strategies to optimize the autoencoding process, such as carefully designing the architecture, loss functions, and training procedures, to maximize the ‘autoencoding gains’ and minimize these failure modes.
Model Limitations#
The limitations section of a research paper about large language models (LLMs) would likely address several key areas. Model scale and context length are often major constraints; larger models are computationally expensive to train and deploy. Smaller models may perform poorly on complex tasks. The ability to process extended contexts is also limited, with computational costs increasing significantly as sequence length grows. There are also methodological limitations, acknowledging that the study may focus on a specific set of LLMs or compression techniques, which may not generalize well to all models or approaches. The study might also need to acknowledge the inherent limitations of the evaluation metrics. Ethical considerations related to bias in training data and potential misuse are relevant. Finally, the scope of any experiment with respect to different model architectures, compression methods, tasks, and datasets will always introduce limitations. The conclusion should explicitly address these limitations to highlight the study’s boundaries and promote future research.
Future Directions#
Future research could explore several promising avenues. Improving the robustness of gist-based methods to handle diverse tasks and unexpected content is crucial. This involves developing more sophisticated gist token generation and representation techniques. Investigating the interplay between compression strategies and model architecture is another key area. Exploring novel architectures specifically designed for efficient gist token handling could unlock significant performance gains. Advanced autoencoding techniques and improved token importance estimation methods could further enhance compression effectiveness. Finally, extending the framework to handle even longer contexts and larger language models would be essential to assess the scalability and real-world applicability of these methods. Addressing these points will contribute to more reliable and efficient long-context processing in LLMs.
More visual insights#
More on figures

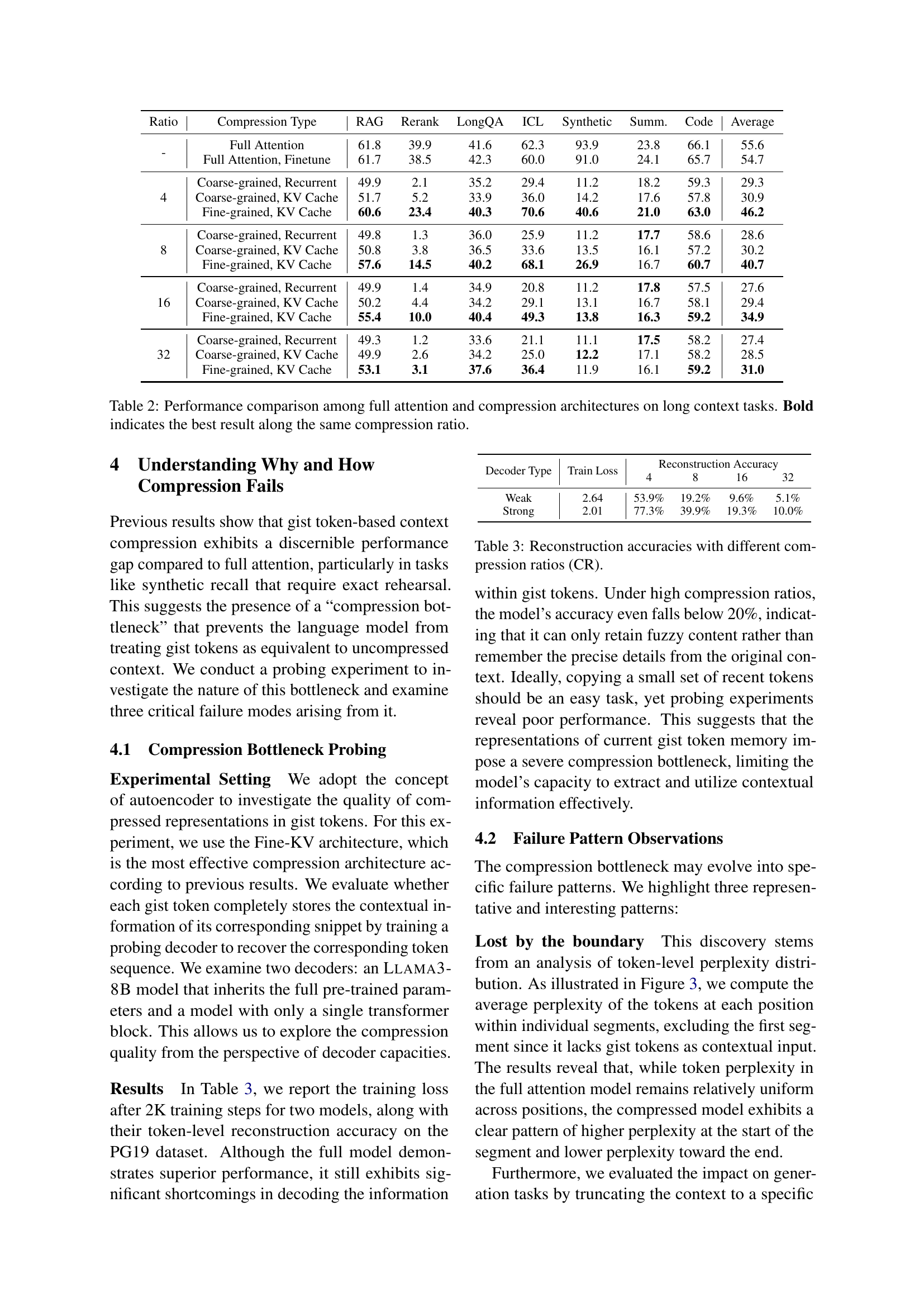
🔼 This figure compares the perplexity scores achieved by various context compression methods against a full attention model for three language modeling datasets: PG19, ProofPile, and CodeParrot. The x-axis represents the compression ratio, indicating the level of context compression applied. The y-axis shows the perplexity, a measure of how well the model predicts the next word in a sequence. Different colored lines represent different compression methods: fine-grained KV cache, coarse-grained KV cache, and coarse-grained recurrent memory. The full attention model serves as a baseline for comparison. The figure helps illustrate the trade-off between compression efficiency and the resulting impact on the model’s language modeling performance.
read the caption
Figure 2: Comparisons of different compression methods on perplexity evaluation for language modeling.

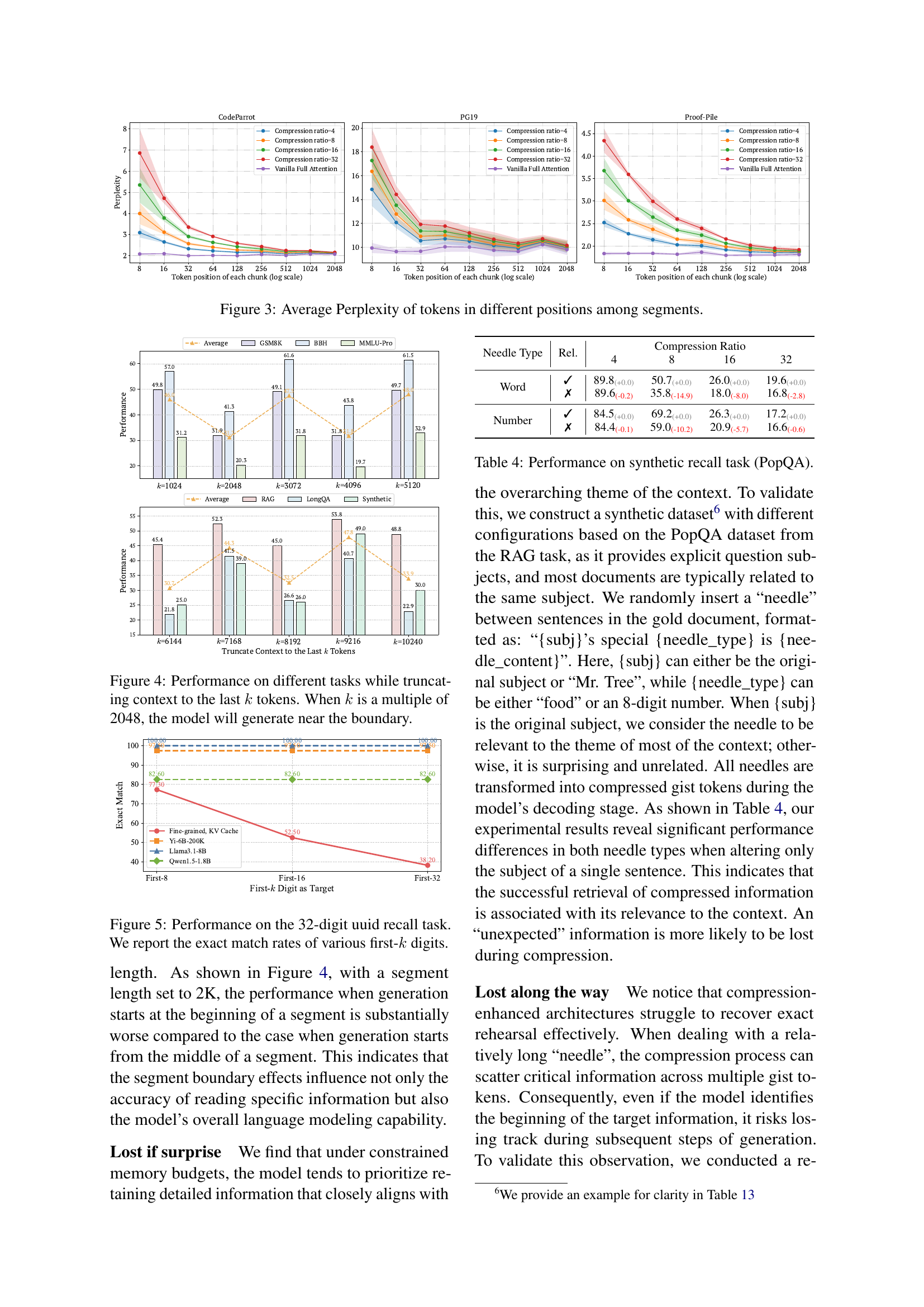
🔼 This figure visualizes the average perplexity scores of tokens within different segments of text. It shows how perplexity changes across the token positions within a segment, comparing compressed models with various compression ratios (4, 8, 16, 32) against a full-attention baseline. This helps to illustrate the ’lost by the boundary’ failure pattern observed in gist-token-based context compression, where the model exhibits higher perplexity near the start of segments and lower perplexity towards the end.
read the caption
Figure 3: Average Perplexity of tokens in different positions among segments.

🔼 This figure displays the performance of different models on various tasks when the context is truncated to the last k tokens. The x-axis represents the number of tokens kept (k), and the y-axis represents the performance metric (e.g., accuracy, exact match). Multiple lines represent different models or compression strategies. The key observation is that when k is a multiple of 2048, model performance tends to be particularly poor, indicating a boundary effect related to the way the context is segmented and compressed in those models. This suggests a failure mode in the compression methods near segment boundaries.
read the caption
Figure 4: Performance on different tasks while truncating context to the last k𝑘kitalic_k tokens. When k𝑘kitalic_k is a multiple of 2048, the model will generate near the boundary.

🔼 This figure illustrates the performance of different models on a 32-digit UUID recall task. The x-axis represents the number of initial digits (k) used as a prompt, and the y-axis shows the percentage of exact matches achieved by the models. The results demonstrate that full-attention models maintain high accuracy regardless of the number of digits used as input, while compressed models show significantly reduced accuracy as the number of input digits increases. This highlights the difficulty that compressed models face in reconstructing the full sequence from a compressed representation. The plot visually compares the accuracy of the full attention and several gist-token based compression methods.
read the caption
Figure 5: Performance on the 32-digit uuid recall task. We report the exact match rates of various first-k𝑘kitalic_k digits.
More on tables
| Ratio | Compression Type | RAG | Rerank | LongQA | ICL | Synthetic | Summ. | Code | Average |
|---|---|---|---|---|---|---|---|---|---|
| - | Full Attention | 61.8 | 39.9 | 41.6 | 62.3 | 93.9 | 23.8 | 66.1 | 55.6 |
| Full Attention, Finetune | 61.7 | 38.5 | 42.3 | 60.0 | 91.0 | 24.1 | 65.7 | 54.7 | |
| 4 | Coarse-grained, Recurrent | 49.9 | 2.1 | 35.2 | 29.4 | 11.2 | 18.2 | 59.3 | 29.3 |
| Coarse-grained, KV Cache | 51.7 | 5.2 | 33.9 | 36.0 | 14.2 | 17.6 | 57.8 | 30.9 | |
| Fine-grained, KV Cache | 60.6 | 23.4 | 40.3 | 70.6 | 40.6 | 21.0 | 63.0 | 46.2 | |
| 8 | Coarse-grained, Recurrent | 49.8 | 1.3 | 36.0 | 25.9 | 11.2 | 17.7 | 58.6 | 28.6 |
| Coarse-grained, KV Cache | 50.8 | 3.8 | 36.5 | 33.6 | 13.5 | 16.1 | 57.2 | 30.2 | |
| Fine-grained, KV Cache | 57.6 | 14.5 | 40.2 | 68.1 | 26.9 | 16.7 | 60.7 | 40.7 | |
| 16 | Coarse-grained, Recurrent | 49.9 | 1.4 | 34.9 | 20.8 | 11.2 | 17.8 | 57.5 | 27.6 |
| Coarse-grained, KV Cache | 50.2 | 4.4 | 34.2 | 29.1 | 13.1 | 16.7 | 58.1 | 29.4 | |
| Fine-grained, KV Cache | 55.4 | 10.0 | 40.4 | 49.3 | 13.8 | 16.3 | 59.2 | 34.9 | |
| 32 | Coarse-grained, Recurrent | 49.3 | 1.2 | 33.6 | 21.1 | 11.1 | 17.5 | 58.2 | 27.4 |
| Coarse-grained, KV Cache | 49.9 | 2.6 | 34.2 | 25.0 | 12.2 | 17.1 | 58.2 | 28.5 | |
| Fine-grained, KV Cache | 53.1 | 3.1 | 37.6 | 36.4 | 11.9 | 16.1 | 59.2 | 31.0 |
🔼 This table presents a comprehensive comparison of the performance of various context compression architectures against a full attention model across a range of long-context tasks. It shows the performance of different gist-based models using various memory locations (recurrent memory, KV cache) and gist granularities (coarse-grained, fine-grained) under different compression ratios (4, 8, 16, 32). The results are presented for several long-context tasks including Retrieval Augmented Generation (RAG), Reranking, LongQA, Many-shot ICL, Synthetic Recall, Summarization, and Code generation. The best performing model for each task and compression ratio is highlighted in bold.
read the caption
Table 2: Performance comparison among full attention and compression architectures on long context tasks. Bold indicates the best result along the same compression ratio.
| Decoder Type | Train Loss | Reconstruction Accuracy | Reconstruction Accuracy | Reconstruction Accuracy | Reconstruction Accuracy |
|---|---|---|---|---|---|
| 4 | 8 | 16 | 32 | ||
| Weak | 2.64 | 53.9% | 19.2% | 9.6% | 5.1% |
| Strong | 2.01 | 77.3% | 39.9% | 19.3% | 10.0% |
🔼 This table presents the results of an experiment evaluating the quality of compressed representations in gist tokens using an autoencoder. It shows the reconstruction accuracy (how well the original token sequence can be recovered) at different compression ratios (CR). A higher accuracy indicates better preservation of information during compression. The experiment uses two decoder models: one with full pre-trained parameters and another with only a single transformer block, to assess compression quality from different perspectives.
read the caption
Table 3: Reconstruction accuracies with different compression ratios (CR).
| Needle Type | Rel. | Compression Ratio | ||||
|---|---|---|---|---|---|---|
| Word | ✓ | 89.8(+0.0) | 50.7(+0.0) | 26.0(+0.0) | 19.6(+0.0) | |
| ✗ | 89.6(-0.2) | 35.8(-14.9) | 18.0(-8.0) | 16.8(-2.8) | ||
| Number | ✓ | 84.5(+0.0) | 69.2(+0.0) | 26.3(+0.0) | 17.2(+0.0) | |
| ✗ | 84.4(-0.1) | 59.0(-10.2) | 20.9(-5.7) | 16.6(-0.6) |
🔼 This table presents the results of experiments conducted on the PopQA dataset, a synthetic recall task designed to evaluate the performance of models in recalling specific information from a given context. The task involves a question and a set of documents, where a specific piece of information (the ’needle’) is inserted into one of the documents. The table shows how well different models perform in retrieving the correct needle, comparing models with varying compression ratios. Different experimental configurations with varied relevance of the added information to the main context are presented in order to reveal specific failure modes.
read the caption
Table 4: Performance on synthetic recall task (PopQA).
| Ratio | Compression Type | RAG | Rerank | LongQA | ICL | Synthetic | Summ. | Code | Average |
|---|---|---|---|---|---|---|---|---|---|
| - | Full Attention | 61.8 | 39.9 | 41.6 | 62.3 | 93.9 | 23.8 | 66.1 | 55.6 |
| 4 | Fine-grained, KV Cache | 60.6 | 23.4 | 40.3 | 70.6 | 40.6 | 21.0 | 62.0 | 46.1 |
| 4 | + Fine-grained AE | 60.9 | 27.4 | 40.8 | 72.0 | 62.0 | 22.3 | 62.9 | 49.8 |
| 4 | + Segment-wise TIE | 60.4 | 27.0 | 41.2 | 72.7 | 54.3 | 20.2 | 62.1 | 48.3 |
| 4 | + Both Strategies | 61.1 | 27.4 | 40.3 | 75.0 | 62.1 | 22.2 | 62.9 | 50.1 |
| 8 | Fine-grained, KV Cache | 57.6 | 14.5 | 40.2 | 68.1 | 26.9 | 16.7 | 60.7 | 40.7 |
| 8 | + Fine-grained AE | 58.3 | 15.6 | 39.8 | 68.7 | 34.8 | 18.5 | 61.3 | 42.4 |
| 8 | + Segment-wise TIE | 58.1 | 17.6 | 40.0 | 70.0 | 30.2 | 17.7 | 60.7 | 42.0 |
| 8 | + Both Strategies | 58.3 | 19.7 | 40.4 | 70.7 | 35.2 | 19.5 | 61.4 | 43.6 |
| 16 | Fine-grained, KV Cache | 55.4 | 10.0 | 40.4 | 49.3 | 13.8 | 16.3 | 59.2 | 34.9 |
| 16 | + Fine-grained AE | 55.6 | 11.3 | 40.4 | 47.1 | 14.7 | 16.2 | 59.6 | 35.0 |
| 16 | + Segment-wise TIE | 55.6 | 10.4 | 40.7 | 55.5 | 14.8 | 15.3 | 58.1 | 35.7 |
| 16 | + Both Strategies | 56.3 | 12.7 | 41.7 | 56.3 | 14.9 | 15.7 | 59.6 | 36.7 |
| 32 | Fine-grained, KV Cache | 53.1 | 3.1 | 37.6 | 36.4 | 11.9 | 16.1 | 59.2 | 31.0 |
| 32 | + Fine-grained AE | 54.3 | 4.6 | 39.3 | 34.1 | 13.1 | 17.1 | 59.8 | 31.8 |
| 32 | + Segment-wise TIE | 53.1 | 4.6 | 40.3 | 43.6 | 13.1 | 17.0 | 59.8 | 33.1 |
| 32 | + Both Strategies | 54.4 | 4.9 | 39.8 | 41.8 | 13.1 | 17.1 | 59.8 | 33.0 |
🔼 This table presents a comprehensive comparison of different gist-based context compression methods on various long-context tasks. It categorizes existing methods along two dimensions: Memory Location and Gist Granularity. For each method and different compression ratios, the performance on tasks such as RAG, Reranking, LongQA, and others is shown. The table also highlights the performance improvement achieved by incorporating the proposed strategies of fine-grained autoencoding and segment-wise token importance estimation. The best average performance across all tasks is highlighted in bold for each compression ratio.
read the caption
Table 5: Performance comparisons using our methods, with the best “average” results bolded for clarity.
| k | Model | MMLU-Pro | BBH | GSM8K |
|---|---|---|---|---|
| 2048 | Fine-grained KV | 20.3(+0.0) | 41.3(+0.0) | 31.9(+0.0) |
| + Fine-grained AE | 23.4(+3.1) | 47.8(+6.5) | 34.3(+2.4) | |
| + Segment-wise TIE | 22.9(+2.6) | 46.3(+5.0) | 32.3(+2.0) | |
| 4096 | Fine-grained KV | 19.7(+0.0) | 43.8(+0.0) | 31.8(+0.0) |
| + Fine-grained AE | 22.5(+2.8) | 51.0(+7.2) | 35.1(+3.3) | |
| + Segment-wise TIE | 22.9(+3.2) | 50.8(+7.0) | 34.7(+2.9) |
🔼 Table 6 presents the results of applying two proposed mitigating methods (Fine-grained Autoencoding and Segment-wise Token Importance Estimation) to address the ’lost by the boundary’ issue, a failure pattern observed in gist token-based context compression. It shows how these methods improve performance on weak context-dependent tasks, particularly on the BBH dataset, which involves complex reasoning tasks where context length significantly impacts performance. The table compares the performance of the original Fine-grained KV Cache method against versions enhanced by each of the two methods individually and a version that incorporates both. This allows assessment of the individual contributions of each method as well as their combined effect on mitigating the boundary problem.
read the caption
Table 6: Improvements of our mitigating methods on the “lost by the boundary” problem.
| Dataset | #Few-shot demos | Answer acquisition |
|---|---|---|
| MMLU-Pro | 12 | Chain-of-Thought |
| BBH | 8 | Chain-of-Thought |
| GSM8K | 16 | Chain-of-Thought |
| HellaSwag | 32 | Logits |
🔼 This table details the experimental setup for evaluating weak context-dependent tasks. It shows the specific datasets used (MMLU-Pro, GSM8K, BBH, HellaSwag), the number of few-shot examples provided as context for each task, and the method used for answer acquisition (Chain-of-Thought or Logits). This information is crucial for understanding how the model’s performance was measured in these experiments, highlighting the methodology used to control for context length and the approach used to generate answers.
read the caption
Table 7: Evaluation setting of weak context-dependent tasks.
| Category | Tasks | Metrics |
|---|---|---|
| RAG | NQ | SubEM |
| TriviaQA | SubEM | |
| PopQA | SubEM | |
| HotpotQA | SumEM | |
| Rerank | MS Marco | NDCG@10 |
| Long-doc QA | ∞Bench QA | ROUGE Recall |
| ∞Bench MC | Accuracy | |
| Many-shot ICL | TREC Coarse | Accuracy |
| TREC Fine | Accuracy | |
| NLU | Accuracy | |
| BANKING77 | Accuracy | |
| CLINIC150 | Accuracy | |
| Synthetic recall | JSON KV | SubEM |
| RULER MK Needle | SubEM | |
| RULER MK UUID | SubEM | |
| RULER MV | SubEM | |
| Summ. | ∞Bench Sum | ROUGE-Sum F1 |
| Multi-LexSum | ROUGE-Sum F1 | |
| Code | RepoBench | Edit Distance |
🔼 Table 8 provides detailed information on the long-context tasks used in the paper’s experiments. It lists the specific tasks evaluated, the metrics used to measure performance on each task, and the datasets employed for each. This allows readers to understand the scope and nature of the long-context experiments, enabling replication of the studies and proper contextualization of the results.
read the caption
Table 8: Details of long context tasks.
| Type | MMLU-Pro | BBH | GSM8K | HellaSwag |
|---|---|---|---|---|
| Full Attention | 35.1 | 59.0 | 50.9 | 79.8 |
| Coarse, Rec | 34.8 | 59.2 | 50.4 | 79.3 |
| Coarse, KV | 35.1 | 58.5 | 51.6 | 79.2 |
| Fine, KV | 35.0 | 59.5 | 50.1 | 79.5 |
🔼 This table presents the performance comparison of different context compression methods on short context tasks. The results are obtained using models trained with short context lengths (i.e., where context length is not a factor). For each of four datasets (MMLU-Pro, BBH, GSM8K, HellaSwag), the table shows the performance of full attention models compared to several compression methods. This allows assessment of the effect of compression on tasks where long contexts aren’t inherent.
read the caption
Table 9: Performance of short context tasks.
| Ratio | Compression Type | RAG | Rerank | LongQA | ICL | Synthetic | Summ. | Code | Average |
|---|---|---|---|---|---|---|---|---|---|
| - | Full Attention | 56.2 | 26.6 | 44.5 | 67.1 | 81.8 | 19.0 | 64.6 | 51.4 |
| 4 | Coarse-grained, Recurrent | 44.1 | 0.9 | 35.6 | 27.9 | 12.1 | 19.3 | 56.9 | 28.1 |
| 4 | Coarse-grained, KV Cache | 45.4 | 1.6 | 36.2 | 29.8 | 12.4 | 17.8 | 59.4 | 29.2 |
| 4 | Fine-grained, KV Cache | 54.8 | 10.6 | 43.8 | 67.5 | 15.5 | 18.2 | 59.4 | 38.9 |
| 8 | Coarse-grained, Recurrent | 49.8 | 1.3 | 36.0 | 25.9 | 11.2 | 17.7 | 58.6 | 28.6 |
| 8 | Coarse-grained, KV Cache | 44.8 | 0.5 | 39.3 | 28.5 | 12.3 | 18.1 | 59.4 | 28.9 |
| 8 | Fine-grained, KV Cache | 52.0 | 5.0 | 44.2 | 62.7 | 11.6 | 17.9 | 61.7 | 36.4 |
| 16 | Coarse-grained, Recurrent | 49.9 | 1.4 | 34.9 | 20.8 | 11.2 | 17.8 | 57.5 | 27.6 |
| 16 | Coarse-grained, KV Cache | 45.1 | 0.9 | 38.6 | 27.9 | 12.2 | 17.8 | 58.7 | 28.7 |
| 16 | Fine-grained, KV Cache | 49.5 | 3.1 | 42.2 | 44.5 | 11.7 | 16.9 | 59.6 | 32.5 |
| 32 | Coarse-grained, Recurrent | 44.2 | 2.4 | 34.1 | 27.5 | 11.5 | 18.5 | 57.3 | 27.9 |
| 32 | Coarse-grained, KV Cache | 45.0 | 1.1 | 37.1 | 23.6 | 12.2 | 17.6 | 57.9 | 27.8 |
| 32 | Fine-grained, KV Cache | 47.5 | 1.7 | 40.6 | 36.9 | 12.1 | 16.8 | 59.5 | 30.8 |
🔼 This table presents the results of experiments conducted using the Qwen2-7B model on long-context tasks. It shows performance comparisons across various compression techniques and a full attention baseline. The metrics used to evaluate the performance are listed for each task. The compression techniques are categorized by the memory location method used and gist granularity. Compression ratios are specified, and average performance across all tasks is provided for each configuration. This allows for a comprehensive comparison of different context compression methods within the Qwen2-7B model.
read the caption
Table 10: Long context performance based on Qwen2-7B.
| Compression Type | RAG | ICL | Synthetic | Summ. | Avg. |
|---|---|---|---|---|---|
| Fine-KV | 59.9 | 75.5 | 54.1 | 21.0 | 52.6 |
| + SFT | 60.2 | 73.3 | 66.3 | 21.7 | 55.4 |
🔼 This table presents the performance of a compression model after undergoing supervised fine-tuning (SFT). The compression ratio used is 4:1. It shows the model’s performance on various tasks (RAG, ICL, Synthetic, Summarization, Average), comparing the model’s performance at different input context lengths (16K and 32K) and both with and without fine-tuning. The table allows for assessing the impact of fine-tuning and the effectiveness of the compression model in maintaining performance even when the input context length exceeds the length during training.
read the caption
Table 11: Performance of the compression model after SFT (compression ratio=4).
| Length | Model | CR. | RAG | ICL | Synthetic | Avg. |
|---|---|---|---|---|---|---|
| 16K | Full | - | 61.8 | 62.3 | 93.9 | 72.7 |
| 16K | Fine-KV | 4 | 60.4 | 72.7 | 62.1 | 65.1 |
| 32K | Full | - | 60.5 | 74.9 | 88.7 | 74.7 |
| 32K | Fine-KV | 4 | 59.3 | 76.8 | 34.9 | 57.9 |
🔼 This table presents the performance of compression models on tasks where the inference length (the length of the input text during testing) is longer than the training length (the length of the input text during training). It shows how well the compression models generalize to longer sequences than those seen during training. Specifically, it compares the performance of a full attention model against fine-grained KV cache compression models with different compression ratios (4, 8, 16, 32) on several tasks under extended context lengths. This evaluation demonstrates the ability of the compression models to extrapolate their capabilities to longer sequences than those encountered during training. The results are important for assessing the efficiency and generalization ability of compression techniques for handling very long input texts in large language models.
read the caption
Table 12: Performance of compression models when inference length exceeds training length.
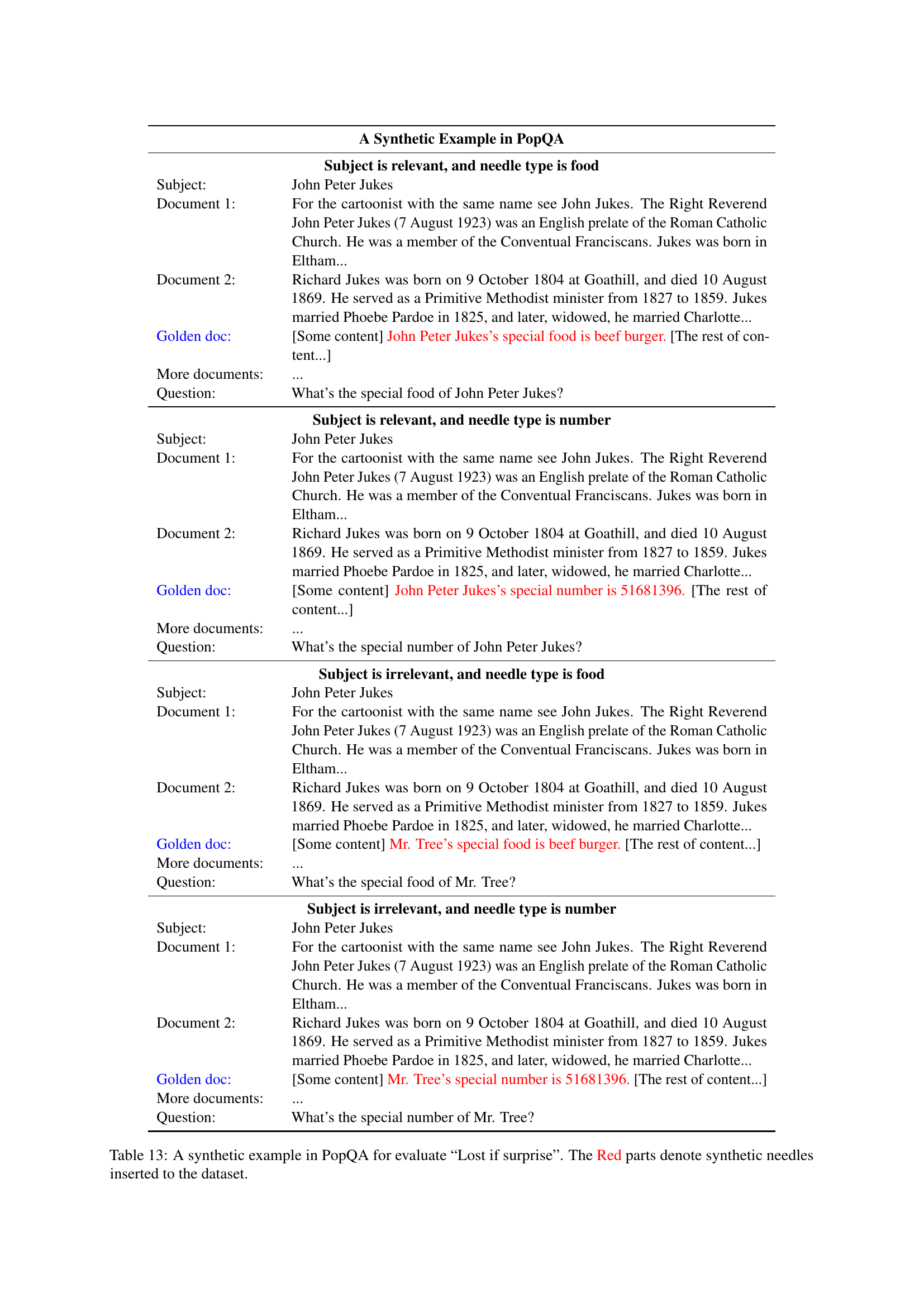
| Subject Relevance | Needle Type | Subject | Document 1 | Document 2 | Golden doc | More documents | Question |
|---|---|---|---|---|---|---|---|
| Relevant | Food | John Peter Jukes | For the cartoonist with the same name see John Jukes. The Right Reverend John Peter Jukes (7 August 1923) was an English prelate of the Roman Catholic Church. He was a member of the Conventual Franciscans. Jukes was born in Eltham… | Richard Jukes was born on 9 October 1804 at Goathill, and died 10 August 1869. He served as a Primitive Methodist minister from 1827 to 1859. Jukes married Phoebe Pardoe in 1825, and later, widowed, he married Charlotte… | [Some content] John Peter Jukes’s special food is beef burger. [The rest of content…] | … | What’s the special food of John Peter Jukes? |
| Relevant | Number | John Peter Jukes | For the cartoonist with the same name see John Jukes. The Right Reverend John Peter Jukes (7 August 1923) was an English prelate of the Roman Catholic Church. He was a member of the Conventual Franciscans. Jukes was born in Eltham… | Richard Jukes was born on 9 October 1804 at Goathill, and died 10 August 1869. He served as a Primitive Methodist minister from 1827 to 1859. Jukes married Phoebe Pardoe in 1825, and later, widowed, he married Charlotte… | [Some content] John Peter Jukes’s special number is 51681396. [The rest of content…] | … | What’s the special number of John Peter Jukes? |
| Irrelevant | Food | John Peter Jukes | For the cartoonist with the same name see John Jukes. The Right Reverend John Peter Jukes (7 August 1923) was an English prelate of the Roman Catholic Church. He was a member of the Conventual Franciscans. Jukes was born in Eltham… | Richard Jukes was born on 9 October 1804 at Goathill, and died 10 August 1869. He served as a Primitive Methodist minister from 1827 to 1859. Jukes married Phoebe Pardoe in 1825, and later, widowed, he married Charlotte… | [Some content] Mr. Tree’s special food is beef burger. [The rest of content…] | … | What’s the special food of Mr. Tree? |
| Irrelevant | Number | John Peter Jukes | For the cartoonist with the same name see John Jukes. The Right Reverend John Peter Jukes (7 August 1923) was an English prelate of the Roman Catholic Church. He was a member of the Conventual Franciscans. Jukes was born in Eltham… | Richard Jukes was born on 9 October 1804 at Goathill, and died 10 August 1869. He served as a Primitive Methodist minister from 1827 to 1859. Jukes married Phoebe Pardoe in 1825, and later, widowed, he married Charlotte… | [Some content] Mr. Tree’s special number is 51681396. [The rest of content…] | … | What’s the special number of Mr. Tree? |
🔼 This table presents a synthetic example used in the PopQA dataset to evaluate the ‘Lost if Surprise’ failure mode in gist-based context compression. Four scenarios are shown, each with a question and two supporting documents. The key difference between scenarios lies in whether the added ‘synthetic needle’ (highlighted in red) is relevant to the main topic of the documents or is surprising and unrelated. The goal is to assess whether the model retains information about unexpected elements after gist-based compression.
read the caption
Table 13: A synthetic example in PopQA for evaluate “Lost if surprise”. The Red parts denote synthetic needles inserted to the dataset.
Full paper#