↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large language models (LLMs) are powerful, but their reasoning processes can be expensive and inefficient due to high token usage. Current methods like Chain-of-Thought (CoT) improve accuracy but substantially increase token costs. This paper addresses this problem.
The researchers propose TALE, a token-budget-aware framework, to optimize LLM reasoning. TALE dynamically adjusts token budgets for different problems based on their complexity, reducing unnecessary token consumption. Experiments show TALE achieves significant cost reduction (~68.64% reduction in token usage) with only a slight performance decrease, showcasing its effectiveness in balancing cost and accuracy. This significantly contributes to making LLM-based reasoning more efficient and accessible.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the high cost of large language model (LLM) reasoning, a significant challenge in deploying LLMs for various applications. TALE offers a practical solution by reducing token usage without substantial accuracy loss, opening avenues for cost-effective LLM reasoning research. It also introduces the concept of ’token elasticity,’ which is a valuable finding for future research on improving LLM efficiency and resource management. This work is highly relevant to the current trends in optimizing LLM performance and reducing environmental impact.
Visual Insights#

🔼 This figure shows a question and its answer generated by a language model without any intermediate reasoning steps. The answer is concise and direct. The number of tokens in the model’s response is specified, highlighting the brevity of the response.
read the caption
(a) Direct answering (15 output tokens).
| Prompt method | Content |
|---|---|
| Vanilla CoT | Let’s think step by step: |
| CoT with Token Budget | Let’s think step by step and use less than budget tokens: |
| Example | Let’s think step by step and use less than 50 tokens: |
🔼 This table illustrates the difference between the standard Chain-of-Thought (CoT) prompting and a modified version that incorporates a token budget. The vanilla CoT prompt simply instructs the LLM to think step by step, leading to potentially lengthy and verbose reasoning. The token-budget-aware prompt adds a constraint, specifying a maximum number of tokens the LLM should use in its response. This encourages more concise reasoning, which can have implications for cost and efficiency.
read the caption
Table 1: Illustrations of the vanilla CoT prompt and the token-budget-aware prompt.
In-depth insights#
LLM Reasoning Cost#
The cost of LLM reasoning is a critical concern, especially as the complexity of tasks increases. Current methods like Chain-of-Thought (CoT) significantly boost accuracy but come at a high price in terms of token usage, leading to increased computational expenses and longer inference times. This paper highlights the issue of unnecessary length in the reasoning process of current LLMs. It argues that this length can be compressed by including a reasonable token budget in prompts. Dynamically estimating optimal token budgets is crucial for efficient reasoning because the effectiveness of compression depends heavily on the chosen budget. The authors introduce the concept of ’token elasticity’ – the tendency for LLMs to produce far more tokens than budgeted when a small budget is set, highlighting the need for a sophisticated budgeting mechanism. The paper explores methods for searching and estimating such optimal budgets, leading to a reduction in token costs while maintaining accuracy. The focus is on balancing efficiency and accuracy, offering practical solutions for managing the cost of LLM reasoning in real-world applications.
Token Budget Impact#
The concept of ‘Token Budget Impact’ in the context of large language models (LLMs) centers on the trade-off between efficiency and accuracy. While techniques like Chain-of-Thought (CoT) improve reasoning abilities, they often lead to increased token usage and higher costs. A token budget, therefore, acts as a constraint to regulate the LLM’s output length, aiming to reduce redundancy in the reasoning process and lower expenses. The impact is twofold: it can significantly decrease computational resources and financial costs associated with LLM inference. However, imposing a strict budget can negatively affect accuracy if the budget is set too low. The challenge lies in finding an optimal balance: a budget that sufficiently constrains the LLM’s verbosity without sacrificing performance. Research in this area focuses on methods for dynamically estimating suitable token budgets based on factors such as problem complexity and LLM capabilities, striving for cost-effective and accurate reasoning.
TALE Framework#
The TALE (Token-Budget-Aware LLM Reasoning) framework is a novel approach to address the high token cost associated with current LLM reasoning methods like Chain-of-Thought (CoT). TALE dynamically estimates optimal token budgets for different problems based on their inherent complexity. This is crucial because using a fixed token budget can be inefficient; excessively large budgets waste resources, while overly small ones might hinder accuracy. The framework uses this estimated budget to guide the LLM’s reasoning process, leading to significantly reduced token usage and monetary costs, all while largely preserving accuracy. The core innovation lies in TALE’s ability to account for ’token elasticity,’ the phenomenon where smaller budgets can unexpectedly inflate token consumption. By incorporating a search algorithm to find the most cost-effective budget while maintaining accuracy, TALE achieves a balance between efficiency and performance, making LLM reasoning more practical for real-world applications. The framework offers a practical solution for organizations and researchers seeking to reduce the financial and computational burden of LLM-based reasoning tasks.
Optimal Budget Search#
The concept of ‘Optimal Budget Search’ in the context of large language model (LLM) reasoning focuses on finding the minimal token budget that yields accurate answers while minimizing computational costs. This search is not a simple linear process; it involves navigating the phenomenon of ’token elasticity’, where reducing the budget below a certain threshold paradoxically increases token usage. Efficient search algorithms like binary search are employed, iteratively adjusting the budget and evaluating the LLM’s performance. A key insight is the existence of an ‘ideal budget range’ – a sweet spot where the cost-accuracy trade-off is optimized. Methods aiming to locate this range involve greedy search strategies, which prioritize minimizing token consumption while maintaining correctness. The ultimate goal is to determine the most economical prompt length for effective LLM reasoning, balancing the need for comprehensive reasoning steps with the desire for efficient computation.
Future Work#
Future research directions stemming from this work could involve several key areas. Extending TALE to other reasoning paradigms beyond chain-of-thought, such as tree-of-thought or self-consistency methods, is crucial to determine the general applicability of the token budget approach. Investigating more sophisticated budget estimation techniques is warranted, perhaps employing more advanced machine learning models or incorporating task-specific features to improve accuracy and reduce reliance on binary search. A particularly promising direction would be to explore integrating TALE with other LLM efficiency optimization strategies, creating a synergistic effect for greater cost reduction. Finally, thorough investigation of the token elasticity phenomenon is needed; a deeper understanding of its root causes could yield highly effective strategies for minimizing token consumption without sacrificing accuracy. This could involve analyzing the interaction between model architecture and training data to identify factors driving excessive token generation.
More visual insights#
More on figures

🔼 This figure shows an example of a question being answered using the vanilla Chain-of-Thought (CoT) prompting method. The question is a word problem about calculating the total time of someone’s after-work activities. The response demonstrates the detailed, step-by-step reasoning process characteristic of vanilla CoT. The caption indicates that this response used 258 tokens.
read the caption
(b) Vanilla CoT (258 output tokens).

🔼 This figure shows an example of Chain-of-Thought (CoT) reasoning with an inappropriately small token budget (set to less than 10 tokens). Despite the budget constraint, the LLM attempts to generate a detailed explanation, resulting in 157 output tokens. This highlights the ‘Token Elasticity’ phenomenon where a severely restrictive budget doesn’t lead to proportionally shorter responses, instead often resulting in significantly longer outputs than with a more reasonable budget.
read the caption
(c) CoT with an unreasonable budget (157 output tokens).

🔼 This figure shows an example of Chain-of-Thought (CoT) reasoning with a reasonable token budget of 50. The question is about calculating the total hours of Peyton’s after-work activities. Unlike the vanilla CoT example that uses many tokens for detailed explanations, this CoT with a budget forces the LLM to be concise in its reasoning. The result is a much shorter chain of thought with 86 output tokens, which is significantly less than the 258 tokens in the vanilla CoT example, while still producing the correct answer.
read the caption
(d) CoT with an reasonable budget (86 output tokens).

🔼 This figure showcases various approaches to solving a math word problem using a large language model (LLM). (a) shows a direct answer approach where the LLM attempts to directly answer the question without intermediate steps. (b) demonstrates the Chain-of-Thought (CoT) method where the LLM breaks down the problem into multiple steps, providing detailed reasoning for each step before arriving at a solution. (c) illustrates CoT with an unreasonable token budget, resulting in an overly long explanation despite the constraint. (d) exhibits CoT with a reasonable token budget; this approach leads to a more concise and effective solution while remaining within the specified token limit. This comparison emphasizes the trade-off between detail in reasoning and efficiency, highlighting how setting an appropriate token budget can improve LLM performance and resource usage.
read the caption
Figure 1: Examples of different problem solving paradigms. The reasoning processes are highlighted.

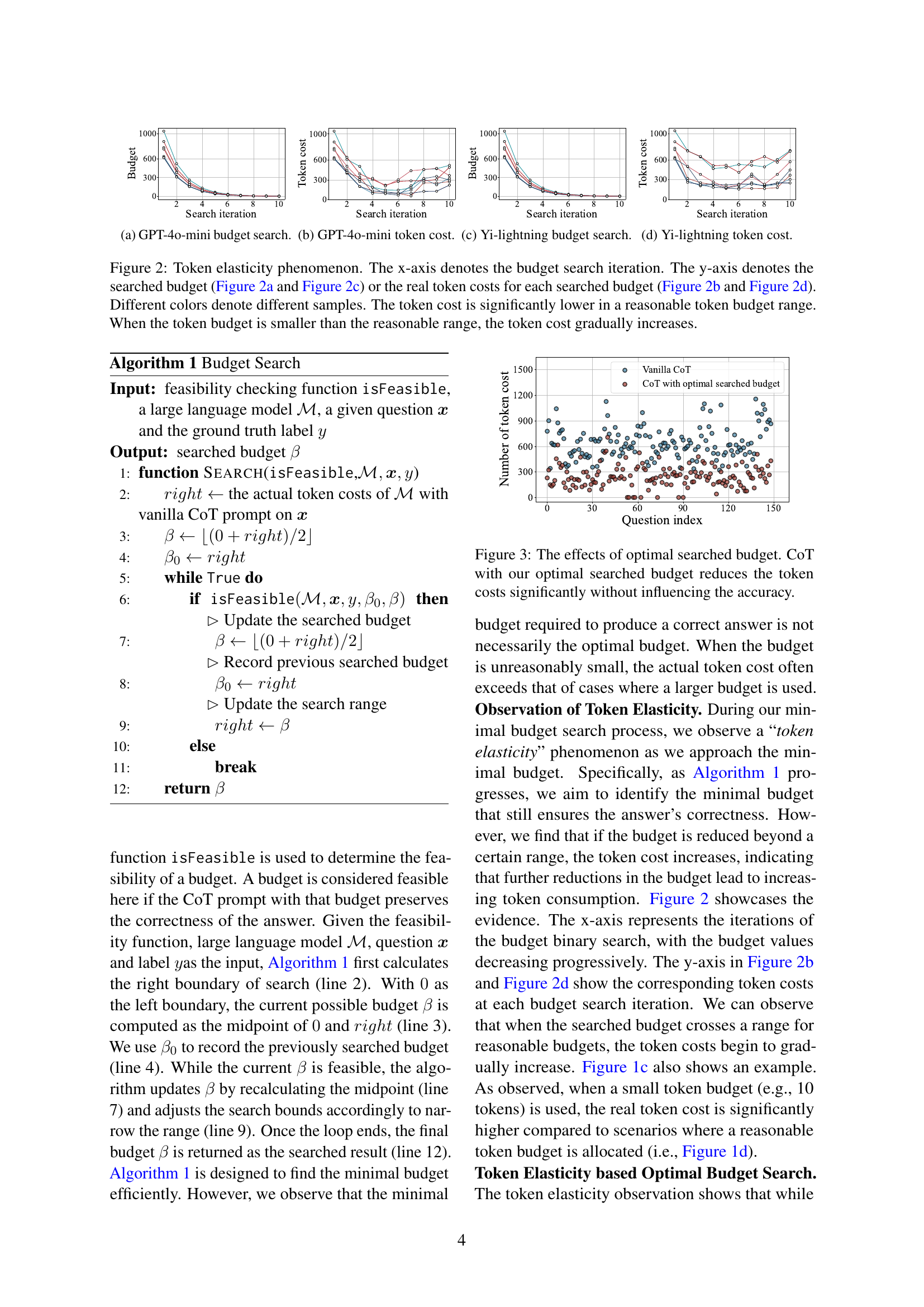
🔼 This figure shows the results of a binary search for the optimal token budget using the GPT-40-mini language model. The x-axis represents the iteration number of the search, and the y-axis represents the token budget being tested at each iteration. Different colored lines represent different samples, showing how the search process varies depending on the specific question. The figure demonstrates the concept of ’token elasticity’, where reducing the budget below a certain threshold can lead to an increase in the actual token usage.
read the caption
(a) GPT-4o-mini budget search.

🔼 The figure shows the relationship between the searched token budget and the actual token cost during the budget search process using the GPT-40-mini language model. The x-axis represents the iteration number of the binary search algorithm used to find the optimal token budget. The y-axis represents the actual token cost incurred by the model for each searched budget. Different colored lines represent different sample questions. The figure demonstrates that there exists a range of reasonable token budgets where the actual cost is significantly lower than when using budgets outside this range. This illustrates the ’token elasticity’ phenomenon observed by the authors, where excessively small budgets lead to unexpectedly high token usage.
read the caption
(b) GPT-4o-mini token cost.

🔼 This figure shows the results of searching for the optimal token budget using the Yi-lightning language model. The x-axis represents the iteration number of the binary search algorithm used to find the optimal budget, and the y-axis shows the searched budget at each iteration. The plot visualizes the ’token elasticity’ phenomenon, where initially decreasing the budget leads to a reduction in token cost, but further reductions beyond a certain point result in increased costs. Different colored lines represent different samples, showing variability in the optimal budget and its relationship to the token cost across different samples.
read the caption
(c) Yi-lightning budget search.

🔼 The figure shows the token costs for different searched budgets during the budget search process using the Yi-lightning large language model. The x-axis represents the iteration number of the budget search, and the y-axis represents the actual number of tokens used by the model. Different colored lines represent different samples, showcasing the variability in token costs across various search instances. The plot illustrates the ’token elasticity’ phenomenon where using an unreasonably small budget can result in a higher token cost than using a more reasonable budget, demonstrating that optimal budget selection significantly influences the cost-effectiveness of the process.
read the caption
(d) Yi-lightning token cost.

🔼 This figure illustrates the concept of ’token elasticity’ in large language models (LLMs). The experiment systematically reduces the token budget provided to the LLM during a chain-of-thought (CoT) reasoning task. The x-axis represents the iterations of the budget reduction process, while the y-axis shows either the target budget (Figures 2a and 2c) or the actual number of tokens used by the LLM (Figures 2b and 2d). Different colored lines represent different samples of the experiment. The figure shows that when the budget is set within a reasonable range, the LLM achieves a significant reduction in token usage. However, if the budget is set too low, the actual number of tokens used increases dramatically, exceeding the token usage when a larger budget was used. This demonstrates that there is an optimal range of token budgets for efficient LLM reasoning.
read the caption
Figure 2: Token elasticity phenomenon. The x-axis denotes the budget search iteration. The y-axis denotes the searched budget (Figure 2a and Figure 2c) or the real token costs for each searched budget (Figure 2b and Figure 2d). Different colors denote different samples. The token cost is significantly lower in a reasonable token budget range. When the token budget is smaller than the reasonable range, the token cost gradually increases.

🔼 This figure demonstrates the impact of using an optimal token budget in Chain-of-Thought (CoT) prompting. It compares the token costs of CoT reasoning using different budget values. The results show that using a carefully searched optimal budget significantly reduces token costs while maintaining similar accuracy. The figure likely includes a graph displaying token costs across different budget levels, showing a minimum point representing the optimal budget.
read the caption
Figure 3: The effects of optimal searched budget. CoT with our optimal searched budget reduces the token costs significantly without influencing the accuracy.

🔼 The figure illustrates the process of TALE (Token-Budget-Aware LLM Reasoning). First, a question is inputted. TALE then uses a budget estimator to predict the optimal number of tokens for the LLM’s response. This estimated token budget is incorporated into a modified prompt that includes both the original question and the budget constraint. The augmented prompt is fed into the large language model (LLM), which generates a response that ideally stays within the specified token budget.
read the caption
Figure 4: The workflow of TALE. Given a question, TALE first estimates the token budget using a budget estimator. It then crafts a token-budget-aware prompt by combining the question with the estimated budget. Finally, the prompt is input to the LLM to generate the answer as the final output.

🔼 This figure shows the prompt used for the zero-shot budget estimation method in the TALE framework. The prompt instructs the large language model (LLM) to analyze a given question and estimate the minimum number of tokens needed to generate a complete and accurate response. The response format is specified as [[budget]], which ensures a consistent numerical output for processing.
read the caption
Figure 5: The prompt for zero-shot estimator.

🔼 This figure shows the instruction prompt used to format the large language model’s (LLM) output when answering multiple-choice questions. The prompt ensures that the LLM’s response is in a standardized format for easier evaluation, making the output directly comparable between different questions and models. The standardized format requests a response in the format
[[choice]], wherechoiceis replaced with the letter corresponding to the selected answer (e.g., [[A]]).read the caption
Figure 6: The instruction prompt used to format the LLM output on multiple-choice questions.

🔼 This figure shows an example of a question being answered using different methods. (a) demonstrates a concise, direct answer generated by the model, using only 10 output tokens. This showcases a minimal response that directly answers the question without any intermediate reasoning steps. It highlights the trade-off between token usage and response detail.
read the caption
(a) Direct answering (10 output tokens).
More on tables
| Dataset | Directly Answering | Vanilla CoT | TALE (Ours) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ACC ↑ | Output Tokens ↓ | Expense ↓ | ACC ↑ | Output Tokens ↓ | Expense ↓ | ACC ↑ | Output Tokens ↓ | Expense ↓ | |
| — | — | — | — | — | — | — | — | — | — |
| GSM8K | 28.29% | 12.46 | 39.43 | 81.35% | 318.10 | 541.09 | 84.46% | 77.26 | 279.84 |
| GSM8K-Zero | 97.21% | 18.85 | 91.69 | 99.50% | 252.96 | 886.79 | 98.72% | 22.67 | 276.12 |
| MathBench-Arithmetic | 59.67% | 41.10 | 9.78 | 75.00% | 313.51 | 78.58 | 73.67% | 39.60 | 18.62 |
| MathBench-Middle | 33.33% | 5.00 | 3.58 | 84.67% | 553.93 | 68.22 | 79.33% | 238.14 | 42.95 |
| MathBench-High | 51.33% | 5.00 | 4.07 | 84.00% | 653.24 | 82.44 | 80.00% | 254.82 | 47.61 |
| MathBench-College | 44.00% | 5.00 | 3.68 | 78.00% | 675.78 | 81.56 | 70.00% | 259.85 | 45.60 |
| Average | 52.31% | 14.57 | 25.37 | 83.75% | 461.25 | 289.78 | 81.03% | 148.72 | 118.46 |
🔼 Table 2 presents a comparative analysis of three different prompt engineering methods: Directly Answering (no reasoning), Vanilla CoT (Chain-of-Thought with no budget constraint), and TALE (Token-Budget-Aware LLM Reasoning using a zero-shot estimator). The evaluation uses the GPT-40-mini language model. Key metrics include accuracy (ACC), average output token cost, and average expense per query. TALE demonstrates a balance between accuracy and efficiency, maintaining competitive accuracy with significantly reduced token costs and expenses compared to Vanilla CoT, while outperforming Directly Answering.
read the caption
Table 2: Comparison of TALE (Zero-shot Estimator Version) and other prompt engineering methods. “Directly Answering” means prompting LLM without any reasoning process. “Vanilla CoT” means the vanilla CoT prompting with budget. The model used in our evaluation is GPT-4o-mini OpenAI (2024a). Observe that TALE achieves an average accuracy (ACC) of 80.22%, with an average output token cost of 138.53 and an average expense of 118.46. TALE reduces output token costs by 67%, lowers expenses by 59%, and maintains competitive performance compared to the vanilla CoT approach. ACC ↑↑\uparrow↑, Output Tokens ↓↓\downarrow↓, Expense (10−5$superscript105currency-dollar10^{-5}\$10 start_POSTSUPERSCRIPT - 5 end_POSTSUPERSCRIPT $ / sample) ↓↓\downarrow↓.
| LLM | Directly Answering | Vanilla CoT | TALE (Ours) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ACC ↑ | Output Tokens ↓ | Expense ↓ | ACC ↑ | Output Tokens ↓ | Expense ↓ | ACC ↑ | Output Tokens ↓ | Expense ↓ | |
| Yi-lightning | 66.67% | 80.01 | 3.09 | 79.33% | 998.10 | 21.55 | 76.67% | 373.52 | 17.25 |
| GPT-4o-mini | 44.00% | 5.00 | 3.68 | 78.00% | 675.78 | 81.56 | 70.00% | 259.85 | 45.60 |
| GPT-4o | 57.33% | 5.00 | 61.34 | 84.00% | 602.29 | 1359.42 | 80.00% | 181.61 | 759.95 |
🔼 Table 3 presents a comparison of the performance of the TALE model (using the zero-shot estimator) across three different large language models (LLMs): Yi-lightning, GPT-40-mini, and GPT-40. The evaluation focuses on the MathBench-College dataset, measuring accuracy (ACC), the number of output tokens generated, and the computational expense (cost) of using each LLM. The table highlights the model’s ability to generalize well across different LLMs while maintaining efficiency by reducing the number of tokens and computational cost.
read the caption
Table 3: The generalization of TALE (Zero-shot Estimator Version) across different LLMs. Yi-lightning Wake et al. (2024), GPT-4o-mini OpenAI (2024a) and GPT-4o OpenAI (2024b) are taken into consideration. We conduct the evaluation on MathBench-College. ACC ↑↑\uparrow↑, Output Tokens ↓↓\downarrow↓, Expense (10−5$superscript105currency-dollar10^{-5}\$10 start_POSTSUPERSCRIPT - 5 end_POSTSUPERSCRIPT $ / sample) ↓↓\downarrow↓.
Full paper#