Graph Generative Pre-trained Transformer

↗ arXiv ↗ Hugging Face ↗ Papers with Code

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel approach to graph generation using a sequence-based representation and a transformer decoder, achieving state-of-the-art results. This method offers efficiency and flexibility, making it suitable for various downstream tasks, opening new avenues for research in molecular design and other graph-related fields. The exploration of fine-tuning strategies for different applications further enhances its value to researchers.

---

Visual Insights

#

🔼 This figure illustrates how a graph is represented as a sequence of actions. First, all nodes are generated, each represented by its type and a unique index. Then, edges are added one by one, each defined by the source node index, the destination node index, and the edge type. The entire graph generation process is thus encoded as a sequence of tokens, which allows the use of a transformer-decoder architecture to model this sequence and predict the next token in the sequence during training. A unified vocabulary is used to represent all node types, edge types, and actions (node creation and edge creation), making this representation suitable for the transformer-decoder.

read the caption

Figure 1: Illustration of our proposed graph sequence representation. This representation can be viewed as a sequence of actions: first generating all nodes (node type, node index), then explicitly adding edges (source node index, destination node index, edge type) step by step until completion. A unified vocabulary is used to map different types of actions into a shared token space.

Model (Rep.)	Likelihood	Illustration	#Network Calls	#Variables	Decomposition
Diffusion ($\mathbf{A}$)	<math alttext=“p(\mathbf{A}^{T})\displaystyle\prod_{t=1}^{T}p(\mathbf{A}^{t-1}	\mathbf{A}^{t})” class=“ltx_Math” display=“inline” id=“S1.T1.2.2.2.2.m1.2”>p,\prod_{t=1}^{T}p(\mathbf{A}^{t-1}	\mathbf{A}^{t})		$T$
Auto-regressive ($\mathbf{A}$)	<math alttext="\displaystyle\prod_{i=2}^{n}\prod_{j=1}^{i-1}p(\mathbf{A}_{i,j}	\mathbf{A}{<i,% <i-1},\mathbf{A}{i,<j})" class=“ltx_Math” display=“inline” id=“S1.T1.7.7.7.2.m1.7”>\prod_{i=2}^{n}\prod_{j=1}^{i-1}p(\mathbf{A}_{i,j}	\mathbf{A}{<i,% <i-1},\mathbf{A}{i,<j})		$O,\backslash prod\_\{i=2\}^\{n\}\backslash prod\_\{j=1\}^\{i-1\}p(\backslash mathbf\{A\}\_\{i,j\}$
Auto-regressive ($E$)	<math alttext=“p(e_{1})\displaystyle\prod_{i=2}^{m}p(e_{i}	e_{<i})” class=“ltx_Math” display=“inline” id=“S1.T1.12.12.12.2.m1.2”>p,\prod_{i=2}^{m}p(e_{i}	e_{<i})		$O,\backslash prod\_\{i=2\}^\{m\}p(e\_\{i\}$

🔼 This table provides a comparison of different graph generative model families, categorized by their data representation (adjacency matrix or edge set) and likelihood decomposition approach (diffusion-based or autoregressive). It shows the computational complexity in terms of the number of network calls and variables involved. The illustration visually explains how each approach generates graph structures, step-by-step, using solid and dashed lines to depict edges and non-edges, with the current step highlighted in blue. Notably, the table highlights that the proposed Graph Generative Pre-trained Transformer (G2PT) is an autoregressive model working with the edge set representation.

read the caption

Table 1: Overview of graph generative model families combined with the used data representation (Rep.). n𝑛nitalic_n: number of nodes. m𝑚mitalic_m: number of edges. In the illustration, we use solid line for edges and dash line for non-edges, (non-)edges generated at current step are colored in blue. Our proposed G2PT is an Auto-regressive model that learns on E𝐸Eitalic_E representation.

In-depth insights

#

GraphSeq Encoding

#

The heading “GraphSeq Encoding” suggests a novel method for representing graphs as sequences, a crucial step in applying sequence-based models like transformers to graph-structured data. A well-designed GraphSeq encoding would likely involve transforming graph elements (nodes and edges) into a sequential format, potentially by incorporating node features, edge types, and topological information. The choice of sequencing (e.g., breadth-first search, depth-first search, random ordering) would significantly impact the model’s ability to learn graph structures. An effective encoding must balance expressiveness with efficiency; it should capture the essential characteristics of the graph while avoiding excessive length or redundancy. The success of this approach hinges on how well the encoding captures graph features and allows the sequence model to accurately reconstruct or generate graphs. Furthermore, the choice of vocabulary for tokenizing the sequence representation and the overall design would directly impact computational performance. Ultimately, the evaluation of GraphSeq would revolve around its effectiveness in downstream applications, such as graph generation and property prediction, demonstrating its capability to improve upon previous methods.

G2PT Model

#

The G2PT model, a Graph Generative Pre-trained Transformer, presents a novel approach to graph generation. Its core innovation lies in representing graphs as sequences of node and edge definitions, shifting away from adjacency matrices. This sequence-based representation allows for efficient encoding and leverages the power of transformer decoders for next-token prediction. The model’s auto-regressive nature enables sequential generation of graph structures, making it suitable for various downstream tasks, including goal-oriented generation and graph property prediction. Fine-tuning strategies are explored for both scenarios, demonstrating the adaptability of the model to specific needs. Overall, G2PT showcases the effectiveness of combining transformer architecture with a carefully designed sequence representation for enhanced graph generation performance and versatility. The model’s strong performance across diverse datasets is a key strength, underlining its potential as a general-purpose graph generation foundation model.

Fine-tuning G2PT

#

The section on “Fine-tuning G2PT” would explore how the pre-trained Graph Generative Pre-trained Transformer (G2PT) model can be adapted for downstream tasks. This involves transfer learning, leveraging the knowledge learned during pre-training on a large graph dataset to improve performance on specific tasks with limited data. The authors likely investigate two main categories of downstream tasks: goal-oriented generation and graph property prediction. Goal-oriented generation focuses on generating graphs with specific properties, perhaps using techniques like reinforcement learning or rejection sampling to guide the generation process towards desired outcomes. Graph property prediction would involve adapting G2PT to predict properties of graphs, such as molecular properties in drug discovery, directly using the learned representations. This could utilize supervised fine-tuning approaches. The results of this fine-tuning would demonstrate G2PT’s adaptability and versatility, showcasing its effectiveness as a general-purpose foundation model for various graph-related applications. The analysis will likely show how the pre-training helps to overcome challenges associated with limited data in downstream tasks and how effectively G2PT can be adapted, highlighting its strengths compared to other models in this area.

Generative Results

#

A dedicated ‘Generative Results’ section in a research paper would ideally present a comprehensive evaluation of a novel graph generative model. This would involve showcasing the model’s ability to generate diverse and realistic graph structures, comparing its performance against existing state-of-the-art methods using established metrics, and providing qualitative visualizations of the generated graphs to illustrate their properties. Quantitative metrics would likely include measures of graph structure such as node degree distribution, clustering coefficient, and path lengths, possibly also evaluating the novelty and uniqueness of generated graphs. Qualitative analysis would involve visual inspection of generated samples, assessing their realism and plausibility within the target domain. The results should be presented across different datasets to show the model’s generalization ability and robustness. Crucially, the analysis should discuss any limitations, addressing challenges encountered during generation and suggesting areas for future improvement. A thorough analysis of generative results is vital to establishing the significance and potential impact of a new graph generative model.

Future Work

#

Future research directions for this Graph Generative Pre-trained Transformer (G2PT) model could explore improving the efficiency and scalability of the training process, particularly for larger and more complex graphs. Investigating alternative training strategies beyond the current autoregressive approach, perhaps incorporating diffusion models or other generative techniques, could potentially unlock improved performance. Another avenue of investigation would be to deepen the understanding of edge ordering techniques. The current approach shows sensitivity to the chosen ordering; therefore, developing a more universal and expressive edge ordering strategy is crucial. Furthermore, exploring different graph representations beyond the sequence-based approach could potentially lead to more efficient models and broader applications. Finally, applying G2PT to a wider range of downstream tasks, especially those involving complex relationship modeling and structural prediction problems, represents a promising area for future development. Benchmarking G2PT against a more extensive set of state-of-the-art baselines on diverse datasets is also important to fully evaluate its capabilities and identify limitations.

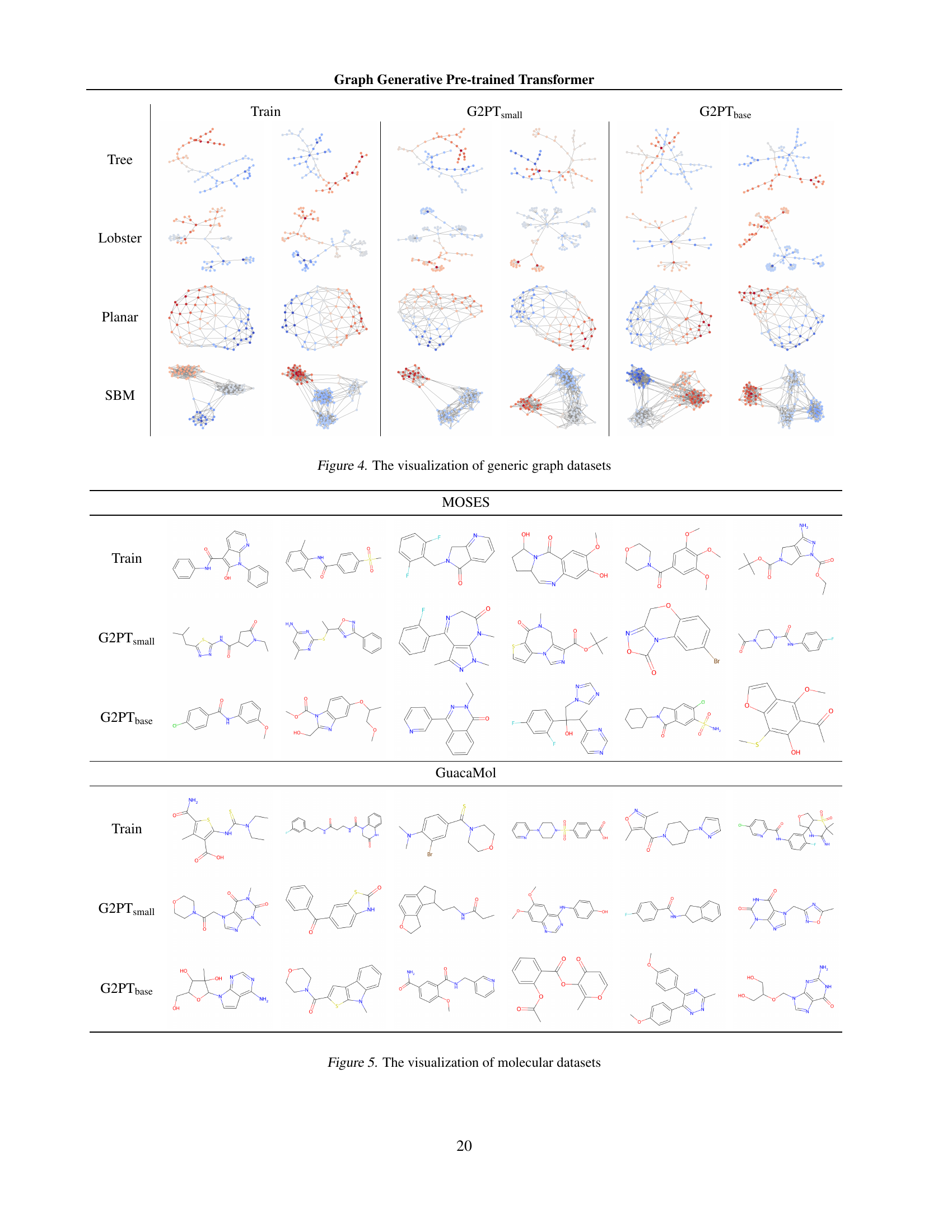
More visual insights

#

More on tables

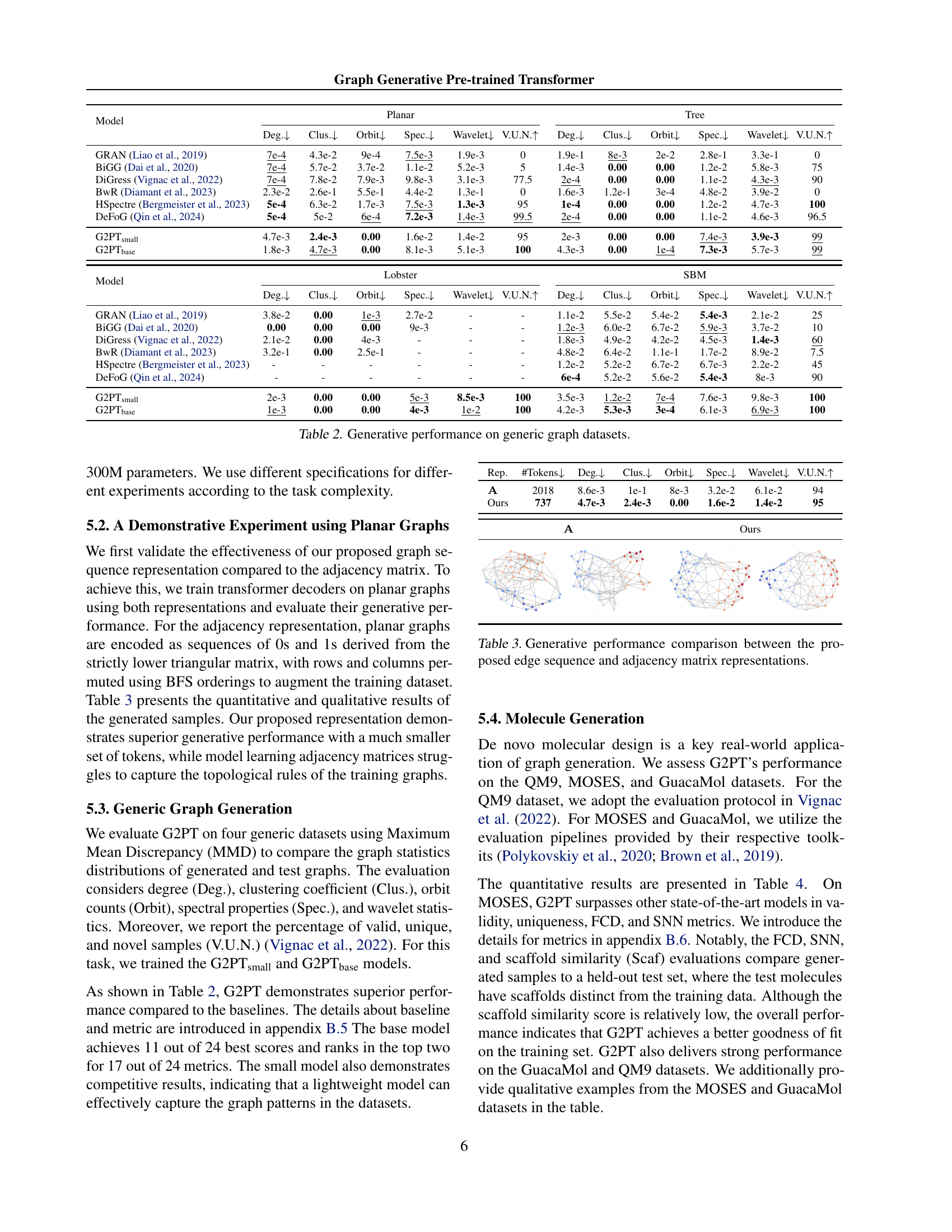
Model	Planar	Planar	Planar	Planar	Planar	Planar	Tree	Tree	Tree	Tree	Tree	Tree
Deg. ↓	Clus. ↓	Orbit ↓	Spec. ↓	Wavelet ↓	V.U.N. ↑	Deg. ↓	Clus. ↓	Orbit ↓	Spec. ↓	Wavelet ↓	V.U.N. ↑
GRAN (Liao et al., 2019)	7e-4	4.3e-2	9e-4	7.5e-3	1.9e-3	0	1.9e-1	8e-3	2e-2	2.8e-1	3.3e-1	0
BiGG (Dai et al., 2020)	7e-4	5.7e-2	3.7e-2	1.1e-2	5.2e-3	5	1.4e-3	0.00	0.00	1.2e-2	5.8e-3	75
DiGress (Vignac et al., 2022)	7e-4	7.8e-2	7.9e-3	9.8e-3	3.1e-3	77.5	2e-4	0.00	0.00	1.1e-2	4.3e-3	90
BwR (Diamant et al., 2023)	2.3e-2	2.6e-1	5.5e-1	4.4e-2	1.3e-1	0	1.6e-3	1.2e-1	3e-4	4.8e-2	3.9e-2	0
HSpectre (Bergmeister et al., 2023)	5e-4	6.3e-2	1.7e-3	7.5e-3	1.3e-3	95	1e-4	0.00	0.00	1.2e-2	4.7e-3	100
DeFoG (Qin et al., 2024)	5e-4	5e-2	6e-4	7.2e-3	1.4e-3	99.5	2e-4	0.00	0.00	1.1e-2	4.6e-3	96.5
G2PTsmall	4.7e-3	2.4e-3	0.00	1.6e-2	1.4e-2	95	2e-3	0.00	0.00	7.4e-3	3.9e-3	99
G2PTbase	1.8e-3	4.7e-3	0.00	8.1e-3	5.1e-3	100	4.3e-3	0.00	1e-4	7.3e-3	5.7e-3	99
Model	Lobster	Lobster	Lobster	Lobster	Lobster	Lobster	SBM	SBM	SBM	SBM	SBM	SBM
—	—	—	—	—	—	—	—	—	—	—	—	—
Deg. ↓	Clus. ↓	Orbit ↓	Spec. ↓	Wavelet ↓	V.U.N. ↑	Deg. ↓	Clus. ↓	Orbit ↓	Spec. ↓	Wavelet ↓	V.U.N. ↑
GRAN (Liao et al., 2019)	3.8e-2	0.00	1e-3	2.7e-2	-	-	1.1e-2	5.5e-2	5.4e-2	5.4e-3	2.1e-2	25
BiGG (Dai et al., 2020)	0.00	0.00	0.00	9e-3	-	-	1.2e-3	6.0e-2	6.7e-2	5.9e-3	3.7e-2	10
DiGress (Vignac et al., 2022)	2.1e-2	0.00	4e-3	-	-	-	1.8e-3	4.9e-2	4.2e-2	4.5e-3	1.4e-3	60
BwR (Diamant et al., 2023)	3.2e-1	0.00	2.5e-1	-	-	-	4.8e-2	6.4e-2	1.1e-1	1.7e-2	8.9e-2	7.5
HSpectre (Bergmeister et al., 2023)	-	-	-	-	-	-	1.2e-2	5.2e-2	6.7e-2	6.7e-3	2.2e-2	45
DeFoG (Qin et al., 2024)	-	-	-	-	-	-	6e-4	5.2e-2	5.6e-2	5.4e-3	8e-3	90
G2PTsmall	2e-3	0.00	0.00	5e-3	8.5e-3	100	3.5e-3	1.2e-2	7e-4	7.6e-3	9.8e-3	100
G2PTbase	1e-3	0.00	0.00	4e-3	1e-2	100	4.2e-3	5.3e-3	3e-4	6.1e-3	6.9e-3	100

🔼 This table presents a quantitative comparison of the generative performance of different graph generative models on four generic graph datasets: Planar, Tree, Lobster, and Stochastic Block Model (SBM). The performance is evaluated using several metrics including degree distribution, clustering coefficient, orbit counts, spectral properties, wavelet statistics, and the percentage of valid, unique, and novel graphs generated. These metrics assess various structural and topological aspects of the generated graphs, offering a comprehensive evaluation of each model’s ability to generate realistic and diverse graph structures.

read the caption

Table 2: Generative performance on generic graph datasets.

Rep.	#Tokens ↓	Deg. ↓	Clus. ↓	Orbit ↓	Spec. ↓	Wavelet ↓	V.U.N. ↑
𝐀	2018	8.6e-3	1e-1	8e-3	3.2e-2	6.1e-2	94
Ours	737	4.7e-3	2.4e-3	0.00	1.6e-2	1.4e-2	95

🔼 This table compares the performance of graph generative models using two different graph representations: the proposed edge sequence representation and the traditional adjacency matrix representation. It evaluates the generative quality on planar graphs, using metrics such as the number of valid, unique and novel graphs generated, and the degree, clustering coefficient, orbital count, spectral properties, and wavelet statistics of the generated graphs. The comparison allows assessment of the effectiveness of the novel edge sequence representation against the standard adjacency matrix method.

read the caption

Table 3: Generative performance comparison between the proposed edge sequence and adjacency matrix representations.

A	A	Ours	Ours

🔼 This table presents a comparison of the performance of different graph generative models on molecular graph datasets. It shows quantitative metrics evaluating the quality of generated molecules, including validity (percentage of valid molecules), uniqueness (percentage of unique molecules), novelty (percentage of novel molecules not present in training data), fraction of molecules that pass certain filters, Frechet ChemNet Distance (FCD), Scaffold similarity, and other metrics specific to the MOSES and GuacaMol benchmarks. This allows for a direct comparison of how well each model generates realistic and diverse molecules.

read the caption

Table 4: Generative performance on molecular graph datasets

Model	MOSES Validity ↑	MOSES Unique ↑	MOSES Novelty ↑	MOSES Filters ↑	MOSES FCD ↓	MOSES SNN ↑	MOSES Scaf ↑	GuacaMol Validity ↑	GuacaMol Unique ↑	GuacaMol Novelty ↑	GuacaMol KL Div ↑	GuacaMol FCD ↑
DiGress (Vignac et al., 2022)	85.7	100	95.0	97.1	1.19	0.52	14.8	85.2	100	99.9	92.9	68
DisCo (Xu et al., 2024)	88.3	100	97.7	95.6	1.44	0.5	15.1	86.6	86.6	86.5	92.6	59.7
Cometh (Siraudin et al., 2024)	90.5	99.9	92.6	99.1	1.27	0.54	16.0	98.9	98.9	97.6	96.7	72.7
DeFoG (Qin et al., 2024)	92.8	99.9	92.1	99.9	1.95	0.55	14.4	99.0	99.0	97.9	97.9	73.8
G2PTsmall	95.1	100	91.7	97.4	1.10	0.52	5.0	90.4	100	99.8	92.8	86.6
G2PTbase	96.4	100	86.0	98.3	0.97	0.55	3.3	94.6	100	99.5	96.0	93.4
G2PTlarge	97.2	100	79.4	98.9	1.02	0.55	2.9	95.3	100	99.5	95.6	92.7

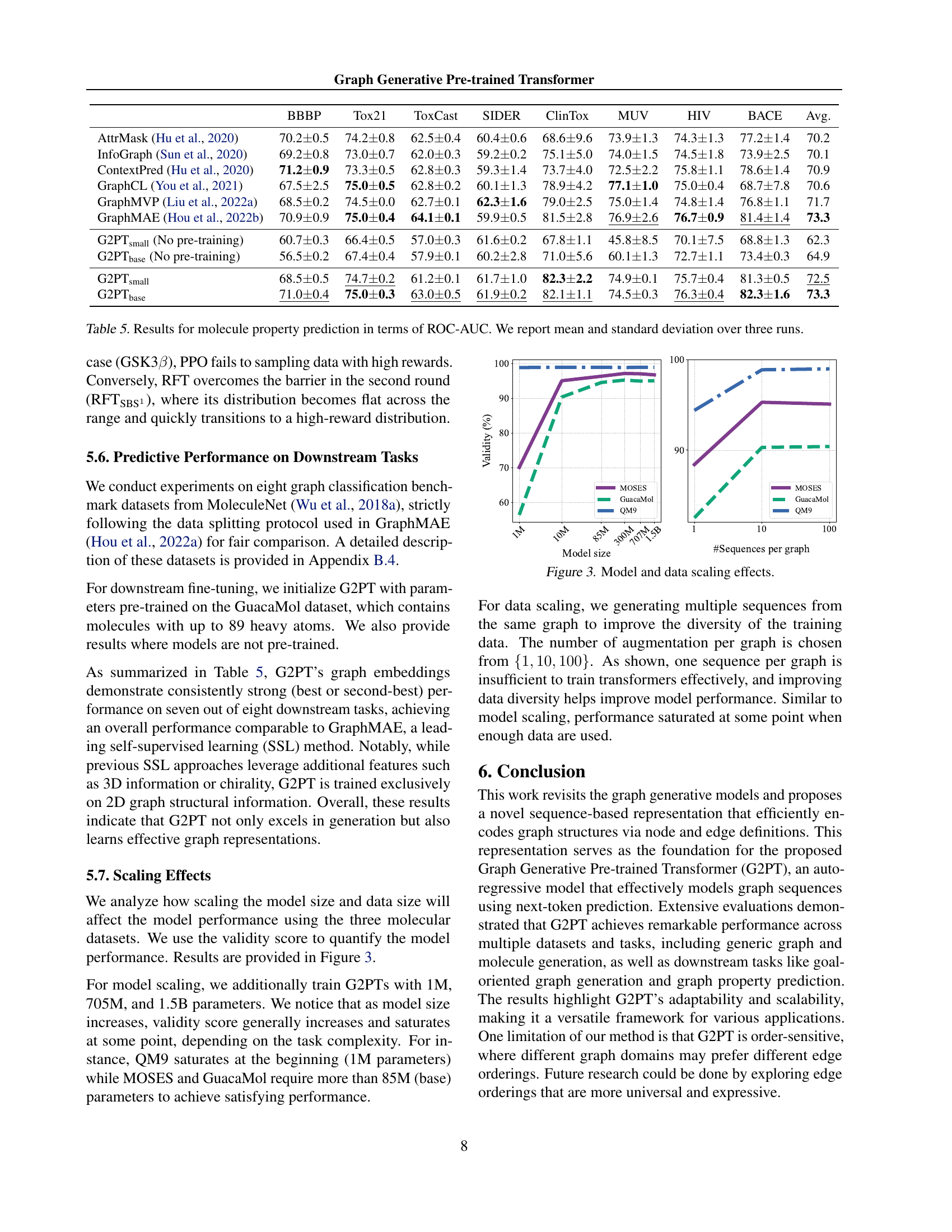
🔼 This table presents the results of molecular property prediction experiments using the Graph Generative Pre-trained Transformer (G2PT) model. The performance is measured by the area under the Receiver Operating Characteristic curve (ROC-AUC). The table shows ROC-AUC scores for multiple datasets (BBBP, Tox21, ToxCast, SIDER, ClinTox, MUV, HIV, BACE) and multiple model sizes, with mean and standard deviation reported across three independent runs, providing a comprehensive evaluation of the G2PT’s predictive capabilities in various molecular property prediction tasks.

read the caption

Table 5: Results for molecule property prediction in terms of ROC-AUC. We report mean and standard deviation over three runs.

Model	QM9
	Validity↑	Unique↑	FCD↓
DiGress (Vignac et al., 2022)	99.0	96.2	-
DisCo (Xu et al., 2024)	99.6	96.2	0.25
Cometh (Siraudin et al., 2024)	99.2	96.7	0.11
DeFoG (Qin et al., 2024)	99.3	96.3	0.12
G2PTsmall	99.0	96.7	0.06
G2PTbase	99.0	96.8	0.06
G2PTlarge	98.9	96.7	0.06

🔼 This table provides a comprehensive overview of the datasets used in the experiments. For each dataset, it lists the number of node types, edge types, the average, minimum, and maximum number of nodes in the graphs, the number of training sequences used for each dataset, and the size of the vocabulary used for tokenization during training. This information is crucial for understanding the scale and complexity of the datasets and how they were prepared for model training.

read the caption

Table 6: Dataset statistics.

MOSES			GuacaMol
Train	G2PTsmall	G2PTbase	Train	G2PTsmall	G2PTbase

🔼 This table details the hyperparameters used during the pre-training phase of the Graph Generative Pre-trained Transformer (G2PT) model. It shows how these settings varied across three different model sizes (10M, 85M, and 300M parameters), impacting aspects like architecture (number of layers, heads, and the model’s embedding dimension), optimization (optimizer, learning rate scheduler, weight decay), training process (batch size, gradient accumulation, gradient clipping), and warmup iterations.

read the caption

Table 7: Hyperparameters for graph generative pre-training.

Density	QED Score	SA Score	GSK3β Score
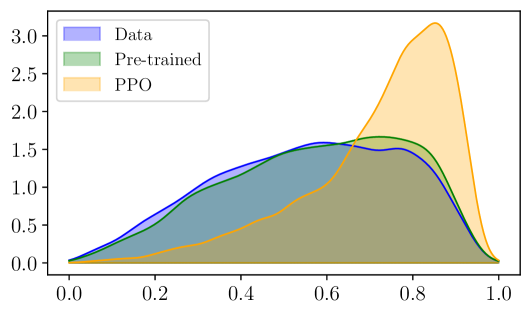
			(a) Rejection sampling fine-tuning (with self-bootstrap)
			(b) Reinforcement learning framework (PPO)

🔼 This table lists the hyperparameters used for training the Proximal Policy Optimization (PPO) algorithm in the goal-oriented molecule generation experiments. It shows hyperparameters specific to three different molecular properties being optimized: Quantitative Evaluation of Druglikeness (QED), Synthetic Accessibility (SA), and Glycogen Synthase Kinase 3 Beta (GSK3β) activity. The table includes settings for advantage and reward normalization and clipping, entropy regularization, learning rates for the actor and critic networks, and the number of training iterations.

read the caption

Table 8: Hyperparameters used for PPO training.

BBBP	Tox21	ToxCast	SIDER	ClinTox	MUV	HIV	BACE	Avg.
AttrMask (Hu et al., 2020)	70.2 ± 0.5	74.2 ± 0.8	62.5 ± 0.4	60.4 ± 0.6	68.6 ± 9.6	73.9 ± 1.3	74.3 ± 1.3	77.2 ± 1.4
InfoGraph (Sun et al., 2020)	69.2 ± 0.8	73.0 ± 0.7	62.0 ± 0.3	59.2 ± 0.2	75.1 ± 5.0	74.0 ± 1.5	74.5 ± 1.8	73.9 ± 2.5
ContextPred (Hu et al., 2020)	71.2 ± 0.9	73.3 ± 0.5	62.8 ± 0.3	59.3 ± 1.4	73.7 ± 4.0	72.5 ± 2.2	75.8 ± 1.1	78.6 ± 1.4
GraphCL (You et al., 2021)	67.5 ± 2.5	75.0 ± 0.5	62.8 ± 0.2	60.1 ± 1.3	78.9 ± 4.2	77.1 ± 1.0	75.0 ± 0.4	68.7 ± 7.8
GraphMVP (Liu et al., 2022a)	68.5 ± 0.2	74.5 ± 0.0	62.7 ± 0.1	62.3 ± 1.6	79.0 ± 2.5	75.0 ± 1.4	74.8 ± 1.4	76.8 ± 1.1
GraphMAE (Hou et al., 2022b)	70.9 ± 0.9	75.0 ± 0.4	64.1 ± 0.1	59.9 ± 0.5	81.5 ± 2.8	76.9 ± 2.6	76.7 ± 0.9	81.4 ± 1.4
G2PTsmall (No pre-training)	60.7 ± 0.3	66.4 ± 0.5	57.0 ± 0.3	61.6 ± 0.2	67.8 ± 1.1	45.8 ± 8.5	70.1 ± 7.5	68.8 ± 1.3
G2PTbase (No pre-training)	56.5 ± 0.2	67.4 ± 0.4	57.9 ± 0.1	60.2 ± 2.8	71.0 ± 5.6	60.1 ± 1.3	72.7 ± 1.1	73.4 ± 0.3
G2PTsmall	68.5 ± 0.5	74.7 ± 0.2	61.2 ± 0.1	61.7 ± 1.0	82.3 ± 2.2	74.9 ± 0.1	75.7 ± 0.4	81.3 ± 0.5
G2PTbase	71.0 ± 0.4	75.0 ± 0.3	63.0 ± 0.5	61.9 ± 0.2	82.1 ± 1.1	74.5 ± 0.3	76.3 ± 0.4	82.3 ± 1.6

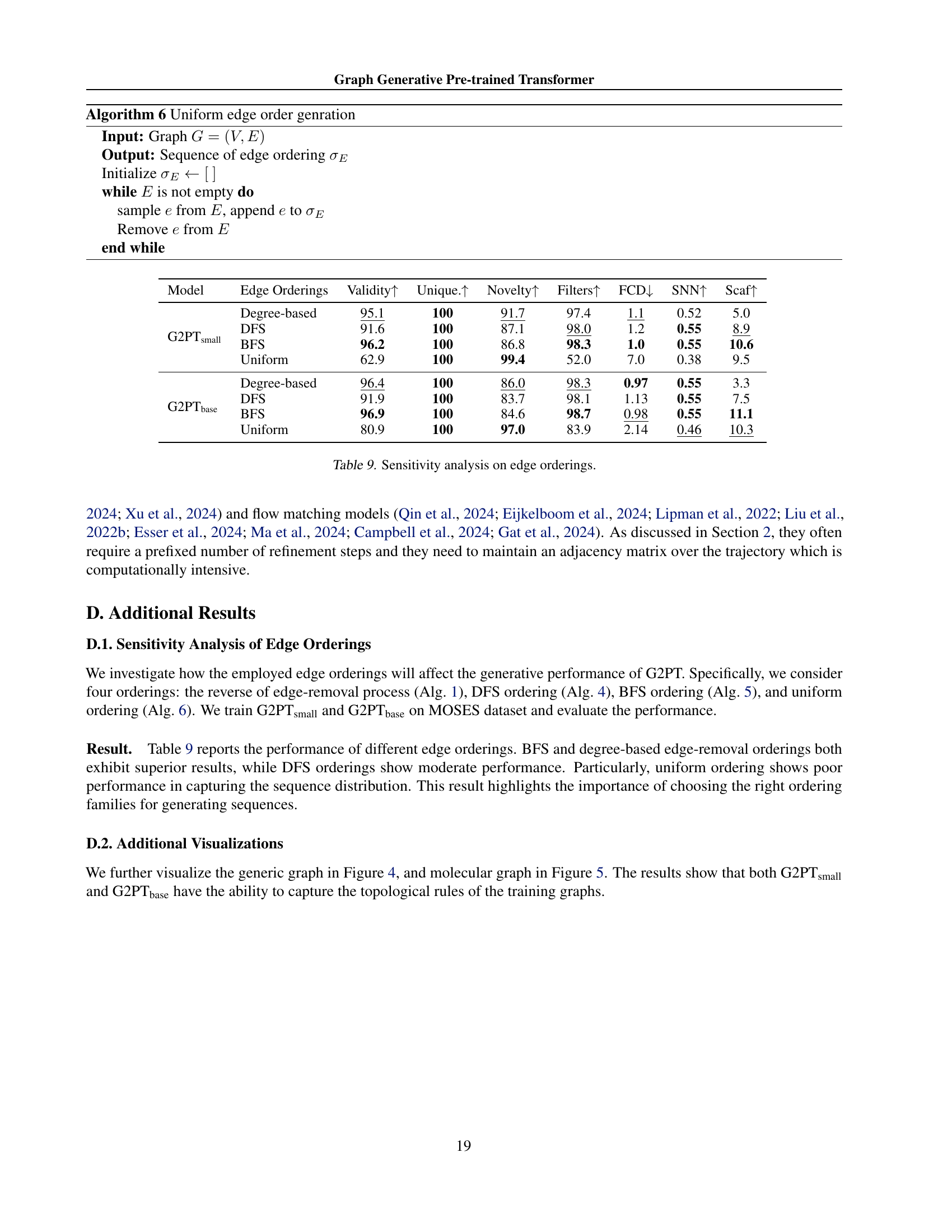
🔼 This table presents a sensitivity analysis of different edge ordering methods used in the Graph Generative Pre-trained Transformer (G2PT) model. It compares the performance of four different edge ordering approaches: degree-based ordering, Depth-First Search (DFS) ordering, Breadth-First Search (BFS) ordering, and uniform random ordering. The evaluation metrics used include validity, uniqueness, novelty, filtering, Frechet ChemNet Distance (FCD), Scaffold similarity, and structural similarity. The results demonstrate that degree-based and BFS ordering strategies generally perform better than DFS and uniform ordering strategies, highlighting the impact of edge ordering on the model’s performance.

read the caption

Table 9: Sensitivity analysis on edge orderings.

Full paper

#