↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Low-precision training, especially using floating-point quantization, is crucial for efficient large language model (LLM) training. However, existing scaling laws primarily focus on integer quantization, which isn’t well-suited for the nuances of floating-point methods. This lack of understanding hinders efforts to optimize training costs and predict model performance. This paper addresses these issues by deeply investigating the effects of different floating-point configurations (exponent bits, mantissa bits, scaling factor granularity) on LLM training performance. The research uses a comprehensive experimental setup involving various data and model sizes, along with multiple precision settings, to establish a robust and accurate scaling law for predicting performance under low-precision training. This new scaling law incorporates these crucial floating-point parameters, unlike prior work that treated precision in a less nuanced way.
The core contribution of this work is the development of a novel, unified scaling law that accurately predicts LLM performance under various data sizes, model sizes, and floating-point configurations (exponent and mantissa bits). This law allows researchers to efficiently select optimal parameter settings before running costly experiments and assists in predicting model behavior across a wide range of conditions. Key insights from the scaling law include discovering the optimal exponent-mantissa bit ratio for various precision levels and determining the critical training data size to prevent performance degradation. This research demonstrates that cost-effective performance can be achieved between 4-8 bits of precision and proposes guidelines for selecting optimal hardware configurations.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language model (LLM) training efficiency and low-precision computation. It provides a novel scaling law for floating-point quantization, offering practical guidance for optimizing LLM training costs and hardware resource allocation. The findings are particularly relevant to current trends in reducing computational expenses and improving LLM deployment on resource-constrained platforms. It opens up new avenues for exploring optimal exponent-mantissa bit ratios and critical data size thresholds in low-precision LLM training.
Visual Insights#

🔼 This figure compares the predictions of Kumar et al.’s (2024) scaling law (Equation 7 in the paper) against actual experimental results for various data sizes (D), exponent bits (E), and mantissa bits (M) during floating-point quantization training. The three subplots show these comparisons, with point sizes in each plot visually representing the magnitude of D, E, and M respectively. The results show that the scaling law significantly deviates from the observed experimental results particularly when both exponent and mantissa bits are small (E1M1), highlighting the limitations of using this model for this scenario. The plot demonstrates the inaccuracies of Kumar et al.’s scaling law in predicting the loss for floating-point quantization training.
read the caption
Figure 1: The fitting results of the scaling law in Eq. (7) deriving from Kumar et al. (2024), which have large bias in E1M1 case. In the three sub-figures on the left, middle and right, the sizes of the data points are approximately proportional to D𝐷Ditalic_D, E𝐸Eitalic_E, and M𝑀Mitalic_M respectively.
| Hyper-parameters | 41M | 85M | 154M | 679M | 1.2B | |
|---|---|---|---|---|---|---|
| Layers | 12 | 12 | 12 | 24 | 24 | |
| Hidden Size | 512 | 768 | 1024 | 1536 | 2048 | |
| FFN Hidden Size | 1536 | 2048 | 2816 | 4096 | 5632 | |
| Attention Heads | 8 | 12 | 16 | 24 | 32 | |
| Attention Head size | 64 | 64 | 64 | 64 | 64 | |
| Optimizer | AdamW | AdamW | AdamW | AdamW | AdamW | |
| Adam $(\beta_1,\beta_2)$ | (0.9, 0.95) | (0.9, 0.95) | (0.9, 0.95) | (0.9, 0.95) | (0.9, 0.95) | |
| Adam $\epsilon$ | $1\times 10^{-8}$ | $1\times 10^{-8}$ | $1\times 10^{-8}$ | $1\times 10^{-8}$ | $1\times 10^{-8}$ | |
| Weight Decay | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| Clip Grad Norm | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| Max LR | $3.0\times 10^{-4}$ | $3.0\times 10^{-4}$ | $3.0\times 10^{-4}$ | $3.0\times 10^{-4}$ | $3.0\times 10^{-4}$ | |
| Min LR | 0 | 0 | 0 | 0 | 0 | |
| LR Decay | Cosine | Cosine | Cosine | Cosine | Cosine | |
| Seqence Length | 2048 | 2048 | 2048 | 2048 | 2048 | |
| Batch Size (# Tokens) | 2M | 2M | 2M | 2M | 2M | |
| Warmup Steps | 500 | 500 | 500 | 500 | 500 |
🔼 This table details the specific hyperparameter settings used for training each of the different sized LLaMA language models. It includes information such as the number of layers, hidden size, feed-forward network (FFN) hidden size, attention heads, attention head size, optimizer, Adam parameters (B1, B2), Adam epsilon, weight decay, gradient clipping norm, maximum learning rate, minimum learning rate, learning rate decay schedule, sequence length, batch size (in tokens), and warmup steps. These parameters are crucial for understanding the experimental setup and for reproducibility.
read the caption
Table 1: Model hyper-parameters for each size.
In-depth insights#
FP Quant. Scaling Laws#
The research explores scaling laws for floating-point quantization training in large language models (LLMs). It challenges existing laws that primarily focus on integer quantization, arguing they don’t accurately capture the nuances of floating-point precision. The study delves into the impact of exponent and mantissa bit allocation on LLM performance, proposing an optimal exponent-mantissa bit ratio for different precision levels. A crucial finding is the identification of a critical data size, beyond which adding more training data hinders performance. The research culminates in a unified scaling law that incorporates data size, model size, exponent, mantissa, and block size of scaling factors, providing a more comprehensive predictive model for low-precision LLM training and guiding cost-effective choices of precision levels for specific computational resources.
Optimal Bit Allocation#
Optimal bit allocation in quantized neural networks, especially for large language models (LLMs), is crucial for balancing model accuracy and computational efficiency. Finding the ideal balance between exponent bits (representing the dynamic range) and mantissa bits (representing precision within that range) is key. A common approach is to explore the scaling laws, which describe the relationship between model performance and different hyperparameters, including bit precision. The research investigates how the choice of exponent and mantissa bits affects LLM performance, aiming to find the optimal allocation for a given total number of bits. This involves extensive experimentation, fitting the results to scaling laws, and analyzing the resulting trade-offs. The optimal allocation often varies based on factors like the model size, dataset size, and the chosen quantization method. Further exploration might consider the impact of hardware limitations and the cost-performance trade-offs associated with different bit allocation strategies. Ultimately, the goal is to minimize the loss in accuracy while maximizing computational efficiency, resulting in a cost-effective solution for low-precision training and inference.
Critical Data Size#
The concept of “Critical Data Size” in the context of low-precision floating-point quantization training for LLMs reveals a crucial limitation. Beyond a certain data size, increasing training data paradoxically leads to performance degradation instead of improvement. This is attributed to the combined effects of limited precision and the “knowledge intensity” of the model. The model’s capacity to effectively utilize and learn from additional information is overwhelmed by the precision constraints. This highlights that optimal performance is not solely determined by the scale of data, but by a careful balance between data size, model size, and the selected precision. Optimal data size varies significantly depending on the precision level, with higher precisions enabling the use of larger datasets before encountering performance decline. This insight has significant implications for resource allocation and efficient training strategies, emphasizing the importance of precise scaling law estimations that account for the interplay between these factors.
Cost-Optimal Precision#
The concept of “Cost-Optimal Precision” in the context of large language model (LLM) training centers on finding the sweet spot between model accuracy and computational cost. The paper explores the trade-offs between using higher precision (e.g., FP32) for better accuracy and lower precision (e.g., FP8) for reduced computational expenses. It highlights that optimal precision isn’t fixed, but rather dynamically depends on factors like model size, training data volume, and available computational resources. The research likely presents a mathematical framework or scaling laws to predict the best precision for a given set of constraints, enabling researchers and developers to optimize training efficiency without significantly sacrificing model performance. Essentially, the “Cost-Optimal Precision” section aims to guide efficient resource allocation by providing a data-driven method for selecting the most appropriate precision level for LLM training, leading to cost savings and faster training times.
Future Work#
The authors suggest several avenues for future research. Extending the scaling laws to larger models and datasets is crucial to validate the model’s generalizability and predictive power beyond the current experimental scope. Investigating the applicability of these laws to different LLM architectures, such as those beyond the Transformer architecture, is vital to broaden the findings’ relevance and practical impact. The study focused on specific floating-point quantization strategies, therefore, exploring other quantization methods will enrich the understanding of the impact of precision on LLM performance. Finally, a deeper investigation into the interaction between various quantization techniques and the scaling laws could reveal valuable insights into the optimization of low-precision LLM training and deployment. Addressing these points would further enhance the practical use and theoretical significance of the presented work.
More visual insights#
More on figures

🔼 The figure shows the comparison of the Chinchilla scaling law with the actual LLM training losses using BF16 precision. The plot visualizes the alignment of predicted losses against empirical losses for various model sizes, demonstrating the accuracy of the Chinchilla scaling law in predicting LLM performance under BF16 precision.
read the caption
(a) Chinchilla basic scaling law.

🔼 This figure shows the comparison of the OpenAI scaling law with the empirical training loss for various model sizes. The plot illustrates the predicted loss versus the actual training loss observed during experiments. This visualization helps assess the accuracy of the OpenAI scaling law in predicting model performance in the context of the paper’s research.
read the caption
(b) OpenAI basic scaling law.

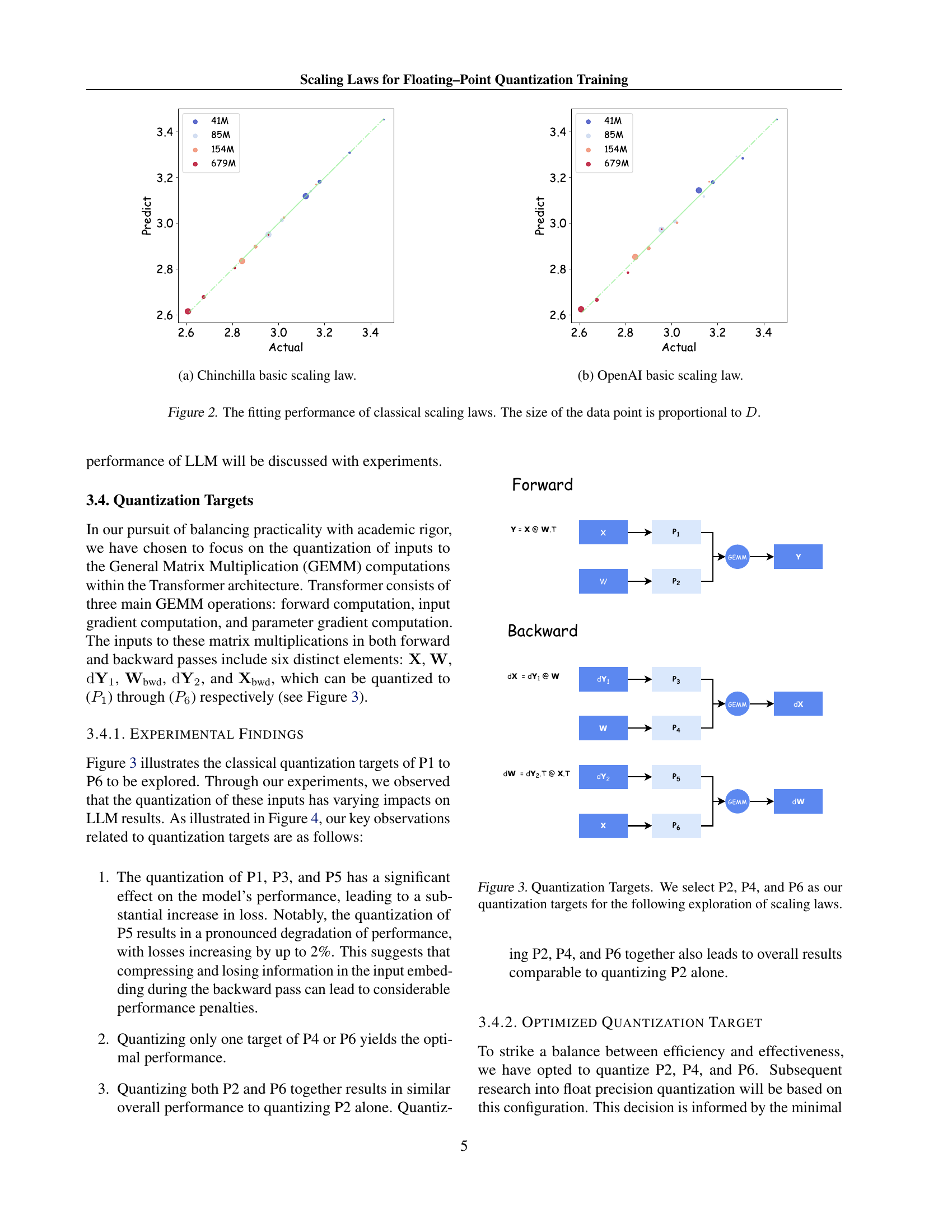
🔼 This figure compares the performance of two established scaling laws – the Chinchilla scaling law and the OpenAI scaling law – against actual results obtained from LLM training. Both laws attempt to predict training loss (L) based on model size (N) and dataset size (D). The plot visually represents the comparison, showing how well each law predicts the observed training losses. The size of each data point corresponds to the dataset size (D). This visualization helps assess the accuracy of the classical scaling laws in predicting LLM training behavior and informs the development of a more precise, precision-aware scaling law.
read the caption
Figure 2: The fitting performance of classical scaling laws. The size of the data point is proportional to D𝐷Ditalic_D.

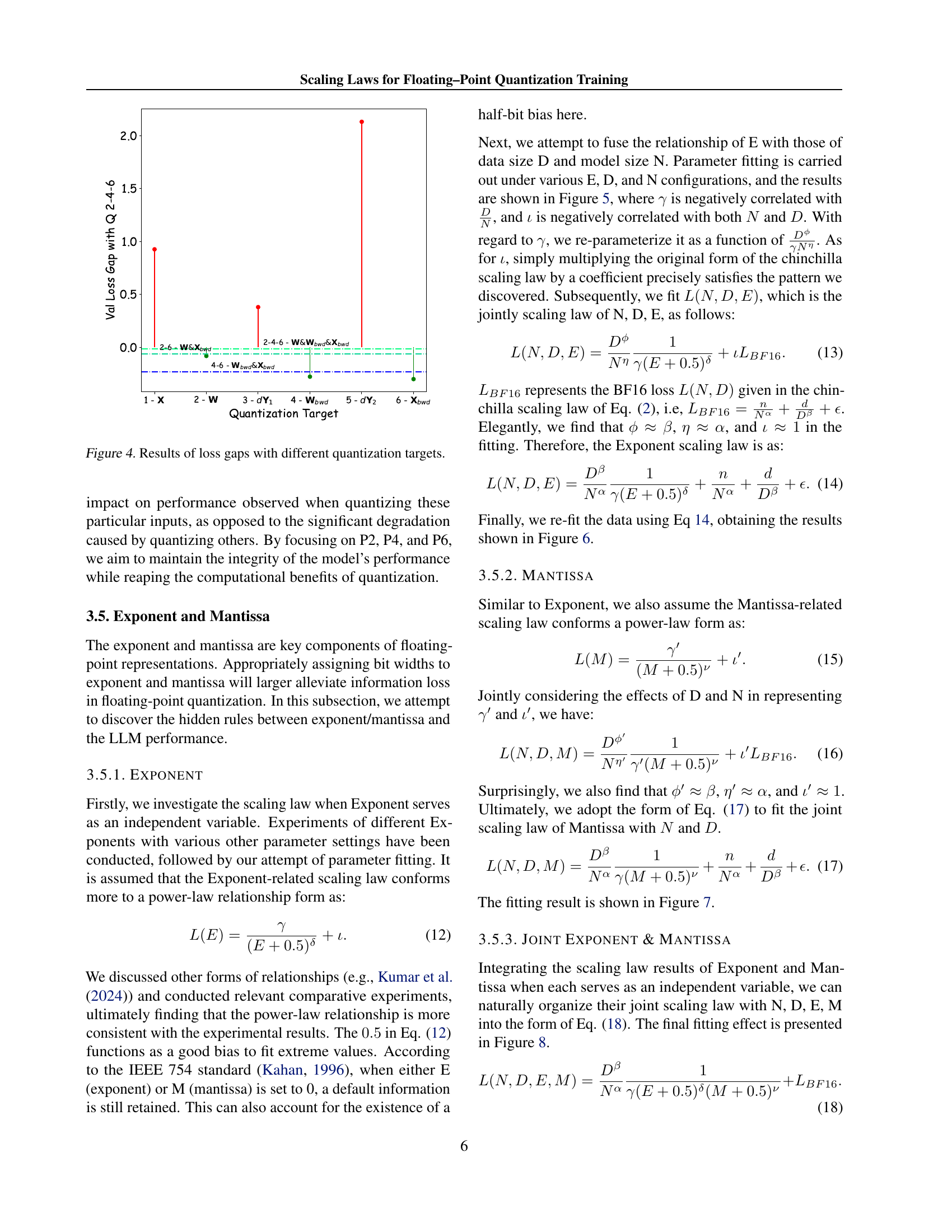
🔼 This figure illustrates the six different quantization targets considered in the paper: P1 to P6. Each target represents a specific input tensor to the GEMM (General Matrix Multiplication) operations within the Transformer architecture. These GEMMs are involved in the forward and backward passes of the model during training. The paper explores the impact of quantizing each of these tensors individually on the overall model’s performance. The authors ultimately choose to focus on quantizing P2, P4, and P6 in subsequent experiments due to their findings regarding the impact on model accuracy.
read the caption
Figure 3: Quantization Targets. We select P2, P4, and P6 as our quantization targets for the following exploration of scaling laws.

🔼 The bar chart visualizes the performance loss differences when applying various quantization strategies to different components of the transformer model (inputs to GEMM computation). It shows that quantizing input embeddings during backward propagation (P5) leads to significant performance degradation, while quantizing other inputs, especially P2, P4, or P6 alone, yields near-optimal results. Quantizing multiple targets together may not always provide additional benefit. The chart highlights the impact of choosing specific inputs for quantization on model performance.
read the caption
Figure 4: Results of loss gaps with different quantization targets.

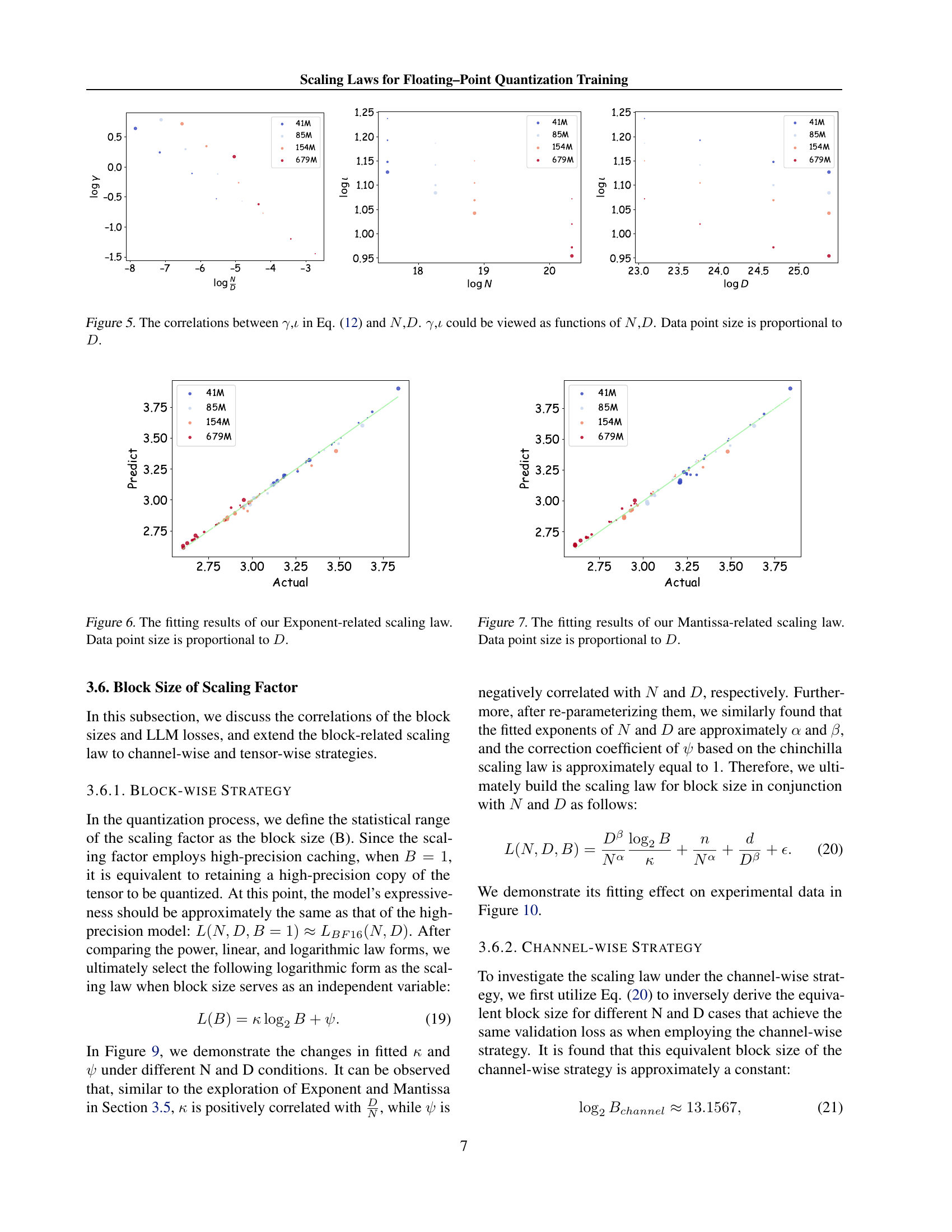
🔼 Figure 5 shows the relationship between the hyperparameters γ and ι (from the exponent scaling law equation 12) and the model size (N) and data size (D). The plots illustrate that γ and ι are not constant values but rather functions of N and D, indicating that their influence on model performance depends on the model and data size. The size of each data point in the plot is proportional to the data size (D), providing a visual representation of the relative data sizes used in the experiments.
read the caption
Figure 5: The correlations between γ𝛾\gammaitalic_γ,ι𝜄\iotaitalic_ι in Eq. (12) and N𝑁Nitalic_N,D𝐷Ditalic_D. γ𝛾\gammaitalic_γ,ι𝜄\iotaitalic_ι could be viewed as functions of N𝑁Nitalic_N,D𝐷Ditalic_D. Data point size is proportional to D𝐷Ditalic_D.

🔼 This figure displays the results of fitting the exponent-related scaling law. The graph shows the relationship between predicted and actual loss values for various LLMs trained under different low-precision settings. The size of the data points is directly proportional to the amount of training data used in each experiment (D). This visualization helps assess the accuracy of the proposed Exponent-related scaling law in predicting LLM performance. The graph provides a visual representation of the efficacy of the scaling law to model the effect of the exponent in floating point quantized training on LLM performance.
read the caption
Figure 6: The fitting results of our Exponent-related scaling law. Data point size is proportional to D𝐷Ditalic_D.

🔼 This figure displays the results of the Mantissa-related scaling law, a part of the study on scaling laws for floating-point quantization training of LLMs. The plot shows the correlation between predicted and actual loss values for different Mantissa configurations. The sizes of the data points in the graph are proportional to the size of the training dataset (D), providing a visual representation of the dataset’s influence on the Mantissa scaling law’s accuracy.
read the caption
Figure 7: The fitting results of our Mantissa-related scaling law. Data point size is proportional to D𝐷Ditalic_D.

🔼 This figure displays the results of the joint exponent and mantissa scaling law. It shows how well the model’s predicted loss matches the actual loss across different combinations of exponent bits (E), mantissa bits (M), data size (D), and other parameters. The size of the data points in the subfigures visually represents the relative contribution of D, M, and E respectively to the overall scaling law, allowing for a better visualization of their individual impacts on the model’s performance.
read the caption
Figure 8: The fitting results of the joint Exponent & Mantissa scaling law: Data point sizes in left, middle, and right sub-figures are proportional to D𝐷Ditalic_D, M𝑀Mitalic_M, and E𝐸Eitalic_E, respectively.

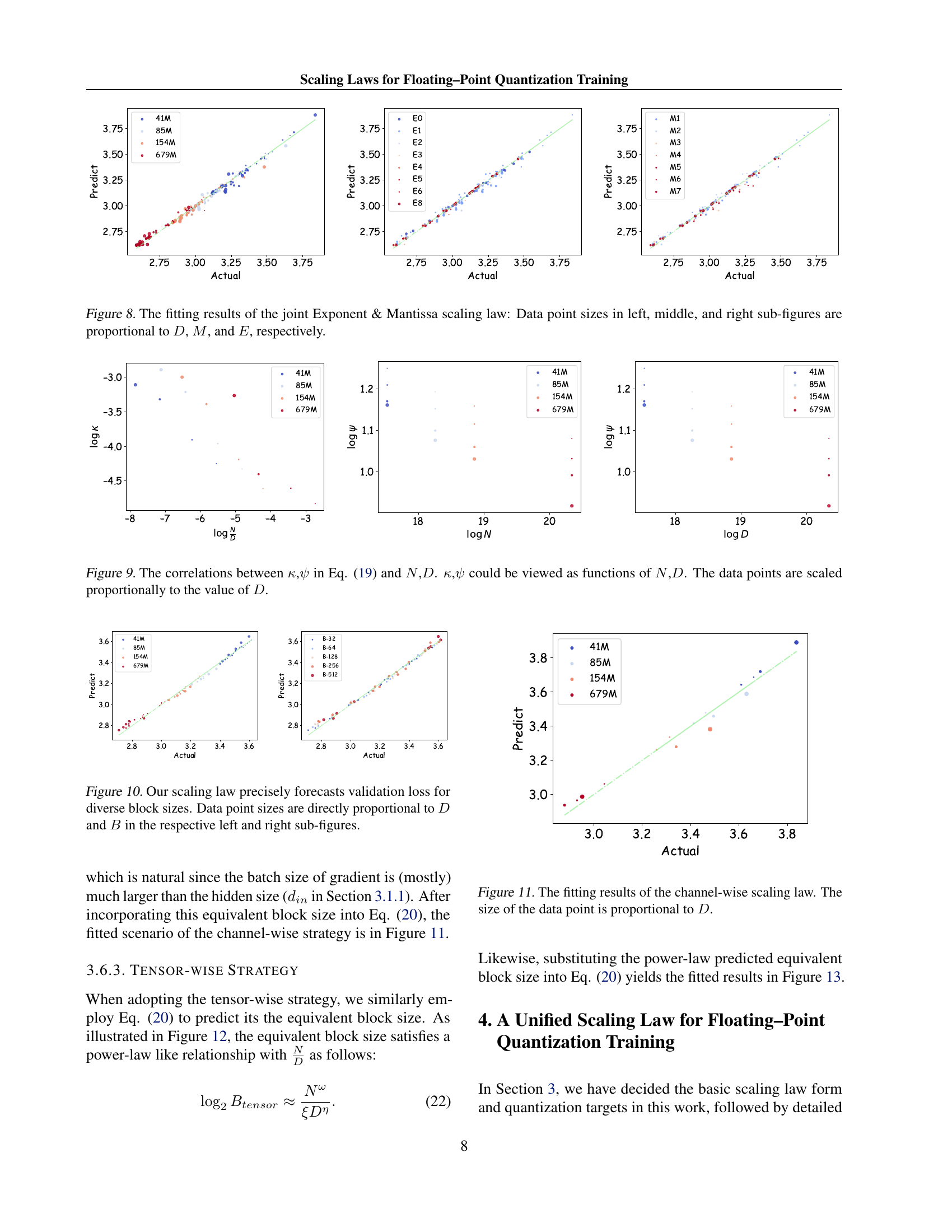
🔼 Figure 9 visualizes the relationship between the hyperparameters κ and ψ (from the logarithmic scaling law in Equation 19) and the model size (N) and dataset size (D). The plots show that κ and ψ exhibit clear correlations with N and D, suggesting that the impact of block size on model performance is dependent on the model and dataset scales. The size of the data points in the figure is scaled proportionally to the dataset size (D), providing a visual representation of data size’s influence on the correlations.
read the caption
Figure 9: The correlations between κ𝜅\kappaitalic_κ,ψ𝜓\psiitalic_ψ in Eq. (19) and N𝑁Nitalic_N,D𝐷Ditalic_D. κ𝜅\kappaitalic_κ,ψ𝜓\psiitalic_ψ could be viewed as functions of N𝑁Nitalic_N,D𝐷Ditalic_D. The data points are scaled proportionally to the value of D𝐷Ditalic_D.
🔼 Figure 10 shows the results of experiments on the impact of block size (B) on the validation loss of LLMs. The scaling law proposed in this work accurately predicts the validation loss for different block sizes (B) and data sizes (D). The left sub-figure shows the correlation between the predicted and actual loss for different data sizes. The right sub-figure emphasizes the relationship between block size (B) and validation loss, showing how accurately the proposed scaling law captures this relationship. In both sub-figures, the size of the data points is directly proportional to the size of the dataset (D) and block size (B), respectively.
read the caption
Figure 10: Our scaling law precisely forecasts validation loss for diverse block sizes. Data point sizes are directly proportional to D𝐷Ditalic_D and B𝐵Bitalic_B in the respective left and right sub-figures.

🔼 This figure shows the fitting results of the channel-wise scaling law. The x-axis represents the actual loss, and the y-axis represents the predicted loss according to the channel-wise scaling law. Each data point corresponds to a specific model trained with a particular combination of model size (N), data size (D), exponent (E), mantissa (M), and block size of scaling factors (B). The size of the data point is proportional to the data size (D). The plot visually demonstrates how well the channel-wise scaling law predicts the loss compared to the actual results. This figure helps assess the accuracy and applicability of the channel-wise scaling law for estimating the performance of low-precision LLMs in training.
read the caption
Figure 11: The fitting results of the channel-wise scaling law. The size of the data point is proportional to D𝐷Ditalic_D.

🔼 Figure 12 shows the relationship between the block size of scaling factors (B) and the ratio of model size (N) to data size (D). Specifically, it plots log₂B against log₁₀(N/D), illustrating how the choice of block size impacts the scaling behavior as model and dataset sizes vary. The size of each point in the graph corresponds to the dataset size (D), making larger datasets more visually prominent.
read the caption
Figure 12: The correlations between log2Bsubscript2𝐵\log_{2}Broman_log start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT italic_B and ND𝑁𝐷\frac{N}{D}divide start_ARG italic_N end_ARG start_ARG italic_D end_ARG. The size of the data point is proportional to D𝐷Ditalic_D.

🔼 Figure 13 presents the results obtained by fitting the tensor-wise scaling law. This scaling law models the relationship between the training loss of a large language model (LLM) and key parameters, specifically the data size, model size, and block size of scaling factors. The figure visually displays the agreement between the predicted loss values (from the scaling law) and the actual losses observed during experiments using the tensor-wise scaling strategy. The size of each data point in the figure is directly proportional to the data size (D), providing a visual representation of how the data size relates to model performance under the tensor-wise scaling approach. This allows for a visual assessment of the accuracy of the tensor-wise scaling law.
read the caption
Figure 13: The fitting results of the tensor-wise scaling law. The size of the data point is proportional to D𝐷Ditalic_D.

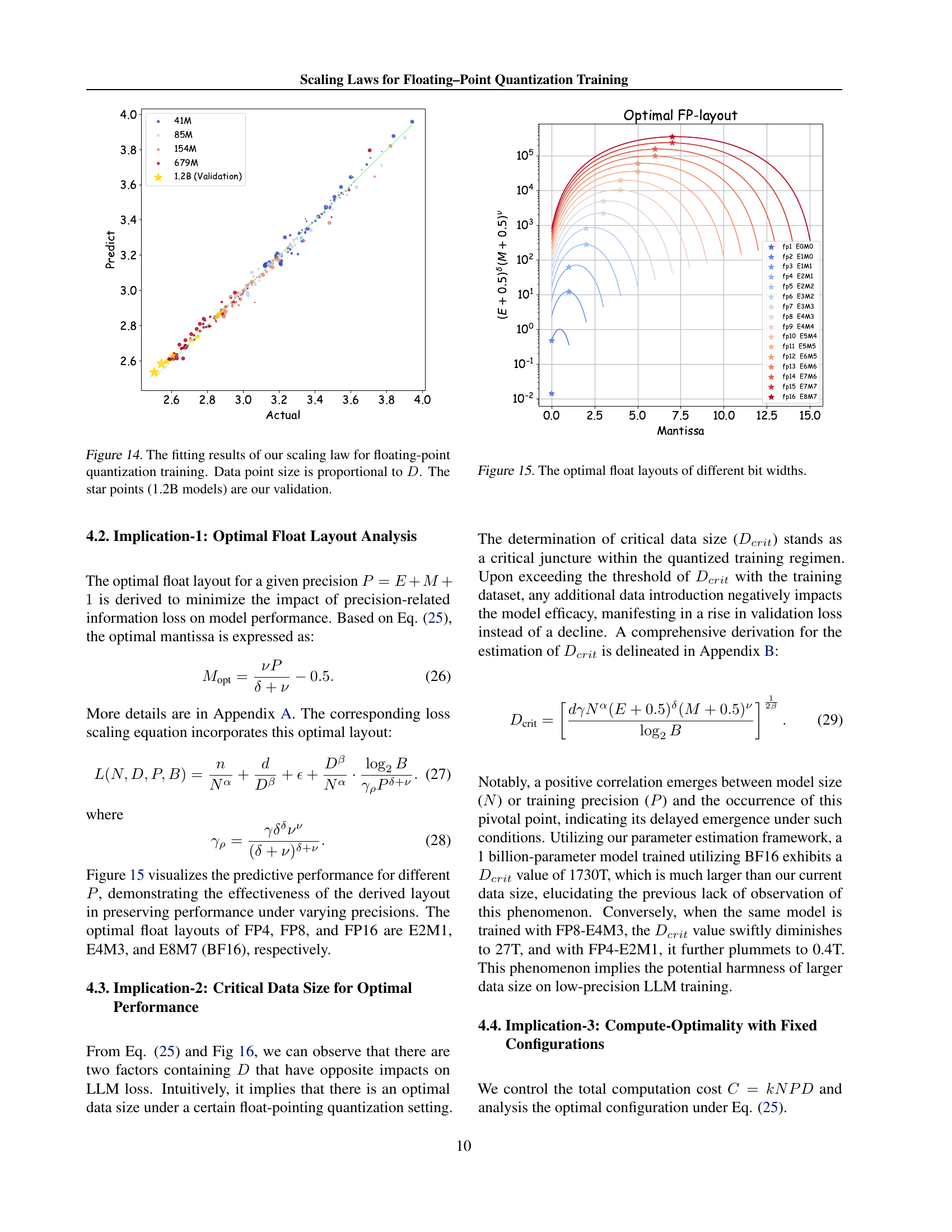
🔼 Figure 14 shows the results of the proposed scaling law for low-precision floating-point training. The plot compares predicted loss values from the scaling law against actual measured losses across a range of training configurations. Each point represents a different training setup. Point size is proportional to the training dataset size (D). The star points show model validation using 1.2 billion parameter models which are not part of the training data used to generate the scaling law.
read the caption
Figure 14: The fitting results of our scaling law for floating-point quantization training. Data point size is proportional to D𝐷Ditalic_D. The star points (1.2B models) are our validation.

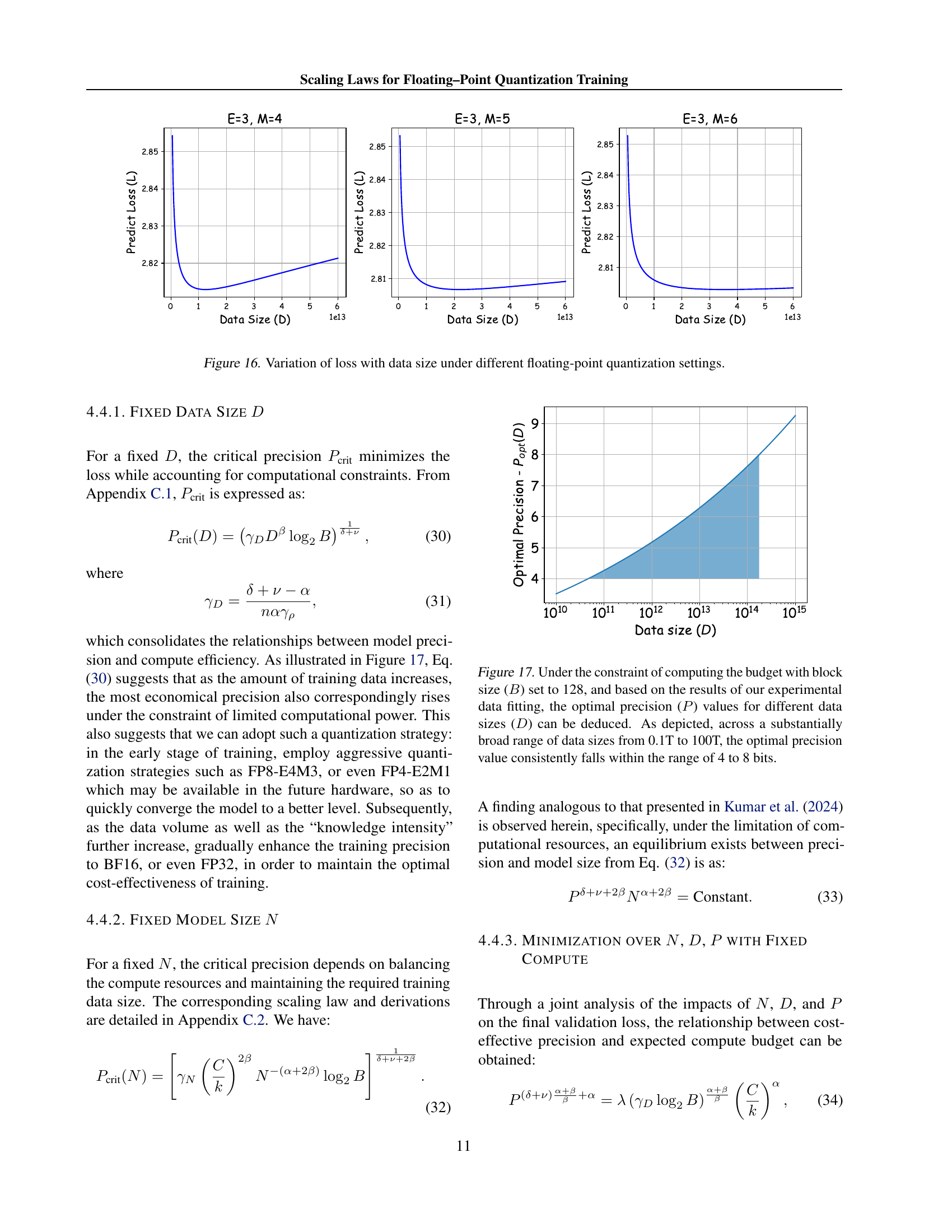
🔼 This figure visualizes the optimal allocation of exponent and mantissa bits for various floating-point precisions (4, 8, and 16 bits). It shows how the optimal bit distribution changes as the total number of bits in the floating-point representation increases. The optimal layout is determined by minimizing the loss of information due to quantization, as derived from the proposed scaling law in the paper.
read the caption
Figure 15: The optimal float layouts of different bit widths.

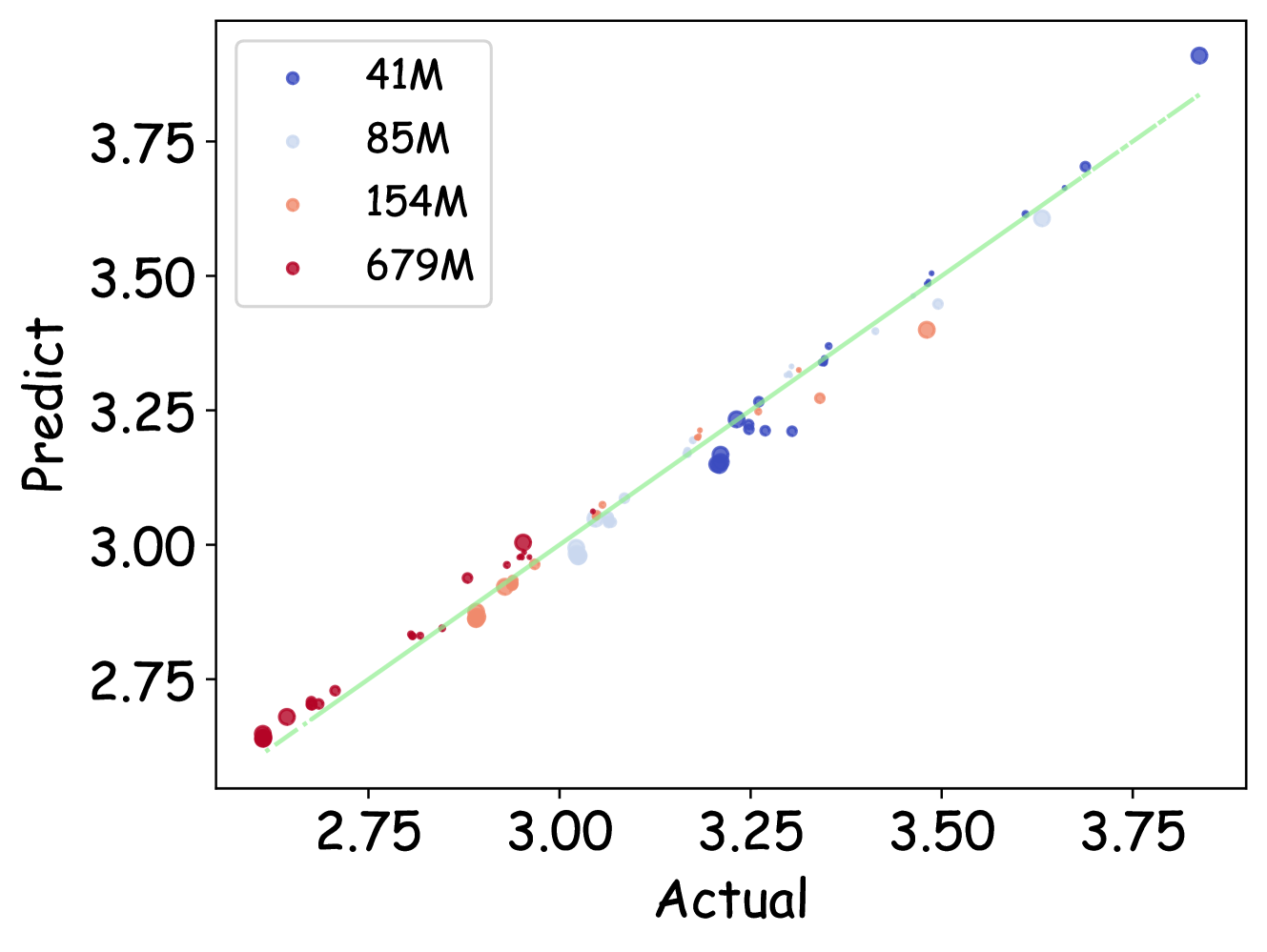
🔼 This figure shows how the training loss changes with respect to the size of the training dataset for different floating-point quantization configurations. The x-axis represents the dataset size (D), and the y-axis represents the training loss (L). Multiple lines are presented, each corresponding to a different combination of exponent (E) and mantissa (M) bits in the floating-point format. This illustrates how the optimal amount of training data might vary depending on the chosen quantization precision.
read the caption
Figure 16: Variation of loss with data size under different floating-point quantization settings.

🔼 This figure shows the relationship between optimal precision and data size under a fixed computational budget. The experiment was conducted with a block size (B) of 128. The results demonstrate that across a wide range of data sizes (0.1T to 100T), the optimal precision consistently falls between 4 and 8 bits. This suggests that a moderate precision is generally optimal, even with very large datasets.
read the caption
Figure 17: Under the constraint of computing the budget with block size (B𝐵Bitalic_B) set to 128, and based on the results of our experimental data fitting, the optimal precision (P𝑃Pitalic_P) values for different data sizes (D𝐷Ditalic_D) can be deduced. As depicted, across a substantially broad range of data sizes from 0.1T to 100T, the optimal precision value consistently falls within the range of 4 to 8 bits.

🔼 Figure 18 shows the relationship between the optimal precision (number of bits used for computation) and the total computational cost. The optimal precision is determined by balancing the trade-off between achieving high accuracy and minimizing the computational resources. As the computational budget increases, the optimal precision increases but eventually plateaus. This is because with a larger budget, the model can afford higher precision without significantly sacrificing performance. This figure highlights that there is a sweet spot for computational cost and precision. It is generated by setting the block size (B) to 128 and k to 6/16 in the equation derived by the authors.
read the caption
Figure 18: The optimal cost-performance ratio precision as a function of the total compute budget, illustrating the relationship between precision (P𝑃Pitalic_P) and computational budget (C𝐶Citalic_C) when the block size (B𝐵Bitalic_B) is set to 128 and k=6/16𝑘616k=6/16italic_k = 6 / 16.
More on tables
| Constant | Value |
|---|---|
| n | 69.2343 |
| α | 0.2368 |
| d | 68973.0621 |
| β | 0.5162 |
| ϵ | 1.9061 |
| γ | 11334.5197 |
| δ | 3.1926 |
| ν | 2.9543 |
🔼 This table presents the fitted hyperparameters and their corresponding values used in the proposed unified scaling law for floating-point quantization training. These parameters, including α, β, δ, ν, γ, η, and ε, quantify the relationships between various factors such as model size, data size, exponent bits, mantissa bits, and block size, all affecting the performance of LLMs during low-precision training.
read the caption
Table 2: Fitted hyper-parameters and their values in our proposed unified scaling law for floating-point quantization training.
| N | D | E | M | B | Fitting support | |
| 0 | 40894464 | 10485760000 | 0 | 7 | channel | ✓ |
| 1 | 40894464 | 10485760000 | 1 | 1 | 32 | ✓ |
| 2 | 40894464 | 10485760000 | 1 | 1 | 64 | ✓ |
| 3 | 40894464 | 10485760000 | 1 | 1 | 128 | ✓ |
| 4 | 40894464 | 10485760000 | 1 | 1 | 256 | ✓ |
| 5 | 40894464 | 10485760000 | 1 | 1 | 512 | ✓ |
| 6 | 40894464 | 10485760000 | 1 | 1 | channel | ✓ |
| 7 | 40894464 | 10485760000 | 1 | 1 | tensor | ✓ |
| 8 | 40894464 | 10485760000 | 1 | 2 | channel | ✓ |
| 9 | 40894464 | 10485760000 | 1 | 3 | channel | ✓ |
| 10 | 40894464 | 10485760000 | 1 | 4 | channel | ✓ |
| 11 | 40894464 | 10485760000 | 1 | 5 | channel | ✓ |
| 12 | 40894464 | 10485760000 | 1 | 6 | channel | ✓ |
| 13 | 40894464 | 10485760000 | 2 | 1 | channel | ✓ |
| 14 | 40894464 | 10485760000 | 2 | 3 | channel | ✓ |
| 15 | 40894464 | 10485760000 | 3 | 1 | channel | ✓ |
| 16 | 40894464 | 10485760000 | 3 | 2 | channel | ✓ |
| 17 | 40894464 | 10485760000 | 4 | 1 | channel | ✓ |
| 18 | 40894464 | 10485760000 | 4 | 3 | channel | ✓ |
| 19 | 40894464 | 10485760000 | 4 | 5 | channel | ✓ |
| 20 | 40894464 | 10485760000 | 5 | 1 | channel | ✓ |
| 21 | 40894464 | 10485760000 | 5 | 2 | channel | ✓ |
| 22 | 40894464 | 10485760000 | 6 | 1 | channel | ✓ |
| 23 | 40894464 | 20971520000 | 0 | 7 | channel | ✓ |
| 24 | 40894464 | 20971520000 | 1 | 1 | 32 | ✓ |
| 25 | 40894464 | 20971520000 | 1 | 1 | 64 | ✓ |
| 26 | 40894464 | 20971520000 | 1 | 1 | 128 | ✓ |
| 27 | 40894464 | 20971520000 | 1 | 1 | 256 | ✓ |
| 28 | 40894464 | 20971520000 | 1 | 1 | 512 | ✓ |
| 29 | 40894464 | 20971520000 | 1 | 1 | channel | ✓ |
| 30 | 40894464 | 20971520000 | 1 | 1 | tensor | ✓ |
| 31 | 40894464 | 20971520000 | 1 | 2 | channel | ✓ |
| 32 | 40894464 | 20971520000 | 1 | 3 | channel | ✓ |
| 33 | 40894464 | 20971520000 | 1 | 4 | channel | ✓ |
| 34 | 40894464 | 20971520000 | 1 | 5 | channel | ✓ |
| 35 | 40894464 | 20971520000 | 1 | 6 | channel | ✓ |
| 36 | 40894464 | 20971520000 | 2 | 1 | channel | ✓ |
| 37 | 40894464 | 20971520000 | 2 | 3 | channel | ✓ |
| 38 | 40894464 | 20971520000 | 3 | 1 | channel | ✓ |
| 39 | 40894464 | 20971520000 | 3 | 2 | channel | ✓ |
| 40 | 40894464 | 20971520000 | 4 | 1 | channel | ✓ |
| 41 | 40894464 | 20971520000 | 4 | 3 | channel | ✓ |
| 42 | 40894464 | 20971520000 | 4 | 5 | channel | ✓ |
| 43 | 40894464 | 20971520000 | 5 | 1 | channel | ✓ |
| 44 | 40894464 | 20971520000 | 5 | 2 | channel | ✓ |
| 45 | 40894464 | 20971520000 | 6 | 1 | channel | ✓ |
| 46 | 40894464 | 52428800000 | 0 | 7 | channel | ✓ |
| 47 | 40894464 | 52428800000 | 1 | 1 | 32 | ✓ |
| 48 | 40894464 | 52428800000 | 1 | 1 | 64 | ✓ |
| 49 | 40894464 | 52428800000 | 1 | 1 | 128 | ✓ |
| 50 | 40894464 | 52428800000 | 1 | 1 | 256 | ✓ |
| 51 | 40894464 | 52428800000 | 1 | 1 | 512 | ✓ |
| 52 | 40894464 | 52428800000 | 1 | 1 | channel | ✓ |
| 53 | 40894464 | 52428800000 | 1 | 1 | tensor | ✓ |
| 54 | 40894464 | 52428800000 | 1 | 2 | channel | ✓ |
| 55 | 40894464 | 52428800000 | 1 | 3 | channel | ✓ |
| 56 | 40894464 | 52428800000 | 1 | 4 | channel | ✓ |
| 57 | 40894464 | 52428800000 | 1 | 5 | channel | ✓ |
| 58 | 40894464 | 52428800000 | 1 | 6 | channel | ✓ |
| 59 | 40894464 | 52428800000 | 2 | 1 | channel | ✓ |
| 60 | 40894464 | 52428800000 | 2 | 3 | channel | ✓ |
| 61 | 40894464 | 52428800000 | 3 | 1 | channel | ✓ |
| 62 | 40894464 | 52428800000 | 3 | 2 | channel | ✓ |
| 63 | 40894464 | 52428800000 | 4 | 1 | channel | ✓ |
| 64 | 40894464 | 52428800000 | 4 | 3 | channel | ✓ |
| 65 | 40894464 | 52428800000 | 4 | 5 | channel | ✓ |
| 66 | 40894464 | 52428800000 | 5 | 1 | channel | ✓ |
| 67 | 40894464 | 52428800000 | 5 | 2 | channel | ✓ |
| 68 | 40894464 | 52428800000 | 6 | 1 | channel | ✓ |
| 69 | 40894464 | 104857600000 | 0 | 7 | channel | ✓ |
| 70 | 40894464 | 104857600000 | 1 | 1 | 32 | ✓ |
| 71 | 40894464 | 104857600000 | 1 | 1 | 64 | ✓ |
| 72 | 40894464 | 104857600000 | 1 | 1 | 128 | ✓ |
| 73 | 40894464 | 104857600000 | 1 | 1 | 256 | ✓ |
| 74 | 40894464 | 104857600000 | 1 | 1 | 512 | ✓ |
| 75 | 40894464 | 104857600000 | 1 | 1 | channel | ✓ |
| 76 | 40894464 | 104857600000 | 1 | 1 | tensor | ✓ |
| 77 | 40894464 | 104857600000 | 1 | 2 | channel | ✓ |
| 78 | 40894464 | 104857600000 | 1 | 3 | channel | ✓ |
| 79 | 40894464 | 104857600000 | 1 | 4 | channel | ✓ |
| 80 | 40894464 | 104857600000 | 1 | 5 | channel | ✓ |
| 81 | 40894464 | 104857600000 | 1 | 6 | channel | ✓ |
| 82 | 40894464 | 104857600000 | 2 | 1 | channel | ✓ |
| 83 | 40894464 | 104857600000 | 2 | 3 | channel | ✓ |
| 84 | 40894464 | 104857600000 | 3 | 1 | channel | ✓ |
| 85 | 40894464 | 104857600000 | 3 | 2 | channel | ✓ |
| 86 | 40894464 | 104857600000 | 4 | 1 | channel | ✓ |
| 87 | 40894464 | 104857600000 | 4 | 3 | channel | ✓ |
| 88 | 40894464 | 104857600000 | 4 | 5 | channel | ✓ |
| 89 | 40894464 | 104857600000 | 5 | 1 | channel | ✓ |
| 90 | 40894464 | 104857600000 | 5 | 2 | channel | ✓ |
| 91 | 40894464 | 104857600000 | 6 | 1 | channel | ✓ |
| 92 | 84934656 | 10485760000 | 0 | 7 | channel | ✓ |
| 93 | 84934656 | 10485760000 | 1 | 1 | 32 | ✓ |
| 94 | 84934656 | 10485760000 | 1 | 1 | 64 | ✓ |
| 95 | 84934656 | 10485760000 | 1 | 1 | 128 | ✓ |
| 96 | 84934656 | 10485760000 | 1 | 1 | 256 | ✓ |
| 97 | 84934656 | 10485760000 | 1 | 1 | channel | ✓ |
| 98 | 84934656 | 10485760000 | 1 | 1 | tensor | ✓ |
| 99 | 84934656 | 10485760000 | 1 | 2 | channel | ✓ |
| 100 | 84934656 | 10485760000 | 1 | 3 | channel | ✓ |
| 101 | 84934656 | 10485760000 | 1 | 4 | channel | ✓ |
| 102 | 84934656 | 10485760000 | 1 | 5 | channel | ✓ |
| 103 | 84934656 | 10485760000 | 1 | 6 | channel | ✓ |
| 104 | 84934656 | 10485760000 | 2 | 1 | channel | ✓ |
| 105 | 84934656 | 10485760000 | 2 | 3 | channel | ✓ |
| 106 | 84934656 | 10485760000 | 3 | 1 | channel | ✓ |
| 107 | 84934656 | 10485760000 | 3 | 2 | channel | ✓ |
| 108 | 84934656 | 10485760000 | 4 | 1 | channel | ✓ |
| 109 | 84934656 | 10485760000 | 4 | 3 | channel | ✓ |
| 110 | 84934656 | 10485760000 | 4 | 5 | channel | ✓ |
| 111 | 84934656 | 10485760000 | 5 | 1 | channel | ✓ |
| 112 | 84934656 | 10485760000 | 5 | 2 | channel | ✓ |
| 113 | 84934656 | 10485760000 | 6 | 1 | channel | ✓ |
| 114 | 84934656 | 20971520000 | 0 | 7 | channel | ✓ |
| 115 | 84934656 | 20971520000 | 1 | 1 | 32 | ✓ |
| 116 | 84934656 | 20971520000 | 1 | 1 | 64 | ✓ |
| 117 | 84934656 | 20971520000 | 1 | 1 | 128 | ✓ |
| 118 | 84934656 | 20971520000 | 1 | 1 | 256 | ✓ |
| 119 | 84934656 | 20971520000 | 1 | 1 | channel | ✓ |
| 120 | 84934656 | 20971520000 | 1 | 1 | tensor | ✓ |
| 121 | 84934656 | 20971520000 | 1 | 2 | channel | ✓ |
| 122 | 84934656 | 20971520000 | 1 | 3 | channel | ✓ |
| 123 | 84934656 | 20971520000 | 1 | 4 | channel | ✓ |
| 124 | 84934656 | 20971520000 | 1 | 5 | channel | ✓ |
| 125 | 84934656 | 20971520000 | 1 | 6 | channel | ✓ |
| 126 | 84934656 | 20971520000 | 2 | 1 | channel | ✓ |
| 127 | 84934656 | 20971520000 | 2 | 3 | channel | ✓ |
| 128 | 84934656 | 20971520000 | 3 | 1 | channel | ✓ |
| 129 | 84934656 | 20971520000 | 3 | 2 | channel | ✓ |
| 130 | 84934656 | 20971520000 | 4 | 1 | channel | ✓ |
| 131 | 84934656 | 20971520000 | 4 | 3 | channel | ✓ |
| 132 | 84934656 | 20971520000 | 4 | 5 | channel | ✓ |
| 133 | 84934656 | 20971520000 | 5 | 1 | channel | ✓ |
| 134 | 84934656 | 20971520000 | 5 | 2 | channel | ✓ |
| 135 | 84934656 | 20971520000 | 6 | 1 | channel | ✓ |
| 136 | 84934656 | 52428800000 | 0 | 7 | channel | ✓ |
| 137 | 84934656 | 52428800000 | 1 | 1 | 32 | ✓ |
| 138 | 84934656 | 52428800000 | 1 | 1 | 64 | ✓ |
| 139 | 84934656 | 52428800000 | 1 | 1 | 128 | ✓ |
| 140 | 84934656 | 52428800000 | 1 | 1 | 256 | ✓ |
| 141 | 84934656 | 52428800000 | 1 | 1 | channel | ✓ |
| 142 | 84934656 | 52428800000 | 1 | 1 | tensor | ✓ |
| 143 | 84934656 | 52428800000 | 1 | 2 | channel | ✓ |
| 144 | 84934656 | 52428800000 | 1 | 3 | channel | ✓ |
| 145 | 84934656 | 52428800000 | 1 | 4 | channel | ✓ |
| 146 | 84934656 | 52428800000 | 1 | 5 | channel | ✓ |
| 147 | 84934656 | 52428800000 | 1 | 6 | channel | ✓ |
| 148 | 84934656 | 52428800000 | 2 | 1 | channel | ✓ |
| 149 | 84934656 | 52428800000 | 2 | 3 | channel | ✓ |
| 150 | 84934656 | 52428800000 | 3 | 1 | channel | ✓ |
| 151 | 84934656 | 52428800000 | 3 | 2 | channel | ✓ |
| 152 | 84934656 | 52428800000 | 4 | 1 | channel | ✓ |
| 153 | 84934656 | 52428800000 | 4 | 3 | channel | ✓ |
| 154 | 84934656 | 52428800000 | 4 | 5 | channel | ✓ |
| 155 | 84934656 | 52428800000 | 5 | 1 | channel | ✓ |
| 156 | 84934656 | 52428800000 | 5 | 2 | channel | ✓ |
| 157 | 84934656 | 52428800000 | 6 | 1 | channel | ✓ |
| 158 | 84934656 | 104857600000 | 0 | 7 | channel | ✓ |
| 159 | 84934656 | 104857600000 | 1 | 1 | 32 | ✓ |
| 160 | 84934656 | 104857600000 | 1 | 1 | 64 | ✓ |
| 161 | 84934656 | 104857600000 | 1 | 1 | 128 | ✓ |
| 162 | 84934656 | 104857600000 | 1 | 1 | 256 | ✓ |
| 163 | 84934656 | 104857600000 | 1 | 1 | channel | ✓ |
| 164 | 84934656 | 104857600000 | 1 | 1 | tensor | ✓ |
| 165 | 84934656 | 104857600000 | 1 | 2 | channel | ✓ |
| 166 | 84934656 | 104857600000 | 1 | 3 | channel | ✓ |
| 167 | 84934656 | 104857600000 | 1 | 4 | channel | ✓ |
| 168 | 84934656 | 104857600000 | 1 | 5 | channel | ✓ |
| 169 | 84934656 | 104857600000 | 1 | 6 | channel | ✓ |
| 170 | 84934656 | 104857600000 | 2 | 1 | channel | ✓ |
| 171 | 84934656 | 104857600000 | 2 | 3 | channel | ✓ |
| 172 | 84934656 | 104857600000 | 3 | 1 | channel | ✓ |
| 173 | 84934656 | 104857600000 | 3 | 2 | channel | ✓ |
| 174 | 84934656 | 104857600000 | 4 | 1 | channel | ✓ |
| 175 | 84934656 | 104857600000 | 4 | 3 | channel | ✓ |
| 176 | 84934656 | 104857600000 | 4 | 5 | channel | ✓ |
| 177 | 84934656 | 104857600000 | 5 | 1 | channel | ✓ |
| 178 | 84934656 | 104857600000 | 5 | 2 | channel | ✓ |
| 179 | 84934656 | 104857600000 | 6 | 1 | channel | ✓ |
| 180 | 154140672 | 10485760000 | 0 | 7 | channel | ✓ |
| 181 | 154140672 | 10485760000 | 1 | 1 | 32 | ✓ |
| 182 | 154140672 | 10485760000 | 1 | 1 | 64 | ✓ |
| 183 | 154140672 | 10485760000 | 1 | 1 | 128 | ✓ |
| 184 | 154140672 | 10485760000 | 1 | 1 | 256 | ✓ |
| 185 | 154140672 | 10485760000 | 1 | 1 | channel | ✓ |
| 186 | 154140672 | 10485760000 | 1 | 1 | tensor | ✓ |
| 187 | 154140672 | 10485760000 | 1 | 2 | channel | ✓ |
| 188 | 154140672 | 10485760000 | 1 | 3 | channel | ✓ |
| 189 | 154140672 | 10485760000 | 1 | 4 | channel | ✓ |
| 190 | 154140672 | 10485760000 | 1 | 5 | channel | ✓ |
| 191 | 154140672 | 10485760000 | 1 | 6 | channel | ✓ |
| 192 | 154140672 | 10485760000 | 2 | 1 | channel | ✓ |
| 193 | 154140672 | 10485760000 | 2 | 3 | channel | ✓ |
| 194 | 154140672 | 10485760000 | 3 | 1 | channel | ✓ |
| 195 | 154140672 | 10485760000 | 3 | 2 | channel | ✓ |
| 196 | 154140672 | 10485760000 | 4 | 1 | channel | ✓ |
| 197 | 154140672 | 10485760000 | 4 | 3 | channel | ✓ |
| 198 | 154140672 | 10485760000 | 4 | 5 | channel | ✓ |
| 199 | 154140672 | 10485760000 | 5 | 1 | channel | ✓ |
| 200 | 154140672 | 10485760000 | 5 | 2 | channel | ✓ |
| 201 | 154140672 | 10485760000 | 6 | 1 | channel | ✓ |
| 202 | 154140672 | 20971520000 | 0 | 7 | channel | ✓ |
| 203 | 154140672 | 20971520000 | 1 | 1 | 32 | ✓ |
| 204 | 154140672 | 20971520000 | 1 | 1 | 64 | ✓ |
| 205 | 154140672 | 20971520000 | 1 | 1 | 128 | ✓ |
| 206 | 154140672 | 20971520000 | 1 | 1 | 256 | ✓ |
| 207 | 154140672 | 20971520000 | 1 | 1 | channel | ✓ |
| 208 | 154140672 | 20971520000 | 1 | 1 | tensor | ✓ |
| 209 | 154140672 | 20971520000 | 1 | 2 | channel | ✓ |
| 210 | 154140672 | 20971520000 | 1 | 3 | channel | ✓ |
| 211 | 154140672 | 20971520000 | 1 | 4 | channel | ✓ |
| 212 | 154140672 | 20971520000 | 1 | 5 | channel | ✓ |
| 213 | 154140672 | 20971520000 | 1 | 6 | channel | ✓ |
| 214 | 154140672 | 20971520000 | 2 | 1 | channel | ✓ |
| 215 | 154140672 | 20971520000 | 2 | 3 | channel | ✓ |
| 216 | 154140672 | 20971520000 | 3 | 1 | channel | ✓ |
| 217 | 154140672 | 20971520000 | 3 | 2 | channel | ✓ |
| 218 | 154140672 | 20971520000 | 4 | 1 | channel | ✓ |
| 219 | 154140672 | 20971520000 | 4 | 3 | channel | ✓ |
| 220 | 154140672 | 20971520000 | 4 | 5 | channel | ✓ |
| 221 | 154140672 | 20971520000 | 5 | 1 | channel | ✓ |
| 222 | 154140672 | 20971520000 | 5 | 2 | channel | ✓ |
| 223 | 154140672 | 20971520000 | 6 | 1 | channel | ✓ |
| 224 | 154140672 | 52428800000 | 0 | 7 | channel | ✓ |
| 225 | 154140672 | 52428800000 | 1 | 1 | 32 | ✓ |
| 226 | 154140672 | 52428800000 | 1 | 1 | 64 | ✓ |
| 227 | 154140672 | 52428800000 | 1 | 1 | 128 | ✓ |
| 228 | 154140672 | 52428800000 | 1 | 1 | 256 | ✓ |
| 229 | 154140672 | 52428800000 | 1 | 1 | channel | ✓ |
| 230 | 154140672 | 52428800000 | 1 | 1 | tensor | ✓ |
| 231 | 154140672 | 52428800000 | 1 | 2 | channel | ✓ |
| 232 | 154140672 | 52428800000 | 1 | 3 | channel | ✓ |
| 233 | 154140672 | 52428800000 | 1 | 4 | channel | ✓ |
| 234 | 154140672 | 52428800000 | 1 | 5 | channel | ✓ |
| 235 | 154140672 | 52428800000 | 1 | 6 | channel | ✓ |
| 236 | 154140672 | 52428800000 | 2 | 1 | channel | ✓ |
| 237 | 154140672 | 52428800000 | 2 | 3 | channel | ✓ |
| 238 | 154140672 | 52428800000 | 3 | 1 | channel | ✓ |
| 239 | 154140672 | 52428800000 | 3 | 2 | channel | ✓ |
| 240 | 154140672 | 52428800000 | 4 | 1 | channel | ✓ |
| 241 | 154140672 | 52428800000 | 4 | 3 | channel | ✓ |
| 242 | 154140672 | 52428800000 | 4 | 5 | channel | ✓ |
| 243 | 154140672 | 52428800000 | 5 | 1 | channel | ✓ |
| 244 | 154140672 | 52428800000 | 5 | 2 | channel | ✓ |
| 245 | 154140672 | 52428800000 | 6 | 1 | channel | ✓ |
| 246 | 154140672 | 104857600000 | 0 | 7 | channel | ✓ |
| 247 | 154140672 | 104857600000 | 1 | 1 | 32 | ✓ |
| 248 | 154140672 | 104857600000 | 1 | 1 | 64 | ✓ |
| 249 | 154140672 | 104857600000 | 1 | 1 | 128 | ✓ |
| 250 | 154140672 | 104857600000 | 1 | 1 | 256 | ✓ |
| 251 | 154140672 | 104857600000 | 1 | 1 | channel | ✓ |
| 252 | 154140672 | 104857600000 | 1 | 1 | tensor | ✓ |
| 253 | 154140672 | 104857600000 | 1 | 2 | channel | ✓ |
| 254 | 154140672 | 104857600000 | 1 | 3 | channel | ✓ |
| 255 | 154140672 | 104857600000 | 1 | 4 | channel | ✓ |
| 256 | 154140672 | 104857600000 | 1 | 5 | channel | ✓ |
| 257 | 154140672 | 104857600000 | 1 | 6 | channel | ✓ |
| 258 | 154140672 | 104857600000 | 2 | 1 | channel | ✓ |
| 259 | 154140672 | 104857600000 | 2 | 3 | channel | ✓ |
| 260 | 154140672 | 104857600000 | 3 | 1 | channel | ✓ |
| 261 | 154140672 | 104857600000 | 3 | 2 | channel | ✓ |
| 262 | 154140672 | 104857600000 | 4 | 1 | channel | ✓ |
| 263 | 154140672 | 104857600000 | 4 | 3 | channel | ✓ |
| 264 | 154140672 | 104857600000 | 4 | 5 | channel | ✓ |
| 265 | 154140672 | 104857600000 | 5 | 1 | channel | ✓ |
| 266 | 154140672 | 104857600000 | 5 | 2 | channel | ✓ |
| 267 | 154140672 | 104857600000 | 6 | 1 | channel | ✓ |
| 268 | 679477248 | 10485760000 | 0 | 7 | channel | ✓ |
| 269 | 679477248 | 10485760000 | 1 | 1 | 32 | ✓ |
| 270 | 679477248 | 10485760000 | 1 | 1 | 64 | ✓ |
| 271 | 679477248 | 10485760000 | 1 | 1 | 128 | ✓ |
| 272 | 679477248 | 10485760000 | 1 | 1 | 256 | ✓ |
| 273 | 679477248 | 10485760000 | 1 | 1 | 512 | ✓ |
| 274 | 679477248 | 10485760000 | 1 | 1 | channel | ✓ |
| 275 | 679477248 | 10485760000 | 1 | 1 | tensor | ✓ |
| 276 | 679477248 | 10485760000 | 1 | 2 | channel | ✓ |
| 277 | 679477248 | 10485760000 | 1 | 3 | channel | ✓ |
| 278 | 679477248 | 10485760000 | 1 | 4 | channel | ✓ |
| 279 | 679477248 | 10485760000 | 1 | 5 | channel | ✓ |
| 280 | 679477248 | 10485760000 | 1 | 6 | channel | ✓ |
| 281 | 679477248 | 10485760000 | 2 | 1 | channel | ✓ |
| 282 | 679477248 | 10485760000 | 2 | 3 | channel | ✓ |
| 283 | 679477248 | 10485760000 | 3 | 1 | channel | ✓ |
| 284 | 679477248 | 10485760000 | 3 | 2 | channel | ✓ |
| 285 | 679477248 | 10485760000 | 4 | 1 | channel | ✓ |
| 286 | 679477248 | 10485760000 | 4 | 3 | channel | ✓ |
| 287 | 679477248 | 10485760000 | 4 | 5 | channel | ✓ |
| 288 | 679477248 | 10485760000 | 5 | 1 | channel | ✓ |
| 289 | 679477248 | 10485760000 | 5 | 2 | channel | ✓ |
| 290 | 679477248 | 10485760000 | 6 | 1 | channel | ✓ |
| 291 | 679477248 | 20971520000 | 0 | 7 | channel | ✓ |
| 292 | 679477248 | 20971520000 | 1 | 1 | 32 | ✓ |
| 293 | 679477248 | 20971520000 | 1 | 1 | 64 | ✓ |
| 294 | 679477248 | 20971520000 | 1 | 1 | 128 | ✓ |
| 295 | 679477248 | 20971520000 | 1 | 1 | 256 | ✓ |
| 296 | 679477248 | 20971520000 | 1 | 1 | 512 | ✓ |
| 297 | 679477248 | 20971520000 | 1 | 1 | channel | ✓ |
| 298 | 679477248 | 20971520000 | 1 | 1 | tensor | ✓ |
| 299 | 679477248 | 20971520000 | 1 | 2 | channel | ✓ |
| 300 | 679477248 | 20971520000 | 1 | 3 | channel | ✓ |
| 301 | 679477248 | 20971520000 | 1 | 4 | channel | ✓ |
| 302 | 679477248 | 20971520000 | 1 | 5 | channel | ✓ |
| 303 | 679477248 | 20971520000 | 1 | 6 | channel | ✓ |
| 304 | 679477248 | 20971520000 | 2 | 1 | channel | ✓ |
| 305 | 679477248 | 20971520000 | 2 | 3 | channel | ✓ |
| 306 | 679477248 | 20971520000 | 3 | 1 | channel | ✓ |
| 307 | 679477248 | 20971520000 | 3 | 2 | channel | ✓ |
| 308 | 679477248 | 20971520000 | 4 | 1 | channel | ✓ |
| 309 | 679477248 | 20971520000 | 4 | 3 | channel | ✓ |
| 310 | 679477248 | 20971520000 | 4 | 5 | channel | ✓ |
| 311 | 679477248 | 20971520000 | 5 | 1 | channel | ✓ |
| 312 | 679477248 | 20971520000 | 5 | 2 | channel | ✓ |
| 313 | 679477248 | 20971520000 | 6 | 1 | channel | ✓ |
| 314 | 679477248 | 52428800000 | 0 | 7 | channel | ✓ |
| 315 | 679477248 | 52428800000 | 1 | 1 | 32 | ✓ |
| 316 | 679477248 | 52428800000 | 1 | 1 | 64 | ✓ |
| 317 | 679477248 | 52428800000 | 1 | 1 | 128 | ✓ |
| 318 | 679477248 | 52428800000 | 1 | 1 | 256 | ✓ |
| 319 | 679477248 | 52428800000 | 1 | 1 | 512 | ✓ |
| 320 | 679477248 | 52428800000 | 1 | 1 | channel | ✓ |
| 321 | 679477248 | 52428800000 | 1 | 1 | tensor | ✓ |
| 322 | 679477248 | 52428800000 | 1 | 2 | channel | ✓ |
| 323 | 679477248 | 52428800000 | 1 | 3 | channel | ✓ |
| 324 | 679477248 | 52428800000 | 1 | 4 | channel | ✓ |
| 325 | 679477248 | 52428800000 | 1 | 5 | channel | ✓ |
| 326 | 679477248 | 52428800000 | 1 | 6 | channel | ✓ |
| 327 | 679477248 | 52428800000 | 2 | 1 | channel | ✓ |
| 328 | 679477248 | 52428800000 | 2 | 3 | channel | ✓ |
| 329 | 679477248 | 52428800000 | 3 | 1 | channel | ✓ |
| 330 | 679477248 | 52428800000 | 3 | 2 | channel | ✓ |
| 331 | 679477248 | 52428800000 | 4 | 1 | channel | ✓ |
| 332 | 679477248 | 52428800000 | 4 | 3 | channel | ✓ |
| 333 | 679477248 | 52428800000 | 4 | 5 | channel | ✓ |
| 334 | 679477248 | 52428800000 | 5 | 1 | channel | ✓ |
| 335 | 679477248 | 52428800000 | 5 | 2 | channel | ✓ |
| 336 | 679477248 | 52428800000 | 6 | 1 | channel | ✓ |
| 337 | 679477248 | 104857600000 | 0 | 7 | channel | ✓ |
| 338 | 679477248 | 104857600000 | 1 | 1 | 32 | ✓ |
| 339 | 679477248 | 104857600000 | 1 | 1 | 64 | ✓ |
| 340 | 679477248 | 104857600000 | 1 | 1 | 128 | ✓ |
| 341 | 679477248 | 104857600000 | 1 | 1 | 256 | ✓ |
| 342 | 679477248 | 104857600000 | 1 | 1 | 512 | ✓ |
| 343 | 679477248 | 104857600000 | 1 | 1 | channel | ✓ |
| 344 | 679477248 | 104857600000 | 1 | 1 | tensor | ✓ |
| 345 | 679477248 | 104857600000 | 1 | 2 | channel | ✓ |
| 346 | 679477248 | 104857600000 | 1 | 3 | channel | ✓ |
| 347 | 679477248 | 104857600000 | 1 | 4 | channel | ✓ |
| 348 | 679477248 | 104857600000 | 1 | 5 | channel | ✓ |
| 349 | 679477248 | 104857600000 | 1 | 6 | channel | ✓ |
| 350 | 679477248 | 104857600000 | 2 | 1 | channel | ✓ |
| 351 | 679477248 | 104857600000 | 2 | 3 | channel | ✓ |
| 352 | 679477248 | 104857600000 | 3 | 1 | channel | ✓ |
| 353 | 679477248 | 104857600000 | 3 | 2 | channel | ✓ |
| 354 | 679477248 | 104857600000 | 4 | 1 | channel | ✓ |
| 355 | 679477248 | 104857600000 | 4 | 3 | channel | ✓ |
| 356 | 679477248 | 104857600000 | 4 | 5 | channel | ✓ |
| 357 | 679477248 | 104857600000 | 5 | 2 | channel | ✓ |
| 358 | 679477248 | 104857600000 | 6 | 1 | channel | ✓ |
| 359 | 1233125376 | 10485760000 | 1 | 2 | 512 | ✗ |
| 360 | 1233125376 | 10485760000 | 4 | 3 | 512 | ✗ |
| 361 | 1233125376 | 20971520000 | 1 | 2 | 512 | ✗ |
| 362 | 1233125376 | 20971520000 | 4 | 3 | 512 | ✗ |
| 363 | 1233125376 | 52428800000 | 1 | 2 | 512 | ✗ |
| 364 | 1233125376 | 52428800000 | 4 | 3 | 512 | ✗ |
| 365 | 1233125376 | 104857600000 | 1 | 2 | 512 | ✗ |
| 366 | 1233125376 | 104857600000 | 4 | 3 | 512 | ✗ |
🔼 This table details the hyperparameter settings used in the ablation experiments conducted in the paper. Each row represents a unique experiment configuration, specifying the model size (N), dataset size (D), exponent bits (E), mantissa bits (M), and block size (B). The ‘Fitting support’ column indicates whether the corresponding experiment’s results were used for fitting the scaling laws presented in the paper. These ablation studies systematically investigated the impact of various floating-point quantization parameters to better understand their contribution to model performance and the accuracy of the scaling laws.
read the caption
Table 3: All configurations for the ablation experiments.
Full paper#