↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Large Language Models (LLMs) show promise in solving complex math problems but struggle with inaccuracies in the reasoning process, particularly due to issues in the granularity of in-context learning examples. Current methods often use problem-level examples, which can lead to irrelevant guidance during the step-wise solution process. This problem is exacerbated by the fact that LLMs can correctly identify what steps are needed but may fail to execute the steps accurately.
BoostStep tackles this by introducing step-level in-context learning and a ‘first-try’ strategy. This approach aligns the granularity between example retrieval and reasoning, providing highly relevant examples for each step. BoostStep demonstrates significant performance improvements on various mathematical benchmarks, especially those with lower similarity to the training data. Importantly, it’s also shown to integrate well with Monte Carlo Tree Search (MCTS) methods, enhancing both candidate generation and decision-making.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical limitation of current large language models (LLMs) in mathematical reasoning. By improving the accuracy of single-step reasoning, it offers a significant advancement in LLM capabilities, impacting various applications like problem-solving and theorem proving. The proposed method is general and robust, paving the way for further research into enhanced reasoning strategies within LLMs. This work’s focus on step-level reasoning provides valuable insights for researchers working on improving LLMs’ performance on complex tasks requiring multi-step reasoning, which is a significant advancement for AI research.
Visual Insights#

🔼 The figure shows a comparison of different mathematical reasoning methods using various benchmarks. The x-axis represents different benchmarks (MATH, AMC10, AMC12, AQUA, MathBench-C, MathBench-H, MathVerse, OlympiadBench, and MathVision), and the y-axis represents the accuracy. The radar chart compares the performance of three methods: 0-shot, few-shot in-context learning (COT), and the proposed BoostStep method. The BoostStep approach consistently outperforms the other two methods across all benchmarks. Notably, on benchmarks with lower similarity to the training data (OlympiadBench and MathVision), the BoostStep method shows significant improvement over few-shot COT, which even demonstrates a negative impact in those cases. This highlights BoostStep’s robustness and effectiveness, especially when dealing with less similar problems. The BoostStep method’s improvement averages about 4% across all benchmarks.
read the caption
Figure 1: Our step-level in-context learning outperforms traditional problem-level few-shot learning for about 4% across in-domain, out-domain and cross-modality mathematical benchmark. Moreover, on benchmarks with lower similarity with example problem set (i.e. OlympiadBench and multi-modal benchmarks), where problem-level few-shot learning may have negative impact, while our strategy still provides valuable guidance.
| Model | Method | in-domain MATH | out-domain AMC12 | out-domain AMC10 | out-domain AQUA | out-domain MathBench(C) | out-domain MathBench(H) | out-domain OlympiadBench-TO |
|---|---|---|---|---|---|---|---|---|
| GPT-4o | 0-shot | 73.4 | 53.6 | 55.8 | 81.1 | 80.0 | 77.3 | 40.6 |
| few-shot | 73.8 | 56.5 | 56.7 | 83.9 | 80.7 | 79.3 | 39.3 | |
| Ours | 76.4 | 63.0 | 60.4 | 85.4 | 82.0 | 84.0 | 43.3 | |
| Qwen | 0-shot | 83.0 | 67.4 | 67.7 | 84.6 | 80.6 | 82.0 | 49.7 |
| few-shot | 83.8 | 67.4 | 66.8 | 85.0 | 81.3 | 82.7 | 49.9 | |
| Ours | 85.2 | 69.2 | 69.6 | 86.6 | 82.7 | 84.7 | 52.7 |
🔼 This table compares the performance of different in-context learning methods on various mathematical reasoning benchmarks using two large language models: GPT-4 and Qwen-2.5-Math-72B. The methods compared are zero-shot, few-shot (traditional problem-level in-context learning), and the proposed BoostStep method (step-level in-context learning). The benchmarks include both in-domain (MATH500, built using the same dataset as the example problem bank) and out-of-domain tasks (AMC10, AMC12, AQuA, MathBench, OlympiadBench). The table highlights the improved accuracy of the BoostStep approach, especially on out-of-domain benchmarks.
read the caption
Table 1: A comparison of different in-context learning strategies on different benchmarks on GPT-4o and Qwen2.5-Math-72B-Instruct. The example problem bank is constructed from PRM800K, so MATH500 is an in-domain benchmark while others are all out-domain benchmarks. Best results are in bold.
In-depth insights#
Step-Level Reasoning#
Step-level reasoning, as described in the research paper, presents a significant advancement in enhancing the mathematical capabilities of Large Language Models (LLMs). Instead of tackling complex problems holistically, this approach decomposes the problem into smaller, manageable steps, allowing for more focused and accurate reasoning at each stage. This granular approach directly addresses the limitations of traditional methods, which often struggle with the intricacy and multiple layers of reasoning inherent in many mathematical problems. By breaking down the process, step-level reasoning reduces the complexity and allows LLMs to leverage in-context learning more effectively by providing highly relevant examples at each step, significantly improving accuracy. The paper highlights a novel ‘first-try’ strategy, which further refines this process by using the LLM’s initial attempt to guide the retrieval of similar examples, thus minimizing irrelevant information. This strategy proves to be particularly beneficial when handling problems with lower similarity to those in the training data, a common challenge for LLMs. Overall, step-level reasoning emerges as a robust and generalizable technique that improves LLM reasoning performance, particularly when integrated with advanced search methods like Monte Carlo Tree Search (MCTS).
First-Try Strategy#
The “First-Try” strategy, employed within the BoostStep model for improved mathematical reasoning, represents a novel approach to in-context learning. Instead of relying solely on pre-selected examples, BoostStep initially allows the model to attempt a solution step independently. This “first-try” provides crucial information about the model’s current understanding and reasoning approach. This initial attempt informs the subsequent retrieval of relevant examples from the step-level example bank. By focusing on the similarity between the model’s initial attempt and available examples, rather than solely relying on problem-level similarity, the strategy ensures that provided examples directly address the model’s specific challenges and misconceptions in that step. This targeted approach reduces noise and distraction from irrelevant example steps, leading to more accurate and efficient single-step reasoning. The “first-try” strategy’s effectiveness is highlighted by its compatibility with Monte Carlo Tree Search methods, further demonstrating its potential as a robust technique for improving the mathematical reasoning capabilities of large language models.
MCTS Integration#
The integration of Monte Carlo Tree Search (MCTS) within the BoostStep framework represents a significant advancement in enhancing Large Language Model (LLM) mathematical reasoning capabilities. MCTS’s inherent ability to explore multiple reasoning pathways synergizes well with BoostStep’s step-level in-context learning. By incorporating example steps during both candidate generation and evaluation phases, BoostStep significantly improves the accuracy of the MCTS process. The integration isn’t merely additive; it’s synergistic. The step-level guidance provided by BoostStep reduces the reliance on overall problem similarity, addressing a crucial limitation of traditional MCTS implementations. This leads to more accurate candidate generation and more reliable evaluation by the critic model, ultimately enhancing the overall effectiveness of the MCTS search. The seamless integration highlights the generalizability of the BoostStep approach, demonstrating its potential as a powerful reasoning enhancement technique applicable to various step-wise reasoning strategies, not just MCTS.
Benchmark Results#
A dedicated ‘Benchmark Results’ section would be crucial for evaluating the proposed BoostStep method. It should present a thorough comparison against existing state-of-the-art (SOTA) models on a range of established mathematical reasoning benchmarks. Key metrics would include accuracy, precision, recall, and F1-score, broken down by problem type and difficulty. The results should clearly demonstrate whether BoostStep significantly outperforms SOTA, especially in scenarios involving complex, multi-step problems. Statistical significance testing (e.g., t-tests or ANOVA) must be applied to confirm the improvements are not merely due to chance. Furthermore, the section should analyze the performance differences across various benchmark datasets. This is important to determine whether BoostStep generalizes well or exhibits biases towards certain problem types. Qualitative analysis of specific successes and failures of BoostStep would add valuable insights. Finally, the results should be presented visually (e.g., tables and charts) for easy comprehension and to effectively communicate the contributions of the method.
Future Directions#
Future research directions for mathematical reasoning in large language models (LLMs) should prioritize addressing the limitations of current in-context learning techniques. Improving the granularity and relevance of examples used for in-context learning is key. This might involve developing more sophisticated methods for retrieving and selecting relevant steps from a problem bank, perhaps incorporating techniques beyond simple TF-IDF. Research into more robust and efficient ways to evaluate the correctness of step-wise reasoning is also crucial, exploring alternatives to current methods that rely on separate critic models. Furthermore, exploring more sophisticated reasoning strategies beyond basic step-by-step approaches (such as integrating more advanced search algorithms like Monte Carlo Tree Search more effectively) and developing more comprehensive mathematical datasets (that explicitly break down solutions into granular, consistent steps) would greatly improve the field. Finally, investigating the potential for transfer learning across different mathematical domains and assessing the robustness of these models in the face of novel problem types is essential for achieving true progress in mathematical reasoning with LLMs.
More visual insights#
More on figures

🔼 Figure 2 illustrates the core concept of the BoostStep method. Panel (a) shows traditional problem-level in-context learning, where the model receives a set of complete example problems before attempting to solve a new problem. This approach offers limited guidance during the reasoning process. Panel (b) presents BoostStep’s step-level in-context learning, which provides more granular guidance by retrieving examples for each individual reasoning step. The ‘first-try’ strategy, where the model attempts the step before retrieving examples, ensures higher relevance. Panel (c) demonstrates how BoostStep integrates with Monte Carlo Tree Search (MCTS), guiding both the candidate generation and decision-making processes by introducing highly relevant example steps.
read the caption
Figure 2: Our strategy refines in-context learning from problem-level granularity (fig.a) to step-level granularity(fig.b) to provide more real-time fine-grained guidance. Moreover, our strategy can guide the reasoning and verifying process in Monte Carlo Tree Search (MCTS) strategies by introducing examples.

🔼 Figure 3 illustrates how step-level in-context learning (BoostStep) overcomes a limitation of problem-level in-context learning. It shows two distinct math problems with different surface-level features. Problem-level methods would deem these problems dissimilar due to their contextual differences and might not find them relevant to each other. However, BoostStep focuses on the underlying steps involved in solving the problem and highlights that both problems share a similar ‘core skill’ or reasoning step (e.g., squaring an expression of the form (x + 1/x) to solve for a polynomial). Step-level learning allows retrieval and use of this highly relevant guidance (the core skill), improving the model’s ability to solve problems with similar underlying steps, even if their overall problem statements differ.
read the caption
Figure 3: An example of different problems may contain similar steps. Problem-level in-context learning will ignore this example due to low problem similarity, while our step-level in-context learning can introduce the core skills by step-level retrieval and guidance.

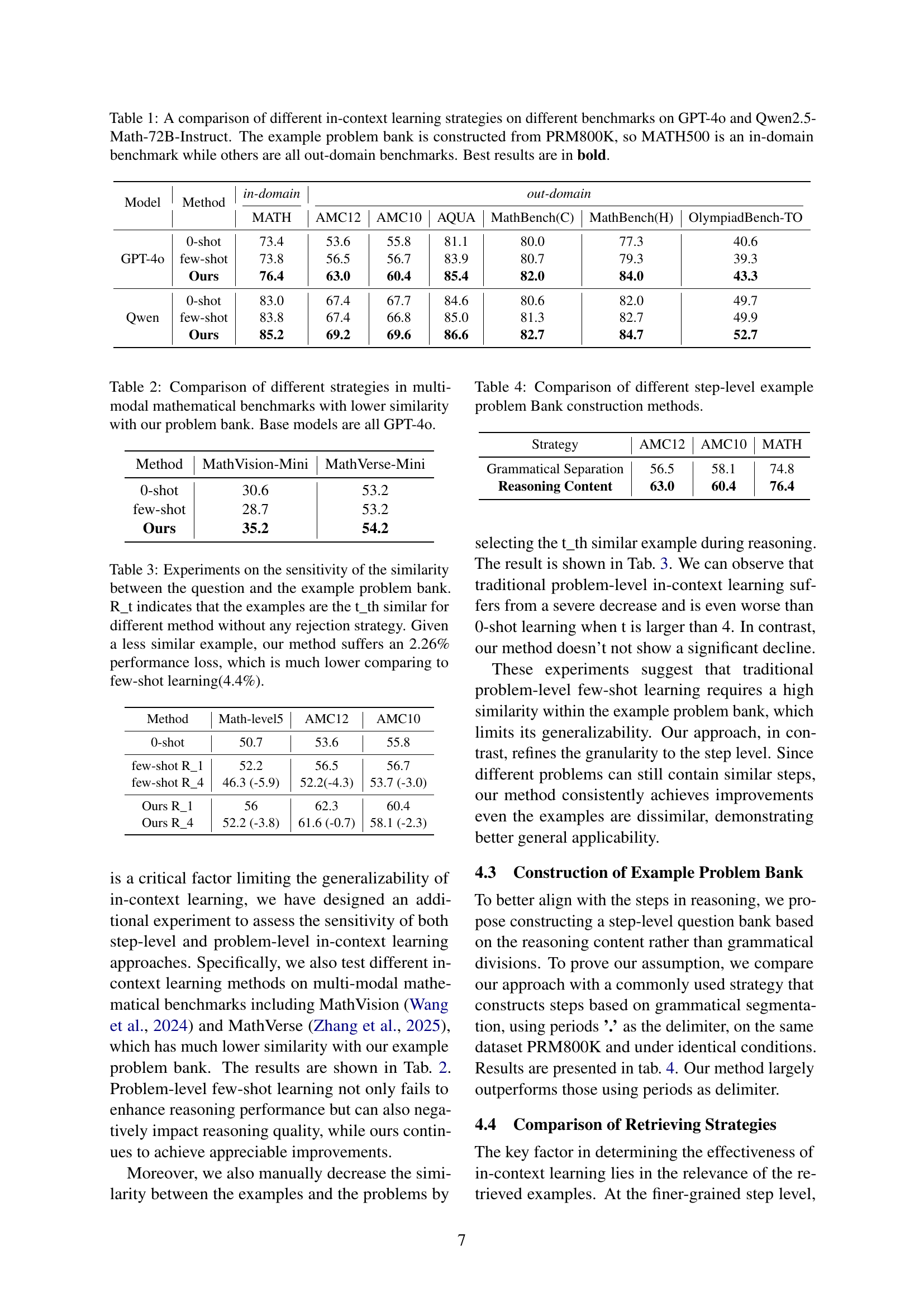
🔼 This figure demonstrates how the step-level in-context learning method helps improve the reasoning process during real-time inference. The example shows the model’s initial attempt (‘first-try’) at solving a step in a mathematical problem, where it incorrectly uses an equation. The step-level in-context learning then retrieves a relevant example from a database, guiding the model to utilize the correct equation and arrive at the correct solution for that step. This highlights the method’s ability to provide targeted guidance and correct errors in the model’s reasoning.
read the caption
Figure 4: A specific example of adjusting reasoning during real-time inference through step-level in-context learning. The first-try uses a wrong equation while the retrieving example step guides the model to use the correct equation and get the correct conclusion.
More on tables
| Method | MathVision-Mini | MathVerse-Mini |
|---|---|---|
| 0-shot | 30.6 | 53.2 |
| few-shot | 28.7 | 53.2 |
| Ours | 35.2 | 54.2 |
🔼 This table presents a comparison of the performance of different reasoning strategies on multi-modal mathematical benchmarks. These benchmarks (MathVision-Mini and MathVerse-Mini) have a lower similarity to the example problem bank used in the study than other benchmarks. The comparison focuses on the impact of different strategies on solving problems in these visually-rich settings. All strategies utilize the GPT-40 language model as a base.
read the caption
Table 2: Comparison of different strategies in multi-modal mathematical benchmarks with lower similarity with our problem bank. Base models are all GPT-4o.
| Method | Math-level5 | AMC12 | AMC10 |
|---|---|---|---|
| 0-shot | 50.7 | 53.6 | 55.8 |
| few-shot R_1 | 52.2 | 56.5 | 56.7 |
| few-shot R_4 | 46.3 (-5.9) | 52.2(-4.3) | 53.7 (-3.0) |
| Ours R_1 | 56 | 62.3 | 60.4 |
| Ours R_4 | 52.2 (-3.8) | 61.6 (-0.7) | 58.1 (-2.3) |
🔼 This table investigates how sensitive different methods are to the similarity between the question and the examples in the problem bank. It tests the performance of a 0-shot method, few-shot learning (using the top 1 and top 4 most similar examples), and the proposed method. The experiment measures the performance drop when using less similar examples and compares the impact on various methods. The results demonstrate that the proposed method shows significantly better robustness than traditional few-shot learning when faced with less similar examples.
read the caption
Table 3: Experiments on the sensitivity of the similarity between the question and the example problem bank. R_t indicates that the examples are the t_th similar for different method without any rejection strategy. Given a less similar example, our method suffers an 2.26% performance loss, which is much lower comparing to few-shot learning(4.4%).
| Strategy | AMC12 | AMC10 | MATH |
|---|---|---|---|
| Grammatical Separation | 56.5 | 58.1 | 74.8 |
| Reasoning Content | 63.0 | 60.4 | 76.4 |
🔼 This table compares the performance of different methods for constructing a step-level example problem bank. It shows how different strategies for segmenting problems into steps (grammatical separation versus reasoning content) affect the performance of a model on mathematical reasoning tasks. The results are presented as accuracy scores on three benchmark datasets: AMC12, AMC10, and MATH.
read the caption
Table 4: Comparison of different step-level example problem Bank construction methods.
| Strategy | AMC12 | AMC10 | MATH | MathVision |
|---|---|---|---|---|
| Path | 56.5 | 58.1 | 73.8 | 31.7 |
| Pre-Step | 57.2 | 56.7 | 74.0 | 31.0 |
| First-try | 63.0 | 60.4 | 76.4 | 35.2 |
🔼 Table 5 presents a comparison of different retrieval strategies within a step-level in-context learning approach for mathematical reasoning. The study uses GPT-40 as the base language model, and all experiments employ the same prompts to ensure consistency. Three retrieval methods are compared: 1. Path: Retrieves relevant examples based on the entire reasoning path up to the current step, including all previous steps (sᵢ₋₁, sᵢ₋₂, …, s₁) and the initial question (q). 2. Pre-Step: Retrieves examples based only on the immediately preceding step (sᵢ₋₁). 3. First-try: This is the proposed method from the paper. It involves a ‘first-try’ step where the model attempts the reasoning task before retrieving examples, using this initial attempt to guide the selection of highly relevant examples. The table displays the performance of each retrieval strategy across four mathematical benchmarks: AMC12, AMC10, MATH, and MathVision. The best performance for each benchmark is highlighted in bold.
read the caption
Table 5: Comparison on different retrieval strategies in step-level in-context learning. The base model is GPT-4o and all the prompts are the same. ’Path’ represents retrieving by the reasoning path including all previous step si−1,si−2,…,s1subscript𝑠𝑖1subscript𝑠𝑖2…subscript𝑠1s_{i-1},s_{i-2},\ldots,s_{1}italic_s start_POSTSUBSCRIPT italic_i - 1 end_POSTSUBSCRIPT , italic_s start_POSTSUBSCRIPT italic_i - 2 end_POSTSUBSCRIPT , … , italic_s start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT and question q𝑞qitalic_q, while ’Pre-Step’ represents retrieving by only the immediately preceding step si−1subscript𝑠𝑖1s_{i-1}italic_s start_POSTSUBSCRIPT italic_i - 1 end_POSTSUBSCRIPT. Best results are in bold.
| Reason | Verify | AMC12 | AMC10 | MATH |
|---|---|---|---|---|
| w/o MCTS | 53.6 | 55.8 | 73.4 | |
| ✗ | ✗ | 58.7 | 59.0 | 77.8 |
| ✓ | ✗ | 64.4 | 62.2 | 79.2 |
| ✗ | ✓ | 61.6 | 60.4 | 78.2 |
| ✓ | ✓ | 65.2 | 63.6 | 79.4 |
🔼 This table presents an ablation study on the impact of incorporating retrieved similar steps into the Monte Carlo Tree Search (MCTS) process for mathematical reasoning. It examines how providing similar examples during both the reasoning and verification phases of the MCTS algorithm affects performance. The study uses GPT-4o as the base reasoning model and compares different configurations of using or not using similar examples in the reasoning and verification steps, measuring the impact on accuracy across three benchmark datasets (AMC12, AMC10, MATH). The prompts used across the different configurations were kept constant to isolate the effect of example retrieval.
read the caption
Table 6: A detailed ablation on incorporating retrieving similar steps to provide fine-grained guidance during the reasoning and verifying phases of Monte Carlo Tree Search (MCTS) methods. Base models are GPT-4o and prompts are the same. Best results are in bold.
Full paper#