↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
Current approaches for training language models to solve mathematical problems often rely on large models or high-quality datasets, which are limited and expensive. This makes it difficult to improve the reasoning abilities of smaller models. The existing methods for training reward models also face challenges due to the scarcity of accurate step-by-step feedback data.
The paper introduces rStar-Math, a novel approach that uses smaller language models and Monte Carlo Tree Search (MCTS) to overcome these limitations. It introduces three key innovations: a code-augmented Chain-of-Thought data synthesis method, a new process reward model training method, and a self-evolutionary training process. These innovations allow rStar-Math to achieve state-of-the-art performance on various math benchmarks, even surpassing larger models in some cases. The results demonstrate the potential for smaller language models to tackle complex reasoning tasks if trained effectively.
Key Takeaways#
Why does it matter?#
This paper is important because it demonstrates that small language models can achieve state-of-the-art performance in mathematical reasoning by using a novel self-evolved deep thinking approach. This opens new avenues for research in low-resource settings and challenges the common assumption that large models are necessary for complex reasoning tasks. It also introduces valuable techniques like code-augmented data synthesis and process preference model training which can benefit a wider AI community.
Visual Insights#

🔼 This figure provides a high-level overview of the rStar-Math system. It illustrates the three key innovations that enable small language models (SLMs) to master math reasoning: (a) shows the generation of step-by-step reasoning trajectories through Monte Carlo Tree Search (MCTS), where each step is verified using Python code execution, ensuring correctness; (b) depicts the construction of per-step preference pairs based on Q-values obtained from MCTS, enabling the training of a process preference model (PPM) without requiring manual step-level annotations; (c) shows the iterative, self-evolutionary process, where the policy SLM and PPM are repeatedly trained and refined using increasingly high-quality data generated by the system.
read the caption
Figure 1: The overview of \sysname.
| Task | rStar-Math (Qwen-7B) | rStar-Math (Qwen-1.5B) | rStar-Math (Phi3-mini) | OpenAI o1-preview | OpenAI o1-mini | QWQ 32B-preview | GPT-4o | DeepSeek-V3 |
|---|---|---|---|---|---|---|---|---|
| MATH | 90.0 | 88.6 | 86.4 | 85.5 | 90.0 | 90.6 | 76.6 | 90.2 |
| AIME 2024 | 53.3 | 46.7 | 43.3 | 44.6 | 56.7 | 50.0 | 9.3 | 39.2 |
| Olympiad Bench | 65.6 | 64.6 | 60.3 | - | 65.3 | 61.2 | 43.3 | 55.4 |
| College Math | 60.5 | 59.3 | 59.1 | - | 57.8 | 55.8 | 48.5 | 58.9 |
| Omni-Math | 50.5 | 48.5 | 46.0 | 52.5 | 60.5 | 49.6 | 30.5 | 35.9 |
🔼 This table presents the performance of the rStar-Math model on various math reasoning tasks. It shows the accuracy (pass@1) achieved by rStar-Math when applied to several small language models (SLMs) of varying sizes. The results are compared against the performance of OpenAI’s models and other baselines, highlighting the significant improvements in math reasoning capabilities achieved by rStar-Math through its deep thinking approach. The table demonstrates the model’s ability to achieve state-of-the-art results on standard benchmarks and even surpass the performance of larger, more powerful models.
read the caption
Table 1: \sysname enables frontier math reasoning in SLMs via deep thinking over 64 trajectories.
In-depth insights#
Self-Evolved Deep Thinking#
The concept of “Self-Evolved Deep Thinking” presents a novel approach to enhancing Large Language Models’ (LLMs) reasoning capabilities. It leverages iterative self-improvement, where the LLM’s reasoning process isn’t static but dynamically evolves through multiple rounds. Each round refines both the policy model (which generates reasoning steps) and a process preference model (which evaluates the quality of generated steps). This iterative refinement relies on synthesized training data, created using Monte Carlo Tree Search (MCTS). The key is the MCTS generates verified reasoning trajectories and step-by-step quality scores that avoid the need for manual data annotation, making the training process significantly more scalable and efficient. The self-evolution aspect is crucial because it enables the system to progressively tackle more challenging problems and generates increasingly high-quality data, ultimately leading to state-of-the-art performance in mathematical reasoning.
Code-Augmented CoT#
The proposed Code-Augmented Chain of Thought (CoT) method represents a significant advancement in generating high-quality training data for mathematical reasoning. By augmenting the traditional natural language CoT with executable Python code, the approach directly addresses the issue of hallucination inherent in large language models (LLMs). The requirement that the code successfully executes acts as a powerful filter, ensuring that only valid and coherent reasoning steps are retained. This verification process not only mitigates errors but also enables the automatic assignment of Q-values through Monte Carlo Tree Search (MCTS) rollouts, thereby eliminating the need for tedious manual annotation. The integration of code execution within the CoT framework is a novel and elegant solution, effectively combining the strengths of symbolic computation with the capabilities of LLMs for a more robust and reliable training dataset. This crucial innovation is a key contributor to the success of the rStar-Math framework, highlighting the potential of code-augmented techniques to improve the accuracy and generalizability of LLMs in complex reasoning tasks.
Process Reward Model#
Process reward models are crucial for effective System 2 reasoning, offering fine-grained feedback on intermediate reasoning steps. However, training data is scarce, requiring extensive human annotation or impractical-to-scale automatic methods which suffer from noisy scores. This paper introduces a novel approach to training a process preference model (PPM) by avoiding naïve step-level score annotation. Instead, it leverages the Q-values from Monte Carlo Tree Search (MCTS) to construct preference pairs, using a pairwise ranking loss to train the PPM. This method enables reliable step-level evaluation without intense human labeling, yielding a more effective model than traditional outcome-based or Q-value based reward models. The iterative self-evolution method further refines the PPM by continually improving the quality of training data. This strategy avoids the limitations of existing approaches which rely on superior LLMs for data synthesis and achieve state-of-the-art results in mathematical reasoning. The novel PPM training method is a key innovation, significantly improving the reliability and efficacy of the process reward component in the overall System 2 framework.
Self-Evolution Recipe#
The ‘Self-Evolution Recipe’ section details a crucial iterative process. The core idea is bootstrapping: starting with relatively weak small language models (SLMs) and iteratively improving them. Each round involves using Monte Carlo Tree Search (MCTS) to generate high-quality training data, which is then used to train stronger SLMs and process preference models (PPMs). This self-improvement cycle, repeated four times, allows the system to progressively tackle more challenging math problems. A key innovation is the use of code-augmented Chain-of-Thought (CoT) data, ensuring the accuracy of intermediate steps. The PPM’s design avoids the need for expensive manual annotation of intermediate steps, further increasing efficiency and scalability. The iterative refinement of both SLMs and PPMs through this cycle is the key to the remarkable performance improvements observed.
Limitations and Future Work#
The study’s limitations center on the reliance on specific model architectures, potentially limiting generalizability. Future work could explore applying the methodology to diverse model types and problem domains, enhancing its robustness. Furthermore, the self-evolution process could benefit from more sophisticated techniques, such as incorporating external knowledge or human feedback. Investigating the scalability and efficiency of the approach for larger datasets and more complex problems remains crucial. Finally, a deeper dive into the self-reflection capabilities observed in the system, and whether it is a consistent feature or artifact of the methodology, would significantly improve the understanding of the deep thinking mechanism.
More visual insights#
More on figures

🔼 This figure shows an example of a Code-augmented Chain of Thought (CoT) used in the rStar-Math model. The example problem is a word problem asking to calculate the direct distance from a starting point after a series of movements. The solution is presented step-by-step using a code-augmented CoT, where each step involves natural language reasoning (the NL CoT) accompanied by executable Python code. The Python code directly implements the reasoning described in the accompanying natural language. This approach ensures the correctness and verifiability of each step, mitigating the problem of hallucination often seen in large language models (LLMs) that generate only natural language reasoning steps.
read the caption
Figure 2: An example of Code-augmented CoT.

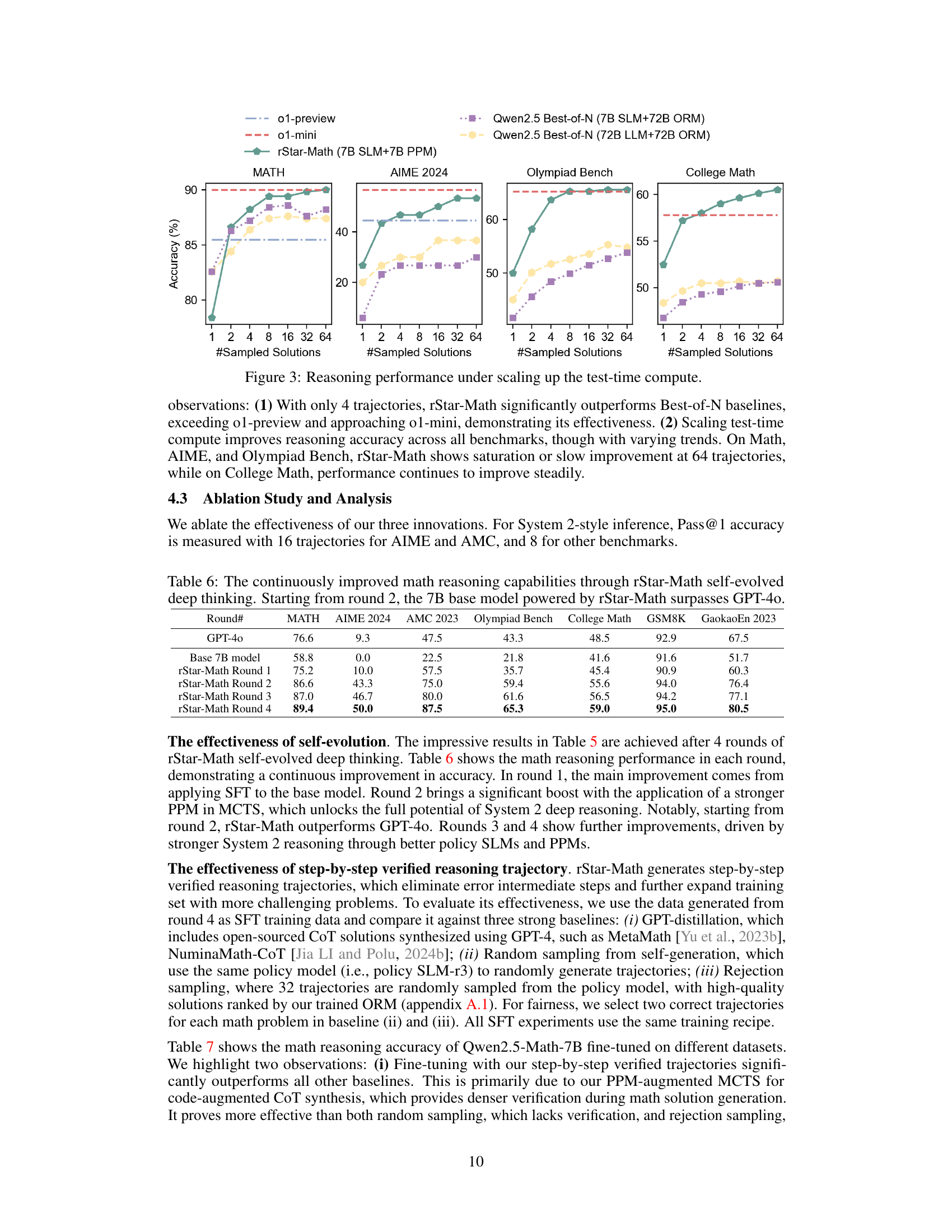
🔼 This figure displays the impact of increasing computational resources during testing on the accuracy of mathematical problem-solving. Four different benchmarks (MATH, AIME 2024, Olympiad Bench, and College Math) are shown, each represented by a separate graph. The x-axis represents the number of solutions sampled during the test-time computation, and the y-axis shows the percentage accuracy achieved. Multiple models are compared: OpenAI’s o1-preview and o1-mini models, and the rStar-Math model with a 7B parameter policy LLM and a 7B parameter PPM, as well as a comparison using Qwen2.5 Best-of-N models with 7B and 72B parameter LLMs and a 72B parameter ORM. This allows for a visual comparison of how different models and levels of computational scaling (number of solution samples) impact the accuracy of mathematical reasoning across the various benchmarks. The plot shows that increasing the number of samples generally improves accuracy, but the rate of improvement varies for different models and benchmarks. It also highlights the competitive performance of rStar-Math, sometimes exceeding even the larger models with less compute.
read the caption
Figure 3: Reasoning performance under scaling up the test-time compute.

🔼 This figure shows an example of the model’s intrinsic self-reflection ability during problem-solving. The model initially attempts a solution using SymPy, but realizes it’s leading to an incorrect answer (as indicated by the low PPM score). It then abandons this approach, and instead finds a simpler and correct solution. This demonstrates the model’s ability to identify and correct its own mistakes, rather than simply continuing down an incorrect path.
read the caption
Figure 4: An example of intrinsic self-reflection during \sysname deep thinking.

🔼 Figure 5 presents a comparative analysis of the performance of various policy models (different sizes) before and after integrating them into a System 2 reasoning framework. The x-axis represents different mathematical benchmarks (MATH, AIME 2024, AMC 2023, Olympiad Bench, College Math), while the y-axis shows Pass@1 accuracy. The bars visually represent the accuracy of individual policy models (various base models) using only System 1 reasoning (i.e., generating a single answer without deep thinking). The bars also show the improved performance achieved by incorporating these models into a System 2 deep thinking approach with various reward models (ORM, PPM). The key takeaway is that the reward model significantly impacts the final performance of the system, highlighting its importance in System 2 deep thinking.
read the caption
Figure 5: Pass@1 accuracy of policy models and their accuracy after applying System 2 reasoning with various reward models, shows that reward models primarily determine the final performance.

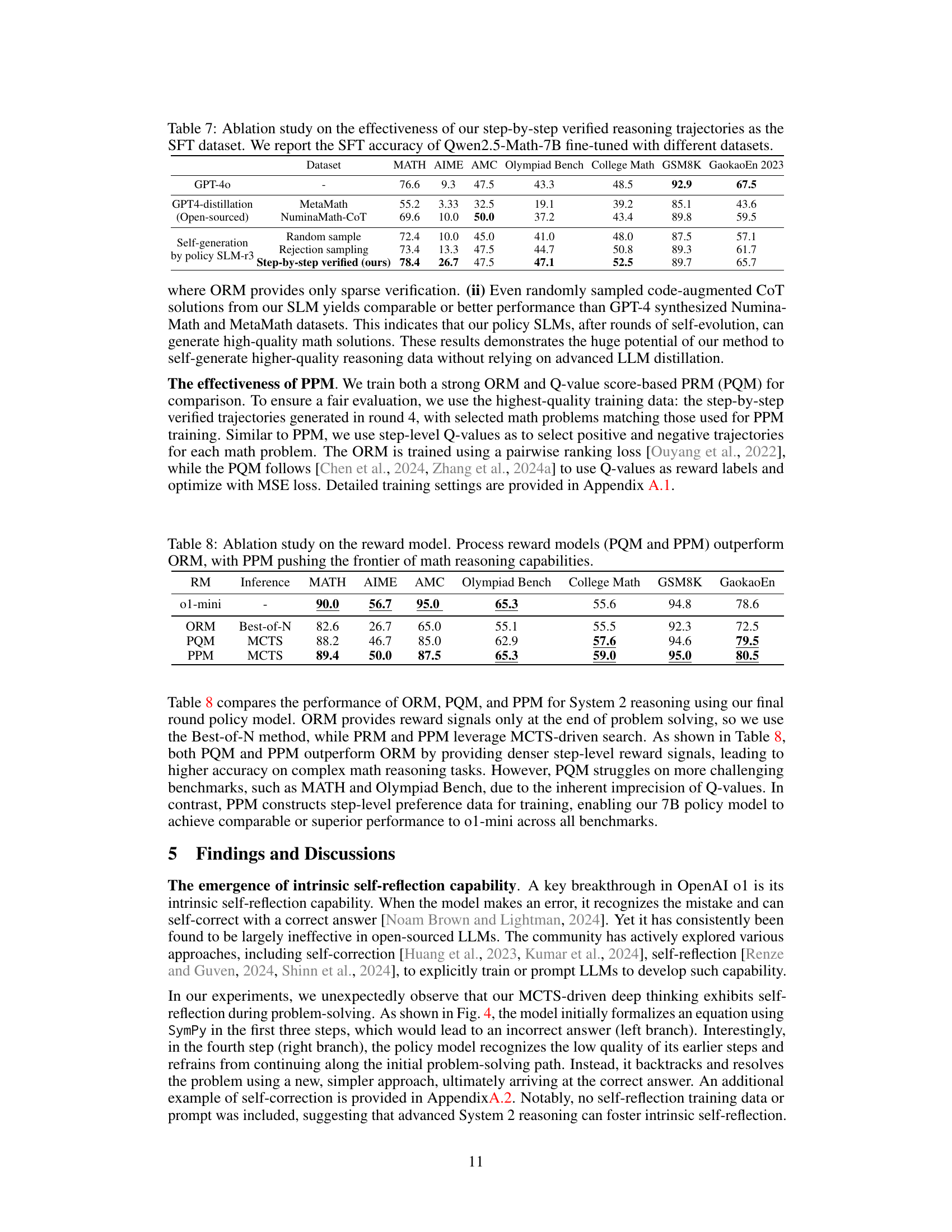
🔼 Figure 6 presents a comparison of the accuracy (Pass@N) achieved using random sampling for solution selection from various policy models. The x-axis represents the number of solutions sampled (N), while the y-axis shows the accuracy. Four different benchmarks are shown: MATH, AIME 2024, Olympiad Bench, and College Math. The results demonstrate that the rStar-Math policy models consistently outperform the official Qwen instruct versions, showcasing their superior ability to generate correct solutions, even when only a small number of samples are considered.
read the caption
Figure 6: Pass@N accuracy with random sampling from different policy models. Compared to the official Qwen instruct version, our policy model exhibits a stronger ability to sample correct solutions.

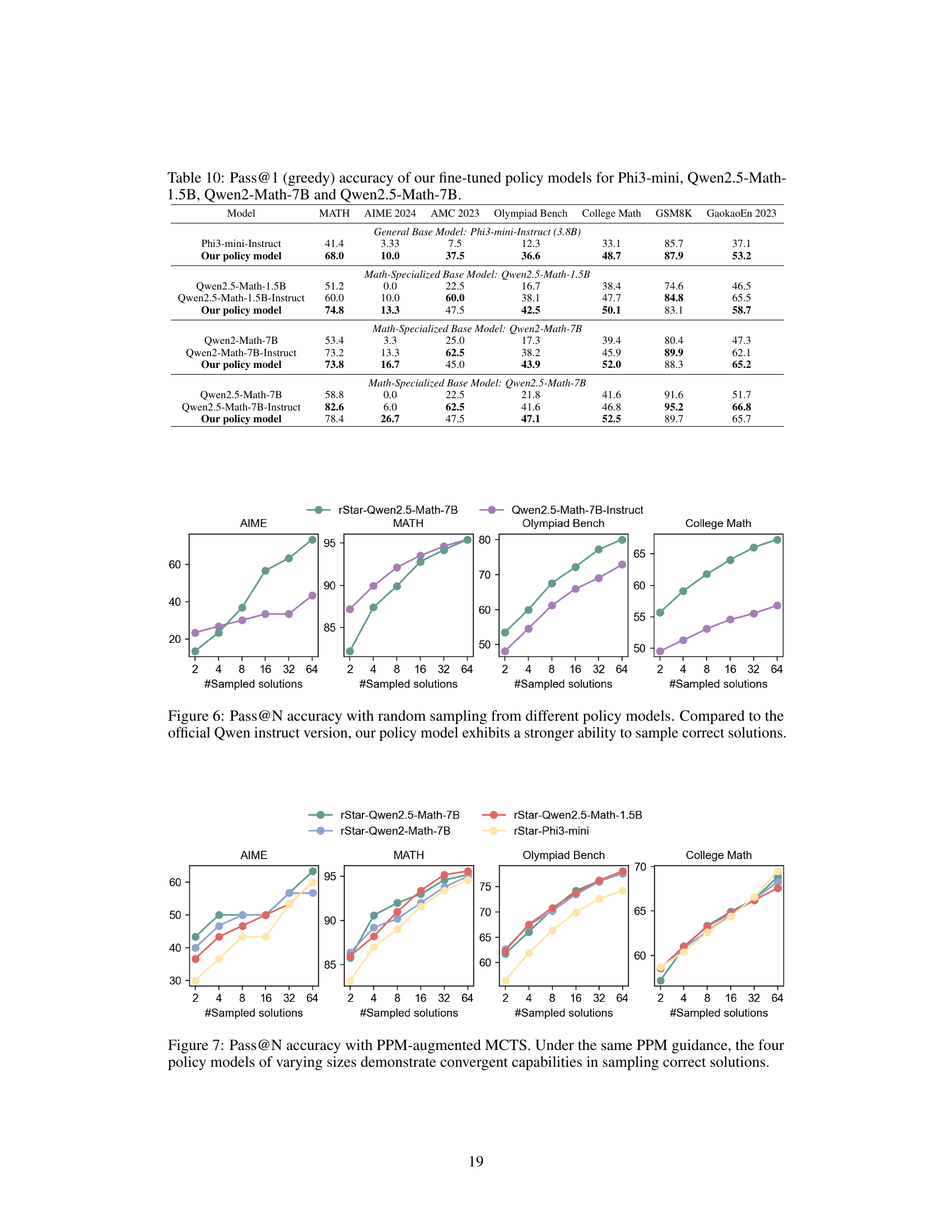
🔼 Figure 7 illustrates the performance of four different sized language models (1.5B, 3.8B, 7B, and 72B parameters) on several math reasoning benchmarks when using Monte Carlo Tree Search (MCTS) with a process preference model (PPM). The key takeaway is that despite the varying sizes of the base models, their accuracy in sampling correct solutions converges as the number of MCTS samples increases. This highlights the effectiveness of the PPM in guiding the search process, regardless of the underlying model’s size.
read the caption
Figure 7: Pass@N accuracy with PPM-augmented MCTS. Under the same PPM guidance, the four policy models of varying sizes demonstrate convergent capabilities in sampling correct solutions.
More on tables
| # | models in MCTS | GSM-level | MATH-level | Olympiad-level | All |
|---|---|---|---|---|---|
| Round 1 | DeepSeek-Coder-V2-Instruct | 96.61% | 67.36% | 20.99% | 60.17% |
| Round 2 | policy SLM-r1 | 97.88% | 67.40% | 56.04% | 66.60% |
| Round 3 | policy SLM-r2, PPM-r2 | 98.15% | 88.69% | 62.16% | 77.86% |
| Round 4 | policy SLM-r3, PPM-r3 | 98.15% | 94.53% | 80.58% | 90.25% |
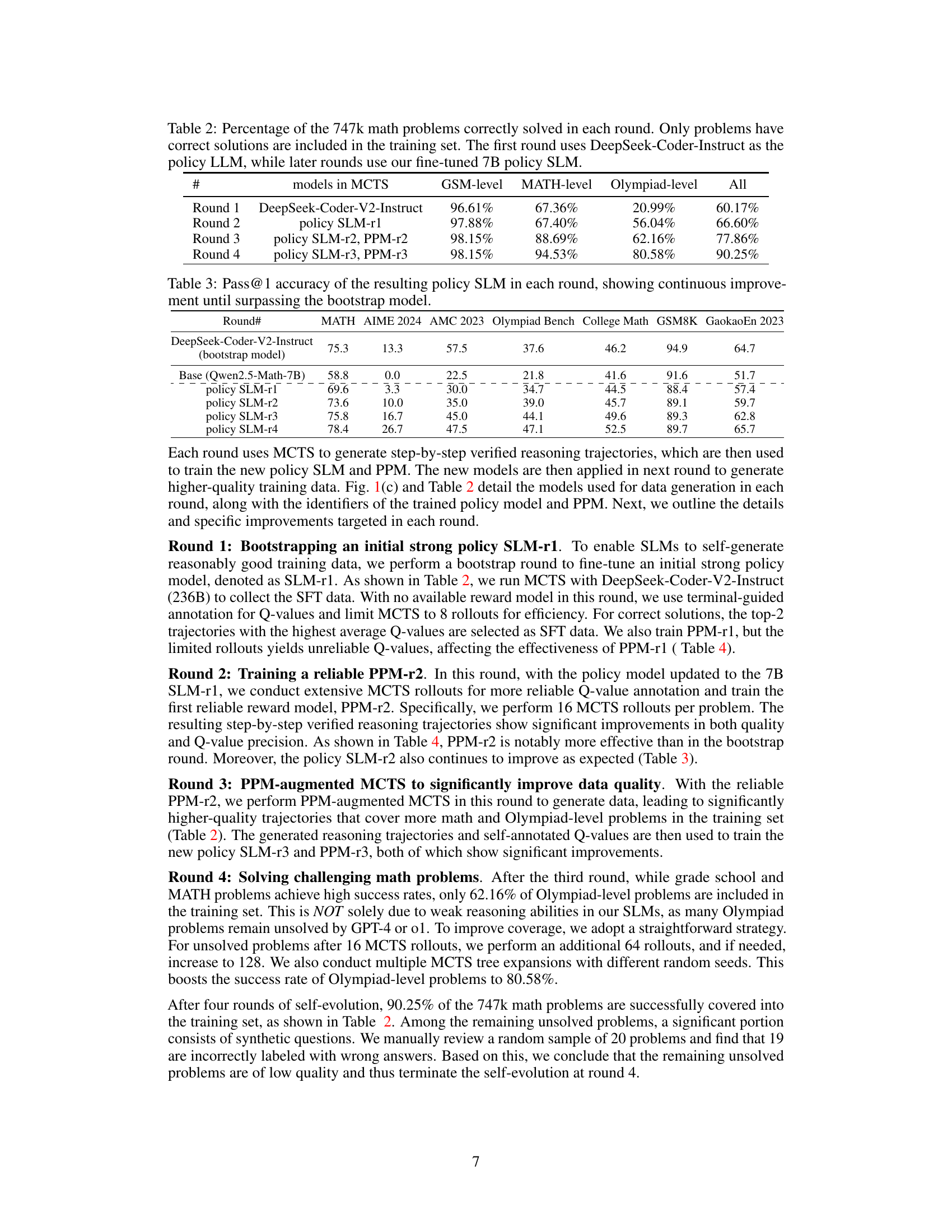
🔼 This table shows the percentage of 747,000 math problems that were correctly solved by the model in each of four training rounds. Only problems with verifiable correct solutions were included in the training data. The first round used a pre-trained large language model (DeepSeek-Coder-Instruct) as the initial policy model. Subsequent rounds used a smaller, fine-tuned 7-billion parameter language model that was iteratively improved during the self-evolution process. The table provides a measure of the model’s progress in solving increasingly difficult math problems across the training rounds.
read the caption
Table 2: Percentage of the 747k math problems correctly solved in each round. Only problems have correct solutions are included in the training set. The first round uses DeepSeek-Coder-Instruct as the policy LLM, while later rounds use our fine-tuned 7B policy SLM.
| Round# | MATH | AIME 2024 | AMC 2023 | Olympiad Bench | College Math | GSM8K | GaokaoEn 2023 |
|---|---|---|---|---|---|---|---|
| DeepSeek-Coder-V2-Instruct (bootstrap model) | 75.3 | 13.3 | 57.5 | 37.6 | 46.2 | 94.9 | 64.7 |
| Base (Qwen2.5-Math-7B) | 58.8 | 0.0 | 22.5 | 21.8 | 41.6 | 91.6 | 51.7 |
| policy SLM-r1 | 69.6 | 3.3 | 30.0 | 34.7 | 44.5 | 88.4 | 57.4 |
| policy SLM-r2 | 73.6 | 10.0 | 35.0 | 39.0 | 45.7 | 89.1 | 59.7 |
| policy SLM-r3 | 75.8 | 16.7 | 45.0 | 44.1 | 49.6 | 89.3 | 62.8 |
| policy SLM-r4 | 78.4 | 26.7 | 47.5 | 47.1 | 52.5 | 89.7 | 65.7 |
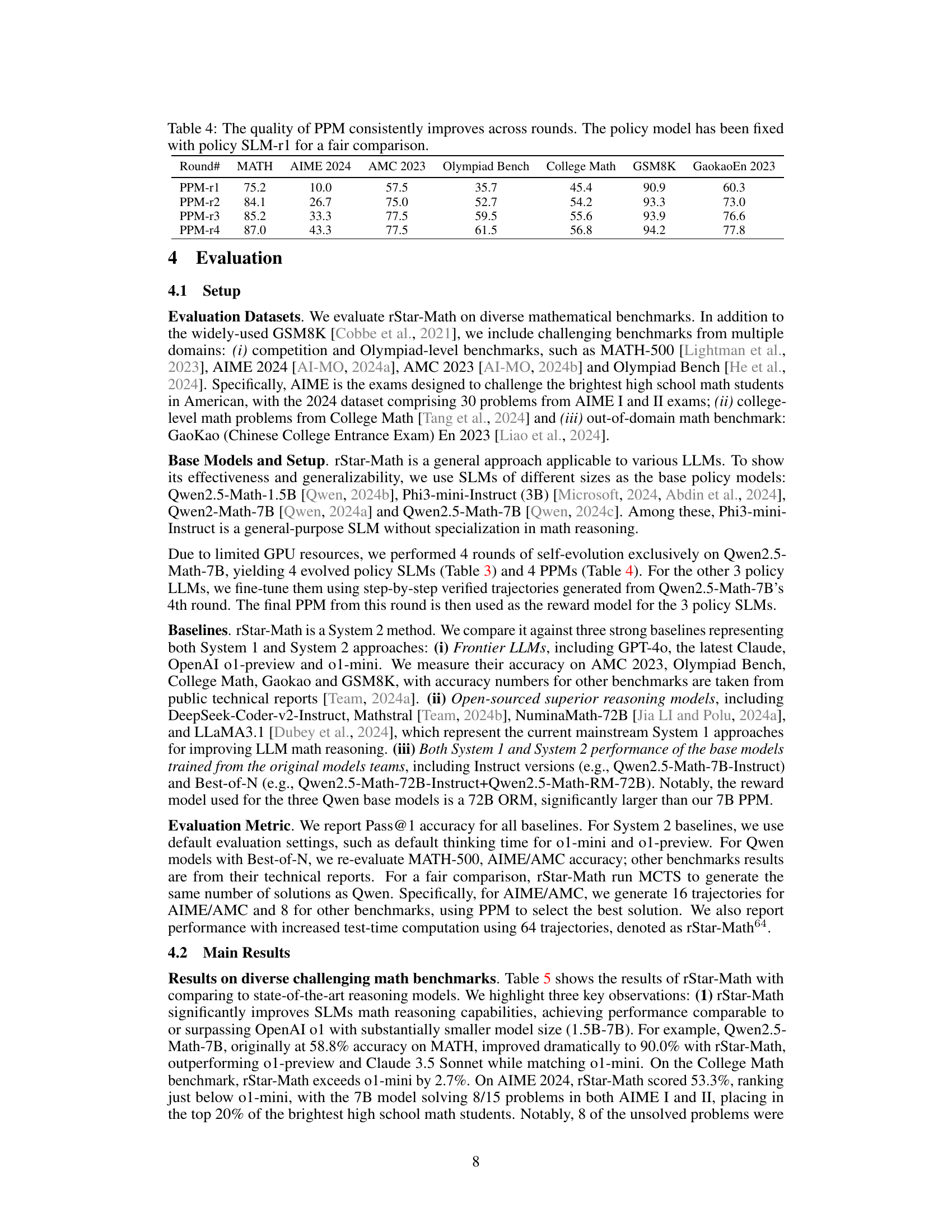
🔼 Table 3 presents the accuracy (Pass@1) of the policy model across four rounds of training. The initial policy model (Round 0, bootstrap model) is a pre-trained model. Each subsequent round represents an iterative improvement of the policy model, trained using data generated by the previous round. The table demonstrates consistent accuracy improvement across rounds, culminating in performance that surpasses that of the initial, pre-trained bootstrap model.
read the caption
Table 3: Pass@1 accuracy of the resulting policy SLM in each round, showing continuous improvement until surpassing the bootstrap model.
| Round# | MATH | AIME 2024 | AMC 2023 | Olympiad Bench | College Math | GSM8K | GaokaoEn 2023 |
|---|---|---|---|---|---|---|---|
| PPM-r1 | 75.2 | 10.0 | 57.5 | 35.7 | 45.4 | 90.9 | 60.3 |
| PPM-r2 | 84.1 | 26.7 | 75.0 | 52.7 | 54.2 | 93.3 | 73.0 |
| PPM-r3 | 85.2 | 33.3 | 77.5 | 59.5 | 55.6 | 93.9 | 76.6 |
| PPM-r4 | 87.0 | 43.3 | 77.5 | 61.5 | 56.8 | 94.2 | 77.8 |
🔼 Table 4 presents the performance of the Process Preference Model (PPM) across four rounds of training. The key point is that the PPM’s ability to accurately evaluate the quality of reasoning steps improves with each round. To ensure a fair comparison and isolate the PPM’s progress, the policy model used remained consistent (policy SLM-r1) throughout the four rounds. The table shows accuracy scores across various math reasoning benchmarks (MATH, AIME 2024, AMC 2023, Olympiad Bench, College Math, GSM8K, GaokaoEn 2023) for each round’s PPM, highlighting the steady improvement in performance.
read the caption
Table 4: The quality of PPM consistently improves across rounds. The policy model has been fixed with policy SLM-r1 for a fair comparison.
| Model | Method | MATH | AIME 2024 | AMC 2023 | Olympiad Bench | College Math | GSM8K | Gaokao En 2023 |
|---|---|---|---|---|---|---|---|---|
| Frontier LLMs | ||||||||
| GPT-4o | System 1 | 76.6 | 9.3 | 47.5 | 43.3 | 48.5 | 92.9 | 67.5 |
| Claude3.5-Sonnet | System 1 | 78.3 | 16.0 | - | - | - | 96.4 | - |
| GPT-o1-preview | - | 85.5 | 44.6 | 90.0 | - | - | - | - |
| GPT-o1-mini | - | 90.0 | 56.7 | 95.0 | 65.3 | 57.8 | 94.8 | 78.4 |
| Open-Sourced Reasoning LLMs | ||||||||
| DeepSeek-Coder-V2-Instruct | System 1 | 75.3 | 13.3 | 57.5 | 37.6 | 46.2 | 94.9 | 64.7 |
| Mathstral-7B-v0.1 | System 1 | 57.8 | 0.0 | 37.5 | 21.5 | 33.7 | 84.9 | 46.0 |
| NuminaMath-72B-CoT | System 1 | 64.0 | 3.3 | 70.0 | 32.6 | 39.7 | 90.8 | 58.4 |
| LLaMA3.1-8B-Instruct | System 1 | 51.4 | 6.7 | 25.0 | 15.4 | 33.8 | 76.6 | 38.4 |
| LLaMA3.1-70B-Instruct | System 1 | 65.4 | 23.3 | 50.0 | 27.7 | 42.5 | 94.1 | 54.0 |
| Qwen2.5-Math-72B-Instruct | System 1 | 85.6 | 30.0 | 70.0 | 49.0 | 49.5 | 95.9 | 71.9 |
| Qwen2.5-Math-72B-Instruct+72B ORM | System 2 | 85.8 | 36.7 | 72.5 | 54.5 | 50.6 | 96.4 | 76.9 |
| General Base Model: Phi3-mini-Instruct (3.8B) | ||||||||
| Phi3-mini-Instruct (base model) | System 1 | 41.4 | 3.33 | 7.5 | 12.3 | 33.1 | 85.7 | 37.1 |
| \sysname (3.8B SLM+7B PPM) | System 2 | 85.4 | 40.0 | 77.5 | 59.3 | 58.0 | 94.5 | 77.1 |
| \sysname64 (3.8B SLM+7B PPM) | System 2 | 86.4 | 43.3 | 80.0 | 60.3 | 59.1 | 94.7 | 77.7 |
| Math-Specialized Base Model: Qwen2.5-Math-1.5B | ||||||||
| Qwen2.5-Math-1.5B (base model) | System 1 | 51.2 | 0.0 | 22.5 | 16.7 | 38.4 | 74.6 | 46.5 |
| Qwen2.5-Math-1.5B-Instruct | System 1 | 60.0 | 10.0 | 60.0 | 38.1 | 47.7 | 84.8 | 65.5 |
| Qwen2.5-Math-1.5B-Instruct+72B ORM | System 2 | 83.4 | 20.0 | 72.5 | 47.3 | 50.2 | 94.1 | 73.0 |
| \sysname (1.5B SLM+7B PPM) | System 2 | 87.8 | 46.7 | 80.0 | 63.5 | 59.0 | 94.3 | 77.7 |
| \sysname64 (1.5B SLM+7B PPM) | System 2 | 88.6 | 46.7 | 85.0 | 64.6 | 59.3 | 94.8 | 79.5 |
| Math-Specialized Base Model: Qwen2.5-Math-7B | ||||||||
| Qwen2.5-Math-7B (base model) | System 1 | 53.4 | 3.3 | 25.0 | 17.3 | 39.4 | 80.4 | 47.3 |
| Qwen2.5-Math-7B-Instruct | System 1 | 73.2 | 13.3 | 62.5 | 38.2 | 45.9 | 89.9 | 62.1 |
| Qwen2.5-Math-7B-Instruct+72B ORM | System 2 | 83.4 | 23.3 | 62.5 | 47.6 | 47.9 | 95.1 | 71.9 |
| \sysname (7B SLM+7B PPM) | System 2 | 88.2 | 43.3 | 80.0 | 63.1 | 58.4 | 94.6 | 78.2 |
| \sysname64 (7B SLM+7B PPM) | System 2 | 88.6 | 46.7 | 85.0 | 63.4 | 59.3 | 94.8 | 79.2 |
| Math-Specialized Base Model: Qwen2.5-Math-7B | ||||||||
| Qwen2.5-Math-7B (base model) | System 1 | 58.8 | 0.0 | 22.5 | 21.8 | 41.6 | 91.6 | 51.7 |
| Qwen2.5-Math-7B-Instruct | System 1 | 82.6 | 6.0 | 62.5 | 41.6 | 46.8 | 95.2 | 66.8 |
| Qwen2.5-Math-7B-Instruct+72B ORM | System 2 | 88.4 | 26.7 | 75.0 | 49.9 | 49.6 | 97.9 | 75.1 |
| \sysname (7B SLM+7B PPM) | System 2 | 89.4 | 50.0 | 87.5 | 65.3 | 59.0 | 95.0 | 80.5 |
| \sysname64 (7B SLM+7B PPM) | System 2 | 90.0 | 53.3 | 87.5 | 65.6 | 60.5 | 95.2 | 81.3 |
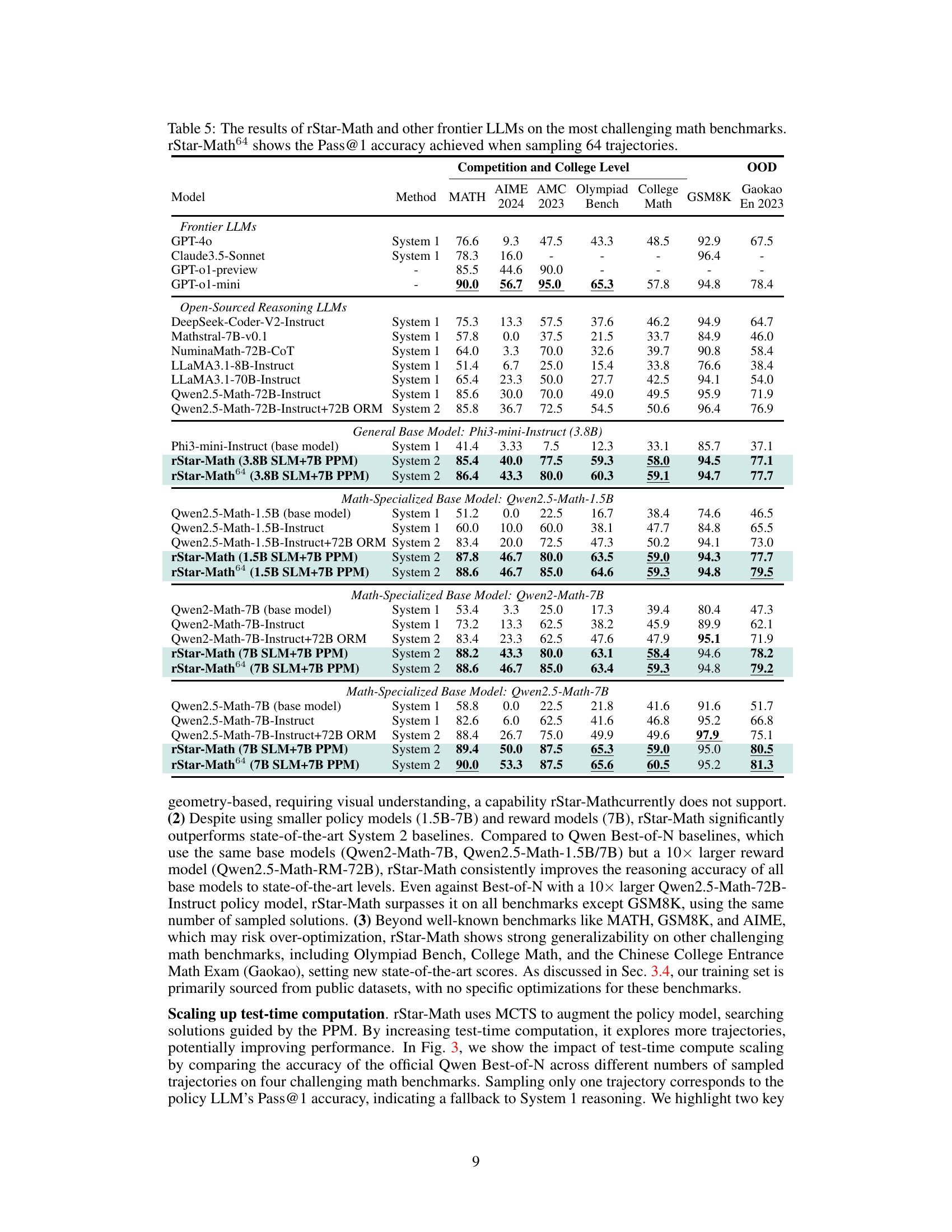
🔼 Table 5 presents a comparison of the performance of the rStar-Math model against state-of-the-art Large Language Models (LLMs) on a variety of challenging mathematical benchmarks. It shows the Pass@1 accuracy (the percentage of problems solved correctly in a single attempt) for each model across different datasets, including MATH, AIME 2024, AMC 2023, Olympiad Bench, College Math, GSM8K, and GaokaoEn 2023. The table also includes results for rStar-Math64, which represents the performance when the model generates 64 solution attempts for each problem, showcasing the impact of increased computational resources on accuracy. The benchmarks range in difficulty, from commonly used datasets like GSM8K to more challenging competition-level datasets such as AIME (American Invitational Mathematics Examination) and Olympiad Bench, providing a comprehensive evaluation of the models’ capabilities.
read the caption
Table 5: The results of \sysname and other frontier LLMs on the most challenging math benchmarks. \sysname64 shows the Pass@1 accuracy achieved when sampling 64 trajectories.
| Round# | MATH | AIME 2024 | AMC 2023 | Olympiad Bench | College Math | GSM8K | GaokaoEn 2023 |
|---|---|---|---|---|---|---|---|
| GPT-4o | 76.6 | 9.3 | 47.5 | 43.3 | 48.5 | 92.9 | 67.5 |
| Base 7B model | 58.8 | 0.0 | 22.5 | 21.8 | 41.6 | 91.6 | 51.7 |
| \sysname Round 1 | 75.2 | 10.0 | 57.5 | 35.7 | 45.4 | 90.9 | 60.3 |
| \sysname Round 2 | 86.6 | 43.3 | 75.0 | 59.4 | 55.6 | 94.0 | 76.4 |
| \sysname Round 3 | 87.0 | 46.7 | 80.0 | 61.6 | 56.5 | 94.2 | 77.1 |
| \sysname Round 4 | 89.4 | 50.0 | 87.5 | 65.3 | 59.0 | 95.0 | 80.5 |
🔼 This table presents the performance of the rStar-Math model across four rounds of self-evolution. It shows how the model’s accuracy improves on various mathematical reasoning benchmarks (MATH, AIME 2024, AMC 2023, Olympiad Bench, College Math, GSM8K, GaokaoEn 2023) as it iteratively learns and refines its reasoning capabilities. Notably, starting from round 2, the 7B base model enhanced by rStar-Math surpasses the performance of GPT-4, a leading large language model, demonstrating the effectiveness of the self-evolution approach.
read the caption
Table 6: The continuously improved math reasoning capabilities through \sysname self-evolved deep thinking. Starting from round 2, the 7B base model powered by \sysname surpasses GPT-4o.
| Dataset | MATH | AIME | AMC | Olympiad Bench | College Math | GSM8K | GaokaoEn 2023 |
|---|---|---|---|---|---|---|---|
| GPT-4o | - | 76.6 | 9.3 | 47.5 | 43.3 | 48.5 | 92.9 |
| GPT4-distillation (Open-sourced) | MetaMath | 55.2 | 3.33 | 32.5 | 19.1 | 39.2 | 85.1 |
| NuminaMath-CoT | 69.6 | 10.0 | 50.0 | 37.2 | 43.4 | 89.8 | 59.5 |
| Self-generation by policy SLM-r3 | Random sample | 72.4 | 10.0 | 45.0 | 41.0 | 48.0 | 87.5 |
| Rejection sampling | 73.4 | 13.3 | 47.5 | 44.7 | 50.8 | 89.3 | |
| Step-by-step verified (ours) | 78.4 | 26.7 | 47.5 | 47.1 | 52.5 | 89.7 | 65.7 |
🔼 This table presents an ablation study evaluating the effectiveness of using step-by-step verified reasoning trajectories as a training dataset for fine-tuning the Qwen2.5-Math-7B language model. It compares the model’s performance after fine-tuning on this dataset against its performance after training on several other datasets, including those generated by GPT-4 and other methods such as random sampling and rejection sampling. The results are reported as Pass@1 accuracy across various mathematical reasoning benchmarks, allowing for a comparison of the different training approaches and their impact on the final model’s accuracy.
read the caption
Table 7: Ablation study on the effectiveness of our step-by-step verified reasoning trajectories as the SFT dataset. We report the SFT accuracy of Qwen2.5-Math-7B fine-tuned with different datasets.
| RM | Inference | MATH | AIME | AMC | Olympiad Bench | College Math | GSM8K | GaokaoEn |
|---|---|---|---|---|---|---|---|---|
| o1-mini | - | 90.0 | 56.7 | 95.0 | 65.3 | 55.6 | 94.8 | 78.6 |
| ORM | Best-of-N | 82.6 | 26.7 | 65.0 | 55.1 | 55.5 | 92.3 | 72.5 |
| PQM | MCTS | 88.2 | 46.7 | 85.0 | 62.9 | 57.6 | 94.6 | 79.5 |
| PPM | MCTS | 89.4 | 50.0 | 87.5 | 65.3 | 59.0 | 95.0 | 80.5 |
🔼 This table presents an ablation study comparing three different reward model approaches for a System 2 math reasoning model: an Outcome Reward Model (ORM), a Process Reward Model using Q-values (PQM), and a Process Preference Model (PPM). The goal is to assess the impact of the reward model on the overall accuracy of the system. The results show that both PQM and PPM outperform the ORM, demonstrating the benefit of using fine-grained feedback on the reasoning process rather than only considering the final outcome. The PPM achieved the best performance and enabled the model to reach state-of-the-art accuracy, surpassing even the ORM used with a much larger model.
read the caption
Table 8: Ablation study on the reward model. Process reward models (PQM and PPM) outperform ORM, with PPM pushing the frontier of math reasoning capabilities.
| MATH | AIME 2024 | AMC 2023 | Olympiad Bench | College Math | GSM8K | GaokaoEn 2023 |
|---|---|---|---|---|---|---|
| 5453 | 15693 | 14544 | 7889 | 4503 | 3299 | 6375 |
🔼 This table presents the average number of tokens generated by the rStar-Math model to produce a single reasoning trajectory for different types of math problems. The token counts reflect the computational cost associated with generating solutions using Monte Carlo Tree Search (MCTS) for various problem difficulty levels (MATH, AIME 2024, AMC 2023, Olympiad Bench, College Math, GSM8K, GaokaoEn 2023). These costs are important for understanding the efficiency and scalability of the proposed method.
read the caption
Table 9: Inference costs of \sysname. We show the average number of generated tokens required to generate a trajectory for a given question.
| Model | MATH | AIME 2024 | AMC 2023 | Olympiad Bench | College Math | GSM8K | GaokaoEn 2023 |
|---|---|---|---|---|---|---|---|
| General Base Model: Phi3-mini-Instruct (3.8B) | |||||||
| Phi3-mini-Instruct | 41.4 | 3.33 | 7.5 | 12.3 | 33.1 | 85.7 | 37.1 |
| Our policy model | 68.0 | 10.0 | 37.5 | 36.6 | 48.7 | 87.9 | 53.2 |
| Math-Specialized Base Model: Qwen2.5-Math-1.5B | |||||||
| Qwen2.5-Math-1.5B | 51.2 | 0.0 | 22.5 | 16.7 | 38.4 | 74.6 | 46.5 |
| Qwen2.5-Math-1.5B-Instruct | 60.0 | 10.0 | 60.0 | 38.1 | 47.7 | 84.8 | 65.5 |
| Our policy model | 74.8 | 13.3 | 47.5 | 42.5 | 50.1 | 83.1 | 58.7 |
| Math-Specialized Base Model: Qwen2-Math-7B | |||||||
| Qwen2-Math-7B | 53.4 | 3.3 | 25.0 | 17.3 | 39.4 | 80.4 | 47.3 |
| Qwen2-Math-7B-Instruct | 73.2 | 13.3 | 62.5 | 38.2 | 45.9 | 89.9 | 62.1 |
| Our policy model | 73.8 | 16.7 | 45.0 | 43.9 | 52.0 | 88.3 | 65.2 |
| Math-Specialized Base Model: Qwen2.5-Math-7B | |||||||
| Qwen2.5-Math-7B | 58.8 | 0.0 | 22.5 | 21.8 | 41.6 | 91.6 | 51.7 |
| Qwen2.5-Math-7B-Instruct | 82.6 | 6.0 | 62.5 | 41.6 | 46.8 | 95.2 | 66.8 |
| Our policy model | 78.4 | 26.7 | 47.5 | 47.1 | 52.5 | 89.7 | 65.7 |
🔼 This table presents the Pass@1 accuracy, a measure of how often the model’s top prediction is correct, for four different sized language models after fine-tuning. The models are evaluated on several math reasoning benchmarks, including MATH, AIME 2024, AMC 2023, Olympiad Bench, College Math, GSM8K, and GaokaoEn 2023. It compares the performance of the base, instruct-tuned, and rStar-Math-fine-tuned versions of each model to demonstrate the impact of the proposed method.
read the caption
Table 10: Pass@1 (greedy) accuracy of our fine-tuned policy models for Phi3-mini, Qwen2.5-Math-1.5B, Qwen2-Math-7B and Qwen2.5-Math-7B.
Full paper#