TL;DR#
Current methods for improving large language model (LLM) reasoning often prioritize final answer accuracy. However, this can lead to unreliable or logically inconsistent intermediate steps, undermining trust. This is especially problematic in domains like mathematics, where the reasoning process itself is crucial.
STEP-KTO tackles this by incorporating both process-level and outcome-level binary feedback during training. This means the model receives feedback not only on the final answer but also on the correctness of each step in its reasoning process. Experimental results show that STEP-KTO significantly improves the accuracy of both final answers and intermediate steps on various mathematical benchmarks. This highlights the promise of integrating stepwise feedback for creating more reliable and interpretable LLM reasoning.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the critical issue of trust and reliability in large language models (LLMs), particularly for reasoning tasks. By introducing a novel training framework, STEP-KTO, that incorporates both process-level and outcome-level feedback, this research offers a significant advancement in enhancing the trustworthiness of LLMs’ reasoning capabilities. This has far-reaching implications for various applications that rely on reliable LLM reasoning, such as scientific discovery, education, and decision-making systems. Moreover, the research opens up new avenues for further exploration into integrating stepwise feedback into LLM training, leading to more interpretable and dependable AI systems.
Visual Insights#

🔼 The figure illustrates the training process of the STEP-KTO method. A math problem is input to a large language model (LLM), which generates a series of reasoning steps and a final answer. The intermediate steps and the final answer are then evaluated by separate reward models: a Process Reward Model (PRM) and an Outcome Reward Model (ORM), respectively. Each model provides binary feedback (correct or incorrect). This binary feedback, along with the input and the LLM’s output, is used to compute a loss function that guides the LLM’s training. The iterative process refines the model’s ability to produce both correct answers and coherent reasoning steps.
read the caption
Figure 1: \method Training Process. Given a dataset of math problems (left), a language model (LLM) produces both reasoning steps and a final answer. Each intermediate reasoning step is evaluated by a process reward model (Process RM), and the final answer is assessed by an outcome reward model (Outcome RM). The binary feedback signals from both levels (outcome-level correctness cosuperscript𝑐𝑜c^{o}italic_c start_POSTSUPERSCRIPT italic_o end_POSTSUPERSCRIPT and stepwise correctness chssubscriptsuperscript𝑐𝑠ℎc^{s}_{h}italic_c start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_h end_POSTSUBSCRIPT) are recorded together with the input (x)𝑥(x)( italic_x ) and the model’s response (y)𝑦(y)( italic_y ) §2.1. These signals are then used to compute the \method loss, guiding the LLM to not only produce correct final answers but also maintain coherent and correct reasoning steps §2.3. Through multiple iterations of this training process §2.4, the model progressively improves both its stepwise reasoning and final answer accuracy.
| 8B Model | Stepwise Errors in Correct Solutions | |
|---|---|---|
| KTO | \method | |
| 27.3% | 27.3% | |
| 24.6% | 22.9% | |
| 22.6% | 20.8% | |
| 21.1% | 19.9% | |
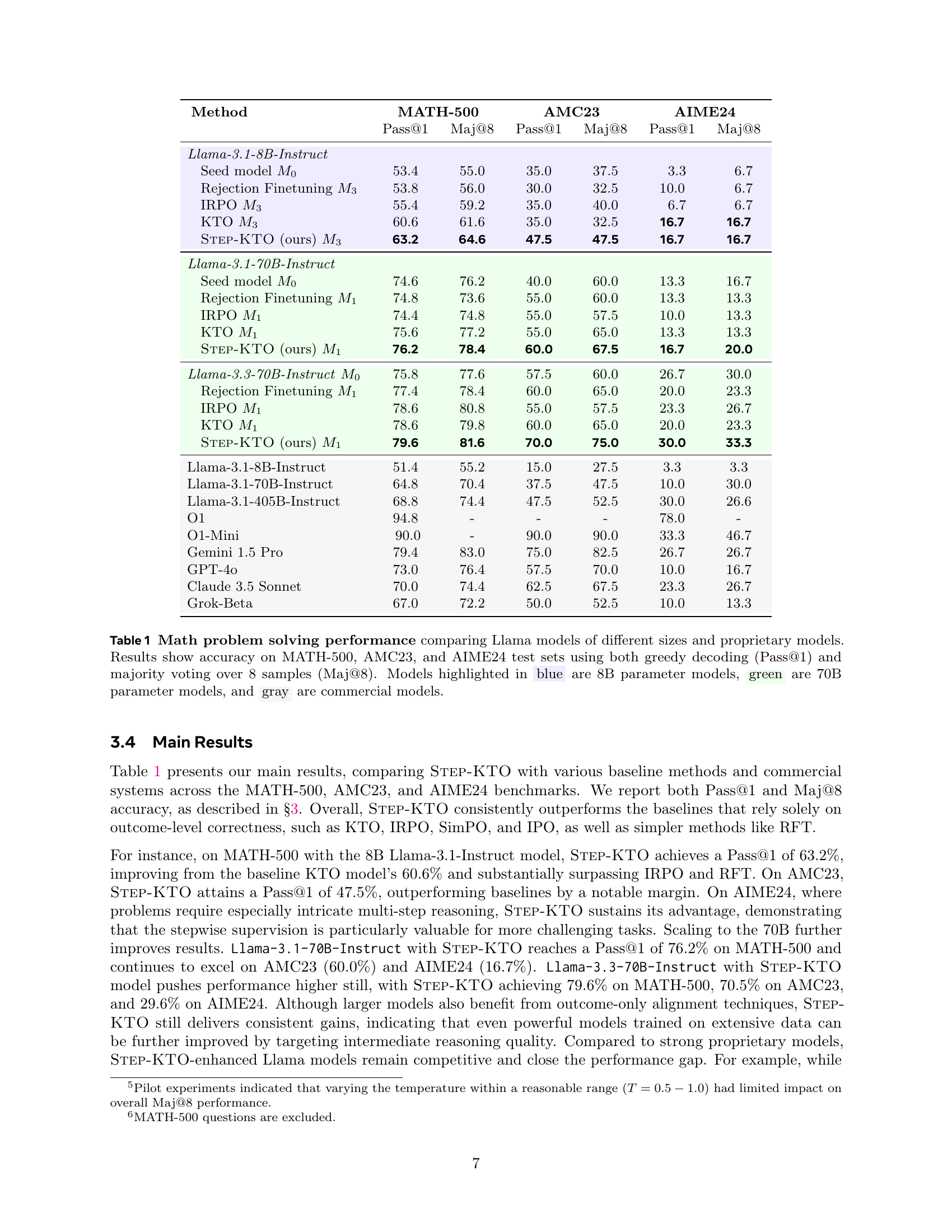
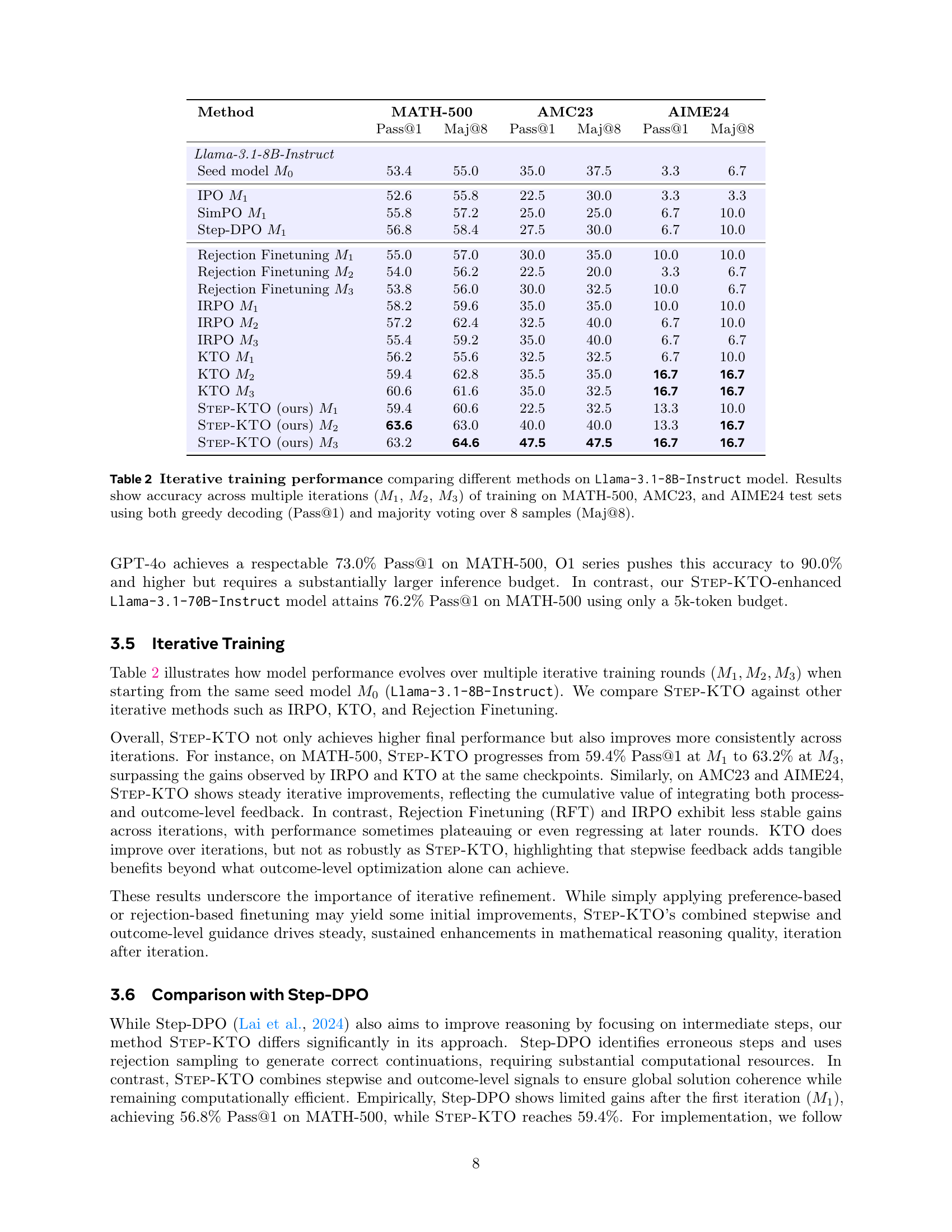
🔼 This table presents the results of math problem-solving experiments using various language models, including different sizes of Llama models and several commercial models. The models’ performance is evaluated on three benchmark datasets: MATH-500, AMC23, and AIME24. The accuracy is measured using two metrics: Pass@1 (the accuracy of a single prediction) and Maj@8 (the accuracy of majority voting among 8 predictions). The table highlights the performance differences between models with varying parameter counts (8B, 70B) and commercially available models. Color-coding is used to distinguish between model sizes: blue for 8B parameter models, green for 70B parameter models, and gray for commercial models.
read the caption
Table 1: Math problem solving performance comparing Llama models of different sizes and proprietary models. Results show accuracy on MATH-500, AMC23, and AIME24 test sets using both greedy decoding (Pass@1) and majority voting over 8 samples (Maj@8). Models highlighted in blue are 8B parameter models, green are 70B parameter models, and gray are commercial models.
Full paper#