TL;DR#
Long-thought reasoning in large language models (LLMs) has shown promising results in problem-solving, but it significantly increases inference time and resource consumption. This is mainly due to length disharmony, where models generate longer reasoning paths than necessary, even when shorter paths can yield accurate solutions. This inefficiency necessitates methods that can improve both accuracy and efficiency.
O1-Pruner tackles this issue by employing a reinforcement learning-based fine-tuning approach. It estimates the LLM’s baseline performance and encourages the model to generate shorter reasoning processes while maintaining accuracy constraints. The method significantly reduces inference overhead and achieves higher accuracy across several mathematical reasoning benchmarks. This shows O1-Pruner’s potential to improve the efficiency of long-thought LLMs while addressing the length disharmony issue. The results demonstrate O1-Pruner’s efficacy in balancing length and accuracy, offering a promising solution for optimizing long-thought reasoning.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical challenge in large language models (LLMs): the high computational cost of long-thought reasoning. By proposing the O1-Pruner method, it offers a novel solution to enhance both the efficiency and accuracy of LLMs, opening up new avenues for research into more efficient and effective LLMs. This is particularly relevant given the increasing computational demands and cost constraints associated with LLMs.
Visual Insights#

🔼 This figure visualizes the relationship between the length of reasoning processes and the accuracy of the model’s predictions on a per-problem basis. For each problem, the model generates multiple solutions of varying lengths. The plot shows that the relationship between length and accuracy is inconsistent across problems. In some cases, the highest accuracy is achieved with short reasoning sequences, while in others, longer sequences are necessary. Importantly, many problems display high accuracy even with short solutions, highlighting the redundancy present in longer reasoning processes.
read the caption
Figure 1: Accuracy-Length Relationship at Instance level. The relationship between length and accuracy varies significantly across problems, with peak accuracy occurring at short, medium, or long intervals. Notably, high accuracy often persists in shorter intervals.
| Model | Interval 1 | Interval 2 | Interval 3 | Interval 4 |
|---|---|---|---|---|
| Marco | 81.1 | 80.2 | 78.8 | 75.3 |
| QwQ | 44.9 | 49.9 | 45.9 | 45.3 |
🔼 This table shows the relationship between the length of generated solutions and their accuracy for two different large language models (Marco and QwQ). The models were given 64 math problems, and for each problem, 512 solutions were generated and grouped into four intervals based on their length (from shortest to longest). The average accuracy within each length interval is presented. The results reveal that, in general, shorter solutions tend to have higher accuracy, suggesting that longer responses are often unnecessarily verbose or contain redundant reasoning steps.
read the caption
Table 1: Accuracy-Length Relationship at Distribution Level. A larger interval number indicates a longer solution length. For both models, the average accuracy is higher when the solution length is short.
In-depth insights#
O1 Reasoning Limits#
The hypothetical heading, ‘O1 Reasoning Limits,’ invites exploration into the inherent constraints within OpenAI’s O1 model and similar long-thought reasoning LLMs. While these models demonstrate enhanced reasoning capabilities exceeding those of conventional LLMs, their performance is bounded by limitations in resource allocation and inference efficiency. The primary constraint is the length disharmony observed, where models often generate excessively lengthy reasoning chains even when concise solutions are feasible. This leads to substantial computational overhead, negating the potential benefits of improved accuracy. Further investigation is needed to understand the root causes of these redundancies, such as the model’s inability to accurately assess problem difficulty and adapt the complexity of its reasoning accordingly. Overcoming this length disharmony is crucial for realizing the full potential of long-thought reasoning, requiring the development of novel techniques to optimize inference efficiency while maintaining accuracy. The efficiency of these models is also dependent on factors such as the size and quality of the training data, highlighting the importance of both model architecture and data curation in determining their ultimate performance limits.
RL Fine-Tuning#
Reinforcement learning (RL) fine-tuning offers a powerful approach to optimize large language models (LLMs) for specific tasks. In the context of long-thought reasoning, where LLMs generate lengthy solution paths, RL can be leveraged to encourage the generation of shorter, more efficient reasoning sequences while maintaining accuracy. A key advantage of RL is its ability to directly optimize for the desired outcome (e.g., shorter length), rather than relying on indirect methods. This is achieved by defining a reward function that penalizes longer solutions and rewards accurate, concise ones. The RL agent learns to balance the trade-off between brevity and accuracy, learning which steps are essential and which are redundant. This approach contrasts with supervised fine-tuning (SFT), which relies on providing many examples of ideal solutions, which can be time-consuming to generate and potentially incomplete. RL’s ability to learn from trial and error makes it particularly suitable for complex reasoning tasks, where optimal solutions are not easily discernible. The challenge lies in designing appropriate reward functions that effectively capture the desired behavior and avoiding reward hacking, which can lead to suboptimal performance. Successfully applying RL necessitates careful consideration of the reward shaping, exploration strategies and handling of sparse rewards, but its potential to improve both efficiency and accuracy of LLMs makes it a promising area of research.
Length Disharmony#
The concept of “Length Disharmony” highlights a crucial inefficiency in long-thought reasoning LLMs. These models, while exhibiting enhanced reasoning capabilities, often generate responses of varying lengths, even when shorter, equally accurate answers exist. This inefficiency stems from the model’s inability to effectively allocate token budgets, leading to redundant computations and increased inference times. Shorter responses are not always inferior; the paper demonstrates that high accuracy can often be achieved with significantly shorter reasoning paths. This observation underscores the need for optimization strategies that encourage concise yet accurate reasoning. Length-Harmonizing Fine-Tuning (O1-Pruner) directly addresses this issue by incentivizing the model to generate shorter solutions while maintaining accuracy, thereby optimizing both efficiency and performance. The existence of length disharmony reveals a fundamental limitation in current long-thought reasoning models and presents a significant opportunity for future research focused on resource-efficient and more human-like reasoning processes.
O1-Pruner Method#
The O1-Pruner method tackles the inefficiency of long-thought reasoning LLMs like OpenAI’s O1 by directly addressing the length disharmony problem. It recognizes that these models often generate excessively long reasoning paths, even when shorter ones would suffice. O1-Pruner employs a reinforcement learning approach, pre-sampling to estimate baseline performance and then fine-tuning the model to produce shorter, yet accurate, solutions. The core innovation lies in formulating a loss function that balances accuracy and length, rewarding shorter solutions while penalizing accuracy loss. This method cleverly avoids overly simplistic solutions by considering problem difficulty and dynamically adapting reasoning length. By combining pre-sampling for baseline estimation with a carefully designed RL-style fine-tuning, O1-Pruner provides a novel and effective means for optimizing inference efficiency in long-thought reasoning LLMs, offering significant improvements in both speed and accuracy. Furthermore, its off-policy training strategy simplifies the training process, enhancing practicality and scalability.
Future Directions#
Future research should focus on several key areas to advance length-harmonizing fine-tuning. Improving the reward function is crucial; exploring alternative reward formulations that better capture the trade-off between accuracy and length could significantly enhance performance. Developing more efficient training methods is also vital, given the computational cost of current approaches. Off-policy methods or techniques leveraging pre-computed information should be investigated. Extending the approach to different reasoning paradigms beyond mathematical problem solving would demonstrate broader applicability and robustness. This could involve adapting the methodology to various tasks, including question answering or commonsense reasoning. Finally, a deeper theoretical understanding of why length disharmony exists in long-thought reasoning models is needed. This understanding could guide the development of more effective solutions to address inference overhead while maintaining accuracy. Investigating the underlying cognitive mechanisms that might parallel this behavior could provide valuable insights.
More visual insights#
More on figures

🔼 Figure 2 illustrates the Length-Harmonizing Fine-Tuning process using the O1-Pruner method. The left panel shows the training phase, where multiple samples are drawn from a reference model for each problem. A sample is then taken from the model being optimized, and a reward is calculated based on the comparison with the reference samples. Reinforcement learning (RL) is used to fine-tune the model. The right panel displays the inference phase, highlighting the significant improvements in both inference speed and accuracy achieved by the O1-Pruner optimized model compared to the original.
read the caption
Figure 2: Length-Harmonizing Fine-Tuning. During the training phase, for each problem, we sample multiple times from the reference model. Subsequently, we sample from the model to be optimized and compute the reward based on the reference samples, followed by a RL-style fine-tuning. During the inference phase, the model optimized through O1-Pruner demonstrates a significant improvement in inference speed, along with a noticeable enhancement in accuracy.

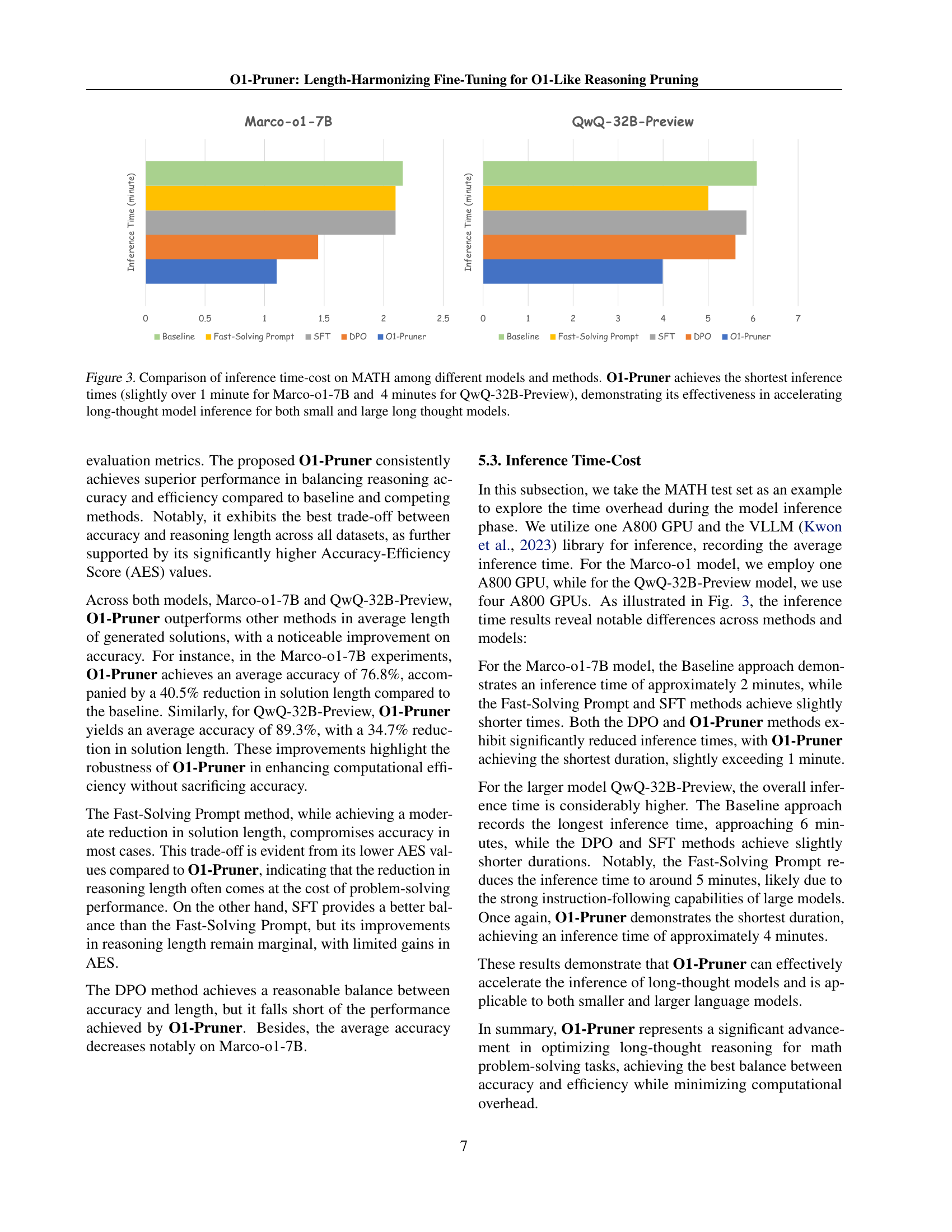
🔼 Figure 3 presents a comparison of inference time costs for different models and methods on the MATH dataset. It shows that the O1-Pruner method significantly reduces inference time compared to baseline models and other optimization methods (Fast-Solving Prompt, SFT, and DPO). Specifically, O1-Pruner achieves inference times of just over 1 minute for the smaller Marco-01-7B model and approximately 4 minutes for the larger QwQ-32B-Preview model. This demonstrates the effectiveness of O1-Pruner in accelerating inference, particularly for large long-thought language models.
read the caption
Figure 3: Comparison of inference time-cost on MATH among different models and methods. O1-Pruner achieves the shortest inference times (slightly over 1 minute for Marco-o1-7B and 4 minutes for QwQ-32B-Preview), demonstrating its effectiveness in accelerating long-thought model inference for both small and large long thought models.

🔼 This figure displays the performance of models trained on subsets of the MATH dataset categorized by difficulty level. The x-axis represents the difficulty level of the training data (e.g., easiest 0-40%, medium 30-70%, hardest 60-100%). The y-axis shows both the average solution length and the average accuracy achieved on the MATH test set by models trained on each difficulty level. The results reveal that models trained on more challenging datasets generate longer solutions, but also achieve higher accuracy on the test set. Conversely, models trained on easier datasets produce shorter solutions without a corresponding increase in accuracy.
read the caption
Figure 4: Performance on MATH Test-set When Trained on Problems of Different Difficulty Levels. Models trained on more challenging datasets tend to generate longer solutions, while learning to solve harder problems enhances model accuracy. In contrast, for less challenging datasets, shorter solutions are produced without a corresponding accuracy improvement.
More on tables
| Model | MATH | GSM8K | GaoKao | AVERAGE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc | Length | AES | Acc | Length | AES | Acc | Length | AES | Acc | Length | AES | |
| Marco-o1-7B | ||||||||||||
| (full fine-tune) | ||||||||||||
| Baseline | 73.8 | 1156 | 0 | 89.2 | 530 | 0 | 57.1 | 1112 | 0 | 73.4 | 932 | 0 |
| Fast-solving Prompt | 71.0 | 1113 | 0.15 | 81.7 | 447 | 0.41 | 57.1 | 1062 | 0.04 | 69.9 | 874 | 0.20 |
| SFT | 73.6 | 1076 | 0.08 | 89.9 | 497 | 0.09 | 56.3 | 1066 | 0.08 | 73.3 | 880 | 0.08 |
| DPO | 71.8 | 761 | 0.42 | 88.6 | 410 | 0.25 | 56.6 | 780 | 0.32 | 72.3 | 650 | 0.33 |
| O1-Pruner | 77.5 | 657 | 0.58 | 91.4 | 343 | 0.43 | 61.6 | 664 | 0.64 | 76.8 | 554 | 0.55 |
| QwQ-32B-Preview | ||||||||||||
| (freeze fine-tune last 48 layers) | ||||||||||||
| Baseline | 90.6 | 2191 | 0 | 95.1 | 777 | 0 | 79.0 | 2183 | 0 | 88.2 | 1717 | 0 |
| Fast-solving Prompt | 90.2 | 1763 | 0.21 | 95.8 | 561 | 0.30 | 78.4 | 1911 | 0.15 | 88.1 | 1411 | 0.22 |
| SFT | 90.4 | 2031 | 0.08 | 95.7 | 717 | 0.10 | 79.5 | 2112 | 0.05 | 88.5 | 1620 | 0.08 |
| DPO | 91.7 | 1999 | 0.12 | 95.3 | 704 | 0.10 | 79.7 | 2021 | 0.10 | 88.9 | 1575 | 0.11 |
| O1-Pruner | 91.0 | 1385 | 0.38 | 96.5 | 534 | 0.36 | 80.3 | 1446 | 0.39 | 89.3 | 1121 | 0.38 |
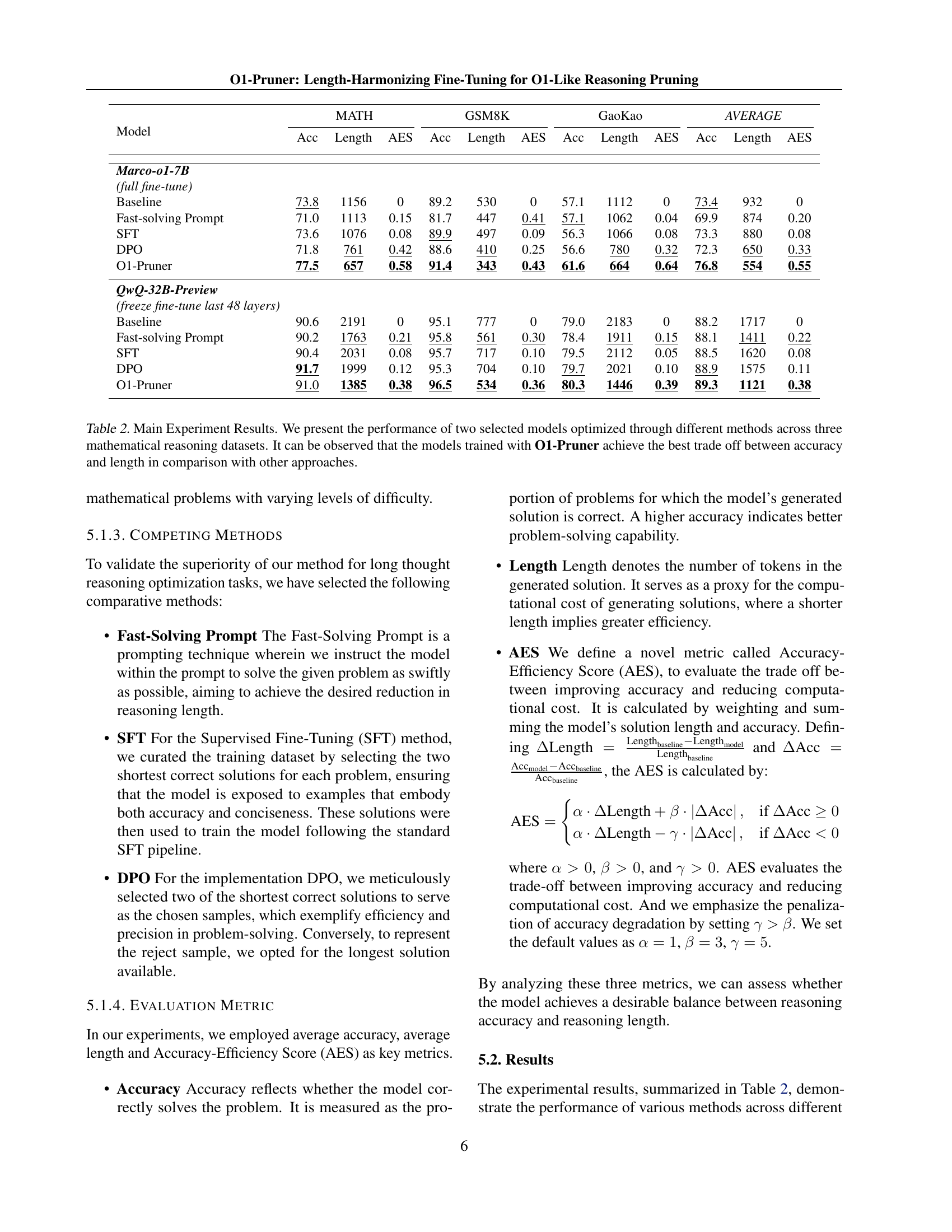
🔼 This table presents the results of experiments comparing different methods for optimizing long-thought reasoning models on three mathematical reasoning datasets. The methods evaluated are Baseline (no optimization), Fast-Solving Prompt, Supervised Fine-Tuning (SFT), Direct Preference Optimization (DPO), and the proposed 01-Pruner. For each method, the table shows the accuracy, average solution length, and Accuracy-Efficiency Score (AES) achieved on the MATH, GSM8K, and GaoKao datasets for two different models: Marco-01-7B and QwQ-32B-Preview. The results demonstrate that O1-Pruner achieves the best balance between accuracy and solution length, outperforming other methods in terms of efficiency and overall performance.
read the caption
Table 2: Main Experiment Results. We present the performance of two selected models optimized through different methods across three mathematical reasoning datasets. It can be observed that the models trained with O1-Pruner achieve the best trade off between accuracy and length in comparison with other approaches.
| Marco-o1-7B | |||
|---|---|---|---|
| 0 | 74.8 | 527 | 0.49 |
| 1 | 76.0 | 532 | 0.54 |
| 2 | 76.8 | 554 | 0.55 |
| 5 | 76.3 | 656 | 0.45 |
🔼 This ablation study investigates the impact of the penalty coefficient (λ) on the model’s performance. The table shows that as λ increases, both the model’s accuracy and the average length of generated solutions also increase. However, λ = 2 represents the optimal balance, providing a good trade-off between accuracy and efficiency.
read the caption
Table 3: Ablation experiments on λ𝜆\lambdaitalic_λ. Overall, the model’s accuracy and solution length increase with the penalty coefficient λ𝜆\lambdaitalic_λ. λ𝜆\lambdaitalic_λ = 2 achieves an optimal balance between accuracy and efficiency.
Full paper#