TL;DR#
Current test-time scaling methods for Large Language Models (LLMs) often rely on reward models that assign scores to individual solutions. However, these scores can be arbitrary and inconsistent, hindering accurate selection of the best solution. This inconsistency significantly impacts the performance of Best-of-N (BON) sampling, a common strategy to improve LLM outputs.
The proposed Pairwise Reward Model (Pairwise RM) tackles this issue by directly comparing pairs of solutions instead of assigning individual scores. It determines which solution is better based on a defined criterion (e.g., correctness). To perform BoN sampling, it employs a knockout tournament, iteratively comparing solution pairs and eliminating inferior ones until only the best solution remains. The evaluation on a large dataset shows that Pairwise RM and its knockout tournament significantly improve BON sampling performance, especially for difficult problems, surpassing traditional methods.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical limitation in large language model (LLM) evaluation, particularly in the context of test-time scaling. By introducing Pairwise RM and the knockout tournament, it offers a more robust and accurate approach for selecting the best among multiple LLM-generated solutions. This method is significant to researchers working on LLM evaluation, ranking, and test-time scaling strategies. It also opens up avenues for developing improved reward models and other LLM evaluation metrics that focus on relative correctness rather than absolute scores.
Visual Insights#

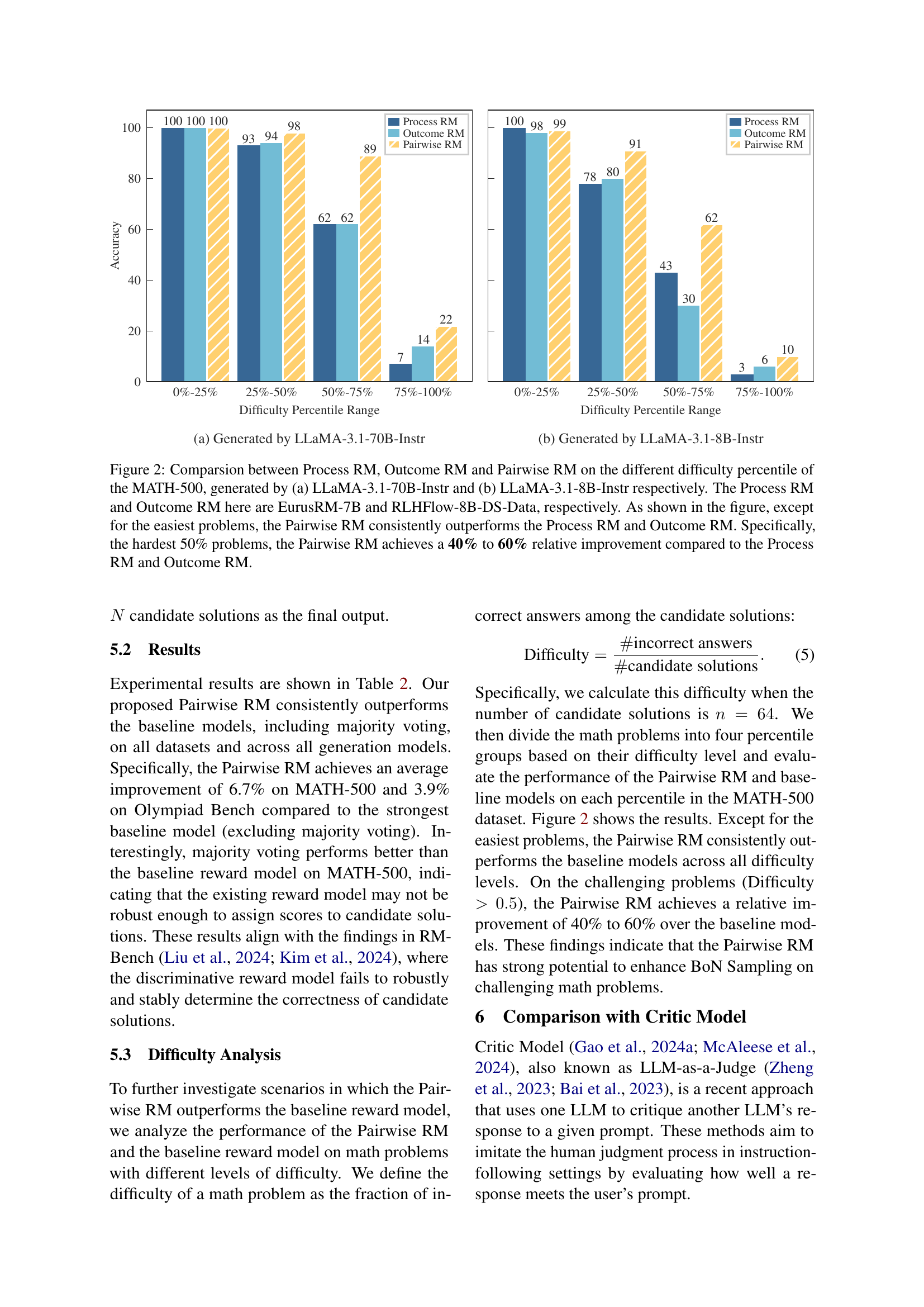
🔼 The figure illustrates the Pairwise Reward Model (Pairwise RM) within a knockout tournament framework for best-of-N sampling. A math problem and two candidate solutions are input. The Pairwise RM compares them, determining correctness. Incorrect solutions are eliminated iteratively until only one remains, which is deemed the best solution. The example shows the process, highlighting how pairwise comparisons lead to the elimination of an incorrect response.
read the caption
Figure 1: An example of the knockout tournament with the Pairwise RM. Pairwise RM takes one question and two responses as the input prompt, and outputs the pairwise comparison results to determine the correctness of the responses. The Pairwise RM correctly identifies the first response as correct and the second response as incorrect, leading to the elimination of the second response. Such pairwise comparisons iteratively proceed in the knockout tournament until only one response remains. The final response is selected as the best candidate solution.
| Input |
| Prompt |
🔼 This table presents a quantitative analysis of dataset sizes before and after data cleaning and filtering. It shows the original number of data points in various datasets used in the paper, along with the count after filtering out low-quality data, multiple-choice questions, and proof-based problems. The significant reduction in AMC-related datasets after filtering highlights the prevalence of multiple-choice questions in these datasets, which were removed as part of the data cleaning process.
read the caption
Table 1: Statistics of the datasets before and after filtering. AMC-related datasets shrink significantly because most AMC tasks are multiple-choice.
In-depth insights#
Pairwise RM: BON#
The proposed Pairwise Reward Model (Pairwise RM) for Best-of-N (BON) sampling offers a novel approach to selecting the best candidate solution from multiple LLM generations. Instead of assigning arbitrary scores, Pairwise RM directly compares two candidate solutions, assessing their correctness simultaneously. This eliminates the inherent inconsistencies of traditional reward models and enables efficient cross-validation. The integration with a knockout tournament further streamlines the selection process, iteratively eliminating incorrect solutions until a single best candidate remains. This method’s strength lies in its reliance on parallel comparison, avoiding the need for absolute scoring and reducing reliance on potentially unreliable individual reward model outputs. A large-scale dataset, PAIRWISE-443K, supports the training of this model. While computationally intensive due to the pairwise comparisons, the approach shows significant promise for more robust and reliable BON sampling in complex tasks, particularly those where human evaluation is subjective and inconsistent, as demonstrated by improved results compared to traditional methods on challenging math problems.
Knockout Tourney#
The proposed “Knockout Tournament” method for Best-of-N sampling presents a novel approach to selecting the optimal candidate solution from a set of model-generated options. Instead of relying on potentially arbitrary scoring mechanisms of traditional reward models, it leverages a pairwise comparison strategy. Each comparison, facilitated by a Pairwise Reward Model (PRM), directly determines which solution is superior, eliminating the need for absolute scoring. This iterative process, mimicking a single-elimination tournament structure, efficiently reduces the candidate pool until only the most accurate solution remains. The strength of this approach lies in its inherent robustness against inconsistent reward model scoring. It leverages the power of pairwise comparisons to reduce bias and enhance the reliability of the selection process. However, scalability is a key consideration, especially with large sets of candidate solutions, because of the computational cost of multiple pairwise comparisons. Further exploration into optimal tournament structures and parallelization strategies could address this limitation. The effectiveness of this method, demonstrated through experimentation, opens up exciting avenues in test-time scaling and beyond. The focus on pairwise comparison and its efficient tournament implementation highlights a significant departure from conventional approaches. This method offers a more reliable and robust solution selection process for applications requiring optimal selection under uncertainty.
PAIRWISE-443K Dataset#
The creation of the PAIRWISE-443K dataset is a significant contribution to the field of large language model (LLM) evaluation, particularly within the context of math problem solving. Its large scale (443K pairwise comparisons) addresses a crucial limitation of existing reward models: the inconsistency and arbitrariness of scores assigned to solutions. By focusing on pairwise comparisons, this dataset directly evaluates the relative correctness of two solutions for the same problem, thereby circumventing the difficulties of absolute scoring. This innovative approach is likely to lead to more robust and reliable reward models that are better suited to the intricacies of nuanced math problem solving. The use of NumiaMath as the source of problems and gemini-1.5-flash for annotation ensures a high-quality dataset that is representative of real-world mathematical reasoning challenges. The detailed description of the dataset’s construction pipeline is essential for reproducibility and facilitates the development of more sophisticated evaluation methods in the future. The resulting dataset is expected to be a valuable resource for researchers working to improve LLMs’ mathematical reasoning abilities and should advance the state-of-the-art in best-of-N sampling and other related areas.
BoN Sampling: Limits#
Best-of-N (BoN) sampling, while a powerful technique for improving LLM performance, has inherent limitations. Computational cost is a major factor; generating and evaluating multiple candidate solutions significantly increases inference time, hindering real-time applications. Reward model reliability is another crucial limitation. Inaccuracies or inconsistencies in the reward model’s scoring can lead to suboptimal selection of candidate solutions, negating the benefits of BoN. The effectiveness of BoN is also heavily dependent on the quality and diversity of generated candidates; a weak LLM will produce poor candidates regardless of the sampling strategy. Finally, data limitations affect reward model training and evaluation, especially the lack of high-quality, diverse data for nuanced evaluation of generated text, directly impacting BoN’s ability to consistently select superior outputs. Addressing these limits is key to unlocking BoN’s full potential.
Future Work: RL#
The heading ‘Future Work: RL’ suggests a promising direction for extending the research presented in the paper. It indicates a plan to explore how the Pairwise Reward Model (and its knockout tournament) can be integrated into a reinforcement learning (RL) framework. This is significant because current RL applications often struggle with the effective evaluation of diverse solutions, a problem directly addressed by the Pairwise RM’s ability to compare candidates simultaneously, rather than assigning arbitrary scores. The integration into RL would allow the algorithm to learn a policy that leverages these pairwise comparisons, potentially leading to more efficient and robust training of RL agents. This approach could be particularly beneficial for complex tasks involving multiple steps, where the ability to discriminate between subtly different solutions is crucial. The success of this future work would depend on effectively defining appropriate reward signals within the RL framework, making judicious choices for RL algorithms, and assessing the resulting performance improvements compared to traditional methods. Furthermore, thorough investigation of scalability will be important, as pairwise comparisons can become computationally expensive as the number of solutions grows. Addressing these challenges will be key to unlocking the full potential of the proposed method within RL applications.
More visual insights#
More on tables
| Pairwise |
| Comparison |
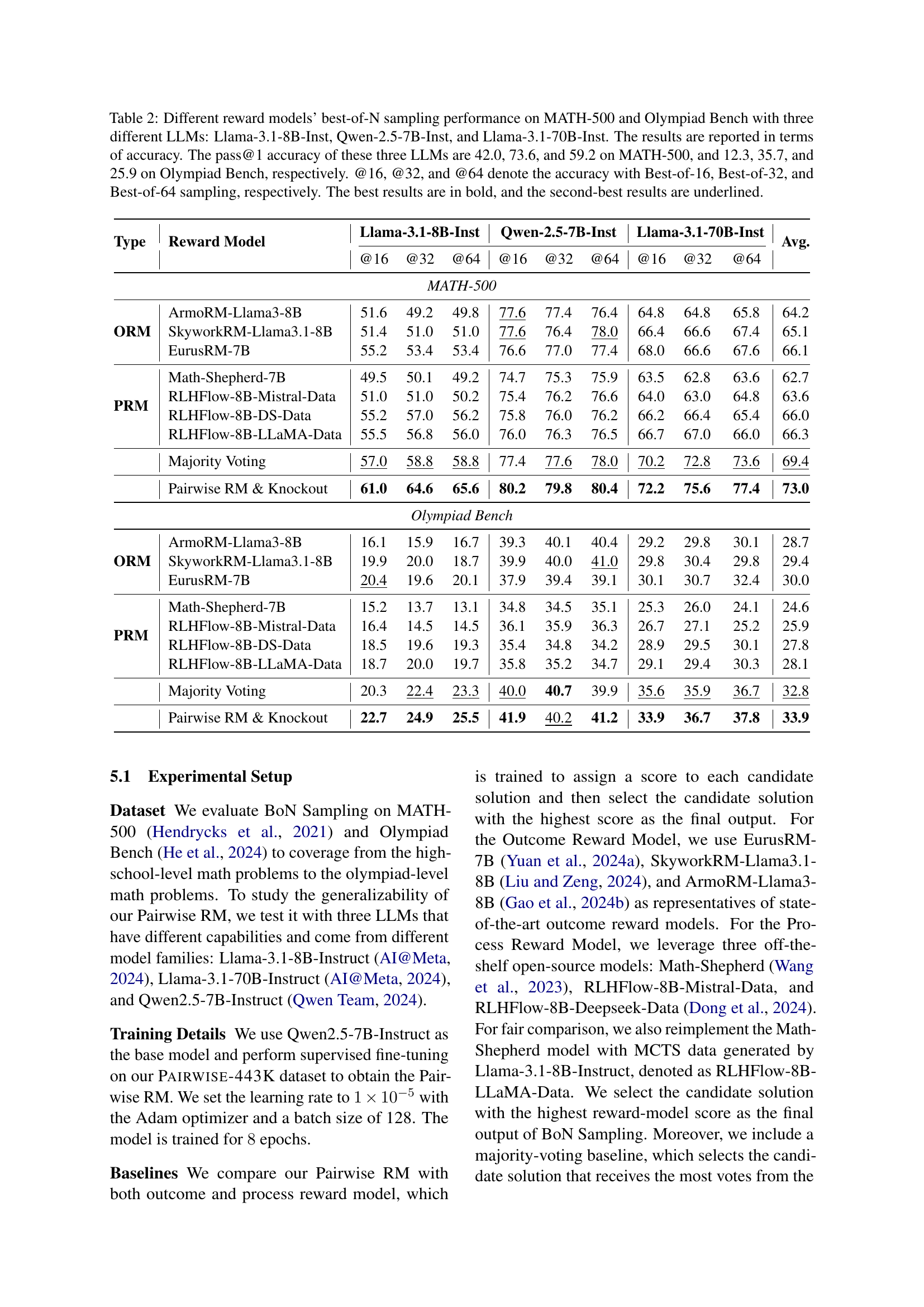
🔼 This table presents a comparison of various reward models’ performance in best-of-N sampling on two benchmark datasets: MATH-500 and Olympiad Bench. Three different large language models (LLMs) were used: Llama-3.1-8B-Inst, Qwen-2.5-7B-Inst, and Llama-3.1-70B-Inst. The table shows the accuracy of each reward model for different best-of-N sampling strategies (best-of-16, best-of-32, and best-of-64). The pass@1 accuracy (accuracy of selecting the single best solution from the initial set) for each LLM on each dataset is also provided for context. The best and second-best results for each scenario are highlighted in bold and underlined, respectively.
read the caption
Table 2: Different reward models’ best-of-N sampling performance on MATH-500 and Olympiad Bench with three different LLMs: Llama-3.1-8B-Inst, Qwen-2.5-7B-Inst, and Llama-3.1-70B-Inst. The results are reported in terms of accuracy. The pass@1 accuracy of these three LLMs are 42.0, 73.6, and 59.2 on MATH-500, and 12.3, 35.7, and 25.9 on Olympiad Bench, respectively. @16, @32, and @64 denote the accuracy with Best-of-16, Best-of-32, and Best-of-64 sampling, respectively. The best results are in bold, and the second-best results are underlined.
| Dataset | Original Count | Filtered Count |
| AMC/AIME | 4,070 | 289 |
| AoPS Forum | 30,192 | 9,017 |
| Chinese K-12 | 276,554 | 63,779 |
| GSM8K | 7,342 | 6,539 |
| Math | 7,477 | 5,988 |
| Olympiads | 150,563 | 52,766 |
| ORCA Math | 153,314 | 149,550 |
| Synthetic AMC | 62,108 | 94 |
| Synthetic Math | 167,874 | 136,921 |
| Total | 859,494 | 425,943 |
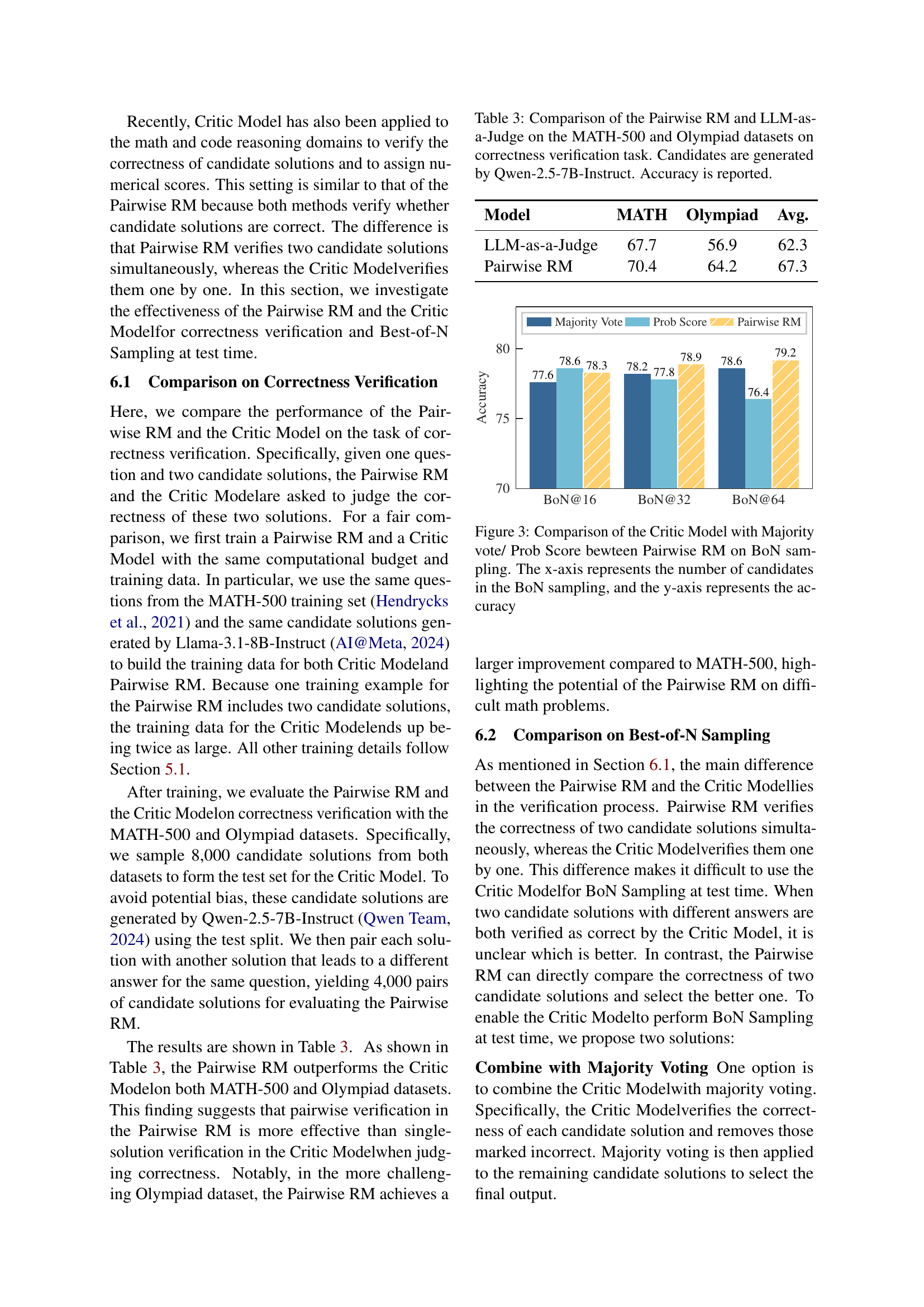
🔼 This table presents a comparison of the Pairwise Reward Model (Pairwise RM) and the LLM-as-a-Judge model’s performance on correctness verification tasks. The models were evaluated on the MATH-500 and Olympiad datasets, using candidate solutions generated by the Qwen-2.5-7B-Instruct language model. The table reports the accuracy of each model on both datasets.
read the caption
Table 3: Comparison of the Pairwise RM and LLM-as-a-Judge on the MATH-500 and Olympiad datasets on correctness verification task. Candidates are generated by Qwen-2.5-7B-Instruct. Accuracy is reported.
| Type | Reward Model | Llama-3.1-8B-Inst | Qwen-2.5-7B-Inst | Llama-3.1-70B-Inst | Avg. | ||||||
| @16 | @32 | @64 | @16 | @32 | @64 | @16 | @32 | @64 | |||
| MATH-500 | |||||||||||
| ORM | ArmoRM-Llama3-8B | 51.6 | 49.2 | 49.8 | 77.6 | 77.4 | 76.4 | 64.8 | 64.8 | 65.8 | 64.2 |
| SkyworkRM-Llama3.1-8B | 51.4 | 51.0 | 51.0 | 77.6 | 76.4 | 78.0 | 66.4 | 66.6 | 67.4 | 65.1 | |
| EurusRM-7B | 55.2 | 53.4 | 53.4 | 76.6 | 77.0 | 77.4 | 68.0 | 66.6 | 67.6 | 66.1 | |
| PRM | Math-Shepherd-7B | 49.5 | 50.1 | 49.2 | 74.7 | 75.3 | 75.9 | 63.5 | 62.8 | 63.6 | 62.7 |
| RLHFlow-8B-Mistral-Data | 51.0 | 51.0 | 50.2 | 75.4 | 76.2 | 76.6 | 64.0 | 63.0 | 64.8 | 63.6 | |
| RLHFlow-8B-DS-Data | 55.2 | 57.0 | 56.2 | 75.8 | 76.0 | 76.2 | 66.2 | 66.4 | 65.4 | 66.0 | |
| RLHFlow-8B-LLaMA-Data | 55.5 | 56.8 | 56.0 | 76.0 | 76.3 | 76.5 | 66.7 | 67.0 | 66.0 | 66.3 | |
| Majority Voting | 57.0 | 58.8 | 58.8 | 77.4 | 77.6 | 78.0 | 70.2 | 72.8 | 73.6 | 69.4 | |
| Pairwise RM & Knockout | 61.0 | 64.6 | 65.6 | 80.2 | 79.8 | 80.4 | 72.2 | 75.6 | 77.4 | 73.0 | |
| Olympiad Bench | |||||||||||
| ORM | ArmoRM-Llama3-8B | 16.1 | 15.9 | 16.7 | 39.3 | 40.1 | 40.4 | 29.2 | 29.8 | 30.1 | 28.7 |
| SkyworkRM-Llama3.1-8B | 19.9 | 20.0 | 18.7 | 39.9 | 40.0 | 41.0 | 29.8 | 30.4 | 29.8 | 29.4 | |
| EurusRM-7B | 20.4 | 19.6 | 20.1 | 37.9 | 39.4 | 39.1 | 30.1 | 30.7 | 32.4 | 30.0 | |
| PRM | Math-Shepherd-7B | 15.2 | 13.7 | 13.1 | 34.8 | 34.5 | 35.1 | 25.3 | 26.0 | 24.1 | 24.6 |
| RLHFlow-8B-Mistral-Data | 16.4 | 14.5 | 14.5 | 36.1 | 35.9 | 36.3 | 26.7 | 27.1 | 25.2 | 25.9 | |
| RLHFlow-8B-DS-Data | 18.5 | 19.6 | 19.3 | 35.4 | 34.8 | 34.2 | 28.9 | 29.5 | 30.1 | 27.8 | |
| RLHFlow-8B-LLaMA-Data | 18.7 | 20.0 | 19.7 | 35.8 | 35.2 | 34.7 | 29.1 | 29.4 | 30.3 | 28.1 | |
| Majority Voting | 20.3 | 22.4 | 23.3 | 40.0 | 40.7 | 39.9 | 35.6 | 35.9 | 36.7 | 32.8 | |
| Pairwise RM & Knockout | 22.7 | 24.9 | 25.5 | 41.9 | 40.2 | 41.2 | 33.9 | 36.7 | 37.8 | 33.9 | |
🔼 This table presents the prompt template used for the Pairwise Reward Model (Pairwise RM). The template guides the model to evaluate the correctness of two responses (Response A and Response B) to a given math question. It instructs the model to perform a step-by-step verification of each response, checking for mathematical accuracy, logical consistency, and completeness. Finally, the model provides a correctness judgment for each response, indicating whether each answer is ‘Correct’ or ‘Incorrect’. Additional tips are included in the template to help the model validate the responses accurately.
read the caption
Table 4: Prompt Template for Pairwise RM, the {question}, {response_a}, and {response_b} are placeholders for the math question, response A, and response B, respectively.
| Model | MATH | Olympiad | Avg. |
| LLM-as-a-Judge | 67.7 | 56.9 | 62.3 |
| Pairwise RM | 70.4 | 64.2 | 67.3 |
🔼 This table details the criteria used to filter the NumiaMath dataset before creating the PAIRWISE-443K dataset. Filtering was necessary to remove data that was low-quality, contained proof-based questions, or included multiple-choice questions. The table lists several filter types (Bad Quality Problems, Equations in Ground Truth, Multiple Questions, Yes/No Questions, Text Answers, Proof Problems, and Multiple Choice Questions) and the specific criteria that were used to identify and remove those types of problems from the dataset.
read the caption
Table 5: Filtering criteria applied to the dataset to remove low-quality, proof-based, or multiple-choice problems.
Full paper#