TL;DR#
Mixture-of-Expert (MoE) models, while effective, suffer from a critical flaw: the separation of routing decisions from expert execution. This leads to suboptimal expert selection and inefficient learning. The router’s inability to directly assess expert capabilities results in mismatches and hinders effective training. This paper proposes a solution by giving experts autonomy.
The proposed Autonomy-of-Experts (AoE) approach removes the router entirely. Instead, experts independently evaluate their capacity to process each input based on internal activations. Only the top-performing experts are activated, reducing computational overhead through a low-rank weight factorization. Experiments on language models demonstrate that AoE significantly outperforms traditional MoE models with comparable efficiency, showcasing improvements in expert selection and effective learning.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a critical limitation in Mixture-of-Experts (MoE) models, a prominent technique in large language models. By introducing the Autonomy-of-Experts (AoE) model, it significantly improves efficiency and performance. This research is relevant to current trends in efficient and powerful large language model development and opens avenues for investigating self-regulating model architectures and improving expert selection methods.
Visual Insights#
| Node for Norm Calculation | MMLU (5-shot) | ARC-C (5-shot) | ||
| Mixtral B | Phi-3.5-MoE-ins. | Mixtral B | Phi-3.5-MoE-ins. | |
| 64.23 (42.70) | 29.43 (33.05) | 50.43 (4.40) | 28.84 (3.47) | |
| 62.06 (42.73) | 34.60 (33.05) | 53.41 (4.40) | 40.36 (3.47) | |
| 61.71 (43.88) | 38.03 (34.32) | 58.79 (4.51) | 47.53 (3.60) | |
| 66.64 (75.53) | 27.89 (52.60) | 58.79 (6.27) | 35.32 (5.42) | |
| Experts’ Final Outputs | 66.66 (76.15) | 29.69 (69.20) | 58.62 (7.42) | 36.35 (7.07) |
| Performance w. Router | 70.35 (24.30) | 78.20 (14.53) | 62.12 (2.50) | 67.41 (1.60) |
🔼 This table presents a preliminary experiment evaluating the feasibility of removing routers from pre-trained Mixture-of-Experts (MoE) Large Language Models (LLMs). Experts are selected during inference based solely on the internal activation norms of specific nodes within the model’s computational graph, without any parameter updates. The results demonstrate the accuracy achieved on two challenging tasks (MMLU and ARC-C) using this simplified method. Time costs (in minutes) are reported for processing on 8×A800-80G GPUs. The analysis shows that while accuracy is partially maintained, the efficiency is significantly suboptimal, indicating a need for optimization.
read the caption
Table 1: We remove routers from pre-trained MoE-LLMs and select experts during inference based on the internal activation norms of specific nodes in the computational graph. The accuracy on two challenging tasks is reported, along with the time cost (in minutes) for 8×A800-80G GPUs, which is given in parentheses. Without parameter updates, we can largely preserve accuracy under certain nodes, but this rudimentary approach requires significant improvements in efficiency.
In-depth insights#
AoE: Expert Autonomy#
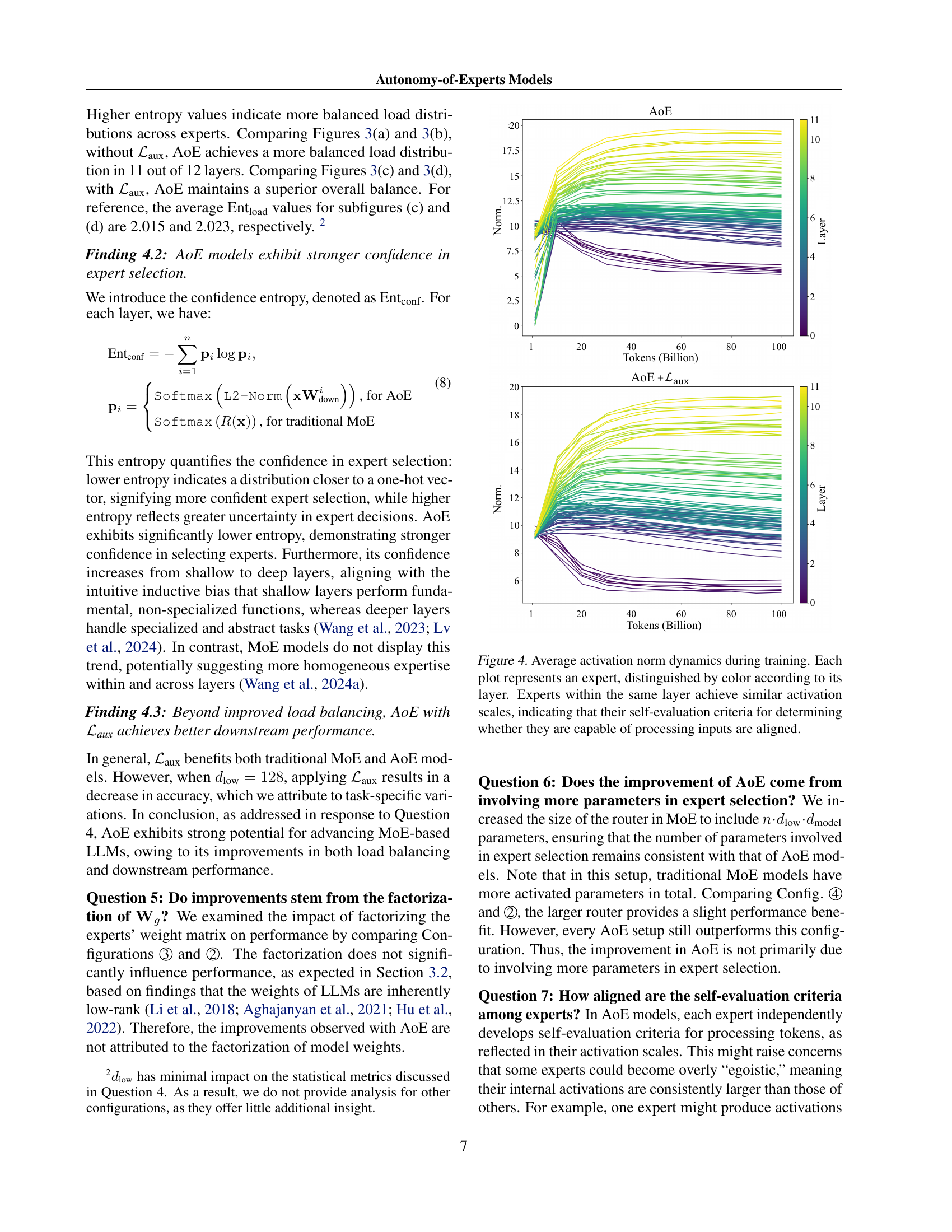
The concept of “AoE: Expert Autonomy” introduces a paradigm shift in Mixture-of-Experts (MoE) models. Traditional MoEs rely on a router to assign inputs to experts, leading to suboptimal expert selection and inefficient learning. AoE empowers experts with the ability to self-select based on their internal activation norms, eliminating the need for a router and improving efficiency. This self-evaluation mechanism allows experts to determine their suitability for a given input, thus ensuring that only the most appropriate experts process it, improving accuracy. The removal of the router also simplifies the model architecture and training process. While the initial implementation may introduce computational overhead due to pre-computed activations, techniques like low-rank weight factorization mitigate this issue. The resulting model demonstrates superior performance and comparable efficiency compared to traditional MoEs. The core idea is that experts implicitly ‘know’ what they know best, leading to a more intuitive and potentially more powerful approach to large-scale language modeling.
Low-Rank Factorization#
Low-rank factorization is a crucial technique in the paper for improving the efficiency of the Autonomy-of-Experts (AoE) model. By decomposing the weight matrices into smaller, low-rank matrices, the authors significantly reduce the computational cost and memory footprint of their approach. This is particularly important in large language models where the sheer number of parameters can be overwhelming. The factorization enables efficient caching of intermediate activations, as experts only need to store and process low-dimensional representations. This reduces the redundancy inherent in the original method, allowing the model to process inputs more efficiently while achieving comparable performance. The low-rank approximation acts as a form of dimensionality reduction, enabling the model to effectively capture relevant information while minimizing storage needs and computational overhead. This is a key innovation for scaling MoE models to larger sizes, enhancing both training and inference speed, making the overall model more practical and efficient.
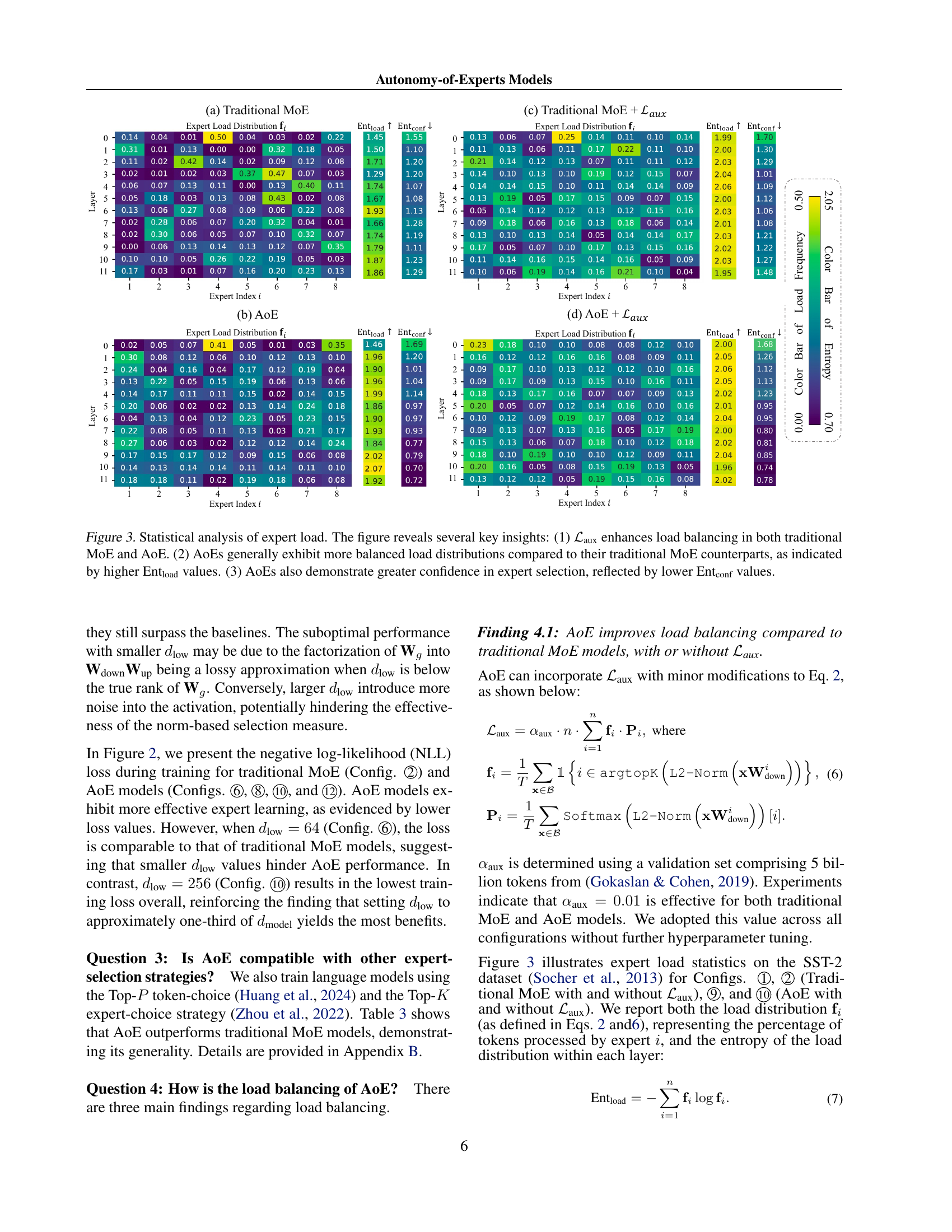
Expert Load Balancing#
Expert load balancing in Mixture-of-Experts (MoE) models is crucial for efficiency and performance. Uneven distribution of tasks among expert networks leads to underutilization of some experts and overloading of others, hindering overall model efficiency. Techniques like adding a load balancing loss function aim to address this by penalizing imbalanced expert usage during training. However, simply balancing the load doesn’t guarantee optimal performance. The choice of routing mechanism significantly influences load distribution; a poorly designed router can still lead to imbalances despite a load balancing loss. Autonomy-of-Experts (AoE) models offer an alternative approach, where experts autonomously select themselves based on their internal activation norms, potentially leading to improved load balancing and more effective knowledge utilization. Further research should explore the interplay between routing strategies, loss functions, and the inherent properties of different model architectures to achieve truly balanced and efficient MoE systems.
Efficiency Tradeoffs#
The concept of ‘Efficiency Tradeoffs’ in large language models (LLMs) is crucial. Balancing computational cost against performance gains is a central challenge. Mixture-of-Experts (MoE) models, while offering potential efficiency through sparsity, introduce complexities. Routing mechanisms, which decide which expert handles which input, can be computationally expensive and may lead to suboptimal expert usage, thus negating some efficiency benefits. Autonomy-of-Experts (AoE) models attempt to address this by letting experts self-select, reducing routing overhead. However, AoE introduces its own tradeoffs. Pre-computing activations for all experts before selection adds computational cost, although this is mitigated by low-rank weight factorization. The optimal balance depends on factors like the number of experts, the dimensionality of the activation vectors, and the specific task. Careful consideration of these tradeoffs is essential for designing efficient and effective LLMs; it’s not simply a choice between dense and sparse, but a nuanced optimization problem.
Future of AoE Models#
The “Future of AoE Models” section would explore several promising avenues. Extending AoE to other modalities beyond language is crucial; its self-selecting mechanism could prove highly effective in vision or multi-modal tasks. Improving efficiency is paramount; research into more efficient low-rank factorization techniques or alternative activation norm calculations could drastically reduce computational costs. Incorporating better load balancing strategies remains a key challenge. While AoE exhibits better balance than traditional MoE, further refinement of load-balancing loss functions or dynamic expert allocation could lead to significant gains. Exploration of different architectural choices within the AoE framework, such as varying the depth or width of expert networks, or integrating different expert types, could improve model performance and generalization. Finally, a critical area of future work involves detailed theoretical analysis. This could help determine the optimal conditions for AoE to outperform traditional methods, leading to more informed model design choices.
More visual insights#
More on tables
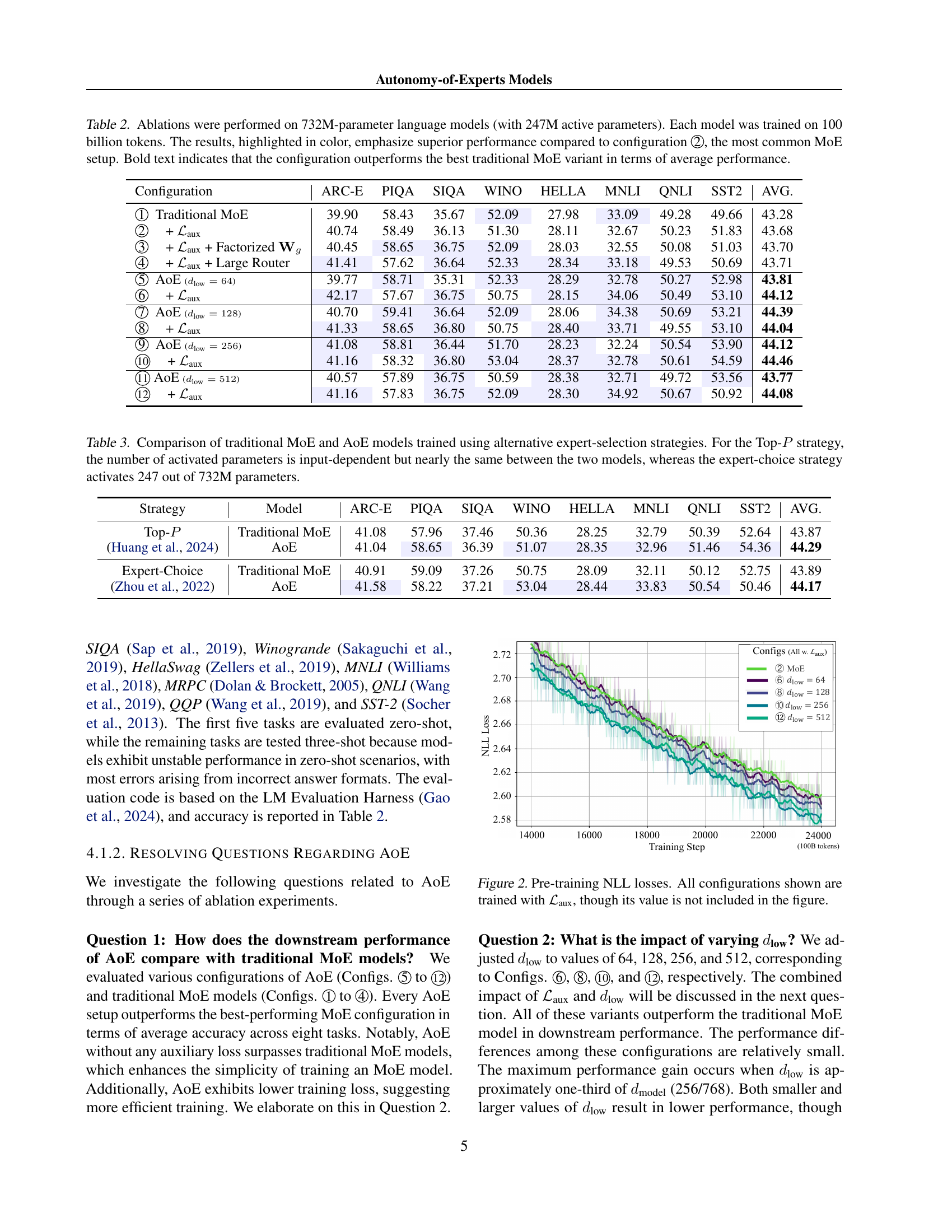
| Configuration | ARC-E | PIQA | SIQA | WINO | HELLA | MNLI | QNLI | SST2 | AVG. |
| Traditional MoE | 39.90 | 58.43 | 35.67 | 52.09 | 27.98 | 33.09 | 49.28 | 49.66 | 43.28 |
| + | 40.74 | 58.49 | 36.13 | 51.30 | 28.11 | 32.67 | 50.23 | 51.83 | 43.68 |
| + + Factorized | 40.45 | 58.65 | 36.75 | 52.09 | 28.03 | 32.55 | 50.08 | 51.03 | 43.70 |
| + + Large Router | 41.41 | 57.62 | 36.64 | 52.33 | 28.34 | 33.18 | 49.53 | 50.69 | 43.71 |
| AoE () | 39.77 | 58.71 | 35.31 | 52.33 | 28.29 | 32.78 | 50.27 | 52.98 | 43.81 |
| + | 42.17 | 57.67 | 36.75 | 50.75 | 28.15 | 34.06 | 50.49 | 53.10 | 44.12 |
| AoE () | 40.70 | 59.41 | 36.64 | 52.09 | 28.06 | 34.38 | 50.69 | 53.21 | 44.39 |
| + | 41.33 | 58.65 | 36.80 | 50.75 | 28.40 | 33.71 | 49.55 | 53.10 | 44.04 |
| AoE () | 41.08 | 58.81 | 36.44 | 51.70 | 28.23 | 32.24 | 50.54 | 53.90 | 44.12 |
| + | 41.16 | 58.32 | 36.80 | 53.04 | 28.37 | 32.78 | 50.61 | 54.59 | 44.46 |
| AoE () | 40.57 | 57.89 | 36.75 | 50.59 | 28.38 | 32.71 | 49.72 | 53.56 | 43.77 |
| + | 41.16 | 57.83 | 36.75 | 52.09 | 28.30 | 34.92 | 50.67 | 50.92 | 44.08 |
🔼 This table presents ablation study results on 732M-parameter language models (using 247M active parameters), trained on 100 billion tokens. Different model configurations are compared, including variations of traditional Mixture-of-Experts (MoE) models and the proposed Autonomy-of-Experts (AoE) method. The results, highlighted in color, show the superior performance of the AoE configurations compared to the standard MoE setup (Configuration 2). Bold text indicates that a specific configuration surpasses the best-performing traditional MoE model in terms of average performance across several downstream tasks. The table helps demonstrate the effectiveness of the proposed AoE method compared to conventional MoE.
read the caption
Table 2: Ablations were performed on 732M-parameter language models (with 247M active parameters). Each model was trained on 100 billion tokens. The results, highlighted in color, emphasize superior performance compared to configuration 2, the most common MoE setup. Bold text indicates that the configuration outperforms the best traditional MoE variant in terms of average performance.
| Strategy | Model | ARC-E | PIQA | SIQA | WINO | HELLA | MNLI | QNLI | SST2 | AVG. |
| Top- | Traditional MoE | 41.08 | 57.96 | 37.46 | 50.36 | 28.25 | 32.79 | 50.39 | 52.64 | 43.87 |
| (Huang et al., 2024) | AoE | 41.04 | 58.65 | 36.39 | 51.07 | 28.35 | 32.96 | 51.46 | 54.36 | 44.29 |
| Expert-Choice | Traditional MoE | 40.91 | 59.09 | 37.26 | 50.75 | 28.09 | 32.11 | 50.12 | 52.75 | 43.89 |
| (Zhou et al., 2022) | AoE | 41.58 | 58.22 | 37.21 | 53.04 | 28.44 | 33.83 | 50.54 | 50.46 | 44.17 |
🔼 Table 3 presents a comparative analysis of traditional Mixture-of-Experts (MoE) and Autonomy-of-Experts (AoE) models, trained using different expert selection strategies. The comparison focuses on performance across various downstream tasks. Two strategies are compared: Top-P, where the number of activated parameters is dynamic and depends on the input data but remains roughly equivalent between MoE and AoE, and expert-choice, where a fixed subset of parameters (247 out of 732 million) is activated. This allows for evaluation of AoE’s effectiveness across differing selection methods.
read the caption
Table 3: Comparison of traditional MoE and AoE models trained using alternative expert-selection strategies. For the Top‑P𝑃Pitalic_P strategy, the number of activated parameters is input-dependent but nearly the same between the two models, whereas the expert-choice strategy activates 247 out of 732M parameters.
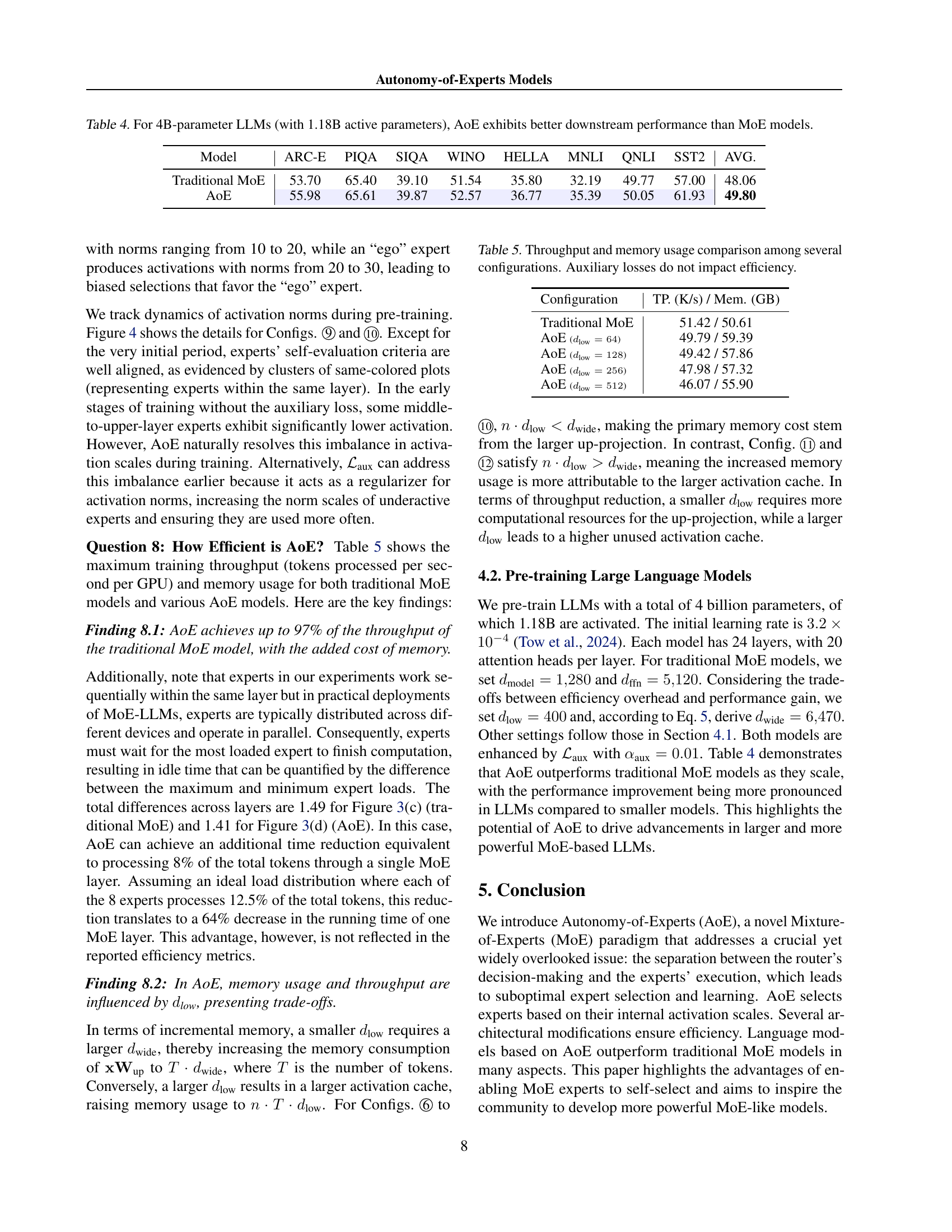
| Model | ARC-E | PIQA | SIQA | WINO | HELLA | MNLI | QNLI | SST2 | AVG. |
| Traditional MoE | 53.70 | 65.40 | 39.10 | 51.54 | 35.80 | 32.19 | 49.77 | 57.00 | 48.06 |
| AoE | 55.98 | 65.61 | 39.87 | 52.57 | 36.77 | 35.39 | 50.05 | 61.93 | 49.80 |
🔼 This table presents the results of downstream performance evaluations for 4-billion parameter Large Language Models (LLMs). Two model architectures are compared: a traditional Mixture-of-Experts (MoE) model and the proposed Autonomy-of-Experts (AoE) model. Both models utilize 1.18 billion active parameters. The table shows the accuracy scores achieved by each model on eight different downstream tasks, including ARC-E, PIQA, SIQA, WINO, HELLA, MNLI, QNLI, and SST2. The average accuracy across these tasks is also provided, demonstrating the superior performance of the AoE model.
read the caption
Table 4: For 4B-parameter LLMs (with 1.18B active parameters), AoE exhibits better downstream performance than MoE models.
| Configuration | TP. (K/s) / Mem. (GB) |
| Traditional MoE | 51.42 / 50.61 |
| AoE () | 49.79 / 59.39 |
| AoE () | 49.42 / 57.86 |
| AoE () | 47.98 / 57.32 |
| AoE () | 46.07 / 55.90 |
🔼 Table 5 presents a detailed comparison of the throughput (tokens processed per second per GPU) and memory usage (in gigabytes) for various model configurations. The configurations include traditional Mixture-of-Experts (MoE) models and several variants of the proposed Autonomy-of-Experts (AoE) models with different values for the hyperparameter
dlow. The table demonstrates the trade-offs between efficiency and model performance associated with different AoE configurations. It also highlights that the auxiliary loss used for load balancing does not significantly affect the computational efficiency.read the caption
Table 5: Throughput and memory usage comparison among several configurations. Auxiliary losses do not impact efficiency.
| Node for Norm Calculation | MMLU (5-shot) | ARC-C (5-shot) | ||
| Mixtral B | Phi-3.5-MoE-ins. | Mixtral B | Phi-3.5-MoE-ins. | |
| 51.14 | 24.15 | 41.98 | 29.01 | |
| 39.79 | 35.87 | 40.19 | 36.35 | |
| 47.29 | 26.37 | 45.73 | 36.09 | |
| 54.37 | 26.95 | 50.09 | 33.79 | |
| Experts’ Final Outputs | 57.84 | 26.56 | 52.73 | 31.31 |
| Performance w. Router | 70.35 | 78.20 | 62.12 | 67.41 |
🔼 This table presents the results of a preliminary study on pre-trained Mixture-of-Experts (MoE) Large Language Models (LLMs). The goal was to assess the effectiveness of using the L1 norm of internal activations to autonomously select experts for processing inputs. The table shows the performance (measured by MMLU and ARC-C scores) achieved when using different nodes within the computational graph to calculate the L1 norm for expert selection. Different pre-trained models (Mixtral 8x7B and Phi-3.5-MoE-ins.) are included in the study. A comparison with the performance achieved when using a standard router is also provided.
read the caption
Table 6: Preliminary study results on pre-trained MoE-LLMs, selecting experts by L1superscript𝐿1L^{1}italic_L start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT norm of internal activation.
| Node for Norm Calculation | MMLU (5-shot) | ARC-C (5-shot) | ||
| Mixtral B | Phi-3.5-MoE-ins. | Mixtral B | Phi-3.5-MoE-ins. | |
| 48.16 | 29.28 | 43.77 | 35.92 | |
| 50.43 | 34.78 | 49.49 | 40.02 | |
| 54.30 | 36.38 | 47.95 | 50.85 | |
| 50.72 | 26.43 | 46.08 | 33.02 | |
| Experts’ Final Outputs | 51.03 | 23.64 | 53.16 | 30.12 |
| Performance w. Router | 70.35 | 78.20 | 62.12 | 67.41 |
🔼 This table presents the results of preliminary experiments evaluating the effectiveness of using the L∞ norm of internal activations to select experts in pre-trained Mixture-of-Experts (MoE) Large Language Models (LLMs). It compares the performance on the MMLU (Massive Multitask Language Understanding) and ARC-C (AI2 Reasoning Challenge) benchmarks, using different nodes within the model’s computational graph for calculating the L∞ norm. The results show the accuracy achieved on both tasks for several different model types (Mixtral 8x7B and Phi-3.5-MoE-instruct), along with the computational time required on 8x A800-80G GPUs. The final row shows the performance using a traditional router-based MoE for comparison.
read the caption
Table 7: Preliminary study results on pre-trained MoE-LLMs, selecting experts by L∞superscript𝐿L^{\infty}italic_L start_POSTSUPERSCRIPT ∞ end_POSTSUPERSCRIPT norm of internal activation.
Full paper#