TL;DR#
Aligning Large Language Models (LLMs) with human values is challenging. Traditional methods involve Reinforcement Learning from Human Feedback (RLHF), but this is complex and resource-intensive. Direct Alignment Algorithms (DAAs) offer a simpler alternative, but their effectiveness varies significantly depending on their design. Existing DAAs lack a unified framework for comparing and understanding their differences.
This paper addresses these issues. It introduces a scaling parameter (β) which unifies existing DAAs and allows for direct comparison. The authors find that two-stage methods (incorporating an explicit supervised fine-tuning (SFT) phase) consistently outperform one-stage methods. Further analysis reveals that the choice between pairwise or pointwise objectives is the key factor influencing alignment quality, more so than the specific reward function. Finally, it’s shown that only a small fraction (5-10%) of supervised data is necessary in the SFT phase for excellent performance.
Key Takeaways#
Why does it matter?#
This paper is crucial because it clarifies the complex landscape of direct alignment algorithms (DAAs), a critical area in aligning large language models with human values. Its findings offer practical guidance for optimizing LLM training pipelines, saving researchers time and resources, and opening new avenues for research into more efficient and effective alignment techniques.
Visual Insights#

🔼 This figure shows the effect of tuning the beta parameter (β) on the performance of two direct alignment algorithms: ASFT and ORPO. The x-axis likely represents different values of β, while the y-axis shows the performance metric (GPT-4 win rate for Llama 3.2 3B TL;DR, and AlpacaEval 2 LC win rate for Llama 3.1 8B UF). The graph likely contains bars or lines comparing the performance of ASFT and ORPO at different values of β. Each algorithm’s performance at β=1 is likely used as a baseline for comparison. The results illustrate how adjusting β impacts the trade-off between alignment quality and potential overfitting.
read the caption
Figure 1: Impact of the β𝛽\betaitalic_β Parameter on ASFT and ORPO Alignment Quality. The plot shows how tuning β𝛽\betaitalic_β (Section 3.1.2) affects both ASFT and ORPO performance. Results are reported for GPT-4 Win Rate in the Llama 3.2 3B TL;DR setup and for AlpacaEval 2 LC Win Rate in the Llama 3.1 8B UF scenario. All other hyperparameters (e.g., learning rates) are selected via grid search, using each method’s best configuration at β=1𝛽1\beta=1italic_β = 1 as the baseline. See Section 5.2 for more details.
| Win / Tie / Lose Rate % |
|---|
| 35.6 / 4.8 / 59.6 |
| 91.2 / 1.0 / 7.8 |
| 91.4 / 0.4 / 8.2 |
| 91.6 / 0.2 / 8.2 |
| 90.2 / 0.6 / 9.2 |
| 92.6 / 0.6 / 6.8 |
| 91.8 / 1.0 / 7.2 |
| 91.4 / 0.4 / 8.2 |
| 87.2 / 1.0 / 11.8 |
🔼 This table compares the performance of different language model alignment methods on the Llama 3.1 8B model using the UltraFeedback dataset. It shows the win rates on AlpacaEval 2 Length-Controlled (LC) and ArenaHard (AH) benchmarks for base models and models that underwent supervised fine-tuning (SFT) before the application of the alignment method. It highlights the performance improvement achieved by incorporating the SFT phase before applying the alignment algorithms. The best hyperparameters used in each case are also detailed.
read the caption
Table 1: Base and SFT-initialized alignment methods on the Llama 3.1 8B model with the UF dataset. SFT-initialized methods demonstrate better performance compared to their traditional formulations without ℒSFTsubscriptℒSFT\mathcal{L}_{\mathrm{SFT}}caligraphic_L start_POSTSUBSCRIPT roman_SFT end_POSTSUBSCRIPT. Results marked with ††{\dagger}† correspond to training with ℒSFTsubscriptℒSFT\mathcal{L}_{\mathrm{SFT}}caligraphic_L start_POSTSUBSCRIPT roman_SFT end_POSTSUBSCRIPT, using the best hyperparameters: lr=1×10−6lr1superscript106\text{lr}=1\times 10^{-6}lr = 1 × 10 start_POSTSUPERSCRIPT - 6 end_POSTSUPERSCRIPT for ORPO and lr=7×10−7lr7superscript107\text{lr}=7\times 10^{-7}lr = 7 × 10 start_POSTSUPERSCRIPT - 7 end_POSTSUPERSCRIPT for ASFT. For other setups, the best hyperparameters are: lr=5×10−7lr5superscript107\text{lr}=5\times 10^{-7}lr = 5 × 10 start_POSTSUPERSCRIPT - 7 end_POSTSUPERSCRIPT for standard SFT ORPO/ASFT, and lr=1×10−5lr1superscript105\text{lr}=1\times 10^{-5}lr = 1 × 10 start_POSTSUPERSCRIPT - 5 end_POSTSUPERSCRIPT/6×10−66superscript1066\times 10^{-6}6 × 10 start_POSTSUPERSCRIPT - 6 end_POSTSUPERSCRIPT for Base ORPO/ASFT.
In-depth insights#
DAA Taxonomy#
A thoughtful exploration of “DAA Taxonomy” in the context of direct alignment algorithms would necessitate a multi-faceted approach. First, it’s crucial to establish a clear definition of what constitutes a DAA, differentiating it from traditional RLHF methods. Then, the taxonomy must consider key differentiating factors, such as the type of loss function used (pairwise vs. pointwise), the reward mechanism (odds ratios vs. reference policies), and the training methodology (single-stage vs. two-stage). A robust taxonomy should go beyond superficial categorizations, exploring the interdependencies and relationships between these characteristics. For example, how does the choice of loss function interact with the reward mechanism? Does a two-stage approach always yield superior results, or are there situations where a single-stage method suffices? A comprehensive taxonomy should also address the impact of hyperparameters, highlighting their influence on algorithm behavior and overall performance. Ultimately, a well-defined DAA taxonomy would provide a valuable framework for researchers to better understand, compare, and improve direct alignment algorithms.
SFT’s Impact#
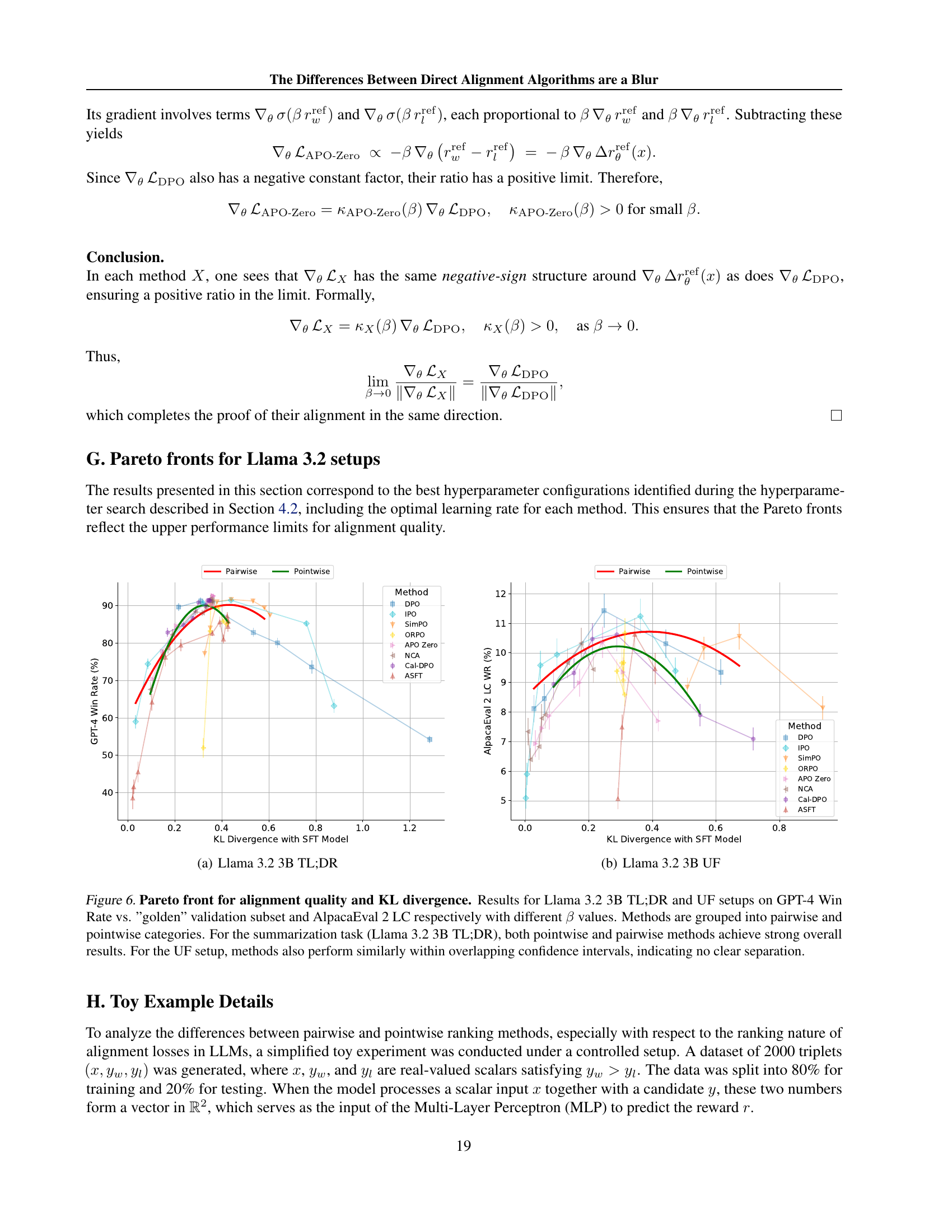
The paper explores the impact of supervised fine-tuning (SFT) on the performance of direct alignment algorithms (DAAs). SFT acts as a crucial preparatory step, enhancing the alignment quality of even single-stage DAAs like ORPO and ASFT, which were initially designed without an explicit SFT phase. The results indicate that incorporating SFT significantly improves the models’ ability to align with human preferences, closing the performance gap between single and two-stage DAAs. The study reveals that while SFT benefits DAAs, using the full dataset isn’t always necessary. Even a relatively small fraction of the SFT data (around 5-10%) can yield substantial gains. This highlights a significant efficiency improvement for implementing DAAs, reducing computational costs without sacrificing much alignment quality. The findings emphasize the importance of a well-defined SFT stage as a critical component, even in approaches aiming to simplify the alignment process by removing the reward modeling and reinforcement learning phases inherent in traditional RLHF.
Beta Tuning#
The concept of “Beta Tuning” in the context of direct alignment algorithms (DAAs) for large language models (LLMs) is crucial for balancing alignment quality and KL divergence. Beta acts as a scaling parameter within the loss function of DAAs like ASFT and ORPO. It controls the intensity of preference optimization. A small beta leads to aggressive optimization, prioritizing preference satisfaction, even at the cost of higher KL divergence from a reference policy. Conversely, a large beta tempers this optimization, aiming for a better balance between alignment quality and divergence from the baseline model. The optimal beta value is data-dependent and requires careful tuning. The research suggests that beta tuning is essential for achieving effective alignment, and that it influences alignment performance more significantly in larger LLMs. This tuning process is critical for managing the trade-off between the quality of alignment and the model’s deviation from the baseline behavior.
Pairwise vs. Pointwise#
The core of the “Pairwise vs. Pointwise” comparison lies in how direct alignment algorithms (DAAs) utilize human preference data for model training. Pairwise methods directly compare two model outputs for a given input, learning from the relative ranking provided by a human evaluator. This approach focuses on the ordering of preferences, making it robust to the absolute strengths of individual preferences. In contrast, pointwise methods assess each model output independently, usually using a numerical score reflecting its quality. This approach learns from the absolute quality of individual outputs, making it sensitive to the scaling and potential biases present in the individual scores. The choice between these methodologies significantly influences the training process and resulting model performance. While pairwise methods tend to offer greater robustness and efficiency, especially in scenarios with noisy or limited data, pointwise methods are more straightforward to implement. The paper explores the trade-offs between these approaches, suggesting that pairwise methods yield superior results, particularly with larger language models, and highlight that the choice is critical for effective DAA design and optimization.
Future Work#
Future research directions stemming from this paper could involve a more in-depth exploration of the interplay between model capacity and the effectiveness of pairwise versus pointwise ranking methods. Larger-scale experiments with diverse datasets and more powerful LLMs are needed to solidify these findings. Investigating the impact of various SFT data sizes across a wider range of DAA algorithms is also crucial, especially given the varying computational costs associated. A deeper dive into the hyperparameter sensitivity across different DAAs should be prioritized, potentially refining the tuning strategies suggested in the paper. The observed improvements in alignment quality through thoughtful hyperparameter selection and the identification of ‘best’ configuration parameters across various DAAs highlights a critical need for more comprehensive and standardized hyperparameter optimization procedures. Furthermore, exploring alternative training methodologies that balance efficiency and quality, potentially leveraging techniques beyond standard gradient descent, warrants future investigation. The development of more robust and sophisticated evaluation metrics which go beyond win-rates would greatly strengthen future work in this domain. Finally, exploring how the integration of different components within alignment strategies impacts overall performance should be addressed to create a more holistic and effective language model alignment pipeline.
More visual insights#
More on figures

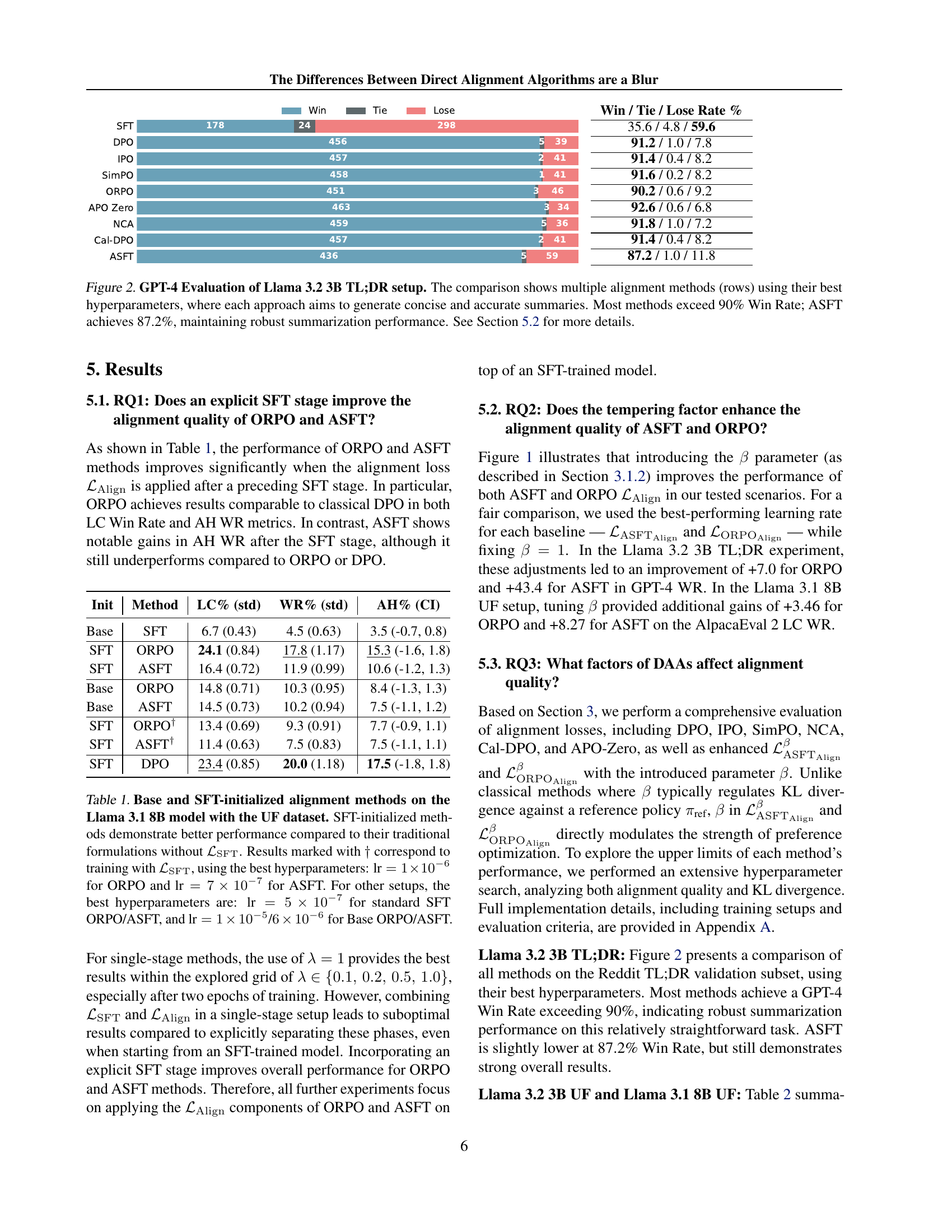
🔼 This figure displays the results of evaluating various language model alignment methods on a summarization task using the Llama 3.2 3B model and the Reddit TL;DR dataset. The evaluation is performed using GPT-4 to compare the quality of summaries generated by different methods. The y-axis represents the win rate (percentage of times a method’s summary was judged superior by GPT-4), and the x-axis shows different methods. The results indicate that most alignment methods achieved a high win rate (over 90%), with ASFT showing a slightly lower but still strong performance of 87.2%. This demonstrates the effectiveness of the alignment techniques in generating high-quality summaries.
read the caption
Figure 2: GPT-4 Evaluation of Llama 3.2 3B TL;DR setup. The comparison shows multiple alignment methods (rows) using their best hyperparameters, where each approach aims to generate concise and accurate summaries. Most methods exceed 90% Win Rate; ASFT achieves 87.2%, maintaining robust summarization performance. See Section 5.2 for more details.

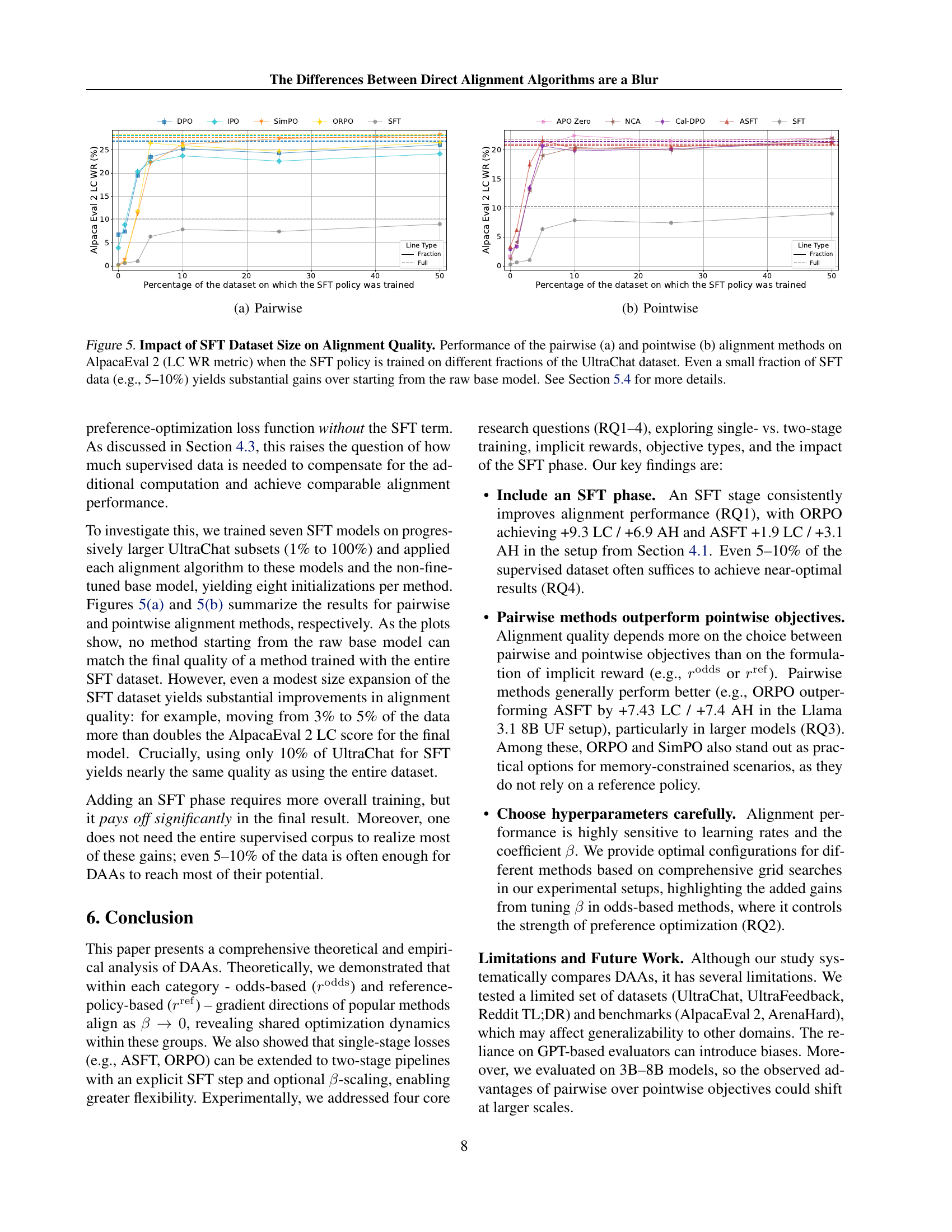
🔼 This figure displays Pareto fronts illustrating the trade-off between alignment quality (measured by AlpacaEval 2 Length-Controlled Win Rate) and KL divergence from a reference model for Llama 3.1 8B UF. The data points are categorized into those using pairwise and pointwise ranking methods. The results show that pairwise methods generally achieve better alignment quality (higher LC Win Rate) compared to pointwise methods, while maintaining KL divergence within overlapping confidence intervals.
read the caption
Figure 3: Pareto front for alignment quality and KL divergence. Results for Llama 3.1 8B UF on AlpacaEval 2 LC. Methods are grouped into pairwise and pointwise categories, with pairwise achieving higher LC values while remaining within overlapping confidence intervals. See Section 5.3 for more details.
More on tables
| Init | Method | LC% (std) | WR% (std) | AH% (CI) |
|---|---|---|---|---|
| Base | SFT | 6.7 (0.43) | 4.5 (0.63) | 3.5 (-0.7, 0.8) |
| SFT | ORPO | 24.1 (0.84) | 17.8 (1.17) | 15.3 (-1.6, 1.8) |
| SFT | ASFT | 16.4 (0.72) | 11.9 (0.99) | 10.6 (-1.2, 1.3) |
| Base | ORPO | 14.8 (0.71) | 10.3 (0.95) | 8.4 (-1.3, 1.3) |
| Base | ASFT | 14.5 (0.73) | 10.2 (0.94) | 7.5 (-1.1, 1.2) |
| SFT | ORPO† | 13.4 (0.69) | 9.3 (0.91) | 7.7 (-0.9, 1.1) |
| SFT | ASFT† | 11.4 (0.63) | 7.5 (0.83) | 7.5 (-1.1, 1.1) |
| SFT | DPO | 23.4 (0.85) | 20.0 (1.18) | 17.5 (-1.8, 1.8) |
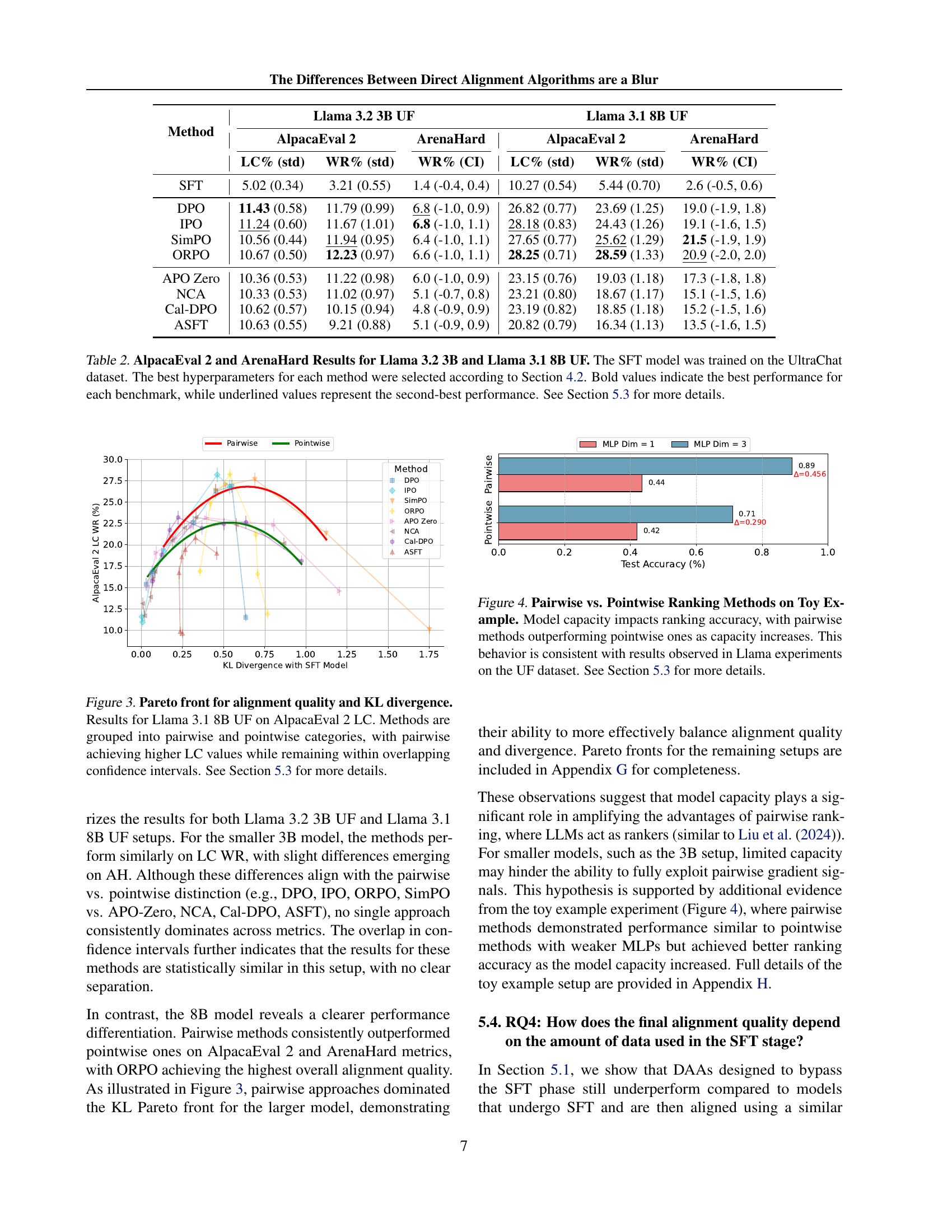
🔼 This table presents the results of AlpacaEval 2 and ArenaHard evaluations on Llama language models (3.2B and 3.1B parameters). The models were fine-tuned using supervised fine-tuning (SFT) on the UltraChat dataset before applying different direct alignment algorithms. The table shows the performance of each alignment method in terms of Win Rate (WR) for length-controlled (LC) and ArenaHard (AH) benchmarks. Optimal hyperparameters for each algorithm (determined in section 4.2) were used. Bold values highlight the top-performing algorithm for each benchmark, while underlined values represent the second-best performance. The details are further discussed in section 5.3.
read the caption
Table 2: AlpacaEval 2 and ArenaHard Results for Llama 3.2 3B and Llama 3.1 8B UF. The SFT model was trained on the UltraChat dataset. The best hyperparameters for each method were selected according to Section 4.2. Bold values indicate the best performance for each benchmark, while underlined values represent the second-best performance. See Section 5.3 for more details.
| Method | Llama 3.2 3B UF | Llama 3.1 8B UF | ||||
|---|---|---|---|---|---|---|
| AlpacaEval 2 | ArenaHard | AlpacaEval 2 | ArenaHard | |||
| LC% (std) | WR% (std) | WR% (CI) | LC% (std) | WR% (std) | WR% (CI) | |
| SFT | 5.02 (0.34) | 3.21 (0.55) | 1.4 (-0.4, 0.4) | 10.27 (0.54) | 5.44 (0.70) | 2.6 (-0.5, 0.6) |
| DPO | 11.43 (0.58) | 11.79 (0.99) | 6.8 (-1.0, 0.9) | 26.82 (0.77) | 23.69 (1.25) | 19.0 (-1.9, 1.8) |
| IPO | 11.24 (0.60) | 11.67 (1.01) | 6.8 (-1.0, 1.1) | 28.18 (0.83) | 24.43 (1.26) | 19.1 (-1.6, 1.5) |
| SimPO | 10.56 (0.44) | 11.94 (0.95) | 6.4 (-1.0, 1.1) | 27.65 (0.77) | 25.62 (1.29) | 21.5 (-1.9, 1.9) |
| ORPO | 10.67 (0.50) | 12.23 (0.97) | 6.6 (-1.0, 1.1) | 28.25 (0.71) | 28.59 (1.33) | 20.9 (-2.0, 2.0) |
| APO Zero | 10.36 (0.53) | 11.22 (0.98) | 6.0 (-1.0, 0.9) | 23.15 (0.76) | 19.03 (1.18) | 17.3 (-1.8, 1.8) |
| NCA | 10.33 (0.53) | 11.02 (0.97) | 5.1 (-0.7, 0.8) | 23.21 (0.80) | 18.67 (1.17) | 15.1 (-1.5, 1.6) |
| Cal-DPO | 10.62 (0.57) | 10.15 (0.94) | 4.8 (-0.9, 0.9) | 23.19 (0.82) | 18.85 (1.18) | 15.2 (-1.5, 1.6) |
| ASFT | 10.63 (0.55) | 9.21 (0.88) | 5.1 (-0.9, 0.9) | 20.82 (0.79) | 16.34 (1.13) | 13.5 (-1.6, 1.5) |
🔼 This table shows whether different Direct Alignment Algorithms (DAAs) use length-based probability normalization in their original implementations. A checkmark (✓) indicates length normalization was used, while an ‘X’ indicates it was not. This is important because the choice of normalization can affect the results and comparability of different DAAs.
read the caption
Table 3: Methods that include (✓) or omit (✗) length-based probability normalization in their original formulation.
| Method | Use normalization |
|---|---|
| DPO (Rafailov et al., 2023) | ✗ |
| IPO (Azar et al., 2023) | ✗ |
| SimPO (Meng et al., 2024) | ✓ |
| NCA (Chen et al., 2024) | ✗ |
| Cal-DPO (Xiao et al., 2024) | ✗ |
| APO-Zero (D’Oosterlinck et al., 2024) | ✗ |
| ORPO (Hong et al., 2024) | ✓ |
| ASFT (Wang et al., 2024) | ✓ |
🔼 This table lists the hyperparameters used during the training of two different Llama language models: Llama 3.2 3B and Llama 3.1 8B. It details settings such as maximum token length, number of epochs, learning rates (for both supervised fine-tuning and alignment), optimizer used (Adam), and its hyperparameters (beta1, beta2), batch size, learning rate schedule, warmup ratio, maximum gradient norm, and memory optimization techniques employed (DeepSpeed and FlashAttention-2). The values provided represent the settings used for experiments in the paper.
read the caption
Table 4: Representative training hyperparameters for Llama 3.2 3B and Llama 3.1 8B models.
| Hyperparameter | Value |
|---|---|
| Max Tokens Length | 1024 (TL;DR setup), 4096 (UF setup) |
| Epochs | 1 (or 2 when specified) |
| Learning Rate (SFT) | |
| Learning Rate (Base Init.) | |
| Learning Rate (Alignment) | |
| Optimizer | Adam (Kingma & Ba, 2014) |
| Adam | 0.9 |
| Adam | 0.95 |
| Batch Size | 128 |
| Learning Schedule | Linear Decay |
| Warm-up Ratio | 0.03 |
| Max Gradient Norm | 2 |
| Memory Optimization | DeepSpeed (Rasley et al., 2020) |
| Attention Mechanism | Flash Attention 2 (Dao, 2023) |
🔼 This table presents a summary of the sizes of the datasets used in the experiments described in the paper. It shows the number of training and validation examples available for three key datasets: UltraChat, UltraFeedback, and Reddit TL;DR. The Reddit TL;DR dataset is further broken down into the number of examples used for supervised fine-tuning (SFT) and those used for preference-based optimization.
read the caption
Table 5: Summary of dataset sizes used for training and validation.
| Dataset | Training Examples | Validation Examples |
|---|---|---|
| UltraChat | 207,865 | 23,110 |
| UltraFeedback | 61,135 | 2,000 |
| Reddit TL;DR (SFT) | 41,947 | 11,941 |
| Reddit TL;DR (Preference) | 73,396 | 21,198 |
🔼 This table presents the range of beta (β) values used in the experiments for each Direct Alignment Algorithm (DAA). The beta parameter controls the strength of the preference optimization, and its impact on performance was evaluated across multiple scenarios. Each DAA’s performance was tested using the provided range of β values to identify optimal configurations for each.
read the caption
Table 6: Range of β𝛽\betaitalic_β values tested for each DAA method on all scenarios.
| Method | Values Tested |
|---|---|
| DPO | |
| IPO | |
| SimPO | |
| ORPO | |
| ASFT | |
| APO-Zero | |
| Cal-DPO | |
| NCA |
🔼 This table presents the best-performing hyperparameter configurations for each Direct Alignment Algorithm (DAA) across three different experimental setups. The setups vary in model size and datasets used, allowing for a comparison of the algorithms’ sensitivity to hyperparameter settings across diverse conditions. The hyperparameters shown include learning rate and the β scaling parameter, key factors influencing the performance of the DAAs.
read the caption
Table 7: Best hyperparameters for each DAA method across setups.
| Method | Llama 3.2 3B TL;DR | Llama 3.2 3B UF | Llama 3.1 8B UF | |||
|---|---|---|---|---|---|---|
| Learning Rate | Learning Rate | Learning Rate | ||||
| DPO | 0.05 | 0.01 | 0.003 | |||
| IPO | 0.005 | 0.001 | 0.001 | |||
| SimPO | 0.5 | 1.0 | 1.0 | |||
| ORPO | 0.5 | 0.2 | 0.5 | |||
| ASFT | 0.001 | 0.2 | 0.1 | |||
| APO Zero | 0.001 | 0.005 | 0.003 | |||
| NCA | 0.0001 | 0.0005 | 0.0003 | |||
| Cal-DPO | 0.00003 | 0.0003 | 0.0003 | |||
🔼 This table lists the hyperparameters used during the text generation phase for the Llama 3.1 8B and Llama 3.2 3B language models. Specifically, it shows the values used for temperature, top-k sampling, top-p (nucleus) sampling, and the maximum number of new tokens generated. These settings control the randomness and length of the generated text sequences.
read the caption
Table 8: Generation hyperparameters for Llama 3.1 8B and Llama 3.2 3B models.
Full paper#