TL;DR#
Current methods for training large language models (LLMs) using reinforcement learning (RL) often rely on sparse outcome-level rewards, leading to issues like training inefficiency and difficulty in assigning credit for intermediate steps. Dense rewards, providing feedback at each step, can address these issues. However, obtaining high-quality dense rewards is costly and prone to reward hacking. This paper introduces PRIME, a novel method that addresses these challenges.
PRIME leverages implicit process rewards derived from policy rollouts and outcome labels. This innovative technique avoids the expensive process of labeling each step and mitigates reward hacking. Experiments show PRIME significantly enhances performance on benchmark reasoning tasks, outperforming existing models and requiring substantially less training data. The results show that PRIME offers a scalable and efficient alternative for training LLMs with dense rewards.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on reinforcement learning for large language models (LLMs). It addresses the significant challenge of efficiently training LLMs with dense rewards, a problem hindering progress in complex reasoning tasks. PRIME’s novel approach, using implicit rewards and online updates, offers a scalable and cost-effective solution, opening new avenues for improving LLM reasoning capabilities.
Visual Insights#

🔼 The bar chart displays the performance of various language models on several competitive mathematics benchmarks. Eurus-2-7B-PRIME, a model enhanced with the PRIME method, demonstrates superior performance compared to other state-of-the-art models, including those with significantly larger parameter counts. The chart highlights the substantial improvement achieved by PRIME (+16.7%) over the Eurus-2-7B-SFT baseline, showcasing the effectiveness of the PRIME technique in enhancing mathematical reasoning capabilities.
read the caption
Figure 1: Overall math performance. Eurus-2-7B-PRIME excels at competition-level mathematics benchmarks, outperforming advanced math models and larger models. Notably, PRIME brings substantial performance gain (+16.7%) over Eurus-2-7B-SFT.
| Model | Eurus-2-7B-PRIME | Qwen2.5-Math-7B-Instruct |
|---|---|---|
| Base Model | Qwen2.5-Math-7B | Qwen2.5-Math-7B |
| SFT Data | 230K (open-source) | 2.5M (open-source & in-house) |
| RM Data | 0 | 618K (in-house) |
| RM | Eurus-2-7B-SFT | Qwen2.5-Math-RM (72B) |
| RL Data | 150K queries 4 samples | 66K queries 32 samples |
🔼 This table compares the computational resources used to train the Eurus-2-7B-PRIME model with the Qwen2.5-Math-7B-Instruct model. It shows a significant difference in the amount of data used for supervised fine-tuning (SFT) and reinforcement learning (RL), highlighting the efficiency gains achieved by PRIME. Specifically, it contrasts the base models used, the size of the SFT datasets, the amount of reward model data, the type of reward model employed, and the size of the RL training data used in each approach.
read the caption
Table 1: The comparison of resource requirements between Eurus-2-7B-PRIME and Qwen2.5-Math-7B-Instruct.
In-depth insights#
Implicit Reward RL#
Implicit Reward RL presents a compelling paradigm shift in reinforcement learning (RL) for large language models (LLMs). Traditional RL approaches often struggle with the high cost and inherent ambiguity of defining explicit, dense rewards for complex reasoning tasks. Implicit reward methods offer a more efficient alternative by leveraging readily available outcome-level feedback (e.g., whether an answer is correct) to indirectly guide the learning process. This circumvents the need for extensive, manual annotation of intermediate steps. The effectiveness of this approach hinges on cleverly designed reward models capable of inferring process-level information from high-level signals. Key challenges include avoiding reward hacking (where the model exploits weaknesses in the reward model to maximize reward without genuine progress) and maintaining scalability for large LLMs. Despite these hurdles, implicit reward RL shows great promise for improving the training efficiency and overall performance of LLMs on complex reasoning benchmarks, making it an exciting area of ongoing research.
Online PRM Updates#
Online updates to Process Reward Models (PRMs) are crucial for effective reinforcement learning (RL) in large language models (LLMs), particularly in addressing the challenge of reward hacking. Continuously adapting the PRM prevents the policy from exploiting loopholes in a static reward function. However, online PRM updates present significant challenges. Acquiring high-quality process-level labels for every step is prohibitively expensive. Therefore, methods like using implicit rewards, derived from outcome labels, offer a scalable solution. Implicit reward methods reduce reliance on expensive annotations, enabling online PRM adjustments using only policy rollouts and outcome feedback. This approach significantly lowers development and computational overhead compared to traditional PRM training. The key is to find a balance between responsiveness and stability: Overly frequent updates could lead to instability, whereas infrequent updates might not effectively address reward hacking or changing policy behavior. Furthermore, sophisticated techniques may be required to handle the inherent noise and uncertainty in both process and outcome feedback, thus ensuring the robust learning process.
Scalable Reward Model#
A scalable reward model is crucial for the effective application of reinforcement learning (RL) to large language models (LLMs). The challenge lies in the high cost of obtaining high-quality, dense process-level rewards for training. Existing methods often rely on expensive human annotation or estimation techniques that lack scalability. A truly scalable solution must leverage readily available data like outcome labels from policy rollouts. This might involve techniques such as implicit reward modeling, which derives process-level rewards from outcome labels and online PRM updates without explicit reward model training, significantly reducing the development overhead. Another aspect of scalability relates to the algorithm’s compatibility and efficiency with various RL algorithms. A successful scalable reward model will need to integrate seamlessly with established RL frameworks and not require substantial modifications. Ultimately, a scalable solution needs to address reward hacking and over-optimization issues commonly found when using simple sparse rewards, providing a robust and effective approach to online RL training for LLMs. Efficiency is also key, reducing the number of rollouts necessary for accurate advantage estimation and model training.
Math & Code Benchmarks#
A dedicated section on “Math & Code Benchmarks” within a research paper would be crucial for validating the effectiveness of a proposed model or approach. It should present a diverse range of well-established benchmarks, encompassing various levels of difficulty and problem types within both mathematical and coding domains. The selection of benchmarks must be justified, highlighting their relevance to the research question and the model’s intended application. Results should be presented clearly, ideally with tables comparing the model’s performance against state-of-the-art baselines. Statistical significance testing should be used to demonstrate the robustness of any performance gains. Furthermore, a detailed analysis of the model’s strengths and weaknesses on each benchmark task should be included, offering valuable insights into its capabilities and limitations. A discussion of potential biases in the benchmark datasets and suggestions for future improvement should also be part of this section to enhance the research’s overall impact and reproducibility.
Future of PRIME#
The future of PRIME hinges on several key aspects. Scalability remains paramount; future work should focus on optimizing its efficiency for even larger language models and more complex reasoning tasks. Robustness is crucial, requiring further investigation into its resilience to various data distributions and potential vulnerabilities like reward hacking, particularly as models become more sophisticated. Generalization to diverse tasks beyond mathematics and coding is vital to demonstrate its broader applicability and impact. Integration with other RL frameworks and model architectures should be explored, promoting seamless collaboration within the existing ecosystem of tools and techniques. Finally, interpretability improvements are necessary to provide greater insights into the inner workings of PRIME, enabling better understanding, debugging, and potential enhancements in its decision-making processes. The ultimate success of PRIME depends on successfully addressing these challenges, unlocking its full potential for advanced AI systems.
More visual insights#
More on figures

🔼 The figure illustrates the PRIME framework’s workflow. It begins by initializing both the policy model and the Implicit PRM using a reference model. Next, multiple responses are generated for each prompt, and a filter based on output accuracy selects the most promising ones. Then, the Implicit PRM calculates implicit process rewards for each token, which are used to update the PRM itself using cross-entropy loss. Finally, advantages are computed based on these rewards, and these are used in calculating the policy loss, enabling the update of the policy model.
read the caption
Figure 2: Illustration of PRIME. PRIME follows that (1) initialize policy model and the Implicit PRM both with the reference model; (2) sample multiple responses for each prompt and filter with output accuracy; (3) obtain implicit process rewards by the Implicit PRM and update it using cross-entropy (CE) loss; (4) compute advantage and policy loss then update the policy model.

🔼 This figure displays the effect of online prompt filtering on the training rewards during reinforcement learning. The blue line shows the training rewards with online prompt filtering applied, while the orange line represents the training rewards without filtering. The plot demonstrates a significant reduction in variance of the training rewards when using online prompt filtering, suggesting improved stability in the learning process.
read the caption
Figure 3: Impact of online prompt filtering on training rewards.

🔼 This figure shows the outcome-based rewards obtained during the training process using a 10-step moving average. It illustrates the trend of training rewards over time, providing insights into the learning progress and the effectiveness of the reward system.
read the caption
(a) Outcome training rewards (10-step moving).

🔼 The figure shows the test accuracy of different models across various gradient update steps during training. It illustrates how the accuracy changes over time as the model is updated and refined using different methods, providing insights into the learning progress and relative performance of the compared models.
read the caption
(b) Test accuracy across different gradient steps.

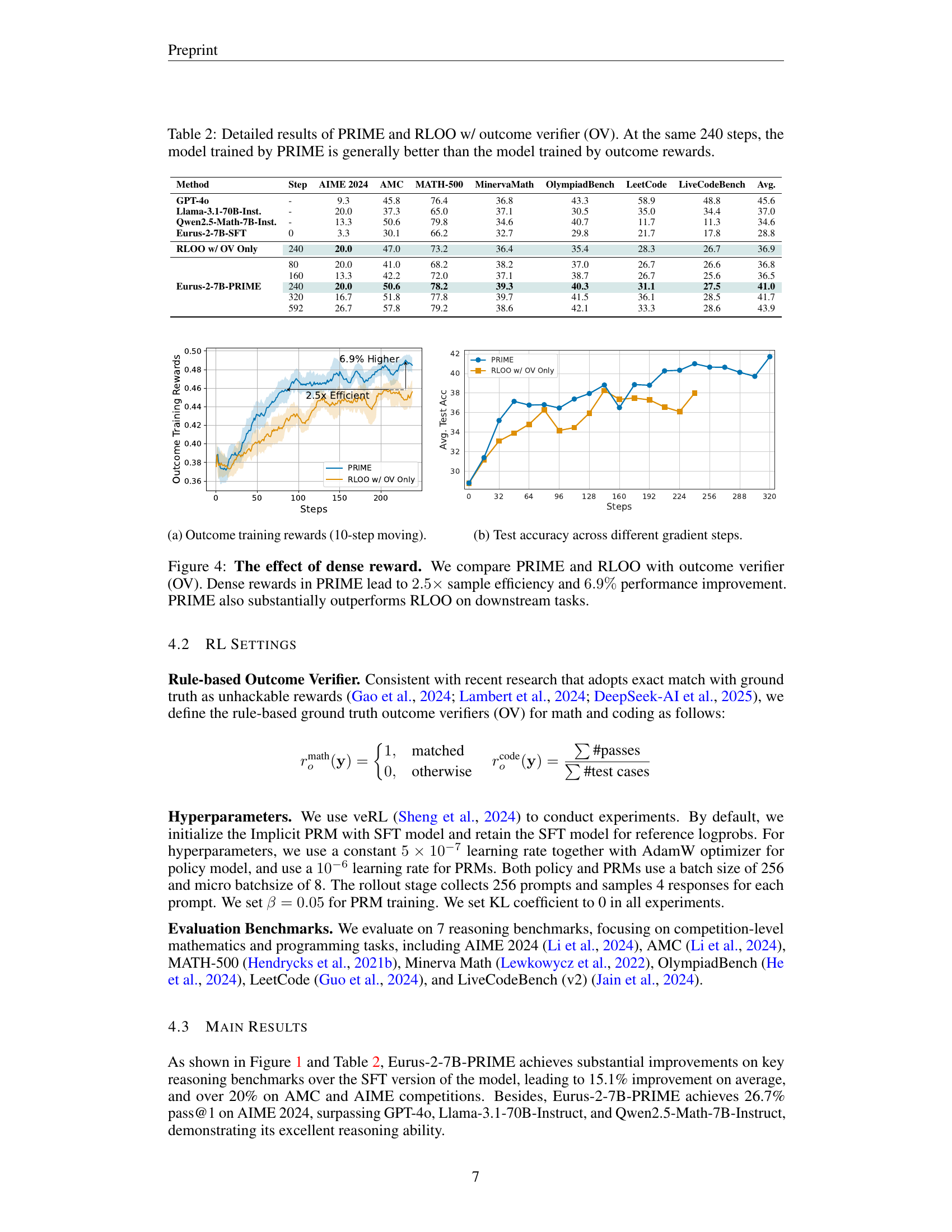
🔼 Figure 4 presents a comparison of the performance of PRIME (Process Reinforcement through Implicit Rewards) and RLOO (Reward-Level Online Optimization) on various tasks. Both methods employ an outcome verifier (OV) to evaluate performance. The results show that PRIME, which utilizes dense rewards, achieves a 2.5x improvement in sample efficiency and a 6.9% increase in performance compared to RLOO, which uses only outcome-level rewards. Moreover, PRIME demonstrates superior performance on downstream tasks, illustrating the advantages of dense rewards in reinforcement learning for LLMs.
read the caption
Figure 4: The effect of dense reward. We compare PRIME and RLOO with outcome verifier (OV). Dense rewards in PRIME lead to 2.5×2.5\times2.5 × sample efficiency and 6.9%percent6.96.9\%6.9 % performance improvement. PRIME also substantially outperforms RLOO on downstream tasks.

🔼 This figure shows the outcome-based rewards obtained during the training process. The rewards are calculated every 10 steps and smoothed using a 10-step moving average to reduce noise and highlight the overall trend. It visually represents the learning progress of the model, indicating how well the model is performing based on its final outputs. Higher reward values suggest improved performance in solving the tasks.
read the caption
(a) Outcome training rewards (10-step moving).

🔼 The graph shows how the test accuracy of the model changes as the number of gradient steps increases. This illustrates the model’s learning progress and performance improvement over time during the training process. It provides insights into how effectively the model learns and generalizes to unseen data as training progresses.
read the caption
(b) Test accuracy across different gradient steps.

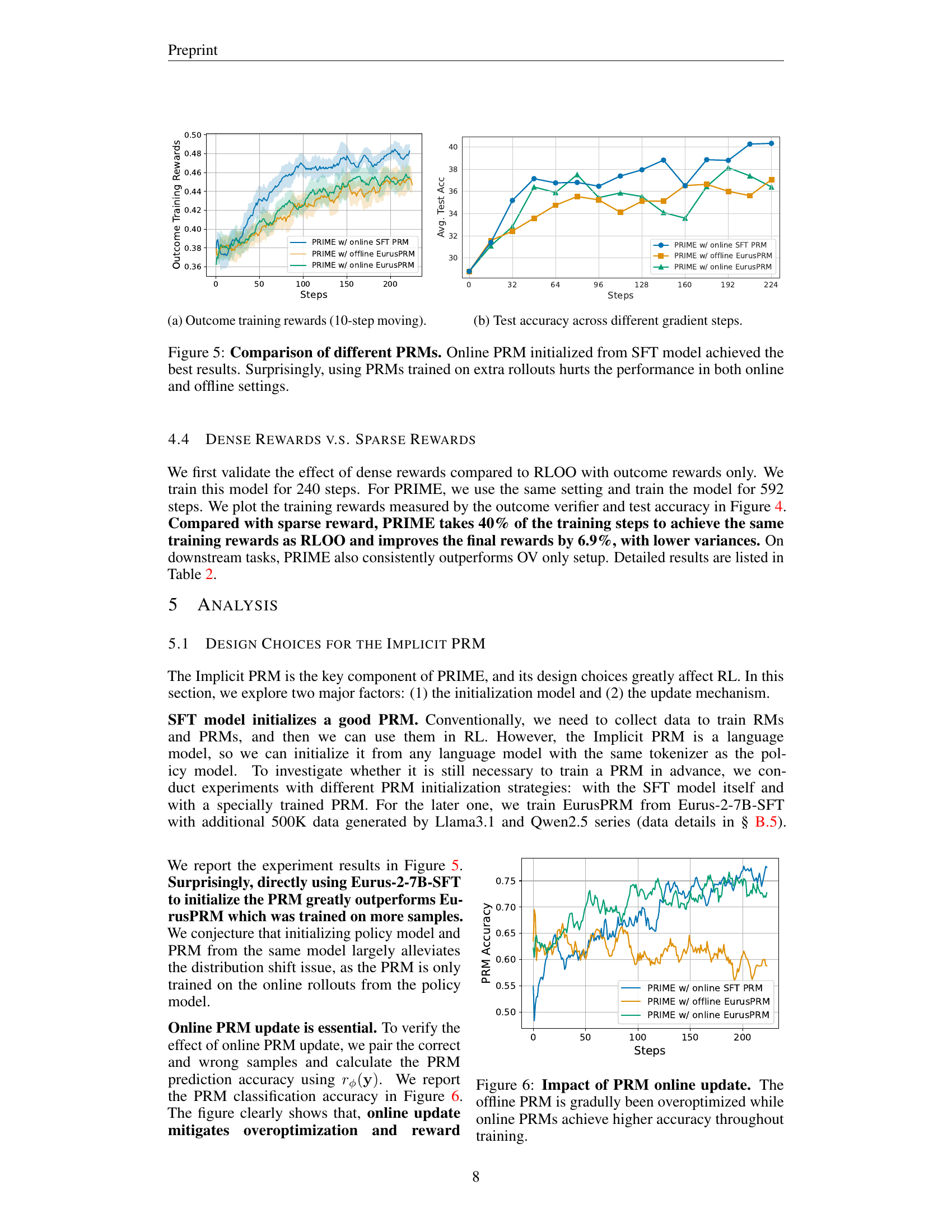
🔼 This figure compares the performance of different process reward models (PRMs) in a reinforcement learning setting. The key finding is that online PRMs, particularly those initialized using the supervised fine-tuning (SFT) model, achieve superior results compared to offline PRMs or online PRMs trained on additional data. The results demonstrate that training a PRM using only the on-policy rollouts from the SFT model is sufficient, and adding extra training data negatively impacts the performance in both online and offline scenarios. This suggests that overfitting is a significant concern when training PRMs outside of the online reinforcement learning context.
read the caption
Figure 5: Comparison of different PRMs. Online PRM initialized from SFT model achieved the best results. Surprisingly, using PRMs trained on extra rollouts hurts the performance in both online and offline settings.

🔼 This figure displays the impact of online vs. offline updates of the process reward model (PRM) on its accuracy. The x-axis represents the training steps, and the y-axis shows the PRM’s accuracy in classifying rewards as correct or incorrect. The online PRM, updated during training, maintains high accuracy, whereas the offline PRM, trained beforehand, gradually loses accuracy due to overoptimization. This highlights the importance of online PRM updates to prevent performance degradation.
read the caption
Figure 6: Impact of PRM online update. The offline PRM is gradully been overoptimized while online PRMs achieve higher accuracy throughout training.

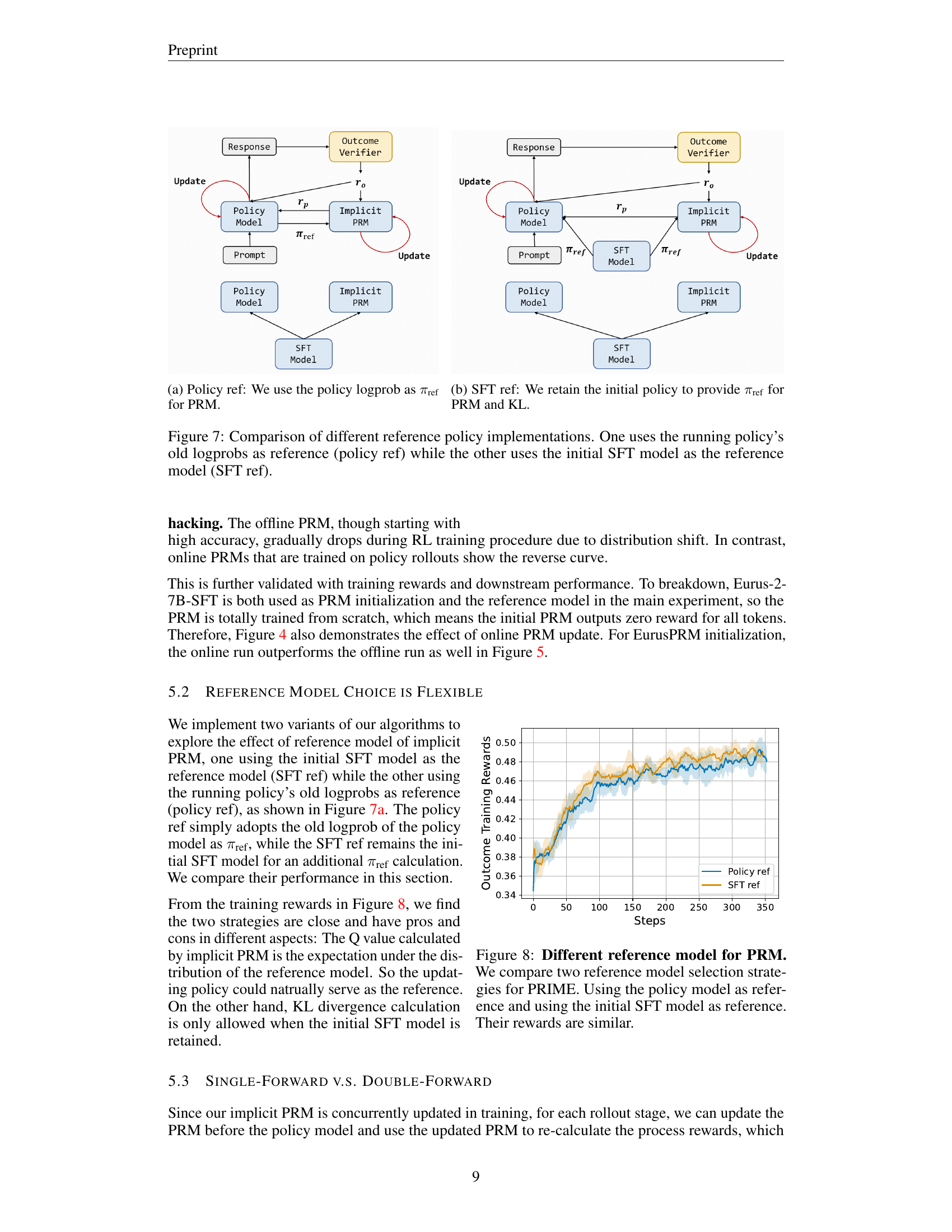
🔼 This figure compares two different methods for implementing the implicit process reward model (PRM) in reinforcement learning. The left panel (a) shows the results when using the policy’s log probabilities as the reference distribution for the PRM. This method directly uses the model’s own estimates of token probabilities to guide the PRM. The right panel (b) shows the alternative method, which employs the initial Supervised Fine-Tuning (SFT) model as the reference. In this case, the PRM is based on a pre-trained model, rather than using the model’s dynamically changing probability estimates.
read the caption
(a) Policy ref: We use the policy logprob as πrefsubscript𝜋ref\pi_{\text{ref}}italic_π start_POSTSUBSCRIPT ref end_POSTSUBSCRIPT for PRM.

🔼 This figure illustrates a design choice in the PRIME framework, specifically how the reference policy (πref) is selected for calculating implicit process rewards. The (b) part of the figure shows a setup where the initial policy model from the supervised fine-tuning (SFT) stage is used as the reference. This means that the probabilities from the initially trained SFT model are used when computing the implicit process reward, providing a consistent baseline against which to measure the current policy. This choice of reference model helps stabilize the training process and mitigates issues related to reward hacking and reward model overoptimization.
read the caption
(b) SFT ref: We retain the initial policy to provide πrefsubscript𝜋ref\pi_{\text{ref}}italic_π start_POSTSUBSCRIPT ref end_POSTSUBSCRIPT for PRM and KL.

🔼 This figure compares two approaches for using a reference policy in the PRIME reinforcement learning framework. The ‘policy ref’ method uses the log probabilities from the current policy model as the reference. The ‘SFT ref’ method uses the initial Supervised Fine-Tuning (SFT) model’s log probabilities as a reference. The comparison highlights how the choice of reference policy impacts the overall performance of the algorithm. Both methods are visually shown in separate diagrams illustrating their process.
read the caption
Figure 7: Comparison of different reference policy implementations. One uses the running policy’s old logprobs as reference (policy ref) while the other uses the initial SFT model as the reference model (SFT ref).

🔼 This figure compares two different methods of selecting a reference model for the Implicit Process Reward Model (PRM) within the PRIME framework. The first method uses the current policy model’s log probabilities as the reference. The second method uses the initial Supervised Fine-Tuning (SFT) model’s log probabilities. The results show that the training rewards obtained using both methods are quite similar, suggesting that the choice of reference model may not be a critical factor in the PRIME framework’s performance.
read the caption
Figure 8: Different reference model for PRM. We compare two reference model selection strategies for PRIME. Using the policy model as reference and using the initial SFT model as reference. Their rewards are similar.
🔼 This figure shows the performance of the Implicit PRM (Process Reward Model) during training. The y-axis represents the classification accuracy of the PRM on the training samples. The x-axis represents the training steps. This plot helps visualize how well the PRM learns to predict process rewards over the course of training. The accuracy is measured on training samples and shows the improvement in the PRM’s ability to correctly classify token-level rewards during training.
read the caption
(a) PRM classification accuracy on training samples.

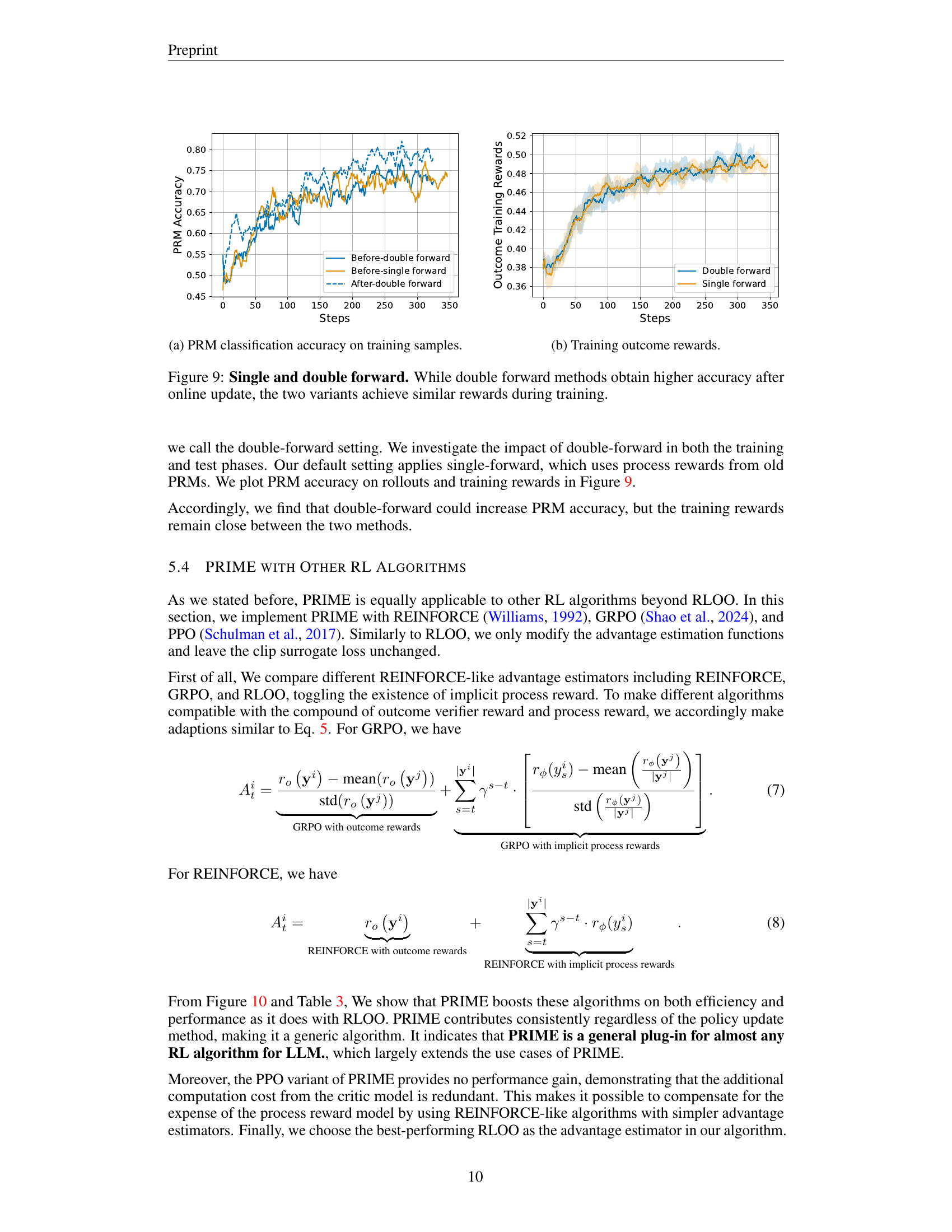
🔼 The graph displays the training outcome rewards over time steps for two different methods: single forward and double forward. It shows the cumulative outcome rewards achieved during the training process. The double-forward approach demonstrates slightly higher rewards, suggesting it might lead to better overall model performance.
read the caption
(b) Training outcome rewards.

🔼 This figure compares the performance of single-forward and double-forward methods in training an implicit process reward model (PRM). Single-forward updates the PRM once per training iteration, using the rewards from the previous PRM, while double-forward updates the PRM twice, first using the older rewards and then again using the newly calculated rewards. The results show that the double-forward method achieves higher PRM accuracy after the online update, suggesting it may be more effective at preventing overfitting. However, both methods yield similar training rewards, indicating comparable overall performance in terms of maximizing the cumulative reward.
read the caption
Figure 9: Single and double forward. While double forward methods obtain higher accuracy after online update, the two variants achieve similar rewards during training.

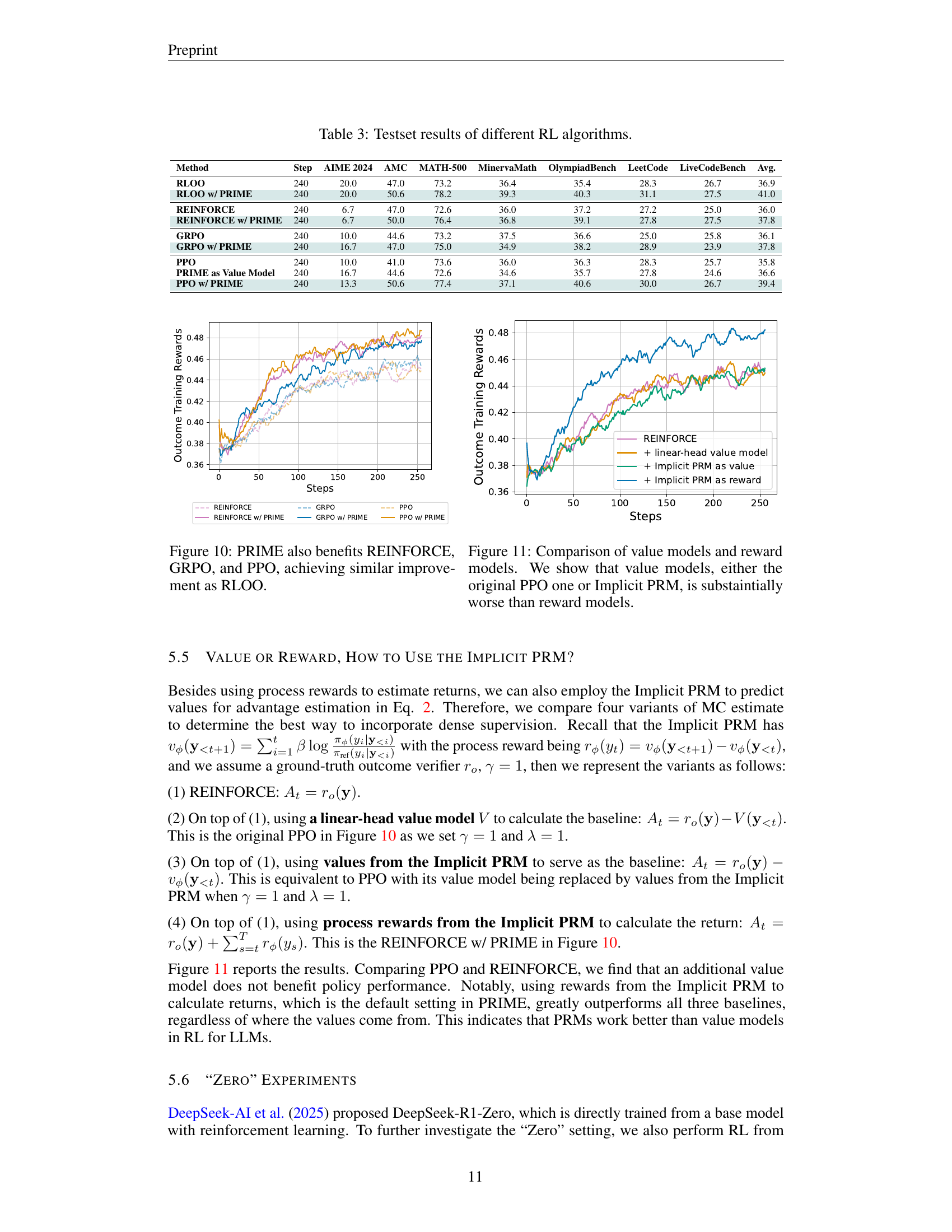
🔼 Figure 10 presents a comparison of the performance of several reinforcement learning algorithms (REINFORCE, GRPO, PPO, and RLOO) when used with and without the PRIME method. The figure demonstrates that incorporating PRIME consistently improves the performance of all four algorithms, achieving similar levels of improvement as seen with RLOO alone. This highlights the general applicability and effectiveness of the PRIME method across different reinforcement learning algorithms.
read the caption
Figure 10: PRIME also benefits REINFORCE, GRPO, and PPO, achieving similar improvement as RLOO.

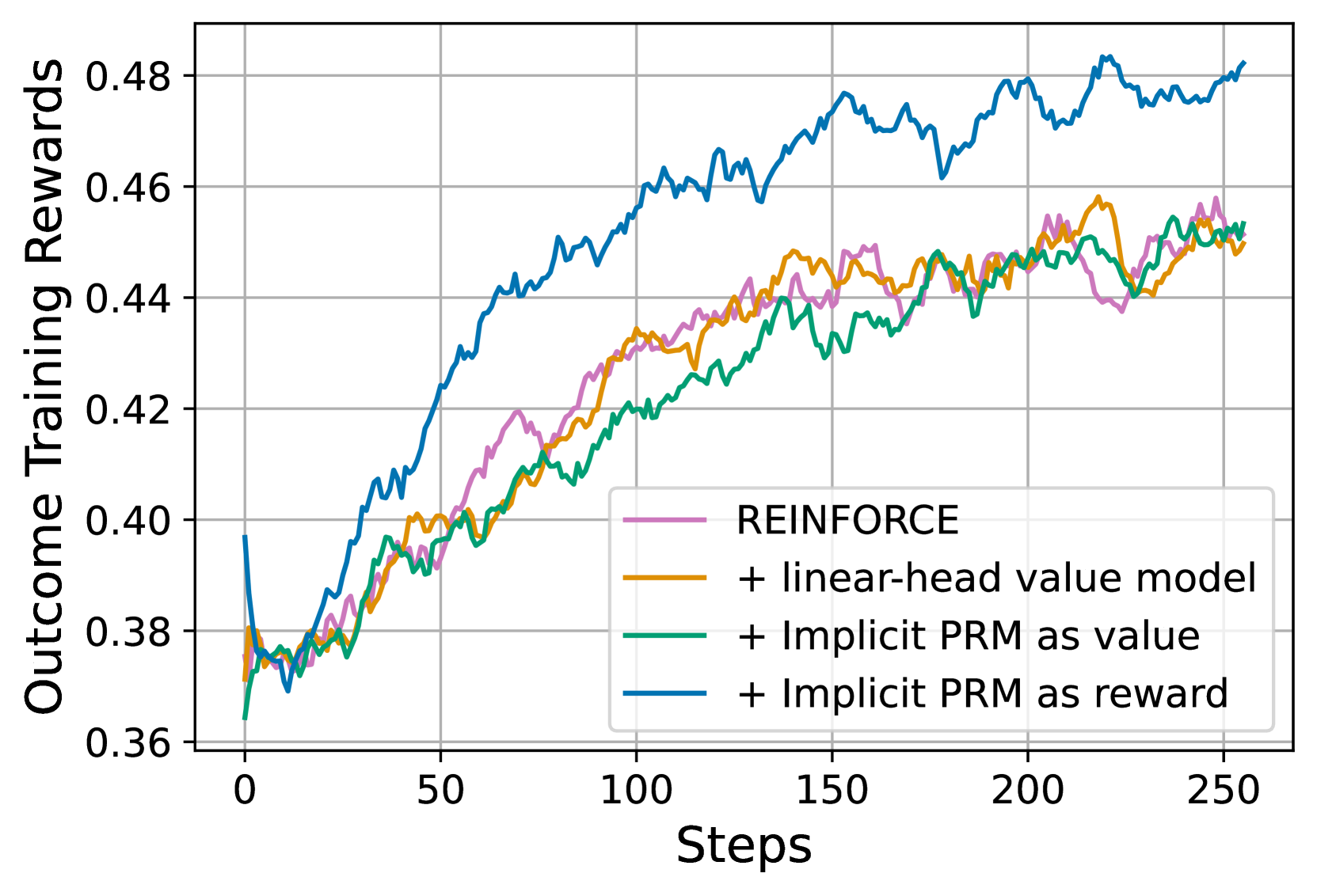
🔼 This figure compares the performance of using value models versus reward models within a reinforcement learning framework for large language models. Specifically, it contrasts the performance of three approaches: (1) a standard value model from Proximal Policy Optimization (PPO), (2) a value model based on the implicit process reward model (PRM) proposed in the paper, and (3) a reward model using the implicit PRM. The results demonstrate that using reward models, particularly the implicit PRM reward model, significantly outperforms value models in terms of training effectiveness.
read the caption
Figure 11: Comparison of value models and reward models. We show that value models, either the original PPO one or Implicit PRM, is substaintially worse than reward models.
More on tables
| Method | Step | AIME 2024 | AMC | MATH-500 | MinervaMath | OlympiadBench | LeetCode | LiveCodeBench | Avg. |
|---|---|---|---|---|---|---|---|---|---|
| GPT-4o | - | 9.3 | 45.8 | 76.4 | 36.8 | 43.3 | 58.9 | 48.8 | 45.6 |
| Llama-3.1-70B-Inst. | - | 20.0 | 37.3 | 65.0 | 37.1 | 30.5 | 35.0 | 34.4 | 37.0 |
| Qwen2.5-Math-7B-Inst. | - | 13.3 | 50.6 | 79.8 | 34.6 | 40.7 | 11.7 | 11.3 | 34.6 |
| Eurus-2-7B-SFT | 0 | 3.3 | 30.1 | 66.2 | 32.7 | 29.8 | 21.7 | 17.8 | 28.8 |
| RLOO w/ OV Only | 240 | 20.0 | 47.0 | 73.2 | 36.4 | 35.4 | 28.3 | 26.7 | 36.9 |
| 80 | 20.0 | 41.0 | 68.2 | 38.2 | 37.0 | 26.7 | 26.6 | 36.8 | |
| 160 | 13.3 | 42.2 | 72.0 | 37.1 | 38.7 | 26.7 | 25.6 | 36.5 | |
| 240 | 20.0 | 50.6 | 78.2 | 39.3 | 40.3 | 31.1 | 27.5 | 41.0 | |
| 320 | 16.7 | 51.8 | 77.8 | 39.7 | 41.5 | 36.1 | 28.5 | 41.7 | |
| Eurus-2-7B-PRIME | 592 | 26.7 | 57.8 | 79.2 | 38.6 | 42.1 | 33.3 | 28.6 | 43.9 |
🔼 This table presents a detailed comparison of the performance of two reinforcement learning (RL) methods: PRIME and RLOO (with an outcome verifier), on several key reasoning benchmarks. Both methods were trained for 240 steps. The results show that the model trained with PRIME consistently outperforms the model trained with RLOO across all benchmarks, demonstrating PRIME’s effectiveness in enhancing reasoning capabilities. Specific metrics shown include accuracy percentages on various benchmarks such as AIME 2024, AMC, MATH-500, Minerva Math, OlympiadBench, LeetCode, and LiveCodeBench, allowing for a comprehensive performance evaluation of both methods.
read the caption
Table 2: Detailed results of PRIME and RLOO w/ outcome verifier (OV). At the same 240 steps, the model trained by PRIME is generally better than the model trained by outcome rewards.
| Method | Step | AIME 2024 | AMC | MATH-500 | MinervaMath | OlympiadBench | LeetCode | LiveCodeBench | Avg. |
|---|---|---|---|---|---|---|---|---|---|
| RLOO | 240 | 20.0 | 47.0 | 73.2 | 36.4 | 35.4 | 28.3 | 26.7 | 36.9 |
| RLOO w/ PRIME | 240 | 20.0 | 50.6 | 78.2 | 39.3 | 40.3 | 31.1 | 27.5 | 41.0 |
| REINFORCE | 240 | 6.7 | 47.0 | 72.6 | 36.0 | 37.2 | 27.2 | 25.0 | 36.0 |
| REINFORCE w/ PRIME | 240 | 6.7 | 50.0 | 76.4 | 36.8 | 39.1 | 27.8 | 27.5 | 37.8 |
| GRPO | 240 | 10.0 | 44.6 | 73.2 | 37.5 | 36.6 | 25.0 | 25.8 | 36.1 |
| GRPO w/ PRIME | 240 | 16.7 | 47.0 | 75.0 | 34.9 | 38.2 | 28.9 | 23.9 | 37.8 |
| PPO | 240 | 10.0 | 41.0 | 73.6 | 36.0 | 36.3 | 28.3 | 25.7 | 35.8 |
| PRIME as Value Model | 240 | 16.7 | 44.6 | 72.6 | 34.6 | 35.7 | 27.8 | 24.6 | 36.6 |
| PPO w/ PRIME | 240 | 13.3 | 50.6 | 77.4 | 37.1 | 40.6 | 30.0 | 26.7 | 39.4 |
🔼 This table presents the test set results achieved by various reinforcement learning (RL) algorithms when combined with the PRIME framework. It compares the performance of several standard RL algorithms (RLOO, REINFORCE, GRPO, and PPO) both with and without the PRIME framework across seven key reasoning benchmarks (AIME 2024, AMC, MATH-500, Minerva Math, OlympiadBench, LeetCode, and LiveCodeBench). The results show the effectiveness of PRIME in boosting the performance of different RL algorithms.
read the caption
Table 3: Testset results of different RL algorithms.
| Action Name | Description |
|---|---|
| ASSESS | Analyze current situation, identify key elements and goals |
| ADVANCE | Move forward with reasoning - calculate, conclude, or form hypothesis |
| VERIFY | Check accuracy of current approach, look for errors |
| SIMPLIFY | Break complex problems into simpler parts |
| SYNTHESIZE | Combine multiple pieces of information into complete solution |
| PIVOT | Change strategy when current approach isn’t working |
| OUTPUT | Summarize thought process and present final answer |
🔼 This table details the actions involved in the action-centric chain-of-thought reasoning framework used in the paper. Each action represents a step in the multi-step reasoning process employed by the language model to solve problems. The actions are: ASSESS (analyzes the problem), ADVANCE (moves forward with reasoning), VERIFY (checks accuracy), SIMPLIFY (breaks down complex problems), SYNTHESIZE (combines information), PIVOT (changes strategy if needed), and OUTPUT (presents the final answer).
read the caption
Table 4: Actions in action-centric chain-of-thought reasoning framework.
| Task | Dataset | Size | Avg. Response Length | Source |
| Math | MathInstruct-MATH (Yue et al., 2023) | 12715 | 964.01 | https://huggingface.co/datasets/TIGER-Lab/MathInstruct |
| OpenMathIns-2-Aug_Math (Toshniwal et al., 2024) | 15086 | 1202.25 | https://huggingface.co/datasets/nvidia/OpenMathInstruct-2 | |
| Numina (Li et al., 2024) | 55845 | 1331.61 | https://huggingface.co/datasets/AI-MO/NuminaMath-CoT | |
| Reasoning-001 (SkunkworksAI, 2024) | 29831 | 1316.49 | https://huggingface.co/datasets/SkunkworksAI/reasoning-0.01 | |
| Coding | Code-Feedback (Zheng et al., 2024) | 27663 | 1805.16 | https://huggingface.co/datasets/m-a-p/Code-Feedback |
| Magicoder (Wei et al., 2024) | 24480 | 1828.72 | https://huggingface.co/datasets/ise-uiuc/Magicoder-Evol-Instruct-110K | |
| Magicoder-OSS (Wei et al., 2024) | 28980 | 1850.05 | https://huggingface.co/datasets/ise-uiuc/Magicoder-OSS-Instruct-75K | |
| Biomedicine | UltraMedical_mc (Zhang et al., 2024) | 35163 | 891.06 | https://huggingface.co/datasets/TsinghuaC3I/UltraMedical |
| Total / Avg. | - | 229763 | 1390.75 | - |
🔼 Table 5 provides a detailed overview of the data used for supervised fine-tuning (SFT). It breaks down the data by task (Math and Code), the source dataset used for each task, the number of instances, the average response length, and the specific URLs to access those datasets. This information is crucial for understanding the scale and composition of the data used to initialize the language model before reinforcement learning.
read the caption
Table 5: Data statistics of SFT data.
| Dataset | Generator Model | Num. Inst | Resp/Inst | Step-level/Response-level |
|---|---|---|---|---|
| UltraInteract | Llama-3.1-8B-Inst | 20177 | 8 | Response-level |
| Llama-3.1-8B-Base | 13570 | 8 | Response-level | |
| Qwen2.5-72B-Inst | 4758 | 8 | Response-level | |
| Qwen2.5-Math-7B-Base | 25713 | 8 | Response-level | |
| Numina-SynMath | Llama-3.1-8B-Inst | 4783 | 8 | Response-level |
| Qwen2.5-Math-7B-Base | 5806 | 8 | Response-level | |
| Numina-Olympiads | Llama-3.1-8B-Inst | 2909 | 8 | Response-level |
| Qwen2.5-Math-7B-Base | 4739 | 8 | Response-level |
🔼 This table presents a summary of the datasets used to train the EurusPRM (Eurus Process Reward Model). For each dataset, it lists the model used to generate the data, the number of instances (training examples), the number of response instances per prompt, whether the reward is assigned at the step level or response level, and the name of the dataset. The datasets include examples from a range of sources and model types, reflecting a variety of mathematical reasoning tasks.
read the caption
Table 6: Data statistics of EurusPRM training dataset.
Full paper#