TL;DR#
Current LLM inference-time scaling methods often rely on reward models and frame the task as a search problem, leading to vulnerabilities like reward hacking. This paper addresses these limitations by presenting a probabilistic inference approach. Existing techniques struggle with imperfect reward models, leading to suboptimal solutions and a reliance on larger models.
The proposed approach uses particle-based Monte Carlo methods to treat inference-time scaling as a probabilistic inference problem. This method explores the typical set of the state distribution, reducing reliance on potentially flawed reward models and achieving a more balanced exploration-exploitation strategy. Experiments show that this approach significantly outperforms traditional search methods, demonstrating a 4-16x improvement in scaling rate and enabling smaller models to achieve performance comparable to much larger, more computationally expensive models.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel approach to inference-time scaling of LLMs using probabilistic inference, which is more robust than existing search-based methods. It opens up new avenues for research by connecting the rich literature in probabilistic inference with LLM inference-time scaling. The results demonstrate a significant improvement in scaling rate, offering a practical solution for enhancing LLM performance with limited resources. This is particularly relevant given the diminishing returns observed from simply increasing model size or training data.
Visual Insights#

🔼 The figure illustrates a state-space model used for inference-time scaling in large language models (LLMs). The model is a probabilistic graphical model where: ‘c’ represents the input prompt; x₁, x₂, …, xₜ are sequences of partial LLM outputs at different time steps; and o₁, o₂, …, oₜ are binary observations indicating whether each partial output was accepted or not. The goal of inference-time scaling is to estimate the latent states (x₁, x₂, …, xₜ) given that all observations are 1 (all partial outputs were accepted). This approach frames the scaling problem as probabilistic inference rather than a search problem, offering a more robust method less prone to reward hacking.
read the caption
Figure 1: State-space model for inference-time scaling. c𝑐citalic_c is a prompt, x1,…,xTsubscript𝑥1…subscript𝑥𝑇x_{1},\dots,x_{T}italic_x start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT , … , italic_x start_POSTSUBSCRIPT italic_T end_POSTSUBSCRIPT are sequence of partial LLM outputs and o1,…,oTsubscript𝑜1…subscript𝑜𝑇o_{1},\dots,o_{T}italic_o start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT , … , italic_o start_POSTSUBSCRIPT italic_T end_POSTSUBSCRIPT are the “observed” acceptance. We cast inference-time scaling as to estimate the latent states conditioned on ot=1subscript𝑜𝑡1o_{t}=1italic_o start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT = 1 for t=1,2,…,T𝑡12…𝑇t=1,2,\dots,Titalic_t = 1 , 2 , … , italic_T, i.e. all being accepted.
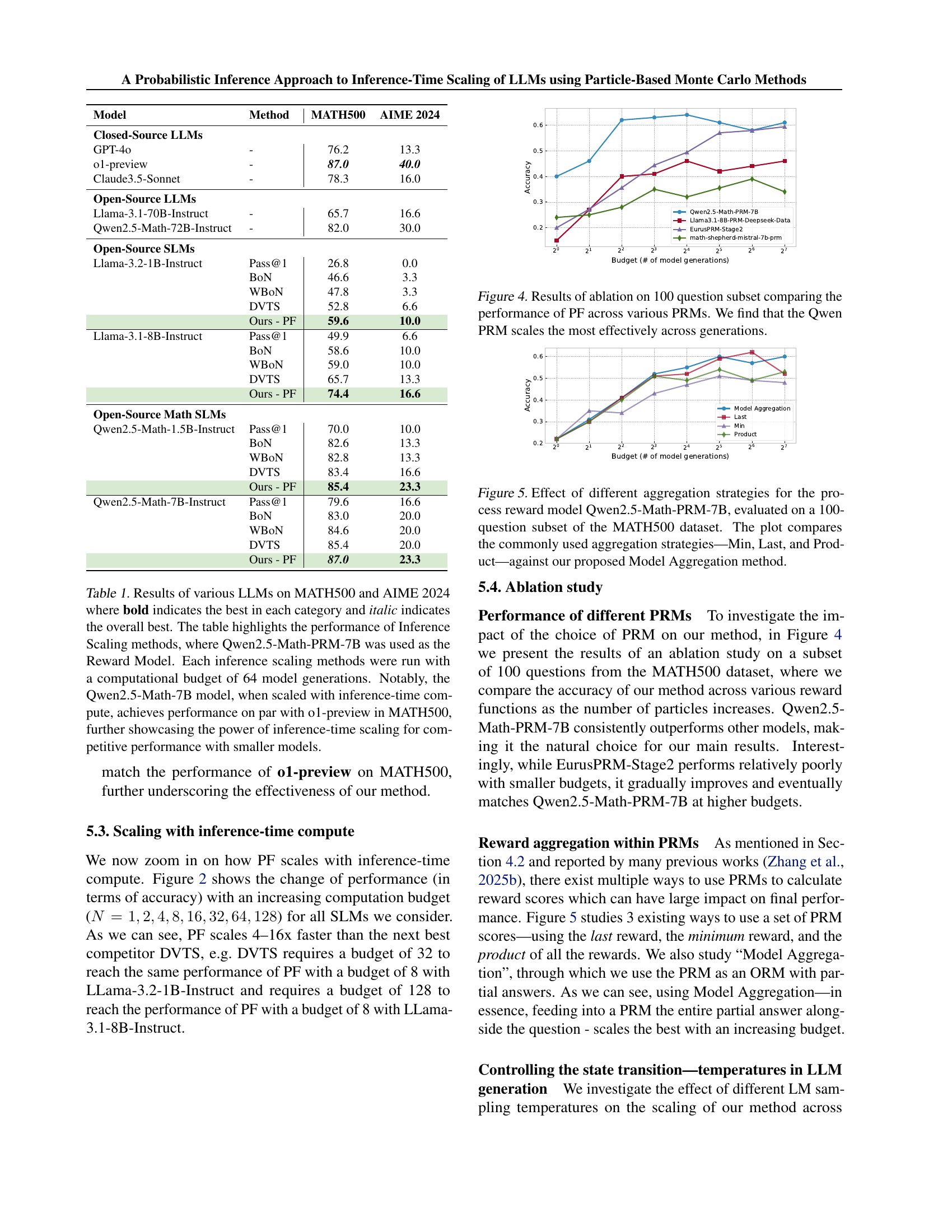
| Model | Method | MATH500 | AIME 2024 |
|---|---|---|---|
| Closed-Source LLMs | |||
| GPT-4o | - | 76.2 | 13.3 |
| o1-preview | - | 87.0 | 40.0 |
| Claude3.5-Sonnet | - | 78.3 | 16.0 |
| Open-Source LLMs | |||
| Llama-3.1-70B-Instruct | - | 65.7 | 16.6 |
| Qwen2.5-Math-72B-Instruct | - | 82.0 | 30.0 |
| Open-Source SLMs | |||
| Llama-3.2-1B-Instruct | Pass@1 | 26.8 | 0.0 |
| BoN | 46.6 | 3.3 | |
| WBoN | 47.8 | 3.3 | |
| DVTS | 52.8 | 6.6 | |
| Ours - PF | 59.6 | 10.0 | |
| Llama-3.1-8B-Instruct | Pass@1 | 49.9 | 6.6 |
| BoN | 58.6 | 10.0 | |
| WBoN | 59.0 | 10.0 | |
| DVTS | 65.7 | 13.3 | |
| Ours - PF | 74.4 | 16.6 | |
| Open-Source Math SLMs | |||
| Qwen2.5-Math-1.5B-Instruct | Pass@1 | 70.0 | 10.0 |
| BoN | 82.6 | 13.3 | |
| WBoN | 82.8 | 13.3 | |
| DVTS | 83.4 | 16.6 | |
| Ours - PF | 85.4 | 23.3 | |
| Qwen2.5-Math-7B-Instruct | Pass@1 | 79.6 | 16.6 |
| BoN | 83.0 | 20.0 | |
| WBoN | 84.6 | 20.0 | |
| DVTS | 85.4 | 20.0 | |
| Ours - PF | 87.0 | 23.3 |
🔼 Table 1 presents the performance comparison of various Large Language Models (LLMs) on two mathematical reasoning benchmarks: MATH500 and AIME 2024. The models are categorized into closed-source LLMs (like GPT-40 and Claude), open-source LLMs (Llama-3.1-70B-Instruct, Qwen2.5-Math-7B-Instruct), and smaller, open-source models specialized for math reasoning (Llama-3.2-1B-Instruct and Qwen2.5-Math-1.5B-Instruct and Qwen2.5-Math-7B-Instruct). For the smaller math-specialized models, the table also shows the performance using different inference-time scaling methods, namely Pass@1 (single generation), Best-of-N (BON), weighted Best-of-N (WBON), Dynamic Variable-Time Search (DVTS), and the authors’ proposed Particle Filtering (PF) method. All inference-time scaling methods used the Qwen2.5-Math-PRM-7B reward model and a computational budget of 64 model generations. The table highlights the best performance within each model category and the overall best performance across all models. Importantly, it shows that inference-time scaling allows smaller models to achieve competitive performance with much larger models, especially the Qwen2.5-Math-7B model which reaches parity with the o1-preview model on MATH500.
read the caption
Table 1: Results of various LLMs on MATH500 and AIME 2024 where bold indicates the best in each category and italic indicates the overall best. The table highlights the performance of Inference Scaling methods, where Qwen2.5-Math-PRM-7B was used as the Reward Model. Each inference scaling methods were run with a computational budget of 64 model generations. Notably, the Qwen2.5-Math-7B model, when scaled with inference-time compute, achieves performance on par with o1-preview in MATH500, further showcasing the power of inference-time scaling for competitive performance with smaller models.
In-depth insights#
Inference-Time Scaling#
Inference-time scaling, as discussed in the research paper, focuses on enhancing Large Language Model (LLM) performance by allocating more computational resources during inference rather than solely relying on increasing model size or training data. The paper highlights the limitations of existing search-based methods, which often suffer from reward hacking due to imperfections in reward models. As an alternative, it proposes a probabilistic inference approach using particle-based Monte Carlo methods. This approach addresses the limitations of search-based methods by casting inference-time scaling as a probabilistic inference task, focusing on exploring the typical set of state distribution rather than solely optimizing for the mode. This probabilistic approach is argued to be more robust to reward model inaccuracies, balancing exploration and exploitation more effectively. The empirical results demonstrate significant improvements in scaling rates compared to search-based methods, showcasing the potential of this innovative approach for improving LLM performance and making advanced AI more accessible to low-resource devices. Particle filtering, a key component of the probabilistic framework, emerges as a robust and effective method, showing impressive results across various challenging mathematical reasoning tasks.
Particle Filtering#
Particle filtering, a sequential Monte Carlo method, is presented as a novel approach to inference-time scaling in LLMs. Instead of treating inference-time scaling as a search problem prone to reward hacking, this method frames it as probabilistic inference. It leverages the inherent robustness of particle filtering to imperfect reward models by maintaining a diverse set of candidate solutions and updating their weights iteratively based on observed evidence. This approach cleverly balances exploration and exploitation, avoiding the pitfalls of search-based methods that can get stuck in local optima. The core idea is to estimate the typical set of the state distribution, rather than solely focusing on the mode, which is especially beneficial when dealing with approximate reward models. By dynamically adjusting particle weights and resampling, the algorithm efficiently explores the solution space, making it effective even with limited computational budgets. The authors’ empirical evaluations demonstrate significant performance gains over existing search-based approaches, highlighting the potential of particle filtering as a more robust and efficient technique for inference-time scaling.
PRM’s Role#
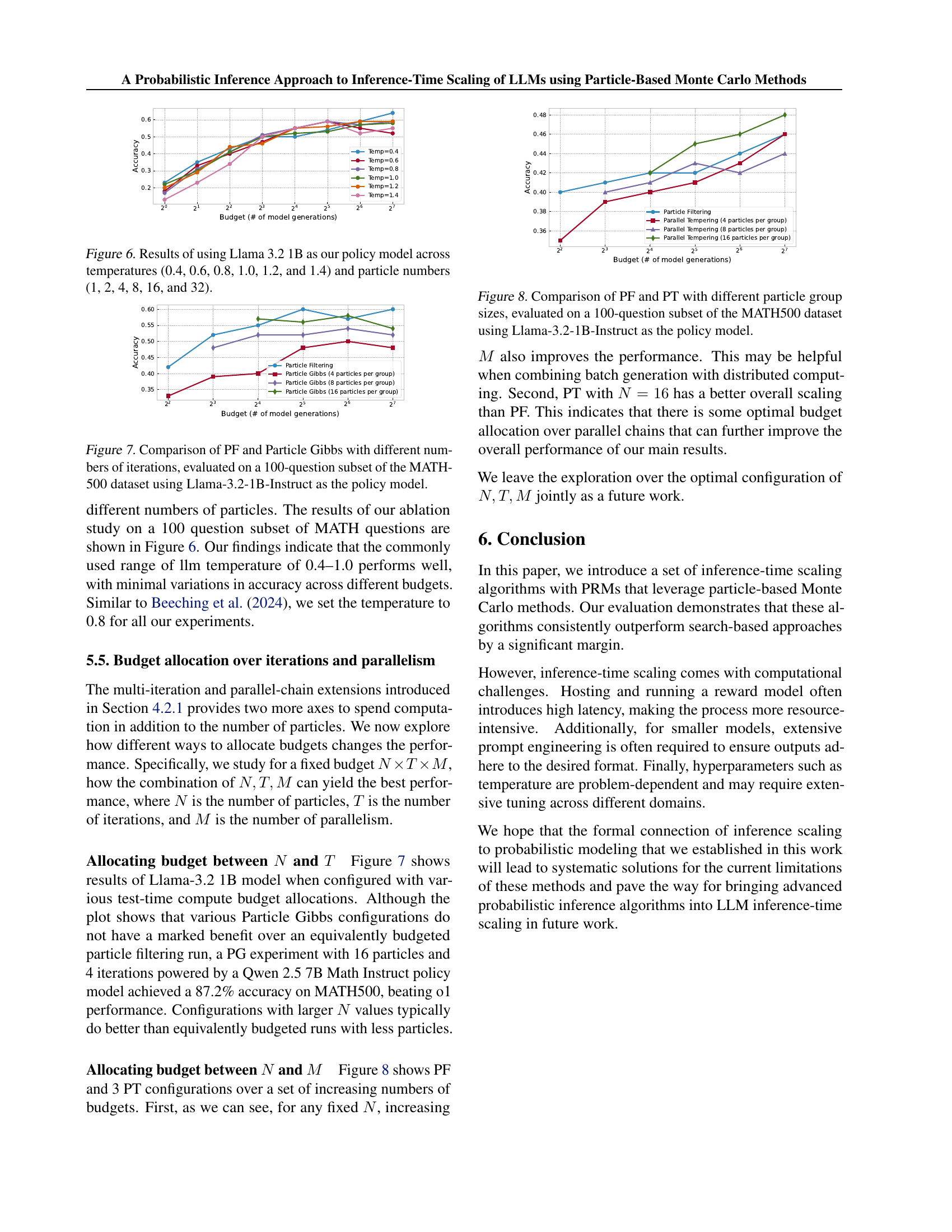
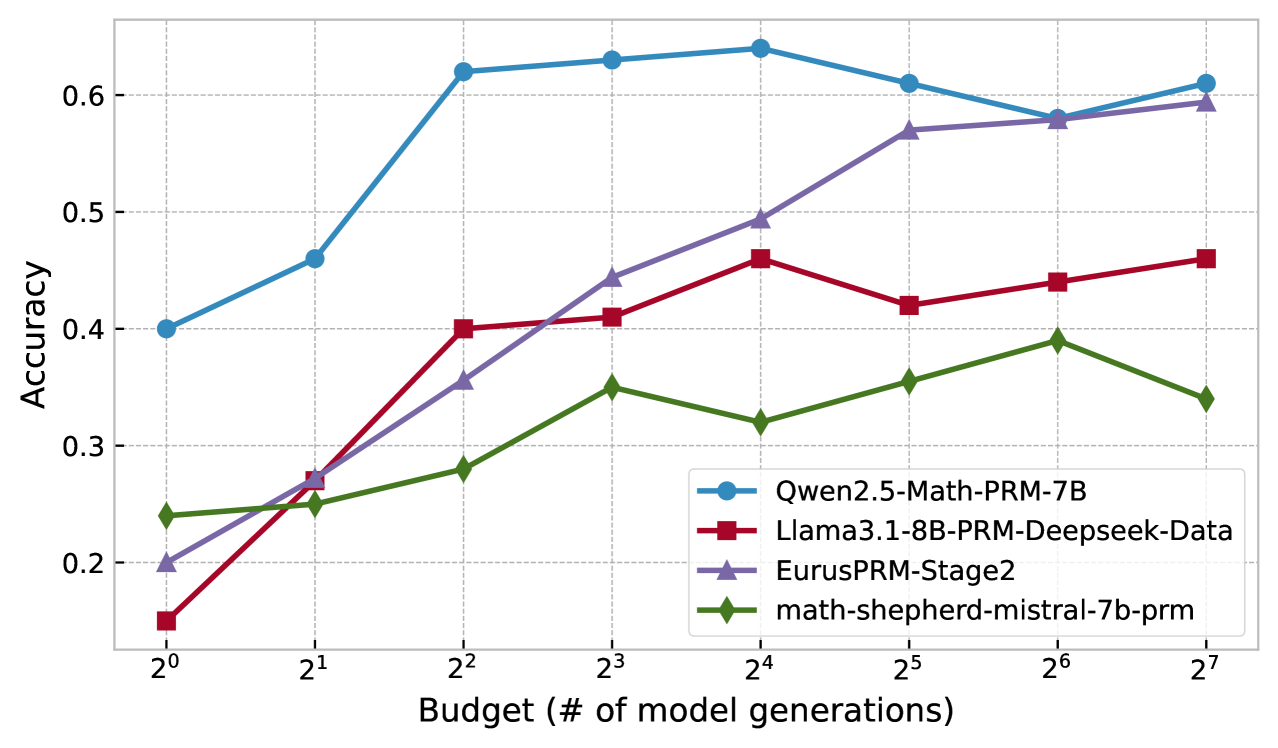
The effectiveness of inference-time scaling hinges critically on the quality of the Process Reward Model (PRM). PRMs provide crucial intermediate feedback, guiding the model’s trajectory towards better solutions. However, imperfect PRMs are vulnerable to reward hacking, where the model prioritizes maximizing the reward signal over achieving genuine problem-solving. This necessitates robust PRM design and aggregation strategies. The paper explores model-based aggregation to address this, advocating for methods that balance exploration and exploitation by relying on the typical set of the reward distribution rather than just its mode. Furthermore, the choice of PRM significantly impacts performance, underscoring the importance of selecting or training PRMs specific to the target task. The interaction between PRM quality, aggregation methods, and the probabilistic inference approach is key to effective inference-time scaling. Choosing an imperfect PRM risks undermining the entire process, thus highlighting the need for careful consideration of this crucial component.
Scaling Limits#
The concept of “Scaling Limits” in the context of large language models (LLMs) refers to the inherent boundaries in performance improvement achievable solely through increasing model size or training data. The paper likely explores how this limitation motivates alternative approaches, such as focusing on inference-time scaling. It investigates whether enhancing the computational resources at the inference stage can overcome these scaling limits and unlock better performance. Diminishing returns from simply scaling up model parameters suggest that optimizing the inference process itself might be a more efficient strategy. The analysis probably delves into the trade-offs between increasing model size/data and improving inference-time efficiency, identifying potential bottlenecks or limitations to scaling that can’t be addressed by simply throwing more resources at the problem. A key aspect of the analysis would likely be identifying the points at which performance gains from scaling plateau, providing a quantitative measure of these limits and offering alternative solutions to bypass them.
Future Work#
Future research directions stemming from this work on inference-time scaling of LLMs using probabilistic methods are numerous and impactful. Improving the robustness and efficiency of reward model aggregation is key; exploring alternative aggregation strategies beyond the proposed method, and potentially integrating learning-based approaches to reward modeling, could significantly improve performance. Further investigation into optimizing the balance between exploration and exploitation within the particle filtering framework is crucial. This includes exploring advanced sampling techniques and adaptive strategies for adjusting the effective temperature. Extending the framework to support more complex model architectures and reasoning tasks beyond mathematical problems is also important. Finally, a detailed empirical study comparing the performance of the proposed probabilistic approach against other state-of-the-art methods, across a broader range of benchmarks and models, is needed to solidify its advantages. This comprehensive evaluation should include rigorous analysis of computational costs and resource requirements.
More visual insights#
More on figures

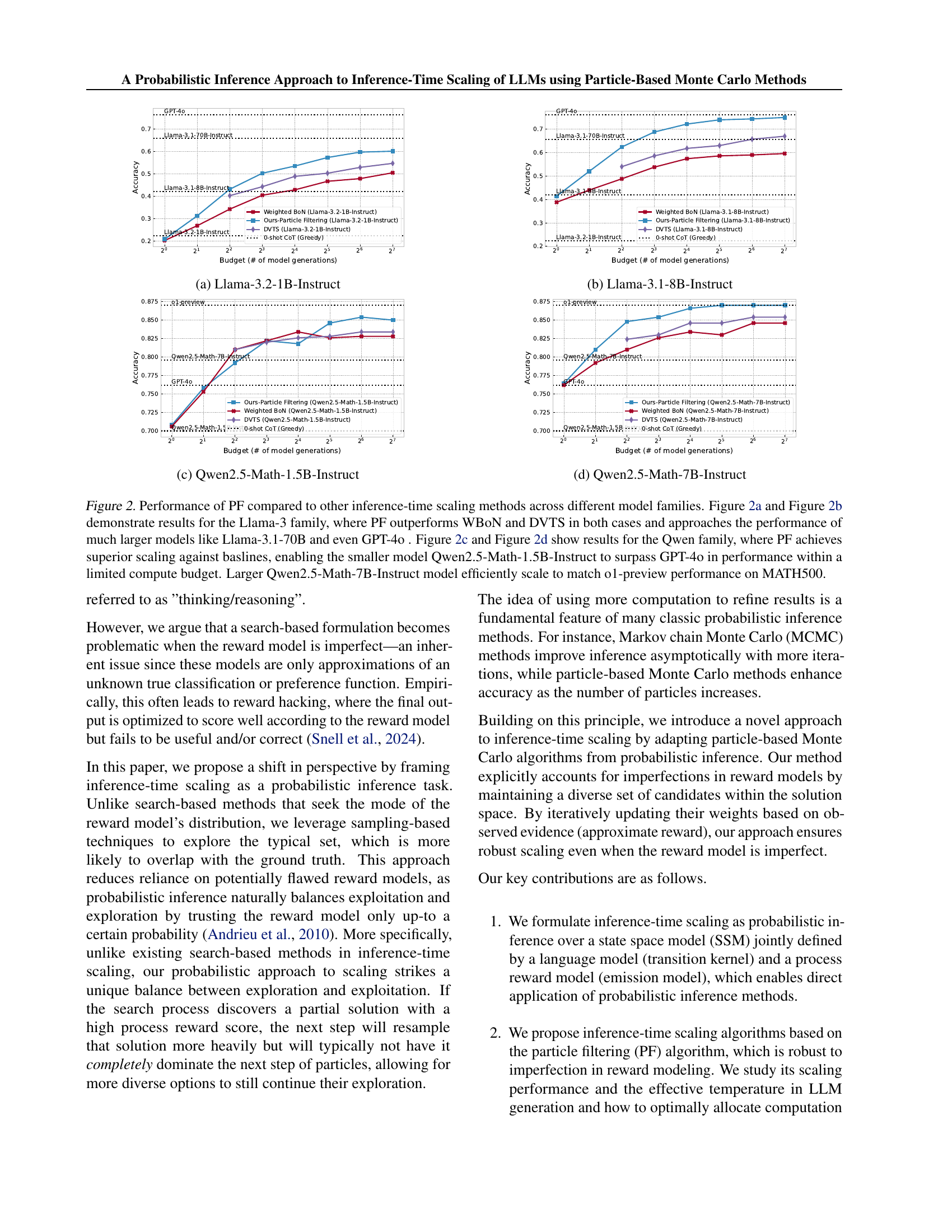
🔼 This figure (Figure 2a) presents the performance comparison of different inference-time scaling methods on the Llama-3.2-1B-Instruct model. It shows how accuracy varies as a function of the computation budget (number of model generations). The comparison includes several baselines: Pass@1 (a single greedy generation), Weighted Best-of-N (WBoN), Dynamic Variable-Time Search (DVTS), and the proposed Particle Filtering (PF) method. The plot visually demonstrates the superior scaling performance of PF compared to the baselines, showing its ability to achieve higher accuracy with a smaller computation budget.
read the caption
(a) Llama-3.2-1B-Instruct

🔼 This figure (Figure 2b) presents the performance comparison of different inference-time scaling methods on the Llama-3.1-8B-Instruct model. It shows how accuracy changes as the computational budget (number of model generations) increases. The methods compared include the proposed Particle Filtering (PF) approach, Weighted Best-of-N (WBON), Dynamic Variable-Time Search (DVTS), and a 0-shot Chain-of-Thought (CoT) baseline. The graph allows for a visual assessment of the scaling efficiency and relative performance of each method on this specific language model.
read the caption
(b) Llama-3.1-8B-Instruct

🔼 This figure shows the performance of the particle filtering (PF) method compared to other inference-time scaling methods (Weighted Best-of-N, DVTS, and 0-shot CoT) on the Qwen2.5-Math-1.5B-Instruct model. The x-axis represents the computational budget (number of model generations), and the y-axis represents the accuracy achieved on a challenging mathematical reasoning task. The graph demonstrates that PF achieves significantly better scaling, surpassing other methods and approaching the accuracy of larger models within a smaller budget.
read the caption
(c) Qwen2.5-Math-1.5B-Instruct
🔼 This figure (2d) presents the performance comparison of different inference-time scaling methods on the Qwen2.5-Math-7B-Instruct model. It shows how accuracy changes as the computation budget (number of model generations) increases. The comparison includes the proposed particle filtering method (PF) and baselines such as weighted best-of-N (WBON), dynamic variable-time search (DVTS), and a simple greedy 0-shot chain of thought approach. The plot illustrates the superior scaling efficiency of PF, highlighting its ability to achieve higher accuracy with significantly fewer model generations compared to the baselines. It also compares the performance against GPT-40 and the o1-preview model.
read the caption
(d) Qwen2.5-Math-7B-Instruct

🔼 This figure compares the performance of the proposed Particle Filtering (PF) method against other inference-time scaling techniques (Weighted Best-of-N, DVTS) across different model families (Llama-3 and Qwen). The plots show that PF consistently outperforms the baselines in terms of scaling. Notably, PF enables smaller models to match or even exceed the performance of significantly larger models (like Llama-3.1-70B and GPT-4) and achieves this with a much lower computational budget.
read the caption
Figure 2: Performance of PF compared to other inference-time scaling methods across different model families. Figure 2(a) and Figure 2(b) demonstrate results for the Llama-3 family, where PF outperforms WBoN and DVTS in both cases and approaches the performance of much larger models like Llama-3.1-70B and even GPT-4o . Figure 2(c) and Figure 2(d) show results for the Qwen family, where PF achieves superior scaling against baslines, enabling the smaller model Qwen2.5-Math-1.5B-Instruct to surpass GPT-4o in performance within a limited compute budget. Larger Qwen2.5-Math-7B-Instruct model efficiently scale to match o1-preview performance on MATH500.

🔼 Figure 3(a) illustrates the core idea of the particle filtering method for inference-time scaling. It contrasts particle filtering with the beam search method. In particle filtering, a reward model generates scores for each partial answer. These scores are converted into weights (using a softmax function) that determine the probability of selecting each partial answer for expansion in the next step. This probabilistic selection allows for exploration of multiple potential solutions, unlike beam search, which deterministically expands only the top-N highest-scoring partial answers. The stochastic nature of particle filtering makes it more robust to imperfections or noise in the reward model.
read the caption
(a) Particle filtering uses the rewards to produce a softmax distribution and does stochastic expansion of N𝑁Nitalic_N based sampling.

🔼 This figure illustrates beam search, a deterministic approach to inference-time scaling. Unlike probabilistic methods that incorporate uncertainty, beam search treats the reward signals from a process reward model (PRM) as completely accurate. It operates by expanding the search space based on a fixed beam size (N) and width (M). The beam size limits the number of candidate sequences explored simultaneously, while the beam width determines how many token options are considered at each step. The algorithm keeps track of the N best sequences according to the PRM’s reward, extending them deterministically until a final output is produced. This contrasts with probabilistic methods, which incorporate stochasticity and uncertainty in the exploration of the search space.
read the caption
(b) Beam search treats the rewards as exact and performs deterministic expansion based on beam size N𝑁Nitalic_N and beam width M𝑀Mitalic_M.

🔼 Figure 3 illustrates the core difference between particle filtering and beam search, two approaches to inference-time scaling. Beam search, shown in 3(b), is deterministic. It uses the reward model’s scores as completely accurate and selects the top-scoring options for expansion. In contrast, particle filtering (3(a)) acknowledges that the reward model’s scores are uncertain. It uses these scores to create a probability distribution and samples from it, making expansion probabilistic. This allows particle filtering to explore a wider range of possibilities and be less sensitive to inaccuracies in the reward model, as opposed to the deterministic and potentially myopic beam search. Further details of particle filtering are found in Figure 9 in Appendix A.1.
read the caption
Figure 3: A side-by-side comparison between particle filtering and its closet search-based counterpart, beam search. Compared with beam search in Figure 3(b) where the selection and expansion is deterministic (implicitly assumes the rewards are correct), particle filtering in Figure 3(a) trust the rewards with uncertainty and propagate the expansion via sampling. A more detailed, step-by-step version of particle filtering can be found in Figure 9 of Appendix A.1.
Full paper#